Macrostructure from Microstructure: Generating Whole Systems from Ego Networks

Abstract

This paper presents a new simulation method to make global network inference from sampled data. The proposed simulation method takes sampled ego network data and uses Exponential Random Graph Models (ERGM) to reconstruct the features of the true, unknown network. After describing the method, the paper presents two validity checks of the approach: the first uses the 20 largest Add Health networks while the second uses the Sociology Coauthorship network in the 1990's. For each test, I take random ego network samples from the known networks and use my method to make global network inference. I find that my method successfully reproduces the properties of the networks, such as distance and main component size. The results also suggest that simpler, baseline models provide considerably worse estimates for most network properties. I end the paper by discussing the bounds/limitations of ego network sampling. I also discuss possible extensions to the proposed approach.

1. INTRODUCTION

Global network measures are notoriously difficult to measure with sampled, or incomplete, information. It is difficult to describe the cohesion (Moody 2004), group structure (Frank and Yasumoto 1998) or diffusion potential (Watts 2002) of a network if we cannot capture the direct and indirect connections among all individuals.¹ Unfortunately, it is often practically impossible to collect full network data on many populations of interest. For example, it may be impossible to interview everyone in a very large network, while an electronic (or easily collected) data source may not exist (Lewis et al. 2008). A smaller network may also prove difficult if one has limited resources or if the population is not institutionally bounded (e.g. adolescents in schools). The problem only becomes worse if one is interested in multiple networks at different locations. In short, while we may be interested in global network features, it is often impossible to collect complete data on the population of interest.

This paper offers a new, practical approach for researchers interested in global network structure where only sampled data can be collected (Frank 1971; Granovetter 1976). There are a number of ways to sample a network, including subgraph (Frank 1971) and snowball sampling (Goodman 1961; Handcock and Gile 2010; Koskinen, Robins and Pattison 2010), but this paper focuses on the simplest possible option—an independent sample of ego networks (Marsden 1987; Krivitsky, Handcock, and Morris 2011). Here, respondents are randomly sampled from the population and describe themselves and their local social network. Ego network data are easy to collect and already found on many social surveys. It is, unfortunately, often infeasible to analytically estimate network properties from ego network data, and past studies have typically used simulation instead (Lee 2004; Morris et al 2009).

This study builds on the ego network simulation tradition, offering a new method for global network inference. The approach takes ego network data and uses two models, Exponential Random Graph Models (Robins et al. 2007) and case control logistic regression (McPherson, Smith and Smith-Lovin 2011), to generate full networks consistent with the sampled data. The method also assumes that the size of the network is known. The simulated networks are then used to estimate the features of the true network. Intuitively, ego network data are drawn randomly from the population: any network consistent with the sampled information is thus a possible construction of the true network.

The method extends past work by exploiting the sampled information more fully. The simulation is built around a new measure of ego network structure, as well as more traditional measures, like homophily. The measure of ego network structure captures the full distribution of ego network types, and is thus more precise than existing options. The paper also assess the validity of the proposed method on known networks.

I begin the paper with background sections on network sampling, simulation and ego network data. I then describe my method of generating full networks from ego network data. I follow the methods section with two validity checks. The first check uses data from the National Longitudinal Study of Adolescent Health, or Add Health, a nationally representative study of adolescents covering grades 7–12 in 1994–1995 (Harris 2009). The analysis uses the 20 largest Add Health networks (N between 1000 and 2200) and compares the estimates produced by my method with the empirically known values. I test my method on a series of network features, including typical measures of connectivity (e.g. distance) and clustering (e.g. modularity). The paper then moves to a larger network, describing the same analysis on the Sociology Coauthorship network in the late 1990's (~60,000 nodes).

2. A SHORT SUMMARY OF NETWORK SAMPLING

Much of the work on network sampling stems from the pioneering analysis of Frank (Frank 1971; 1977; 1978a). Frank derived formulas to estimate network-level measures from a sample (Frank 1971; 1978b). The formulas were often based on a random sample of nodes in the network, or a subgraph sample, where all ties between sampled respondents are recorded. Unfortunately, a subgraph sample is impractical for many, if not most, network settings. For example, a subgraph sample on a large network may yield few, or even zero, ties between sampled respondents unless the sample is very large or the density is very high. A subgraph sample without ties tells the researcher the network is not very dense, but not much else.

As an alternative, researchers have employed sampling schemes that capture more local information, such as ego network sampling (Marsden 1987) and snowball sampling (see Thompson and Frank 2000; Handcock and Gile 2010; Koskinen et al. 2010; Goodman 2011). Both of these sampling strategies record local tie information, thus avoiding the large N problem of subgraph samples. In a snowball sample, researchers interview respondents, the friends of respondents, the friends of the friends, and so on.² Snowball sampling avoids the limitations of subgraph sampling but is quite complex in its own right—as one must identify, find, and interview the associates of the respondents. Additionally, a snowball sample is not easily embedded in an existing survey.

Ego network data, in contrast, are easy to collect and already widely used by network scholars (e.g. Moore 1990; McPherson, Smith-Lovin and Brashears 2006). The survey randomly samples individuals from a known population (i.e. the population is not hard-to-reach). The survey then gathers information about the respondents and their local social network: we know the number of associates, or alters, per respondent; the characteristics of those alters; the characteristics of the respondent; and the presence of ties between alters.³ The ego networks are completely independent and the alters are not identified. Ego network data are also easily added to existing surveys, even if that survey was not designed with networks in mind. The promise of ego network sampling is thus considerable: for it becomes possible to make global network inference from data that are, potentially, already at hand (or at least easily collected).

I design my method with these practical issues in mind, focusing solely on an ego network sampling scheme (Marsden 1987). I do, however, consider snowball sampling more thoroughly in the conclusion, noting where the extra information from a snowball sample will be particularly useful.

Past work on ego network sampling has employed simulation techniques as a means of analysis, and the proposed method follows in this simulation tradition (Morris and Kretzschmar 2000; Lee 2004; Lee 2008; Morris et al. 2009). Simulation based inference is an ideal option as analytical solutions are infeasible: one can explore the properties of the network by generating full networks consistent with the local ego network information. It is important to recognize that the generated networks are consistent with the local information in the sample, but need not, necessarily, be consistent with the macro properties of the true network. Despite this limitation, simulation methods can produce excellent approximations of the full network: for ego network data provide a surprisingly large amount of information about the network.

Some network types will yield more accurate estimates than others, however, and I describe the networks most appropriate for the simulation method in the conclusion.⁴ Briefly, the method will be most appropriate for networks that exhibit homophily (as the simulations rely on group mixing patterns), are undirected (as there is no asymmetry information) and capture strong tie relationships (as it is impractical for a respondent to list every person they know or recognize).

3. EGO NETWORK DATA AND THE SIMULATION APPROACH

The proposed method proceeds in three steps. First, it calculates the local information available from the sampled data. Second, it uses the local information to simulate full networks consistent with the sampled data. And third, it uses the generated networks to calculate the statistics of interest. The key to the simulation approach is extracting the maximum amount of information from the sample.

Ego network data provide information on the local social world of respondents, but also provide a wealth of information about the full, unknown network from which the ego networks were drawn. At the simplest, an ego network sample provides compositional information about the true network. Respondents answer basic demographic questions, thus providing a count of males/females, blacks/whites, etc. in the network.⁵

More importantly, ego network surveys ask respondents to nominate their alters.⁶ The list of alters provides an estimate of the degree distribution, or the number of alters per person.⁷ The list of alters also provides information on differential degree, or the average degree by demographic group (as we know the demographic characteristics of the respondents). Some surveys may employ a truncated naming scheme, where a respondent can name a maximum of X alters (say 10). A truncated naming scheme will yield biased estimates of the degree distribution (although one could possibly simulate, or project, the truncated part). I assume, for the sake of this paper, that that the degree distribution is not truncated: respondents are allowed to name a small but non-trivial number of alters.⁸

Ego network data also provide information about homophily. Respondents report on their own demographic characteristics as well as the characteristics of their alters. The paired respondent/alter information captures the demographic similarity among social contacts.⁹

The measures described so far, including composition, degree distribution, differential degree and homophily, can be measured unbiasedly from ego network data. The measures are unbiased as they depend on node or dyad level information, and thus do not depend on information outside the ego network. Past sampling/simulation studies have measured homophily and the degree distribution from ego network data and used those estimates to generate full networks consistent with the sampled data (Lee 2008; Morris et al. 2009; Krivitsky, et al. 2011).

Past simulation methods have made less use of the structural information, which captures the pattern of social ties among alters. In ego network data, the respondent describes the relationship between each alter pair (is there a tie between alter one and two, one and three…?). This structural information has rarely been the focus of past work, although some studies have discussed the limitations of the data (Newman 2003; Grannis 2010). For example, transitivity (where a friend of friend tends to be a friend) is estimated inaccurately because it depends on information outside the ego network, such as the degree of the named alters (Soffer and Vazquez 2005; Bansal, Khandelwal and Meyers 2009). In a similar manner, we cannot estimate the rate of assortative degree mixing, or the tendency for individuals with similar degree to be socially tied.

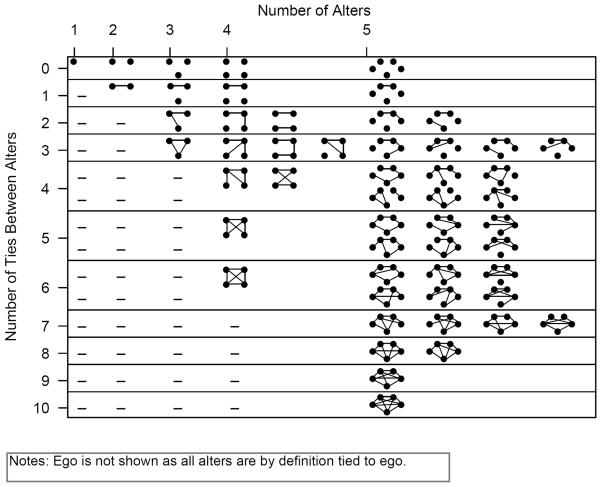
Given these limitations, this paper offers a new measure of ego network structure that makes the most of the available data.¹⁰ Specifically, I take the alter-alter tie data and form a distribution of ego network patterns, or a distribution of ego network configurations (see Holland and Leinhardt 1976 and Middendorf et al. 2005 for related intuition).¹¹ Figure 1 summarizes the 53 possible ego network configurations of size 5 and below (see Freeman 1979). The distribution of ego network configurations is formed by placing each respondent in the appropriate structural category. Ego networks are placed in a unique category based on three attributes: size; the degree distribution among alters (ignoring ego); and the number of triangles (ignoring ego).¹² We can write this formally as: Let X be a square matrix of dimensions m × m, consisting of the alters in the ego network of respondent p. Let X_tj = 1 if a tie exists between alter i and alter j. Define ego network configuration p by the unique combination of:

$$\{\begin{array}{c}1.{\mathit{Size}}_p=m\hfill \\ \hfill \\ 2.{\left(d_i\right)}_p=X_{i+},\mathit{where}{d}_i\mathrm{is}\mathrm{the}\mathrm{degree}\mathrm{of}\mathrm{alert}i\hfill \\ \hfill \\ 3.T_p=\sum _t{X}_{ij}\ast X_{jk}\ast X_{ik},\mathrm{where}t\mathrm{is}\mathrm{the}\mathrm{set}\mathrm{of}\mathrm{all}\mathrm{triads}\mathrm{in}X.t=(t_{123},t_{124},\dots ,t_{(i-2),(i-1),i}).\hfill \end{array}\phantom{\}}$$ (1)

FIGURE 1.

All Possible Ego Network Configurations for Symmetric Ego Networks of Size 5 and Below

Figure 2 offers two example distributions. The figure plots the proportion of (hypothetical) respondents in each ego network category.¹³ The left hand panel plots the ego network distribution from a random network (with a specified degree distribution), while the right hand panel plots the ego network distribution from a clustered network—where there are group divisions and moderate transitivity. It is clear from this simple example that networks with different structural features yield very different ego network distributions (see Johnsen 1985 for this same idea applied to the triad distribution).

FIGURE 2.

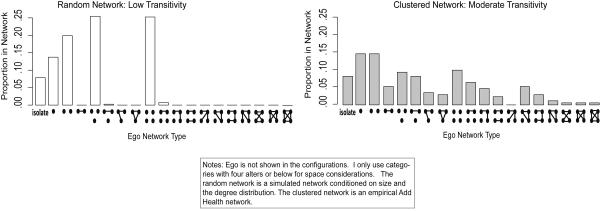
Example Ego Network Configuration Distributions

More generally, the ego network distribution is a reflection of the larger network: for the distribution faithfully mirrors the data generating process and captures the structural heterogeneity across respondents. For example, the distribution captures the structural heterogeneity around size, where smaller ego networks may be denser than larger ego networks. The distribution also captures more subtle heterogeneity, where ego networks of the same size and density may have very different structural patterns.¹⁴ The measure's precision is ultimately crucial for the simulation: for the algorithm uses the distribution to choose between seemingly similar networks. A simple density score would obscure such differences.

More substantively, the ego network distribution serves as a latent signal for many properties not captured by ego network data. For the same underlying forces that structure the real network (e.g. structural balance) similarly constrain the ego network configurations. Simulated networks with the right ego network patterns are thus shaped by the same local processes as the real network, and are thus more likely to have the right structural features—even if those features are not directly captured by the individual level data.

For example, a network with the right ego network configurations is likely to have the right level of transitivity, even though ego network data cannot directly measure transitivity without bias. The key is fitting the entire ego network distribution, where the local clustering patterns (by degree) aggregate to create global transitivity. We can see this in Figure 3, which plots the ego network distributions from two networks with the same local density (i.e. the density of the ego networks) but different levels of global transitivity. The ego network distributions are significantly different across the two networks. The ego network distribution thus differentiates the networks in terms of transitivity, even though the ego networks offer the same direct, local estimate of clustering.

FIGURE 3.

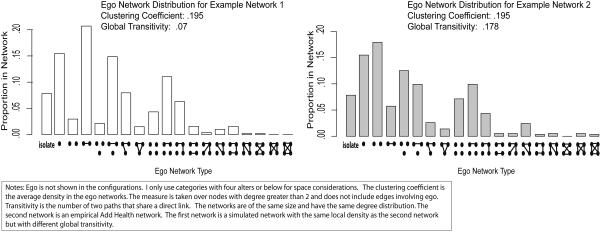
Example Ego Network Configuration Distributions: Transitivity Comparison

4. METHODS: BACKGROUND

The methods section is divided into two parts. In the first section, I describe the models employed during the simulation, Exponential Random Graph Models (ERGM) and case control logistic regression. In the second part, I describe the simulation process itself.

4.1. ERGM

ERGMs are statistical models used to test hypotheses about the structural features of a network (Holland and Leinhardt 1981; Frank and Strauss 1986; Wasserman and Pattison 1996; Snijders et al. 2006; Handcock et al. 2008). Formally, for each pair of actors, or nodes, i,j in the set N (N=1,2…n), let Y_ij= 1 if there exists a tie from i to j and Y_ij=0 if no tie exists (all Y_ii are definitionally assumed to be zero). Y_ij=Y_ji in undirected networks (the focus in this paper). Furthermore, let y_ij be the observed values of Y_ij while y is the observed, or realized, network. Y is then a random graph on N, where each possible network tie may be seen as a random variable Y_ij. The ERG models the Pr(Y=y) to capture the structural features of the network. The independent variables are counts of network measures (e.g. number of edges) and take a variety of forms, including individual, dyadic and higher order terms (Robins et al. 2007; Goodreau, Kitts and Morris 2009). We can write the model as:

$$P(\mathit{Y}=\mathit{y})=\frac{\mathit{exp}\left({\theta }^{T}g\right(\mathit{y}\left)\right)}{K\left(\theta \right)}$$ (2)

where g(y) is vector of network statistics, θ is vector of parameters, and κ(θ) is a normalizing constant.

ERG models are particularly useful for testing hypotheses about the formation, or generation, of a network, but can also be used to simulate networks (Robins, Pattison, and Woolcock 2005). The model coefficients measure the strength of various micro processes shaping the formation of the network. One can take those coefficients and (stochastically) predict the presence or absence of a tie between pairs of people.

Traditionally, ERG models have been estimated on full networks without missing data, but more recent work has extended the model to sampled data. For example, Handcock and Gile (2010), estimated ERG models under a two wave link tracing design (or a snowball sample on a not hard-to-reach population—Goodman 2011). They compared the estimated parameters from the sample to the parameters from the complete network (N=36), finding the bias to be relatively small. In a similar manner, Koskinen et al. (2010) introduced a Bayesian approach for estimating ERGMs with missing data. Unlike Handcock and Gile (2010), they also used the ERGM coefficients to make inference about global network measures: where the estimated parameters were first used for missing link prediction; once the missing data was “filled in”, the network was used to calculate various measures of interest, such as betweenness. They also considered their model in the context of snowball sampling on a not hard-to-reach population.

Both papers estimated the properties of a network from sampled data, and thus had similar goals as this paper. The sampling schemes employed by Handcock and Gile (2010) and Koskinen et al. (2010) are, however, more complex than the ego network sampling scheme considered here. Still, the work on snowball sampling highlights a crucial idea: if one can estimate parameters from sampled data, the model can be used to simulate networks based on the estimated coefficients.

Past work on ERG models and ego network sampling has explored this idea (primarily) using degree and homophily terms (Morris et al. 2009; Krivitsky et al. 2011). For example, Morris et al. (2009) used an ERGM to simulate sexual networks from ego network data, including terms in the model for racial mixing, differential degree and the degree distribution. Sexual ego network data do not provide configurational information (i.e. did the alters share other sexual partners?) and the model was specified without a local clustering term (transitivity, for example). The parameters could then be estimated from ego network data and used to simulate synthetic networks. A degree/homophily approach is appropriate for sexual networks as the structure is likely to be captured through the degree distribution, differential degree and mixing rates.¹⁵ A model without a local clustering term is not, however, appropriate for many other network types of interest—say a friendship network, where there is strong transitive closure.

4.2. Case Control Logistic Regression

The case control framework is used for two tasks: to estimate homophily on the ego network data; and, more crucially, to update the homophily coefficients as the simulation progresses. This ensures that the simulated networks reflect the empirical level of homophily.

Past work on network sampling has typically used log-linear models to estimate homophily (Mare 1991; Morris 1991). Log-linear models compare the frequency of observed ties between categories (e.g. blacks and whites) to the frequency expected by chance. Log-linear models are limited, however, as it is difficult to include a large number of predictors (especially if they are not categorical). Given this practical limitation, McPherson et al. (2011) introduced an extended log-linear model based on case control models. Case control methods are employed in medical research to study rare events, such as having cancer, which are difficult to capture with random sampling (Breslow and Day 1980). Instead, case control methods take the cases, those individuals with the disease, and compare them to individuals without the disease, or the controls, on some behavior or condition of interest (such as smoking).

The case control method is a natural fit for ego network data. Rather than take a random sample of dyads, ego network data capture the rare event of interest, the social ties between individuals. We can then view the cases, or those dyads with a social relationship, as the respondent-alter ties in the ego network data. The controls, in turn, are dyads that do not have a social relationship. The controls are formed independent of the cases and need not come from the same data source. It is, however, typical to create the controls by randomly pairing respondents together, thus capturing random mixing in the population, or chance expectations. In this case, the “0s”, or non-ties, are a random sample of respondent-respondent dyads.

The case control model compares a behavior, or condition, between the cases and the controls. Here the condition of interest is the social distance between i and j in each dyad: for example, absolute distance on age or match/no match on race. For categorical variables, social distance can also take the form of a mixing matrix. A mixing matrix describes the frequency of ties between all categories, where there is one term for every combination of categories a pair could fall into (e.g. black-white, white-white…). The social distance between respondents and alters is then compared to the social distance between individuals in the control part of the dataset. The model takes the form of a logistic regression, where the “1s” are the respondent-alter pairs and the “0's” are those pairs where a tie does not exist. Formally we can write the model as:

$$\ln \left(\frac{p\left(\mathit{O}\right)}{1-p\left(\mathit{O}\right)}\right)={\theta }_o\mathbf{X}$$ (3)

where O_ij is the presence or absence of a tie; X_ij is the social distance between i and j for each dyad, and θ_o is the vector of coefficients. The case control model is conceptually close to a dyadic independent ERGM, where both models compare the counts of dyadic properties (e.g. matching on race) to the level expected by chance (see Koehly, Goodreau and Morris 2004 for a related discussion). There are, however, important estimation differences between the models. In an ERGM, chance expectations are constructed from all individuals in the network. In the case control models, chance expectations are constructed independently from the network tie information. Thus, an ERGM on the ego networks would include the alter information in the random baseline, while the case control model would not.

More generally, the case control model offers a great deal of flexibility: because the controls are separate from the cases, the controls can easily be constructed to represent a different comparison. The case control model is ultimately useful because of this flexibility, making it easier to update the homophily coefficients as the simulation proceeds.

5. METHODS: THE SIMULATION APPROACH

5.1. Setup and Assumptions

The proposed simulation approach uses ERGM and case control logistic regression to generate full networks from ego network data.¹⁶ I divide the discussion of the method into three parts: gathering information prior to the simulation; setting up the simulation; and the simulation itself. In the first part, the method extracts the local information from the sampled data; in the second and third parts, the method generates networks consistent with the local information. And more specifically, the method searches for the “best” fitting network, using the empirical ego network distribution as the benchmark (while also maintaining the correct level of homophily). I present the method as a series of steps and offer a summary in Table 1.

Table 1.

Summary of Simulation Steps

Part I: Gathering Information Prior to the Simulation

Step 1: Calculate degree distribution and differential degree from the sampled data.

Step 2: Calculate ego network configuration distribution from the sampled data.

Part II: Setting up the Simulation

Step 3: Simulate network of size N with the degree distribution from Step 1; assign demographic characteristics to the nodes in the network (based on the sampled data).

Set ERG Model to Simulate Network From:

Step 4: Specify terms in the model.

Model terms capture:

Differential degree (nodecovariate term)

Homophily (absolute difference or mixing matrix)

Ego network configuration distribution (GWESP or alternative clustering term)

Step 5: Set initial coefficients on terms from Step 4.

Step 6: Constrain model on the observed degree distribution (from Step 1)

Part III: Simulation Procedure

Step 7: Simulate network using the model specified in Steps 4–6. Start from network simulated in Step 3.

Step 8: Compare homophily in simulated network (from Step 7) to homophily in sampled data. Update homophily coefficients if bias is found.

Step 9: Simulate new network using the updated coefficients from Step 8. Start from the network in Step 7.

Step 10: Use chi square value to compare ego network configuration distribution in simulated network (from Step 9) to ego network configuration distribution in sampled data (from Step 2)

Step 11: Update coefficient on clustering term to find better fitting network. A “better” network has a lower chi square value (compared to the chi square value from Step 10), or has an ego network configuration distribution closer to the empirical distribution. Steps 7–10 are repeated for each proposed change to the clustering term coefficient (with the new clustering term coefficient used in the set of coefficients).

Repeat Step 11 until the expected chi square value does not improve over the last iteration.

For the purposes of discussion, assume that the ego network survey has demographic information on the respondents and alters. Also assume that the researcher knows the number of alters per respondent, but can only ask alter-alter tie information for a subset of the alters (e.g. for four randomly selected alters).¹⁷ Also assume that the size of the true network is known.

5.2. Gathering Information Prior to the Simulation

Step 1: Calculate the degree distribution and differential degree from the sampled data.

Step 2: Calculate the ego network configuration distribution from the sampled data (using Formula 1). See Figure 2 for an example.

5.3. Setting up the Simulation

Step 3: Simulate an initial network of size N (assumed to be known) with the same degree distribution as the sampled data (estimated in Step 1); also assign demographic characteristics to the nodes in the network.¹⁸ Specifically, nodes in the simulation are randomly assigned the demographic profile (e.g. black, college graduate) of someone in the sample with the same degree as themselves.¹⁹ The initial network will thus have the right size, degree distribution (estimated from the sampled data), and demographic composition. The network will also reflect differential degree, where some demographic groups have higher degree than others.²⁰

Step 4: Specify an ERG formula from which to simulate the full networks. The ERG formula determines which micro features are used to generate the full network. The model terms should thus capture all of the information available from ego network data: differential degree, homophily and the ego network configuration distribution. The initial coefficients for the terms are set in Step 5, while the degree distribution is handled separately as a constraint in Step 6.

Differential degree: include a nodecovariate term for initial degree, or the degree of each node from the initial network (from Step 3). A nodecovariate term serves as a main effect: in this case, a tie is more likely if person i has high initial degree and less likely if person i has low initial degree (assuming a positive coefficient). The nodecovariate term thus maintains the degree of node i throughout the simulations (with some stochastic variation). By holding expected degree constant, the nodecovariate term maintains the empirical correlation between degree and the demographic characteristics (as the demographic characteristics are held fixed and the empirical correlation is reflected in the initial network—see Step 3). Nodes falling into a given category in the simulation will thus have the same mean degree as that category in the sampled data.²¹

Homophily

One should also include homophily terms for each demographic dimension available in the sampled data. An absolute difference term is appropriate for continuous variables, such as age, while a mixing matrix is appropriate for categorical variables (“absdiff” or “nodemix” in the statnet package—Handcock et al. 2008). The mixing matrix for race, for example, may include terms for the number of black-black, black-white, white-white, etc. ties in the network.²² Formally, the count of black-white ties (for example) can be written as:

$$\sum _{i\in B}\sum _{j\in W}{Y}_{ij}∕2,\mathit{where}\mathit{Y}\mathrm{is}\mathrm{an}\mathrm{undirected}\mathrm{network}.$$ (4)

Ego Network Configuration Distribution

The ego network configuration distribution offers a more difficult specification problem than homophily or differential degree. There are a large number of configurations, and the model must include a term, or terms, that will reproduce the distribution in the simulated networks. One could include a term for each possible configuration, but this yields a very large number of (similar) clustering terms. Such a model is difficult to estimate and simulate from.

As an alternative, one could specify a model with a single clustering term. This specification has two key advantages: first, the model is considerably simpler; and second, the model is less likely to yield degenerate networks (Handcock 2003), likely under the dummy variable specification (i.e. one term for each configuration).²³ The question is what single term will yield non-degenerate networks with the right ego network configuration distribution. There are a number of possible options, but I suggest that GWESP (geometrically weighed edgewise shared partner) is the most appropriate choice, where GWESP is a weighted summation of the shared partner distribution (Snidjers et al. 2006). Formally:

$$\mathit{GWESP}=e^{\alpha }\sum _{i=1}^{n-2}\{1-{(1-e^{-\alpha })}^i\}{p}_i$$ (5)

where α is a scalar, determining the rate of decay on the summation (where lower values weight the initial shared partners to a much larger extent than the 10^th, 11^th, etc. shared partner) and p_i is the number of dyads (with an edge) who have i partners in common. A GWESP coefficient is positive when pairs of tied nodes have a high number of shared partners (relative to chance). Substantively, GWESP captures transitivity and higher order clustering in the network (Hunter 2007).

GWESP is a particularly appropriate choice as it mirrors the structural features of the ego networks. For example, the shared partner distribution in an ego network (from ego's point of view) is equivalent to the degree distribution of the alters.²⁴ The degree distribution of the alters is largely sufficient to differentiate the ego network configurations, given size. Similarly, GWESP captures structural heterogeneity through the α parameter, while the ego network configurations vary systematically by size. By decreasing α, one implicitly decreases the density in larger ego networks relative to smaller ego networks (as adding another shared partner has a smaller effect and larger ego networks have a higher number of possible shared partners).

I suggest that GWESP is the most theoretically and technically appropriate option, but there is nothing inherent in the simulation that says GWESP must be used. A researcher could easily specify another clustering term: for example, one term for each ego network configuration or a triangle term. I only suggest that GWESP is an ideal option; it is certainly not the only one.

Step 5: Set the initial coefficients for the terms specified in Step 4. The nodecovariate coefficient, for example, must be positive, so that initial degree is highly correlated with final degree. A coefficient that is too large, however, limits the flexibility of the simulation.²⁵ The initial homophily coefficients, defined as θ_o, are set using case control logistic regression. The model predicts a tie as a function of social distance (as specified in Step 4).²⁶

Unlike homophily or differential degree, the coefficient for the clustering term (e.g. GWESP) cannot easily be assigned: for it is not possible to analytically solve for the correct coefficient (i.e. the coefficient that will yield networks with the right ego network configuration distribution). The method thus generates an initial (naïve) value by estimating a dyadic independent ERGM on the ego networks. The model predicts ties as a function of the specified term (e.g. GWESP), and the estimated parameter is used as the initial coefficient.²⁷

Step 6: Set the constraints for the model. The model is constrained on the degree distribution, where only networks consistent with the observed degree distribution (from Step 1) have a non-zero probability of remaining in the set of generated networks.²⁸

5.4. Simulation Procedure

Step 7: Simulate a network using the model specified in Steps 4–6. The simulation takes the network from Step 3 as the starting point.

Given the simulated network from Step 7, Steps 8–11 adjust the model to find a better fitting network, specifically updating the homophily coefficients and the coefficient for the clustering term.

Step 8: Compare homophily in the simulated network (from Step 7) to homophily in the sampled data; update homophily coefficients if any error is found. The generated networks may have incorrect mixing rates due to the initial estimation process. The initial homophily model (see Step 5) only includes homophily terms, so that all non-homophily terms are implicitly set to 0. The simulation model, in contrast, is conditioned on a non-zero clustering term. The homophily estimates are therefore biased when they are used to simulate the network (as the initial estimates are not conditioned on the positive value for clustering) (Goodreau et al. 2009).²⁹

The simulation method consequently checks for inconsistencies between the simulated network and the sampled data. The method then updates the homophily coefficients to adjust for any error. A coefficient is decreased if mixing is too strong in the simulated network (between category i and category j) and increased if mixing is too weak.

Formally, the homophily coefficients are updated using case control logistic regression. The method first takes the tied dyads from the simulated network and the respondent-alter dyads from the sampled data and creates a combined dataset. The dataset includes the demographic characteristics of person i and j in each dyad. A 0/1 indicator variable is then created, where the sample dyads are “1s” and the dyads from the simulated network are “0s”. The method then runs a simple logistic regression, predicting 1s as a function of the social distance between i and j. The regression thus compares the social distance in the sampled data (between respondents and alters) to the social distance in the simulated network (among pairs where a tie exists). The estimated coefficients are then added to the original homophily coefficients, thus scaling the original homophily coefficients up or down, depending on the error in the simulated network. This procedure can be written formally as: Construct matrices A and D from:

• 1all i,j Respondent Alter pairs, defined as R_ij
• 2
  all i,j pairs ∈ S_ij == 1 where S is the simulated network.

  $$\begin{array}{cc}\hfill & A_n=\{\begin{array}{c}\hfill 1,\mathrm{if}i,j\in R_{ij}\hfill \\ \hfill 0,\mathrm{if}i,j\notin R_{ij}\hfill \end{array}\phantom{\}}\hfill \\ \hfill & D_n=\mathrm{Social}\mathrm{Distance}\mathrm{between}i\mathrm{and}j\hfill \\ \hfill & \ln \left(\frac{p\left(\mathit{A}\right)}{1-p\left(\mathit{A}\right)}\right)={\theta }_a\mathbf{D}\hfill \\ \hfill & {\theta }_u={\theta }_a+{\theta }_o\hfill \end{array}$$ (6)

  where θ_o is the original homophily coefficients, θ_a is the vector of estimated coefficients, and θ_u is the updated homophily coefficients. For categorical variables (e.g. a racial mixing matrix), θ_a will be positive when the simulated network has too few ties for that term (e.g. black-white ties) and will be negative when the simulated network has too many. And more generally, θ_a measures the upward or downward error in the original homophily coefficients: for θ_a compares the empirical level of homophily to the homophily generated by θ_o, conditioned on the other terms in the model. By adding θ_a to θ_o, the coefficients are brought back into line with the proper values.

Step 9: Simulate a new network using the updated coefficients from Step 8 (starting from the network in Step 7 and using the model formula from Step 4 and 6). Steps 8 and 9 are repeated a small number of times to ensure that homophily is correct in the simulated network.

Step 10: Evaluate the ego network configuration distribution in the simulated network (from Step 9). The generated network from Step 9 will have the correct degree distribution and mixing patterns, but need not, necessarily, have the right ego network configuration distribution. The simulation procedure thus allows the coefficient on the clustering term (e.g. GWESP) to vary, looking for networks that better fit the empirical ego network distribution. The ego network configuration distribution is evaluated in this step, while the coefficient is updated in the next.

There are two steps to evaluating the ego network configuration distribution: first, calculating the ego network configuration distribution from the simulated network; and second, comparing the distribution from the simulated network to the distribution from the sampled data (calculated in Step 3). The method compares the distributions using Pearson's chi square value:

$$\sum _{i=1}^n\frac{{(O_i-E_i)}^2}{E_i}$$ (7)

where O_i is the observed frequency in the simulated network, E_i is the empirical frequency, and n is the total number of possible configurations (53 in the five alter case). Larger chi square values indicate a worse fit, so that the ego networks in the simulated network do not structurally match the ego networks in the sampled data.

Step 11: Update the coefficient on the clustering term to find a better fitting network (given the chi square value from Step 10). A “better” network has a lower chi square value, or has an ego network configuration distribution closer to the empirical distribution (estimated from the sampled data). The ego network configuration distribution thus serves as the benchmark, or ruler, by which the generated networks are judged. The question is what coefficient on the clustering term will yield simulated networks with the lowest chi square value. In updating the model, the nodecovariate coefficient is held constant, while the homophily coefficients are updated using the framework from Step 8.³⁰

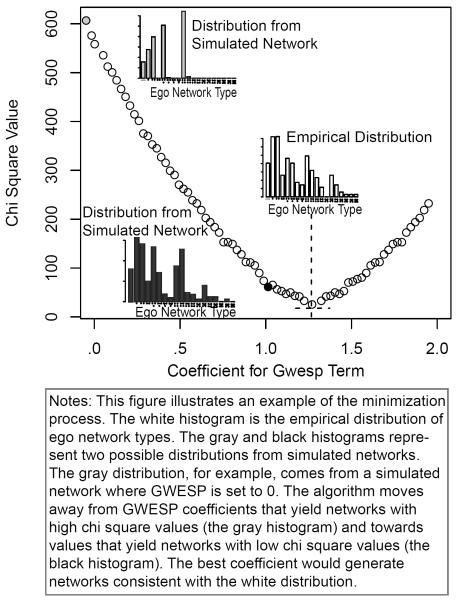
Figure 4 offers a snapshot of the minimization process. Assume, for this example, that the researcher has included a GWESP term in the model. The x-axis represents a (restricted) range of GWESP coefficients. The y-axis represents the chi-square value associated with that GWESP coefficient. The GWESP coefficient is used to simulate a network (along with the other terms in the model) and the chi square value is calculated from the simulated network. The optimization process moves away from points with high chi square values, like the “grey” distribution in Figure 4, and towards points, or coefficients, with lower chi square values—like the “black” distribution in Figure 4. The “black” distribution matches the sampled ego networks more closely and thus offers a better fit.

FIGURE 4.

Example Optimization Curve

I present two options for minimizing the chi square value. The first is a simple hill climbing algorithm. The algorithm moves the current coefficient in the positive and negative direction, looking for a better fitting network. For each potential move, the method takes the coefficients (from Step 9 but with the new coefficient for the clustering term) and simulates a network; the method also adjusts for homophily bias if necessary (Steps 7–9). The method then calculates the chi square value for each network, comparing the ego network distribution in the simulated networks to the distribution in the sampled data. The algorithm settles on whichever move maximizes the drop in chi square from the current coefficient. The method then returns to Step 7 and starts the process over again, using the new coefficients to simulate the networks. The search process ends when all local moves yield a worse chi square value than the current coefficients.

The second minimization process is similar to the hill climbing algorithm, but requires a less exhaustive search of the solution space. Under this option, the method first simulates a sample of networks at different values of the (clustering) coefficient— specifically values above and below the starting coefficient. For each simulated network, the method adjusts for homophily bias and calculates the chi square value (i.e. Steps 7–10). The method then takes the coefficients for the clustering term and the chi square values and fits an OLS regression to the data. The regression predicts chi square as a function of a linear and quadratic term:

$${\chi }_i^2={\beta }_0+{\beta }_1\left(C_i\right)+{\beta }_2{\left(C_i\right)}^2$$ (8)

where ${\chi }_i^2$ equals the chi-square value for network i, and C_i equals the coefficient on the clustering term for network i. The regression coefficients are then used in an optimization routine. The method uses the Nelder-Mead algorithm to find the clustering term coefficient with the lowest chi square value (based on the fitted regression line). The solution, or coefficient, is then used as the starting point for the next iteration. The method then repeats Steps 7–10 again, ending the process when the expected chi square value does not improve over the last iteration.

At the end of the search process, the method generates networks from the best set of coefficients.³¹ One then calculates the statistics of interest (e.g. component size) on the simulated networks and summarizes over the estimated values. The simulated networks yield a distribution of statistics, capturing the stochastic uncertainty in the estimates. Sampling error provides another source of uncertainty, and a researcher would have to perform a bootstrap analysis to take this into account.³²

The simulation, in short, rests on a kind of approximated likelihood ratio test: the coefficients are updated to find a more likely full network, where a network is more likely if its ego network configuration distribution is closer to the empirical distribution (estimated from the sampled data). The simulation approach thus draws (implicitly) on formal statistical properties, increasing the probability that the generated networks approximate the true network—as the method finds the most likely full network given the local data and the specified model. One could even run the simulations with different specifications of the clustering term, checking to see if the fit (i.e. chi square) improves under different models.

More generally, I argue that simulation based inference holds great promise: for social networks are highly constrained by size, the degree distribution, and social/physical distance (Butts 2001; Faust 2006), all properties captured by the simulation. If the simulated networks correctly capture these constraining dimensions, then the space of possible networks is greatly reduced. The number of possible networks is reduced further by finding networks with the right ego network configurations. For the empirical ego networks are shaped by the same processes that shape the true network; a network consisting of the sampled ego networks thus represents a possible construction of the real network.

6. TESTING THE METHOD ON EMPIRICAL NETWORKS

6.1. Summary of the Analytical Strategy, Measures and Baseline Comparisons

I now present a set of empirical tests checking the validity of the method. For each test, I first sampled ego networks from a completely known, empirical network. I then applied my method to the sampled data and compared the properties of the generated networks to the properties of the real network. I examined the accuracy and variability of the estimates and compared my results with those of simpler, baseline models. I tested my method on the 20 largest Add Health networks and the Sociology Coauthorship network in the 1990's. The Add Health networks ranged from 1000 to 2200 students and varied in structure and composition, offering a robustness check for the method (see McFarland et al. 2009). The Coauthorship network offered a different type of test: here the method was used on a relatively large, highly transitive network (N~60000).

The network properties of interest were divided into two broad categories: connectivity and clustering/group structure. For connectivity, the measures included size of the largest component and bicomponent, where a component is a set of nodes connected by at least one path (a path exists if two nodes are reachable through a series of adjacent ties). Bicomponent size is the largest set of people connected by at least two independent paths (Moody and White 2003). There were also measures for reachability and mean distance, where distance is the length of the shortest path between any two nodes (restricted to reachable pairs). Reachability was measured as the proportion of people reachable 5 steps out into the network (averaged over all starting nodes). The analysis used modularity as the measure of group structure. I used the group detection algorithm of Clauset, Newman and Moore (2004) to divide the network into groups. I then calculated modularity on the found groups, where modularity measures the strength of group divisions in the network; modularity is high when there are many ties within groups and few between (Newman 2006).³³ The analysis used transitivity and the triad census as the measures of clustering. Transitivity is the relative number of two-step paths that also share a direct link. The triad census was measured as the proportion of 102 triads, or triads with one symmetric tie, and the proportion of closed triads, or 300 triads (Cartwright and Harary 1956).³⁴

The proposed method estimates the global features of a network from sampled ego network data; it is possible, however, that simpler, existing methods will produce equally valid results. I thus compared my method to two baseline models. The first model generated random networks with the correct size and degree distribution (Newman et al. 2001).³⁵ This model is called the Degree (D) model in the figures and tables. The second baseline model incorporated homophily into the Degree model, capturing both the degree distribution and the pattern of group mixing. This model is called the Homophily model in the tables and figures (H). The full model included the degree distribution, homophily and the newly introduced ego network configuration distribution. I refer to my own method as the Ego Network Configuration Model (ENC).

The three models are directly nested. This makes it possible to discuss the “value added” for each term in the model. The question is whether the ego network configuration distribution is necessary to produce good estimates, or if homophily and the degree distribution are sufficient.

6.2. Add Health Networks: Data, Sampling and Models

Add Health is a nationally representative survey of public and private schools covering grades 7–12. Students were asked to nominate up to five male and five female friends. The constructed, symmetrized networks were used in two sets of analyses. The networks were symmetrized using a “weak” rule: if there was a directed link between i and j or a directed link between j and i, then i and j were tied in the undirected network. The first analysis used the 20 largest networks and randomly sampled 25 percent of the students within each school. The 25 percent sample results were used to compare across models. In the second analysis, I focused solely on my method, exploring the bias and sampling variability of the estimates under different sample sizes. I limited the analysis to the five largest networks but considered sampling rates of 10 percent, 25 percent, 50 percent and 75 percent. I varied the sample size to test my method under more or less favorable samples.

Each sampled student provided the following information: first, the number of alters and the ties between alters; second, the characteristics of the respondent; and third, the characteristics of the alters. The characteristics included grade, race, sex, and club affiliations. Club affiliations were limited to broad categories: music, sports and academic. The survey was “realistic” as I only recorded alter characteristics and alter-alter ties for up to five friends, although there was no limit on the number of friends one could name. The five friends were randomly selected from the set of all friends for that respondent.³⁶ The respondent described the ties between the randomly selected friends and answered questions about their demographic characteristics. The decision to use five friends was made independent of the Add Health study design. I used five alters for two reasons: first, it makes counting the ego networks more tractable; and second, it is more realistic for data collection purposes, where respondent burden is kept to a reasonable amount.

The simulation method requires an ERG model and I included the following terms in the formula: nodemix terms for grade, race, gender and club affiliation; a nodecovariate term on initial degree; and GWESP.³⁷ The simulations were also constrained on the degree distribution. The Homophily model was equivalent but did not include GWESP.

My method takes the model formula and initial coefficients and produces estimates for the statistics of interest. The analysis captured the variability of the estimates by repeating the procedure 30 times for each school, starting with a new sample of ego networks for each iteration.³⁸ There were parallel analyses for the baseline models (under 25 percent sampling).

6.3. Sociology Coauthorship Network: Data, Sampling and Models

The second validity check used the Sociology Coauthorship network as the empirical, known network. I constructed the network from article level data drawn from Sociological Abstracts. The database includes information on all sociology related articles going back to 1963, but the network was restricted to articles published between 1995 and 1999. An edge existed in the network if person i and person j coauthored a paper between 1995–1999. The empirical network included 60098 people and I worked with a random sample of 5 percent of the network. I produced estimates for only one sample due to the computational burden of the analysis (where a network of that size and transitivity requires a rather extended run time). I thus did not consider sampling variability for the Coauthorship network.

As with Add Health, the hypothetical survey collected the following information: the number of alters (with no limit); the ties between alters (for five randomly selected alters); the characteristics of the respondent; and the characteristics of the alters (for five randomly selected alters). The characteristics included gender, prestige (defined as having ever published in AJS, ASR, or Social Forces), subfield specialty, and quantitative/qualitative identification. I specified an ERG model with mixing terms for each characteristic as well as a nodecovariate term for initial degree. The model also included a GWESP term.³⁹ All simulations were conditioned on the degree distribution. The Homophily model was exactly the same but did not include the GWESP term.

7. RESULTS

7.1. Qualitative Comparison

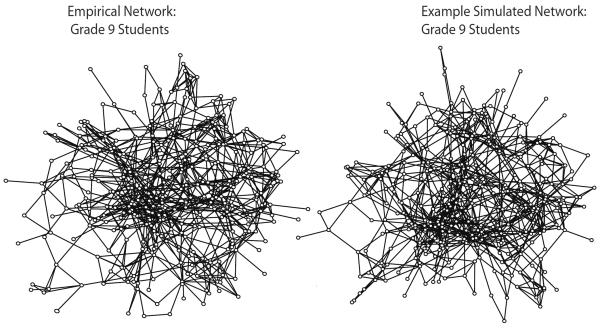
The results section begins with a qualitative comparison, showing that the simulation produces realistic looking networks. Figure 5 offers a snapshot comparison for one typical Add Health network. The left hand panel presents the true network while the right hand panel presents one realization from the simulation process.⁴⁰ The networks, while not identical, are strikingly similar—the macro structure in the real network is reflected in the overall shape of the simulated network. The comparison is similarly encouraging in Figure 6, which presents a more detailed view of the network. Here the figure is limited to nodes in grade 9. The simulation performs well even at this more fine grained level, generally reproducing the core-periphery structure of the grade 9 network.

FIGURE 5.

Comparing Add Health Network #6 to Example Simulated Network

FIGURE 6.

Comparing Add Health Network #6 to Example Simulated Network: Grade 9 Only

Given these positive qualitative results, I now move to a more formal test of the approach. I first compare my results to those of simpler models. I then examine my model in more detail, looking at the results at different levels of sampling. In both sections, the results begin with the connectivity measures before moving to clustering and group structure.

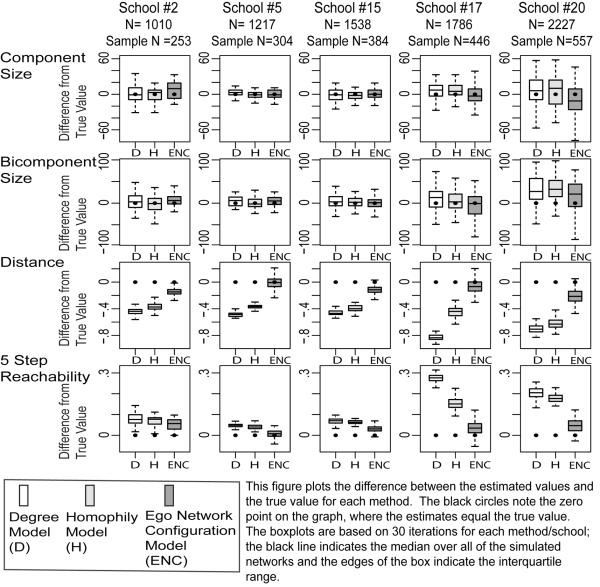
7.2. Connectivity: Baseline Model Comparisons

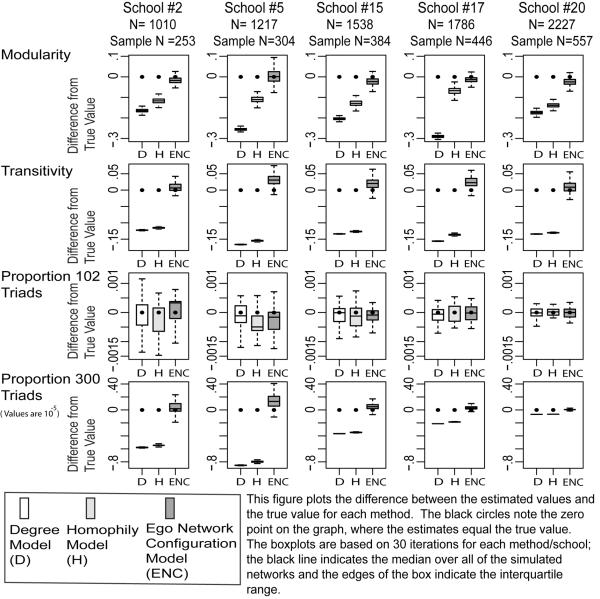
The connectivity results begin with the Add Health networks (under 25 percent sampling). It is difficult to visually summarize the results over all 20 networks. I simplify the presentation by focusing on five typical networks of different sizes. Figure 7 presents the results for my model as well as the baseline models. For each model (and measure), the analysis subtracts the empirical value from the estimated values from the 30 samples. The figure presents these differences in a series of box plots. The black dot marks the zero point, where there is zero difference between the true and estimated value. The paper offers more precise information about bias and sampling variability in Appendix A (where bias is the difference between the mean estimate and the true value). For each measure and network, the tables report the bias and the proportion bias (bias divided by the true value). The tables also report the standard deviation of the sampling distribution. See Tables A1–A8 for the 25 percent sample results.

FIGURE 7.

Comparison between True and Estimated Values for 5 Illustrative Add Health Schools: Connectivity Measures, 25 Percent Ego Network Samples

It is clear from Figure 7 that all three methods successfully estimate the size of the largest component and bicomponent. For example, my method yields an average bias less than 1 percent of the true bicomponent size (across all networks). The simpler models also perform well. The Homophily and Degree models are thus good options if one is only interested in component or bicomponent size.

The story is quite different for distance, where only the ENC model accurately estimates mean distance in the network. Looking at row 3 of Figure 7, the Degree and Homophily models underestimate the true distance while the ENC model does not. The results are similar across all 20 Add Health networks: the average bias for my model is 3.5 percent of the true value, while the bias is upwards of 15 percent for the Degree model and 11.8 percent for the Homophily model (on average). The Degree model is thus improved by including homophily, while the Homophily model is improved by including the ego network configuration distribution. See Table A3 for more detailed results.

The reachability results are qualitatively similar: the baseline models overestimate reachability in the network while my method is quite accurate. In Figure 7, the empirical values are close to the ENC estimates but below those provided by the baseline models (especially for the larger networks). For example, the empirical 5 step reachability is .59 in Add Health Network #17; the Degree and Homophily estimates are .87 and .75 while my estimate is .626. More generally, the ENC model performs well for all of the networks, with an average bias of .053.

The connectivity results for the Coauthorship network offer a substantially different story than the Add Health networks. Here, both of the baseline models badly overestimate the size of the main component and bicomponent. The real bicomponent size, for example, is 6807 while the baseline estimates are 36432 (D) and 34280 (H). The baseline models perform poorly as they underestimate the level of transitivity in the network. The empirical network has high transitivity and low density, leading many small components to break off from the main component. By underestimating the level of transitivity, the baseline models undercount the number of disconnected components, thus overestimating the connectivity of the network. In the real network, an average node can reach 2.4 percent of people in 10 steps, yet the Degree model puts the value at almost 90 percent.

The ENC model fares considerably better than the baseline models (see Table 2). For example, my method puts component size between 18262 and 21895 while the real value is 19155; the estimates for bicomponent size fall between 8698 and 10620 while the true value is 6807. The results are similar for distance and reachability (10 step): the median estimates are 13.52 and 2.2 percent, compared to the true values of 13.25 and 2.4 percent.

Table 2.

Summary of Coauthorship Results: Connectivity

		Degree			Homophily			Ego Network Configuration
Statistic	True Value	Min	Median	Max	Min	Median	Max	Min	Median	Max
Component	19155	57218	57275	57330	55360	55640	55850	18262	20887	21895
Bicomponent	6807	36219	36342	36437	34230	34280	34310	8698	9975	10620
Distance	13.250	8.002	8.009	8.018	8.427	8.461	8.467	13.055	13.524	14.049
5 Step Reachability	.0014	.031	.031	.032	.025	.025	.025	.0012	.0014	.0015
10 Step Reachability	.024	.867	.869	.872	.758	.764	.769	.016	.022	.026

Note: The values are taken from a single sample and thus do not capture variability due to sampling error. Rather, the estimates capture the stochastic variation inherent in the simulation procedure, where a single sample will produce a range of possible values.

7.3. Group Structure and Clustering: Baseline Model Comparisons

The results now turn to the group structure and clustering measures, beginning with the Add Health networks under 25 percent sampling. The results for modularity are plotted in row 1 of Figure 8. The proposed method performs quite well: the estimated values are close to the empirical value, with bias under 5 percent of the true value (on average). The baseline models, in contrast, badly underestimate the group divisions in the network (although the Homophily model outperforms the Degree model).

FIGURE 8.

Comparison between True and Estimated Values for 5 Illustrative Add Health Schools: Clustering Measures, 25 Percent Ego Network Samples

The results are similar for transitivity, where the ENC model estimates the empirical values quite well with relatively small standard deviations—see row 2 in Figure 8. The Degree and Homophily models perform poorly, systematically underestimating transitivity. For example, Add Health Network #19 has a transitivity value of .14; the estimated values are .147, .01 and .006 for the ENC, Homophily and Degree models. The average bias for transitivity is .016 in the ENC model (with a mean true value of .17). See Table A6 for details.

The triad distribution offers a more complicated story. The closed triad (300) is estimated far better by my method than the simpler baseline models. In contrast, all three models effectively estimate the proportion of 102 triads (see row 3 in Figure 8). A researcher interested in balanced triads could use the baseline models to make inference, although my model more accurately captures the closed triads.

The Coauthorship network results are similar, but less consistent, than the Add Health results. The ENC model accurately estimates modularity and the 102 triad, while the Degree and Homophily models only estimate the 102 triad well. Modularity is .979 in the true network and .978 in the ENC model (compared to .64 and .66 for the Degree and Homophily models). Transitivity and the 300 triad are also estimated more accurately by the ENC model, but the error is larger than with modularity or the 102 triad (or with the Add Health networks).⁴¹ For example, the true transitivity value is .6 while the estimated values are .47 (ENC), .0004 (Homophily) and .00013 (Degree).

The Coauthorship results raise an important question about the bounds of the method: can the method capture clustering measures when transitivity is high, such as in the Coauthorship network? And more specifically, is the method appropriate when local clustering is high but not complete?⁴² This paper offers an initial answer to the question in a supplementary simulation analysis (not shown for space considerations). The analysis measured transitivity bias in a series of generated networks (size 500) that ranged from very low clustering (0 transitivity) to very high clustering (.62 transitivity). The results for this supplementary analysis are encouraging: the bias and sampling variability for transitivity (as well as the other clustering measures) are small overall and change only slightly as clustering increases. The transitivity bias in the Coauthorship network is thus not indicative of larger, systematic problems (i.e. of estimating transitivity when transitivity is high).⁴³

7.4. Bias and Sampling Variability by Sample Size: ENC Model

The ENC model clearly offers a better option than the baseline models. Having established this, it is important to examine the method on its own terms, and I now turn to a more detailed assessment of the ENC model. Using the Add Health networks, I tested my method at different levels of sampling (in terms of bias and uncertainty).

Table 4 presents the connectivity results for the 5 largest Add Health networks under 10 percent, 25 percent, 50 percent, and 75 percent sampling. Sampling variability clearly decreases with larger samples, although even a 10 percent sample yields low levels of uncertainty. The standard deviation for component size, for example, decreases from 22 to 5.6 for Network #17 (10 percent to 75 percent sampling).

Table 4.

Connectivity Results for 5 Largest Add Health Networks by Sample Size

			Bias a				SE b
Net ID	Statistic	True Value	10% Sample	25% Sample	50% Sample	75% Sample	10% Sample	25% Sample	50% Sample	75% Sample
16	Component	1570	−1.042	−2.245	−1.097	−.896	16.263	9.209	5.734	3.696
17	Component	1707	5.813	.765	1.439	−2.039	21.993	16.013	8.516	5.625
18	Component	1745	−.360	.181	−.937	.060	18.768	10.245	8.319	4.723
19	Component	1894	−1.061	.772	.572	.769	14.633	9.308	6.015	4.002
20	Component	1954	−9.903	−10.846	−.193	−1.608	50.711	26.636	17.323	13.457
16	Bicomponent	1517	.769	−6.641	−4.453	−3.506	24.894	20.319	9.944	6.421
17	Bicomponent	1594	15.735	−3.531	−2.865	−1.842	32.292	27.695	11.580	8.363
18	Bicomponent	1648	8.945	7.374	5.150	3.216	38.663	20.124	11.688	6.835
19	Bicomponent	1838	−3.634	1.543	1.485	2.047	22.986	17.441	11.029	5.881
20	Bicomponent	1664	10.920	16.564	25.134	18.619	76.119	34.949	26.401	16.470
16	Distance	4.253	−.155	−.163	−.194	−.186	.094	.058	.039	.033
17	Distance	5.038	−.034	−.067	−.073	−.066	.154	.098	.076	.073
18	Distance	4.751	−.226	−.264	−.286	−.264	.142	.088	.054	.049
19	Distance	4.302	−.133	−.143	−.147	−.146	.076	.041	.034	.029
20	Distance	5.497	−.175	−.212	−.225	−.204	.201	.103	.068	.062
16	5 Step Reachability	.881	.041	.043	.049	.048	.024	.016	.019	.008
17	5 Step Reachability	.591	.030	.035	.036	.032	.051	.033	.026	.024
18	5 Step Reachability	.720	.090	.104	.110	.104	.050	.027	.018	.015
19	5 Step Reachability	.882	.032	.037	.038	.038	.019	.012	.009	.006
20	5 Step Reachability	.393	.039	.047	.055	.048	.063	.033	.021	.018

Note: The values for Bias and SE are calculated over 30 independent samples, where each sample yields one estimate of the network measure. All estimates come from the ENC model.

^aBias=E(estimates)−True Value.

^bThe Standard Error is the standard deviation of the sampling distribution.

The bias results provide a more complicated story. The 10 percent estimates are (again) quite good, so that a 10 percent sample is sufficient to produce quality estimates of connectivity. The average bias for distance, for example, is approximately 3.6 percent of the true value under 10 percent sampling. Bias does not, however, decrease systematically as the sampling rate increases. The bias does not decrease appreciably as the connectivity measures are not directly captured by the sampled information. A larger sample provides more precise estimates of homophily, the degree distribution, and other inputs into the method. But as these local measures are estimated well enough in smaller samples, and the connection between the inputs and the connectivity measures is not one to one, we see little improvement in bias after a reasonable sample size (e.g. 10 percent).

The method thus offers the greatest payoff when sampling rates are low. And more specifically, a 10 percent sample would have been an ideal choice in this setting— given the low levels of bias and uncertainty. Conversely, if one could really interview 75 percent of the network, one should simply collect full network data and follow a more traditional route of analysis.

Table 5 presents the sample size results for the clustering/group structure measures. As with the connectivity results, sample variability decreases as sample size increases. For example, the standard error for modularity decreases from .026 to .015 in Network #18 (with a true value of .611). The bias results, in contrast, do not follow the pattern of the connectivity measures: here the bias for transitivity and the triad census decreases as the sample rate increases, although there is a plateau at the 75 percent level. The bias for transitivity in Network #16, for example, is .027 (10 percent), .019 (25 percent), .015 (50 percent), and .015 (75 percent). The bias decreases because the clustering measures are more directly tied to the sample information (i.e. the ego network configurations) than the connectivity measures.

Table 5.

Clustering Results for 5 Largest Add Health Networks by Sample Size

			Bias a				SE b
Net ID	Statistic	True Value	10% Sample	25% Sample	50% Sample	75% Sample	10% Sample	25% Sample	50% Sample	75% Sample
16	Modularity	.575	−.038	−.041	−.052	−.049	.022	.023	.017	.016
17	Modularity	.667	−.009	−.014	−.014	−.013	.019	.014	.013	.013
18	Modularity	.611	−.045	−.051	−.052	−.051	.026	.021	.016	.015
19	Modularity	.545	−.034	−.028	−.035	−.037	.016	.016	.013	.013
20	Modularity	.627	−.020	−.025	−.029	−.026	.026	.017	.012	.012
16	Transitivity	.140	.027	.019	.015	.015	.015	.014	.011	.011
17	Transitivity	.161	.028	.024	.021	.022	.019	.016	.015	.015
18	Transitivity	.178	.025	.013	.013	.015	.024	.019	.014	.013
19	Transitivity	.141	.012	.007	.006	.008	.017	.013	.011	.011
20	Transitivity	.138	.020	.010	.004	.006	.025	.017	.015	.014
16	Proportion 102 Triad	.015	.000	.000	.000	.000	.001	.000	.000	.000
17	Proportion 102 Triad	.010	.000	.000	.000	.000	.000	.000	.000	.000
18	Proportion 102 Triad	.011	.000	.000	.000	.000	.001	.000	.000	.000
19	Proportion 102 Triad	.012	.000	.000	.000	.000	.000	.000	.000	.000
20	Proportion 102 Triad	.006	.000	.000	.000	.000	.000	.000	.000	.000
16	Proportion 300 Triadc	.424	.078	.043	.042	.036	.058	.043	.037	.033
17	Proportion 300 Triadc	.219	.041	.032	.026	.026	.034	.026	.022	.020
18	Proportion 300 Triadc	.309	.037	.019	.024	.023	.047	.031	.025	.023
19	Proportion 300 Triadc	.267	.022	.012	.009	.012	.041	.028	.021	.020
20	Proportion 300 Triadc	.070	.011	.005	.002	.002	.015	.010	.008	.007

Note: The values for Bias and SE are calculated over 30 independent samples, where each sample yields one estimate of the network measure. All estimates come from the ENC model.

^aBias=E(estimates)−True Value.

^bThe Standard Error is the standard deviation of the sampling distribution.

^cValues are 10⁻⁵

7.5. ERGM Coefficients and the ENC Model

The results presented thus far have focused on network measures, where the analysis generated networks from an ERG model and examined the properties of the generated networks. It is also possible to examine the ERGM coefficients themselves for bias. Here I compared the true coefficients (estimated on the full network) to the coefficients found during the simulation procedure. This comparison is presented in Appendix B (see Table A9), and is limited to the Add Health networks and the coefficient for GWESP. It is clear from Table A9 that the simulation coefficients do not necessarily map onto the true GWESP coefficients; although, predictably, the simulation coefficients are close to the true values. Thus, while GWESP is included in the ERG model, the method need not produce accurate estimates for the GWESP coefficient: for the coefficient is updated to match the ego network configurations, and not the shared partner distribution. See Appendix B for a more detailed discussion.

The Add Health comparison is, unfortunately, complicated by the fact that we do not know the “true” model generating the networks. It is thus difficult to judge what GWESP parameter should have been recovered by the simulation method. I consequently offer another, more controlled comparison in Appendix C. I tested my method on a network generated from a known, or “true”, model (the network is size 1000). The model was based on the degree distribution, homophily (for race and education) and GWESP. Thus, the only processes affecting the network were clustering and homophily. It is clear from Table A10 that the simulation approach performs quite well here. The mean estimate for the GWESP coefficient is 1.199 under a 20 percent sample, while the true coefficient is 1.2.

Thus, when the “true” model only includes a GWESP term (as well as degree and homophily parameters), the simulation accurately captures the coefficient for GWESP. The GWESP coefficient is updated to fit the ego network configuration distribution. If the only local process affecting the configurations is GWESP, then the coefficient on GWESP will be directly estimated through the simulation process.⁴⁴

8. CONCLUSION

This paper has presented a simulation technique that uses sampled ego network data to make inference about the properties of the full, unknown network. The simulation extends past work by using a new, distributional measure of ego network structure (as well as more traditional measures, like homophily). I tested the validity of the method on the 20 largest Add Health networks and the Sociology Coauthorship network in the 1990's. The simulation method performs quite well in both cases, producing excellent approximations of the true network from a sample of ego networks. The method fares better than simpler baseline models for most statistics, and equally well for the rest.

The proposed technique is a practical option for researchers interested in global network structure where census data cannot be collected. Ego network data are easy to collect and already found on many social surveys. The respondent burden is relatively light and the researcher does not require a full network roster, a potentially difficult item to come by in certain settings (Morgan and Rytina 1977). Additionally, the method makes heavy use of ERGMs, which are widely used by network scholars. Finally, the method is quite general, as any statistic can be calculated on the generated networks. The potential of the method, and network sampling in general, is thus quite large: if a researcher can make inference using a random sample of individuals, it becomes (more) feasible to undertake comparative network work (i.e. comparing the network structure across different settings and locations) and to move beyond small, institutionally bounded populations.

The advantages of the proposed method are partly offset by limitations which need to be addressed in future work, or, at a minimum, must be considered before using the method. For example, the method may produce poor estimates for networks with certain features. In particular, the method may have difficulty with networks that are disconnected, or consist of many separate components. In a supplementary simulation analysis (not presented here), I tested my method on a disconnected network (size 500) close to its phase transition (where the network becomes a fully connected network).⁴⁵ The method, while performing well overall, produces uncertain estimates for connectivity: some samples yield a disconnected network while others yield a connected one, leading to high standard errors for measures such as distance and bicomponent size (see also Grannis 2010). A researcher could still use the method on a network below its phase transition; for as we saw in the Coauthorship analysis, the method can produce accurate estimates of connectivity in a disconnected network.⁴⁶ One must, however, be willing to accept the possibility of large bounds around the connectivity statistics.

Similarly, a network with a badly skewed degree distribution may propose problems for the method: for the few high degree nodes are unlikely to be sampled, leading to a distorted degree distribution. The method is thus most appropriate for strong tie relationships—where the maximum degree is relatively small (e.g. under 75).⁴⁷ Other more complex sampling techniques, such as a snowball sample, may be a better option when the degree distribution is skewed (as one is likely to reach the hub of the network quite quickly). This is especially true of smaller networks, where the high degree nodes have a proportionally larger effect on the network structure.

In a similar manner, the method will be less successful when the sampled data miss important demographic or geographic information. For example, a large hill in the middle of a village may strongly shape interaction patterns (by making it difficult to travel across the village and creating distinct communities). A respondent's location relative to the hill, however, is not easily captured by a standard ego network survey. The simulation approach will thus fare better when the researcher has prior knowledge of the population of interest. And more specifically, a researcher should know the demographic (or geographic) characteristics exhibiting homophily.⁴⁸ There is little gained in asking about alter hair color (for example) if hair color is irrelevant as a predictor of ties. A researcher could improve the quality of their survey by performing a small pilot study on the population of interest. The initial survey would collect detailed information on respondents and their alters, thus identifying the key social/physical dimensions in the network.

More generally, the simulation approach will be most successful when the true network is strongly shaped by the local properties found in the sampled data. The more homophily constrains the network, the more likely the simulation will reproduce the features of the true network. Networks strongly shaped by organizational foci (e.g. associations, work) (Feld 1981) or physical geography are also appropriate.

Future work should consider the scope conditions not simply as practical limitations, but also as methodological opportunities to extend the method. For example, researchers could improve the efficiency of my algorithm. Currently, the full network of interest must be relatively small due to computational limitations (say under 75000 nodes). This upper limit could be extended by making better use of parallel processing (for example). A faster algorithm would also make bootstrapped standard errors a more practical option for large networks.

Future work could also extend the method to other network types and sampling schemes. I restricted the current paper to ego network data and undirected networks, but one could perform a very similar analysis using a two step sample and directed networks. In a two step sample, the researcher interviews the alters of the respondents. The alters describe their personal network, thus providing information on asymmetry (in relation to the respondent) and assortative degree mixing (as we know the degree of the alters and the respondent). A two step sample thus opens the simulation to directed networks and adds assortative degree mixing to the set of local information.

And perhaps more importantly, future work could compare ego network sampling to more complicated sampling schemes, such as snowball sampling (on not hard-to-reach populations). For example, under what conditions, if any, does ego network sampling perform as well as snowball sampling (or perhaps even better)? It is possible that future work also could develop a hybrid sampling scheme that skirts the limitations of both methods.⁴⁹

In a similar manner, future work could examine the effect of measurement error on the estimates. If the degree distribution is truncated, how biased are the estimates? And are there any ways to reduce the bias?⁵⁰ Researchers could also explore the bias due to respondent error. For example, Marin (2004) found that respondents are more likely to forget certain types of alters.⁵¹ This could lead to an undercounting of degree.⁵² As a possible solution, Marin and Hampton (2007) suggested using multiple name generators, while Brewer and Garret (2001) offered survey techniques to reduce the number of missed alters. More work in this vein is clearly needed to describe the costs and benefits of different survey options, especially given the respondent burden in a long ego network survey (see McCarty et al. 2007).

Future work could similarly consider the respondent error in the alter-alter ties. There are two potential sources of bias in the alter-alter data. First, some relationships could be difficult to describe secondhand, as respondents may be unaware if a tie exists between two other people. And second, the data could be biased towards transitive relationships, as respondents try to maintain cognitive consistency in their local network (Kumbasar, Romney and Batchelder 1994; Krackhardt and Kilduff 1999). The severity of these problems will likely vary by the type of relation in the survey. For example, a broadly defined tie (friends with, socialize with, like, etc.) will be easier to describe than a content specific tie. A respondent may know if their alters talk to one another but not whether they discuss politics.⁵³ Future work is clearly needed to describe which relations can be measured accurately via secondhand reports.

Future work should also consider the effects of alter-alter tie error on the ego network configuration distribution, and, ultimately, the macro network statistics. Ideally, we would know how the alter-alter tie error varies by name generator and how the measurement error affects different macro network estimates (Grannis 2010). Finally, one could explore possible solutions to the measurement problems, offering options to increase the validity of the survey without interviewing the alters.⁵⁴ The bias in the alter-alter ties is thus a potential limitation to the method as well as a rich source of material for future studies.

In sum, the approach presented here has been quite successful, but there are a number of methodological questions left unanswered. The hope is that future work will extend this analysis, and the simulation will become a general option for network scholars. For now, the results offer an initial glimpse, or perhaps a reminder, of the great promise of network sampling: to bring the relational, connected nature of social life to standard survey research.

Table 3.

Summary of Coauthorship Results: Clustering

		Degree			Homophily			Ego Network Configuration
Statistic	True Value	Min	Median	Max	Min	Median	Max	Min	Median	Max
Modularity	.979	.642	.643	.644	.660	.661	.663	.976	.978	.981
Transitivity	.604	.00008	.00013	.00017	.0003	.0004	.0004	.459	.469	.479
Proportion 102 Triad (values are 10−3)	.157	.155	.155	.155	.150	.150	.150	.156	.156	.156
Proportion 300 Triad (values are 10−8)	.267	.00003	.00005	.00007	.0001	.00013	.00014	.206	.210	.215

Note: The values are taken from a single sample and thus do not capture variability due to sampling error. Rather, the estimates capture the stochastic variation inherent in the simulation procedure, where a single sample will produce a range of possible values.

Biography

Jeffrey Smith is a doctoral candidate in sociology at Duke University. His research focuses on networks, quantitative methodology and stratification. He is particularly interested in questions of status, homophily and mobility.

Appendix A. Detailed Add Health Tables: 25 Percent Sampling

Table A1.

Add Health Results: 25 Percent Sample, Component Size

		Ego Network Configuration Model				Degree Model		Homophily Model
Net ID	True Value	Mean Estimate	SEa	Biasb	Relative Biasc	Biasb	Relative Biasc	Biasb	Relative Biasc
1	815	817.232	23.182	2.232	.003	8.996	.011	14.220	.017
2	957	963.428	10.873	6.428	.007	.652	.001	−1.915	.002
3	987	991.508	10.674	4.508	.005	−1.268	.001	2.923	.003
4	1025	1032.327	14.337	7.327	.007	13.196	.013	9.625	.009
5	1201	1201.303	7.098	.303	.000	1.436	.001	.090	.000
6	1145	1157.201	14.306	12.201	.011	16.568	.014	19.172	.017
7	1180	1182.274	11.072	2.274	.002	2.680	.002	3.683	.003
8	1214	1222.823	7.318	8.823	.007	6.348	.005	7.005	.006
9	1250	1249.536	15.461	−.464	.000	5.096	.004	11.800	.009
10	1283	1290.029	12.253	7.029	.005	4.308	.003	6.548	.005
11	1278	1275.285	11.339	−2.715	.002	−2.252	.002	−5.610	.004
12	1411	1410.387	14.482	−.613	.000	−.516	.000	−.348	.000
13	1441	1442.547	10.210	1.547	.001	5.144	.004	3.372	.002
14	1355	1372.817	16.940	17.817	.013	23.568	.017	22.367	.017
15	1509	1509.036	8.173	.036	.000	−1.804	.001	−2.463	.002
16	1570	1567.755	9.209	−2.245	.001	−.748	.000	−2.352	.002
17	1707	1707.765	16.013	.765	.000	5.072	.003	7.170	.004
18	1745	1745.181	10.245	.181	.000	1.260	.001	.693	.000
19	1894	1894.772	9.308	.772	.000	1.100	.001	−1.185	.001
20	1954	1943.154	26.636	−10.846	.006	7.628	.004	5.795	.003

Note: The values for Mean Estimate, SE, Bias, and Relative Bias are calculated over 30 independent samples, where each sample yields one estimate of the network measure

^aThe Standard Error is the standard deviation of the sampling distribution.

^bBias=E(estimates)−True Value

^cRelative Bias= |Bias/True Value|

Table A2.

Add Health Results: 25 Percent Sample, Bicomponent Size

		Ego Network Configuration Model				Degree Model		Homophily Model
Net ID	True Value	Mean Estimate	SEa	Biasb	Relative Biasc	Biasb	Relative Biasc	Biasb	Relative Biasc
1	678	684.651	29.146	6.651	.010	22.032	.032	25.133	.037
2	888	897.066	16.309	9.066	.010	4.096	.005	−3.008	.003
3	898	908.140	14.096	10.140	.011	2.584	.003	6.312	.007
4	936	937.162	22.975	1.162	.001	13.572	.014	8.022	.009
5	1166	1170.421	10.644	4.421	.004	5.028	.004	−.293	.000
6	1023	1038.197	26.164	15.197	.015	28.288	.028	30.435	.030
7	1119	1124.328	16.484	5.328	.005	6.064	.005	9.640	.009
8	1164	1173.450	13.855	9.450	.008	5.844	.005	11.728	.010
9	1126	1136.715	24.125	10.715	.010	21.260	.019	27.318	.024
10	1200	1217.067	17.055	17.067	.014	14.508	.012	15.028	.013
11	1175	1177.974	22.917	2.974	.003	4.300	.004	2.155	.002
12	1306	1307.993	20.899	1.993	.002	1.116	.001	−3.758	.003
13	1355	1373.731	18.691	18.731	.014	18.332	.014	21.913	.016
14	1200	1212.092	27.118	12.092	.010	19.244	.016	16.043	.013
15	1449	1448.535	15.260	−.465	.000	5.224	.004	2.250	.002
16	1517	1510.359	20.319	−6.641	.004	.328	.000	−2.435	.002
17	1594	1590.469	27.695	−3.531	.002	9.852	.006	5.703	.004
18	1648	1655.374	20.124	7.374	.004	4.212	.003	15.532	.009
19	1838	1839.543	17.441	1.543	.001	1.648	.001	.520	.000
20	1664	1680.564	34.949	16.564	.010	29.380	.018	35.447	.021

Note: The values for Mean Estimate, SE, Bias, and Relative Bias are calculated over 30 independent samples, where each sample yields one estimate of the network measure

^aThe Standard Error is the standard deviation of the sampling distribution.

^bBias=E(estimates)−True Value

^cRelative Bias= |Bias/True Value|

Table A3.

Add Health Results: 25 Percent Sample, Distance

		Ego Network Configuration Model				Degree Model		Homophily Model
Net ID	True Value	Mean Estimate	SEa	Biasb	Relative Biasc	Biasb	Relative Biasc	Biasb	Relative Biasc
1	5.433	5.308	.195	−.125	.023	−.915	.168	−.770	.142
2	4.253	4.126	.083	−.127	.030	−.437	.103	−.370	.087
3	5.069	4.829	.122	−.240	.047	−.737	.145	−.611	.121
4	5.370	5.180	.150	−.190	.035	−.044	.194	−.754	.140
5	4.076	4.069	.086	−.008	.002	−.485	.119	−.369	.091
6	6.550	6.282	.216	−.268	.041	−1.559	.238	−1.130	.172
7	4.495	4.303	.094	−.192	.043	−.649	.144	−.548	.122
8	4.065	3.961	.073	−.104	.026	−.473	.116	−.425	.105
9	5.091	4.866	.108	−.224	.044	−.859	.169	−.728	.143
10	4.801	4.626	.105	−.176	.037	−.818	.170	−.596	.124
11	4.898	4.664	.104	−.234	.048	−.733	.150	−.619	.126
12	4.515	4.363	.069	−.152	.034	−.449	.099	−.415	.092
13	4.462	4.283	.085	−.179	.040	−.681	.153	−.532	.119
14	5.463	5.262	.145	−.201	.037	−.942	.172	−.797	.146
15	4.272	4.160	.058	−.113	.026	−.459	.107	−.394	.092
16	4.253	4.090	.058	−.163	.038	−.546	.128	−.440	.103
17	5.038	4.972	.098	−.067	.013	−.829	.164	−.447	.089
18	4.751	4.487	.088	−.264	.056	−.741	.156	−.667	.140
19	4.302	4.159	.041	−.143	.033	−.470	.109	−.384	.089
20	5.497	5.285	.103	−.212	.039	−.698	.127	−.625	.114

Note: The values for Mean Estimate, SE, Bias, and Relative Bias are calculated over 30 independent samples, where each sample yields one estimate of the network measure

^aThe Standard Error is the standard deviation of the sampling distribution.

^bBias=E(estimates)−True Value

^cRelative Bias= |Bias/True Value|

Table A4.

Add Health Results: 25 Percent Sample, 5 Step Reachability

		Ego Network Configuration Model				Degree Model		Homophily Model
Net ID	True Value	Mean Estimate	SEa	Biasb	Relative Biasc	Biasb	Relative Biasc	Biasb	Relative Biasc
1	.348	.380	.049	.032	.091	.224	.643	.195	.562
2	.801	.851	.024	.049	.061	.078	.098	.068	.085
3	.564	.649	.041	.085	.150	.230	.408	.196	.347
4	.464	.526	.049	.062	.133	.340	.732	.244	.526
5	.926	.932	.020	.006	.006	.047	.050	.040	.043
6	.233	.267	.034	.034	.146	.381	1.639	.227	.975
7	.775	.844	.029	.069	.090	.140	.181	.134	.173
8	.882	.924	.015	.042	.048	.063	.072	.065	.074
9	.565	.640	.038	.075	.133	.265	.469	.242	.428
10	.687	.746	.035	.058	.085	.221	.321	.174	.253
11	.610	.691	.037	.081	.133	.206	.338	.180	.294
12	.763	.812	.022	.049	.065	.108	.142	.101	.133
13	.800	.859	.024	.059	.074	.139	.173	.123	.154
14	.420	.492	.044	.072	.171	.313	.745	.265	.631
15	.881	.910	.016	.029	.033	.069	.078	.063	.071
16	.881	.924	.016	.043	.048	.082	.093	.073	.083
17	.591	.626	.033	.035	.059	.276	.466	.153	.260
18	.720	.824	.027	.104	.145	.203	.282	.193	.268
19	.882	.919	.012	.037	.042	.071	.080	.063	.072
20	.393	.440	.033	.047	.119	.202	.514	.177	.451

Note: The values for Mean Estimate, SE, Bias, and Relative Bias are calculated over 30 independent samples, where each sample yields one estimate of the network measure

^aThe Standard Error is the standard deviation of the sampling distribution.

^bBias=E(estimates)−True Value

^cRelative Bias= |Bias/True Value|

Table A5.

Add Health Results: 25 Percent Sample, Modularity

		Ego Network Configuration Model				Degree Model		Homophily Model
Net ID	True Value	Mean Estimate	SEa	Biasb	Relative Biasc	Biasb	Relative Biasc	Biasb	Relative Biasc
1	.697	.669	.025	−.027	.039	−.216	.310	−.173	.248
2	.526	.512	.022	−.014	.027	−.164	.312	−.117	.222
3	.658	.601	.021	−.057	.086	−.225	.342	−.157	.239
4	.696	.668	.019	−.028	.040	−.265	.380	−.122	.175
5	.569	.572	.032	.002	.004	−.256	.449	−.111	.195
6	.768	.730	.021	−.038	.050	−.274	.356	−.151	.196
7	.594	.560	.022	−.034	.057	−.243	.409	−.140	.236
8	.520	.519	.026	−.002	.003	−.206	.395	−.133	.255
9	.661	.617	.021	−.043	.066	−.257	.389	−.179	.270
10	.631	.608	.017	−.022	.036	−.264	.418	−.100	.159
11	.599	.576	.022	−.023	.038	−.204	.340	−.145	.242
12	.566	.505	.019	−.060	.107	−.195	.344	−.163	.289
13	.600	.585	.017	−.015	.025	−.270	.450	−.092	.153
14	.681	.647	.021	−.034	.050	−.244	.358	−.179	.263
15	.535	.513	.020	−.022	.041	−.204	.381	−.129	.241
16	.575	.534	.023	−.041	.072	−.262	.455	−.127	.221
17	.667	.652	.014	−.014	.021	−.290	.435	−.069	.103
18	.611	.560	.021	−.051	.083	−.263	.431	−.185	.304
19	.545	.517	.016	−.028	.052	−.227	.417	−.111	.203
20	.627	.603	.017	−.025	.039	−.174	.277	−.138	.221

Note: The values for Mean Estimate, SE, Bias, and Relative Bias are calculated over 30 independent samples, where each sample yields one estimate of the network measure

^aThe Standard Error is the standard deviation of the sampling distribution.

^bBias=E(estimates)-True Value

^cRelative Bias= |Bias/True Value|

Table A6.

Add Health Results: 25 Percent Sample, Transitivity

		Ego Network Configuration Model				Degree Model		Homophily Model
Net ID	True Value	Mean Estimate	SEa	Biasb	Relative Biasc	Biasb	Relative Biasc	Biasb	Relative Biasc
1	.174	.218	.022	.044	.251	−.167	.957	−.154	.884
2	.132	.140	.018	.008	.061	−.123	.930	−.115	.876
3	.180	.168	.023	−.012	.069	−.173	.964	−.163	.908
4	.206	.202	.018	−.004	.022	−.199	.968	−.185	.899
5	.175	.207	.018	.031	.179	−.166	.950	−.155	.885
6	.265	.257	.032	−.007	.028	−.261	.986	−.253	.955
7	.168	.191	.017	.022	.132	−.161	.956	−.152	.903
8	.153	.180	.015	.027	.179	−.143	.937	−.134	.878
9	.188	.206	.019	.018	.098	−.182	.968	−.172	.916
10	.183	.198	.017	.015	.082	−.177	.963	−.166	.905
11	.151	.180	.021	.029	.190	−.144	.958	−.136	.903
12	.132	.140	.017	.008	.057	−.126	.954	−.120	.907
13	.186	.183	.022	−.002	.013	−.178	.960	−.168	.906
14	.202	.213	.019	.011	.056	−.197	.976	−.189	.934
15	.141	.162	.016	.021	.151	−.134	.953	−.127	.901
16	.140	.158	.014	.019	.135	−.133	.950	−.122	.872
17	.161	.185	.016	.024	.148	−.156	.970	−.137	.849
18	.178	.191	.019	.013	.074	−.173	.969	−.164	.918
19	.141	.147	.013	.007	.049	−.135	.961	−.129	.921
20	.138	.148	.017	.010	.074	−.134	.973	−.130	.944

Note: The values for Mean Estimate, SE, Bias, and Relative Bias are calculated over 30 independent samples, where each sample yields one estimate of the network measure

^aThe Standard Error is the standard deviation of the sampling distribution.

^bBias=E(estimates)-True Value

^cRelative Bias= |Bias/True Value|

Table A7.

Add Health Results: 25 Percent Sample, Proportion 102 Triad

		Ego Network Configuration Model				Degree Model		Homophily Model
Net ID	True Value	Mean Estimate	SEa	Biasb	Relative Biasc	Biasb	Relative Biasc	Biasb	Relative Biasc
1	.011	.011	.001	.000	.006	.000	.004	.000	.000
2	.018	.018	.001	.000	.000	.000	.006	.000	.015
3	.014	.014	.000	.000	.005	.000	.019	.000	.008
4	.013	.013	.001	.000	.003	.000	.011	.000	.015
5	.020	.020	.001	.000	.011	.000	.008	.000	.020
6	.010	.010	.000	.000	.009	.000	.005	.000	.003
7	.016	.016	.001	.000	.003	.000	.012	.000	.013
8	.019	.019	.001	.000	.006	.000	.016	.000	.004
9	.012	.012	.000	.000	.001	.000	.001	.000	.004
10	.014	.014	.000	.000	.009	.000	.012	.000	.001
11	.012	.012	.000	.000	.002	.000	.002	.000	.016
12	.012	.012	.000	.000	.001	.000	.008	.000	.001
13	.015	.015	.000	.000	.010	.000	.003	.000	.014
14	.009	.009	.000	.000	.002	.000	.000	.000	.005
15	.014	.014	.000	.000	.006	.000	.006	.000	.009
16	.015	.015	.000	.000	.012	.000	.005	.000	.002
17	.010	.010	.000	.000	.001	.000	.007	.000	.000
18	.011	.011	.000	.000	.003	.000	.004	.000	.005
19	.012	.012	.000	.000	.002	.000	.002	.000	.007
20	.006	.006	.000	.000	.000	.000	.003	.000	.001

Note: The values for Mean Estimate, SE, Bias, and Relative Bias are calculated over 30 independent samples, where each sample yields one estimate of the network measure

^aThe Standard Error is the standard deviation of the sampling distribution.

^bBias=E(estimates)-True Value

^cRelative Bias= |Bias/True Value|

Table A8.

Add Health Results: 25 Percent Sample, Proportion 300 Triad

		Ego Network Configuration Model				Degree Model		Homophily Model
Net ID	True Value	Mean Estimate	SEa	Biasb	Relative Biasc	Biasb	Relative Biasc	Biasb	Relative Biasc
1	.351	.431	.055	.080	.229	−.335	.957	−.310	.885
2	.622	.652	.096	.030	.048	−.579	.931	−.546	.878
3	.469	.438	.061	−.031	.067	−.452	.965	−.426	.909
4	.507	.492	.064	−.015	.030	−.491	.969	−.457	.902
5	.898	1.035	.107	.137	.153	−.854	.951	−.798	.889
6	.319	.318	.046	−.001	.004	−.315	.986	−.305	.955
7	.599	.672	.080	.073	.122	−.573	.957	−.542	.905
8	.774	.895	.100	.121	.156	−.727	.938	−.680	.879
9	.375	.412	.045	.037	.097	−.363	.968	−.344	.916
10	.504	.548	.051	.044	.087	−.486	.964	−.456	.904
11	.302	.358	.048	.056	.187	−.289	.957	−.273	.906
12	.275	.290	.038	.014	.052	−.263	.955	−.250	.907
13	.565	.546	.073	−.019	.034	−.542	.960	−.513	.909
14	.256	.269	.027	.013	.050	−.250	.976	−.240	.935
15	.384	.439	.048	.055	.142	−.366	.953	−.347	.902
16	.424	.467	.043	.043	.103	−.403	.951	−.369	.872
17	.219	.251	.026	.032	.146	−.212	.971	−.186	.848
18	.309	.328	.031	.019	.062	−.299	.970	−.283	.917
19	.267	.279	.028	.012	.046	−.256	.961	−.246	.922
20	.070	.076	.010	.005	.077	−.069	.973	−.067	.945

Note: The values for Mean Estimate, SE, Bias, and Relative Bias are calculated over 30 independent samples, where each sample yields one estimate of the network measure. Estimates, SE, and bias values are 10⁻⁵

^aThe Standard Error is the standard deviation of the sampling distribution.

^bBias=E(estimates)−True Value

^cRelative Bias= |Bias/True Value|

Appendix B. Estimated ERGM Coefficients: Add Health Networks

In this appendix section, I present a table of ERGM parameter estimates from the Add Health analysis (25 percent sample). I compare the true coefficients estimated on the full network to the coefficients found during the simulation procedure. I limit the table to the GWESP coefficient. I focus on GWESP as it offers a particularly telling inferential problem. For the GWESP coefficient in the simulation is updated to minimize the chi square value, where the chi square value is low when the ego network configurations in the simulated network match the empirical distribution. The GWESP term, in contrast, measures the shared partner distribution; the coefficient in the simulation is therefore updated without explicitly considering what GWESP actually measures.

I take all of the Add Health networks and compare the true GWESP coefficients to the simulation GWESP coefficients. The true GWESP coefficients are estimated on the full network, conditioned on the other terms in the model. The simulation GWESP coefficients are taken from the best set of coefficients for each iteration (for each school).

I present the results in the table below, where the Add Health networks offer a somewhat muddled picture: for about half of the networks the true GWESP coefficient falls in the interval of the simulated values; for the other half, the simulation coefficients are clearly higher than the true coefficient. This suggests that the simulation coefficients do not necessarily map onto the ERGM estimates, although the coefficients from the simulations are generally close to the true values.

Table A9.

Comparing True GWESP Coefficients to Simulation GWESP Coefficients: Add Health Networks

	GWESP: True Value	GWESP: from Simulation
Net ID		Min	Median	Max
1	1.059	1.160	1.353	1.569
2	1.035	.908	1.109	1.289
3	1.190	.898	1.227	1.445
4	1.217	1.099	1.272	1.346
5	1.248	1.281	1.505	1.689
6	1.526	1.388	1.580	1.790
7	1.268	1.279	1.435	1.633
8	1.188	1.270	1.417	1.617
9	1.290	1.247	1.447	1.619
10	1.287	1.248	1.441	1.642
11	1.157	1.120	1.361	1.555
12	1.182	1.014	1.275	1.533
13	1.283	1.302	1.525	1.736
14	1.381	1.315	1.494	1.652
15	1.192	1.166	1.408	1.596
16	1.088	1.132	1.350	1.573
17	1.060	1.071	1.268	1.452
18	1.301	1.338	1.541	1.712
19	1.368	1.263	1.463	1.639
20	1.321	1.274	1.432	1.636

Appendix C. Estimated ERGM Coefficients: Known Model Analysis

In this appendix, I test my method on a network generated from a known, or “true”, model, testing whether my model can reproduce the parameters of the known model. I specifically use a model based on the degree distribution, mixing terms (for race and education) and GWESP to generate the test network. Thus, the only processes affecting the network are clustering and homophily. I set the GWESP coefficient to 1.2 and use a network of size 1000 as my test case. I take 10 percent, 20 percent, and 30 percent random samples from the network and use that as the input into my method. I then check if the simulation approach captures the true, known value for GWESP.

I present the results below. My simulation approach performs quite well, with accurate estimates of the true GWESP coefficient. The mean estimate for the coefficient is 1.199 under 20 percent sampling, with a standard deviation of .095. The bias is thus only −.001 under 20 percent sampling. The results for the 10 percent sampling are predictably worse than the 20 percent or 30 percent results but even here the bias is only 10 percent of the true coefficient.

Table A10.

Estimated GWESP Coefficients for Known Model Analysis

		Biasa			SEb
Statistic	True Value	10 Percent Sample	20 Percent Sample	30 Percent Sample	10 Percent Sample	20 Percent Sample	30 Percent Sample
GWESP Coefficient	1.2	.129	−.001	−.015	.144	.095	.086

Note: The values for Bias and SE are calculated over 30 independent samples, where each sample yields one estimate of the network measure. All estimates come from the ENC model.

^aBias=E(estimates)−True Value.

^bThe Standard Error is the standard deviation of the sampling distribution.