Spatiotemporal receptive fields of barrel cortex revealed by reverse correlation of synaptic input

Abstract

Of all sensory areas, barrel cortex is among the best understood in terms of circuitry, yet least understood in terms of sensory function. We combined intracellular recording in rats with a novel multi-directional multi-whisker stimulator system to estimate receptive fields by reverse correlation of stimuli to synaptic inputs. Spatiotemporal receptive fields were identified orders of magnitude faster than by conventional spike-based approaches, even for neurons with little spiking activity. Given a suitable stimulus representation, a linear model captured the stimulus-response relationship for all neurons with surprisingly high accuracy. In contrast to conventional single-whisker stimuli, complex stimuli revealed dramatically sharpened receptive fields, largely due to adaptation. This phenomenon allowed the surround to facilitate rather than suppress responses to the principal whisker. Optimized stimuli enhanced firing in layers 4-6 but not 2/3, which remained sparsely active. Surround facilitation through adaptation may be required for discriminating complex shapes and textures during natural sensing.

The rodent barrel cortex has become a popular model system for diverse neuroscience studies ranging from tactile sensation, sensorimotor integration, structural and functional plasticity, cortical development, to neurological disease. Perhaps surprisingly, the sensory properties of barrel cortex neurons have remained mysterious. For technical reasons, most previous studies have investigated response properties by isolated deflections of single facial whiskers^1-6. Barrel cortex neurons may, however, be highly sensitive to multi-whisker stimuli involving complex interactions of space, time, and direction of whisker movement. During exploration, a rodent contacts objects simultaneously with multiple whiskers^7,8 and discriminates object textures, shapes, and locations with psychophysical thresholds similar to humans with their fingertips⁹. The importance of multi-whisker integration is further suggested by the axons of pyramidal neurons spanning multiple cortical columns, and in some cases the entire barrel field¹⁰. How do neurons in barrel cortex respond to spatiotemporally complex stimuli?

Studies using single-whisker stimuli have concluded that the surround receptive field is largely suppressive, with stimulation of the central principal whisker alone being an equally or more potent driver of neural activity than co-stimulation of the principal whisker and surrounding whiskers^11-15. Facilitatory surrounds have been noted only in a minority of cells under specific conditions, such as short delays between whisker deflections^16,17. Several groups have applied complex multi-whisker stimuli^13,14,17,18 but had to predict in advance the relevant stimulus dimensions. An alternative approach with a long history in the visual and auditory systems is “reverse correlation”, mathematically deducing a neuron’s receptive field from its responses to a set of random stimulus patterns sampled from a large space of relevant dimensions¹⁹.

When the dimensionality of a stimulus space is high, a large number of spikes are required to identify the receptive field. However, many neurons in the cortex have low firing rates²⁰, and sparse firing has been well documented in barrel cortex under a variety of conditions, including anesthesia, sedation, quiet wakefulness, and active behavior^21,22. Indeed, a recent study found that, even when focusing on the most active layers of barrel cortex, only one quarter of all extracellular recordings discharged a sufficient number of spikes for reverse correlation²³. Seemingly silent neurons may reflect overall sparse firing among neurons or experimental inability to identify the optimal stimuli for highly selective neurons²⁰.

Here, we overcome these low firing rates to study receptive fields by recording intracellularly, gaining access to information contained in the subthreshold synaptic inputs normally hidden to extracellular recording. Combining this with a novel multi-whisker stimulator system that moves 9 whiskers independently in any direction allowed exploration of a vast stimulus space. Our method identified spatiotemporal receptive fields (STRFs) even for neurons with little or no spiking activity, orders of magnitude faster than conventional spike-based approaches. Surprisingly, given a suitable stimulus representation, the response of a neuron could be captured by a simple model where responses to movements of different whiskers add linearly. In contrast to conventional single-whisker stimuli, complex stimuli revealed dramatically sharpened receptive fields, largely due to the effects of adaptation. Under these conditions, the surround facilitated rather than suppressed responses to the principal whisker. This switch in spatiotemporal receptive fields may be essential for discriminating complex shapes and textures during natural sensing.

Results

Subthreshold stimulus-response model

We performed whole-cell recordings from the barrel cortex of rats, administered local anesthetics and a sedative, which better approximate wakefulness than general anesthesia does²¹. The receptive field center or “principal whisker” (PW) and eight surround whiskers (SWs) simultaneously received spatiotemporally complex stimuli (Fig. 1a, left) via piezo-electric actuators that could move in arbitrary angles and at speeds up to 2200°/sec. This system allowed exploration of a greater amount of the stimulus space than multi-whisker stimulator systems used in previous studies, which were often restricted to motion along a single axis^18,23. Each of the nine whiskers was stimulated with high-velocity deflections of fixed temporal structure (5-ms rise and 5-ms decay; Supplementary Fig. 1a), mimicking the stick-slip events known to occur during natural contact with surfaces⁷. Deflections occurred stochastically in time at a frequency of ~9.1 Hz, similar to natural whisking frequencies⁸, as well as in arbitrary directions (“complex multi-whisker stimulation”; Fig. 1a, right). Thus, our paradigm had naturalistic features while still exploring the stimulus space thoroughly.

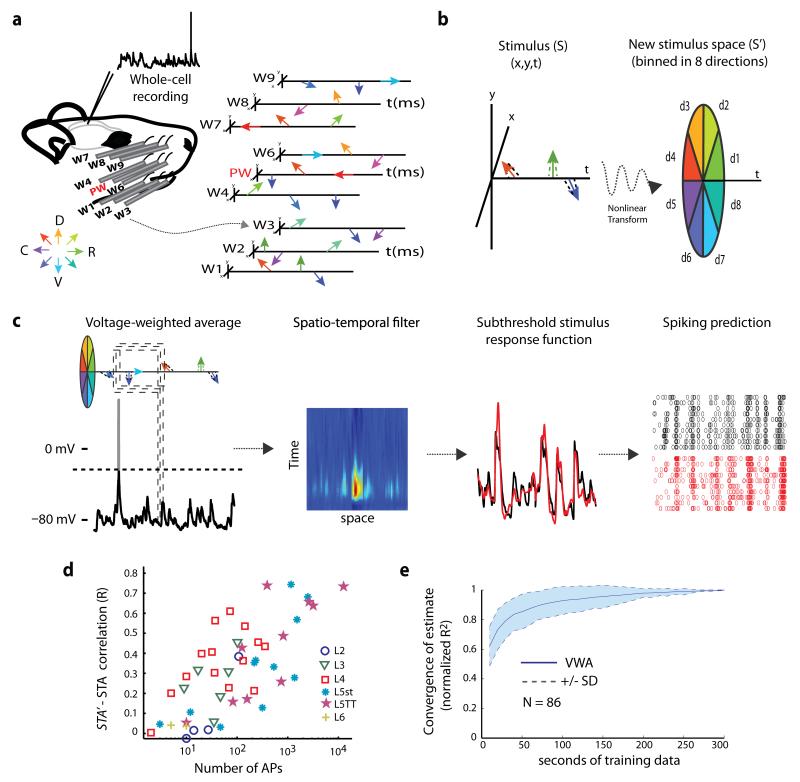
Figure 1. Reverse correlation of intracellular recordings can rapidly and accurately identify spatiotemporal receptive fields (STRFs).

a, Schematic of the experimental setup. Left, barrel cortex neurons were recorded intracellularly during complex multi-whisker stimulation (sparse noise) to 9 whiskers. Right, schematic of complex multi-whisker stimulation. Arrows represent independent deflections of 9 whiskers. Deflections occur stochastically in time and direction (any of 360°). b, Nonlinear stimulus representation. Whisker movements are represented in an 8 angle-binned space instead of Cartesian space. c, The voltage-weighted average (VWA) of stimulus patterns estimates the spatiotemporal filter (K) for an individual neuron. The accuracy of the spatiotemporal filter is tested by predicting the response of the neuron to novel stimuli (cross-validation). The filter accurately predicts both the subthreshold response of the neuron as well as the spiking response. d, The relationship between the VWA and the STA is plotted as the correlation coefficient (R) between the predicted STA (STA’) and the true spike-triggered average (STA). The STA’ is the prediction calculated using the VWA and the appropriate noisy-threshold operation. As the number of spikes used for STA estimation increases, the mean correlation between the STA’ and STA becomes stronger, irrespective of laminar location or cell type of the recorded neuron. e, The speed of convergence for the VWA as a function of the amount of amount of data (seconds) used to train the model. The plot is on population data, dashed lines and shaded areas represent ± 1 SD.

We initially investigated models in which responses were a nonlinear function of the stimulus (further discussed below). Surprisingly, we ultimately found that response variance was best explained by a model in which responses were a linear function of the stimulus, but after a nonlinear stimulus transform (an input nonlinearity model²⁴). The stimulus, initially represented as the x-y positions of each stimulator over the last 100 msec (the “X-Y” representation), was transformed into an “8-directional” representation using 45° bins (Fig. 1b; Supplementary Fig. 1a). This new stimulus representation, in which each directional bin is an independent stimulus with no explicit relationship to other directions, is similar to the sensory transformation occurring at the whisker follicles, where individual primary afferents innervate a limited circumference of a follicle and are consequently tuned to a limited range of directions²⁵.

Because the stimuli are uncorrelated with regard to whisker and time, the relationship between the stimulus and instantaneous membrane potential can be computed as the voltage-weighted average stimulus (VWA, Fig. 1c), an intracellular analogue of the classic spike-triggered average stimulus (STA). The VWA yields the neuron’s filter, an estimate of its subthreshold spatiotemporal receptive field, illustrated as a matrix of 72 possible spatial dimensions (9 whiskers × 8 directional bins) by 100 1-ms time bins (Fig. 1c, left). Its dot product with the stimulus vector predicts the instantaneous voltage, which can also be used to infer spiking responses (Fig. 1c, right).

We measured the trial-to-trial variability and spike-threshold experimentally for neurons that fired at least 1 spike during stimulation (53/86) and predicted the average spiking response by applying the appropriate noisy-threshold operation to the VWA (Supplementary Fig. 1b). Applying a spike threshold nonlinearity to the membrane potential in the presence of substantial trial-to-trial variability (noise) results in an established power law relationship²⁶. The predicted STA of the noisy-threshold model (STA’) was, on average, only weakly correlated with the actual STA calculated from spikes (0.323 ± 0.242). However, many of our neurons fired sparsely throughout the recording (31/57 fired < 100 spikes), possibly causing STAs to poorly estimate their receptive fields. Indeed, the correlation of STA’ and STA was proportional to cells’ firing rates, being strongest for highly active neurons (Fig. 1d). The VWA therefore provides an effective surrogate for the STA and may be used to obtain accurate receptive field estimates for neurons in all layers, even for low firing rates or high noise.

Finally, the VWA provides an additional advantage over the STA: speed. Under a conservative estimate of 1000 spikes to accurately estimate receptive fields, most neurons would require prohibitively long recording times to produce a sufficient number of spikes. Median firing rates throughout the period of complex multi-whisker stimulation were 0.057 (L2), 0.03 (L3), 1.01 (L4), 0.84 (L5 slender-tufted), 8.86 (L5 thick-tufted), and 0.02 Hz (L6). The least active neurons, such as in L2/3, would require ~7 hours of recording for STA estimation. By contrast, the VWA converges after 200 seconds of recorded data for all neurons, irrespective of laminar location, and reaches 80% of that estimate within 30 seconds (Fig. 1e, N = 86). Subthreshold estimation is therefore highly efficient, providing in minutes a receptive field that would otherwise take hours of spike recording. This further allows receptive fields to be determined online and immediately played back.

Linearity of cortical responses in S1

We calculated subthreshold spatiotemporal filters for 86 neurons. Model accuracy was tested by using the filters to predict neuronal responses to novel stimuli not used in filter calculations (cross-validation). The linearized model predicted subthreshold responses with an average accuracy (R²) of 0.488 ± 0.149 (mean ± SD) throughout the depths of a cortical column (Fig. 2a, red lines). The highest R² values occurred at depths of 500-900 μm (0.513 ± 0.126) corresponding to lower layer 3 (L3) and upper layer 4 (L4), and at depths of 1400-1800 μm (0.605 ± 0.126) corresponding to layer 6 (L6). The worst performance occurred at depths of 200-600 μm (0.473 ± 0.121) corresponding to layers 2/3 (L2/3), and at depths of 1000-1400 μm (0.331 ± 0.155) corresponding to layer 5 (L5).

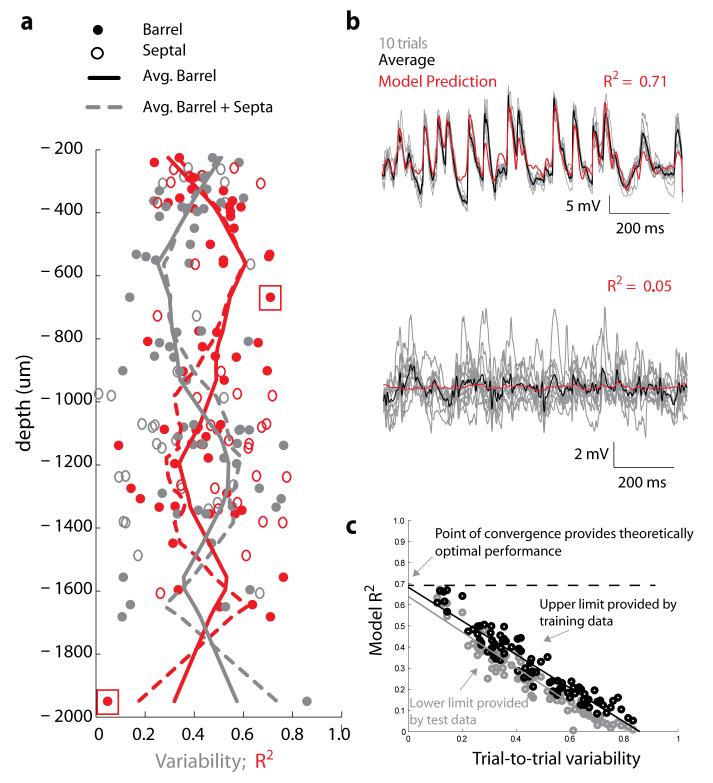
Figure 2. Linearized model captures a majority of the predictable synaptic input for neurons in all layers of S1.

a, Depth dependent relationship of the model performance and neural variability. Model performance (red) – defined as the cross-validated prediction of the VWA on trial averaged responses; – and neural variability (grey) – defined as the trial-to-trial variability between repeated presentations of identical stimuli, are plotted as a function of recording depth for each neuron. There is an inverse relationship between the model performance and neural variability in all neurons and layers. b, Responses of a neuron to ten repetitions of the same stimulus (gray traces) to illustrate neural variability along with the average response (blue) and predicted response (red). The two examples correspond to the data points inside red boxes in 2A, and represent examples of neurons with high prediction quality and low variability (top) and low prediction quality and high variability (bottom). c, The model performance (R²) tested on single-trial responses using training data (black) and cross-validation/test data (grey) is plotted against the trial-to-trial variability for each neuron. Convergence of the test-performance and training-performance at zero variability between an R² of 0.64 and 0.68.

In the visual and auditory systems, L2/3 and L5 have been reported to exhibit more nonlinear behavior than L4 (ref ^27,28). The drop in model performance in L2/3 and L5 might simply reflect inability of the linearized model to capture such nonlinearity. Alternatively, these layers might simply have more variable responses and neural noise. While background synaptic inputs may be behaviorally relevant, neural variability is noise with regard to the model and cannot be predicted from the stimulus. To determine whether noise accounts for weaker prediction of L2 and L5 activity, we measured the trial-to-trial variability of responses (Fig.2a, gray line) to repeated trials of identical stimuli (frozen noise; Fig. 2b). This measure estimates the fraction of neural response variance attributable to noise, with the sensory stimulus driving the remainder, the predictable variance. The model captured less response variance in L2/3 and L5, where the variability was correspondingly higher, than in other layers (Fig. 2a). As a result, the fraction of predictable variance captured by the model was not significantly different between layers (p = 0.36, ANOVA) and was remarkably high for all neurons (0.729 ± 0.207).

For each neuron, we plotted the performance of the model on training data and testing data against the trial-to-trial variability (noise) of the neuron (Fig. 2c). Extrapolating the regressions of both data sets to the y-intercept gives the predicted performance of the model under conditions of zero-noise, here between an R² of 0.64 and 0.68 (Fig. 2c). These metrics, while intuitive, are known to potentially overestimate trial-to-trial variability and, conversely, underestimate performance due to noise²⁹. However, unbiased estimators²⁹ yielded a similar upper bound of predictable variance of 0.75 ± 0.06 and a lower bound of 0.58 ± 0.03 (Supplementary Fig. 2).

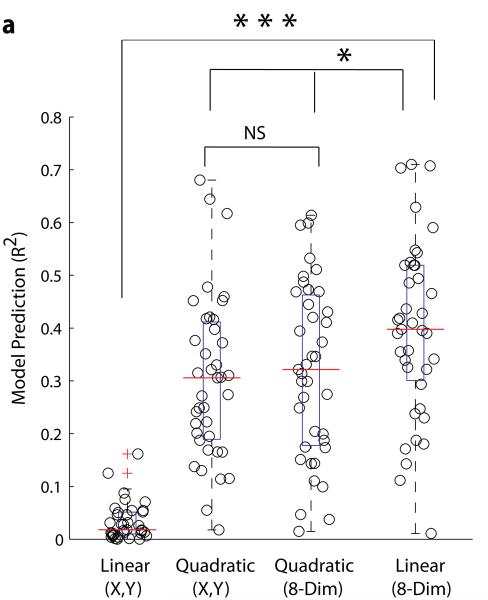
Prediction by a quadratic model, widely used in reverse correlation studies, was also checked. Such models should capture nonlinear interactions between whiskers. Predictions of responses to novel stimuli were calculated for linear and quadratic models in the X-Y space (X,Y) or the 8-dimensional (8-Dim) stimulus transformed space (Fig. 3a; n = 39 cells). The linear model in the X-Y space was inadequate (mean R² 0.034 ± 0.0362, median 0.0179), and the quadratic model performed far better (mean R² 0.303 ± 0.155, median 0.306). One might interpret this as evidence of strong non-linear interactions between whiskers, but linear models are constrained to produce equal and opposite responses along a stimulus dimension (X or Y) and will fail for neurons driven equally by opposing directions (e.g., 0° and 180°). Indeed, the quadratic model given an 8-dimensional representation is not significantly better (mean R² 0.319 ± 0.165; p = 0.65, t-test), demonstrating that the main nonlinearity captured here by the quadratic model relates to directional tuning, rather than whisker interactions. In fact, the linear model in the 8-dimensional representation (mean R² 0.397 ± 0.167, median 0.398) outperformed the quadratic models (p = 0.01, 0.04; t-tests), suggesting that the linear model is a sufficient and parsimonious description of neural responses and that the more complex quadratic model is prone to fitting noise. Prediction was unaffected by rotating the directional bins of the 8-dimensional representation, indicating that cardinal directions play no special role in barrel cortex coding and that the level of directional discretization used in our model is adequate (Supplementary Fig. 3). Furthermore our linear model was successful over a substantial range of whisker deflection frequencies, demonstrating model robustness across conditions (Supplementary Fig. 4). Linear approaches are further appealing, being simple to calculate and producing filters (receptive fields) that are visually intuitive and biologically interpretable.

Figure 3. Comparison of models.

a, In order to verify the superiority of the stimulus-transformed linear model over other linear and nonlinear models (quadratic regression), we compared the performance of these different models on a subset of neurons (N=39). For the four models, calculated either in the (x,y) space or the 8 dimensional stimulus transformed space (8-dim) we show jitterplots and boxplots of the cross-validated prediction, R². The red line indicates median values. The linear model in the (x,y) space had an R² 0.0340 ± 0.0362 and a median value of 0.0179, and performed significantly worse than the linear model in the 8-Dim representation (p-value < 0.001, t-test). The quadratic regression in the (x,y) space had an R² 0.303 ± 0.155 and a median value of 0.306. The quadratic regression in the 8-Dim representation had an average R² of 0.319 ± 0.165, a median value of 0.322, and did not perform significantly better than the quadratic regression in the (x,y) space (p-value = 0.65, t-test). The linear model in the 8-Dim representation performed significantly better than the quadratic (x,y) and the quadratic 8-Dim (p-values = 0.0113, 0.0416 respectively; t-test) and had an average R² of 0.397 ± 0.167.

Spatiotemporal receptive fields in S1

Having validated the linear model, we analyzed the filters, which are an estimate of the spatiotemporal receptive field. For each STRF, time preceding neural activity is represented on the y-axis, and whisker identities and angles are represented on the x-axis (Fig. 4a). Metrics such as latency, angular tuning, receptive field size, degree of excitation and inhibition, directional consistency of the whiskers, and inter-whisker temporal relationships can be extracted from this single plot. Whiskers are ordered from whisker 1 (W1) through 9 (W9) with the PW in the center. Each whisker is represented by eight columns corresponding to the eight angle bins (0-45°, 46-90°, and so on).

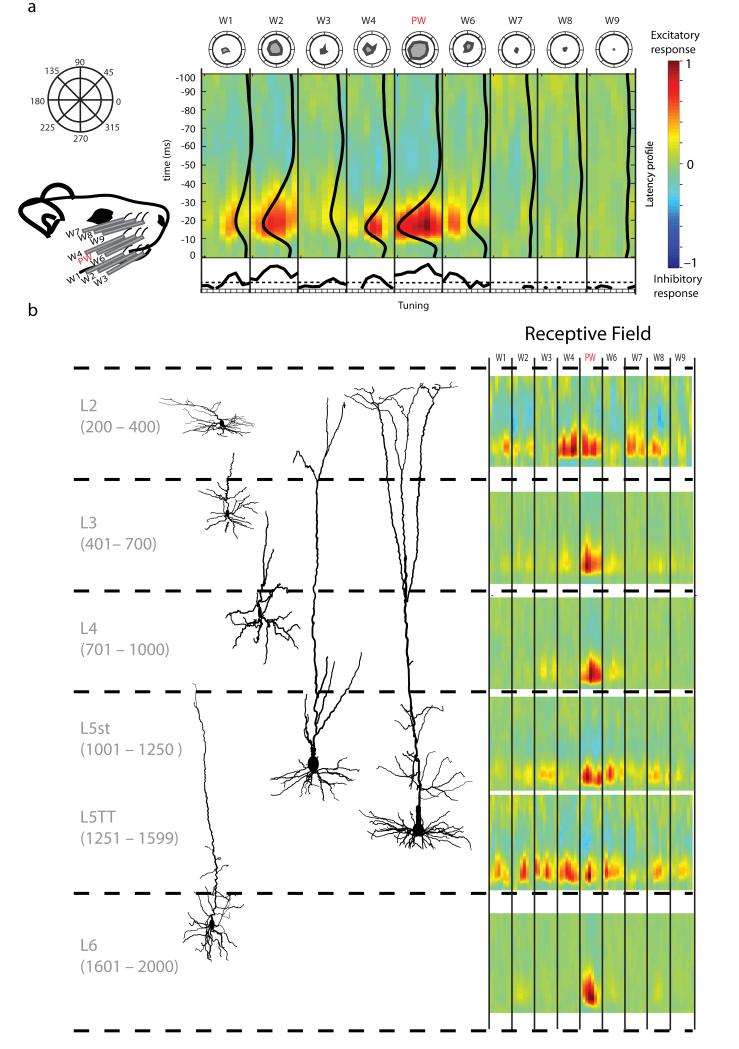
Figure 4. Example whisker spatiotemporal receptive fields (STRFs) for morphologically identified cells across layers.

a, Left top, the pinwheel corresponds to 8 angle bins used to represent the tuning of the individual whiskers. Left bottom, schematic of the 9 whisker stimulators arranged on the rat’s face with the PW in the center and 8 SWs. Middle, a representative STRF for a layer 5 slender tufted (L5st) neuron. Each whisker contains 8 columns corresponding to movement in one of the 8 angle bins. Collapsing over time reveals the angular tuning for each whisker (bottom, dashed lines represent 99% significance) and is equivalent to unwrapping the polar plots of the same data (top). Collapsing over space reveals the average latency of response for each neuron, illustrated by the 9 black vertical curves overlying the STRF. b, Example STRFs for morphologically identified and reconstructed neurons from each layer.

STRFs were normalized for each neuron so the maximum excitatory excursion from baseline is red and an equally large inhibitory excursion would be blue. The example neuron (Fig. 4a) responds predominantly to 5 whiskers, the PW, W2, W4, W6 and W1, in that order, and weakly to W3. The tuning for the PW and W2 is broad, peaking at 270° and 180°, respectively. Conversely, W1, W4, and W6 have comparatively sharper tuning, with peaks at 270°, 225°, and 90°. The vector strength for these 5 whiskers, a measure of the consistency of preferred directions across whiskers, is 0.48 (0: no consistency, 1: perfect consistency). Subtle timing differences suggest that the best combination of stimuli for this neuron is to move W1, W2, and W6 simultaneously, followed 2 milliseconds later by the PW and W4.

We examined the STRFs for all neurons that could be unambiguously identified morphologically and classified according to cell type and laminar location (N = 71). Cells were classified into six excitatory types: L2 (N = 9), L3 (N = 14), L4 (N = 13), layer 5 slender-tufted neurons (L5st) (N = 16), layer 5 thick-tufted neurons (L5TT) (N = 11), and L6 (N = 8). Reconstructions and STRFs for example cells are shown in Fig. 4b. Simple single-whisker receptive fields are seen predominantly in L4, L3, and L6, while more complex multi-whisker receptive fields are seen in L2, L5st, and L5TT cells. Strong inhibition was seldom seen, and inhibitory excursions were generally weaker and longer lasting than excitatory excursions.

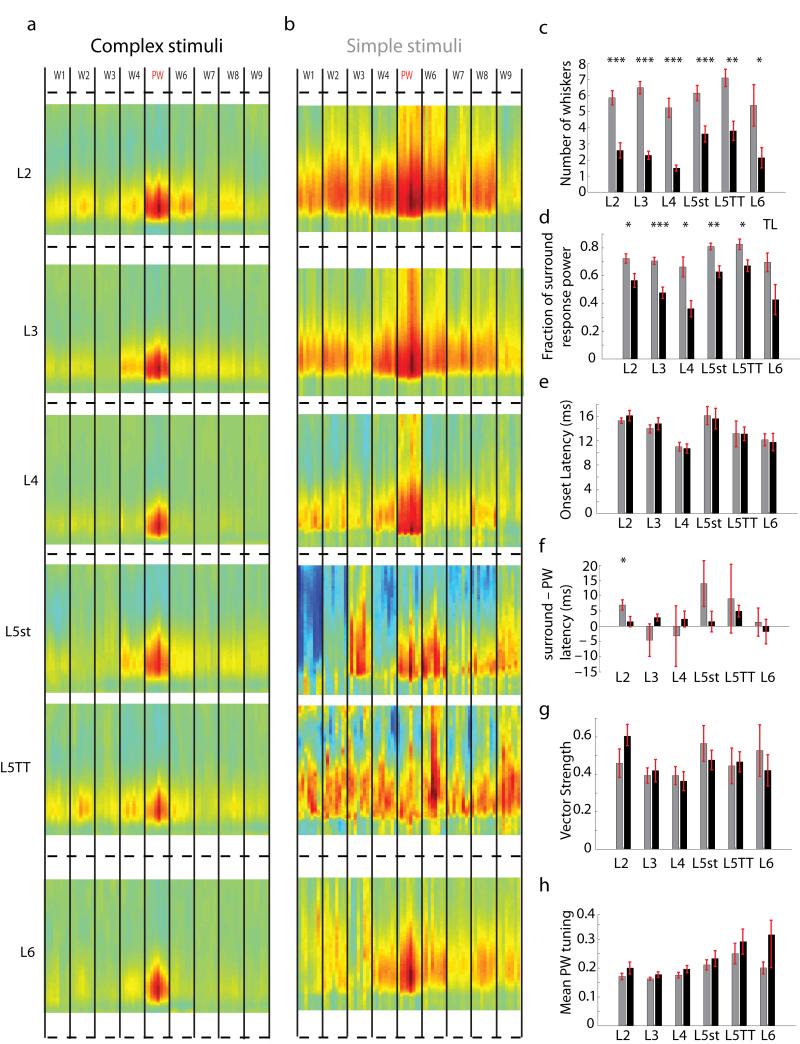
STRFs were averaged according to layer and cell type. To our surprise the PW was overwhelmingly the strongest stimulus for neurons in all layers (Fig. 5a), and the temporal structure of the RF was similar across neurons and layers (i.e., low rank; Supplementary Fig. 5). This contrasts starkly with previous reports of ubiquitous broad subthreshold responses spanning multiple whiskers^1-4. Previous studies, however, inferred receptive field size by overlaying the activity measured from individual whiskers stimulated in isolation with substantial inter-trial intervals^1-5. STRFs of neurons calculated from such conventional, sequentially-presented single-whisker stimuli (Fig. 5b) were strikingly different from their STRFs obtained using complex stimuli (Fig. 5a). In particular, STRFs measured using simple stimuli were broad in all layers, especially for L2 and L5TT cells as observed previously^1,2, unlike STRFs for complex stimuli.

Figure 5. Complex stimuli reveal dramatically sharpened receptive fields relative to conventional stimuli.

Population averaged STRFs were calculated for neurons of the same cell type. a, Population STRFs based on complex multi-whisker stimuli. b, Population STRFs simple single-whisker stimulation for the same neurons as in A. c – h, Receptive field properties for complex (black) versus simple (gray) stimuli (* p < 0.05; ** p < 0.01; *** p < 0.001; TL, p < 0.1; all tests were non-parametric two sided rank-sum test). Bars, means ± SEM. c, Adapted STRFs had significantly fewer responsive whiskers than unadapted STRFs. d, For adapted STRFs the total fraction of the response power contained in the surround receptive field was significantly less than in unadapted neurons. e, Onset latency of the receptive field (usually, but not always, the onset of the PW response) was unchanged between groups. f, The average latency between the onset of the PW response and the mean onset of the SW responses was shortened for adapted STRFs, and was significant in L2 (p<0.05, t-test). g, The vector strength, a measure of coherence or directional similarity between significantly responsive whiskers, was highest in infra and supra-granular layers but was unchanged between simple stimuli and complex stimuli (0 anti-coherent, 1 perfectly coherent). h, Directional tuning of the PW, defined as strength of response to the preferred direction divided by the summed response to all directions, was always higher during complex stimuli but results were not significant (0.125 = no tuning preference; 1.0 = tuned to a single direction).

Complex multi-whisker stimuli shrunk STRFs, both in number of whiskers eliciting responses (Fig. 5c) and fraction of response power accounted for by the surround (Fig. 5d). Asymmetric surrounds, potentially resulting from asymmetric cross-whisker inhibitory effects^11,12, were absent in complex stimulus filters (Supplementary Figs. 6 and 7). Response onset latencies were similar for simple versus complex stimuli (Fig. 5e). On the other hand, complex stimuli predict that neurons’ maximal responses should result from PW deflections lagging surround deflections by only a few milliseconds (Fig. 5f, black). This timescale mirrors instances of facilitation seen previously in minorities of cells^16,17. The consistency of preferred directions across significantly responsive whiskers was moderate in all layers (Fig. 5g; ref ⁶). Directional correspondence of center and surround whiskers spanned a broad range, indicating that neurons are not exclusively tuned to correlated or antagonistic surrounds (Supplementary Fig. 7c). PW directional tuning was sharpest in deep layer neurons, particularly L5TT and L6, yet unaffected by the use of simple vs complex stimuli (Fig. 5h).

Facilitatory surrounds through adaptation

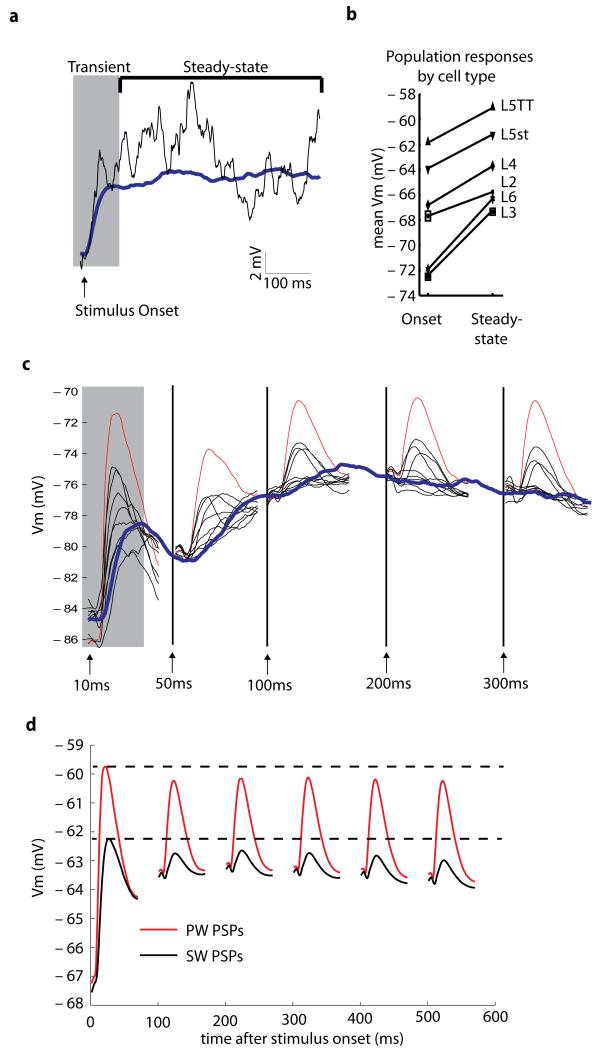
While simple single-whisker stimuli are brief isolated events, complex multi-whisker stimuli engage the whiskers in a sustained and continuous fashion. Adaptation to sustained stimuli could potentially explain the reduction in RF size seen during complex multi-whisker stimulation. To examine the underlying membrane potential dynamics involved in the adaptation process, we averaged responses of neurons across many trials of complex multi-whisker stimuli (Fig. 6a). Trial-averaged responses showed clear stimulus-onset transients and tonic sustained depolarizations of 1-5 mV for all neurons and layers (Fig. 6b). Both PW and SW deflections at the beginning of a trial induced large depolarizations relative to baseline (Fig. 6c). As the neuron adapted to the stimulus and reached a steady state in the mean membrane potential, both the PW and SW post-synaptic potentials (PSPs) became smaller, and SW PSPs were often no longer able to drive responses above the steady-state voltage (Fig. 6c). SW responses adapted far more than PW responses (Fig. 6d; PW: 9.02 ± 4.98 vs 6.23 ± 3.62 mV, SW: 3.06 ± 2.64 vs 0.811 ± 0.526 mV), leading to the overall sharpening of the receptive field (Fig. 5).

Figure 6. Neural adaptation underlying receptive field changes.

a, The trial averaged response of a neuron over 300 unique trials of complex stimulus (blue) and the response to a single trial (black) reveals a strong stimulus transient and tonic depolarization that is dependent on stimulus onset. b, Comparison of the mean V_m at stimulus onset and during steady-state response reveals a tonic depolarization of 1-5 mV for each cell type and layer. c, The response to PW deflections (red) and the eight SW deflections (black) depends on the state of the neuron and/or circuit. The average PW and SW deflections were measured during the five epochs indicated by the arrows. The trial averaged response is shown in blue. d, For all neurons (N = 86), the average PSP amplitude and peak V_m for PW and the average for the eight SWs (as in C) are plotted in time. Peak potentials for the PW (red) and SWs (black) remain relatively invariant and the main factor affecting PSP size is the tonic depolarization of membrane potential during adaptation.

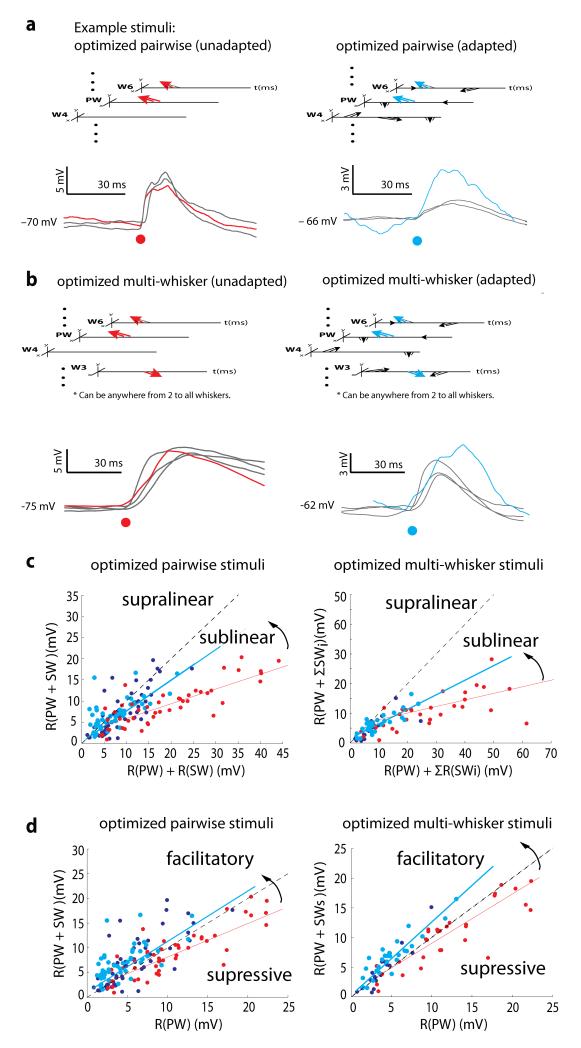
To examine how adaptation might affect multi-whisker integration, we played back predicted optimal stimuli to a subset of neurons. The combination of whiskers, angles, and times predicted to drive the maximal peak response was determined from on-line calculation of the STRF (see Methods). We delivered the optimized pairwise (best 2-whisker) combination of whisker deflections as well as the optimized multi-whisker combination to the neurons in the absence of background stimuli (unadapted) and embedded within our otherwise random complex stimuli (adapted) (Fig. 7a,b). We then checked whether responses could be predicted by the sum of responses to individual whisker deflections. Consistent with previous studies¹⁵, unadapted responses to both pairwise and multi-whisker optimized stimuli added sublinearly (Fig. 7c, red; p < 0.0001 for both, sign test). Responses were, however, significantly more linear in the adapted state (blue; p < 10⁻⁵ for left; p = 0.005 for right; comparison of slopes test). Summation of pairwise stimuli was highly sublinear prior to adaptation (slope 0.346, r 0.738) but more linear under adapted conditions (left; slope 0.723, r 0.506). Responses to optimized multi-whisker deflections also showed greater linearity after adaptation (right; adapted: slope 0.491, r 0.631; unadapted: slope 0.223, r 0.442).

Figure 7. Adaptation linearizes summation of synaptic inputs and allows surrounds to facilitate rather than suppress responses.

a, The best pairwise stimulus for each neuron was determined from the VWA and played back in isolation (unadapted, left) or embedded within random surround stimuli (adapted, right). Black, trial-averaged responses of a neuron to each of the two whiskers, R(PW) or R(SW). Circles, stimulus onset. The pairwise deflection, R(PW+SW), is shown in red (unadapted) or cyan (adapted). b, same as in panel a but for the best multi-whisker stimuli (2-9 whiskers). c, For all neurons (N = 46 unadapted in red; N = 75 adapted in blue/cyan) response to the pairwise deflection R(PW+SW) was plotted against the sum of responses to individual deflections R(PW)+R(SW). Cyan points represent neurons observed during both adapted and unadapted conditions and therefore have a red counterpart. Blue points represent neurons observed only during adaptation. Pairwise summation is nearly linear during adaptation (blue and cyan) (slope 0.723, r 0.506, p < 10⁻⁸) and sub-linear under unadapted conditions (red) (slope 0.346, r 0.738, p < 10⁻⁹). Similar behavior was observed for the optimal multi-whisker stimuli (right) (N=33 unadapted, 36 adapted; 33 matched pairs) (adapted: slope 0.491, r 0.631, p < 10⁻⁷; unadapted: slope 0.223, r 0.442, p < 10⁻⁹). d, For the same data as in c responses to pairwise deflections [R(PW+SW)] were compared to responses to the PW deflections alone [R(PW)]. Surround inputs facilitated the PW response during adaptation but suppressed the PW response without adaptation.

Approximate linearity due to adaptation suggests that surround inputs should enhance the response of the neuron to the PW alone, despite surround suppression observed in barrel cortex neurons during conventional stimulation^{8,11,12,30,31}. To examine the degree to which the surround was facilitatory versus suppressive, we compared the PSP responses of neurons to pairwise and multi-whisker stimuli versus PW stimulation. In the adapted state, responses to pairwise stimuli were 1.33 ± 1.15 times greater than to PWs alone (Fig. 7d, left, blue; p = 0.002, sign test). When neurons were unadapted, however, responses to pairwise stimuli were only 0.895 ± 0.373 times the amplitudes of responses to PWs alone (red; p = 0.002, sign test). For the optimized multi-whisker stimuli, the surround inputs facilitated the response in the adapted neuron by a factor of 1.28 ± 0.43 (Fig. 7d, right, blue; p < 10⁻⁹, sign test) but suppressed activity in unadapted neurons by 0.893 ± 0.269 (red; p = 0.36, sign test). This transition from a suppressive surround to a facilitatory surround during adaptation occurred for neurons in all layers and was independent of how closely the preceding surround deflections (not involved in the optimal stimulus) occurred as well as the number of SWs deflected (Supplementary Fig. 8).

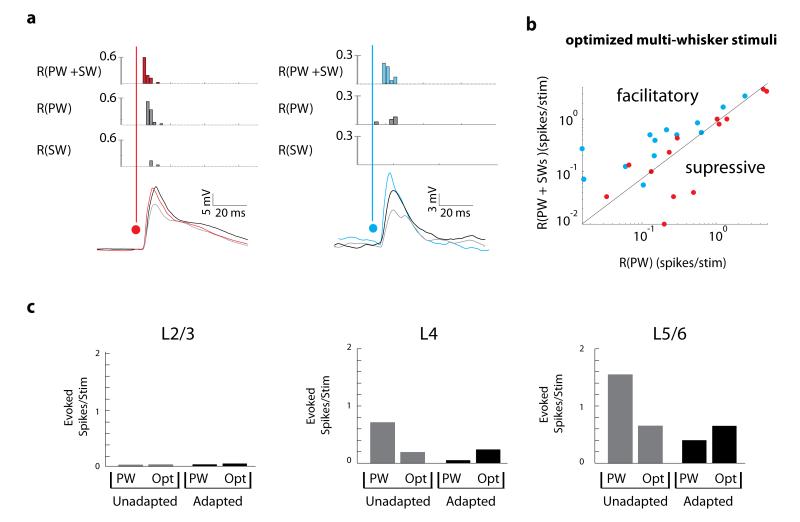
Spiking output followed a pattern similar to subthreshold input (Fig. 8a). Of 33 neurons presented with both single-whisker and optimized stimuli, only half ever fired spikes (4/17 L2/3, 6/9 L4 and 7/7 L5/6). The log-log plot in Fig. 8b shows those that responded to both types of stimuli, with adaptation significantly facilitating spiking by a factor of 1.78 ± 1.04 and unadapted conditions weakly suppressing or not facilitating spiking (0.85 ± 0.3; p = 0.02, 0.30, respectively; sign tests). Neural adaptation therefore allows surround inputs to become facilitatory in S1 while they remain suppressive when the neuron is unadapted. Moreover, while optimized multi-whisker stimuli were able to increase firing rates of adapted L4 and L5/6 neurons, firing in L2/3 was not significantly driven by optimized stimulus playback (Fig. 8c) suggesting that coding in the superficial layers in particular is not purely tactile.

Figure 8. Spiking responses are facilitated by the surround in adapted neurons yet spiking remains sparse in superficial layers.

a, Examples of spiking neurons during the delivery of optimal stimuli in unadapted neurons (left) and adapted neurons (right). b, Surround inputs facilitate the PW response in adapted neurons but suppress the PW response in unadapted neurons (p = 0.02, 0.30, respectively; two-sided sign test). c, Evoked spiking activity in adapted and unadapted neurons demonstrates that the PW alone is the most effective driver of spiking activity in unadapted neurons but optimal multi-whisker stimuli are more effective in adapted neurons.

Discussion

Spatiotemporal receptive fields of barrel cortex neurons have been largely enigmatic. Nevertheless, pioneering studies of spatial and temporal interactions uncovered substantial surround suppression, depending on the combination and sequence of whiskers and their directions of movement¹¹. Subsequent studies by multiple groups parametrically exploring 2-whisker deflections have repeatedly confirmed suppressive interactions^17,32-34. However, while surrounds are normally suppressive for pairs of whisker deflections at low frequency, high frequency stimulation can reveal facilitation in 19% of neurons¹⁷ and even short sequences of whisker deflections (i.e., PW-SW-PW) can “suppress suppression”³³. That weakening of suppression is consistent with the transition we observed as neurons adapted to stimuli and surrounds became facilitatory. Moreover, by playing back optimized multi-whisker stimuli we demonstrated that facilitation may in fact dominate over suppression during sustained stimuli.

A recent study deflecting 24 whiskers along the rostrocaudal axis found that the relative directions of center and surround movements also impact activity. Specifically, discharges of ~15% of recorded neurons are enhanced by deflecting the center whisker in the same direction or opposite direction of the surround²³. Indeed we observed some neurons strongly tuned to correlated or anticorrelated surrounds, but our data, based on 360° of movement, additionally reveal a broad spectrum of center-surround relationships (Fig. 4; Supplementary Fig. 7c).

Reverse correlation in S1

Our linear STRF model captured the correct subthreshold stimulus-response relationship for neurons in all cortical layers (Fig. 2). Sensory physiology has a long history of studying spiking receptive fields by reverse correlation using both linear models and linear-nonlinear Poisson models. The combination of intracellular recordings and our stimulator system allowed us to extensively sample the stimulus space and map STRFs for neurons spanning the depths of an S1 cortical column. Our simple linear model of the stimulus-response relationship was able to account for 73% of predictable synaptic input after an appropriate stimulus transformation. Our data reveal that neurons receiving substantial background synaptic input, particularly in L2 and L5, are the most difficult to predict (Fig. 2a,d). Isolating the neural noise from the predictable component of the responses revealed that the linear model works equally well across layers. Thus, nonlinear interactions cannot necessarily be inferred from poor overall linear model performance, which may reflect high levels of neural noise in specific cell types.

The accuracy of our linear model could be partially due to our re-representation of stimuli in a manner similar to their natural encoding at the periphery and by central synapses. In the whisker system, primary afferents initially encode direction and space using discrete clusters of mechanoreceptors around a limited circumference of individual whisker follicles²⁵. Relatively labeled lines maintain this code from the periphery to the cortex^35-37. We represented direction in 45° bins, similar to the half widths of neurons’ directional tuning curves. With a standard Cartesian representation of direction instead, prediction would require a nonlinear model simply because many neurons respond equally well to opposite directions of motion whereas linear models using Cartesian representations require opposite responses to opposing motions. Linear sensory integration is consistent with active synaptic inputs being spatially or temporally distributed across dendritic arbors^38,39. Models of other sensory modalities may benefit from finding analogous stimulus representations encoded by presynaptic inputs in which the stimulus-response relationship can be estimated using linear methods²⁴.

Another contributor to the model’s accuracy is likely our use of intracellular recording, which reveals additional information normally masked by the spike generation nonlinearity and removes noise inherent therein. An intracellular study of auditory cortex using a reasonable stimulus transform found that linear models performed poorly, predicting on average only 11% of subthreshold response variance⁴⁰, and a similar spike-based study captured ~19% of suprathreshold response variance²⁹. It remains unclear how to compare the percentage of predictable variance explained by a subthreshold model to that by a suprathreshold model. While subthreshold receptive fields may seem irrelevant as information is propagated by spike output rather than subthreshold input, ultimately the stimulus driving the maximal synaptic input is the same stimulus driving spike output. To the extent presently known, spike output is a power law function of synaptic input²⁶. Indeed our VWAs correlated well with actual STAs when adequate numbers of spikes were available (Fig. 1, Supplementary Fig. 1).

Finally, our stimuli were purposefully chosen to mimic the high-velocity events common during natural whisking and thought important for sensation^7,34,41. Though naturalistic in their kinematics, these stimuli were stochastic (“white”) with regard to space, direction, and time, sampling unbiasedly along potentially important stimulus dimensions while keeping data collection and analysis tractable. Models built using white noise stimuli can be poor predictors of responses to natural visual scenes, which contain strong spatial correlations⁴². Strong correlation of neighboring whiskers is not apparent from videography of rats during sustained contact with textures⁷, but initial encounters with an object may induce significant spatial and temporal correlations, such as arc contacts being near synchronous and row contacts being sequentially ordered. Object shapes could further contribute to such correlations. Studies of possible high-order correlations during natural whisking, which might necessitate the use of nonlinear models, are needed.

Coding in barrel cortex

Rodents repetitively sweep all of their whiskers back and forth across surfaces when exploring their environments^7,8. Our results show that a major consequence of sustained multi-whisker input during natural whisking will be to dramatically sharpen receptive fields in spatial extent and tighten the temporal latencies between whiskers (Fig. 5). For example, L5 thick-tufted pyramidal neurons were equally well driven by most whiskers when mapped with conventional single-whisker stimuli as noted previously^2,5 but became highly focused on the PW during complex stimuli. In fact identifying the PW of this cell type is very difficult using only single-whisker stimuli. The switch in coding with repetitive whisking may be especially important for corticofugal cells such as those in L5 that signal numerous subcortical, behaviorally relevant structures (i.e., thalamus, striatum, spinal cord, brainstem, superior colliculus).

Similar laminar analyses of visual cortex showed that thalamorecipient layers, such as L4 and L6, possess simple receptive fields reminiscent of their thalamic inputs²⁷. Recently, we discovered that thalamocortical synapses converge even more densely onto L5TT neurons than L6 cells⁴³, but our L5TT STRFs here look nothing like those in L6. This likely reflects local, rather than thalamocortical, circuit differences between the two layers. This disparity also underscores the challenge in inferring connectivity from receptive fields and vice versa.

In contrast to L5, coding in superficial layers has been particularly difficult to study²³. This stems from the sparse activity in L2/3 under a variety of conditions^5,20,22,43. Conceivably, the effective stimuli for L2/3 barrel cortex neurons have been previously missed. Our study is the first able to explore a large stimulus space for L2/3 despite its seemingly low firing rates. We observed that optimized stimuli for activating synapses onto L2/3 cells are very similar to those for other, more robustly spiking layers (Fig. 5a), but still do not reliably drive L2/3 to threshold (Fig. 8c). Impoverished stimuli are therefore unlikely to explain previous reports of sparse firing in L2/3. The activity of L2/3, rather than being highly selective for stimuli, may be gated by top-down and/or neuromodulatory inputs present only during active behavior⁴⁴ or may be a sparse coding system under all conditions.

The role of surround receptive fields

Complex stimuli induced a tonic depolarization in all layers (Fig. 6). Further studies are needed to determine whether this reflects the number of whiskers stimulated or a general activation of the cortical network. During these depolarized steady-state conditions, all whiskers evoked smaller PSPs than at stimulus onset. Counterintuitively, the surround receptive field under steady-state conditions facilitated responses to the PW, contrary to the well-established surround suppression observed in numerous studies of barrel cortex^11-15. Surround suppression between pairs of whisker deflections at fixed latencies does not derive from hyperpolarizing or shunting inhibition^32,45, but rather reduced synaptic input. Synaptic depression at the thalamocortical and corticocortical synapses as well as reduced cellular driving force may contribute to this adaptation^46,47. Our results not only confirm such observations regarding initial transient responses but also demonstrate that persistently adapted conditions render the integration of whisker inputs more nearly linear relative to unadapted conditions, allowing surround facilitation (Fig. 7). Stimulus-dependent linearization has been observed in subthreshold responses of visual cortical neurons⁴⁸ and may be a ubiquitous feature of cortical processing. Finally, the sufficiency of a linear model for 9 whiskers moving in 360° suggests that spiking models predicting activity evoked by rostrocaudal movements of two individual whiskers³⁴ may scale to many whiskers and directions. Incorporating adaptation in those spiking models was critical for accurate prediction. Linear models of barrel cortex may benefit from incorporating such history dependence, perhaps especially for arbitrary and natural stimuli.

Ethologically, adaptation may allow neurons to transition from simple stimulus detectors to discriminators of stimuli^3,49,50. Indeed, adaptation enhanced the acuity of individual neurons (Fig. 5). Additionally, adaptation allowed multi-whisker stimuli to more effectively drive responses than the PW alone (Fig. 8). Such effects may allow neurons in S1 to discriminate objects during active tactile exploration employing multiple whiskers, yet still serve as indiscriminate detectors of salient stimuli when not actively exploring. Adaptation induced by repetitive whisking might be required to classify object shapes and textures. Behavioral studies examining the effect of adaptation on detection versus discrimination are needed.

Conclusion

By exploiting additional information available from intracellular recording, we have been able to explore the sensitivity of neurons to stimuli varying in space, direction, and time by reverse correlation. Our results demonstrate that a linear model, given an appropriate stimulus transform, accounts well for the predictable subthreshold activity in rat barrel cortex. This method reveals STRFs an order of magnitude faster than conventional spike-based techniques, even for neurons firing few or no spikes. These STRFs differ starkly from receptive fields based on conventional stimuli. The surround receptive field, long thought to be predominantly suppressive, becomes facilitatory during more natural conditions.

Methods

Animal Preparation and Physiology

All procedures were approved by the Columbia University Institutional Animal Care and Use Committee. Forty adult female (weight 130-340 g, mean 210 g) Wistar rats (Hilltop Laboratories) were used. During surgery animals were deeply anesthetized with isoflurane (1-3% in O₂), and body temperature was maintained at 37° by a heating blanket. Eyes were coated with lubricating ointment to prevent drying. Cannulae were inserted into the trachea (for mechanical ventilation), left femoral artery (for blood pressure monitoring) and right jugular vein (for drug infusion). A metal post for stabilizing the head was attached to the skull by dental acrylic. Screws were inserted in the right frontal and parietal bones for electrocorticogram (“EEG”) recording. Small (~0.5 × 0.5 mm) craniotomies were made over left barrel cortex, and the dura removed. The acrylic was extended around the craniotomies to create a well for retaining artificial cerebrospinal fluid (ACSF; in mM: 135 NaCl, 5.4 KCl, 1.8 CaCl₂, 1.0 MgCl₂, and 5.0 HEPES; pH 7.2). Bupivacaine was applied to cannulae incisions and the scalp surrounding the acrylic and reapplied periodically.

For neural recordings, isoflurane was discontinued, and the rat was maintained in a lightly narcotized state by intravenous infusion of fentanyl (~10 μg / kg / hr). To prevent spontaneous whisker movement, neuromuscular blockade was induced with pancuronium bromide (1.6 mg / kg / hr), and the animal artificially respired (90-100 breaths/min) using a positive-pressure ventilator. A computer continuously monitored electrocorticogram, mean arterial pressure (MAP), arterial pulse rate, and tracheal airway pressure. Experiments were terminated if these indicators could not be maintained within normal physiological ranges.

Craniotomies were mapped extracellularly to identify the underlying barrel.Glass pipettes with tips of ~5 μm inside diameter (ID) were filled with aCSF and inserted vertically to a microdrive depth of 700-1000 μm. Signals were amplified, band-pass filtered at 0.3-9 kHz, and played over an audio monitor. Whiskers were deflected manually using hand-held probes to determine the principal whisker (PW) corresponding to locations within a craniotomy.

Patch pipettes were pulled from 2 mm unfilamented borosilicate glass. Tip ID was ~0.5-1 μm. Pipettes were tip-filled with (in mM) 135 K-gluconate, 10 HEPES, 10 phosphocreatine-Na₂, 4 KCl, 4 ATP-Mg, 0.3 guanosine triphosphate, and 0.4% biocytin (pH 7.2, osmolarity ~300). Cells were searched for blindly in voltage-clamp mode using pulses. Whole-cell recordings were made in Bridge mode and digitized at 32 kHz. Seal resistance was > 1 GΩ, access resistance 5.2-51.5 MΩ (mean 26.3 MΩ), and spike height and overall membrane potential (V_m) were stable throughout the recording. No holding current was used. Pipette capacitance was neutralized prior to break in. A large ground shield was placed between the electrodes and whisker-stimulator system to minimize stimulus artifact.

Histology and Morphological Analysis

After recordings, the rat was deeply anesthetized with sodium pentobarbital (50 mg/ml) until a drop in MAP and desynchronization of EEG was observed. Rats were perfused transcardially with cold 0.1 M sodium phosphate buffer followed by 4% paraformaldehyde (in 0.1 M buffer). Barrel cortex was cut tangentially in 100-μm vibratome sections. Sections were stained for cytochrome oxidase (CO) and subsequently biocytin. Seventy-one cells were recovered and could be unambiguously identified morphologically. Cells were classified as barrel- or septal-related and by layer according to methods described previously⁴³. Example cells were reconstructed using a Neurolucida system with a 40X/1.3NA oil-immersion objective.

Stimulus Presentation

Whiskers were trimmed to a length of ~10 mm. Nine multi-directional piezoelectric stimulators were used to deflect individual whiskers. After mapping the barrel identity, the 9 stimulators were arranged around the face so that the stimulator corresponding to the PW was located at the center and the remaining 8 stimulators occupied the immediate surrounding whiskers. The opening of a stimulator was slipped over the whisker and positioned at ~7mm from the base of the hair.

Two different stimulus protocols were used to probe whisker responses: a complex multi-whisker stimulus protocol, and a simple single-whisker stimulus protocol. Complex multi-whisker stimulus trials lasted 1000 ms with a 1-second inter-trial interval. The nine whiskers moved simultaneously and continuously in random directions in any of 360° (1° resolution) and at random times as a Poisson process with a mean rate of 10 Hz during non-refractory periods, with a refractory period after each pulse initiation of 10ms (the length of each pulse). This made the actual pulse rate on each whisker ~9.1Hz. All pulses followed the same trajectory of velocity vs. time with maximum speed of 2200°/second and a maximum excursion of 850 um (~7°). The pulse was a symmetric parabolic movement with a 5-ms rise, no hold, and 5-ms fall.

During each trial of simple single-whisker stimuli, one of the 9 whiskers was selected randomly and moved in one of the eight cardinal directions with ramp-and- hold movement having a total amplitude of 850 um (~7°), rise-time of 10 ms, a hold of 200 ms, and decay time of 10 ms. Trials lasted 500 ms with a 1-second interval between consecutive trials. Each whisker and angle combination occurred at least 10 times, resulting in a total of 720 trials.

Receptive Field Mapping

Data were analyzed using custom-written MATLAB (Mathworks, Natick, MA) routines running on an 8-core Linux server with 64GB RAM.

Whole-cell recordings were preprocessed before calculating the stimulus-response function or STRFs. Action potentials were removed by linearly interpolating between the points just before and just after the action potential, and a median filter (200-ms) was subtracted to remove slow changes over the course of the experiment due to fluctuations in the animal’s state or network dynamics. The trace was then zero-meaned.

Standard reverse correlation, applied in a nonlinearly transformed stimulus space, was used to map receptive fields to complex multi-whisker stimuli. The stimulus ensemble s was transformed from an (x, y, t) representation to a binned polar representation (d1, d2, …, d8, t). Specifically, stimulus pulses occurring in each of the full 360° were re-encoded in 45° bins (Supplementary Fig. 1a) where s’ is the stimulus in the new 8-dimensional representation. This transform roughly approximates the transformation occurring at the whisker follicle.

The subthreshold stimulus response function of the neuron can then be described using the following linear model:

$$v\left(t\right)={\overrightarrow{K}}^T{{\overrightarrow{S}}^{\prime }}_t+b+{\epsilon }_t$$

The model gives the expected instantaneous voltage of the neuron, at time t given the (transformed) stimulus that occurred before the voltage response, ${{\overrightarrow{s}}^{\prime }}_t$. The stimulus is passed through a spatiotemporal filter, $\overrightarrow{k}$, and has an offset and noise added, b and ε_t, respectively. The vector ${{\overrightarrow{s}}^{\prime }}_t$ represents the stimulus movements that occurred in all 9 whiskers over the 100 ms preceding the voltage response. Only steady-state (adapted) responses were modeled.

Note that each whisker is represented with 8 directional dimensions, making the spatial dimensionality of the stimulus segment 72, and the temporal dimensionality 100. Thus the stimulus segments preceding each voltage response can be described as a matrix of size 100 × 72, which is vectorized to obtain a stimulus vector ${{\overrightarrow{s}}^{\prime }}_t$, which is size 7200 × 1. Because both the voltage and the stimulus are zero-meaned, the offset b becomes zero.

The parameters for the spatiotemporal filter $\overrightarrow{k}$ can be estimated in general using linear, ordinary least squares, multiple regression (OLS).

$$\overrightarrow{k}={\left(S^{\prime }{S}^{{\prime }^T}\right)}^{-1}{S}^{\prime T}\overrightarrow{v}$$

S’ is a matrix whose columns are the vectors ${{\overrightarrow{s}}^{\prime }}_t$ for each time t, and is therefore dimensionality [N × 7200] where N is the number of 1ms time bins of data. The vector $\overrightarrow{v}$ is a column vector that contains the voltage observation at each time t, and is size [N × 1]. Because our stimulus is binary with respect to the presence of absence of a stimulus and the movements between whiskers and angles are uncorrelated, the stimulus prior (S’S’T) can be approximated as proportional to the identity matrix. The filter $\overrightarrow{k}$ is therefore easily calculated as the voltage-weighted average (the “reverse correlation” estimate),

$$\overrightarrow{k}=\frac{1}{N}{\Sigma }_t{{\overrightarrow{S}}^{\prime }}_{t}v\left(t\right)$$

where N is the total number of voltage observations. Rank-reduced regression approaches, which place stronger priors on the form of the filter $\overrightarrow{k}$ and should lead to stable estimates given less data, did no better (see Separability and shared structure below).

To test the accuracy of the model we used the spatiotemporal filter, $\overrightarrow{k}$, to predict activity of the neuron to novel stimuli (cross-validation). We first trained our model on 300 trials of unique complex multi-whisker stimuli. We next tested the model on the trial averaged response to 10 trials of unique stimuli, averaged over 10 stimulus presentations (frozen noise). The rationale here is to train the model on as general a stimulus as possible, but test it on as “noise-free” a neural response as attainable. Additionally, the frozen noise approach allows estimation of the predictable variance of a neuron, var_p,:

$$r_i=\left(\frac{cov(trai{l}_i,<trail>)}{\sqrt{var\left(trai{l}_i\right)\times var(<trail>)}}\right)$$

$$va{r}_p={\Sigma }_{i=1}^n\frac{{r_i}^2}{n-1}$$

As well as the noise variance var_n,:

$$va{r}_n=1-va{r}_p$$

where the brackets 〈 〉 represent an average over the trials, the subscript (i) denotes the response of the i-th trial of frozen noise (i = 1,…, 10), and the notation cov refers to covariance, and n is the number of trials of frozen noise (10). For covariance and variance calculations, expectations are with respect to time. A similar calculation can be made for the average signal power, and the average noise power in the response²⁹.

To calculate STRFs using simple single-whisker stimuli, we used the conventional approach (“forward correlation”), taking the average zero-meaned voltage response for 100 ms following each possible stimulus presentation (9 stimulators × 8 angles = 72 possible stimulus presentations). Each average voltage response corresponds to the equivalent of a single column in the STRF and the 72 responses were assembled in appropriate order.

To predict the STA from VWA, the STA’ (see Supplementary Fig. 1), we first measured the mean spike threshold and mean V_m variance of each neuron that fired at least 1 action potential during recording. Threshold was determined by detecting large changes in dV/dt, indicative of spike onset. V_m variance was calculated from 10 trials of frozen noise. The actual stimuli were projected through the VWA to predict subthreshold responses to the 300 trials and added to temporally correlated Gaussian noise that matched the cell’s true variance. When the modeled response passed threshold, a binary spike followed by a 10-ms refractory period was recorded. This spike train was then used to produce the STA’. For additional simulation trials, new random stimuli were generated.

Quadratic Model

The subthreshold stimulus response function of the neuron can be described with the following quadratic model:

$$v\left(t\right)={\overrightarrow{s^{\prime T}}}_{t}A{{\overrightarrow{S}}^{\prime }}_t+{\overrightarrow{K}}^T{{\overrightarrow{S}}^{\prime }}_t+b+{∊}_t$$

where ${{\overrightarrow{s}}^{\prime }}_t$, $\overrightarrow{k}$, b and ε_t, and, represent the same as above. The matrix A represents an additional quadratic term, where off-diagonal values can be thought of as pairwise interactions of all whiskers across times, and has dimensionality 7200 × 7200. As above, the quadratic model is fit using regression analysis. Because the dimensionality of parameters in the quadratic model is high, the quadratic model is prone to overfitting. We therefore initially reduced the dimensionality of the stimulus space by performing voltage-weighted covariance analysis (VWC), an analogue of classic STC. The stimulus is weighted by the voltage and then a PCA-like analysis is performed which identifies dimension (eigenvectors) which account for the majority of the variance in responses. Significant positive and negative eigenvectors are then used to filter the stimulus. Regression analysis was then performed on the filtered subspace. This significantly reduced the dimensionality of the analysis, allowing for more efficient estimates that are less prone to overfitting.

Separability and shared structure

Supplementary Fig. 5 decomposes the receptive field of each neuron into temporal and spatial (whisker) basis components. Each RFs is characterizable by the “rank,” the number of basis components required to reconstruct the RF (a “separable” RF has rank one). To fit a rank-R RF we followed the method proposed in ref ²⁴ with the voltage response of each neuron modeled as a linear function of temporal and spatial features of the binned input. We re-write the linear model of the voltage response:

$$v^{\left(t\right)}={\overrightarrow{K}}^T{\overrightarrow{S}}_t$$

as (for each neuron, indexed by i)

$${v_i}^{\left(t\right)}=\sum _{r=1}^R{{\overrightarrow{q}}_i}^{\left(r\right)}{S_i}^{\left(t\right)}{{\overrightarrow{a}}_i}^{\left(r\right)}$$

where v(t) is the voltage response of neuron i at time t. ${\overrightarrow{s}}_t$ is reshaped into S(t), a matrix version of the stimulus (100 × 72, generally L lags by P features), and indexed to correspond to the binary stimulus at each time for T timesteps. We ignore bias for notational convenience, but a bias term is included in the analysis.

The desired rank R of each individual RF is specified in advance. The set of vectors ${\overrightarrow{q}}_i^{\left(r\right)}$ and ${\overrightarrow{a}}_i^{\left(r\right)}$ for r = 1…R are respectively the temporal and spatial basis components for the neuron i. These vectors are equivalent to the RF represented in $\overrightarrow{k}$ with ${\Sigma }_{r=1}^R{\overrightarrow{q}}^{\left(r\right)}{\overrightarrow{a}}^{{\left(r\right)}^T}$ yielding the rank R voltage weighted average of L lags by P features. Our empirical analysis showed that R = 1…3 is adequate (see also Fig. 4) to capture the full RF for each of the neurons analyzed (Supplementary Fig. 5). See also ref ⁵¹ for related results.

The shared structure of temporal basis components can also be leveraged to estimate the RFs using less data (a regularization) by sharing information across neurons. To fit the separable RF model for all neurons jointly while enforcing shared components (${\overrightarrow{q}}_i^{\left(r\right)}$ and ${\overrightarrow{a}}_i^{\left(r\right)}$ for r = 1…R, & i = 1…N), we alternate between the following convex optimization problems:

$$\underset{Q}{\min }\sum _{i=1}^N\mid \mid {\overrightarrow{v}}_i-{\overrightarrow{q}}_i^T\left(\sum _{r=1}^R{X}_i^{\left(t\right)}{\overrightarrow{a}}_i^{\left(r\right)}\right)\mid {\mid }_F^2+{\lambda }_q{\mid \mid Q_{reshaped}\mid \mid }_{\ast }$$

$$\underset{A}{\min }\sum _{i=1}^N\mid \mid {\overrightarrow{v}}_i-\left(\sum _{r=1}^R{\overrightarrow{q}}_i^{\left(r\right)}{X}_i^{\left(t\right)}\right){\overrightarrow{a}}_i\mid {\mid }_F^2+{\lambda }_a{\mid \mid A_{reshaped}\mid \mid }_{\ast }$$

where ${\overrightarrow{q}}_i$ and ${\overrightarrow{a}}_i$ are the vectors formed by concatenating ${\overrightarrow{q}}_i^{\left(r\right)}$ and ${\overrightarrow{a}}_i^{\left(r\right)}$ vertically over r = 1…R, and Q and A are the matrices formed by concatenating vectors ${\overrightarrow{q}}_i$ and ${\overrightarrow{a}}_i^{\left(r\right)}$ horizontally over neurons i = 1…N (such that Q has dimensions (L × R) by N and A has dimensions (P × R) by N). Q_reshaped is a reshaped matrix Q with dimensions L by (N × R). A_reshaped is a reshaped matrix A with dimensions angles by (whiskers × N × R). λ_q & λ_a are tunable parameters specifying the extent to which the neurons share a basis, fit by cross-validation here. The nuclear norm penalty $\mid \mid \cdot \mid {\mid }_{\ast }$ is a convex relaxation of the rank of the matrix⁵² and therefore enforces low rank structure. Applied here, this penalty will enforce that the temporal components across neurons will be shared. We similarly regularize for appropriate components in A_reshaped which enforces a shared basis of tuning to different stimulation angles across whiskers and neurons. To solve this penalized problem, we alternate between objectives (in the style of alternating least squares), using the alternating direction method of multipliers⁵³ to solve each regularized subproblem.

The resulting solutions Q and A correspond to the RFs, and due to the pooling of information across neurons, the RFs can be fit much better when less data is available than they could if they were fit independently. For example, when the VWAs are fit in a particularly low data regime (5-sec worth of data per neuron), they are underfit and perform poorly when used to predict voltage. In this regime, the R = 1 regularized model improves the prediction quality dramatically (increasing the correlation on average by a factor of almost 2).

Analysis of Receptive Field Properties

To estimate significant whisker responses, 99% confidence limits on noise were calculated using a selected portion of the STRF representing spontaneous background activity (the first 5 ms of each STRF, for all whiskers and directions). Whisker responses exceeding these limits were deemed significant. Surround power was defined as the power contained in the SWs over the total power contained in the receptive field. Power was calculated as the average square deviation from the mean over the full STRF.

Onset latency was defined as the first time the receptive field exceeded these 99% confidence limits. Surround latency was defined as the average latency difference between the PW and the significantly responsive SW’s. Surround latency was not calculated for neurons lacking significantly responsive SWs.

The preferred direction for a whisker was defined as the direction with largest STRF time-peak response. For the vector strength calculation, the preferred direction for each significantly responsive whisker is first represented as a unit-vector (length 1) in the appropriate direction. Each significantly responsive whisker is thus given equal influence in the calculation of the vector strength. The vector strength is then calculated by taking the algebraic mean of the unit vectors. A vector strength of 1 signifies that all unit vectors are aligned, or coherent, and a vector strength of 0 signifies that unit vectors are anti-coherent and cancel out.

The mean PW directional tuning was defined as the strength of response (peak value) to the preferred direction of the PW divided by the summed strength of the PW response to all directions. Tuning can take on values anywhere from (0.125-1), where a 1 indicates that all of the response is contained within the preferred direction and a value of 0.125 indicates a flat tuning curve where all values are preferred equally.

Average STRFs for each layer (Figs. 4 and 5) were plotted with the PW in the middle. SW identities were always the same with respect to the PW, i.e. SW2 and SW8 were always in the same arc as the PW, while SW4 and SW6 were always in the same row as the PW. PW tuning was always shown with the preferred response in the middle bin (180-225° in Fig. 5a,b), and the tuning curves, or polar plots, were shifted accordingly.

Stimulus Playback

For stimulus playback experiments, STRF of complex multi-whisker stimuli were calculated online and significant whisker responses were determined as above. The best combination of whiskers, times, and angles was defined as the combination that produced the largest peak voltage response. This combination was extracted from the STRF, for both pairwise stimuli and multi-whisker stimuli. Because the model is linear, the best pairwise or multi-whisker stimuli can easily be determined by examining the STRFs and finding the direction with largest peak response for all significantly responsive whiskers, as well as the optimal time lags between them to make their peaks coincide in time. This exact stimulus combination was then delivered back to the neuron in the absence of any background stimuli to measure the response to optimal stimuli when the neuron was in an unadapted state and compared to the same stimuli when embedded within the complex multi-whisker presentation, the adapted state.

Statistics

Statistical tests were implemented in Matlab. Sample sizes were not pre-determined, but retrospective analysis shows that the power of our significance tests was generally >90%. Our sample sizes are also similar to those of previous studies^5,23,27.Stimuli were computer randomized (see Stimulus Presentation), but no randomization of samples (cells or animals) was needed in our design.