Abstract
We describe a comprehensive modeling approach to combining genomic and clinical data for personalized prediction in disease outcome studies. This integrated clinicogenomic modeling framework is based on statistical classification tree models that evaluate the contributions of multiple forms of data, both clinical and genomic, to define interactions of multiple risk factors that associate with the clinical outcome and derive predictions customized to the individual patient level. Gene expression data from DNA microarrays is represented by multiple, summary measures that we term metagenes; each metagene characterizes the dominant common expression pattern within a cluster of genes. A case study of primary breast cancer recurrence demonstrates that models using multiple metagenes combined with traditional clinical risk factors improve prediction accuracy at the individual patient level, delivering predictions more accurate than those made by using a single genomic predictor or clinical data alone. The analysis also highlights issues of communicating uncertainty in prediction and identifies combinations of clinical and genomic risk factors playing predictive roles. Implicated metagenes identify gene subsets with the potential to aid biological interpretation. This framework will extend to incorporate any form of data, including emerging forms of genomic data, and provides a platform for development of models for personalized prognosis.
Genomic information, in the form of gene expression patterns, has an established capacity to define clinically relevant risk factors in disease prognosis. Recent studies have generated such patterns related to lymph node metastasis and disease recurrence in breast cancer (1–8), as well as in other cancers and disease contexts (9–16). The challenge now is the integration of such genomic information into prognostic models that can be applied in a clinical setting to improve the accuracy of treatment decisions.
Achievement of this goal requires modeling approaches that focus on the generation of predictions for the individual patient and that can evaluate and combine multiple risk factors to produce informed predictions. Gene expression profiles may indeed prove to be powerful individual indicators of tumor behavior, but analysis should not force a choice of one form of data over the other; rather, analysis should evaluate and combine all forms of potentially relevant information. This integrative view underlies our development of clinicogenomic models and should underlie prognostic systems in support of personalized health planning.
Consistent with this view, the example of breast cancer recurrence presented here highlights the predictive value of multiple genomic patterns in models defining accurate predictions at the individual patient level. This analysis uses integrative models that combine clinical and genomic factors, such as multiple gene expression patterns, clinical risk factors, and treatment information, and that predict recurrence for individual patients. The example shows improved recurrence prediction accuracy at the individual patient level based on multiple risk factors in combination and the relevance of multiple summary measures of gene expression. Prediction accuracy in the combined clinicogenomic models exceeds that achieved by using either clinical data or single genomic predictors alone, and the analysis highlights the importance of representing and communicating uncertainties in prediction. The analysis also identifies gene candidates that can now be studied to shed light on potential regulatory pathways.
Methods
The example study involves 158 breast cancer patients at the Koo Foundation Sun Yat-Sen Cancer Center in Taipei, with primary tumor biopsies collected and banked between 1991 and 2001. The patient sample represents a heterogeneous population, and sample selection was enriched for high-risk cases for the purposes of this example. Samples were collected under Duke (IRB no. 3157-01) and Koo Foundation Sun Yat-Sen Cancer Center (September 21, 2001) Institutional Review Board guidelines. Summaries of clinical risk factors, such as axillary lymph node status, estrogen receptor (ER) status, age, tumor size and others, appear in Table 1, which is published as supporting information on the PNAS web site.
Gene expression assays were performed with RNA extracted from the banked tissue. Total RNA was extracted with Qiagen RNeasy kits and assessed for quality with an Agilent Lab-on-a-Chip 2100 Bioanalyzer. Probes for hybridization were then prepared according to standard Affymetrix protocols on the Human U95Av2 GeneChip. Affymetrix GeneChip scanning and analysis produced the Affymetrix mas version 5.0 expression signal intensity estimates.
The core methodology uses statistical classification and prediction tree models, and the gene expression data enter into these models in the form of metagenes. As previously described (7, 17, 18), metagenes represent the aggregate patterns of variation of subsets of potentially related genes. In this example, metagenes were constructed as the first principal components (singular factors) of clusters of genes created by using k-means clustering. Bayesian methods of analysis were used to fit multiple candidate classification tree models, each candidate model based on varying the selection of predictor variables, and trees were individually generated by using a forward selection process. Predictions were based on weighted averages across multiple candidate tree models, and the combinations of genomic and clinical predictor variables appearing in highly weighted tree models provide insights on the interactions of risk factors determining the predictions. Full details of the statistical approach appear in the supporting information.
Results
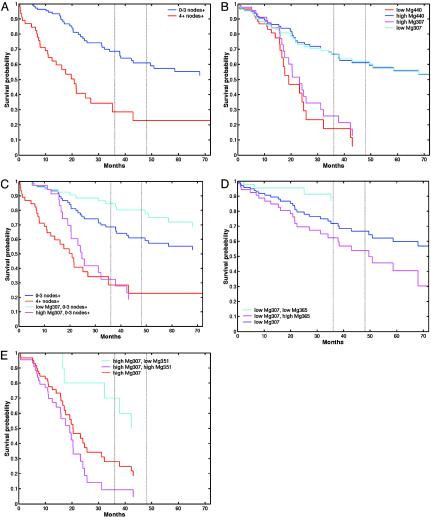
Combining Multiple Metagene Signatures Improves Accuracy of Recurrence Prediction. Data summaries in terms of raw survival curve and relative risk estimates illustrate the traditional view of stratifying patients into high versus low risk of recurrence based on clinical factors such as lymph node involvement (Fig. 1A). Similar summaries using any one of a number of metagenes (Tables 2 and 3, which are published as supporting information on the PNAS web site) indicate strong association with recurrence. Two closely related (negatively correlated) metagenes, Mg307 and Mg440, provide strongly discriminating genomic signatures (Fig. 1B) and are able to stratify individuals into significantly different risk categories, with discrimination stronger than that defined by the key clinical predictor, lymph node status. This result is similar to a recent study (6) employing a single 70-gene predictor that classified breast cancer patients in risk categories based on a “good” or “poor” signature. Although the prediction of low risk (good signature) was accurate, the prediction of high risk (poor signature) was highly uncertain, because individuals in this group had a 50/50 probability of recurrence at 10 years. Either Mg307 or Mg440 alone is more accurate, in this sense, and on a clinically much shorter (and more challenging) 4- to 5-year time horizon, but this analysis only begins the process of understanding personal-level recurrence risks. Further factors may refine these risk categories toward personalized prediction for the patient.
Fig. 1.
Kaplan–Meier survival curves for recurrence based on high-risk/lowrisk categorization of breast cancer patients. (A) Empirical survival estimates based on lymph node involvement (low risk, 0–3 positive nodes; high risk, 4 or more positive nodes). (B) Empirical survival estimates based on partition into two groups defined by a threshold in the gene expression pattern of Mg307 and, separately, Mg440. (C) Empirical survival estimates showing evidence of interaction between clinical factors (lymph node status) and genomic factors (in this example, Mg307). (D) Refined empirical survival estimates for two subgroups of the low Mg307 group, defined by a partition on Mg365. (E) Refined empirical survival estimates for two subgroups of the high Mg307 group, defined by a partition on an ER-related metagene, Mg351.
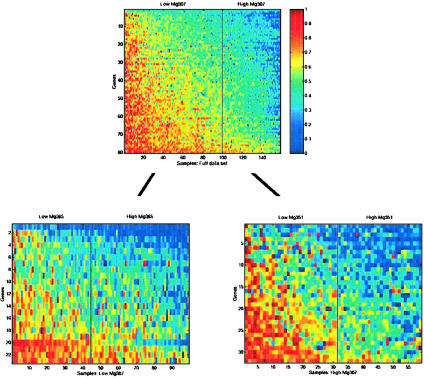
For example, some of the remaining heterogeneity in outcomes within the two groups defined by the initial partition of Mg307 may be resolved by additional genomic factors, as exhibited through partitions of the “low Mg307” group based on Mg365 and of the “high Mg307” group based on Mg351 (Fig. 2). This effect of the refinement on evaluating risk of recurrence (Fig. 1 D and E) shows how the incorporation of additional metagenes changes the survival estimates by partitioning into more homogenous subgroups. This combination of multiple metagenes through the further categorization of patients into refined risk groups underlies the use of statistical tree models. The same principle applies to combining clinical factors with metagenes (Fig. 1C). Evidently, multiple metagenes are capable of playing significant roles in such analyses (Tables 2 and 3), and it is clear that there is a resulting potential for different models to generate different, even potentially conflicting, predictions. Understanding this point is vital in developing an appreciation of the true nature of the genomic state, reflected in multiple, related measures of expression. Hence, there is a need to consider multiple models that define successive partitions of patient groups with a mechanism to formally compare, contrast, and combine them.
Fig. 2.
Use of successive metagene analyses to improve predictions of breast cancer recurrence. (Upper) The expression pattern of the genes in Mg307 (ordered vertically by their weighted value in the metagene) on the entire group of 158 patients. Samples are ordered (horizontally) by the value of Mg307, and the vertical black line indicates the split of the patients into two subgroups underlying the empirical survival curves in Fig. 1B. The two subgroups of patients defined by this split were then further split with two additional metagenes. The low Mg307 subgroup is split based on Mg365, and the high Mg307 group is split based on Mg351. (Lower) The subsequent images show the patterns of genes within Mg365 (Left) and Mg351 (Right) for the corresponding two subgroups of patients, arranged similarly within each group and also indicating the second-level splits. These splits underlie the refined survival curve estimates in Fig. 1 D and E.
Statistical Tree Models Using Multiple Metagenes to Predict Cancer Recurrence. To explore multiple metagenes for optimal predictions, we use classification trees (18–23) and Bayesian statistical methods of tree model generation and evaluation. A single tree defines successive partitions of the sample into more homogenous subgroups. At any node of the tree, the corresponding subset of patients may be divided in two at a threshold on a chosen metagene analogous to the standard low-risk/high-risk grouping already discussed. The analysis shown in Fig. 2 represents one node of a tree in which Mg307 splits the samples into two groups that are then further split by additional metagenes. The logical extension is to tree models with more levels and also to multiple trees. At any node, the optimal metagene/threshold pair for dividing the sample in the node is chosen by screening all metagenes and, for a range of thresholds on any metagene, by testing for the significance of a split of the data into two subgroups based on that metagene/threshold pair. Splits deemed significant lead to growth of the tree; otherwise, tree growth is restricted and ends when no metagene can be found to define a significant split. Multiple possible splits generate copies of the tree and so underlie the generation of forests of trees. The specific statistical test used is a Bayes factor test (24) that is generally conservative relative to standard significance tests and so tends to generate less elaborate trees than do traditional tree programs.
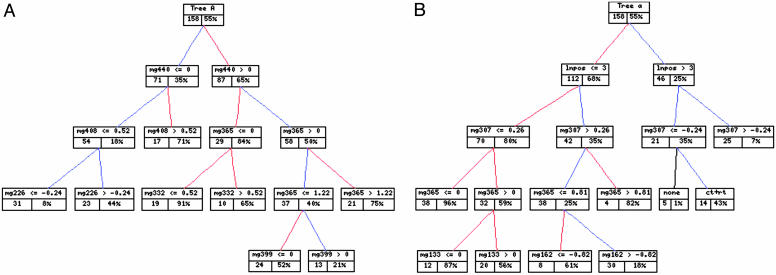
A tree model involving several metagenes is shown in Fig. 3A, where the development of branches involving additional metagenes and the resulting predictions of recurrence within the population subgroups are defined by each leaf. An individual patient is successively categorized down the tree to a unique terminal node, and the model-based survival probability in that node represents the point estimate of her risk.
Fig. 3.
Predictive genomic and clinicogenomic tree models. (A) Metagene tree model. The left box at each node of the tree identifies the number of patients, and the right box gives (as a percentage) the corresponding model-based point estimate of the 4-year recurrence-free probability based on the tree model predictions for that group. (B) Clinicogenomic tree model in a format as described in A. Note the appearance of interactions between lymph node status and Mg307 and Mg365, for example, in relation to the empirical survival curves and metagene expression images in Figs. 1 and 2.
At any given node of a tree model, there may be several metagenes defining significant subgroups, so it is important to consider multiple tree models. A resulting set of tree models is evaluated statistically by computing the implied value of the statistical likelihood function for each tree; the set of likelihood values is then converted to tree probabilities by summing and normalizing with respect to all selected trees. Predictions are based on all trees in combination, by means of weighted averages of predictions from individual trees with the tree probabilities acting as weights. This “model averaging” is well known to generally improve prediction accuracy relative to choosing one “best” model (25, 26), especially when several or many models fit the data comparably.
Statistical Prediction Tree Models Combining Metagenes and Clinical Risk Factors Predict Individual Breast Recurrence Most Accurately. The tree models were extended to explore all forms of input data, both genomic and clinical. Key clinical factors are lymph node status (represented as 0, 1–3, 4–9, and 10 or more positive nodes), ER status (represented as 0, 1, and 2 or more to reflect intensity of staining), tumor size, and treatment factors. Fig. 3B displays a highly significant tree contributing to the prediction of recurrence. The key clinical variable identified by these trees is nodal status; its appearance in highly weighted trees indicates that it supersedes some of the metagene predictors selected in the exclusively genomic analysis. ER status and tumor size also define secondary aspects of some of the top trees. Of hundreds of trees generated in the model search, others involve clinical predictors and also treatment variables, although these trees receive low relative statistical likelihood measures and resulting tree probabilities. Treatment protocols closely follow the traditional clinical risk groups that are dominated by lymph node status, and so the inclusion of nodal status substitutes for treatments in some trees. Others include treatment variables, as illustrated by the partition on the right branch in Fig. 3B into subgroups of patients receiving no treatment (none) versus combined chemotherapy and radiotherapy (ct+rt).
Once lymph node status is a candidate predictor, it defines key aspects of predictive trees and reduces the number of metagenes required to achieve accurate predictions. This result mainly reflects colinearity of predictors, indicating metagenes related to nodal status. ER status is a second clinical factor selected in some of the top trees. Some trees involve Mg20 with ER; Mg20 defines a group of genes related to the known risk factor Her-2-neu/Erb-b2 and represents the gene expression-based measure of this risk factor.
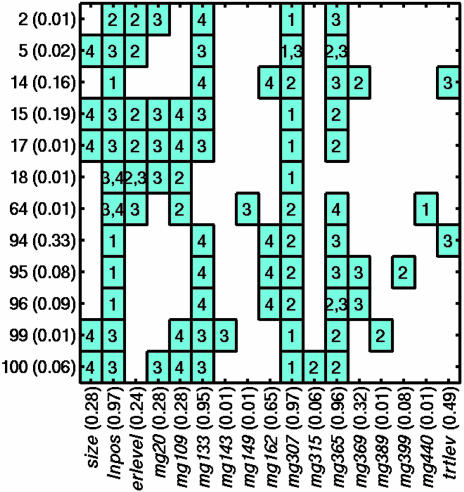
Fig. 4 summarizes the clinicogenomic model predictor variables selected. The figure indicates the predictor variables (columns) that appear in the selected top trees (rows), and the levels (boxed numbers) of the trees in which they define node splits. The probability of each tree and the overall probability of occurrence of each of the clinical and metagene factors across the set of trees are also given. Metagene Mg307 and the clinical lymph node predictor dominate the initial splits, with Mg440, a close correlate of Mg307, defining the initial split of other trees. The two models, based on genomic data alone and on the combined clinicogenomic data, thus share features. However, the clinicogenomic model statistically dominates the genomic data-only framework; the difference in approximate log-model likelihoods is >7, a substantial weight of evidence in favor of the clinicogenomic model. (The corresponding weight of evidence of the clinicogenomic model to that based only on clinical predictors is >26 units on the log-likelihood scale, indicating the latter to be of no interest at all relative to the clinicogenomic model.)
Fig. 4.
Predictor variables in top clinicogenomic tree models. Summary of the level of the tree in which each variable appears and defines a node split. The numbers on the y axis simply index trees, with probabilities (in parentheses) indicating the relative weights of trees based on fit to the data. On the x axis, probabilities (in parentheses) associated with clinical or metagene predictor variables are sums of the probabilities of trees in which each occurs and so define overall weights, indicating the relative importance of each variable to the overall model fit and consequent recurrence predictions.
Predicting Risk of Recurrence Based on Tree Model Summaries. Predictive accuracy assessment uses a one-at-a-time cross-validation study in which the analysis is repeatedly performed: holding out one tumor sample at each reanalysis and predicting the recurrence time distribution for that holdout patient. With many candidate predictors, the sensitivity of predictions to selection of variables is usually important, because the subsets of variables selected across cross-validation analyses can vary substantially (1, 3, 7, 22, 27, 28). Importantly, therefore, the entire model-building process, selection of metagenes and clinical factors and their combination in sets of trees to be weighted by the data analysis, forms part of each reanalysis to understand how prediction accuracy is impacted by the selection process.
The predictive probability of survival beyond any time point defines the predicted survival curve for an individual (Fig. 5). The statistical uncertainty about the model parameters in terminal nodes of a tree combined with the uncertainties across candidate trees generates uncertainties about these predicted survival curves. The estimated receiver operator characteristic (ROC) curves for 4- and 5-year survival (Fig. 6, which is published as supporting information on the PNAS web site) indicate the capacity to achieve up to 90% sensitivity and 90% specificity in predicting recurrence of disease even at such short time horizons. These figures are crude summaries of overall prediction accuracy that neglect consideration of uncertainties about predicted probabilities. Nevertheless, these numbers serve to indicate a high degree of accuracy. Also, consistent with the likelihood-based model-fit comparison, the combined clinicogenomic analysis exceeds the cross-validation predictive accuracy of the exclusively genomic analysis (<75% sensitivity to achieve comparable specificity) and also that of proportional-hazards-based analysis, which properly accounts for variable selection in model refitting for cross-validation predictions (<70% sensitivity to achieve comparable specificity).
Fig. 5.
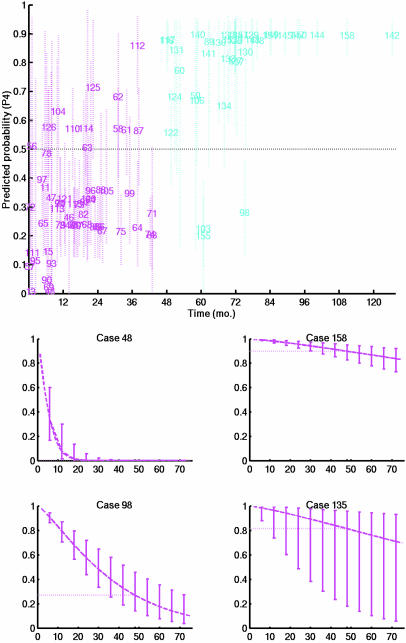
Predictions from a clinicogenomic tree model. (Upper) Estimates and approximate 95% confidence intervals for 4-year survival probabilities for each patient. The survival probability of each patient is predicted in an out-of-sample cross-validation based on a model completely regenerated from the data of the remaining patients. Each patient is located on the x axis at the recorded recurrence or censoring time for that patient. Patients indicated in blue are the 4-year recurrence-free cases, and those in red are patients with symptoms that recurred within 4 years. The interval estimates for a few cases that stand out are wide, representing uncertainty due to disparities among predictions from individual tree models that are combined in the overall prediction. (Lower) Summary of predictive survival curves and uncertainty estimates for four patients whose clinical and genomic parameters match four actual cases in the data set (cases indexed as 48, 158, 98, and 135).
Patients with <4 years of follow-up appear in Fig. 7, which is published as supporting information on the PNAS web site; their status at 4 years is predicted conditionally on their observed time of recurrence-free follow-up, again at the individual level.
Metagenes Can Predict and Substitute for Clinical Risk Factors. The combined clinicogenomic predictive tree analyses reveal that lymph node involvement appears in the key predictive trees, consistent with the wide recognition of lymph node involvement as the most significant clinical risk factor (1, 29–31). Because axillary node dissection carries significant morbidity, we proposed previously that a metagene analysis would be preferable to clinical lymph node diagnosis (1). We see in these analyses that the metagene signatures do indeed have some capacity to replace nodal counts, although the latter still aids in the construction of the most significant models in this study. As mentioned above, tree analysis without the use of clinical factors has good predictive capability but is dominated, in that predictive respect and in terms of statistical likelihood, by the combined clinicogenomic model.
Metagene Mg307 and, to a lesser extent, its close correlate Mg440 appear as candidates for initial splits in some of the top trees, with an initial lymph node risk categorization defining the initial split of other top trees. Also clearly of interest are Mg315 and Mg351, two of several metagenes that correlate strongly with ER status and involve genes within the estrogen pathway (7, 18); these metagenes now apparently substitute for ER status in the genomic data-only analysis.
A further metagene that appears with ER status in the combined model, Mg20, is based on 15 genes that define the Her-2-neu/Erb-b2 metagene cluster (Table 4, which is published as supporting information on the PNAS web site). Her-2-neu/Erb-b2 has previously been defined as a risk factor primarily among ER-negative cases (32), so its appearance here within a subset of ER-positive cases implicates Her-2-neu/Erb-b2 more broadly.
Prediction of Recurrence to Achieve Personalized Prognosis. The 4-year survival probability predictions in Figs. 5 Upper and 7 are taken from the full survival distributions that result from the statistical model analysis. At each terminal leaf of each tree, the analysis estimates a full survival time distribution that represents the survival characteristics of individuals assigned to the subpopulation with predictors defining that leaf. Formal predictions for an individual are based on averaging these survival distributions across tree models, each tree weighted by its corresponding data-based probability. The analysis also provides assessments of uncertainty about predicted survival curves; communicating these uncertainties along with estimates is critical to interpretation and assessment of survival prospects at an individual level. Fig. 5 Lower displays the resulting predictions for four example patients. Each panel gives the predicted survival curve for one patient. At a number of time points, the vertical intervals represent ≈95% uncertainty intervals for the predicted survival probabilities at those time points. Cases 48 and 158 are examples in which the confidence of prediction, whether for early recurrence or longer-term survival, is high, indicated by the narrow intervals around the predicted survival curve. The two additional cases are examples where uncertainty is higher.
Discussion
The breast cancer example shows the capacity of this analysis framework to evaluate the relative contributions of multiple forms of data, both clinical and genomic, in predicting disease outcomes. This study shows what is possible, in principle and by example, in terms of refining predictions to be specific for individual patients. Multiple, related metagene patterns have predictive value in association with breast cancer recurrence. Several key metagenes are each individually interesting risk factors, but, when combined in predictive models, small sets of metagenes together define improved predictions in the overall model that mixes over generated classification trees.
Prediction accuracy can be improved by combining clinical factors with genomic data. Key metagenes can, to a degree, replace traditional risk factors in terms of individual association with recurrence, but the combination of metagenes and clinical factors currently defines models most relevant in terms of statistical fit and also, more practically, in terms of cross-validation predictive accuracy. The resulting tree models provide an integrated clinicogenomic analysis that generates substantially accurate, cross-validated predictions at the individual patient level.
The models deliver formal predictive survival assessments, in terms of estimates of survival distributions for future patients and current patients being followed-up, together with measures of uncertainty about the predictions. The latter are critical in guiding clinical decisions. A point prediction of a survival probability, such as a 4-year-recurrence probability, is only part of the story; it is critical to also communicate how uncertain that probability estimate is, as measured by an interval estimate that integrates uncertainty due to sample size and sampling fluctuations together with uncertainty arising from potentially conflicting predictors. The specific approach using tree models highlights the latter issue, helping to identify individual patients for whom there is evidence of conflict within or between the genomic and clinical predictors; this conflict is reflected in increased uncertainty about the resulting recurrence predictions.
The technical modeling framework represents an approach that builds on standard classification trees (21, 23) and utilizes Bayesian methods in forward tree generation. These methods rely on prespecification of grids of potential thresholds for splitting nodes on chosen predictor variables and on the use of statistical approximations in inference on hyperparameters (see the supporting information). This approach represents a simplification and approximation to what is theoretically a fully Bayesian analysis, which is possible, in principle, with simulation methods (19, 20). The development of such an analysis is a major computational and technical challenge in problems like this one, when the number of potential predictor variables (clinical data and metagenes) is more than a few and research advances in statistical computation are needed to anticipate its implementation. The current analysis represents a first-step approximation to Bayesian posterior inference in the full theoretical framework; progress on computational aspects may lead to improvements with practical implications.
Our use of aggregate expression summaries, metagenes, follows our earlier work with empirical factors based on screened gene subsets (3, 7), then termed “supergenes.” Principal components (or singular factors) as aggregate measures of expression of sets of genes have been used in a number of recent studies in molecular phenotyping, whether applied to a full array profile or to selected gene subsets (3, 7, 33) or in the “gene shaving” framework (34), which aims to identify genes with coherent patterns of expression and large variation across samples (and which also, independently, used the term “supergene”). Our use of metagenes derived from direct clustering of genes into a larger number of gene subsets aims to reduce dimension while capturing key patterns, or “factors,” in the full set of genes across samples. This method is closely related, although somewhat reciprocal, to the use of “eigengenes” (33) to cluster genes according to common patterns. The goals of metagene construction are more closely allied to the method of gene shaving (34) that develops sequences of nested clusters of genes that successively remove from consideration genes apparently contributing little to the evaluation of dominant principal components. In contrast, however, our direct construction uses all genes and aims to construct larger numbers of clusters of generally smaller numbers of genes; the key goals are to reduce dimension (from thousands of genes to hundreds of metagenes) while keeping clusters relatively small, with a view to maintaining more homogenous patterns within each cluster so that the resulting, dominant principal component within each is properly representative of the cluster. Improvements in statistical methods for clustering and large-scale factor analysis (35) can be expected to refine and improve the specific method of metagene construction, the current cluster-based method being clearly very empirical and representing an initial step toward model-based improvements.
Key metagenes that provide predictive power also define sets of genes suggestive of biologically relevant pathways associated with clinical phenotypes. Of note are the primary metagenes Mg307 and Mg440, which involve a number of genes identifying growth-signaling pathways that are altered in a variety of oncogenic settings, as well as genes implicated in predicting lymph node status (1) that are generally associated with tumor immunosurveillance, which may relate to the involvement of processes associated with immunological response to the tumor. Additional implicated metagenes, including Mg109, Mg133, and Mg162, contain further oncogenes and genes involved in growth-signaling, and a number of ER-related metagenes, as already described, are identified in predictive trees. Thus, multiple metagenes represent patterns of expression related to multiple, distinct biological properties, suggesting that different aspects of biology are contributing to the prediction and ultimately reflecting the heterogeneity of the disease process.
The modeling process provides a framework for future studies in which other forms of clinical data (such as improvements in clinical phenotyping) as well as new forms of genomic data (DNA structure, protein patterns, metabolic profiles, single nucleotide polymorphisms, and haplotype data) will likely make significant contributions to the ultimate prediction of outcome. As technologies evolve to generate data that might better describe the clinical state, technology-independent models will provide mechanisms to evaluate such new information. This adaptability is immediately relevant in the context of developing extended studies that aim to refine and evolve our understanding of multiple forms of data relevant to moving genomic analysis through clinical trials to clinical practice.
Acknowledgments
We thank two anonymous reviewers for constructive comments on the original version of the manuscript. This work was supported by Synpac (Research Triangle Park, NC), the Koo Foundation Sun Yat-Sen Cancer Center Research Fund, and National Science Foundation Grants DMS-0102227 and DMS-0112340.
Abbreviation: ER, estrogen receptor.
References
- 1.Huang, E., Cheng, S., Dressman, H., Pittman, J., Tsou, M.-H., Horng, C.-F., Bild, A., Iversen, E., Liao, M., Chen, C.-M., et al. (2003) Lancet 361, 1590-1596. [DOI] [PubMed] [Google Scholar]
- 2.Perou, C. M., Sorlie, T., Eisen, M. B., van de Rijn, M., Jeffrey, S. S., Rees, C. A., Pollack, J. R., Ross, D. T., Johnsen, H., Akslen, L. A., et al. (2001) Nature 406, 747-752. [DOI] [PubMed] [Google Scholar]
- 3.Spang, R., Zuzan, H., West, M., Nevins, J., Blanchette, C. & Marks, J. (2002) In Silico Biol. 2, 369-381. [PubMed] [Google Scholar]
- 4.Sorlie, T., Perou, C., Tibshirani, R., Aas, T., Geisler, S., Johnsen, H., Hastie, T., Eisen, M. B., van de Rijn, M., Jeffrey, S. S., et al. (2001) Proc. Natl. Acad. Sci. USA 98, 10869-10874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.van' t Veer, L., Dai, H., van de Vijver, M., He, Y., Hart, A., Mao, M., Peterse, H., van der Kooy, K., Marton, M., Witteveen, A., et al. (2002) Nature 415, 530-536. [DOI] [PubMed] [Google Scholar]
- 6.van de Vijver, M., He, Y., van' t Veer, L., Dai, H., Hart, A., Voskuil, D., Schreiber, G., Peterse, J., Roberts, C., Marton, M., et al. (2002) N. Engl. J. Med. 347, 1999-2009. [DOI] [PubMed] [Google Scholar]
- 7.West, M., Blanchette, C., Dressman, H., Ishida, S., Spang, R., Zuzan, H., Marks, J. & Nevins, J. (2001) Proc. Natl. Acad. Sci. USA 98, 11462-11467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bertucci, F., Nasser, V., Granjeaud, S., Elsinger, F., Adelaide, J., Tagett, R., Loriod, B., Giaconia, A., Benziane, A., Devilard, E., et al. (2002) Hum. Mol. Gen. 11, 863-872. [DOI] [PubMed] [Google Scholar]
- 9.Pomeroy, S. L., Tamayo, P., Gaasenbeek, M., Sturla, L. M., Angelo, M., McLaughlin, M. E., Kim, J. Y., Goumnerova, L. C., Black, P. M., Lau, C., et al. (2002) Nature 415, 436-441. [DOI] [PubMed] [Google Scholar]
- 10.Alizadeh, A., Eisen, M., Davis, R., Ma, C., Lossos, I., Rosenwald, A., Boldrick, J., Sabet, J., Tran, T., Yu, X., et al. (2000) Nature 403, 503-511. [DOI] [PubMed] [Google Scholar]
- 11.Rosenwald, A., Wright, G., Chan, W., Connors, J., Campo, E., Fisher, R., Gascoyne, R., Muller-Hermelink, K., Smeland, E. & Stoudt, L. (2002) N. Engl. J. Med. 346, 1937-1947. [DOI] [PubMed] [Google Scholar]
- 12.Bhattacharjee, A., Richards, W., Staunton, J., Li, C., Monti, S., Vasa, P., Ladd, C., Beheshti, J., Bueno, R., Gillette, M., et al. (2001) Proc. Natl. Acad. Sci. USA 98, 13790-13795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ramaswamy, S., Tamayo, P., Rifkin, R., Mukherjee, S., Yeang, C.-H., Angelo, M., Ladd, C., Reich, M., Latulippe, E., Mesirov, J., et al. (2001) Proc. Natl. Acad. Sci. USA 98, 15149-15154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Golub, T., Slonim, D., Tamayo, P., Huard, C., Gaasenbeek, M., Mesirov, J., Coller, H., Loh, M., Downing, J., Caligiuri, M., et al. (1999) Science 286, 531-537. [DOI] [PubMed] [Google Scholar]
- 15.Shipp, M., Ross, K., Tamayo, P., Weng, A., Kutok, J., Aguiar, R., Gaasenbeek, M., Angelo, M., Reich, M., Pinkus, G., et al. (2002) Nat. Med. 8, 68-74. [DOI] [PubMed] [Google Scholar]
- 16.Yeoh, E.-J., Ross, M., Shurtleff, S., Williams, W., Patel, D., Mahfouz, R., Behm, F., Raimondi, S., Relling, M., Patel, A., et al. (2002) Cancer Cell 1, 133-143. [DOI] [PubMed] [Google Scholar]
- 17.Huang, E., Ishida, S., Pittman, J., Dressman, H., Bild, A., Kloos, M., D'Amico, M., Pestell, R., West, M. & Nevins, J. (2003) Nat. Genet. 34, 226-230. [DOI] [PubMed] [Google Scholar]
- 18.Pittman, J., Huang, E., Wang, Q., Nevins, J. & West, M. (2004) Biostatistics, in press. [DOI] [PubMed]
- 19.Chipman, H., George, E. & McCulloch, R. (1998) J. Am. Stat. Assoc. 93, 935-960. [Google Scholar]
- 20.Denison, D., Mallick, B. & Smith, A. F. M. (1999) Biometrika 85, 363-377. [Google Scholar]
- 21.Breiman, L., Friedman, J., Olshen, L. & Stone, C. (1984) Classification and Regression Trees (Chapman & Hall/CRC, Boca Raton, FL).
- 22.Breiman, L. (2001) Stat. Sci. 16, 199-225. [Google Scholar]
- 23.Ripley, B. (1996) Pattern Recognition and Neural Networks (Cambridge Univ. Press, Cambridge, U.K.).
- 24.Kass, R. & Raftery, A. (1998) J. Am. Stat. Assoc. 90, 773-795. [Google Scholar]
- 25.Hoeting, J., Madigan, D., Raftery, A. & Volinsky, C. (1999) Stat. Sci. 14, 382-401. [Google Scholar]
- 26.Clyde, M. (1999) Bayesian Stat. 6, 157-185. [Google Scholar]
- 27.Ambroise, C. & McClachan, G. J. (2002) Proc. Natl. Acad. Sci. USA 99, 6562-6566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Simon, R., Radmacher, M. D., Dobbin, K. & McShane, L. M. (2003) J. Natl. Cancer Inst. 95, 14-18. [DOI] [PubMed] [Google Scholar]
- 29.Jatoi, I., Hilsenbeck, S., Clark, G. & Osborne, C. (1999) J. Clin. Oncol. 17, 2334-2340. [DOI] [PubMed] [Google Scholar]
- 30.Cheng, S. H., Tsou, M. H., Liu, M. C., Jian, J. J., Cheng, J. C., Leu, S. Y., Hsieh, C. Y. & Huang, A. T. (2000) Breast Cancer Res. Treat. 63, 213-223. [DOI] [PubMed] [Google Scholar]
- 31.McGuire, W. (1987) Breast Cancer Res. Treat. 10, 5-9. [DOI] [PubMed] [Google Scholar]
- 32.Tandon, A., Clark, G., Chamness, G., Ullrich, A. & McGuire, W. (1989) J. Clin. Oncol. 7, 1120-1128. [DOI] [PubMed] [Google Scholar]
- 33.Alter, O., Brown, P. O. & Botstein, D. (2000) Proc. Natl. Acad. Sci. USA 97, 10101-10106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hastie, T., Tibshirani, R., Eisen, M. B., Alizadeh, A., Levy, R., Staudt, L., Chan, W., Botstein, D. & Brown, P. (2000) Genome Biol. 1, 1-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.West, M. (2003) Bayesian Stat. 7, 733-742. [Google Scholar]