Task-Driven Evaluation of Aggregation in Time Series Visualization

Abstract

Many visualization tasks require the viewer to make judgments about aggregate properties of data. Recent work has shown that viewers can perform such tasks effectively, for example to efficiently compare the maximums or means over ranges of data. However, this work also shows that such effectiveness depends on the designs of the displays. In this paper, we explore this relationship between aggregation task and visualization design to provide guidance on matching tasks with designs. We combine prior results from perceptual science and graphical perception to suggest a set of design variables that influence performance on various aggregate comparison tasks. We describe how choices in these variables can lead to designs that are matched to particular tasks. We use these variables to assess a set of eight different designs, predicting how they will support a set of six aggregate time series comparison tasks. A crowd-sourced evaluation confirms these predictions. These results not only provide evidence for how the specific visualizations support various tasks, but also suggest using the identified design variables as a tool for designing visualizations well suited for various types of tasks.

INTRODUCTION

Visualizations can support judgments over collections using two strategies: they may present raw data requiring the viewer to determine the aggregate properties, or they may compute these aggregate properties and present the derived data. For example, if the designer knows that the viewer is trying to find the maximal value in a series, they may either explicitly compute and encode the maximum, or choose a design that facilitates visual search for the maximum. While such computational aggregation can be precise, it requires knowing a priori which properties are relevant to the task. In contrast, visual aggregation relies on the capabilities of the viewer's visual system, necessitating visual encodings that allow for relevant properties to be determined effectively. Both strategies require a good match between design and task. However, aside from specific examples of designs that apply to specific tasks, there has been little exploration of the tradeoffs in how various design elements may apply to different tasks. By understanding how aggregation strategies combine with other design elements, we can better guide the design and selection of visualizations to support aggregate comparison tasks.

In this work, we identify three key variables in the design of visual displays, and explore their effect on viewers’ ability to carry out various aggregate judgment tasks. Visual variables [7] refer to the visual channels used to represent the data values, such as color, position, or orientation. Mapping variables refer to the the selection of which particular properties of the data to display, for instance choosing not to visualize an irrelevant data dimension, or creating a derived dimension from existing data. Computational variables describe the methods used to compress the signal, such as whether the aggregate is computed continuously or segmented over discrete regions of the series. Since no one choice of encoding will be appropriate for all tasks, and the tasks to be completed may not be known a priori, understanding the relationship between these three design variables and different types of aggregate comparisons provides guidance into the design of effective visualizations for sets of tasks.

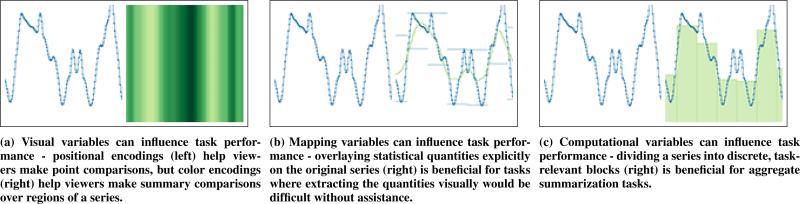
We explore the ability of these variables to characterize the relationship between task and design in the domain of time series data. Each design variable considers how a choice in the design of a visualization will affect its performance on different types of tasks. We analyze tasks requiring the comparison of individual data points as well as tasks which involve calculating and comparing higher order statistics through model problems using time series data. Our results show that all three variables offer robust predictions about performance. Figure 1 shows how consideration of these variables might lead to different design choices for different tasks.

Figure 1.

We can infer how well a particular encoding support a given task by examining the interplay of visual variables (what visual channels are used to encode value), mapping variables (which raw or derived quantities are visualized), and computational variables (how these quantities are computed).

BACKGROUND

Prior work considers connecting task analysis with visual design. The literature provides an extensive nomenclature for defining broad categories of tasks (see Roth [30] for a survey). Many task taxonomies, such as [4, 32], attempt to characterize the full breadth of visualization tasks. More recent work has focused on understanding design as a function of specific tasks, such as comparison [20], or domain-driven analytic workflows [3]. Our work attempts to empirically inform design specifically for visual aggregation tasks.

Existing literature suggests methods for tailoring visualization design to specific tasks. For example, visual boosting can assist in identification tasks [28] and comparison tasks can be helped by co-locating similar values [33]. The perception literature suggests principles that can be used for other task-specific designs, such as segmenting an encoding to support visual search [26] and numerosity estimation [17]. Our goal is to create a more general understanding of the connection of task and design elements, not just a particular one.

Graphical Perception of Time Series

Studies in graphical perception, beginning with Cleveland & McGill [12], have investigated how well viewers can extract specific details from displays and found that the choice of visual encoding matters a great deal. Time series are among the most common type of data explored in such studies. Graphical perception of time series has traditionally focused on line graphs, evaluating how different properties of the line, such as shape [27] and curvature [8], impact the types of judgments viewers make. Additional studies have explored how the visual variables of a line graph influence viewers’ abilities to compare values [22], how different representations support comparison across multiple series [23], and how interaction techniques could facilitate comparisons between series [24].

Studies of the graphical perception of time series have traditionally focused on tasks involving small sets of point values, yet these point tasks are only a subset of visualization tasks. More recently experiments have considered higher-level tasks and the perception of aggregate properties [13, 1, 19, 21]. For example, Aigner et al. [1] found that composite visualization techniques that leverage both color and position encodings better support multiple simultaneous judgment tasks than traditional techniques. Fuchs et al. [19] suggest the effectiveness of position encodings for trend comparisons.

Correll et al. [13] explore how time series displays can be specifically designed to support visual aggregation. The key to their design is to exploit the visual system's ability to make judgements over a field. The understanding of the visual system to see such ensemble statistics is an emerging topic in perceptual science (c.f. [5, 18]). In this paper, we seek to understand the connection between the design elements enabled by these perceptual phenomena, and the tasks they support.

Aggregate Visualization

Designers of visualizations are increasingly concerned with the problem of the scale of data. Several approaches to overcome scale constraints involve computationally reducing the dataset, see [16] for a survey. Alternatively, visual approaches, such as those used for graphs [15], compress and visualize structures drawn from the dataset. Several approaches for visually compressing time series data have been proposed. For example, Lammarsch et al. [25] focus on preserving details of an aggregate series by leveraging temporal hierarchies in calendar data, mapping averages from different time scales to color and nests these averages as a calendar.

Most work on aggregation has focused on average value. Recent work in sequence visualization considers other kinds of aggregates. In particular, both the Sequence Surveyor [2] and LayerCake [14] systems offer multiple techniques for aggregation. These systems suggest the value of tuning encodings to match aggregation tasks. In this work, we seek general guidelines and empirical support for such matchings.

INFORMING DESIGN THROUGH TASK

In contrast to prior work on graphical perception that focuses on how design influences the extraction of specific values, we seek to understand the relationship between elements of visualization design and their effectiveness for aggregate comparison tasks, which require comparisons between ranges of points. We consider two specific classes of aggregate comparison task: point comparisons and summary comparisons. Point comparisons require viewers to identify and compare points drawn from specific subsets of the data, such as monthly ranges, whereas summary comparisons compare values computed from entire ranges of the data, such as monthly averages. We explore these tasks using locate tasks [4], requiring comparisons of aggregated monthly data.

We identify three design variables that we believe offer predictive insight for matching task and encoding: visual variables, mapping variables, and computational variables. These variables arise from the types of choices a designer must consider when creating a visual encoding meant to deal with information in the aggregate. While these variables do not attempt to define the full breadth of encoding choices made by a designer, we believe that these design variables help characterize the tasks an encoding supports and, by understanding the relationship between variable and task, we can then tailor visualizations to better support the needs of viewers.

Visual variables refer to the choices in low-level visual properties used to represent data, such as position and color [7]. While graphical perception results suggest what encodings may provide the most precise extraction [12], results on visual aggregation suggest that different visual variables may be better for statistical summarization [13].

Mapping variables refer to which aggregate properties are computed and presented. For example, a visualization may show the raw data, averages, or extrema. The use of such computed aggregates allows the visualization to do work that would otherwise need to be done by the viewer, and can offer a degree of precision that cannot be achieved mentally. However, these computed statistics are task specific: the system must know which statistics are relevant to the viewer's goals, and avoid overwhelming the viewer with too many irrelevant ones. Mapping variables are more nuanced than simply encoding the “right” answer for a given task, a statistic that is not directly relevant may still help the viewer by serving as a benchmark for a related task.

Computational variables refer to how these aggregate properties are computed. For example, a given statistic, such as mean, may be computed over discrete ranges of the data or as a continuous moving average. Some of these choices allow the computation to fit the task, for example by blocking in groups relevant to the task, but this requires foreknowledge of the task. Interaction is commonly used to adjust computational variables to support tasks at different scopes.

These design variables make explicit the choices in designing a visualization that will affect the visualization's applicability to specific tasks. They allow a designer some predictive insight into how a proposed design may fit a set of tasks. These variables conceptually align with the filtering and mapping stages of the visualization pipeline [11] used to characterize visualization designs. However, our approach differs as we seek to inform design using task by characterizing explicit design choices rather than to more generally characterize visualization approaches. Further, the distinction between the granularity at which each encoded statistic is computed (computational variables) and how these statistics are encoded (visual variables) is important for constructing designs that support different varieties of aggregate tasks at different granularities within a series.

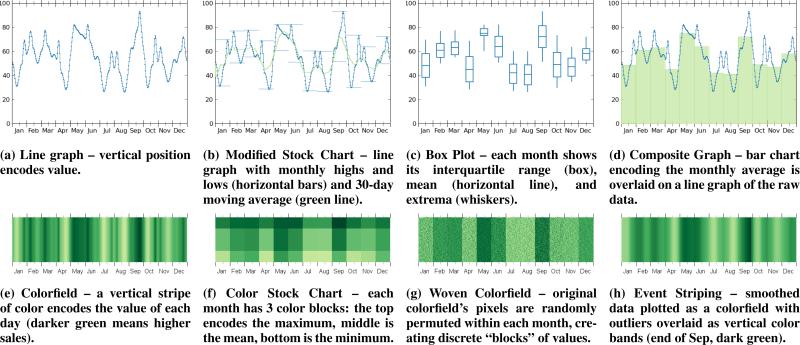
In the next section, we consider a range of existing designs (shown in Figure 2) for displaying times series data using these variables to predict each design's appropriateness for a range of tasks. This provides both a validation of the predictive power of these variables, as well as a better understanding of a set of known tasks and encodings.

Figure 2.

Visual designs explored in this experiment. The first two rows of encodings use position to encode value; the bottom two use color. Conditions 2d, 2b, 2c, 2g, 2f, and 2h calculate and display different statistics at the per-month scale, which requires prior task knowledge ( e.g. that the tasks will be performed at the scale of months).

HYPOTHESES AND EXAMPLES

Considering how each design variable is processed visually may help predict how different encodings support different visual aggregate judgments. In particular, each design variable independently allows us to make predictions about the performance of different visual encodings for various tasks:

• H1: Visual variables that support preattentive summarization, such as color, will better support summary comparisons for designs where aggregation is not done computationally, whereas visual variables with higher perceptual fidelity, such as position, will better support point comparisons.

• H2: Mapping variables that explicitly convey relevant statistics (either the exact task statistic or a benchmark statistic, such as the mean when estimating variance) will support more accurate comparisons, but will still be limited by how each statistic is computed and visualized.

• H3: Computational variables that provide task-aligned discrete aggregation will support more accurate aggregate comparisons than variables which are encoded continuously.

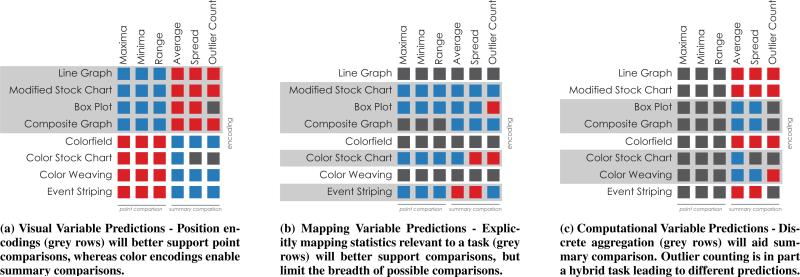
We confirm these predictions through an empirical study of eight encodings for time series data over six aggregate comparison tasks. For each task, we performed a between-subjects experiment to compare viewer accuracy for each encoding. The tasks, detailed in the Methods section, include three point comparison tasks (identifying the month with the largest value, smallest value, and largest range) and three summary comparison tasks (identifying the month with the highest average, spread, and outlier numerosity). The encodings, detailed in the next sections, vary with respect to each design variable: primary visual variable (position versus color), the set of mapping variables (value statistic explicitly encoded, benchmark statistics explicitly encoded, and no explicit task statistics), and the computational variable defining the continuity of the encoding (continuous versus discrete). Figure 3 summarizes the performance predictions made by each design variable for each encoding.

Figure 3.

We consider the design variables of a visualization in order to make predictions about how it supports different aggregate comparison tasks. We analyzed 8 time series visualization techniques using 3 variables, considering how each variable aligns with task requirements to hypothesize about their performance for 6 tasks. Blue squares indicate the variable aligns with the task, red show misalignments, and grey indicate no prediction.

Position-Based Encodings

Line graphs (Figure 2a) are the canonical approach for visualizing time series data using position. Position encodings support extracting exact values from a visualization [12]. However, prior theory suggests that their ability to convey summary insights, such as average, is limited [13].

Modified Stock Charts (Figure 2b) supplement summary judgments in line graphs by layering a moving average over the original series. Extrema of discrete regions are encoded using range bars. We anticipate that the presence of the moving average will help with summary comparisons, albeit the continuous mean aggregation may still limit value extraction from discrete regions. The increased saliency of the extrema as discrete range bars will better afford minimum, maximum, and range comparisons. However, the amount of information encoded by the chart may cause issues of visual clutter.

For some comparison tasks, summary statistics may sufficiently summarize the necessary information in a series. Box plots (Figure 2c) discretely compute and visualize the range, interquartile range (IQR), and mean of the series for each temporal region. The explicit encoding of these statistics may better afford comparisons of the encoded statistics, but does so at the expense of the raw data.

Composite graphs (Figure 2d) layer a line graph over a bar chart representing averages of discrete subregions. By explicitly mapping the mean value aggregated over each month, this approach may enhance the viewer’s ability to extract averages from the visualization without inhibiting their ability to extract point-level information from the original series. Visually encoding the average may also provide a benchmark statistic for comparisons requiring average extraction, such as spread (average distance from the average).

Color-Based Encodings

Recent work demonstrates that color encodings, such as those used in colorfields (Figure 2e), may better support average comparisons than position encodings [13]. Colorfields map each datapoint within a series to a point on a color scale, creating a one-dimensional heatmap. We anticipate that the perceptual system's ability to preattentively summarize color will support summary comparisons; however, we also anticipate that colorfields will be less effective for point comparisons due to the limited perceptual fidelity of color.

Color Stock Charts (Figure 2f) explicitly map the local extrema and average of each temporal range using color (average in the center, with top and bottom runners representing local maxima and minima respectively). This approach simplifies the visual computation required to extract point values from a colorfield while preserving some high-level statistics from the series; however, the performance benefit of this mapping may be limited by the ability of the color encoding to communicate each statistic. Further, encoding only these tasks statistics sacrifices the ability to extract data about local features or other distributional information.

Color weaving [2, 13] (Figure 2g) breaks local structures in a colorfield by randomly permuting data values at the pixel-level within each month. This technique encodes a series as task-blocked woven glyphs whose pixel-level distribution mirrors the distribution of values in each month. Prior studies have shown that by breaking this local structure, color weaving improves the perceptual system's ability to summarize the encoded values [13, 17]. The enhanced visual structures of color weaving may better afford average and spread comparisons; however, the increased difficulty of extracting a particular datapoint may complicate point comparisons using color.

Event striping [2, 14] (Figure 2h) highlights outliers in the dataset by representing outlier values as broad “stripes” drawn over a smoothed colorfield representation of the original series. Explicitly mapping outlier values within the series visually boosts unusual values while the smoothed colorfield preserves the context of the series. Event striping provides an example of an encoding designed specifically for a given task. Its visual design is very similar to colorfields; however, the design choices made to support outlier identification may influence how well the encoding supports other tasks.

METHODS

A series of experiments, one for each of six tasks (discussed below), compared the performance of viewers asked to make comparative judgments from time series data across the eight different visual encodings (described above). The experiments shared some common features across both tasks and encodings that we describe here. The Experiments and Results section describes the specifics of each experiment along with their results for clarity.

Each experiment focused on one aggregate comparison task. The encoding used to visualize the time series data was a between-subjects factor (see Figure 2). Accuracy (number of correct answers in a forced-choice setting) was the principle measure. Participants were instructed to be as accurate as possible, and allowed as much time as they needed, although exposure time was limited to promote progress through the task. We chose accuracy, rather than response time, as our performance metric, as accuracy allowed us to present stimuli that were more difficult, and thus more generalizable to real world datasets (see [21] for more discussion of this choice).

In piloting we observed a learning effect. To partially counteract this we presented participants with an initial set of four stimuli designed to show the heterogeneity of difficul-ties present in the task and also to help participants develop an initial understanding of the task and encoding. These initial “training” stimuli were excluded from analysis. We also randomly interspersed stimuli that were intentionally “easy” to serve as validation questions to gauge both validity of responses and participant understanding of task. For each task, we determined a minimum acceptable accuracy on validation questions based on piloting. We recruited additional participants to replace participants failing to reach this level. Validation stimuli were otherwise excluded from analysis. Each participant saw a total of 44 stimuli (4 training, 6 validation, and 32 experimental) and was paid $1.00.

We recruited all participants using Amazon's Mechanical Turk infrastructure. Each participant saw a brief tutorial explaining the encoding they were going to see as well as the statistical property they were meant to compare. After the tutorial, participants saw a series of individual graphs which we exposed for 20 seconds, after which we hid the stimulus. Participants could submit their answer at any point after the exposure of the graph. In very few cases (less than 4%) did participants take so long to answer that the graph was hidden. We informed participants whether or not they got the previous question right, and gave complete feedback at the end of the task. After the participant had answered every question, we collected demographics data.

Previous research has shown that Turk offers a reliable and diverse participant pool and provides a mechanism for rapidly recruiting a large number of participants [10]. While there are known limitations to using Turk, with proper care in experimental design, Turk studies have proven to be a reliable source of human subjects data for understaning the efficacy of designs for information visualization.

Tasks

Each experiment involved a comparison rather than exact calculation. For instance, rather than asking “what is the highest number in this time series?” (an extraction of a particular value) we might ask “in which month does the highest number occur?” (an extraction and then comparison amongst values). We had no knowledge of our participants’ statistical backgrounds, so the specific task questions had to be carefully phrased. For instance, range is the difference between the local minimum and maximum whereas spread sounds similar but considers variation amongst all points. There is little existing research on asking lay audiences about outliers and spread. For our experiments, we needed to determine effective ways of asking about these statistics. We generated candidate wordings by consulting the Simple English Wikipedia and evaluated these candidates in a pilot study on Mechanical Turk by asking participants to asses their comprehensibility and accuracy. We tested the following statistical properties, using the following final wordings:

1. Maxima: Which month had the day with the highest sales for the year?

2. Minima: Which month had the day with the lowest sales for the year?

3. Range: Which month had the largest range of values?

4. Average: Which month had the highest average sales for the year?

5. Spread: Look at the average sales from each month. Which month had the sales which were the most spread out from their monthly average?

6. Outliers: Which month had the most unusual (outlier) sales days?

For all experiments we presented time series of sales data for a fictional company over the course of a 12 month, 360 day “year” (to ensure months of equal length). For each task, we asked participants to make comparisons on the scale of months – e.g. “which month had the highest average sales?”. We believe this scale of data is substantial enough to make explicit calculation impossible given the time available to participants, but small enough to not overwhelm.

For all of these tasks, since the viewer's specific goal was known to the designer, the answer could have been given directly. However, our goal is to understand how visualizations work in settings where the designer may not know the exact goal of the viewer, or the viewer may have multiple goals.

Stimulus Generation

In order to run a controlled experiment, we needed to create data for our stimuli with a high degree of control. The data needed to have a sufficient balance of apparent randomness so that it appeared realistic but was unpredictable. We needed to control task difficulty and to vary the correct answer. Also, to ensure that the participant was answering the right question, we needed to explicitly decorrelate the answer from other statistics. For example, unless care is taken, the month with the highest average often contains the highest single point. If we do not explicitly decorrelate these statistics, the participant may find a strategy where they give the answer to the wrong question.

Because of these constraints, it was impractical to use real-world data. Therefore, we developed procedures to synthesize stimulus data. For all tasks, the data was created by blending together signals created by structured random noise [29] that gave control over perceived noisiness and allowed for local adjustment to create variation. A set of constraints were created that ensured that the resulting signals were valid data, and met the requirements of decorrelation and specific difficulties. The synthesizer fit each signal to these constraints, while minimizing the adjustment from the initial random signal. The final signals were created either by solving an optimization problem or by locally adjusting signals to achieve the correct properties. The data was pregenerated for each experiment, and checked for the appropriate properties. The same data was used for all encoding conditions in each experiment.

The stimuli for each experiment were generated from the data as pre-rendered images. Stimuli were presented to the viewer as losslessly compressed images to avoid variation in browser display. Color encodings used a green-yellow ColorBrewer sequential ramp [9].

Hardness Parameters

For each task, we considered a set of parameters which were associated with task difficulty either in past research or in our piloting. We leveraged three main dimensions of hardness: ▲, the difference in value between the correct month and the next highest months (lower ▲ meaning more difficult to discriminate between months), the number of distractor months (the number of months with the value x − ▲, where x is the correct highest value), and a qualitative dimension of noise. Each participant saw an equal number of each level of noise, while the number of distractors was randomly sampled across all stimuli. In each experiment there were two levels of noise ( “smoother” and “noisier” levels) and between one and four distractor months. Acceptable levels of ▲ were highly dependent on the task and were modified for each experiment based on piloting. In our experiments and in piloting, each hardness parameter was highly correlated with performance overall, although different encodings could reduce or eliminate this correlation. For example, two box plots encoding signals with equal variation and extrema look identical regardless of the frequency of the underlying signal, so noise would likely not impact task difficulty for box plots.

EXPERIMENTS AND RESULTS

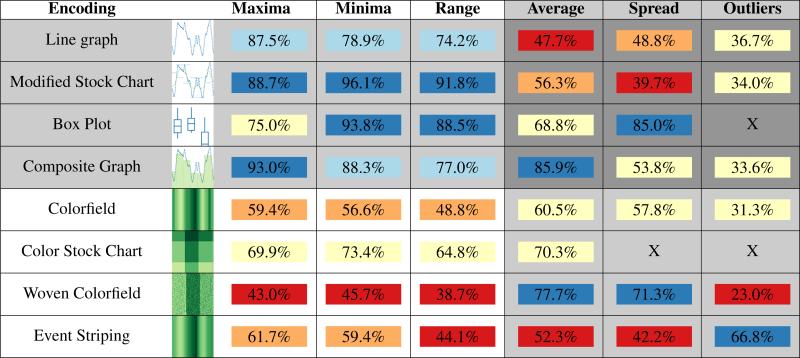
In this section, we detail each experiment and its results. Figure 4 summarizes our findings. For each experiment, we performed an Analysis of Covariance (ANCOVA) to determine the effect of encoding type on accuracy. The model also tested for interaction effects between encoding type and our hardness parameters (▲, distractor count, and noise level). Hardness parameters had generally highly significant effects in the expected direction (noisier signals underperform smoother signals, smaller ▲s are more difficult, etc.), and so we omit these factors from reporting unless unusual. For significant results, we performed Tukey's Test of Honest Significant Difference (HSD) with α = 0.05 to extract clusters of performance. We also performed post-hoc mean squared contrast tests to verify significant differences within clusters.

Figure 4.

A summary of our experimental results. All measures are in accuracy across all participants. Gray rows indicate position encodings; white indicate color encodings. Gray columns indicate summary comparison tasks; white columns indicate point comparison tasks. An ”X” indicates that the encoding does not afford that task. and so no experiment was conducted for this combination of task and encoding. Since performance is not strictly comparable across tasks, cell color encodes the number and direction of standard deviations from the task mean: −1,(-0.5,-1),[0.5,-0.5],(1,0.5), ≥1.

Including piloting and the main tasks, we recruited a total of 582 participants, 306 male and 276 female (μ_age=31.3, σ_age=10.3). A Student's t test showed no significant differences in performance across gender (μ_f=60.1%, μ_m=64.4%, p = .0938). For each experiment, 8 participants were recruited per encoding, totalling 64 participants for tasks evaluating all eight encodings, 56 for the spread experiment (which excluded color stock charts), and 48 for the outlier experiment (which excluded box plots and color stock charts), totaling 360 participants for the main experiments. If a participant failed to achieve acceptable performance on validation stimuli, we discarded their data and recruited additional participants for that condition. Across all experiments, 37 additional participants were recruited for this reason. Although accuracy was our performance metric, we tracked response time for each task and found the longer a participant spent on a particular question, the more likely they were to be incorrect (b = −1.6% accuracy/sec, Pearson's r = 0.83).

Maxima

For this task, participants were asked to locate the month containing the day with the highest absolute sales.

Maxima within the series were created by amplifying the peak in the base series and constraining all remaining values to be at least ▲ less. Especially in the color conditions where detecting individual points is difficult, we considered that picking the month with the highest average sales could be a confounding strategy, so we decorrelated the month with the highest average sales from the month with the highest absolute sales. We sampled evenly across ▲s of 1,2,3,4 with validation stimuli with ▲ = 20.

Encoding had a significant main effect (F (7, 2016) = 45.8, p < .0001). Generally, position encodings outperformed color encodings, with one exception. Box plots significantly under-performed all other positional encodings (F (1, 2016) = 24.5, p < .0001), and were not statistically significantly different from the color stock chart (F (1, 2016) = 1.70, p = .1930). The remaining color encodings performed significantly worse than the color stock charts (F (1, 2016) = 28.8, p < .0001) and the position encodings as a group.

These results support H1 – as this was a point comparison task, we expected position encodings to outperform color encodings, which are not as accurate for extracting exact values. There is partial support for H2 – color stock charts, which were the only color encoding to explicitly encode the maximum value in each month, outperformed other color encodings, while box plots, which were one of two position encodings to explicitly encode maximum values, undeperformed the other position encodings. This may be due to biases arising from visual properties of box plots that have been shown to impact the perception of whisker values [6].

Minima: For this task, participants were asked to locate the month containing the day with the lowest absolute sales. This task was functionally identical to the Maxima task – ques tions about “highest” were changed to “lowest” and the stimuli were derived using the same constraints as the Maxima task. Despite the similarities in the tasks, prior work [31] suggests that there are differences in performance between the two and that different encodings may be appropriate.

Encoding had a significant main effect (F (7, 1984) = 59.1, p < .0001). Within groups, line graphs significantly underper-formed the rest of the position encodings (F (1, 1984) = 25.5, p < .0001), and were only marginally better than color stock charts (F (1, 1984) = 2.76, p = .0966). The remaining color encodings proved significantly worse than the color stock charts (F (1, 1984) = 46.1, p < .0001), and also the position encodings as a group. Unlike other experiments (even the similar Maxima experiment), the noisiness of the signal had no significant effect on accuracy (F (1, 1984) = 0.18, p = .6725).

As in the Maxima experiment, these results support H1 – position encodings tended to outperform color encodings. H2 was more strongly supported than in the Maxima experiment – box plots and modified stock charts, which both explicitly encode monthly minima, outperformed line graphs, and color stock charts outperformed all other color encodings.

Range

For this task, participants were asked to locate the month with the largest range of sales – the largest gap between the maximum day and the minimum day. Initial piloting showed that participants would frequently confound the range with the maximum. To avoid confounds with the maximum and the related measure of spread, we explicitly decor-related these three quantities. The task proved more difficult than either of the extrema tasks as it required participants to compare the difference between two points. To avoid floor effects we sampled from ▲s of 4, 7, 10, and 15, with validation stimuli with ▲ = 20.

Encoding had a significant main effect (F (7, 1984) = 59.3, p < .0001). The color encodings all significantly underper-formed the position conditions. Encodings which explicitly encoded extrema performed significantly better than the other encodings of their type: color stock charts outperformed the other color encodings (F (1, 1984) = 45.8, p < .0001), and box plots and modified stock charts outperformed the other positional encodings (F (1, 1984) = 28.9, p < .0001).

As the range task is a pairwise point comparison task, these results support H1 – position encodings afford greater fidelity in extracting point values than color encodings. H2 is also supported. Box plots, modified stock charts, and color stock charts all explicitly encode local extrema values and all outperformed other encodings with equivalent visual variables.

Averaging

For this task, participants were asked to compare means of months. In piloting, the highest average value was often confused with the highest absolute value, so these values were decorrelated in the stimuli. We sampled ▲s of 1,2,3,4, with validation stimuli at ▲ = 20.

Encoding had a significant main effect (F (7, 1984) = 22.6, p < .0001). Encodings which explicitly encoded discrete monthly averages (the composite graph, box plot, and color stock chart) and discretely blocked woven colorfields significantly outperformed the remaining encodings (F (1, 1984) = 122, p < .0001) Within clusters, there were several pairwise results. In particular, composite charts outperformed woven color fields (F (1, 1984) = 4.24, p = .0395), and regular color-fields outperformed line graphs (F (1, 1984) = 11.4, p = .0008).

These results partially support H1 – colorfields, which support preattentive methods of summarization, outperformed line graphs, which do not. The data also partially support H2 – composite graphs, which explicitly encode mean, outperformed woven colorfields, which do not; however, color stock charts, which also explicitly encode montly averages, did not outperform woven colorfields, which leverage visual aggregation. The data more fully support H3 – all of the encodings which discretely aggregated the data per-month outperformed the other encodings.

Spread

For this task, participants were asked to compare the spread of each month. Since strict control over standard deviation requires complex optimization, we measured spread using the more practical related statistic of absolute deviation $\left(\frac{1}{n}{\sum }_{i=1}^n\mid x_i-\stackrel{‒}{x}\mid \right)$. Linear scaling about the monthly mean was used to tune the absolute deviation of individual months to fit our constraints. Even so, it is difficult to generate large differences in variation as each point must remain in the [0,100] interval. As “spread” is an ambiguous term, we decorrelated the month with the highest absolute deviation from the month with the largest range. To avoid floor effects for what was in piloting a difficult task, we sampled ▲s of 2,3,4, and 10, with validation stimuli with ▲ = 15 - the largest that could be reliably generated in sufficient numbers.

Encoding had a significant main effect (F (6, 1736) = 36.8, p < .0001). Box plots outperformed color weaving (F (1, 1736) = 13.7, p = .0002), which in turn outperformed all the remain ing encodings (F (1, 1736) = 50.0, p < .0001). Standard colorfields outperformed both boosted colorfields and modified stock charts (F (1, 1736) = 17.9, p < .0001). Noise had only a marginal effect on performance (F (1, 1736) = 3.39, p = .0656), and the number of distractors had no significant effect (F (3, 1736) = 0.847, p = .4679).

These results provide partial support for H1 – woven color-fields performed better than nearly all other encodings, as weaving allows for quick visual summarization of the variance of a region despite not explicitly encoding this value. H2 was fully supported – only box plots explicitly encoded a statistical variable that was highly correlated with absolute deviation ( IQR) and best supported this task. There was little support for H3 – while the top two encodings both explicitly blocked data together into months, composite graphs were not statistically different from any of the other encodings despite being blocked with respect to a benchmark statistic (average).

Outliers

For this task, participants were asked which month contained the highest number of outliers. The task required both extracting summary statistics and numerosity estimation of points violating these statistics. We generated outliers from existing signals by amplifying days varying largely from the series mean to between 2.25-2.75 standard deviations from the mean. To avoid visual “plateaus” where consecutive outliers appear as on data point, outliers were at least 3 days apart and no month contained more than 8 outliers. Spread can confound outlier count, so we decorrelated the month with the highest absolute deviation from the month with the most outliers by reducing the absolute deviation of the high outlier month. To avoid confounds between the month with the greatest number of outliers and the month with the largest outlier, we decorrelated the largest value from the month with the most outliers. For this task, ▲ means that if the winning month had x outliers, the other months had at most x ▲ outliers. We used ▲s of 1,2,3,4, with ▲ = 5 for validation.

Encoding had a significant main effect (F (5, 1488) = 28.3, p < .0001). A Tukey HSD showed two clusters - event striping outperformed all other displays (F (1, 1488) = 127, p < .0001). The only other significant difference among conditions was the color woven display, which under-performed all of the remaining conditions (F (1, 1488) = 11.4, p = .0008).

These results support H2 – by explicitly devoting space to outliers, event striping outperformed all other encodings.

DISCUSSION

Our results, summarized in Figure 4, confirm that different designs support different tasks. Our three identified design variables provide a mechanism for identifying elements of these designs that may be responsible for these differences.

• The choice of visual variables can allow the viewer to perform aggregation visually in cases where the quantity of interest is not explicitly encoded, or can facilitate discrimination between values which have been explicitly encoded.

• The choice of mapping variables can help the viewer by explicitly encoding the quantity of interest, but only if the relevant information is known.

• The choice of computational variables can align displayed information with the viewer's task if the task is known.

The results support the importance of these decisions: the predictions of how choices in these variables should influence the performance of the resulting designs are supported. For example, by matching display and task granularity, composite graphs, which display discrete monthly averages rather than as a continuous moving average, significantly outperformed modified stock charts for average comparison. They also suggest that substantial tradeoffs occur when designing for a specific task. For example, event striping underperformed standard colorfields for all summary tasks except for outlier detection, despite their visual similarity.

Our results further indicate interactions between design variables. For example, explicitly encoding relevant statistics may not overcome natural deficits in point value extraction in color displays, as with color stock charts for extrema and range tasks. In contrast, the affordances of color weaving for visual aggregation outweigh these issues with color for average and spread. This suggests the potential for designs informed by perceptual mechanisms.

Value for Design

Matching designs to tasks is important. Beyond providing empirical evidence of this importance to aggregation tasks in time series visualization, our findings provide actionable advice in how to consider such matching. As no design is likely to be effective for all tasks, designers must consider not only their understanding of the target tasks for a display, but also how specifically they want the display to support this task, at potential cost for other tasks.

By identifying three key design variables, our work provides specific questions for a designer to consider in matching visualizations to tasks. For aggregation tasks, the variables make explicit three key choices. Our work provides not only a set of questions to consider in matching designs to tasks, but also predictions as to how the choices will impact performance for different tasks. The variables can guide a structured exploration of the design space, for example, to generate composite designs for multiple tasks or to inform the design of multiple views, or can be used post-hoc to assess potential designs.

The possibility of effective visual aggregation provides new opportunities for designers to create visualizations that support aggregation tasks. The design variables provide connection between the emerging perceptual science and design goals, coupling task features to performance predictions. Our work demonstrates the benefits and costs of different design approaches enabling designers to make informed choices about using each approach.

Limitations and Future Work

Our experiment considers a small set of encodings and tasks for a specific but common data type. We believe these findings generalize to a wider range of situations, but have not confirmed this empirically. Our ability to more exhaustively test our theory is limited not only by the practical problem of running a vast number of experiments, but also in choosing tasks that can be assessed in our experimental setting. Our current evaluations focus on comparisons measured through a variety of locate tasks [4]. In the future, we plan to apply this analysis in more situations.

Our work does not consider the various costs and tradeoffs in combining design elements. For example, a design encoding multiple statistics may support multiple tasks, or cause clutter reducing its effectiveness at any one. Similarly, our present study does not consider the costs of misalignment between design and task. For example, does presenting data aggregated by month hurt performance at questions about weeks or data at weeks hinder tasks at months? In the future, we hope to better understand the tradeoffs of misalignment.

Our work focuses on static visualizations, emphasizing the importance of aligning tasks and design. However, interaction offers a mechanism for the user to specify their task, rather than requiring the designer to make assumptions about statistics and granularities of interest. Extending our work to consider interaction, including identifying new design variables, is important future work.

Other potential tradeoffs of design elements are not considered in this work. For example, when viewers must visually compute a statistic, there may be a performance cost, but they may also gain familiarity with the data, We hope to explore the benefits of such visual aggregation in the future.

CONCLUSION

We have provided an empirical evaluation of visualization design choices that helps match visual encodings to various aggregate comparison tasks. By identifying visualization design choices and showing how they affect performance for different types of task, we provide a mechanism for predicting performance and potentially designing new displays that better support combinations of tasks. In validating these choices, we have shown that viewers can reliably make aggregate judgments of various kinds, although their performance depends predictably on how the data is presented. Our results also suggest that no one encoding will dominate in every task – good visualization design must be merged with deep knowledge of the data and tasks to be considered. With careful consideration of design variables (how to encode, what to show, how to simplify), designers can make grounded choices about how data, visualization, and task interact.