Autoregulation of blood flow: Vessel diameter changes in response to different temperatures

Abstract

Autoregulation of blood flow is a marvelous phenomenon balancing blood supply and tissue demand. Although many chemically-based explanations for this phenomenon have been proposed and some of them are commonly used today, biomechanical aspects of this phenomenon was neglected. The biomechanical aspect provides insights to us to model vessel diameter changes more precisely and comprehensively. One important aspect of autoregulation phenomenon is temperature changes of the tissue resulted from tissue metabolism. We hypothesize that temperature changes can affect the mechanical properties of the vessel wall leading to vessel diameter changes during autoregulation. Mechanical modeling of vessel diameter changes can also be useful to explain other phenomena in which the vessel diameter changes in response to temperature alterations. Through the mechanical modeling of any vessel, the analysis of temperature-induced changes in vessel diameter can be done more precisely.

Introduction

Autoregulation of blood flow to body tissues is a marvelous phenomenon regulating blood flow in proportion to tissue demand: supplying high blood flow to a hyperactive tissue as well as low blood flow to a hypoactive tissue [1].

Many experimental data have been collected to explain this phenomenon through chemically-based approaches [2-5]. Broadly accepted today, blood flow to a tissue is autoregulated by tissue pressure of oxygen (O₂) and carbon dioxide (CO₂) as well as tissue concentration of cellular waste materials [1]. However, biomechanical aspects of this phenomenon have been neglected, which may provide us insights to upgrade the modeling of vessel diameter changes to a more integrated one. In this article, we describe a mechanically-based explanation for vessel diameter changes.

Mechanics of blood flow

Blood flow between two points of the circulation is determined as below:

$${\text{Q}}_{\left(\text{ml/s}\right)}=\frac{\partial {\text{P}}_{\left(\text{mmHg}\right)}}{{\text{R}}_{\left({\text{dyne.s/cm}}^{\text{5}}\right)}}\left(\text{Eq. 1}\right)$$

Where Q is the blood flow rate, ∂P is the blood pressure gradient, and R is the resistance to blood flow. The resistance, itself, is determined by (according to Poiseuille's Law):

$${\text{R}}_{\left({\text{dyne.s/cm}}^5\right)}=\frac{8{\eta }_{\left({\text{dyne.s/cm}}^2\right)}\text{.}{\text{L}}_{\left(\text{cm}\right)}}{\pi {\text{r}}_{\left(\text{cm}\right)}^4}\left(\text{Eq. 2}\right)$$

Where L is the length of the vessel, h is the blood viscosity, and r is the radius of the vessel lumen.

Therefore, blood flow is strongly proportional to the vessel radius. As the radius of the vessel lumen increases (called vasodilation), blood flow increases dramatically, and vice versa [1].

A vessel as an elastic tube

Elastic materials respond to any applied stress by elongating (strain), according to its Young’s modulus [6]. Young's modulus, E, which is a characteristic index of a material is calculated by dividing the tensile stress, s, by the tensile strain, e:

$$\text{E}=\frac{\text{tensile stress}}{\text{tensile strain}}=\frac{\sigma }{\epsilon }\left(\text{Eq. 3}\right)$$

where tensile strain, itself, is defined in an elastic tube as:

$$\epsilon =\frac{\partial \text{L}}{{\text{L}}_{\circ }}=\frac{2\pi \left(\text{r}-{\text{r}}_{\circ }\right)}{2\pi {\text{r}}_{\circ }}=\frac{\left(\text{r}-{\text{r}}_{\circ }\right)}{{\text{r}}_{\circ }}=\frac{\partial \text{r}}{{\text{r}}_{\circ }}\left(\text{Eq. 4}\right)$$

where ∂L is the amount of the length changes; L_o is the original length of the object, and r is the radius of the tube lumen if the object is transformed to a tube.

Tensile stress (TS) applied on the tube wall is directly proportional to the intraluminal hydrostatic pressure, Figure 1. TS is defined as:

Figure 1.

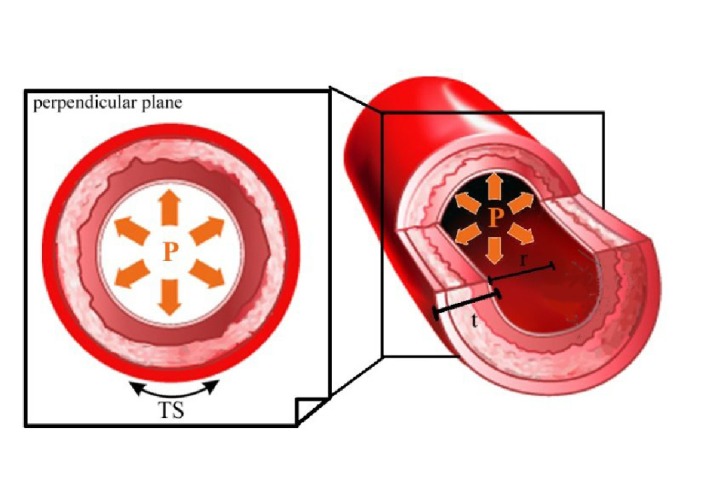
Tensile stress (TS) applied circumferentially on the vessel wall is derived from the hydrostatic blood pressure (TS=Pr/t; P = hydrostatic blood pressure, r = lumen radius, t = wall thickness).

$$\text{TS}=\sigma =\frac{\text{P.r}}{\text{t}}\left(\text{Eq. 5}\right)$$

where P is the intraluminal hydrostatic pressure, r is the radius of the tube lumen, and t is the thickness of the tube wall.

If we consider a segment of a vessel as an elastic tube, Figure 1, TS applied on the vessel wall can be calculated by determining the intravascular hydrostatic blood pressure, the radius of the lumen, and the thickness of the vessel wall (Eq. 5). Tensile strain can be determined experimentally (Eq. 4). Therefore, Young’s modulus of the vessel wall can be achieved (Eq. 3).

Hypothesis

When parenchymal cells of a tissue become more active, higher amount of heat energy is emitted from the hyperactive cells making the tissue warmer. The heat energy is transferred to the vessel wall causing it warmer. We hypothesize that temperature changes can alter Young’s modulus of the vessel wall. Therefore, as temperature of the vessel wall increases, Young’s modulus of the wall decreases, and vice versa.

$$\text{E}\propto \frac{1}{\text{T}}$$

where E is Young's modulus and T is the temperature of the vessel wall.

Thus, in a vascular segment, if TS of the vessel wall is assumed to be constant (Eq. 5), any decrease in Young’s modulus leads to increase in tensile strain (Eq. 3). In this condition, the amount of the vessel radius changes, ∂r, increases resulting in vasodilation (Eq. 4). On the other hand, when temperature of the vessel wall decreases, Young’s modulus of the wall increases leading to vasoconstriction.

Discussion

The present explanations for autoregulation of blood flow are commonly based on chemically-mediated approaches [2-5]. It is commonly accepted that tissue pressure of O₂ and CO₂ as well as tissue concentration of cellular waste substances have essential roles on autoregulation [1]. If tissue pressure of O₂ in a hyperactive tissue decreases, blood flow to the tissue increases via vasodilation. Moreover, high tissue concentration of waste substances and CO₂ in the hyperactive tissue may enhance this effect. On the other hand, in a relatively hypoactive tissue, high tissue pressure of O₂ and low tissue concentration of waste substances may decrease the radius of the vessel lumen. This scenario described a simple chemically-based explanation for vessel diameter changes occurred during autoregulation.

Although the above scenario may be a reasonable explanation for autoregulation phenomenon, we have looked for a more integrated model through which vessel diameter changes can be explained and analyzed more precisely. If we take into account the biomechanical properties of the vessel wall and the effects of temperature changes on them, we may model and calculate vessel diameter changes in response to different tissue temperatures resulted from tissue metabolism.

In addition to autoregulation phenomenon, our proposed model can be useful to explain other phenomena leading to vessel diameter changes in response to changes in temperature. For example, skin vessels become dilated when they are exposed to high temperature [7, 8], and cooling of them leads to vasoconstriction [9]. Although many explanations for this phenomenon have been proposed including neurally or chemically-mediated [9-14], no definite neural or chemical agents have been proved to be responsible for temperature-induced changes in vessel diameter. Any agent which is released into the vessel wall may alter the mechanical characteristics of the wall. Therefore, in our model, the role of neural or chemical agents released into the vessel wall is to change the mechanical properties and Young’s modulus of the vessel wall. Thus, in order to explain and analyze the changes in vessel diameter, we should consider the effect of neural and chemical agents as well as temperature changes on Young’s modulus of the vessel wall.

In some conditions, neuro-chemical agents and temperature changes may counteract. For example, in some pathologic conditions, like sepsis or heat stroke, clinical data show that splanchnic vessels become constricted despite increase in body temperature upto 41.5 ^oC [15, 16]. Although according to our model, it is predicted that the vessels become dilated in response to increase in temperature, the effect of high tissue concentration of neuro-chemical agents on Young’s modulus of the vessel wall should not be neglected. In these catastrophic conditions, the increasing effect of high tissue concentration of neuro-chemical agents on Young’s modulus of the vessel wall is more potent than the decreasing effect of high temperature. However, clinical evidences show that higher temperature (over 41.5 ^oC) overwhelms the strong effect of neuro-chemical agents leading to decrease of Young’s modulus and vasodilation [17-22]. Moreover, in all conditions in which vessels are isolated and relatively free of the counteracting effects of neuro-chemical agents, the diameter of vessels, even splanchnic vessels, increases in response to moderate increase in temperature, even below 41.5 ^oC [21, 23, 24].

Conclusion

Temperature change of the vessel wall affects its mechanical properties, and it may be inversely proportional to Young’s modulus of the vessel wall. Therefore, through the mechanical modeling of any vessel, temperature-induced changes in vessel diameter can be explained more accurately than that through neurochemically-mediated approaches alone. Moreover, the analysis of the vascular response to different temperatures can be done more precisely and comprehensively.

Conflict of Interests: The authors do not have any conflict of interests, and any funding source.