Linking ecophysiological modelling with quantitative genetics to support marker-assisted crop design for improved yields of rice (Oryza sativa) under drought stress

Abstract

Background and Aims

Genetic markers can be used in combination with ecophysiological crop models to predict the performance of genotypes. Crop models can estimate the contribution of individual markers to crop performance in given environments. The objectives of this study were to explore the use of crop models to design markers and virtual ideotypes for improving yields of rice (Oryza sativa) under drought stress.

Methods

Using the model GECROS, crop yield was dissected into seven easily measured parameters. Loci for these parameters were identified for a rice population of 94 introgression lines (ILs) derived from two parents differing in drought tolerance. Marker-based values of ILs for each of these parameters were estimated from additive allele effects of the loci, and were fed to the model in order to simulate yields of the ILs grown under well-watered and drought conditions and in order to design virtual ideotypes for those conditions.

Key Results

To account for genotypic yield differences, it was necessary to parameterize the model for differences in an additional trait ‘total crop nitrogen uptake’ (N_max) among the ILs. Genetic variation in N_max had the most significant effect on yield; five other parameters also significantly influenced yield, but seed weight and leaf photosynthesis did not. Using the marker-based parameter values, GECROS also simulated yield variation among 251 recombinant inbred lines of the same parents. The model-based dissection approach detected more markers than the analysis using only yield per se. Model-based sensitivity analysis ranked all markers for their importance in determining yield differences among the ILs. Virtual ideotypes based on markers identified by modelling had 10–36 % more yield than those based on markers for yield per se.

Conclusions

This study outlines a genotype-to-phenotype approach that exploits the potential value of marker-based crop modelling in developing new plant types with high yields. The approach can provide more markers for selection programmes for specific environments whilst also allowing for prioritization. Crop modelling is thus a powerful tool for marker design for improved rice yields and for ideotyping under contrasting conditions.

INTRODUCTION

Rice (Oryza sativa) yield has been successfully improved during the last 60 years for both favourable and stressful environments (Peng et al., 2008), through extensive, largely empirical, selection. Developments in genomics provided useful tools and information for dissecting complex traits into single quantitative trait loci (QTLs). QTLs related to important agronomic traits, such as yield and stress tolerance, have been mapped, cloned and characterized (e.g. Xing et al., 2008; for reviews, see Miura et al., 2011; Xing and Zhang, 2011). These developments have provided a firm basis for further improving yield through marker-assisted selection or genetic transformation of crops. However, selection for, or transformation of, only a few or even a complex of genes may not result in a major yield increase (Sinclair et al., 2004; Yin and Struik, 2008). While proven for disease and quality traits, the marker based approach has rarely been proven successful for complex traits such as yield, which typically have low heritabilities and exhibit strong genotype × environment (G × E) interactions (Collard and Mackill, 2008).

The complexity of the yield trait stems from its many underlying processes, which are often environment dependent and show strong feedback and feedforward mechanisms during crop growth. Crop yield can be evaluated using ecophysiological crop simulation models that integrate information about processes at lower levels (Yin and Struik, 2008; Hammer et al., 2010; Zhu et al., 2011). Such models quantify causality between relevant physiological processes and responses of these processes to environmental variables (e.g. irradiance, temperature and availability of water and nutrients). By feeding crop models with weather data from other locations, these models predict yield beyond the environments in which the model parameters were derived and could explain variation in yield of a specific genotype among contrasting environments (Yin et al., 2000a; Sinclair, 2011).

The other type of model inputs are model parameters, often referred to as ‘genetic coefficients’ (Messina et al., 2006; White et al., 2008; Boote et al., 2013). Compared with yield itself, these parameters are thought to be less affected by variation in environment (Yin et al., 2000a). Modelling could thus assist in quantifying the G × E interactions and genotype–phenotype relationships (Yin et al., 2004; Reymond et al., 2004; Hammer et al., 2005; Yin et al., 2005a; Hammer et al., 2006; Chenu et al., 2008; Bertin et al., 2010; Tardieu and Tuberosa, 2010; Messina et al., 2011). This is especially true given advances in the use of molecular markers to map QTLs for model parameters and to integrate this QTL information into the crop models (Yin et al., 2000b; Reymond et al., 2003, 2004; Nakagawa et al., 2005; Quilot et al., 2005; Uptmoor et al., 2008; Xu et al., 2011). This ‘QTL-based modelling’ approach can dissect complex traits into physiologically relevant component traits, integrate effects of QTLs on the component traits over time and space at the whole-crop level and predict a complex trait of various allele combinations under different environmental conditions (Chenu et al., 2009; Yin and Struik, 2010). Such a QTL-based modelling approach was proven to be robust in predicting genetic differences in traits, such as leaf elongation rate in maize (Reymond et al., 2003), flowering time (Nakagawa et al., 2005; Yin et al., 2005a; Uptmoor et al., 2008, 2012) and fruit quality (Quilot et al., 2004, 2005; Bertin et al., 2010; Prudent et al., 2011), under different environmental conditions. A major challenge is to predict phenotypic differences in crop yield between relatively similar lines from a genetic population on the basis of QTL-based model parameters (Yin et al., 2000a, b), especially under stressful conditions.

In the present study, we followed the same approach and used the crop model GECROS (Yin and van Laar, 2005) to simulate variation in grain yield and biomass of biparental crosses of rice under well-watered and drought stress environments. Based on the experience of using an older crop model (Yin et al., 2000a, b), the GECROS model was designed in such a way that its input parameters include those close to the traits breeders score for selection. Given the plethora of genetic factors underlying yield, we aimed to analyse the relative importance of individual markers in accounting for variation in yield. To that end, we calibrated the GECROS model to account for yield differences among introgression lines (ILs) of rice. We identified markers for each model input parameter, and incorporated the effects of these markers to develop a marker-based model. In addition, the marker-based model was extrapolated to account for yield variation among recombinant inbred lines (RILs) derived from the same parents. Finally, we examined whether our modelling approach could enhance marker-assisted crop design for improving yields.

MATERIALS AND METHODS

To achieve the above objectives, we followed a pair-wise methodology (Fig. 1). Its individual steps are described in the following sections.

Fig. 1.

Diagram of the methodology used in this study, which combines a simple genetic model, eqn (1), and an ecophysiological crop model, GECROS, into the marker-based crop modelling, in order to rank the relative importance of the identified markers and to design ideotypes for improving rice yield. For acronyms of parameters of GECROS, see Table 1. IL(s), introgression line(s); RIL(s), recombinant inbred line(s).

Plant material and field experiments

The genetic population consisted of 94 advanced backcross ILs and two parents, as described by Gu et al. (2012a). The parents were the lowland cultivar ‘Shennong265’ (japonica, recurrent parent) and the upland rice ‘Haogelao’ (indica–japonica intermediate, donor parent). ‘Haogelao’ is drought tolerant, but low-yielding; ‘Shennong265’ is drought susceptible, but high-yielding under irrigated conditions. After a cross between the two parents, the resultant F₁ plants were backcrossed with ‘Shennong265’ three times, and these BC₃F₁ plants were consecutively self-pollinated five times to construct the genetic population by the single-seed descent method.

Field experiments were conducted to assess model parameters and to measure grain yield and shoot biomass (two major model output traits). The ILs and the two parents were sown on 10 May 2009 by direct seeding at the experimental station of China Agricultural University, Beijing (39°54′N, 116°24′E; elevation 50 m a.s.l.), China (Gu et al., 2012a). The mean temperature was 24·8 °C, the total precipitation was 384 mm and the mean global radiation was 16·7 MJ m⁻² d⁻¹ during the growing season. During grain set, maximum temperatures reached values up to 39·6 °C. The soil was classified as a calciaquoll, containing 23·5 % sand, 57·1 % silt and 19·4 % clay. The field experiments followed a randomized complete block design, with two replications, four rows of 2·5 m per plot, 0·30 m between rows, in both rainfed upland and fully irrigated lowland conditions. Seed was hand sown at a depth of 0·03–0·04 m. At the seedling stage, plants were thinned to a 0·075 m distance between plants within each row, resulting in a plant density of 44·4 plants m⁻². Weeds in both conditions were controlled by a combination of chemical and manual methods. Insects and diseases were controlled chemically. Basal fertilizer application included 48 kg N ha⁻¹ (as urea), 120 kg P₂O₅ ha⁻¹ and 100 kg K₂O ha⁻¹; in addition, 86 kg N ha⁻¹ was applied at the tillering stage and 28 kg N ha⁻¹ at the booting stage. For fully irrigated lowland conditions, rice was grown under continual standing water until harvest. For rainfed upland conditions, besides rainfall, irrigation was only applied when necessary at critical stages (i.e. at sowing, 120 mm; at tillering, 150 mm; and at booting, 130 mm).

An independent population of 251 RILs derived from the same parents (La, 2004; Zhang, 2006) was sown on 7 May 2005 by direct seeding at the experimental station in Zhuozhou (39·29′N, 115·59′E; elevation 45 m a.s.l.), China (Zhang, 2006). The mean temperature was 25·3 °C, the total precipitation was 331 mm and the mean global radiation was 16·7 MJ m⁻² d⁻¹ during the growing season. The experiment design and management for both irrigated lowland and rainfed upland conditions were the same as in the field experiments in Beijing in 2009.

Measurements conducted in the experiment for ILs were: grain yield and yield components (grains m⁻² and grain weight), above-ground biomass, flowering date, maturity date, plant height, leaf area and weight, and grain nitrogen concentration which was determined by means of micro-Kjeldahl digestion and distillation. ‘Total crop nitrogen uptake at maturity’ (N_max) was determined based on dry weight and the nitrogen concentration in plant organs, assuming that nitrogen concentration in straw was conservative at 0·463 % (see data of Singh et al., 1998), and nitrogen accumulation in the roots was assumed to be 5 % of N_max (Yin and van Laar, 2005)_. Phenology, grain yield and biomass were also measured from the experiment for RILs.

The crop growth model

The model used in this study was the crop growth model GECROS, first described by Yin and van Laar (2005). GECROS is a generic model that simulates the growth and development of the crop on a daily basis. It generates phenotypes for a multitude of traits, based on concepts of the interaction and feedback mechanisms among various contrasting components of crop growth, carbon–nitrogen interaction in particular (Yin and Struik, 2010). Crop phenology, canopy photosynthesis, canopy transpiration, crop respiration, nitrogen uptake, partitioning of carbon and nitrogen assimilates among growing organs, green surface area index and senescence are among the physiological processes or traits that the model simulates. The summary information about the latest GECROS model (v3.0) is given in Supplementary Data, Model Description (see also Yin, 2013). For a given set of model parameters and environmental conditions, the model produces simulated grain yield and biomass as output variables.

Model inputs, parameterization, calibration and test

The weather inputs for the GECROS model are daily radiation, vapour pressure, maximum and minimum temperature, rainfall and wind speed. These required weather data were collected from a nearby weather station in 2005 (experiment with RILs) and 2009 (experiments with ILs) at Zhuozhou and Beijing, respectively. Atmospheric CO₂ concentration and the amount of irrigated water were also used as model input.

A complete set of model parameters (Table 1) was determined for each IL from data collected in the experiment under well-watered conditions in 2009. These parameters, covering various morphological, phenological and physiological characteristics of the crop, are: individual seed dry weight (S_W), seed nitrogen concentration (n_SO), maximum plant height (H_max), the minimum number of days for the vegetative growth phase (m_V) or for the reproductive (seed-fill) phase (m_R) provided both photoperiod and temperature are optimal, and specific leaf area constant for newly appeared leaves (S_la). Table 1 also lists measured N_max as a model parameter. N_max per se, as an accumulative quantity in the crop life cycle, is not considered as a model parameter of the original GECROS. However, there was not sufficient information about the soil at the experimental sites, and modelling of nitrogen availability for transition between flooded and non-flooded soil environments is complex and usually full of uncertainties (Gaydon et al., 2012). The model without using observed N_max did not simulate yield differences among the ILs sufficiently (see the Results). To reduce an influence of uncertainties in predicting edaphic variables for nitrogen supply on our model-based sensitivity analysis to identify important markers (see below), we treated N_max as if it were a model parameter.

Table 1.

List of genotype-specific parameters of the GECROS model (see the Materials and Methods)

Trait	Description	Units
SW	Seed dry weight	g d. wt seed−1
nSO	Seed (storage organ) N concentration	g N g−1 d. wt
Hmax	Maximum plant height	m
mV	Minimum days for vegetative growth phase	d
mR	Minimum days for reproductive (seed fill) phase	d
Sla	Specific leaf area constant of newly appeared leaves	m2 leaf g−1 d. wt
Nmax	Total crop N uptake at crop maturity*	g N m−2 ground

d. wt, dry weight; N, nitrogen.

*Not an input parameter in the original GECROS (see the text).

All model parameters were estimated for each genotype from the well-watered treatment of the 2009 experiment in Beijing. Parameters m_V and m_R are calculated based on a flexible bell-shaped non-linear function of phenological response to temperature (Yin et al., 2005b), flowering time and harvest time for each IL. For other non-genotype-specific model parameters and setting initial conditions of simulation, default values described by Yin and van Laar (2005) for rice were used for all lines.

To test the model, simulated dry grain yield and dry shoot biomass were compared with measured data for both ILs and RILs. To evaluate the model outputs, we used the relative root mean square error (rRMSE; Wallach et al., 2006), calculated as the root mean square error divided by the mean of the observed value. In addition, the R² coefficient of linear regression between simulated and observed values was used to indicate the percentage of phenotypic variation accounted for by the model.

Statistical identification of markers for model parameters and yield

A total of 130 simple sequence repeat (SSR) markers and their position for the IL population were reported previously (Gu et al., 2012a; see also Supplementary Data Fig. S1). In order to select markers which could be potentially used for breeding, the effects of markers were analysed using a two-stage approach as described by Gu et al. (2012a). First, using the general linear model (GLM) procedure in the statistical package SAS 9·2 (SAS Instute Inc.), one-way analysis of variance (ANOVA) was used to test the significance (P < 0·05) of markers across the whole genome. Secondly, all significant markers were put into a multiple regression model in a GLM procedure, using eqn (1) where a model parameter value Y (listed in Table 1) of introgression line k, as affected by N markers, was presented as:

$$Y_k=\mu +{\mathrm{\Sigma }}_{n=1}^N{a}_n{M}_{k,n}$$ (1)

where μ is the intercept and a_n is the additive effect of the nth marker; M_{k, n} is the genetic score of the nth marker of the individual introgression line k that takes either the value –1 if the allele comes from recurrent parent ‘Shennong265’ or the value 1 if it comes from donor parent ‘Haogelao’. We used this simple additive model, as additive genetic effects are predictably transmitted to progeny and more complex effects on model parameters are presumbly taken into account by ecophysiological crop models (Chapman et al., 2003). There may be non-significant markers in the multiple regression because of the collinearity of markers (Martens and Næs, 1992; Næs and Mevik, 2001). The non-significant marker with the highest P-value was excluded in the next round of multiple regression. This approach left out one marker at a time, until all markers in the multiple regression became significant (P < 0·05) (Ott and Longnecker, 2010).

Incorporating the effects of identified markers into a crop model

Using the principle as described previously (Yin et al., 2000b, 2005a), the effects of the markers identified in the preceding step were fed to GECROS for simulating differences in yield and biomass among the ILs (Fig. 1). This was achieved by replacing the measured parameter values with the marker-based parameter values of GECROS. The marker-based parameter values were calculated using eqn (1) for each genotype, based on the estimated additive effects, i.e. a_n in eqn (1), for each parameter and the marker allelic information of the ILs. The same approach was used to derive parameter values, based on addititive effects of markers and the marker alleles of RILs, when using GECROS to simulate yield differences among individuals of the RIL population.

Identifying important yield-determining markers and ideotype design

Linear regression analyses were performed to identify which model parameter in Table 1 influenced yield most. A sensitivity analysis using the GECROS model was performed to identify the contribution of single markers to yield production, by following the approach of Yin et al. (2000a), i.e. examining yield variation accounted for by the GECROS model when the tested marker was excluded in estimating the marker-based model parameters. First, the baseline simulation was conducted, where IL-specific allelic values for all markers were used as input for simulation. Then, allelic values were fixed, one marker at a time, at zero (Fig. 1). The extent to which the percentage of yield variation accounted for (R²) was decreased relative to the percentage accounted for in the baseline simulation was used to rank the relative importance of the markers in determining grain yields: the more R² decreases, the more important is the marker. The ranking of markers identified by GECROS was compared with that from the conventional analysis of yield data per se. Furthermore, simulated yields of ideotypes designed by pyramiding yield-increasing alleles of model-identified markers were compared with the simulated yields of ideotypes designed by pyramiding those markers identified by analysing yield per se.

RESULTS

Phenotypic variation in yield and physiological model parameters

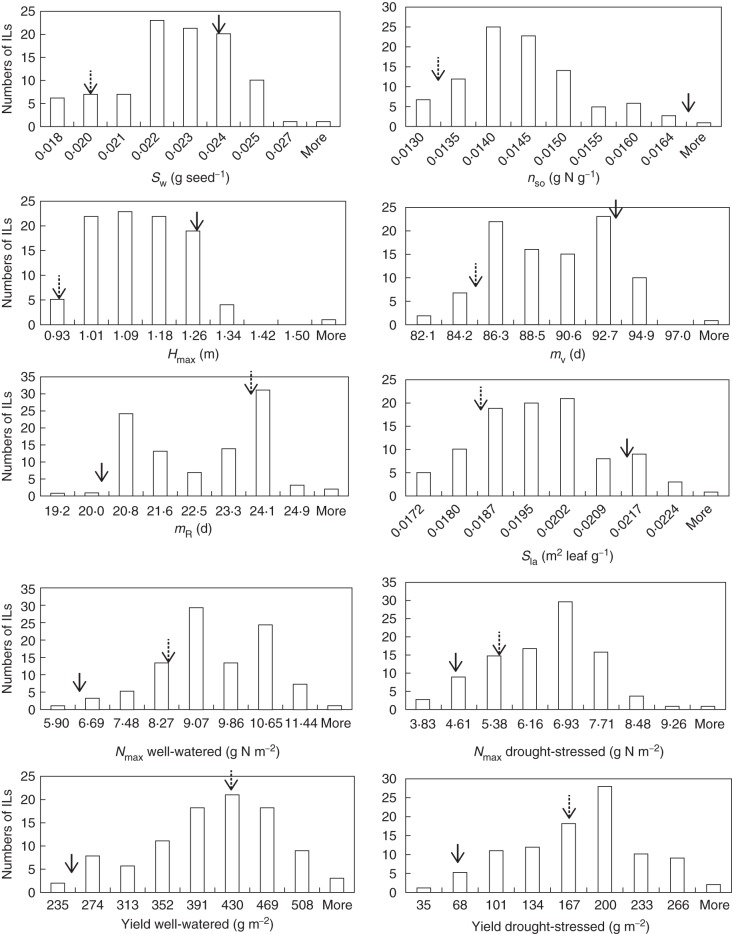
There was no yield difference between replicates in either well-watered or drought-stressed conditions (P > 0·05). The IL population exhibited considerable phenotypic variation in model parameters N_max and grain yield (Fig. 2), showing transgressive segregation. Model parameters S_W, n_SO, H_max and S_la, N_max in a drought-stressed environment and yield presented a unimodal distribution. For parameters m_V and m_R, and N_max in a well-watered environment, a bimodal distribution was observed. Parent ‘Shennong 265’ yielded more than ‘Haogelao’, even under drought.

Fig. 2.

Frequency distribution of seven model parameters and yield in the population of introgression lines (ILs). Arrows show values for the two parents (full arrow for ‘Haogelao’ and dotted arrow for ‘Shennong265’).

Contribution of individual model parameters to yield

Effects of individual model parameters on yield were analysed, for both well-watered and drought-stressed environments as assessed in the 2009 experiments. Simple regression and correlation based on data of all genotypes revealed that yield correlated with most model parameters (Supplementary Data Table S1). Among them, N_max was correlated with yield most. N_max alone accounted for 57·6 and 59·2 % of the variation in yield under well-watered and drought-stressed environments, respectively (Table 2). N_max was also associated with other model parameters (Supplementary Data Table S1). For example, N_max under well-watered conditions correlated with S_w, H_max, m_V and m_R (r = 0·29, 0·44, –0·29 and 0·32, respectively; P < 0·01). Therefore, N_max was used as covariate when multiple regression was conducted relating yield to each model parameter (Table 2). The results showed that yield correlated significantly with all model parameters, except for S_W. Besides N_max, n_SO was best correlated to yield under well-watered conditions, and m_V was best correlated to yield under drought-stressed conditions. Except for the correlation of m_R with yield, all other significant correlations with yield were negative (Table 2). These results agreed well with the simple correlation analysis for yield and model input parameters (Supplementary Data Table S1), and suggested that lower grain N concentrations, shorter vegetative and longer grain-filling phases, lower stem lengths and thicker leaves were associated with higher grain yields.

Table 2.

Linear regression of rice yield (Y) against total crop N uptake (N_max) and one other parameter trait of both well-watered and drought-stressed input parameters (n = 96; for definition of these traits, see Table 1)

Equation	b0	b1	b2	R2
Y = b0 + b1Nmax	−15·43/–62·61	44·49***/37·13***		0·576/0·592
Y = b0 + b1Nmax + b2SW	−39·73/–44·54	43·86***/37·37***	1356·6/–881·1	0·577/0·593
Y = b0 + b1Nmax + b2nSO	466·60/86·83	47·11***/35·94***	−35698·7***/–10033·9*	0·749/0·614
Y = b0 + b1Nmax + b2Hmax	77·43/48·84	49·70***/40·49***	−128·5**/–120·7***	0·609/0·646
Y = b0 + b1Nmax + b2mV	630·66/553·40	39·03***/29·32***	−6·73***/–6·41***	0·668/0·714
Y = b0 + b1Nmax + b2mR	−310·43/–339·14	38·54***/29·04***	15·69***/14·63***	0·669/0·710
Y = b0 + b1Nmax + b2Sla	161·52/92·18	42·74***/36·78***	−8334·2*/–7903·0**	0·598/0·625

Values are presented as ‘well-watered/drought-stressed’.

*, **, ***Significant at the 0·05, 0·01 and 0·001 probability levels, respectively.

Phenotypic calibration of the GECROS model

The GECROS model was evaluated for both well-watered and drought-stressed experiments in 2009. The model did not simulate well differences among the ILs in N_max, and, therefore, in grain yield. Similarly when using the across-IL mean value of observed N_max, the model did not simulate well the differences in grain yield (for well-watered, R² = 0·24; rRMSE = 0·17; for drought-stressed, R² = 0·12, rRMSE = 0·34).

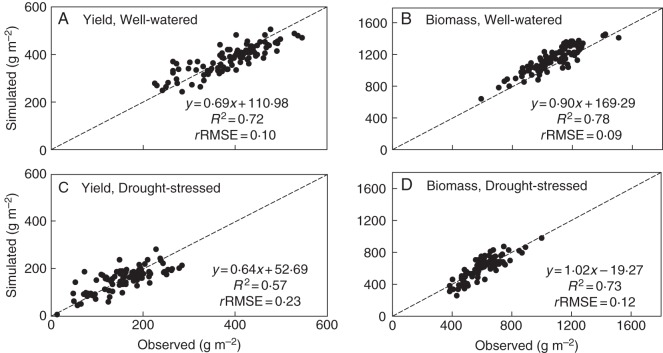
After using the genotype-specific values for N_max, the model accounted for 72 % of the variation in yield (Fig. 3A) and for 78 % of the variation in biomass (Fig. 3B), with rRMSE values of 0·10 and 0·09, respectively, for the well-watered conditions.

Fig. 3.

Comparison between observed and simulated values of grain yield (A, C) and biomass (B, D) of rice introgression lines for both well-watered (A, B) and drought-stressed (C, D) environments. The simulation was based on the phenotypic values of seven parameters (Table 1) estimated from the 2009 experiment. The diagonal line is the 1:1 line.

For simulating yield in the drought-stressed environment, first, all parameter values as used for the well-watered environment were applied. This procedure resulted in systematic overestimations, as the actual nitrogen uptake was much less, resulting in reduced growth under drought. Therefore, observed N_max from the drought-stressed environment was used. The model accurately simulated biomass, but still overestimated grain yield by overestimating the number of grains per m² (results not shown). A calibration was applied by reducing the seed number (i.e. approx. 6171 m⁻²) for all ILs, based on the difference between simulated average population mean and experimental data. After such a calibration, the model accounted for 57 % of the variation in grain yield (Fig. 3C) and 73 % of the variation in biomass (Fig. 3D), with rRMSE values of 0·23 and 0·12, respectively.

Both estimations of yield for well-watered and drought-stressed environments were slightly poorer than the best fit of linear regression in Table 2. This suggests that the input parameters required for GECROS (S_w, n_SO, H_max, m_V, m_R and S_la) were not all important for defining yield for this IL population, as confirmed by later analysis.

Coupling the effects of identified markers to the crop model

First, a multiple regression analysis was conducted to identify markers for each model parameter. In total, 20 markers were detected for all seven model parameters, with 3–6 markers per parameter (Table 3; Supplementary Data Fig. S1). The total fraction of the phenotypic variation accounted for by the markers ranged from 27·3 to 51·7 %. Marker RM410 showed pleiotropic effects on n_SO, H_max, m_V, m_R and S_la; marker RM8030 had pleiotropic effects on S_W, H_max, and N_max under well-watered conditions; marker RM11 was related to phenology influencing both m_V and m_R; marker RM338 influenced both m_V and N_max in the drought-stressed environment; marker RM475 was related to N_max in both well-watered and drought-stressed environments. Also based on eqn (1), we detected five or four markers when analysing yield per se (Table 3). These markers were generally among those markers identified for one or more model parameters; however, RM4085 for yield in the well-watered environment, and RM538 for yield in the drought-stressed environment (Table 3; Supplementary Data Fig. S1) were not detected for any model parameter.

Table 3.

Coefficients of eqn (1) used to identify markers conferring seven physiological model input parameters and for grain yield, using data from the well-watered conditions in 2009 and also from drought-stressed conditions for total nitrogen uptake

Trait	μ	Chromosome	Location (cM)	Markers	Additive effect (an)	P-value	R2 (%)
SW	0·0222	1	124·8	RM1152	0·0010	0·0002	45·2
		2	110·9	RM1367	0·0008	0·0007
		2	139·3	RM8030	−0·0009	0·0035
		4	123·8	RM2799	−0·0006	0·0039
nSO	0·0148	3	79·1	RM251	0·0009	<0·0001	36·8
		9	64·4	RM410	0·0003	0·0002
		12	61·6	RM1261	−0·0004	0·0039
Hmax	1·174	1	9·5	RM8068	0·037	0·0213	51·7
		2	139·3	RM8030	−0·057	0·0004
		4	25·5	RM518	−0·035	0·0042
		7	43·5	RM432	0·081	<0·0001
		9	64·4	RM410	0·042	<0·0001
		10	87·1	RM294A	0·058	0·0021
mV	90·78	1	124·8	RM1152	−1·38	0·0041	33·6
		3	108·4	RM338	1·31	0·0487
		7	47	RM11	1·61	0·0191
		9	64·4	RM410	1·23	0·0002
mR	21·71	1	124·8	RM1152	0·52	0·0127	27·3
		7	47	RM11	−0·81	0·0086
		9	64·4	RM410	−0·59	0·0001
Sla	0·0203	1	25·4	RM8145	0·0007	0·0006	31·0
		7	81·05	RM3753	0·0006	0·0020
		9	64·4	RM410	0·0003	0·0098
Nmax well-watered	7·83	2	92·5	RM475	−0·44	0·0082	37·0
		2	139·3	RM8030	−0·50	0·0052
		8	83·7	RM284	−0·53	0·0004
		9	0·8	RM5799	−0·35	0·0460
Nmax drought-stressed	5·13	1	98·1	RM306	0·62	0·0011	36·2
		2	92·5	RM475	−0·46	0·0066
		3	108·4	RM338	−0·76	0·0042
		5	20·6	RM7302	−0·47	0·0277
Yield well-watered	325·3	2	92·5	RM475	−21·7	0·0288	56·5
		2	139·3	RM8030	−34·9	0·0009
		8	35·7	RM4085	−14·5	0·0431
		8	83·7	RM284	−22·4	0·0113
		9	64·4	RM410	−19·5	0·0048
Yield drought-stressed	137·2	3	108·4	RM338	−42·2	0·0002	45·4
		5	20·6	RM7302	−22·2	0·0067
		5	132·7	RM538	25·7	0·0328
		9	64·4	RM410	−18·8	0·0004

For definitions and units of these parameters, see Table 1. Marker positions were based on the SSR marker linkage map established for the rice introgression lines population (Gu et al., 2012a; see Supplementary Data Fig. S1).

Positive values of the additive effect indicate that increasing alleles of the trait score came from ‘Haogelao’.

R² denotes the percentage of phenotypic variation accounted for by all markers identified for a given parameter or trait.

Secondly, based on the additive effects estimated by the regression analysis and allele information at each detected locus, marker-based values for each of the model parameters were calculated using eqn (1) for each IL. The performance of GECROS with marker-based estimates of model parameters was examined (Fig. 4). The marker-based GECROS model accounted for 52 % of the across-IL phenotypic variation of yield in the well-watered environment and for 43 % of the across-IL phenotypic variation in the drought-stressed environment, with rRMSE of 0·13 and 0·27, respectively. These percentages were almost comparable with those percentages accounted for by the markers identified for yield per se (Table 3).

Fig. 4.

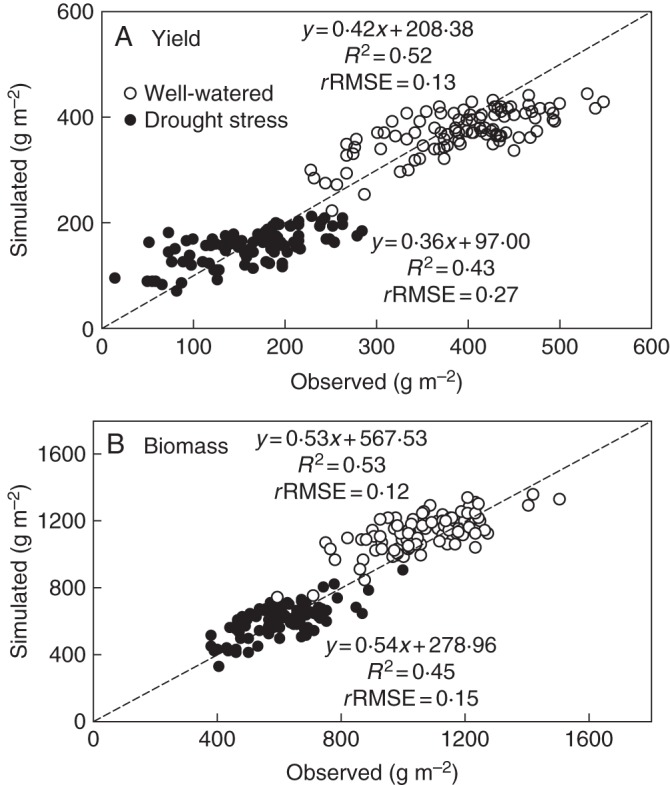
Comparison between observed values and those simulated by the marker-based trait inputs for 96 rice genotypes of the IL population, (A) for grain yield and (B) for biomass, for well-watered and drought-stressed environments (see key in A). The diagonal line is the 1:1 line.

The GECROS model using marker-based parameters gave less accurate simulations than using measured model parameters (Fig. 4 vs. Fig. 3). In both well-watered and drought-stressed cases, the marker-based model seemed to overestimate the lower end of observed yield and biomass, and to underestimate the higher end of observed yield and biomass, and, as a result, the range of simulated values was narrower than that of the observed data. This narrower range could be caused by the fact that the detected markers only explained part of the variation of model parameters (Table 3). The marker-based simulations correlated with the original simulations in grain yield for both the well-watered (r = 0·73) and the drought-stressed (r = 0·70) environment (Supplementary Data Fig. S2). Similar correlations were obtained in biomass (r = 0·75 and 0·71 for the two environments, respectively; Supplementary Data Fig. S2).

For predicting yield differences within an independent, larger population of RILs derived from the same parents, marker-based estimates of model parameters were used according to the same approach as in the IL population using eqn (1) and values of the additive effects shown in Table 3. The model explained 21 % of the phenotypic variation among 251 RILs under well-watered conditions and 20 % of the phenotypic variation under drought-stressed conditions (Fig. 5), with rRMSE = 0·31 and 0·45, respectively.

Fig. 5.

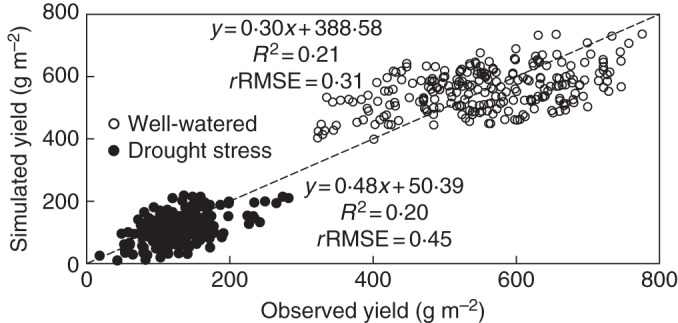
Comparison between observed values of grain yield and those simulated by additive effects of marker-based parameters for a population of 251 recombinant inbred lines grown under well-watered and drought-stressed environments. The diagonal line is the 1:1 line.

Model-based sensitivity analysis to identify important yield-defining markers

The sensitivity of crop yield in response to selection for an individual marker was analysed by excluding the effect of the marker in estimating marker-based model parameters. Marker RM8030 on chromosome 2 contributed most to the yield of the IL population under well-watered conditions. When the additive effect of RM8030 was excluded, the phenotypic variation accounted for by the GECROS model decreased most: from 51·6 to 34·2 % (Table 4). A different marker, RM338 on chromosome 3, contributed most under drought-stressed conditions. Excluding the additive effect of RM338 decreased the explained phenotypic variation in yield most: from 42·6 to 29·8 %. The extents to which the model accounted for the phenotypic variation decreased from that of the baseline simulation were used to rank the markers in importance for determining crop yield (Table 4). This ranking agreed well with the linear regression analysis of rice yield against model parameters (Table 2). As shown by the linear regression, N_max contributed most to the variation in yield. In accordance with that observation, the markers identified for N_max (Table 3) proved to be the most important yield-influencing markers identified by the sensitivity analysis (Table 4).

Table 4.

Percentage of the phenotypic variation in yield among rice ILs (R²) accounted for by different sets of simulations using the marker-based version of the GECROS model, when markers were fixed one at a time to calculate different sets of marker-based parameter inputs for GECROS

Fixed marker		Well-watered		Drought-stressed
Chr_cM	Name	R2 (%)	Rank	R2 (%)	Rank
1_9.5	RM8068	51·6	11	42·6	13
1_25.4	RM8145	53·9	18	41·4	10
1_98.1	RM306	51·6	11	39·5	6
1_124.8	RM1152	50·9	9	44·6	18
2_92.5	RM475*	46·2	3	37·7	5
2_110.9	RM1367	51·7	14	45·5	19
2_139.3	RM8030*	34·2	1	40·9	9
3_79.1	RM251	47·9	5	46·2	20
3_108.4	RM338†	52·6	17	29·8	1
4_25.5	RM518	59·4	20	44·1	17
4_123.8	RM2799	51·8	16	40·2	7
5_20.6	RM7302†	51·6	11	33·2	2
7_43.5	RM432	50·7	8	36·9	4
7_47	RM11	51·7	14	43·8	16
7_81.05	RM3753	49·4	7	41·9	11
8_83.7	RM284*	45·7	2	42·6	13
9_0.8	RM5799	48·3	6	42·6	13
9_64.4	RM410*,†	47·3	4	35·9	3
10_87.1	RM294A	51·1	10	40·5	8
12_61.6	RM1261	53·9	19	42·1	12
Baseline simulation		51·6		42·6

Marker positions are denoted as ‘Chr_cM’, i.e. chromosome_centiMorgan, as identified in Table 3.

The baseline simulation gives the R² values for the simulation, in which no marker was fixed, i.e. IL-specific allelic values (–1 or 1) were used for all markers in calculating marker-based inputs; for other sets of simulations, markers were fixed one at a time, in which all ILs were assumed to carry an identical allele (i.e. 0) at the locus of the considered marker in calculating marker-based inputs.

*These markers were also identified for yield per se under well-watered conditions (see Table 3);

^†These markers were also identified for yield per se under drought-stressed conditions (see Table 3).

Table 4 also shows that under well-watered conditions, markers RM410 and RM251 related to n_SO had a higher ranking than RM5799 related to N_max; in drought-stressed conditions, marker RM410 and RM432 influencing H_max had a higher ranking than RM306 and RM475 influencing N_max. These results were in line with an earlier regression analysis, which showed that parameters n_SO and H_max also had significant effects on yield for well-watered and drought-stressed conditions, respectively (Table 2).

Most high-ranking markers found in this approach were consistent with the markers identified for yield per se in Table 3; for example, the four highest-ranking markers in the well-watered environment (i.e. RM8030, RM284, RM475 and RM410) and the three highest-ranking markers in the drought-stressed environment (i.e. RM338, RM7302 and RM410). Our approach detected a total of 20 markers for each of well-watered and drought-stressed conditions (Table 4), more than the markers identified from multiple regression analysis for yield (Table 3). However, only ten markers mattered for the model to account for yield variation for each of the environments. The remaining markers listed in Table 4 were not important in accounting for yield as removing these markers had no effect on, or even increased the value of, the explained percentage (Table 4). For example, by removing the additive effect of marker RM251, the simulation for drought-stressed conditions could improve from 42·6 to 46·2 % variation accounted for.

Designing ideotypes based on identified markers

Given the markers identified above, it is possible to simulate yields of ideotypes designed by pyramiding yield-increasing alleles of relevant identified markers. We hypothetically designed three ideotypes: one based on the markers in Table 4 that mattered for the GECROS to account for yield variation (Ideotype I), one based on the complete set of the markers in Table 4 (Ideotype II) and one based on only those markers identified by analysing yield per se (Ideotype III). Figure 6 shows GECROS-simulated yields for these three ideotypes as well as the population mean of observed yields. Compared with Ideotype III, Ideotype I was simulated to have 10 and 23 % higher yields, and Ideotype II had 19 and 36 % higher yields, under the well-watered and drought-stressed environments, respectively. On across-environment average, there was only 3 % yield advantage for Ideotype III over the population mean, whereas average yield advantages for Ideotypes I and II were 18 and 29 %, respectively.

Fig. 6.

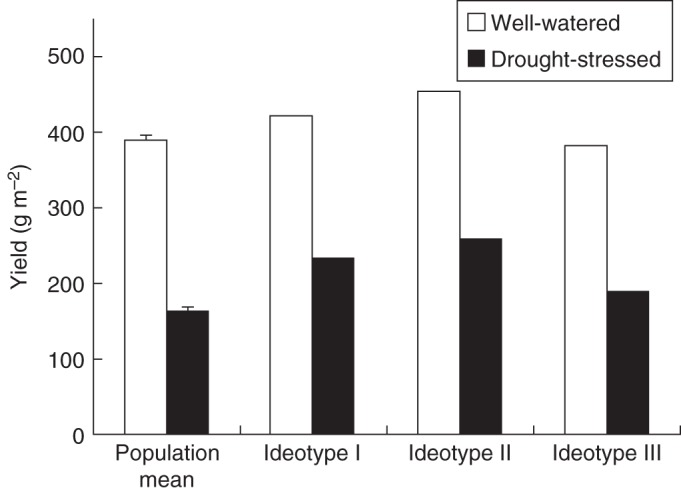
The population mean in the observed yield (with standard error of the mean) of 94 ILs and two parents, and simulated yields using the GECROS model for three hypothetical ideotypes, under well-watered and drought-stressed environments. Ideotype I is the hypothetical genotype designed by pyramiding positive alleles of the ten markers in Table 4 that mattered in improving the percentage of yield variation explained by the GECROS model. Ideotype II is the hypothetical genotype designed by pyramiding positive alleles of all 20 markers in Table 4. Ideotype III is the hypothetical genotype designed by pyramiding positive alleles of 4–5 markers identified by analysing yield per se as shown in Table 3. The ‘pyramiding’ was done by summing up the additive effect of all relevant markers affecting GECROS model parameters that are expected to have positive impacts for improving yield. It is worth noting that in simulating the yield of Ideotype III, the effect of the marker identified by analysing yield per se that had not been detected by analysing model parameters (i.e. RM4085 for well-watered and RM538 for drought-stressed environments, see the text) needs to be accounted for. This was done by multiplying the simulated yield based on the remaining three or four markers found by analysing yield per se with the factor derived as the ratio of the best yield expected from additive effects of 4–5 markers to the best yield expected from additive effects of 3–4 markers.

DISCUSSION

Simulating genotypic differences using the (marker-based) GECROS model

The GECROS model uses the concept of carbon–nitrogen interactions for simulating crop growth (Yin and van Laar, 2005; Yin and Struik, 2010; Yin, 2013). Unlike those of earlier Wageningen models, the input parameters of GECROS are few and most of them are related to the traits that breeders usually measure (Table 1), which may facilitate the use of crop modelling in support of breeding (Yin et al., 2004). Using as few as seven parameters (Table 1), the calibrated GECROS model accounted for observed differences in yield among the 96 ILs including the parents (Fig. 3). Marker-based GECROS also simulated yield differences among the 96 genotypes (Fig. 4).

Since the marker-based model parameters were based on the estimated genetic effects, the marker-based crop model should be able to simulate the variation within any progeny from the same parents. This was shown to be the case, using independent lines of the same cross that were not included in the QTL mapping step (Reymond et al., 2003). Here we tested this possibility using a different population, i.e. RILs derived from the same parents. The comparatively low percentage of yield variation accounted for by the RIL population (Fig. 5) could have been caused by the comparatively larger number of RILs (n = 251), which might have involved segregations that were not revealed by markers found in the smaller IL population. The limited number of markers with small additive effects only accounting for from 27·3 to 51·7 % of the phenotypic variation of model input parameters in the IL population (Table 3) could be another reason.

There were also problems to overcome when applying this approach. This is reflected by the fact that GECROS, like many models, tended to overestimate low yield and underestimate high yield. Specifically, we first showed that the model performance was sensitive to nitrogen uptake, as plant nitrogen content affects not only canopy dynamics but also leaf photosynthesis, and, therefore, biomass and yield, in line with the long recognized role of nitrogen in determining crop yield (Sinclair and de Wit, 1975). However, due to the complexity in modelling the transition between flooded and non-flooded soil environments (Gaydon et al., 2012) and the lack of accurate information on soil-related parameters needed to simulate nitrogen uptake, N_max was used in this study as if it were an input parameter of GECROS (Table 1).

We secondly showed that the drought treatment changed the sink–source relationships. In our simulation, model parameters were estimated from the 2009 well-watered experiment in Beijing. However, a further calibration was found necessary for simulating spikelet numbers when the model was applied to the drought-stressed environment (see the Results). Drought environments reduce transpirational cooling, leading to high tissue organ temperature and high spikelet sterility in rice; this effect can be highly genotype dependent (Jagadish et al., 2007). The generic model GECROS relates potential seed number to carbon and nitrogen accumulation in the vegetative phase, and does not have algorithms to account for the direct effect of panicle temperature on spikelet fertility (Yin and van Laar, 2005).

Boote et al. (2013) emphasized the needs for more mechansims in crop models when used for characterizing genotype–phenotype relationships. Our study suggests that there is an obvious need for robust algorithms to dissect N_max involving rooting density and depth for resource capture from the soil (King et al., 2003). Similarly, better estimation of the final spikelet number of rice when applying the model for stress conditions is needed by considering floret opening time in the flowering day and transpirational control of panicle tissue temperature (Jagadish et al., 2007).

Role of crop models in dissecting complex traits

Crop modelling can dissect complex traits into physiological components. Using the crop model GECROS, yield was connected to, and dissected into, seven model parameters in this study. By dissecting complex traits into physiologically meaningful components – model parameters – it is possible to assess genetic variation for each component and evaluate its relative importance by sensitive analyses or regression analyses. Regression analyses showed that N_max had the most significant effect on yield (Table 2). This is in line with the result showing that the important yield-determining markers identified by GECROS-based sensitivity analysis (Table 4) were mainly those for N_max (Table 3). Similarly, Prudent et al. (2011), combining a fruit sugar model and QTL analysis, identified key elementary processes and genetic factors underlying tomato fruit sugar concentration. These results show that the dissection approach based on physiological models can indicate where the QTLs for complex traits come about (Yin et al., 2002), thereby revealing biological insights into complex traits. Given that the number of QTLs identified for any single trait is always limited (Kearsey and Farquhar, 1998), model-based dissection can detect more QTLs/markers than analysing yield per se (Table 3).

The power of model-based dissection may depend on whether model parameters represent ultimate physiological components. For example, H_max is chosen as a GECROS parameter because it is among the traits that breeders measure; but it can be further dissected into parameters for stem extension rate and duration. Nevertheless, the current GECROS can indicate traits and markers that have the least impact on grain yield (Table 4). Such an analysis may suggest whether or not the model has incorporated the correct parameters for explaining yield differences among genotypes in a population. One of our initial thoughts was to explore the role of leaf photosynthesis in improving rice yield given extensive reports in the literature on this subject (e.g. Richards, 2000; Fischer and Edmeades, 2010); so, our previous major effort was to map QTLs for leaf photosynthesis (Gu et al., 2012a, b). Based on marker effects on individual biochemical parameters of leaf photosynthesis identified by Gu et al. (2012b) using representative ILs, we attempted to introduce these marker effects into the biochemical photosynthesis sub-model of GECROS. The variation accounted for by the model decreased significantly for both well-watered and drought-stressed conditions (results not shown). This suggests that biochemical parameters of leaf photosynthesis are not important for defining yield in our population of ILs.

The lack of importance of some other parameters for our IL population was suggested by the result showing that the marker-based GECROS accounted for 43–52 % of yield variation (Fig. 4) while identified markers typically accounted for only 25–30 % of variation in individual parameters (Table 3). Removing some markers even increased the explained percentage, as was the case for marker RM251 under drought-stressed conditions (Table 4). This could have been caused by the fact that marker RM251 only influenced n_SO (Table 3), which only had a marginally significant effect on yield under drought-stressed conditions (Table 2). The irrelevance of parameters in another crop model in defining yield differences has been noted previously (Yin et al., 2000a) for a barley RIL population of similar size. Whether or not this type of result is general requires further research using a larger population with more recombinant events that probably show more diverse relationships between yield and model parameters.

The model-based dissection approach, despite many advantages (see also the next section), may never replace the approach of the yield per se, because the latter not only is simple but also identified markers (e.g. RM4085 for well-watered, and RM538 for drought-stressed environment, Table 3; Supplementary Data Fig. S1) that were not detected by the model-based approach. This arises from the possibility that markers under the statistical threshold of detection for component traits can be detected when the aggregated complex trait itself was analysed (Yin et al., 2002). The other possibility is that the present GECROS model might miss some yield-influencing traits as input parameters, especially those important for determining the spikelet number.

Marker-based modelling to improve the efficiency of designing crop ideotypes

Combined with conventional breeding, marker-based approaches have been used to integrate major genes or QTLs with large effect into widely grown varieties (Jena and Mackill, 2008). However, so far, the marker-based approach has only had a moderate impact on breeding for complex traits such as yield and drought tolerance for which many genes with only small effect are involved, and which are highly environment dependent (Collard and Mackill, 2008). A crop model-based dissection approach can identify the most determinant yield-defining traits, and can suggest how to create the combination of component traits for an ideal plant type that will perform best under given conditions (Peng et al., 2008). QTL-based models can be used to evaluate the contribution of a single QTL to yield (Chenu et al., 2009), and, therefore, could assist in finding the most important markers.

We showed that the GECROS model, if well parameterized and calibrated, can be a useful tool to enhance the efficiency of selection for improved yields. The markers were first identified for various yield-determining physiological traits that are input parameters of GECROS (Table 3). The relative importance of these markers was then ranked by sensitivity analysis using the marker-based model (Table 4). Such an analysis detected markers that breeders can prioritize in their programmes for specific environments. Our analysis also confirms the assertion that rather than looking only for QTLs for a complex trait (yield) itself, determining QTLs for underlying component traits will provide more genetic information (Yin et al., 2002; Tardieu and Tuberosa, 2010; Prudent et al., 2011). Notably, the GECROS model-based approach identified some markers that were otherwise unidentified by analysis of yield per se, e.g. marker RM432 for the drought-stressed environment (Tables 3 and 4). This approach provides breeders with more choice of markers for selection. Alleles of these markers can be pyramided to create ideotypes (Gu et al., 2012b). Simulations showed that ideotypes based on more markers identified by the model (Ideotypes I and II) had a higher yield potential than the ideotype based on the markers identified for yield per se (Ideotype III) (Fig. 6). It remains to be tested through actual breeding whether this additional information does indeed result in better genotypes.

Quantitative trait locus/marker-based modelling combined with sensitivity analysis (Table 4) can also directly evaluate the effect of a a single QTL/marker on yield level, which could be used to evaluate a specific genotype in silico, thus potentially reducing labour-intensive selection in the field. Crop modelling quantifies causality between relevant physiological processes and the responses of these processes to environmental variables, and might therefore help to resolve the QTL × environment interaction (Hemamalini et al., 2000; Asins, 2002). Using the CROPGRO-soybean model, Messina et al. (2006) estimated the effects of QTL markers from a set of near-isogenic lines and satisfactorily predicted the variation of yield across 5 years and eight sites among an independent set of soybean cultivars. Chenu et al. (2009), using the crop model APSIM-Maize, simulated that a QTL accelerating leaf elongation will increase yield in an environment with water deficit before flowering, but reduced yield under terminal drought stress. Our model analysis showed that the marker RM338 contributed the greatest to yield under a stressed environment, but had no effect at all under a well-watered environment (Table 4). This modelling analysis will greatly improve the selection efficiency for traits which are greatly influenced by environment factors.

Concluding remarks

This study outlines a genotype-to-phenotype approach that exploits potential values of marker-based crop modelling in developing new plant types with high yields. The approach can provide more, yet prioritize, markers in the selection programmes for specific environments. Although the modelling approach may never replace the analysis of yield per se approach, our simulation analysis showed that ideotypes based on the modelling approach had 10–36 % yield advantages. Further work could be achieved by upgrading crop models for rice, based on the identified weakness of the model, especially for drought stress conditions. As pointed out recently by Boote et al. (2013), ‘model linkage to genetics is a new area with good potential’, and incorporating new mechanisms and algorithms into crop models to identify more relevant traits is needed to better account for genotype–phenotype relationships.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Model Description: description of the crop growth model GECROS. Figure S1: chromosome locations of markers associated with the seven model input parameters and with yield per se. Figure S2: correlation between simulated values from marker-based model parameters and those from measured model parameter values for 96 rice genotypes of the IL population for grain yield and biomass, for well-watered and drought-stressed environments. Table S1: simple correlation coefficients for rice yield and model input parameters for well-watered and drought-stressed environments.