Branching patterns of root systems: quantitative analysis of the diversity among dicotyledonous species

Abstract

Background and Aims

Root branching, and in particular acropetal branching, is a common and important developmental process for increasing the number of growing tips and defining the distribution of their meristem size. This study presents a new method for characterizing the results of this process in natura from scanned images of young, branched parts of excavated roots. The method involves the direct measurement or calculation of seven different traits.

Methods

Young plants of 45 species of dicots were sampled from fields and gardens with uniform soils. Roots were separated, scanned and then measured using ImageJ software to determine seven traits related to root diameter and interbranch distance.

Results

The traits exhibited large interspecific variations, and covariations reflecting trade-offs. For example, at the interspecies level, the spacing of lateral roots (interbranch distance along the parent root) was strongly correlated to the diameter of the finest roots found in the species, and showed a continuum between two opposite strategies: making dense and fine lateral roots, or thick and well-spaced laterals.

Conclusions

A simple method is presented for classification of branching patterns in roots that allows relatively quick sampling and measurements to be undertaken. The feasibilty of the method is demonstrated for dicotyledonous species and it has the potential to be developed more broadly for other species and a wider range of enivironmental conditions.

INTRODUCTION

The degree to which root systems are branched is striking. Even on small plants, with only one shoot and a few leaves, observing a very large number of roots which are highly branched is common. This number and branching complexity become extraordinarily high on well-developed plants. If we assign the order 1 to those roots which are directly attached to the shoot, one can commonly observe that roots branch up to order 4 or even 5. Moreover, the branching density, i.e. the number of laterals per unit length of parent root, can be so high that the resulting system appears extremely complex. Only a small number of species, mainly epiphytes or aquatic species, are exceptions to this rule (Esau, 1977).

Thus, branching is a very important developmental process in root systems, which enables them to extend and to increase their surface in contact with the soil. This basic process is generally further extended by the production of root hairs and in some cases by the symbiotic association with fungi in mycorrhizae.

In root systems, new roots can be produced in slightly different ways. Acropetal branching is a general process, in which new lateral roots are produced, generally along files facing the internal vascular poles, towards the apex of the parent root (Esau, 1977; Charlton, 1996). These roots originate from primordia that are initiated close to the meristem of the parent root, develop as meristems during a given period (typically several days) and eventually give rise to new lateral roots, generally at a distance from the tip of the mother root. Because this process is very important and general, it is the focus here. Nevertheless, it should not be forgetten that root systems can also produce a significant number of new roots by other developmental processes. Nodal roots can be developed on the shoots (e.g. Poaceae species) and adventitious roots can emerge from well-established and already branched roots (especially on the taproot near the collar).

Acropetal branching is a well-known process, but its quantitative characterization is not that common, especially in natura or field conditions, where the dynamics of root length are described without distinction between growth and branching. When branching is specifically considered, branching density (number of laterals per unit length of parent root) is often used as the descriptive variable. Branching density has been measured on several species, particularly on the nodal roots of monocotyledonous species (which are easy to identify), and sometimes on their laterals [Varney et al. (1991) on Zea; Pagès and Pellerin (1994) on Zea; Lecompte and Pagès (2006) on Musa; Arredondo and Johnson (2011) on several grass species]. In dicotyledonous species, characterization has often been restricted to the taproot, usually at young stages [e.g. Pagès et al. (1993) on Prunus persica; Tsegaye et al. (1995) on Pisum sativum].

Another approach, at the root system scale, has been suggested by Fitter (1982, 1987) to characterize the branching pattern of root systems. Fitter's approach consists of using topological indices (altitude and magnitude) which define the level of branching complexity globally and can be evaluated on excavated root systems. The approach was extended later by also considering metric information on the distance between the branching points (called link length by Fitter). Another very synthetic approach, based on fractals, was proposed by several groups, such as Tatsumi et al. (1989), Van Noordwijk et al. (1994), Spek and Van Noordwijk (1994), Berntson (1994, 1997) and Nielsen et al. (1997, 1999). The fractal dimension was regarded as an easy way of quantifying branching complexity, even though simulation studies have shown the influence of measurement methods on the estimates of fractal dimensions (Nielsen et al., 1997). Those approaches (overall topological indices and fractal dimension) may be convenient to circumvent the difficulty in characterizing the dynamic developmental characteristics of complex root systems. The data they provide summarize and combine several developmental effects: growth, branching, adventitious emission and self-pruning. All these concurrent processes are likely to affect topological indices, link lengths and fractal dimensions.

In order to improve the characterization of branching patterns, it was chosen to develop a new approach, with two main features. The first is to focus on the particular process of acropetal branching, because it is specific, well identified and of prime importance in overall development and function. The second is to link the characteristics of the branching pattern with another key characteristic of individual roots, namely their tip diameter. Branching is not only a process by which new connected roots are developed and can extend laterally away from their parent root. It is also a means for the plant to allot efficiently the size of its meristems, which are also sinks for shoot-derived resources. As an integrated system, the plant must distribute the size of its roots in a consistent and economic pattern throughout this developmental process.

Therefore, this paper aims to present: (1) a new approach and methods to study branching traits; (2) quantitative results on a number of species (dicotyledons in this case) to validate the practical feasibility and value of the approach; and (3) a definition of the branching types observed among these species, with a focus on the relationships between the traits studied.

MATERIALS AND METHODS

Sampling plants and soil

A total of 45 species of dicots were sampled during spring 2013, from March to June. Most of these species grew spontaneously in kitchen gardens and cultivated fields as weeds, in two different sites with uniform soils. The first site is near Thouzon, in the south-east of France (Provence region: latitude 43°57′, longitude 4°59′, altitude 50 m a.s.l.). The soil was a deep calcareous silty soil developed on loess. The second site is near Nozeyrolles, located in the Massif Central (Auvergne region: latitude 44°59′, longitude 3°24′, altitude 1100 m a.s.l.). The soil was a sandy brown soil developed on a granitic arena. The list of species is given in Table 1. One species (Plantago major) was sampled at both sites.

Table 1.

List of species and sampling sites

Species	Sampling site
Anagallis arvensis	Thouzon
Aquilegia vulgaris	Thouzon
Arabidopsis thaliana	Nozeyrolles
Bryonia dioica	Thouzon
Capsella bursapastoris	Thouzon
Chelidonium majus	Thouzon
Chenopodium album	Thouzon
Clematis vitalba	Thouzon
Conyza canadensis	Thouzon
Digitalis purpurea	Nozeyrolles
Eupatorium cannabinum	Thouzon
Fragaria vesca	Nozeyrolles
Galeopsis segetum	Nozeyrolles
Galium aparine	Nozeyrolles
Glaucium flavum	Thouzon
Hedera helix	Thouzon
Lactuca seriola	Thouzon
Lamium amplexicaule	Thouzon
Medicago lupulina	Thouzon
Melilotus albus	Thouzon
Melissa officinalis	Thouzon
Mercurialis annua	Thouzon
Nigella damascena	Thouzon
Oenothera biennis	Thouzon
Oxalis corniculata	Thouzon
Papaver rhoeas	Thouzon
Parthenocissus inserta	Thouzon
Pisum sativum	Thouzon
Plantago lanceolata	Nozeyrolles
Plantago major	Nozeyrolles, Thouzon
Polygonum aviculare	Thouzon
Prunus persica	Thouzon
Silene latifolia	Thouzon
Silene vulgaris	Thouzon
Solanum nigrum	Thouzon
Sonchus oleraceus	Thouzon
Stellaria media	Thouzon
Tanacetum parthenium	Thouzon
Torilis nodosa	Thouzon
Trifolium repens	Thouzon
Urtica urens	Thouzon
Verbena officinalis	Thouzon
Veronica hederifolia	Thouzon
Veronica persica	Thouzon
Viola odorata	Thouzon

The main characteristics of the soils (Laboratory of Soil Analyses, INRA Arras, France) are given in Table 2.

Table 2.

Main characteristics of the soils in the two sampling sites

Sampling site	Thouzon	Nozeyrolles
Clay (<2 μm)	129	127
Fine silt (2–20 μm)	299	117
Coarse silt (20–50 μm)	157	54
Fine sand (50–200 μm)	243	111
Coarse sand (200–2000 μm)	173	592
pH (water)	8·93	7·38
Carbon (g kg–1)	16·6	13·0
Nitrogen	1·46	0·865
Total organic matter	28·6	22·5

Masses are given on a dry matter basis (g kg^–1).

Plant collection and root system excavation

Young plants at different stages (typically from five to 20 unfolded leaves on the main shoot) were sampled. Two to five plants per species were excavated, depending on their availability at suitable stages. In this sampling, isolated plants grown in recently cultivated soils (kitchen gardens or fields) or on recent mole-hills (in the case of pastures) were favoured. A garden fork was used to demarcate a monolith around the chosen plant (radius 15–20 cm around the collar, 30–50 cm deep), and to extract it before putting it in a large bucket with water. Then, the monolith was gently washed with running water. When the root system was nearly free of soil and organic debris, it was left for several minutes to 1 h in a tray with salt water (5 g L^–1) and liquid soap to complete cleaning.

Measurements

Root systems were separated and spread carefully in a layer of water several millimetress deep in a glass tray, using mounted needles. The densest root systems were cut into several pieces in order to minimize root overlap in the tray. Then they were scanned with a flatbed scanner (EPSON perfection V700) at a resolution of 1200–4800 dots per inch, using the transparent mode. The resolution was adjusted for each species in order to obtain least 8 pixels transversally to the finest roots in order to measure them with sufficient accuracy. Previous tests had shown that this adjustment did not induce any bias, since the same values (on average) were obtained when measuring the same objects at these various resolutions.

Measurements were made on the computer screen by mouse clicking using the measuring tools (i.e. length of straight line and segmented line) provided by the ImageJ software (http://rsbweb.nih.gov/ij/). On the loaded images laid on the screen, we identified sub-structures, consisting of young parts of roots together with their laterals (Fig. 1). On each sub-structure, we measured the diameter of the parent root, the diameter of the laterals and the distance along the parent root from each lateral to its proximal closest neighbour (from centre to centre). Branching density was quantified using the interbranch distance (its reciprocal), because this variable could be measured for each lateral root.

Fig. 1.

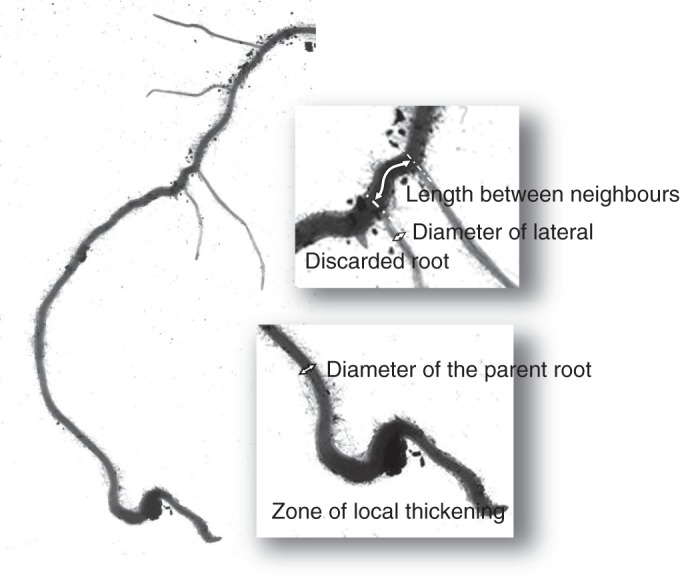
Image of a sub-structure consisting of the young part of a parent root together with its young (distal) laterals. This schema illustrates the principle of the measurements that were carried out on the scanned images.

Depending on the branching order, the sub-structures studied had 1–15 laterals. For each species, we measured from 60 to 200 lateral roots, for a total number of 8091 roots.

All diameters (also called ‘apical diameter’ hereafter) were measured on the young part of the root, at a position where it was nearly cylindrical. The distance from this position to the very tip was typically 5–50 mm on the thickest roots, and 2–20 mm on the finest. Even when the apex was broken, this young zone could be distinguished by the combination of several visual criteria (e.g. the age of the laterals if any, tissue transparency and structure, and stage of the root hairs). The youngest (most distal) lateral roots, <3 mm long, were discarded from these measurements (see example on Fig. 1). Their diameter could be erroneous, and the distance from their neighbour could have been modified later by emergence of another proximal root. Short zones of local thickening were often observed along the roots (Fig. 1), due to local mechanical constraints (Konôpka et al., 2009). They were systematically avoided for diameter measurements.

Data analysis

All data treatments, plots and analyses were carried out using the R software (R Development Core Team, 2013). Linear models were estimated with the ‘lm’ function in order to estimate parameters and perform analyses of variance and covariance. To study graphically the shape of the trends between two variables (Figs 2 and 3), we used the ‘LOESS’ smoothing function of R. Principal components analysis (PCA) and classification were calculated using the FactoMineR package (Husson et al., 2010).

Fig. 2.

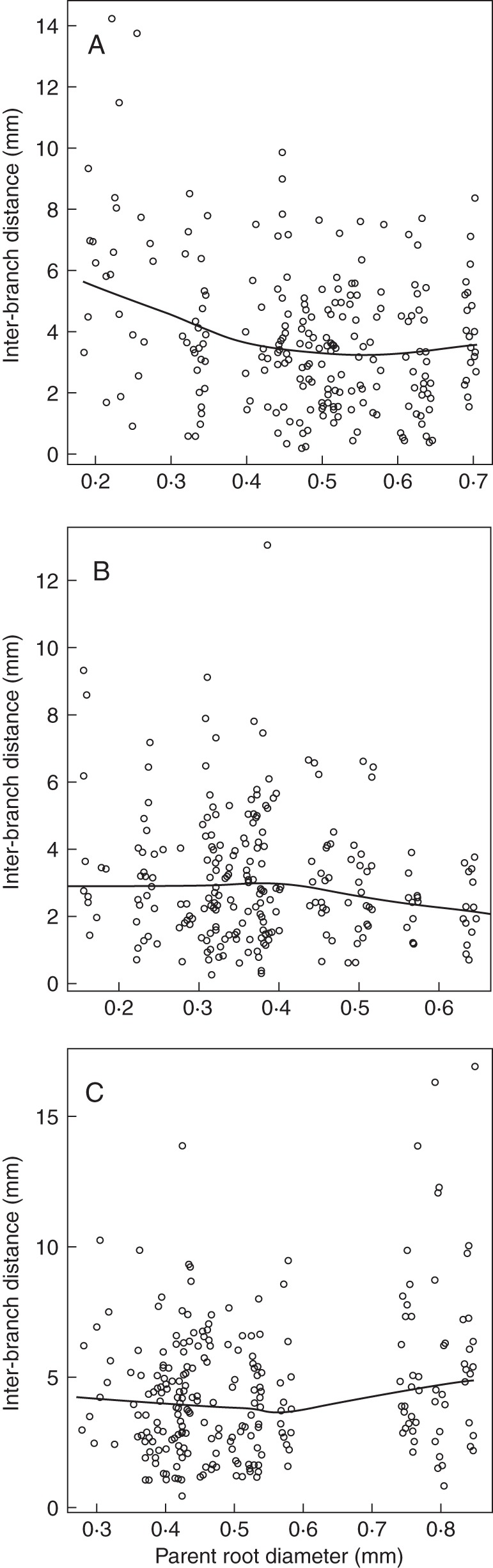
Relationships between interbranch distance and diameter of the parent root. The lines represent the trends between these variables (calculated by the ‘LOESS’ smoother of R). The three graphs illustrate the three cases that were observed for the different species: decrease of interbranch distance with parent root diameter (A: Chelidonium majus); independence (B: Silene vulgaris); and slight increase (C: Melilotus albus).

Fig. 3.

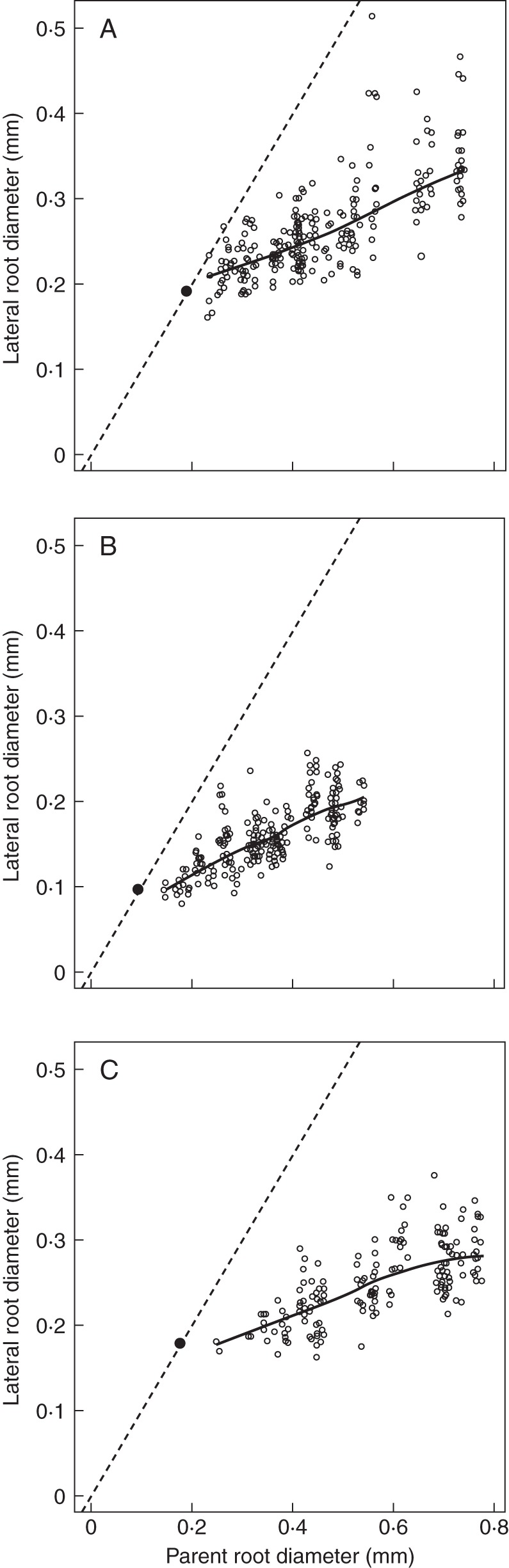
Relationships between lateral and parent diameter illustrated for three different species (A, Lactuca seriola; B, Lamium amplexicaule; C, Solanum nigrum). The solid lines represent the trends between these variables (calculated by the ‘LOESS’ smoother of R). The bisecting line (dashed line) is also drawn, as well as the point with co-ordinates (D_min, D_min), to show that the trends would intersect the bisecting line near this particular point.

RESULTS

The names, definitions and extreme values of the measured and calculated traits are presented in Table 3.

Table 3.

Abbreviations, meanings, units and extreme values of the different traits (one value was estimated per species)

Parameter abbreviation	Meanings	Units	Extreme values
Dmin	Minimal diameter (quantile 2 %)	mm	0·063–0·33
Dmax	Maximal diameter	mm	0·29–1·3
Drange	2·0 × (Dmax – Dmin)/(Dmax + Dmin)	–	0·77–1·6
IBD	Interbranch distance on the thick roots	mm	1·0–5·6
RIBD	Relative interbranch distance of the fine roots to that of the thick roots	–	0·74–2·1
DlDm	Slope of the regression of lateral diameter vs. parent diameter	–	0·14–0·36
VarD	Coefficient of variation of the diameter of lateral roots for a given parent diameter	–	0·10–0·20

Diameter distribution

The maximal diameter (D_max), is defined as the maximal value that was observed on the root sample for each species. When measuring the roots from the images, care was taken to include the root with the largest apical diameter.

The minimal diameter (D_min) is defined as the 2 % quantile of diameters that were measured. We took this quantile instead of the strict minimal value in order to obtain a more robust estimate of the finest diameters. This precaution was useful for the minimal diameter because its value was relatively more sensitive to measurement uncertainty than D_max.

We observed a 4- to 5-fold difference for these traits between species. For D_min, the values were between 0·063 and 0·33 mm and for D_max between 0·29 and 1·30 mm.

The correlation between minimal and maximal diameter over species was significant (P < 0·001) but the relationship was weak (r² = 0·26), showing that the range of diameters was also variable from one species to another.

Interbranch distance

When the relationship between interbranch distance and diameter of the parent root was examined systematically, on each species, three different types of relationship were observed, which are illustrated in Fig. 2. In the first and most frequent type (Fig. 2A), interbranch distance decreased with diameter of the parent root. However, in a few cases, the interbranch distance was rather stable whatever the parent root diameter (Fig. 2B) or even tended to increase (Fig. 2C). Moreover, the spread of interbranch distance was often lower on the thick roots (as in Fig. 2A, B).

Hence, these different patterns of variation were averaged within species using two parameters (see Table 3): IBD, the mean interbranch distance of the laterals emerging from thick parent roots, i.e. parent roots thicker than the middle of the range of diameters for the given species; and RIBD, the ratio of interbranch distance of laterals emerging from fine roots (parent roots thinner than the middle of the range) to that of the thick ones. The interbranch distances of the thick roots were significantly dependent on the species (P-value <0·001). This was shown by an analysis of variance made on the logarithms instead of natural values to obtain a Gaussian distribution for the residuals. The IBD exhibited large interspecific variations, between 1·0 and 5·6 mm. The ratios (RIBD) varied much less, between 0·74 and 2·06. The mean and median values of RIBD across all species were 1·34 and 1·29, respectively. Values >1 confirmed that a majority of species tended to have a lower interbranch distance on the thick roots.

Relationship between diameters of parent and lateral roots

The Pearson correlation coefficients between the diameters of a parent root and those of its laterals were highly significant for all species (values ranged between 0·31 and 0·87; the highest P-value was 0·006). Moreover, when examined graphically (examples are given in Fig. 3), the smooth trends (represented by solid lines) were approximately linear. Some small discrepancies from linearity were observed, but they did not exhibit any common shape from one species to another.

These trend lines did not intercept the vertical axis close to the origin (0, 0) but appeared to intersect the bisecting line near the point of co-ordinates (D_min, D_min). Thus, the hypothesis of passing through this point was tested independently on all species. The test of a zero intercept was used for the regression of the lateral root diameter (with D_min subtracted) on that of its parent (with D_min subtracted). This test was rejected only four times at the 1 % confidence level, and nine times at the 5 % confidence level. In these cases, the estimated intercepts were very small (<0·02 mm) and were either positive or negative. Therefore, it was decided to constrain the regression lines of lateral root diameter against parent root diameter to pass through this particular point (D_min, D_min) for all species, in order to obtain a more robust estimate of the slope following the same protocol on all species.

A covariance model was used to test the effect of the individual species on the slope of lateral root diameter against the parent root diameter (used as covariable). The model account for all species was shown to be highly significant, when compared with the simpler model considering a single common slope. The slope estimates (DlDm) for each species varied within a 3-fold range, with the extreme species being Eupatorium cannabinum on the one hand, exhibiting a strong dominance of the parent over its laterals (slope 0·135), and Nigella damascena on the other hand, exhibiting a low dominance (slope 0·361).

From the same dataset, the coefficient of variation of the lateral root diameter (VarD) was also estimated. This was done because it was observed that the variations in lateral root diameter on the same parent root always tended to increase from the finest to the thickest (see Fig. 3). For this estimation, classes of parent root diameter were made with approximately the same number of lateral roots (around ten in each class) and, for each class, the mean and the standard deviation of the lateral root diameter were calculated. A linear model (standard deviation vs. average of the lateral roots) without intercept, whose slope was the coefficient of variation (VarD), was fitted. This coefficient also varied substantially between species, from 10 to 20 % (Table 3).

Relationships between traits and definition of branching types

From all these branching traits estimated on the whole set of species and locations, their correlations and the possibility of defining different types of branching patterns were studied in order to associate particular levels for these traits. A centred and normalized PCA was achieved on the dataset defined by the variables (traits) presented in Table 3, each line of the dataset being a species (45 species) at a given location (two different locations).

The first component of this PCA (Fig. 4) was mainly determined by D_min and IBD. It represents the fineness of the finest roots and the branching density. These two variables were highly correlated (r² = 0·48; P < 0·001). Species with fine roots also had a high branching density and, conversely, species without fine roots had spaced branches.

Fig. 4.

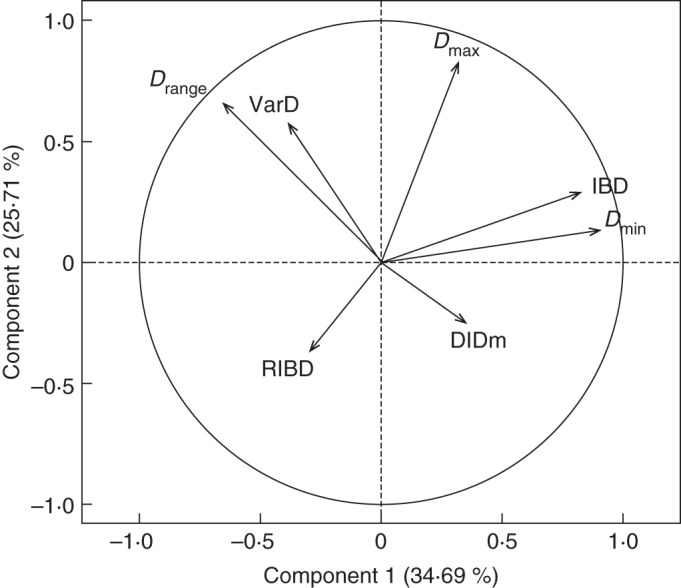
Principal component analysis. Variables (traits) located on the plane defined by component 1 (horizontally) and 2 (vertically). See the text and Table 3 for the names of the traits.

Component 2 was mainly correlated to D_max, i.e. the thickness of the thickest roots of the species. The position of D_range, which was also well represented in this first plane, equally by component 1 and component 2, confirms the interpretation. Both D_min and D_max contributed to D_range. The correlation was positive with D_max, and negative with D_min. Although less represented in this plane, VarD was linked to D_range. The potential of a species to make lateral roots of variable diameters was linked to its diameter range. This correlation between D_range and VarD was also highly significant (r² = 0·28; P < 0·001).

In the plane containing component 1 and component 3 (not shown), it was seen that the third component was mainly correlated to the slope DlDm, i.e. the dominance level. Beyond its correlation with D_range, which was visible on Fig. 4, VarD was also positively correlated with this third component, along which species with a high value of DlDm (low dominance) also had variable diameters. Nevertheless, the overall correlation between VarD and DlDm was rather weak (r = 0·13), and not significant.

Furthermore, a hierarchical classification was made, using the same variables as in the PCA, based on the Euclidean distance. The classification criterion was that of Ward (Husson et al., 2010). On the basis of the hierarchical tree, five different groups were defined, with the following characteristics. The groups were illustrated by paragons (i.e. typical individual species) presented in Fig. 5.

Fig. 5.

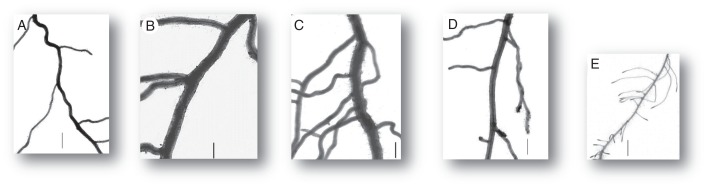
Illustration of the five groups defined in the classification by five different species. Images are at the same scale. Vertical segments on each image are 1 mm long. (A) group 1, Conyza canadensis; (B) group 2, Nigella damascena; (C) group 3, Prunus persica; (D) group 4, Bryonia dioica; (E) group 5, Galium aparine.

Group 1 (typically represented by Medicago lupulina and Conyza canadensis) had rather intermediate and homogenous roots. D_max was low and D_range was minimal, associated with low values for VarD.

Group 2 (Nigella damascena and Melilotus albus) was characterized by thick roots with spaced laterals. D_min was particularly high (maximal values), and D_max moderately high, giving minimal values for D_range. Branching density had minimal values in this group.

Group 3 (Eupatorium cannabinum and Prunus persica) was remarkable because it contained the thickest and the most heterogeneous roots (highest D_max and D_range). This was associated with strong dominance (low values for DlDm) and high values for VarD.

Group 4 (Papaver rhoeas and Bryonia dioica) was characterized by a low branching dominance (high DlDm) and high values for VarD. Branching density was low.

Group 5 (Urtica urens and Galium aparine) was specifically characterized by fine and densely branched roots, i.e. the opposite of group 2. This group contained the lowest values for D_min, D_max and IBD. RIBD was high, and other variables had intermediate values.

DISCUSSION

A suitable practical method for observing and quantifying root branching

In this paper, a new method for characterizing the acropetal branching patterns including the distribution of apical diameters between parent and lateral roots has been proposed and it has been applied to a large set of dicotyledonous species. From a practical point of view, this exercise showed that it was feasible to make these measurements on the young parts (branched tips), because they could be separated and sampled. The sampling, scanning and measurements took about 1·5 d per person per species. This first estimate needs to be refined when we have more experience. A manifest advantage of the method is that it was not necessary to define the developmental branching orders of the roots, as in the method of Fitter (1982) where orders are defined from the tips (external links, number 1) to the base. On some of the species, and especially at advanced stages, defining the developmental order would have been very difficult, because of the complexity of the whole system. Particular care was taken to sample roots with various diameters, and especially the extreme ones, in order to be able to estimate the parameters that were used for the quantification. Nevertheless, it is believed D_max could have been underestimated on some species, because it seemed to increase with age and rather young plants were sampled. The young parts are sometimes very fragile, so washing must be done with care. However, accidentally breaking the very tip of the root, which is usually the most brittle part, does not prevent valuable measurements of diameters to be made, since the roots are approximately cylindrical along a significant distance from their tip. More important was to discard the parts where roots were thickened because of the soil mechanical impedance they experienced during elongation (Konôpka et al., 2009). The reliable quantification of acropetal branching requires sampling rather young parts of the root system, where this process occurs. In older parts, the quantification would have been made more difficult since other processes would make lateral roots disappear (e.g. self-pruning, root decay), add new ones (e.g. emergence of late adventitious roots) or change parent root diameter (radial growth). In a recent study, Pagès et al. (2010) have shown the advantage of looking at the root tips, especially the unbranched apical zone, in order to estimate root elongation rates. The present work can be seen as an extension, with specific observations on the young branched part of the roots. Thus, the peripheral parts of the root systems exhibit several morphological markers which can be used to measure several dynamic developmental processes.

The method is associated with specific morphological traits

Applying this method led us to define new parameters (or traits sensu largo) to characterize our objects quantitatively. These parameters were inspired by previous modelling work (Pagès, 2011). Regarding diameters, extreme diameters (D_min and D_max) rather than average diameters were considered. This is unusual and requires explanation. Average diameter or associated traits such as specific root length (SRL) (Cornelissen et al., 2003) are probably more robust variables because of the smoothing effect of averaging. They have become popular during recent years because they can be measured automatically by several dedicated programs. However, they cannot provide an idea of the diameter range, which can be an easy-to-measure (even manually) and an important trait per se, with developmental and functional meaning. More precisely, we have shown that complementary information was provided by these two characteristics D_min and D_max: they were not closely correlated, and they had clearly different locations in the PCA and the classification (see discussion below). Lastly, the root diameter distribution, when examined at the root system level, is far from symmetrical, because the number of fine roots is much greater than the number of thick roots. Thus, such distributions are not well represented by average values.

Other original variables are the dominance slope (DlDm) which quantifies the subordination of laterals to their parent root, and the coefficient of variation (VarD) which quantifies how lateral roots differ from one another. The linearity of the relationship between lateral and parent root diameter validated the use of the dominance slope parameter (DlDm). DlDm can be related to the herringbone/dichotomous description which was proposed by Fitter (1982), but it is focused on the acropetal branching process. Characterizing the variations (through VarD) was also an important aspect of the method, since such variations also have functional consequences (Forde, 2009; Pagès, 2011) and they were not considered in previous descriptions of branching patterns. Thus, both DlDm and VarD conveniently summarized how the growth potential is distributed among lateral roots and related to that of the parent root. In the relationship of lateral vs. parent root diameter, we have also seen that the regression line intersected the point defined by the minimum diameters (co-ordinates: D_min, D_min). This means that when the finest roots branch, they give rise to roots similar to themselves. Conversely, the biggest roots exert higher subordination of their laterals when they branch. These facts were clearly visible on the scanned pictures, and they were common to all species. A proportionality coefficient would not have been sufficient to describe this hierarchical relationship.

Species exhibited large differences for these traits

The measured traits were highly variable from one species to another. The variation factors between species (ratios of the maximal to the minimal values) were typically between 2 and 5. For example, a factor of approx. 5 was observed in the set of species for both diameters (5·2 for D_min and 4·5 for D_max). These variations are very large, since they have a considerable impact on the construction cost of a given length of root, which is approximately proportional to the squared diameter when root tissue density is constant. Similarly, a factor of 5·3 was observed between extreme values of IBD, again having a huge impact on the overall root length, especially because roots branch on several orders, typically between two and five. The values found in the literature for IBD, often measured on monocotyledonous species (Varney et al., 1991; Pagès and Pellerin, 1994; Tsegaye et al., 1995; Lecompte and Pagès, 2006; Arredondo and Johnson, 2011), fall into the range of the values obained here, except for the most proximal parts of the nodal roots, where IBD could be locally smaller, namely <1 mm, according to Varney et al. (1991). Although very significant, the magnitudes of variation were smaller on DlDm (2·6-fold) and VarD (1·9-fold), but they are also amplified in the whole root system because their effects are repeated over several branching orders.

Therefore, these large variations must be pointed out, because of their general consequences on the branching patterns, and because they justify the use of the chosen traits. Moreover, our sample of species contained mainly weeds growing in disturbed environments such as cultivated fields or kitchen gardens. We can expect to observe even larger variations of the traits if we consider other species among monocotyledons, or additional trees or species from other different environments. This requires further study. It was possible to compare our findings with literature data only for IBD values, because other traits were either not measured by other authors or else were averaged in the case of diameters.

Correlations between traits, and branching types

We observed significant correlations between traits in our species population. This fact can be considered as a corollary of the previous point: since each trait is very variable from one species to another, and has serious consequences for the whole branching system, one can expect that the different traits cannot be distributed independently from one to another. The functional harmony and economy of the whole system define constraints on the overall distribution of traits.

The correlation between D_min and IBD was very interesting and novel. The dense branching patterns (low IBD) were associated with the capacity of the species to make fine roots (low D_min). Conversely, those root systems which do not make fine roots (high D_min) also space their roots well apart (high IBD). This trade-off between the branching density and diameter of roots is rather logical from an economic point of view (e.g. Eissenstat, 1992). It is also consistent with the trade-off between ‘scale’ and ‘precision’ foraging proposed by Campbell et al. (1991). Making large roots allows the root system to extend and forage in a large volume, because roots with a large meristem are able to grow faster and longer (see, for example, Lecompte et al., 2005). However, such large roots cannot be densely distributed because they have a high cost. Conversely, making fine roots is an economic way to increase the exchange surface, but only locally, because such roots cannot extend very far. It is interesting to note that only D_min is correlated with IBD, but not D_max. This confirms the value of considering both diameters independently and looking separately at these extreme roots.

Another interesting correlation was observed between the range of diameters (D_range) and the coefficient of variation of diameter among laterals (VarD). It means that species which develop a wide range of diameters tend to distribute more variable laterals at each branching level. This is probably a way to forage more efficiently, and to enhance their performance in the ‘scale–precision’ trade-off by alternating roots with different growth and branching capacities. Pagès (2011) demonstrated in a theoretical study the potential value of such variations for increasing the soil foraging performance.

Since several traits were correlated, not all trait combinations were represented in the sample set of species, and some trait values were associated in particular syndromes. Therefore, we found it relevant to define branching types that could illustrate these associations or syndromes for particular species. Five different groups were defined, essentially separated by the two main components of the PCA. They summarized the two main features that were observed: branching density of the species was closely related to its minimal diameter; and the attribution of diameters to the laterals through branching (dominance and variation) was related to the overall range of diameters expressed by the species.

Future prospects

This work, which has proven the feasibility and value of this original method for observation and quantification, is a starting point for new studies on a larger set of situations. It will be particularly interesting to characterize the branching patterns of other species, and particularly of monocots that were not represented in this first step. We also intend to evaluate the sensitivity of the branching traits to some environmental conditions, and to study further the ecological significance of the morphological traits and syndromes that we have defined. Finally, whilst it was important to identify specific traits for quantifying branching patterns, it will be equally necessary to link them to traits dedicated to the quantification of elongation.