Abstract
The aim was to elucidate how steps in drug translocation by a solute carrier transporter impact Michaelis-Menten parameters Km, Ki, and Vmax. The first objective was to derive a model for carrier-mediated substrate translocation and perform sensitivity analysis with regard to the impact of individual microrate constants on Km, Ki, and Vmax. The second objective was to compare underpinning microrate constants between compounds translocated by the same transporter. Equations for Km, Ki, and Vmax were derived from a six-state model involving unidirectonal transporter flipping and reconfiguration. This unidirectional model is applicable to co-transporter type solute carriers, like the apical sodium-dependent bile acid transporter (ASBT) and the proton-coupled peptide cotransporter (PEPT1). Sensitivity analysis identified the microrate constants that impacted Km, Ki, and Vmax. Compound comparison using the six-state model employed regression to identify microrate constant values that can explain observed Km and Vmax values. Results yielded some expected findings, as well as some unanticipated effects of microrate constants on Km, Ki, and Vmax. Km and Ki were found to be equal for inhibitors that are also substrates. Additionally, microrate constant values for certain steps in transporter functioning influenced Km and Vmax to be low or high.
Keywords: transporter, model, Michaelis-Menten, apical sodium-dependent bile acid transporter
1. INTRODUCTION
The Michaelis-Menten model was developed to describe enzymatic conversion of substrate to product. The two steps are substrate binding to enzyme (and its reverse, disassociation) and irreversible product formation. These steps are parameterized as k1, k−1, and k2, such that the Michaelis-Menten parameters in terms of the microrate constants are Km = (k−1 + k2)/k1 and Vmax = k2·[ET] where [ET] is the total enzyme concentration (1, 2). The competitive inhibition model is an extension, where inhibitor can bind reversibly to enzyme (i.e. k3 forward and k−3 reverse), where Ki = k−3/k3 (1). A strength of the Michaelis-Menten model is its simplicity, including Km being the substrate concentration for catalysis to be one-half Vmax.
A large number of methodical investigations have been applied to elucidating mechanisms of enzymatic catalysis, which have yielded many elegant descriptions of enzymes. For example, these include the ternary complex mechanism for glutathione S-transferases (3), the ping-pong mechanism for thioredoxin peroxidase (4), the random-sequential mechanism for IκB kinases α and β (5), and the ordered-sequential mechanism for thymidylate synthase (6). These models have benefited from a large number of experimental methods to study enzyme structure and function, resulting in models that are more elaborate than the Michaelis-Menten model.
Drug transporters are generally more complex than many enzyme systems. Hence, when drug flux data is modeled, drug interaction with carrier systems is often characterized by Km (affinity for transporter), Ki (inhibition potency), and Vmax (maximum velocity of substrate transport) values, from the simple Michaelis-Menten model. These parameters are experimentally determined through a series of in vitro uptake and inhibition studies. Application of the simple Michaelis-Menten model efficiently reduces data to these few parameters, allowing for greater data interpretability. For example, Ki values are frequently determined to allow for rapid assessment of potential drug inhibitors of transporters (7). While convenient for data reduction, the Michaelis-Menten model is presumably overly simplified to represent a detailed description of transporter-mediated drug inhibition and drug flux. Interestingly, while there have been recent large developments in transporter identification and drug studies with transporters, kinetic model development for transporter functioning has perhaps lagged. This work aims to contribute to closing this gap. Importantly, a greater mechanistic understanding of transporter kinetics will allow for a greater understanding of translocation differences by a transporter for different substrates, as well as by different transporters for the same substrate. A mechanistic analysis of transporter function can lead to greater kinetic interpretability of simplified Ki, Km, and Vmax parameters that are typically used to describe transporter flux data.
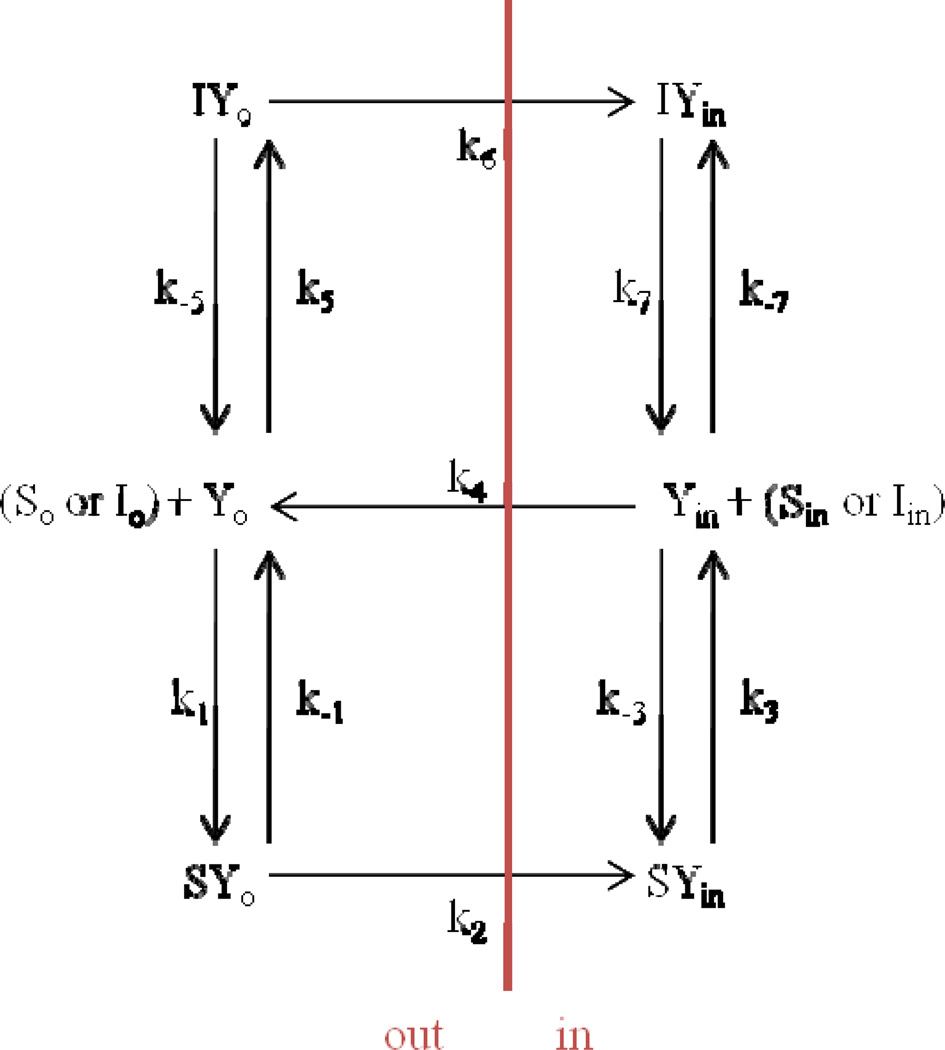
The overall aim was to understand how steps in drug translocation by a solute carrier transporter impact Michaelis-Menten parameters Km and Vmax. As discussed below, a six-state model (Fig. 1) was selected as a model for transporter translocation of drug, and allows for inhibition. The six-state model possesses 11 microrate constants. This model reflects a carrier system where substrate (including translocation of an inhibitor that is a substrate) is translocated by the protein in a unidirectional fashion, and where subsequent free protein re-configuration is unidirectional. Motivation for this work is that Michaelis-Menten parameters from transporter studies are generally not interpreted, with regard to any underpinning mechanistic transporter model. This aim was pursued through two objectives.
Fig 1.
Six-state model for unidirectional transporter-mediated substrate translocation in the presence of inhibitor. This model is more briefly denoted the six-state model. The model entails that free drug outside of the cell (So) binds with free transporter at exo-face (Yo) in order to be translocated to be free drug inside of cell (Sin). Three steps are needed for substrate flux: free drug binding to transporter, re-configuration of drug-transport complex from exo-facial oriention to endo-facial oriention, and release of drug intracellularly from transporter. In a fourth forward step, free transporter is re-configured from endo-facially oriented to its initial free, exo-facially oriented configuration. In this model, only unidirectional protein flipping that involves substrate (or inhibitor) translocation or free protein re-configuration is allowed. The model also allows free inhibitor outside of the cell (Io) to compete for Yo by an identical process, forming Iin inside the cell. Eqn 10 is the general solution for net transporter-mediated drug flux from outside of cell to the inside of cell when Sin = 0. Subscript o denotes outside of cell or on exo-face (i.e. left side). Subscript in denotes inside of cell or on endo-face (i.e. right side). Each microrate constant except k−3 and k−7 impacted Km, Ki, and/or Vmax.
The first objective was to derive a model for carrier-mediated substrate translocation (incorporating competitive inhibition where the inhibitor is also a substrate); and perform sensitivity analysis with regard to the contributions of the impact of individual microrate constants on Km, Ki, and Vmax. For the six-state model, equations for Km, Ki, and Vmax were derived in terms of underlying microrate constants. Sensitivity analysis identified which microrate constants impacted Km and Vmax. The second objective was to compare underpinning microrate constants between compounds translocated by the same transporter using nonlinear regression. Results yielded some expected findings, as well as some unanticipated effects of microrate constants on Km and Vmax.
2. THEORETICAL
2. 1. Derivation of Model Equations
The six-state model shown in Fig. 1 was used as a model for substrate and competitive inhibitor to cross a membrane, along with re-orientation of the transporter. In this model, both substrate and inhibitor cross the membrane by an identical mechanism (i.e., the competitive inhibitor is also a substrate that binds to the same binding domain).
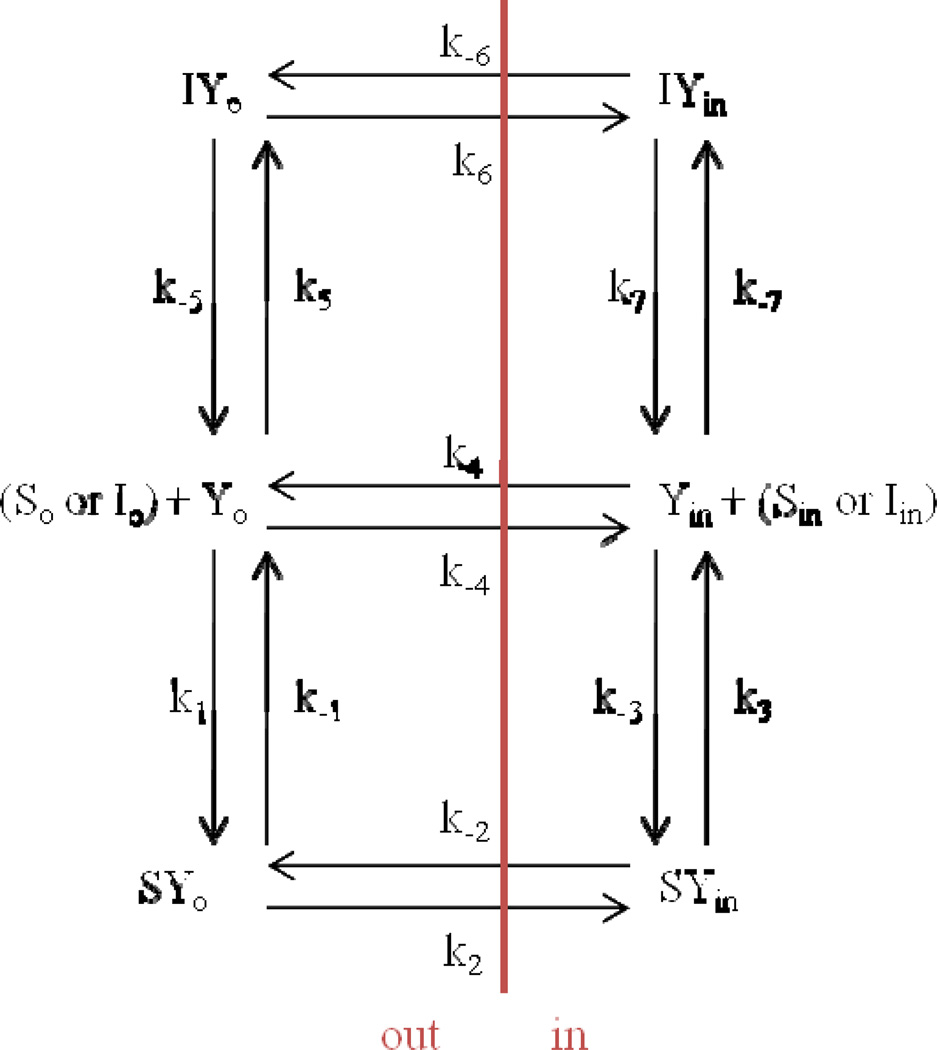
The model starts with free transporter (Yo), substrate (So), and inhibitor (Io) outside of the membrane, with the membrane shown as a red line. The transporter can bind then to substrate (forming SYo complex) or inhibitor (forming IYo complex). If the transporter binds to substrate, the transporter can move on to the next step in the cycle, where the transporter changes configuration from exo-facially oriented to endo-facially oriented (i.e. forming SYin). At this point, the substrate can be released inside the membrane (Sin), and then the transporter can reassume its original exo-facially oriented position (Yo). Similarly, if the transporter forms IYo, it can change configuration to form IYin and subsequently release inhibitor as Iin. Steps in this model that do not cross the membrane are reversible, and all components are in steady state. However, steps involving translocation across the membrane are unidirectional. This model therefore represents unidirectional transporter-mediated substrate translocation in the presence of inhibitor. This unidirectional model of transport is applicable for carriers such as the co-transporter type solute carriers (SLCs), where physiological conditions do not allow for back-flux of the substrate-carrier complex or in cases where back-flux is negligible. An example is the human apical sodium dependent bile acid transporter (ASBT, SLC10A2). ASBT requires sodium for substrate transport; thus, because of the sodium gradient present and the electrochemical potential of the cell, it is assumed that steps involving transporter reconfiguration are unidirectional (i.e. transporter can only move "forward"). k1, k−3, k5, and k−7 are second order microrate constants with units of µM−1s−1, while all other microrate constants are first order and have units of s−1. Concentrations of free inhibitor, substrate, and transporter are in µM. A general model of facilitative transport where all steps are reversible is presented in the Appendix and Supplementary Material (Fig A1 and Eqns S1–14), and represents a more complex model relative to the model in Fig. 1.
Fig. A1.
Six-state model for facilitative transporter-mediated substrate translocation in the presence of inhibitor. Compared to Fig. 1, this model for facilitative transporter-mediated substrate translocation is more complex in that all steps are reversible. Eqn S10 (supplementary material) is the general solution for net transporter-mediated drug flux from outside of cell to the inside of cell when Sin = 0. Subscript o denotes outside of cell or on exo-face (i.e. left side). Subscript in denotes inside of cell or on endo-face (i.e. right side). Each microrate constant except k−3 and k−7 impacted Km, Ki, and/or Vmax.
The system of equations to define transporter movement is defined and solved in a similar manner as in Falk et. al (8). Rate equations for the six transporter states are as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Additionally, the sum of all transporters states (YT) is described by:
| (7) |
To solve for this system, the rate equations were organized into matrix form. In order to obtain six independent equations, equation 7 was substituted for equation 1. Steady state was assumed to set all transporter concentration rate equations to 0.
The system of equations in matrix form above was solved in Matlab (The Mathworks, Inc., Natick, MA) to yield equations for each transporter state. The full matrix solution equations are presented in the Supplementary Material (equations S15– 20).
Velocity of each compound was defined by the following equations:
| (8) |
| (9) |
Putting the matrix solution into equation 8, and assuming sink conditions so that [Sin] and [Iin] = 0, the equation for VS becomes:
| (10) |
In eqn 10, the units of velocity are µM/s. Eqn 10 can be formulated in terms of the Michaelis Menten competitive inhibition model, which is (1, 2):
| (11) |
In the form of eqn 11, with [S] = [So] and [I] = [Io], the six-state model has apparent Michaelis-Menten parameters:
| (12) |
| (13) |
| (14) |
Solving equation 9 in the same manner and assuming SO = 0 (i.e. the “inhibitor” I is the only substrate available to bind to the transporter), Km and Vmax for I are obtained:
| (15) |
| (16) |
Hence, eqn 12–16 show the dependence of Michaelis-Menten parameters on the six-state model microrate constants. Km and Ki have units of µM, while Vmax has units of µM/s−1. Interestingly, when the inhibitor is also substrate transported by an identical mechanism to the compound designated as the substrate as in the case described above, Ki = Km (i.e. equation 13 equals equation 15 for “inhibitor” I). The determinants of Km and Vmax for the two compounds are identical, although each possesses their own corresponding microrate constants, such that they do not have the same Km values and Vmax values.
3. METHODS
Two types of analyses were performed on the six-state model (Fig. 1): microrate constant sensitivity analysis and compound comparison. Based on the results of the model equation derivation, Km and Ki were treated as equal for all subsequent analysis. Sensitivity analysis assessed the impact of individual microrate constants on each Km and Vmax. Compound comparison employed regression to estimate microrate constant values for four scenarios, each representing compound pairs with observed Km and Vmax values (four combinations of high and low values).
3. 1. Sensitivity Analysis
Eqn 12 and 14 (i.e. Km and Vmax) were subjected to sensitivity analysis for the six-state model. For each equation, each microrate constant was individually varied to assess its impact on the Michaelis-Menten parameters. Microrate constants were varied from a value of 1 to a value of 1,000,000 (in their respective units), while all remaining microrate constants were fixed at 1. Additionally, each microrate constant was varied from a value of 1,000,000 to a value of 1, while all remaining microrate constants were fixed at 1,000,000. For example, k1 was assigned 1 or 1,000,000, while all other constants were 1, then 1,000,000. The resulting fold changes in Km and Vmax were recorded. Those microrate constants which caused a 1000-fold or more change in Michaelis-Menten constants were deemed significant.
3. 2. Compound Comparison
Nonlinear regression was performed using eqn 12 and 14 (i.e. Km and Vmax) in order to elucidate microrate constant values that underpin four observed cases, representing four previously observed combinations of high and low Km and Vmax values. The four comparisons considered experimental data from four compounds (9, 10, 11), illustrated in Table 1. Briefly, the four compounds are bile acid derivatives (see Fig. S1 and Table S1 in the Supplementary Material) whose Michaelis-Menten parameters were characterized against ASBT. Case 1 compared two compounds with similarly high Km values, but differing Vmax values (compound 2 vs compound 1). Case 2 compared two compounds with similarly low Km values, but differing Vmax values (compound 4 vs. compound 3). Case 3 compared a compound with low Km and Vmax values with a compound with high Km and Vmax (compound 4 vs. compound 1). Case 4 compared a compound with low Km and high Vmax against a compound with high Km and low Vmax (compound 3 vs. compound 2). This design was intended to assess the relative values of microrate constants when Km and Vmax have various values across compounds.
Table 1.
Compounds 1–4 and their Km and normalized Vmax values when measured against the bile acid transporter ASBT. Compounds 1–4 were applied to compare underlying microrate constants in compound pair analysis. Compounds are conjugates of chenodeoxycholate. Normalized Vmax is compound Vmax divided by Vmax of taurocholate, where taurocholate is a prototypical native bile acid.
| Compound | Km (µM) | Norm Vmax | Characterization |
|---|---|---|---|
| 1 | 16.3 ± 4.7 | 2.15 ± 0.23 | High Km, High Vmax |
| 2 | 17.5 ± 4.7 | 0.250 ± 0.022 | High Km, Low Vmax |
| 3 | 1.69 ± 0.71 | 1.72 ± 0.14 | Low Km, High Vmax |
| 4 | 1.20 ± 0.38 | 0.242 ± 0.013 | Low Km, Low Vmax |
Since eqn 12 and 14 are only two equations, yet collectively contain five unknown parameters (i.e. k1 through k−1), any set of Km and Vmax values does not offer an exact solution, in terms of microrate constants. Hence, in order to elucidate the distribution of microrate constant values for each case, 1000 regressions were performed, with the expectation that certain microrate constants have a larger influence on whether Michaelis-Menten parameters are relatively large or small.
In each regression, each k1, k2, k3, k4, and k−1 were assigned a random number between zero and one (either µM−1s−1 or s−1, depending on the constant). Using these randomly generated numbers as initial estimates, Matlab’s lsqnonlin function (i.e. least squares regression) was employed to estimate microrate constant values until the specified Km and Vmax values were attained. Regression employed the Levenberg-Marquardt method. All regressions required that each microrate value was greater than 0. For each of the four cases, this method was applied to obtain 1000 solutions. From every regression, each fitted microrate constant was normalized against the corresponding microrate constant of the compared compound. Median values for these ratios were recorded, as well as the percent of ratios greater than one, in order to characterize microrate constant values that underpin Km and Vmax and the distribution of those values.
In the defined model, there were three equations with nine unknown variables when comparing two compounds. Two of these equations are Km (i.e. eqn 12) for each compound; the ratio of their Vmax values was a fifth equation (using eqn 14). The ratio of Vmax values was used to account for the unknown exact number of transporter proteins. Rather than 10 unknown variables (i.e. two times the number of microrate constants), there are only 9 unknown variables, since k4 is assumed to be the same value for each compound, as they were measured against the same transporter in the same expression system and k4 is purely transporter-specific. While there has been evidence k4 can be partially influenced by exchanged substrates in limited cases (12), it is assumed here that k4 is substrate-independent. Compound pair analysis is of practical value, as Michaelis-Menten parameters are typically interpreted in the context of other compounds.
3.3. Previously Observed Km and Ki Data and Error Simulations
To determine if the model-supported conclusion Km = Ki is also supported by observed data, parameters of 50 previously tested non-native bile acids were analyzed (9, 10, 11, 13). In addition to examining previous data, Matlab error simulations were performed to evaluate the extent that error explains observed differences between Km and Ki. Km and Ki values were assigned to be either 1, 10, or 100 µM (n = 50, Km and Ki for each designated value), representing typically observed values. Vmax was set as 0.0005 nmol/cm2/s, along with taurocholate concentration of 2.5 µM and Km of 5.03 µM, from historical data (7). Taurocholate was used in Ki simulations as the prototypical native ASBT substrate that was inhibited. Eight inhibitor/substrate concentrations were used, which reflect typical experimental concentrations: 0, 1, 5, 10, 25, 50, 100, and 200 µM. Flux values were calculated by multiplying true flux values by a random number with mean 1 and standard deviation 0.1 or 0.3, representing coefficient of variation (CV) values of 10 or 30% (14). Calculated flux values were regressed against the Michaelis-Menten competitive inhibition model to identify Km and Ki. Although truely equal in these Matlab error simulations, Km and Ki, were compared against one another for each of 50 simulated compound cases, and their fold-differences were calculated.
4. RESULTS
4.1. Sensitivity Analysis
Table 2 indicates the fold-impact of a 1,000,000-fold change in each individual microrate constant on Km and Vmax in the six-state model. Table 2 involves two types of sensitivity analysis for each microrate constant. In one type, the microrate constant under study (i.e. kn) was increased from a value of 1 to a value of 1,000,000, while all other microrate constants remained a value of 1. The second type is when kn was decreased from a value of 1,000,000 to a value of 1, while all other microrate constants remained a value of 1,000,000. For example, in Table 2, Km was reduced many-fold when k1 was increased from one to 1,000,000 when all other microrate constants were one. Meanwhile, Km was increased 500,000.5-fold when k−1 was increased from 1 to 1,000,000. Km only increased 1.5-fold when k2 was decreased from 1,000,000 to 1. In Table 2, a large impact of a microrate constant is defined as changing Km or Vmax by at least 1000-fold, and is highlighted in red (and underlined).
Table 2.
Sensitivity analysis for impact of microrate constants on Km and Vmax for the six-state model. Values in red (and underlined) denote changes that were over 1000-fold higher or lower. kn is either k1-k−1 and denotes the microrate constant that was varied. For example, compared to when all microrate constants were 1 µM−1s−1 or 1 s−1, increasing k1 to 1,000,000 µM−1s−1 decreased Km by 1,000,000-fold (i.e. 0.000001-fold change, noted in table). Meanwhile, compared to when all microrate constants were 1,000,000 µM−1s−1 or 1,000,000 s−1, decreasing k1 to 1 µM−1s−1 increased Km by 1,000,000-fold.
| kn | Fold change in Km when… | Fold change in Vmax when… | ||
|---|---|---|---|---|
| kn increased to 1,000,000 a |
kn decreased to 1 b |
kn increased to 1,000,000 a |
kn decreased to 1 b |
|
| k1 | 0.000001 | 1000000 | 1 | 1 |
| k2 | 0.75 | 1.50 | 1.50 | 0.000003 |
| k3 | 1.50 | 0.000003 | 1.50 | 0.000003 |
| k4 | 1.50 | 0.000003 | 1.50 | 0.000003 |
| k−1 | 500000.5 | 0.50 | 1 | 1 |
Sensitivity analysis involved increasing kn from a value of 1 to a value of 1,000,000, while all other microrate constants retained a value of 1.
Sensitivity analysis involved decreasing kn from a value of 1,000,000 to a value of 1, while all other microrate constants retained a value of 1,000,000.
Using the six-state model, each microrate constant except k−3 significantly impacted Km or Vmax. Km was sensitive to k1, k−1, k3 and k4. k1 had a significantly favorable impact on Km (i.e. decreased Km), while k−1, k3 and k4 had a detrimental impact (i.e. increased Km). In the context of Fig. 1, faster substrate binding increased Km potency. Meanwhile, faster substrate disassociation decreased potency. Each of these effects was expected. An unexpected result was that a slower transporter re-configuration from endo-facially oriention to exo-facially orientation (i.e. k4) decreased potency. Additionally, faster release of substrate inside the membrane (i.e. k3) increased Km potency. No other microrate constants impacted Km at the defined significance level. Vmax was favorably impacted by k2, k3, and k4 (i.e. all three forward microrate constant after substrate binding).
Some results from sensitivity analysis of the six-state model were unexpected. Since Michaelis-Menten rate constants were derived from an enzyme-substrate model, intuitively expected influences are perhaps k1 and k−1 on Km and k2 on Vmax. However, from the six-state model (i.e. Fig. 1), additional microrate constants impacted Michaelis-Menten parameters. k4 impacted both Vmax and Km. This sensitivity analysis indicates that a compound’s Km and Vmax can also be affected by the free transporter protein’s rate of re-configuration (i.e. k4), a step that does not involve compound binding or compound translocation. For example, an especially large k4 favors Km and an especially slow k4 disfavors Vmax. These dependencies anticipate that Michaelis-Menten parameters for any compound-transporter pair cannot be exclusively attributed to compound structure or compound properties, but can reflect the structural biology of the transport itself.
These sensitivity analysis results imply that free transporter kinetics (i.e. k4) may explain variation in typical Km and Ki values for different transporter proteins. For instance, Km and Ki values of many compounds for ASBT are on the order of µM, including bile acids, which are native ASBT substrates. Meanwhile, native peptide substrates of peptide transporter 1 (PEPT1, SLC15A1) are on the order of mM (15). It is possible that peptides are poor substrates for PEPT1, compared to bile acids as substrates for ASBT, due to potentially higher binding affinity of bile acids for ASBT (i.e. better k1 and k−1 values). Alternatively, this sensitivity analysis suggests the difference between ASBT and PEPT1 could possibly be due to free transporter protein kinetics.
4.2. Compound comparison
Compound comparison was conducted on the six-state model to build upon sensitivity analysis findings. While sensitivity analysis involved assessing the impact of each individual microrate constant on resulting Michaelis-Menten parameters by varying microrate constant values, compound pair analysis employed regression to determine sets of microrate constants that explain observed Michaelis-Menten parameters across compounds. For each of four cases, 1000 simulations were performed. Simulations only differed in initial values. The strength of compound pair analysis is its focus on identifying which transporter steps explain variation in Michaelis-Menten parameters across compounds, which is of practical value in studying a homologous series of compounds.
Table 3 summarizes compound pair analysis results. Results shown in red (and underlined) signify a 3-fold or more difference in microrate constant values between the compounds compared. The median ratio of 1,000 runs for each comparison is shown, as well as the percent of all solutions which were greater than 1 (i.e. the percent of instances where the microrate constant is larger than the microrate constant of the reference compound). Table S2 in the Supplementary Material presents additional compound comparison results using 100 and 10,000 runs, showing that 1,000 runs are sufficient to obtain a stable distribution of underlying microrate constant values. By looking at the distribution of microrate constants from 1,000 runs, the microrate constants that can cause these scenarios are identified. Additionally, those that have no clear trend of higher or lower values (i.e. median close to 1) can thus be any value without affecting the resulting Km and Vmax. These microrate constants are found to have limited impact. In this way, compound comparison is a multivariate sensitivity analysis using actually observed endpoints.
Table 3.
Summary of results from compound pair analysis using the six-state model. Comparisons were performed r compounds 2 versus 1 (high Km low Vmax vs. high Km high Vmax), 4 versus 3 (low Km low Vmax vs. low Km high Vmax), 4 versus 1 (low Km low Vmax vs. high Km high Vmax), and 3 versus 2 (low Km high Vmax vs. high Km low Vmax) in Table 1. The median ratio of 1000 simulations for each comparison is shown, as well as the percent of the all solutions which were greater than 1. Median values that differ by at least a factor of 3 are shown in red (and underlined). For example, in Case 1, the k2 solution values of compound 2 have a median value 0.06 times the k2 solution values of compound 1. Also, 11.7% of the 1000 solutions for compound 2’s k2 value were greater than compound 1’s k2 value. These results suggest that generally, between two compounds, k2 is slower when Vmax is lower.
| k1 | k2 | k3 | k−1 | ||||
|---|---|---|---|---|---|---|---|
| Case 1 | Median | 0.74 | 0.06 | 0.42 | 1.03 | ||
| %>1 | 40.7 | 11.7 | 17.3 | 51.6 | |||
| Case 2 | Median | 1.01 | 0.08 | 0.23 | 0.97 | ||
| %>1 | 50.1 | 9.2 | 13 | 47.9 | |||
| Case 3 | Median | 10.48 | 0.06 | 0.27 | 0.94 | ||
| %>1 | 94.1 | 9.5 | 13.8 | 46.0 | |||
| Case 4 | Median | 9.25 | 15.68 | 1.70 | 0.86 | ||
| %>1 | 99.6 | 89.7 | 76 | 40.1 |
Case 1
In this comparison (i.e. compound 2 vs. compound 1), compound 2 had a much lower Vmax than compound 1 (0.250 vs. 2.15 in Table 1), while Km for the two compounds were similarly high (17.5 µM vs. 16.3 µM). Results show that when Vmax is lower (i.e. slower), k2 is slower (i.e. median 0.06, respectively). This finding supports the broadly held notion that the k2 microrate constant (e.g. substrate bound transporter changing configuration from exo-facially oriented to endo-facially oriented) is the most important step in determining Vmax. From this data, it is evident that a larger Vmax but similar and potent Km can be caused by a faster rate of transport across the cell membrane. Of note, although the k3 ratio median did not meet the 3-fold lower cut-off, the ratios of k2 and k3 in a given run were never both greater than 1 (i.e. 0 of 1000 runs), indicating that at least one of these microrate constants must be low for Vmax to be low. This implies that k3 (i.e. release of substrate from transporter inside the cell) also has an influence on Vmax.
Case 2
In this comparison (i.e. compound 4 vs. compound 3), compound 4 had a much lower Vmax than compound 3 (0.242 vs. 1.72 in Table 1), while Km for the two compounds were similarly potent (1.20 µM vs. 1.69 µM). This case confirms that k2 is responsible for changes in Vmax, consistent with sensitivity analysis and case 1, and that whether Km values are low or high does not influence this. Additionally, in this case where compound Km values were highly potent, k3 (i.e. release of substrate from transporter inside the cell) has a large impact on Vmax. As in case 1, in 0% of all iterations were both k2 and k3 ratios greater than 1, indicating that at least one of these must be slower for Vmax to be low.
Case 3
In this comparison, compound 4 (Km = 1.20 µM, Vmax = 0.242) was compared against compound 1 (Km = 16.3 µM, Vmax = 2.15). Results in Table 3 show that low Vmax and low (potent) Km can be caused by high k1 (i.e. fast substrate binding to transporter outside the membrane) and low k2 and k3. Interestingly, when both Vmax and Km are taken into account, k−1 value has little impact, contrary to sensitivity results from only the Km equation. The k1 ratio has a value greater than one 94.1% of the time, while k−1 has a value greater than one 46.0% of the time.
Case 4
In this comparison, compound 3 (Km = 1.69 µM, Vmax = 1.72) was compared against compound 2 (Km = 17.5 µM, Vmax = 0.250). Results in Table 3 confirm that, like in case 3, fast binding (k1) causes low Km. Additionally, as seen in case 1, fast k2 has more of an impact on high Vmax than k3 (i.e. bound substrate translocation across the membrane vs. release of substrate inside the cell).
Overall, the results of these four cases suggest that when two compounds are taken up by the same transporter (i.e. no difference in k4), the k1 microrate constant is the most influential determinant of Km, while k2 is the most influential determinant of Vmax.
4.3. Previously Observed Km and Ki Data and Error Simulations
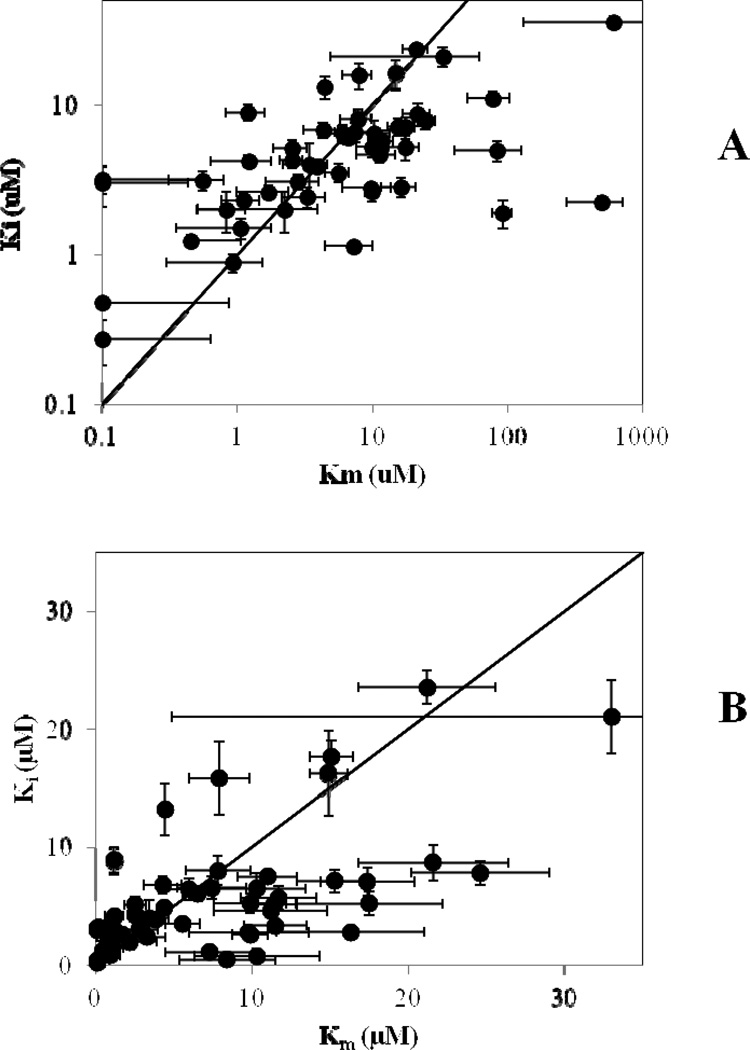
In Figure 2, previously observed Km and Ki values of 50 compounds for ASBT are plotted against one another, along with the line of Km = Ki, to examine differences between Km and Ki Compound structures and corresponding data values are presented in the Supplementary Material, Fig. S1 and Table S3. A general positive relationship is observed between Km and Ki. Using the Student’s t-test between Km and Ki data of the 50 compounds tested, no Km-Ki pair had a P-value less than 0.01, concluding that Km was indistinguishable from Ki at this significance level. Only five of the 50 had a P-value less than 0.05. Thus, experimental evidence generally does not refute our model’s claim that Km is equal to Ki when an inhibitor is also a substrate and inhibition and uptake occur at the same binding site. While measured Km and Ki are of course not identical, an approximately equal number of the 50 examined compounds yielded Km>Ki versus Ki>Km. Across all ranges of compound Km and Ki fold-differences, Km was greater than Ki 52% of the time.
Fig 2.
ASBT Ki vs Km values of 50 compounds from previous studies (9, 10, 11, 13). Each compound is an ASBT substrate and inhibitor. The trend line shown represents Ki=Km. In Panel A, all 50 compounds are shown, while Panel B is an enlarged view of Km and Ki < 30 µM.
Another comparison of these Km and Ki values is presented in Table 4. Table 4 illustrates that 40.0% of the 50 compounds showed Km and Ki values to be within a factor of two. An additional 38.0% of compounds exhibited Km and Ki values were beyond 2-fold different from one another but less than 5-fold different. Only 22.0% of compounds showed over a 5-fold difference in Km and Ki. Interestingly, for each of these three categories (i.e. less than 2-fold, 2-to-5-fold, and more than 5-fold), there was about an equal number of compounds where Km was greater than Ki (45.0%, 52.6%, and 63.6% of cases showed Km > Ki in each group, respectively). This observation implies that Km or Ki is not predominantly larger than the other.
Table 4.
Comparison of Km versus Ki distribution frequencies from simulations to observed distribution frequency. The simulation on the far right (i.e. Km=Ki=100 mM with 30% CV) was the simulation that was most similar to the observed Km versus Ki distribution frequency from 50 non-native bile acids. The observed distribution frequency was 40%, 38%, and 22% for Km and Ki to be 1–2 fold different, 2–5 fold different, and beyond 5 fold different, respectively. Distribution frequencies were obtained from six simulated senarios: Km = Ki = 1 µM and 10% CV, Km = Ki = 1 µM and 30% CV, Km = Ki = 10 µM and 10% CV, Km = Ki = 10 µM and 30% CV, Km = Ki = 100 µM and 10% CV, and Km = Ki = 100 µM and 30% CV. Simulation results support that a majority of a compound's Km and Ki values are about equal, with only a minor number of compounds exhibiting a 5-fold difference in Km and Ki values.
| Fold- Difference between Km and Ki |
Frequency from Previous Experimental Studies |
Frequency from Simulated Pairs | |||||
|---|---|---|---|---|---|---|---|
| 1 µM, 10% CV |
1µM, 30% CV |
10µM, 10% CV |
10µM, 30% CV |
100 µM, 10% CV |
100 µM, 30 % CV |
||
| 1 to 2 | 40 % | 100 % | 72 % | 100 % | 76 % | 94 % | 52 % |
| 2 to 5 | 38 % | 0 % | 24 % | 0 % | 24 % | 6 % | 40 % |
| beyond 5 | 22 % | 0 % | 4 % | 0 % | 0 % | 0 % | 8 % |
Additionally, Table 4 presents the results of experimental error simulations. Distribution frequencies were obtained from six simulated scenarios: Km = Ki = 1 µM and 10% CV, Km = Ki = 1 µM and 30% CV, Km = Ki = 10 µM and 10% CV, Km = Ki = 10 µM and 30% CV, Km = Ki = 100 µM and 10% CV, and Km = Ki = 100 µM and 30% CV. Simulated Km and Ki pairs had the largest fold-differences when Km and Ki were large valued (e.g. 100 µM) and the assigned percent CV was higher. For example, in the right-most column of Table 4 (Km, Ki = 100 µM, 30% CV), 40% of simulated Km and Ki pairs were between 2 and 5-fold different, while 8% were greater than 5-fold different. Hence, results from 50 non-native bile acids show that a majority any one compound's Km and Ki values are within a factor of 5 apart, and that some of the differences in observed Km and Ki values may be attributed to experimental error. Alternatively, differences in observed Km and Ki values could occur if a compound binds to an exterior binding site which inhibits uptake but does not result in transport across the membrane (i.e. if an individual compound does not adhere to Fig. 1).
5. DISCUSSION
Transporter study results are frequently summarized as Michaelis-Menten parameters. For example, an initial inhibition study yields a Ki value. If the compound is an inhibitor (e.g. “binds with the transporter”), subsequent flux studies may be performed, yielding Km and Vmax values. Infrequently, Km and Ki values are compared. Even less frequently, these Michaelis-Menten parameters are interpreted within a kinetic context (e.g. What is the rate limiting step in substrate translocation?).
Since transporters and their catalytic cycles are biophysically complex, even compared to water soluble enzymes, the interpretation of Michaelis-Menten parameters with regard to underlying transporter dynamics is difficult. For example, Michaelis-Menten parameter interpretations with respect to substrate-transporter interactions and with respect to translocation mechanism are not easily performed. However, several studies have linked flux result to transporter catalytic cycles (16, 17, 18). Loo et. al analyzed a model for substrate transport by the Na+/glucose cotransporter (SGLT1, SLC5A1), incorporating both Na+ and substrate binding (19). In Loo et. al, transporter protein conformations in the presence of different substrates were compared by observing resulting current and fluorescence in response to induced voltage changes. Simulations were used to vary microrate constants until a fit was obtained. Hoare et. al examined L-leucine transport into red blood cells using a four step model for simple carrier transport similar to the model in our analysis (20). The study concludes that in the case of L-leucine transport, the carrier re-orientation process (i.e. k4 in our model) is rate-limiting, confirming that free transporter kinetics can greatly affect flux data. Fontana et. al also independently confirms that the carrier re-orientation step can be rate-limiting, as they identified for glutamate transport by the excitatory amino-acid transporters (EAATs) (21). This reinforces what we have seen in our analysis. Experiments such as these represent significant progress toward a mechanistic understanding of transport processes. Specifically for ASBT, structure activity relationships (22, 23, 24) and crystal structures of bacterial homologues of ASBT (25, 26) have identified regions of transporters involved in substrate translocation. However, the carrier models above and the identified structure-activity relationships and crystal structures do not attempt to understand how underpinning microrate constants influence Michaelis-Menten parameters Km, Ki, and Vmax.
The overall aim of this work was to elucidate the contribution of individual steps in drug translocation (and inhibition) to apparent transporter Michaelis-Menten parameters. To achieve this, first a model was derived for transporter-mediated substrate translocation (with competitive inhibition); model flux is presented via Michaelis-Menten parameters in eqn 12–16 (Fig. 1).
An interesting observation from this work is that Km was derived to be equal to Ki for cases when the inhibitor is also a substrate, as is the case in many inhibition/substrate screenings. In multiple studies, we have previously speculated that bile acid translocation by ASBT is rate-limited by substrate binding, as Ki and Km are often the same value (10, 27). In Balakrishnan et. al, a plot for native bile acids showed that compounds fell close to a Km = Ki line (27). In this work and in contrast to our prior explanations, rate-limiting substrate binding is not the cause of Km being equal to Ki. Our analysis here of past Km/Ki data from non-native bile acids confirms that in the vast majority of the compounds examined, Km was not significantly different from Ki. Additionally, simulations showed that some of these observed differences may be attributed to experimental error. Other studies have identified cases of substrate-dependent inhibition, where a single compound can have multiple Ki values depending on the substrate being inhibited (28, 29). Substrate-dependent inhibition could potentially be caused by multiple inhibitor binding sites, whereas in this manuscript, inhibition and uptake are assumed to occur from interaction at the same transporter binding domain.
Sensitivity analysis aimed to assess the impact of individual microrate constants on the Km and Vmax equations (eqn 12 and 14). Interestingly, the kinetics associated with free transporter orientation change (i.e. k4) had a large effect on both Km and Vmax. This analysis clearly shows that this substrate-independent re-orientation step is significant and could explain why potent substrates for different transporters differ in Km by orders of magnitude. Additionally, compound pair analysis built upon sensitivity analysis findings and allowed for the elucidation of microrate constant distributions under specific cases of Km and Vmax values across differing compounds measured against the same transporter.
5.1. Future directions
Pharmaceutical transporter science has progressed in terms of availability of transporter targets and related molecular biology technology (30, 31, 32); relevance of transporters in drug disposition (33) and drug-drug interactions (34); and well as computational and QSAR approaches to better leverage drug screening data sets (35, 36). However, a molecular understanding of the influence of transporter biophysics and compound structure on transporter-mediate drug flux is broadly undeveloped. Interestingly, little transporter kinetic interpretation is currently extracted from Michaelis-Menten parameters. For a specific transporter, what is the interpretation of a lower Km of one compound relative to another? A future direction in pharmaceutical transporter science is to better understand the key kinetic steps in transporter functioning and how those steps impact the translocation of various drugs. Such a molecular understanding has the promise to aid in the design of drugs, or screening of drugs, with favorable attributes (e.g. weak Ki, weak Km, but high Vmax; or potent Ki but non-substrate).
6. CONCLUSION
The overall aim was to elucidate the contribution of individual steps in drug translocation by (and inhibition of) a carrier to apparent transporter Michaelis-Menten parameters (e.g. Km, Ki, and Vmax). Such Michaelis-Menten parameterization is commonly employed to interpret drug uptake data, without regard to the underpinning mechanism behind these simplified Km, Ki, and Vmax terms. This work contributes to a greater understanding of transporter kinetics, which can aid in understanding differences in substrate uptake by one or more transporters. Results show that Km and Ki are equal for inhibitors that are also substrates, where uptake and inhibition occur at the same binding site. Results also reveal the most influential underlying microrate constants on Km and Vmax values.
Supplementary Material
ACKNOWLEDGEMENTS
Financial support for this work was received by T32 DK067872 Research Training in Gastroenterology. This work was supported in part by National Institutes of Health grant DK67530 and Food and Drug Administration collaborative agreement U01FD004320.
ABBREVIATIONS
- ASBT
apical sodium-dependent bile acid transporter
- SLC10A2
PEPT1, peptide transporter 1
- SLC15A1
solute carrier (SLC)
APPENDIX
The objective of this appendix is to present a more generalized six-state model than that provided in Fig. 1. This generalized model is a six-state model for facilitative transporter-mediated substrate translocation in the presence of inhibitor and is illustrated in Fig. A1. Compared to Fig. 1 (i.e. the six-state model for unidirectional transporter-mediated substrate translocation in the presence of inhibitor), this model for facilitative transporter-mediated substrate translocation is more complex in that all steps are reversible.
The model entails that free drug outside of the cell (So) binds with free transporter at exo-face (Yo) in order to be translocated to be free drug inside of cell (Sin). Three steps are needed for substrate flux: free drug binding to transporter, re-configuration of drug-transport complex from exo-facial oriention to endo-facial oriention, and release of drug intracellularly from transporter. In a fourth forward step, free transporter is re-configured from endo-facially oriented to its initial free, exo-facially oriented configuration. Similarly, the reverse of this fourth step simply involves flipping of free transporter (i.e. k−4 does not involve translocation of substrate). The model also allows free inhibitor outside of the cell (Io) to compete for Yo by an identical process, forming Iin inside the cell. Eqn S10 (supplementary material) is the general solution for net transporter-mediated drug flux from outside of cell to the inside of cell when Sin = 0. Subscript o denotes outside of cell or on exo-face (i.e. left side). Subscript in denotes inside of cell or on endo-face (i.e. right side). Each microrate constant except k−3 and k−7 impacted Km, Ki, and/or Vmax.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Garrett R, Grisham C, editors. Biochemistry. 3rd ed. Belmont (CA): Thomson Brooks/Cole; 2005. [Google Scholar]
- 2.Michaelis L, Menten ML, Johnson KA, Goody RS. The original Michaelis constant: translation of the 1913 Michaelis-Menten paper. Biochemistry. 2011;50:8264–8269. doi: 10.1021/bi201284u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dirr H, Reinemer P, Huber R. X-ray crystal structures of cytosolic glutathione S-transferases: Implications for protein architecture, substrate recognition and catalytic function. Eur. J Biochem. 1994;220:645–661. doi: 10.1111/j.1432-1033.1994.tb18666.x. [DOI] [PubMed] [Google Scholar]
- 4.Sztajer H, Gamain B, Aumann K, Slomianny C, Becker K, Brigelius-Flohé R, Flohé L. The putative glutathione peroxidase gene of Plasmodium falciparum codes for a thioredoxin peroxidase. J Biol Chem. 2001;276:7397–7403. doi: 10.1074/jbc.M008631200. [DOI] [PubMed] [Google Scholar]
- 5.Peet GW, Li J. IκB kinases α and β show a random sequential kinetic mechanism and are inhibited by staurosporine and quercetin. J Biol Chem. 1999;274:32655–32661. doi: 10.1074/jbc.274.46.32655. [DOI] [PubMed] [Google Scholar]
- 6.Finer-Moore JS, Montfort WR, Stroud RM. Pairwise specificity and sequential binding in enzyme catalysis: thymidylate synthase. Biochemistry. 1990;29:6977–6986. doi: 10.1021/bi00482a005. [DOI] [PubMed] [Google Scholar]
- 7.Zheng X, Polli JE. Identification of inhibitor concentrations to efficiently screen and measure inhibition Ki values against solute carrier transporters. Eur J Pharm. Sci. 2010;41:43–52. doi: 10.1016/j.ejps.2010.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Falk S, Guay A, Chenu C, Patil SD, Berteloot A. Reduction of an eight-state mechanism of cotransport to a six-state model using a new computer program. Biophys J. 1998;74:816–830. doi: 10.1016/S0006-3495(98)74006-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zheng X, Pan Y, Acharya C, Swaan P, Polli JE. Structural requirements of the ASBT by 3D-QSAR analysis using aminopyridine conjugates of chenodeoxycholic acid. Bioconjugate Chem. 2010;21:2038–2048. doi: 10.1021/bc100273w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rais R, Acharya C, Tririya G, MacKerell A, Polli JE. Structural determinants for transport across the intestinal bile acid transporter using C-24 bile acid conjugates. Mol Pharm. 2010;7:2240–2254. doi: 10.1021/mp100233v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rais R, Fletcher S, Polli JE. Synthesis and in vitro evaluation of gabapentin prodrugs that target the human apical sodium-dependent bile acid transporter (hASBT) J Pharm Sci. 2011;100:1184–1195. doi: 10.1002/jps.22332. [DOI] [PubMed] [Google Scholar]
- 12.Martinez-Becerra P, Briz O, Romero MR, Macias RI, Perez MJ, Sancho-Mateo C, Lostao MP, Fernandez-Abalos JM, Marin JJ. Further characterization of the electrogenicity and pH sensitivity of the human organic anion-transporting polypeptides OATP1B1 and OATP1B3. Mol Pharmacol. 2011;79:596–607. doi: 10.1124/mol.110.069971. [DOI] [PubMed] [Google Scholar]
- 13.Rais R, Acharya C, Tririya G, MacKerell A, Polli JE. Molecular switch controlling the binding of anionic bile acid conjugates to human apical sodium-dependent bile acid transporter. J Med. Chem. 2010;53:4749–4760. doi: 10.1021/jm1003683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kolhatkar V, Polli JE. Reliability of inhibition models to correctly identify type of inhibition. Pharm Res. 2010;27:2433–2445. doi: 10.1007/s11095-010-0236-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bretschneider B, Brandsch M, Neubert R. Intestinal transport of β-lactam antibiotics: analysis of the affinity at the H+/peptide symporter (PEPT1), the uptake into Caco-2 cell monolayers and the transepithelial flux. Pharm Res. 1999;16:55–61. doi: 10.1023/a:1018814627484. [DOI] [PubMed] [Google Scholar]
- 16.Macey RI, Moura TF. Basic Principles of Transport. In: Hoffman JF, Jamieson JD, editors. Handbook of Physiology: Section 14: Cell Physiology. New York: Oxford University Press, USA; 1997. pp. 181–259. [Google Scholar]
- 17.Macey RI. Mathematical models of membrane transport processes. In: Andreoli TE, Hoffman JF, Fanestil DD, Schultz SG, editors. Physiology of Membrane Disorders. New York: Plenum; 1986. pp. 111–131. [Google Scholar]
- 18.Aronson PS. Kinetic properties of the plasma membrane Na+-H+ exchanger. Annu Rev Physiol. 1985;47:546–560. doi: 10.1146/annurev.ph.47.030185.002553. [DOI] [PubMed] [Google Scholar]
- 19.Loo DF, Hirayama A, Sala-Rabanal M, Wright E. How drugs interact with transporters: SGLT1 as a model. J Membrane Biol. 2008;223:87–106. doi: 10.1007/s00232-008-9116-6. [DOI] [PubMed] [Google Scholar]
- 20.Hoare HG. The transport of L-leucine in human erythrocytes: a new kinetic analysis. J Physiol. 1972;221:311–329. doi: 10.1113/jphysiol.1972.sp009753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fontana AC, de Oliveira Beleboni R, Wojewodzic MW, Ferreira Dos Santos W, Coutinho-Netto J, Grutle NJ, Watts SD, Danbolt NC, Amara SG. Enhancing glutamate transport: mechanism of action of Parawixin1, a neuroprotective compound from Parawixia bistriata spider venom. Mol Pharmacol. 2007;72:1228–1237. doi: 10.1124/mol.107.037127. [DOI] [PubMed] [Google Scholar]
- 22.Hussainzada N, Claro Da Silva T, Swaan PW. The cytosolic half of helix III forms the substrate exit route during permeation events of the sodium/bile acid cotransporter ASBT. Biochemistry. 2009;48:8528–8539. doi: 10.1021/bi900616w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hussainzada N, Da Silva TC, Zhang EY, Swaan PW. Conserved aspartic acid residues lining the extracellular loop 1 of sodium-coupled bile acid transporter ASBT Interact with Na+ and 7alpha-OH moieties on the ligand cholestane skeleton. J Biol Chem. 2008;283:20653–20663. doi: 10.1074/jbc.M802885200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Moore RH, Chothe P, Swaan PW. Transmembrane domain V plays a stabilizing role in the function of human bile acid transporter SLC10A2. Biochemistry. 2013;52:5117–5124. doi: 10.1021/bi400028q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hu NJ, Iwata S, Cameron AD, Drew D. Crystal structure of a bacterial homologue of the bile acid sodium symporter ASBT. Nature. 2011;478:408–411. doi: 10.1038/nature10450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhou X, Levin EJ, Pan Y, McCoy JG, Sharma R, Kloss B, Bruni R, Quick M, Zhou M. Structural basis of the alternating-access mechanism in a bile acid transporter. Nature. 2014;505:569–573. doi: 10.1038/nature12811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Balakrishnan A, Wring SA, Polli JE. Interaction of native bile acids with human apical sodium-dependent bile acid transporter (hASBT): influence of steroidal hydroxylation pattern and C-24 conjugation. Pharm Res. 2006;23:1451–1459. doi: 10.1007/s11095-006-0219-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Soars MG, Barton P, Ismair M, Jupp R, Riley RJ. The development, characterization, and application of an OATP1B1 inhibition assay in drug discovery. Drug Metab Dispos. 2012;40:1641–1648. doi: 10.1124/dmd.111.042382. [DOI] [PubMed] [Google Scholar]
- 29.Noé J, Portmann R, Brun ME, Funk C. Substrate-dependent drug-drug interactions between gemfibrozil, fluvastatin and other organic anion-transporting peptide (OATP) substrates on OATP1B1, OATP2B1, and OATP1B3. Drug Metab Dispos. 2007;35:1308–1314. doi: 10.1124/dmd.106.012930. [DOI] [PubMed] [Google Scholar]
- 30.Sai Y. Biochemical and molecular pharmacological aspects of transporters as determinants of drug disposition. Drug Metab Pharmacokinet. 2005;20:91–99. doi: 10.2133/dmpk.20.91. [DOI] [PubMed] [Google Scholar]
- 31.Schinkel AH, Jonker JW. Mammalian drug efflux transporters of the ATP binding cassette (ABC) family: an overview. Adv Drug Deliv. Rev. 2003;55:3–29. doi: 10.1016/s0169-409x(02)00169-2. [DOI] [PubMed] [Google Scholar]
- 32.Hediger MA, et al. The ABCs of solute carriers: physiological, pathological and therapeutic implications of human membrane transport proteins. Pflugers Arch. 2004;447:465–468. doi: 10.1007/s00424-003-1192-y. [DOI] [PubMed] [Google Scholar]
- 33.Wu C, Benet L. Predicting drug disposition via application of BCS: transport/absorption/elimination interplay and development of a biopharmaceutics drug disposition classification system. Pharm Res. 2005;22:11–23. doi: 10.1007/s11095-004-9004-4. [DOI] [PubMed] [Google Scholar]
- 34.Giacomini KM, Huang S, Tweedie D, Benet L, Brouwer K, Chu X, et al. Membrane transporters in drug development. Nature Rev Drug Discov. 2010;9:215–236. doi: 10.1038/nrd3028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ekins S, Freundlich J, Choi I, Sarker M, Talcott C. Computational databases, pathway and cheminformatics tools for tuberculosis drug discovery. Trends Microbiol. 2010;19(2):65–74. doi: 10.1016/j.tim.2010.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zientek M, Stoner C, Ayscue R, Klug-McLeod J, Jiang Y, West M, Collins C, Ekins S. Integrated in silico–in vitro strategy for addressing cytochrome P450 3A4 time-dependent inhibition. Chem Res Toxicol. 2010;2:664–676. doi: 10.1021/tx900417f. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.