Abstract
In recent years, techniques have been developed to explore spatial non-stationarity and to model the entire distribution of a regressand. The former is mainly addressed by geographically weighted regression (GWR), and the latter by quantile regression (QR). However, little attention has been paid to combining these analytical techniques. The goal of this article is to fill this gap by introducing geographically weighted quantile regression (GWQR). This study briefly reviews GWR and QR, respectively, and then outlines their synergy and a new approach, GWQR. The estimations of GWQR parameters and their standard errors, the cross-validation bandwidth selection criterion, and the non-stationarity test are discussed. We apply GWQR to U.S. county data as an example, with mortality as the dependent variable and five social determinants as explanatory covariates. Maps summarize analytic results at the 5, 25, 50, 75, and 95 percentiles. We found that the associations between mortality and determinants vary not only spatially, but also simultaneously across the distribution of mortality. These new findings provide insights into the mortality literature, and are relevant to public policy and health promotion. Our GWQR approach bridges two important statistical approaches, and facilitates spatial quantile-based statistical analyses.
Introduction
In empirical studies, researchers typically are interested in examining possible associations between regional characteristics and outcomes of interest observed for different geographic locations. The standard approach is to specify a spatial linear mean regression model, and analyze the average relationship between the variables of interest after accounting for spatial dependence among locations; examples include the spatial error or lag, conditional autoregressive (CAR), and simultaneous autoregressive (SAR) models (Banerjee, Gelfand, and Sirmans 2003). These spatial models, commonly used in spatial statistics and econometrics, are designated to estimate a single, or “global” regression equation based on spatial data. Their underlying assumption is that relationships between the regressors and regressand are homogeneous (stationary) over space (Fotheringham 1997). However, in practice the associations among variables might be different across space and vary geographically (Cressie 1993; Jones and Hanham 1995; Fotheringham and Brunsdon 1999; Fotheringham, Brunsdon, and Charlton 2002). In addition, from a modeling perspective, “global” modeling may be a misspecification of reality, and the variables included in models may not be represented with correct function forms (Fotheringham, 1997). A global model is useful, but the model specification may not be sufficient to detect nonstationarity (Fotheringham, Brunsdon, and Charlton 1997, 2002).
To address these limitations, the trend in spatial data analysis has been to analyze spatial non-stationarity by fitting a regression model that allows for geographically varying (local) coefficients. A review of the history of the local forms of spatial analysis can be found elsewhere (Fotheringham and Brunsdon 1999). A widely applied approach for exploring local associations (Huang and Leung 2002; Calvo and Escolar 2003; Longley and Tobon 2004; Mennis and Jordan 2005; Yu, Wei, and Wu 2007; Chen et al. 2010) is the geographically weighted regression (GWR) proposed by Fotheringham, Brunsdon, and Charlton (Fotheringham, Brunsdon, and Charlton 1997, 2002; Fotheringham et al. 1998; Brunsdon, Fotheringham, and Charlton 1998a, 1998b). The GWR locally quantifies “average” relationships among variables and estimates regression parameters through the use of local regression and smoothing techniques. The local estimates of regression parameters for a specified linear mean regression model are derived for each location in space so that spatial variations of regression relationships can be investigated. The output from GWR is a set of statistics that can be mapped, depicting the spatial variation of a relationship. Like other analytic methods, GWR has several limitations, including multicollinearity in local coefficients, multiple hypothesis testing, and the incapability of decomposing the global estimates into local estimates (Wheeler and Tiefelsdorf 2005; Wheeler and Calder 2007; Wheeler and Waller 2009; Boots and Okabe 2007; Griffith 2008). Most of these issues have been discussed, and several solutions and alternatives have been proposed (Wheeler, 2007; 2009; Wheeler and Calder, 2007; Griffith, 2008). Despite concerns, GWR is still regarded as a useful tool for exploring spatial non-stationarity and interpolation (Páez, Long, and Farber 2008; Wheeler and Páez 2010).
Currently GWR is only able to compute the parameter estimates for a mean function of the conditional distribution of a dependent variable. While the mean quantifies the central behavior of a response distribution, little information is known about the full distribution. In applications, interest often lies in estimating different percentiles (or quantiles) on an outcome distribution and in determining the spatial pattern associated with a set of explanatory variables. For example, Yang, Jensen, and Haran (2011) investigate the spatial associations between mortality and both natural and social environment factors across the United States. In studies such as this, researchers are more interested in how social determinants explain the variation in low-mortality (lower quantile) and high-mortality (upper quantile) areas than in how they explain variation in average-mortality regions. The GWR approach does not allow such an investigation. A spatial analysis tool that permits estimating various quantile functions of a conditional distribution would be valuable.
Quantile regression (QR), first introduced by Koenker and Bassett (1978), is a statistical procedure that extends the natural linear mean regression model to a range of models estimating various conditional quantile functions. With multiple quantiles being modeled, QR can provide a thorough picture of how independent variables are associated with the underlying conditional distribution of a dependent variable, especially when the conditional distribution is heterogeneous and does not follow a standard normal distribution. QR is useful in practice because of its robustness against outliers and flexibility in dealing with error distributions (Koenker and Hallock 2001; Yu, Lu, and Stander 2003). These appealing features have led to other applications or generalizations of QR in medical statistics, survival analysis, labor economics, and financial econometrics (Buchinsky, 1998; Yu, Lu, and Stander 2003; Koenker 2005; Wei et al. 2006; Li, Graubard, and Korn 2007; Taylor 2008). Less attention has been focused on the application to spatial statistics.
Su and Yang (2007) report a QR generalization of the spatial lag model that relies on the assumption of spatial stationarity. Hallin, Lu, and Yu (2009) propose a local linear spatial QR. This technique estimates the QR coefficients using nonparametric methods, but its methodology is not undertaken with the assumption of stationarity. Although the authors also provide an “ad hoc” two-stage alternative to cope with non-stationarity, the procedure does not directly take it into account in the modeling process, and thus can not retrieve the spatially varying patterns of the estimated regression coefficients.
The aforementioned studies are among the first to conduct spatial quantile-based regression analysis. Few spatial modeling techniques (Salvati et al. 2007; Reich, Fuentes, and Dunson 2010) exist that permit the estimation of conditional quantile functions and analysis of spatial non-stationarity. Our objective is to address this methodological gap. We endeavor to integrate the features of QR into GWR and to develop a geographically weighted quantile regression (GWQR) method for continuous outcomes that simultaneously accounts for the heterogeneity of a regressand and spatial nonstationarity.
Methodology
QR fundamentals
Koenker and Bassett (1978) introduced QR for modeling the relation between a set of independent variables and specific percentiles (or quantiles) of a response variable. Assume that Yi (i = 1, …, n) are the observations with the associated covariate vectors Xi = (1, Xi1, Xi2, ···, Xip)t of dimension (p + 1), including the constant one for the intercept. The QR specifies
| (1) |
where εi, 1 ≤ i ≤ n, are continuous random variables satisfying P (εi ≤ 0) = τ (i.e., the distribution of εi whose τth quantile conditional on Xi is zero). Note that the εis are assumed to be independent but may not be identically distributed. Equation (1) amounts to assuming , where qτ (Xi) ≡ inf{y: F (y|Xi) ≥ τ } is the τth conditional quantile of Yi given the covariate Xi. The QR coefficient βτ is estimated by minimizing the following loss function:
| (2) |
where ρτ (z) = z(τ − I[z < 0]), known as the “check” function, is a V-shaped piecewise linear loss function, and I(·) denotes the indicator function. See Koenker (2005) for a comprehensive framework of QR.
GWR Fundamentals
We briefly review the GWR modeling approach. Now let Yi, i = 1, …, n, be the response observations collected from a set of locations in space. The corresponding geospatial covariate vector is then Xi of dimension (p + 1), including the intercept. Fotheringham, Brunsdon, and Charlton (2002) defined GWR as
| (3) |
where β(ui, vi) = [β0(ui, vi), β1(ui, vi), …, βp(ui, vi)]t, (ui, vi) captures the coordinate location of i in space, and εi is the error term with mean zero and common variance σ2. The βks regression coefficients in equation (3) are the local regression coefficients for the explanatory variables at location i. These parameters are estimated with the geographically weighted least squares on a pointwise basis using kernel-based methods. Specifically, for a given location (u0, v0) in a studied region, the βs at (u0, v0) are locally estimated by minimizing the weighted square loss function
| (4) |
where K is a kernel function, usually a symmetric probability density function, and h is the bandwidth that controls the smoothness of the resultant estimates. The term represents the geographical weight assigned locally to observation (Xi, Yi) and depends upon the distance di0 between the given location (u0,v0) and the ith designed location (ui,vi). Explicitly, the weight is determined by a kernel function that places more weights on observations closer to, than those farther away from, (u0,v0). Many choices exist for the kernel functions, including the Gaussian, the exponential, and the bisquare nearest neighbor function. Using this estimation technique, the local estimates of βk(ui, vi) in equation (4) can be derived by taking (u0,v0) to be each of the designed locations (ui,vi). We refer to Fotheringham, Brunsdon, and Charlton (2002) for a more detailed presentation of the methodology and theory behind GWR.
Although a local model should inform its global model counterpart (Fotheringham 2009), GWR also has been criticized (Wheeler and Tiefelsdorf 2005; Griffith 2008). Specifically, GWR’s local statistics can not be linearly combined to produce their global statistics, making the linkage between GWR modeling and global modeling elusive (Boots and Okabe 2007). Griffith (2008) uses spatial filtering, an eigenvector-based approach, to obtain GWR-type local coefficients. He concludes that GWR is a special case of spatial filtering modeling and that the global/local statistics issue was addressed with spatial filtering. Given the nonparametric setting, however, QR is more compatible with GWR than spatial filtering. Our attention in this article focuses on synthesizing QR with GWR.
Geographically weighted quantile regression (GWQR)
We extend the GWR (equation [3]) to a QR setting (equation [1]) with the specification
| (5) |
where is the random error for the τth quantile conditional on Xi equals zero, and the vector is the local regression quantile coefficients (0 < τ < 1) at location (ui,vi). The QR coefficient measures the change in a specified quantile τ of the response variable Y corresponding to one unit change in the independent variable Xk. This conceptualization allows a comparison between how some percentiles of a response may be more (or less) affected by certain independent variables than other percentiles.
Implicit in equation (5) is that the τ conditional quantile function of Yi given observation vector Xi for location i with coordinates (ui,vi), namely qτ (Xi, ui, vi) ≡ inf{y: F (y|Xi, ui, vi) ≥ τ }, is assumed to be
| (6) |
In contrast to equation (3), the regression coefficients βτ (ui, vi) in equation (5) for each location i are unknown functions of the location coordinates and are now τ dependent. The GWQR model given by equation (5) can be viewed as a variant of Cai and Xu’s (2008) framework with effect modifiers equal to the geographical coordinates (u, v) in space.
Estimation in GWQR
Suppose that each of the GWQR coefficients (k = 0, 1, 2, …, p) in equation (5) has second continuous partial derivatives with respect to the geographical location coordinates u and v. Then for a given location (u0, v0) in a study region (hereafter called a regression point), we approximate by the linear function
| (7) |
for (u, v) in a neighborhood of (u0, v0), where , and . With equation (7) and the local modeling principles, we choose to minimize the following locally weighted function:
| (8) |
where X̃i = [1, Xi1, …, Xip, (ui−u0), Xi1(ui−u0), …, Xip(ui−u0), (vi−v0), Xi1(vi−v0), …, Xip(vi−v0]t, and . Notice that θτ (u0, v0) is the parameter vector corresponding to the linear approximation given by equation (7).
In equation (8), the aim of geographical weighting is to specify spatial neighborhoods around location i according to the given kernel function K so that the locally weighted QR at location i is calculated by using only the data in the kernel window. A popular choice for the kernel function is the bisquare function given by
| (9) |
in which observations with distances greater than the bandwidth are zero weighted and excluded from any calculation. An alternative may be the Gaussian kernel function of the form
| (10) |
This function is infinitely supported, resulting in nonzero weights for all data observations. If a geographical data point coincides with (u0, v0), the weighting of the data is maximum. For all other data points, their assigned weight decreases as their distance to the regression point (u0, v0) increases.
Two types of weighting schemes can be used for calculating K(di0/h). One is the fixed kernel weighting routine, which assumes the bandwidth h at each location is a constant across the geographical region of interest. The other is the adaptive kernel weighting technique, where the bandwidth is selected such that the number of observations with nonzero weights is the same at each location. The adaptive, as implied, changes the smoothing window size to the density of data points, and usually is preferable to the fixed scheme because it avoids “weak data” problems encountered in sparse regions (Fotheringham, Brunsdon, and Charlton 2002). Comparisons of these two weighting schemes in GWR modeling can be found in Fotheringham, Brunsdon, and Charlton (1997, 2002).
According to QR theory, the solution for parameter vector θτ (u0, v0), which minimizes the equation (8) loss function, has no explicit form. The weighted QR problem defined by equation (8) can be equivalently formulated as a linear programming optimization problem. See, for example, Chen and Wei (2005) and Koenker’s (2005) monograph for more details. Therefore, a linear programming solution yields the parameter estimate . According to the Taylor theorem, we then take the solution for each k = 0, 1, …, p as the local linear estimator for at location (u0, v0). If one chooses to minimize the following loss function
| (11) |
then the resulting minimum { } serves as the local constant estimator of { }.
By employing the preceding estimation procedure, and by letting (u0, v0) = (ui, vi) (i = 1, 2, …, n), we obtain the estimates of each QR coefficient for equation (5). The corresponding estimated τth conditional quantile is given by
| (12) |
where β̂τ (ui, vi) denotes the vector of estimates , k = 0, 1, …, p, and Xi is the vector of observed covariates at location (ui, vi).
The preceding methodology also allows for out-of-sample predictions. For an additional covariate vector Xn+1 associated with a new set of location coordinates (un+1, vn+1) that is not in the original sample but in the original studied region, the estimated coefficients , k = 0, 1, …, p, can be obtained through minimization of equation (8) by taking (u0, v0) = (un+1, vn+1). Consequently, the prediction for an out-of-sample location is
| (13) |
The notation (u0, v0) here is generic for both in-sample and out-of-sample estimation within a research area.
Standard errors of GWQR estimators
Because the check function is piecewise linear, equation (8) can be rewritten as
| (14) |
Given equations (8) and (14), and based on the asymptotic theorems described in Koenker (2005), the estimates θ̂τ (u0, v0) have an asymptotically normal distribution, with their mean being the true regression coefficients θτ (u0, v0) and a covariance matrix given by
| (15) |
with and , where the quantity is a weighted version of X̃i, and represents the conditional density of Yi given the vector at location coordinate (ui, vi), evaluated at the τth conditional quantile.
The preceding results can be used to examine the statistical significance of the local QR parameters (k = 0, 1, …, p) at (u0, v0). To implement the desired test, the asymptotic covariance matrix for equation (15) must be estimated. According to Koenker (2005) and Hao and Naiman (2007), we estimate the covariance matrix for θ̂τ (u0, v0) using , in which and . Thus the hypothesis testing for the parameter can be constructed using the t statistics where is the (k + 1)th element of θ̂τ (u0, v0); is the corresponding standard error obtained with the (k + 1)th diagonal element of the estimated covariance matrix .
The estimation D1 relates to the unknown density function . Different techniques have been developed to estimate this quantity for traditional QR (Powell, 1991; Koenker and Machado 1999; Koenker 2005). The estimating procedure introduced by Koenker and Machado (1999), using a local estimator of the conditional quantile function with a difference quotient, has been commonly used (Chen and Wei 2005). Specifically, the formula used in our study is
| (16) |
where hn is a bandwidth parameter that tends to zero as n → ∞. To determine the bandwidth hn, we use the following Hall–Sheather bandwidth rule recommended by Koenker (1994):
| (17) |
for zα satisfying Φ(zα) = 1 − α/2, in which Φ represents a standard normal distribution function whose density function is denoted as ϕ. The parameter α denotes the desired significance level for hypothesis testing or confidence interval construction. Note that a potential difficulty may arise because is not necessarily always positive. In such circumstances, we replace by the following quantity suggested by Koenker and Machado (1999):
| (18) |
where ε > 0 is a small perturbation parameter that avoids division by zero.
The asymptotic methods described in the previous sections require estimation of a conditional density function and the selection of a bandwidth when using a difference quotient. This task can be burdensome for practical implementation. As an alternative to the asymptotic method, a bootstrap technique resampling {Xi, Yi, (ui, vi)} with replacement provides a computationally efficient approach that suppresses the use of and hn for deriving the covariance matrix of θ̂τ (u0, v0). Nevertheless, while bootstrapping is simple, it may be time consuming for a high dimensional and/or large data set such as the one analyzed in this article.
Bandwidth selection for GWQR
The bandwidth controls the smoothness and efficiency of the resultant estimator β̂τ. Choosing an optimal bandwidth h associated with the kernel fitting of equation (8) is necessary. A commonly used procedure to determine the appropriate bandwidth is based on cross-validation (CV). Therefore, following Abberger (1998) and Fotheringham, Brunsdon, and Charlton (2002), we construct the following CV score:
| (19) |
where is the leave-one-out version estimate of qτ (Xi, ui, vi) obtained with the ith observation (Yi, Xi, ui, vi) dropped during estimation. The cross-validated bandwidth is selected from the model with the smallest CV score. Note that the CV score is defined analogous to the mean regression, but with the square loss function replaced by a V-shaped check function.
Although other possible bandwidth selection tools exist that could be considered for GWR, such as the Akaike information criterion (AIC), the bias-corrected AIC (AICc), and the Bayesian information criterion (BIC), the CV score is technically more feasible for GWQR. Our GWQR estimators are built on QR theory, and have no mathematically explicit expression. The AICc or AIC used in GWR could not be directly adopted because of the difficulty of computing the degrees of freedom in our GWQR framework. We revisit this issue in the discussion section.
Assessment of spatial nonstationarity
To examine spatial nonstationarity in regression coefficients of GWQR, we utilize a simple and conventional approach similar to that in Nakaya et al. (2005). We compare, at a specified quantile τ, the inter quartile range (IQR) of the local estimates of βs computed by GWQR with the standard error of the global estimates derived with a traditional QR. A range between the first and third quartiles twice as large as the standard error indicates that spatial nonstationarity exists in the relationships between a dependent and its accompanying independent variables.
In statistics, the basic approach to testing spatial nonstationarity is to calculate the variance of (k = 0, 2, …, p) across all locations (i = 1, …, n) as a measure of the variability of the GWQR estimators, then to determine the sampling distribution of the variance, and finally to test the variability based on the sampleing distribution of the variance. However, implementing such a concept empirically is difficult because the sampling distribution of the variance cannot be identified under the framework of GWQR. Therefore, the conventional IQR approach is used in the present form of GWQR. A possible assessment tool for non-stationarity is briefly described in the discussion section.
An empirical application
The data
Yang, Jensen, and Haran (2011) model the mortality distributions across U.S. counties, conditional on different social determinants, such as population composition, inequality, and socioeconomic covariates. While the authors realize that the associations between the dependent and independent variables may not necessarily be constant across space and the entire mortality distribution, no method was available to address this issue. The proposed GWQR approach provides one possible solution, and we reanalyze the data from Yang, Jensen, and Haran (2011) as an empirical application of GWQR.
The primary outcome is the five-year (1998–2002) average mortality rates (NCHS 2003, 2006) in 3,109 U.S. counties (the lower 48 states and the District of Columbia [DC]), standardized using the U.S. age–sex population structure of year 2000. The independent variables of interest here include five area-based social determinants of human health: race/ethnic composition, income inequality (inequality hereafter), social affluence, concentrated disadvantage, and safety.
The first four explanatory variables were derived from the 2000 Census of Population and Housing SF3 Files. Specifically, race/ethnic composition is represented by the percentage of the black population in a county. Inequality is captured by the Gini coefficient (Kawachi and Kennedy, 1997), which is defined as a ratio with values between zero and one. A smaller Gini coefficient indicates a more even distribution of household income within a county and hence higher levels of equality. Social affluence is a measure of more economically privileged areas, and is measured with a scale defined by the percentage of families that have incomes of more than $75, 000, percentage of workers in managerial and professional positions, and the percentage of adults with at least a bachelor’s degree. Concentrated disadvantage describes conditions of economic disadvantage. Its measurement utilizes the following covariates: poverty rate, percentage of persons receiving public assistance, unemployment rate, and percentage of female-headed households with children. Our fifth variable, safety, is based on the following crimes: embezzlement, forgery/counterfeiting, fraud, and Total Part I property crimes (FBI, 2009). This variable is used to reflect the absence of mutual trust and safety within a county. Detailed discussions of these variables can be found elsewhere (Yang, Jensen, and Haran 2011; Yang, Teng, and Haran 2009). Table 1 lists the descriptive statistics for all variables used in our study.
Table 1.
Descriptive Statistics of Variables (N = 3,109)
| Minimum | Maximum | Mean | Std. Deviation | |
|---|---|---|---|---|
| Percent black | 0.0000 | 86.0780 | 8.7150 | 14.5035 |
| Income inequality | 0.3140 | 0.6050 | 0.4343 | 0.0377 |
| Affluence | −2.4281 | 6.0110 | 0.0000 | 1.0000 |
| Disadvantage | −2.5365 | 9.0560 | 0.0000 | 1.0000 |
| Safety | −1.3703 | 12.1190 | 0.0000 | 1.0000 |
| Mortality (per 1,000) | 0.0000 | 19.7770 | 8.8984 | 1.3766 |
The adaptive bisquare kernel weighting function described in the section on “Estimation in GWQR” was used in this application. We computed the local linear quantile estimates of regression coefficients for five different percentiles, τ = 0.05, 0.25, 0.50, 0.75, and 0.95. The selected optimal bandwidths that yield the same number of nonzero weights for each location in the analysis were h = 471 for τ = 0.05, 319 for τ = 0.25, 287 for τ = 0.5, 389 for τ = 0.75, and 457 for τ = 0.95.
Results
Table 2 reports the GWQR results for the five selected percentiles. All of the IQRs of the local parameter estimates are all at least twice the standard errors of the global estimates. These results suggest that all relationships varied across space. Explicitly, the stationarity assumption does not hold across both space and the distribution of mortality rates. Knowing that the relationships between the five social determinants and mortality are non-stationary (standard GWR) across space is valuable; knowing that these relationships also vary across the distribution of mortality rates is particularly valuable. That is, different relationships between variables exist in different geographical spaces and across different parts of the mortality distribution. Figs. 1–3 exemplify these findings, furnishing maps of the non-stationary process across space and the distribution of mortality for percentage of the black population (hereafter percent black), inequality, and safety. One of the advantages of our approach is that it provides local statistics that are mappable and GIS-friendly. The maps are constructed in ArcGIS 9.x (ESRI) and show only the parts of the mapped surface where the local t-values exceed +/−1.96. Following Fotheringham, Brunsdon, and Charlton (2002), these local values place emphasis on the differences across space, and facilitate the search for exceptions or local hot/cold spots rather than for regularities or global relationships.
Table 2.
GWQR Results for 5, 25, 50, 75, and 95 Percentiles
| Parameters | Minimum* | First Quartile | Median | Third Quartile | Maximum | Inter-quartile | Std Err† | Status |
|---|---|---|---|---|---|---|---|---|
| τ = 0.05 | ||||||||
| Intercept | −5.4525 | 8.4508 | 9.6701 | 11.1269 | 15.3477 | 2.6761 | 0.5720 | Nonstationary |
| Percent black | −0.2175 | −0.0032 | 0.0168 | 0.0551 | 1.4181 | 0.0583 | 0.0031 | Nonstationary |
| Income inequality | −21.2196 | −6.9196 | −4.0858 | −1.3783 | 25.4410 | 5.5413 | 1.3020 | Nonstationary |
| Affluence | −3.0698 | −0.3420 | −0.2134 | −0.1141 | 0.4766 | 0.2279 | 0.0596 | Nonstationary |
| Disadvantage | −0.5255 | 0.3713 | 0.5250 | 0.6823 | 1.1569 | 0.3110 | 0.0700 | Nonstationary |
| Safety | −0.3615 | 0.1351 | 0.2295 | 0.3502 | 2.8933 | 0.2151 | 0.0185 | Nonstationary |
| τ = 0.25 | ||||||||
| Intercept | 3.4092 | 8.9462 | 9.8996 | 10.8330 | 15.2883 | 1.8868 | 0.2492 | Nonstationary |
| Percent black | −0.2951 | −0.0007 | 0.0145 | 0.0442 | 0.6876 | 0.0449 | 0.0017 | Nonstationary |
| Income inequality | −17.6957 | −5.4330 | −3.0879 | −0.9481 | 8.8962 | 4.4849 | 0.6820 | Nonstationary |
| Affluence | −1.1270 | −0.3625 | −0.2534 | −0.1681 | 0.4869 | 0.1944 | 0.0139 | Nonstationary |
| Disadvantage | −0.6315 | 0.3922 | 0.5482 | 0.6935 | 1.3326 | 0.3013 | 0.0384 | Nonstationary |
| Safety | −0.2173 | 0.0793 | 0.1561 | 0.2448 | 1.1315 | 0.1655 | 0.0150 | Nonstationary |
| τ = 0.50 | ||||||||
| Intercept | −0.8215 | 8.8620 | 9.8840 | 10.8772 | 17.0898 | 2.0152 | 0.2682 | Nonstationary |
| Percent black | −0.4055 | −0.0070 | 0.0105 | 0.0285 | 0.4968 | 0.0355 | 0.0013 | Nonstationary |
| Income inequality | −17.6957 | −5.4330 | −3.0879 | −0.9481 | 8.8962 | 4.4849 | 0.6161 | Nonstationary |
| Affluence | −1.0168 | −0.3817 | −0.2955 | −0.2091 | 0.3428 | 0.1726 | 0.0170 | Nonstationary |
| Disadvantage | −0.5446 | 0.3565 | 0.5365 | 0.6786 | 1.4687 | 0.3221 | 0.0339 | Nonstationary |
| Safety | −0.2026 | 0.0174 | 0.0827 | 0.1786 | 1.1997 | 0.1612 | 0.0174 | Nonstationary |
| τ = 0.75 | ||||||||
| Intercept | 0.9190 | 9.1884 | 10.0725 | 10.8434 | 16.6343 | 1.65500 | 0.3024 | Nonstationary |
| Percept black | −0.9976 | −0.0089 | 0.0035 | 0.0183 | 0.3399 | 0.0272 | 0.0018 | Nonstationary |
| Income inequality | −18.6581 | −3.3341 | −1.4577 | 0.5062 | 15.7788 | 3.8403 | 0.6892 | Nonstationary |
| Affluence | −0.8104 | −0.4011 | −0.3228 | −0.2274 | 0.1171 | 0.1737 | 0.0208 | Nonstationary |
| Disadvantage | −0.5118 | 0.3346 | 0.5157 | 0.6608 | 1.6005 | 0.3262 | 0.0419 | Nonstationary |
| Safety | −0.2510 | 0.0106 | 0.0846 | 0.1680 | 0.9127 | 0.1574 | 0.0278 | Nonstationary |
| τ = 0.95 | ||||||||
| Intercept | 2.5717 | 9.4470 | 10.9908 | 12.6140 | 21.3847 | 3.1670 | 0.3811 | Nonstationary |
| Percent black | −1.3904 | −0.0193 | 0.0009 | 0.0186 | 0.3462 | 0.0379 | 0.0036 | Nonstationary |
| Income inequality | −23.3930 | −6.1277 | −2.2793 | 1.3382 | 15.6609 | 7.4659 | 0.8304 | Nonstationary |
| Affluence | −1.3049 | −0.5254 | −0.3789 | −0.2268 | 2.4076 | 0.2986 | 0.0273 | Nonstationary |
| Disadvantage | −0.6832 | 0.2337 | 0.4695 | 0.7183 | 2.0989 | 0.4846 | 0.0697 | Nonstationary |
| Safety | −0.7304 | −0.0770 | 0.0623 | 0.1971 | 1.1333 | 0.2741 | 0.0237 | Nonstationary |
The summary statistics for the 3109 GWQR parameter estimates are listed.
Standard error of the global estimates from classical quantile regression.
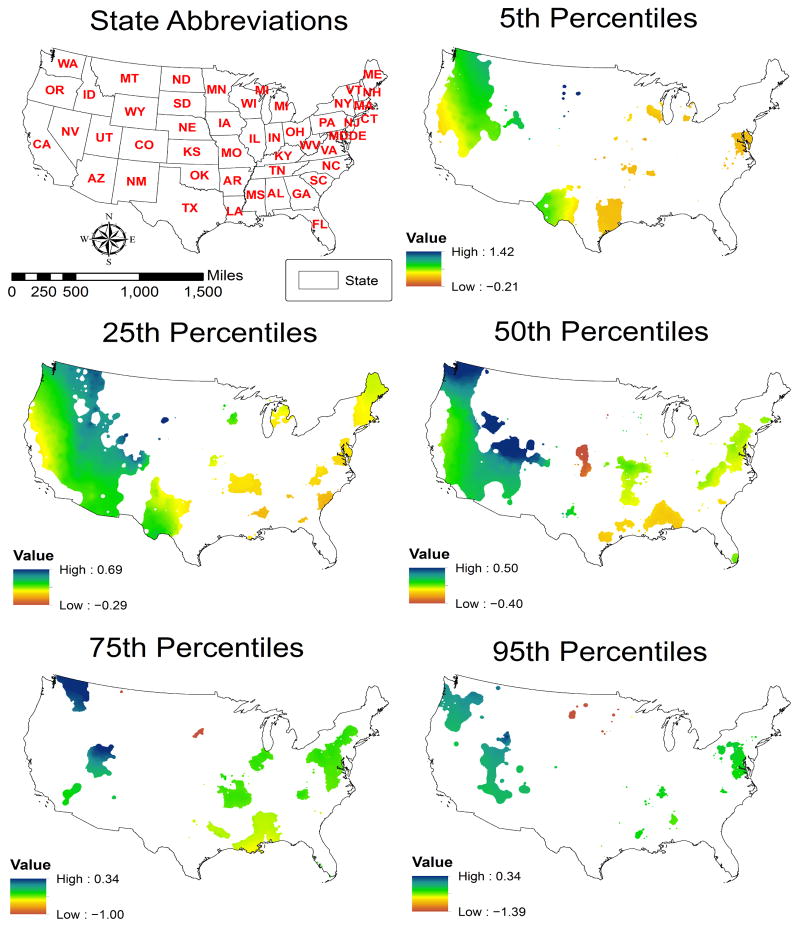
Figure 1.
Map of GWQR estimates for black population, significant areas at +/−1.96 level.
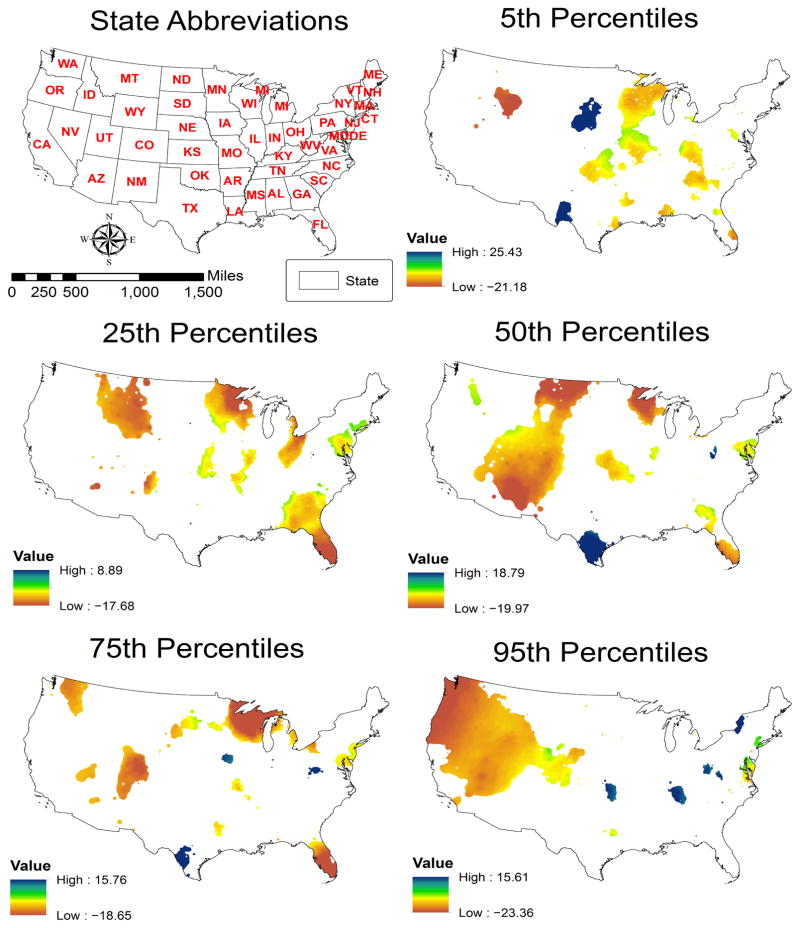
Figure 3.
Map of GWQR estimates for safety, significant areas at +/− 1.96 level.
Fig. 1 illustrates how the percent black associates with mortality over space and percentiles. Beginning with the 50th percentile map, the main general patterns reveal a strong positive relationship between percent black and mortality in three relatively low percent black areas of the United States (mostly inland West Coast states, parts of Oklahoma, Arkansas, and Missouri, and parts of north and central Appalachia in the East). This strong positive relationship is not found in any other areas of the United States with a low percentage of black population. Interestingly, percent black is negatively associated with mortality in parts of the traditional “Black Belt”. A pocket also exists in central Nebraska/Kansas that exhibits a negative relationship. At the 5th percentile for mortality all statistically significant areas have a positive relationship with percent black. This group includes a diverse set of areas in terms of population density and percent black (surrounding Baltimore/DC, Chicago, parts of Texas, and the inland north-west). At the 25th percentile, small pockets in the southeastern United States display a negative relationship. Where mortality is high (75th and 95th percentiles), the relationship between percent black and mortality across most of the United States is not significant. A general contraction of significant areas in the West exists, with a slight expansion for the 75th percentile in the East and Midwest.
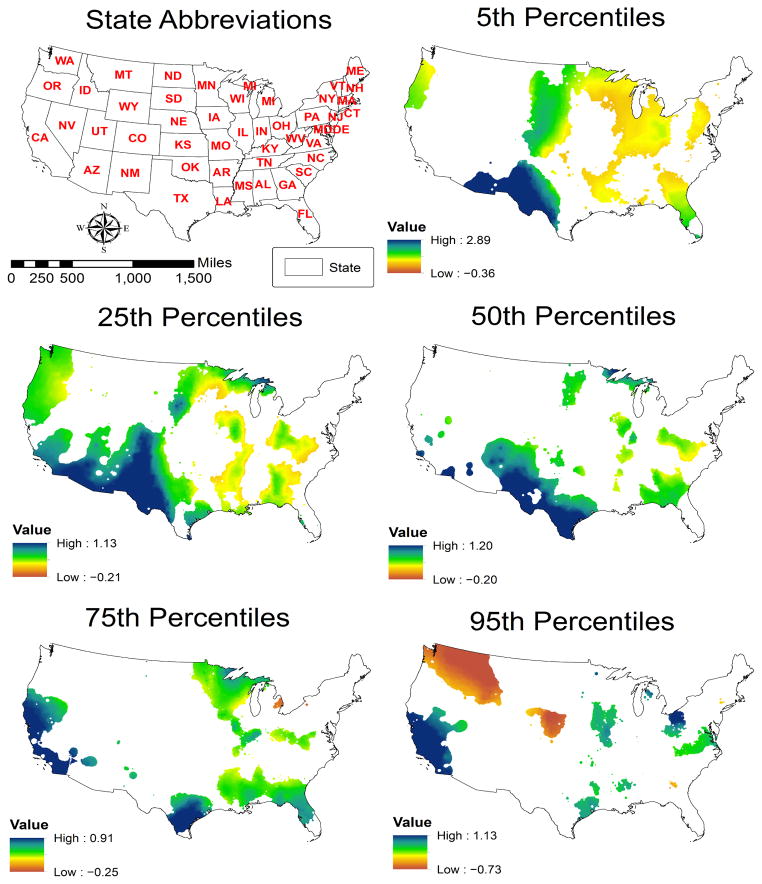
The GWQR estimates of inequality are summarized in Fig. 2. The local estimates vary widely across all percentiles, including both positive and negative values. At the 50th percentile, the relationship between income inequality and mortality is positive only in southern Texas. The non-stationarity of the relationship between inequality and mortality is evident in any single map as well as when comparing across percentiles. The relationship is consistently negative across the distribution of mortality in some areas including around parts of the Baltimore/Washington, DC area and less so in parts of northern Florida, the Midwest, and the Mountain West regions.
Figure 2.
Map of GWQR estimates for income inequality, significant areas at +/− 1.96 level.
Fig. 3 portrays the estimates and significant areas for safety. In the 5th, 25th, and 50th percentile maps, all significant areas show a positive association between safety and mortality. While the significant areas covered in these three maps are different, some commonalities exist: along the U.S./Mexico border between Arizona and Texas, parts of Florida and Georgia, along the Mississippi River, and in parts of Minnesota and Wisconsin. The commonality in statistical relationship belies the diversity between these areas. At both the 75th and 95th percentiles, the map surfaces include areas of the United States where negative relationships also exist between safety and mortality. In general, safety is associated with mortality in more areas of the country at the 50th and lower percentiles.
Finally, affluence is found to be negatively associated with mortality across space and percentiles, with this relationship covering most places in the United States, and with few areas showing no significant association (e.g., parts of the Ohio valley). In contrast, disadvantage demonstrates a positive relationship with mortality across most of the U.S., with the significant areas shrinking toward both lower and higher ends of the mortality distribution1.
Discussion and conclusion
We present an approach that analyzes spatially nonstationary relationships between explanatory and dependent variables within the framework of QR. Although GWR considers spatial nonstationarity only for mean regression models, GWQR generalizes GWR to allow for the computation of conditional quantiles. We apply the approach to a U.S. county-level mortality rates dataset. The results indicate that the changing spatial patterns in regression relationships across the response distribution can be summarized by estimating a range of different conditional quantiles functions. Specifically, the GWQR approach enables researchers to explore whether spatial nonstationarity is stable across the distribution of a dependent variable. Although an increasing interest in exploring nonstationarity across space (e.g., Yang et al. 2009; Chen et al. 2010) has emerged in recent years, to date no published study has tried to examine this issue in terms of QR; our proposed technique fills this gap in the literature.
By bringing QR into GWR, the proposed technique accounts for both spatial structure and the stochastic distribution of a dependent variable. Most research studies, especially in epidemiology and public health, concentrate on only one of these two dimensions, either modeling mean values across space, or showing quantile plots without considering spatial structure. Our approach aims to synthesize these two techniques. Although we focuse on a health-related empirical example, the approach can be used in other kinds of studies. The key message we wish to convey is that without a GWQR approach, researchers cannot explore associations between predictors and a dependent variable, how these associations vary spatially, and how these associations simultaneously vary across the distribution of the dependent variable. Knowing the local estimates via a GWQR helps to place emphasis on variations and on the differences in relationships across space. Of relevance to public policy and applied research, this emphasis on local estimates (and their comparison to single model global estimates) can reveal geographic areas (both hot or cold spots) where detailed case studies might be implemented. Our hope is that GWQR is a method that contributes to the growing trend in which spatial analysis becomes an interdisciplinary geospatial science (Berry, Griffith, and Tiefelsdorf 2008).
We demonstrate in this article that the proposed GWQR is an innovative approach toward spatial quantile-based analysis that simultaneously accounts for the heterogeneity of a regressand and spatial non-stationarity. Several methodological issues remain that deserve further discussion and that future work should try to address. The first issue is the kernel bandwidth. A method developed by Cai and Xu (2008) provides a potential bandwidth selection criterion for GWQR. Specifically, they propose an AICc for a varying coefficient QR to select the optimal bandwidth for time-series data. Our current work attempts to integrate the Cai and Xu approach into the GWQR framework, and our ongoing work seeks to provide users with an alternative bandwidth selection tool. However, this transformed AIC bandwidth selector for GWQR will be more computationally demanding than the current CV approach.
The second issue is the nonstationarity test in GWQR. Monte Carlo techniques offer a potential approach for testing spatial nonstaionarity in the nonparametric analysis setting (Brunsdon, Fotheringham, and Charlton 1996). If an independent variable is found to have a spatially stationary relationship with its regressand, a semiparametric GWQR framework should be applied to account for the stationarity. That is, in a semiparametric GWQR model, the parameter coefficient of a stationary independent variable is fixed across a research area, with other regressors varying spatially. This semiparametric approach is important because it would account for both stationarity and non-stationarity in the same model. These issues are currently being explored.
Finally, because the GWQR framework is built on GWR, our approach shares the same criticisms of GWR described in the introduction. Several strategies have been proposed to overcome the limitations of GWR. Wheeler and Calder (2007), for instance, use a Bayesian spatially varying coefficient process (SVCP) model that estimates spatially varying coefficients as a multivariate spatial process. Their model is specified in a hierarchical manner, producing more robust statistical inference than does GWR, particulary in the presence of explanatory variable collinearity. Another way to explore spatially nonstationary association is spatial filtering (Griffith 2008). As discussed in the section on “GWR fundamentals,” this method bridges the global and local statistics with a decomposition technique. While these methods have several modeling advantages over GWR, they may not be easily combined with QR; but further investigations are warranted.
Although spatial quantile-based analytic approaches are underexplored, some parallels exist with GWQR. One is the M-quantile GWR (MQGWR) developed by Salvati et al. (2007), and the other is the Bayesian spatial QR developed by Reich, Fuentes, and Dunson (2010). The MQGWR is designed to improve small area estimation. Its underlying framework is M-QR, which is generalized from both quantile and expectile regression (Chambers and Tzavidis 2006). Whereas MQGWR is similar to our GWQR approach, and both share some advantages (e.g., data-based modeling without modeling assumptions), we identify three major differences between these two methods. First, MQGWR is less flexible than GWQR when extended to discrete dependent variables. Recent developments in QR (see Bottai, Bo, and McKeown 2010) open the door for our GWQR approach to handle binary dependent variables. Second, the issue of bandwidth selection has not been fully addressed in MQGWR. Our GWQR uses the CV method to determine the bandwidth “specific to each quantile,” but MQGWR only applies one bandwidth (chosen for an entire dataset) to every quantile (Salvati et al. 2007). Third, developing a non-stationarity diagnostic tool is necessary for MQGWR, but our GWQR can adopt the methods used in GWR (Fotheringham et al. 2002; Salvati et al. 2007). We want to emphasize that these differences do not necessarily make our GWQR approach better than MQGWR. A comprehensive study is needed to compare these methods using the same datasets.
Reich, Fuentes, and Dunson (2010) extend a Bayesian SVCP model by Gelfand et al. (2003) to the QR setting in which the conditional quantile function is modeled using a finite number of basis functions varied across locations and smoothed with a spatial prior. This approach handles spatial dependence in data through a single statistical model, and can simultaneously analyze several quantile levels. Although Bayesian spatial QR offers some appealing model properties, difficulties may arise because of computational complexities in the implementation and the choice of prior distributions. In contrast, our GWQR provides a different and relatively easy alternative for spatial quantile-based regression analysis, with a trade-off regarding robust statistical inference.
The goal of this article is to introduce the GWQR framework and to demonstrate it empirically. Many opportunities and challenges exist in implementing GWQR, and our work, in many ways, is only just beginning. We hope that GWQR and similar emerging methods (e.g., MQGWR and Bayesian SVCP) can help stimulate new conversations and methods that continue to push forward the field of geographical analysis.
Footnotes
The maps for these two determinants are available upon request.
References
- Abberger K. Cross-Validation in Nonparametric Parametric Quantile Regression. Allgemeines Statistisches Archiv. 1998;82(2):149–61. [Google Scholar]
- Banerjee S, Gelfand AE, Sirmans CF. Directional Rates of Change under Spatial Process Models. Journal of the American Statistical Association. 2003;98(464):946–54. [Google Scholar]
- Berry BJL, Griffith DA, Tiefelsdorf MR. From Spatial Analysis to Geospatial Science. Geographical Analysis. 2008;40(3):229–38. [Google Scholar]
- Boots B, Okabe A. Local Statistical Spatial Analysis: Inventory and Prospect. International Journal of Geographical Information Science. 2007;21(4):355–75. [Google Scholar]
- Bottai M, Bo C, McKeown RE. Logistic Quantile Regression for Bounded Outcomes. Statistics in Medicine. 2010;29(2):309–17. doi: 10.1002/sim.3781. [DOI] [PubMed] [Google Scholar]
- Brunsdon C, Fotheringham AS, Charlton ME. Geographically Weighted Regression: A method for Exploring Spatial Nonstationarity. Geographical Analysis. 1996;28(4):281–98. [Google Scholar]
- Brunsdon C, Fotheringham AS, Charlton ME. Spatial Nonstationarity and Autoregressive Models. Environment and Planning A. 1998a;30(6):957–973. [Google Scholar]
- Brunsdon C, Fotheringham AS, Charlton ME. Geographically Weighted Regression-Modelling Spatial Non-Stationarity. Journal of the Royal Statistical Society Series D (The Statistician) 1998b;47(3):431–43. [Google Scholar]
- Buchinsky M. Recent Advances in Quantile Regression Models: A Practical Guideline for Empirical Research. Journal of Human Resources. 1998;33(1):88–126. [Google Scholar]
- Cai Z, Xu X. Nonparametric Quantile Estimations for Dynamic Smooth Coefficient Models. Journal of the American Statistical Association. 2008;103(484):1595–1607. doi: 10.1198/016214508000000788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calvo E, Escolar M. The Local Voter: A Geographically Weighted Regression Approach to Ecological Inference. American Journal of Political Science. 2003;47(1):189–204. [Google Scholar]
- Chambers R, Tzavidis N. M-Quantile Models for Small Area Estimation. Biometrika. 2006;93(2):255–68. [Google Scholar]
- Chen C, Wei Y. Computational Issues for Quantile Regression. Sankhyā. 2005;67(2):399–417. [Google Scholar]
- Chen VYJ, Wu PC, Yang TC, Su HJ. Examining Non-Stationary Effects of Social Determinants on Cardiovascular Mortality after Cold Surges in Taiwan. Science of the Total Environment. 2010;408(9):2042–49. doi: 10.1016/j.scitotenv.2009.11.044. [DOI] [PubMed] [Google Scholar]
- Cressie NA. Statistics for Spatial Data. New York: Wiley, USA; 1993. [Google Scholar]
- Federal Bureau of Investigation [FBI] Uniform Crime Reports. U.S. Department of Justice; Washington, D.C: 2009. [Google Scholar]
- Fotheringham AS. Trends in Quantitative Methods I: Stressing The Local. Progress in Human Geography. 1997;21(1):88–96. [Google Scholar]
- Fotheringham AS. The Problem of Spatial Autocorrelation and Local Spatial Statisitics. Geographical Analysis. 2009;41(4):398–403. [Google Scholar]
- Fotheringham AS, Brunsdon C. Local Forms of Spatial Analysis. Geographical Analysis. 1999;31(4):340–58. [Google Scholar]
- Fotheringham AS, Brunsdon C, Charlton ME. Two Techniques for Exploring Non-Stationarity in Geographical Data. Geographical Systems. 1997;4(1):59–82. [Google Scholar]
- Fotheringham AS, Charlton ME, Brunsdon C. Geographically Weighted Regression: A Natural Evolution of the Expansion Method for Spatial Data Analysis. Environment and Planning A. 1998;30:1905–27. [Google Scholar]
- Fotheringham AS, Brunsdon C, Charlton ME. Geographically Weighted Regression: The Analysis of Apatially Varying Relationships. New York: Wiley, USA; 2002. [Google Scholar]
- Gelfand AE, Kim HJ, Sirmans CF, Banerjee S. Spatial Modeling with Spatially Varying Coefficient Processes. Journal of the American Statistical Association. 2003;98(462):387–96. doi: 10.1198/016214503000170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffith DA. Spatial-Filtering-Based Contributions to a Critique of Geographically Weighted Regression (GWR) Environment and Planning A. 2008;40(11):2751–69. [Google Scholar]
- Hallin M, Lu Z, Yu K. Local Linear Spatial Quantile Regression. Bernoulli. 2009;15(3):659–86. [Google Scholar]
- Hao L, Naiman DQ. Quantitative Applications in the Social Sciences. Vol. 149. London: Sage; 2007. Quantile Regression. [Google Scholar]
- Huang Y, Leung Y. Analyzing Regional Industrialization in Jiangsu Province using Geographically Weighted Regression. Journal of Geographical Systems. 2002;4(2):233–49. [Google Scholar]
- Jones JP, Hanham RQ. Contingency, Realism, and the Expansion Method. Geographical Analysis. 1995;27(3):185–207. [Google Scholar]
- Kawachi I, Kennedy BP. The Relationship of Income Inequality to Mortality: Does the Choice of Indicator Matter? Social Science & Medicine. 1997;45(7):1121–27. doi: 10.1016/s0277-9536(97)00044-0. [DOI] [PubMed] [Google Scholar]
- Koenker R. Confidence Intervals for Regression Quantiles. In: Mandl P, Huskova M, editors. Asymptotic Statistics: Proceedings of the 5th Prague Symposium. New York: Springer-Verlag; 1994. pp. 349–359. [Google Scholar]
- Koenker R. Quantile Regression. Cambridge, U.K: Cambridge University Press; 2005. [Google Scholar]
- Koenker R, Bassett G. Regression Quantiles. Econometrica. 1978;46(1):33–50. [Google Scholar]
- Koenker R, Hallock KF. Quantile regression. Journal of Economic Perspectives. 2001;15(4):143–56. [Google Scholar]
- Koenker R, Machado JAF. Goodness of Fit and Related Inference Processess for Quantile Regression. Journal of the American Statistical Association. 1999;94(448):1296–1310. [Google Scholar]
- Li Y, Graubard B, Korn EL. Application of Nonparametric Quantile Regression to Body Mass Index Percentile Curves from Survey Data. Statistics in Medicine. 2007;29(5):558–72. doi: 10.1002/sim.3810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longley PA, Tobon C. Spatial Dependence and Heterogeneity in Patterns of Hardship: An Intra-Urban analysis. Annals of the Association of American Geographers. 2004;94(3):503–19. [Google Scholar]
- Mennis JL, Jordan LM. The Distribution of Environmental Equity: Exploring Spatial Nonstationarity in Multivariate Models of Air Toxic Releases. Annals of the Association of American Geographers. 2005;95(2):249–68. [Google Scholar]
- Nakaya T, Fotheringham AS, Brunsdon C, Charlton M. Geographically Weighted Poisson Regression for Disease Association Mapping. Statistics in Medicine. 2005;24(17):2695–717. doi: 10.1002/sim.2129. [DOI] [PubMed] [Google Scholar]
- National Center for Health Statistics (NCHS) Machine-readable data file and documentation. National Center for Health Statistics; Hyattsville, MD: 2003. Compressed Mortality File, 1989–98. CD-ROM series 20, No. E. [Google Scholar]
- National Center for Health Statistics (NCHS) Machine-readable data file and documentation. National Center for Health Statistics; Hyattsville, MD: 2006. Compressed Mortality File, 1999–2002. CD-ROM series 20, No. F. [Google Scholar]
- Páez A, Long F, Farber S. Moving Window Approaches for Hedonic Price Estimation: An Empirical Comparison of Modelling Techniques. Urban Studies. 2008;45(8):1565–81. [Google Scholar]
- Powell JL. Estimation of Monotonic Regression Models under Quantile Regressions. In: Barnett W, Powell J, Tauchen G, editors. Nonparametric and Semiparametric Models in Econometrics. Cambridge, U.K: Cambridge university Press; 1991. pp. 357–86. [Google Scholar]
- Reich BJ, Fuentes M, Dunson D. Bayesian Spatial Quantile Regression. Journal of the American Statistical Association. 2010;106(493):6–20. doi: 10.1198/jasa.2010.ap09237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvati N, Tzavidis N, Pratesi M, Chambers R. Small Area Estimation via M-Quantile Geographically Weighted Regression. Centre for Statistical and Survey Methodology, University of Wollongong; 2007. [accessed on 30 June, 2011]. Working Paper 07-09. Avaliable at http://ro.uow.edu.au/cssmwp/29. [Google Scholar]
- Su L, Yang Z. Working Paper 05-2007. Singapore Management University; Singapore: 2007. Instrumental Variable Quantile Estimation of Spatial Autoregression Models. [Google Scholar]
- Taylor JW. Using Exponnentially Weighted Quantile Regression to Estimate Value at Risk and Expected Shortfall. Journal of financial Econometrics. 2008;6(3):382–406. [Google Scholar]
- Wei Y, Pere A, Koenker R, He M. Quantile Regression Methods for Reference Growth Charts. Statistics in Medicine. 2006;25(8):1369–82. doi: 10.1002/sim.2271. [DOI] [PubMed] [Google Scholar]
- Wheeler DC. Diagnostic Tools and a Remedial Method for Collinearity in Geographically Weighted Regression. Environment and Planning. D, Society &Space. 2007;39(10):2464–81. [Google Scholar]
- Wheeler DC. Simultaneous Coefficient Penalization and Model Selection in Geographically Weighted Regression: The Geographically Weighted Lasso. Environment and Planning. D, Society &Space. 2009;41(3):722–42. [Google Scholar]
- Wheeler DC, Calder CA. An Assessment of Coefficient Accuracy in Linear Regression Models with Spatially Varying Coefficients. Journal of Geographical Systems. 2007;9(2):145–66. [Google Scholar]
- Wheeler DC, Páez A. Geographically Weighted Regression. In: Fischer MM, Getis A, editors. Handbook of Applied Spatial Analysis. New York: Springer; 2010. pp. 461–86. [Google Scholar]
- Wheeler DC, Tiefelsdorf MR. Multicollinearity and Correlation among Local Regression Coefficients in Geographically Weighted Regression. Journal of Geographical Systems. 2005;7(2):161–87. [Google Scholar]
- Wheeler DC, Waller LA. Comparing Spatially Varying Coefficient Models: A Case Study Examining Violent Crime Rates and Their Relationships to Alcohol Outlets and Ilegal Drug Arrests. Journal of Geographical Systems. 2009;11(1):1–22. [Google Scholar]
- Yang TC, Jensen LI, Haran M. Social Capital and Human Mortality: Explaining the Rural Paradox with County-Level Mortality Data. Rural Sociology. 2011;76(3):347–74. doi: 10.1111/j.1549-0831.2011.00055.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang TC, Teng HW, Haran M. The Impacts of Social Capital on Infant Mortality in the U.S.: A Spatial Investigation. Applied Spatial Analysis and Policy. 2009;2(3):211–27. [Google Scholar]
- Yang TC, Wu PC, Chen VYJ, Su HJ. Cold Surge: A Sudden and Spatially Varying Threat to Health? Science of the Total Environment. 2009;407(10):3421–24. doi: 10.1016/j.scitotenv.2008.12.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu K, Lu Z, Stander J. Quantile Regression: Applications and Current Research Areas. The Statistician. 2003;52(3):331–50. [Google Scholar]
- Yu D, Wei YD, Wu C. Modeling Spatial Dimensions of Housing Prices in Milwaukee, WI. Environment and Planning B. 2007;34(6):1085–102. [Google Scholar]