Abstract
The kinetic adsorption profile at the DNA–gold nanoparticle (AuNP) interface is probed by following the binding and organization of thiolated linear DNA and aptamers of varying chain lengths (15, 30, 44, and 51 mer) to the surface of AuNPs (13.0 ± 1.0 nm diameter). A systematic investigation utilizing dynamic light scattering has been performed to directly measure the changes in particle size during the course of a typical aging-salting thiolated DNA/AuNP preparation procedure. We discuss the effect of DNA chain length, composition, salt concentration, and secondary structure on the kinetics and conformation at the DNA–AuNP interface. The adsorption kinetics are chain-length dependent, composition independent, and not diffusion rate limited for the conditions we report here. The kinetic data support a mechanism of stepwise adsorption of thiols to the surface of AuNPs and reorganization of the thiols at the interface. Very interestingly, the kinetic increases of the particle sizes are modeled accurately by the pseudo-second-order rate model, suggesting that DNA could possess the statistically well-defined conformational evolution. Together with other experimental evidence, we propose a dynamic inner-layer and outer-tail (DILOT) model to describe the evolution of the DNA conformation after the initial adsorption of a single oligonucleotide layer. According to this model, the length of the tails that extend from the surface of AuNPs, capable for hybridization or molecular recognition, can be conveniently calculated. Considering the wide applications of DNA/AuNPs, the results should have important implications in sensing and DNA-directed nanoparticle assembly.
DNA-functionalized gold nanoparticles (DNA/AuNPs) are attractive systems with applications ranging from the construction of self-assembled materials to biosensors.1−7 The most widely used DNA in DNA/AuNPs includes single stranded linear DNA (ssDNA) and secondary structure-rich DNA, such as aptamers.8−12 Aptamers can undergo substantial structural changes upon target binding or preassemble certain secondary structures to fit a target.12−14 Generally, DNA is self-assembled onto AuNP directly via thiol–Au linkage, then assuming the bases available for hybridization to their complement or for target binding. However, many studies have demonstrated that the proper function of DNA/AuNP highly depends on the right conformation of DNA.15−20 Therefore, it is of considerable interest to know more about the conformation nature of DNA on AuNP surfaces.
The self-assembled alkanethiol monolayer on gold has been demonstrated to be highly labile, and the defects migrate across the surface.21 The recent studies have shown that DNA tends to adsorb to gold surfaces through the interaction between bases and Au.16,22,23 The conformation of DNA on Au surfaces is rather complicated. Even though the DNA conformation on flat Au surfaces has been studied using many techniques such as X-ray photoelectron spectroscopy (XPS), ellipsometry, radioisotopic techniques, surface plasmon resonance (SPR), and atomic force microscopy (AFM).15,24 The effect of surface curvature has to be taken into account, and the results obtained for planar Au surfaces may not be applied to spherical AuNPs.25−27 However, the study of the DNA conformation on the surfaces of AuNPs was quite limited due to the lack of the suitable characterization techniques.16,23
Gel electrophoresis has been reported to probe the conformation of DNA on the surfaces of AuNPs.23 According to the effective diameter of the DNA/AuNP derived from the electrophoretic mobility of these conjugates, three conformations of DNA at low, medium, to high capacity were proposed: the wrap-around, random coiled, and fully stretched conformations, respectively.23 The wrap-around conformation favors the decease of the surface energy of AuNP, and in contrast, the stretched conformation favors the increase of entropy. The wrap-around conformation of DNA at the low surface coverage has been widely accepted and evidenced by other techniques.28 However, from the free energy point of view, the random coiled shape is not the most free energy favored conformation. It is also hard to understand how the wrap-around conformation is transformed to the stretched conformations as the capacity is increased.
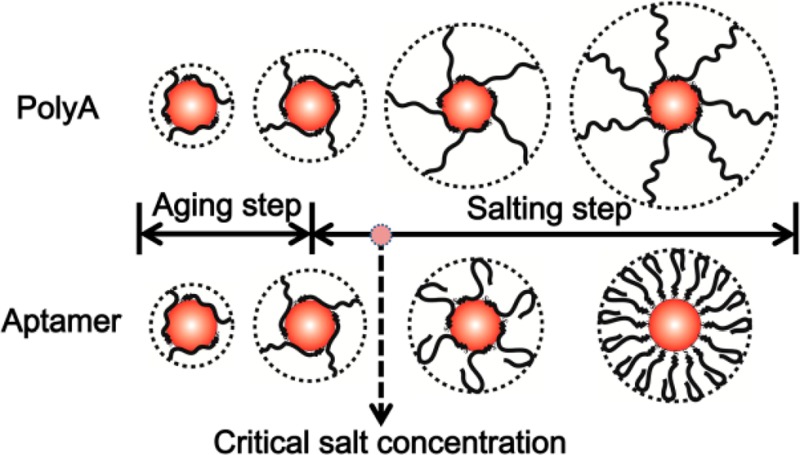
Here, we propose a more stable conformation, referred to as a dynamic inner-layer and outer-tail (DILOT) conformation, to describe the conformational evolution of DNA on AuNP (Figure 1). The DILOT conformation consists of an inner single oligonucleotide monolayer and a stretched section pointing perpendicular to the surface. Under the same immobilization conditions, the longer DNA possess the longer stretched tails to balance between enthalpic and entropic forces in DNA/gold monolayer self-assembly (Figure 1A). During the DNA immobilization process, the AuNP should be always coated by an inner layer to maintain the lowest surface energy until it is completely replaced by the Au–S layer. With the increase of the DNA loadings, the extended tails of DNA become longer and longer as more and more of the DNA bases are away from the surface of AuNP (Figure 1B).
Figure 1.
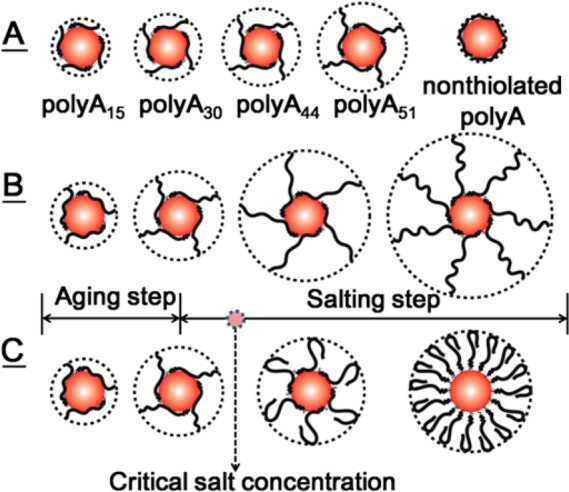
Proposed dynamic inner-layer and outer-tail (DILOT) conformation model of the thiolated linear DNA on the surface of AuNP as shown (A) with varied chain lengths and (B) in the typical aging-salting thiolated DNA/AuNP preparation procedure. The conformations of aptamers in the aptamer/AuNP preparation process are depicted in C. Their conformation still follows the DILOT model when the salt concentration is lower than the critical salt concentration [Na+]c. When the salt concentration is higher than [Na+]c, the aptamers are folded on the surfaces. The conformation of the nonthiolated DNA on AuNP is shown in A to demonstrate its difference with DILOT conformation.
In order to find out if the DILOT conformation is reasonable, the kinetic adsorption profile was acquired. Such a kinetic study requires the continuous acquiring of the conformation related information, which is beyond the capability of most common techniques. Gel electrophoresis would be rather expensive, tedious, and time-consuming. In order to get an estimate about the accuracy of the data, gels of different percentages have to be compared.29 In addition, gel electrophoresis is not able to provide the single-strand resolution for shorter DNA (less than 40-mer) that have more practical applications than the longer ones. Moreover, the surfaces of AuNPs need to be precoated with triphenyl phosphine sulfonate (TPPS) to enhance the stability of the conjugates to avoid aggregation in the gel. However, the pretreatment of AuNPs with TPPS may affect the conformation of DNA. Aptamers could fold into more compact structures, which strongly affects the electrophoretic mobility of the conjugate on the gel and then make the conformation study rather difficult. Thus, it is highly desired to have a more efficient and accurate way to kinetically probe the conformation of DNA on the surfaces of AuNPs.
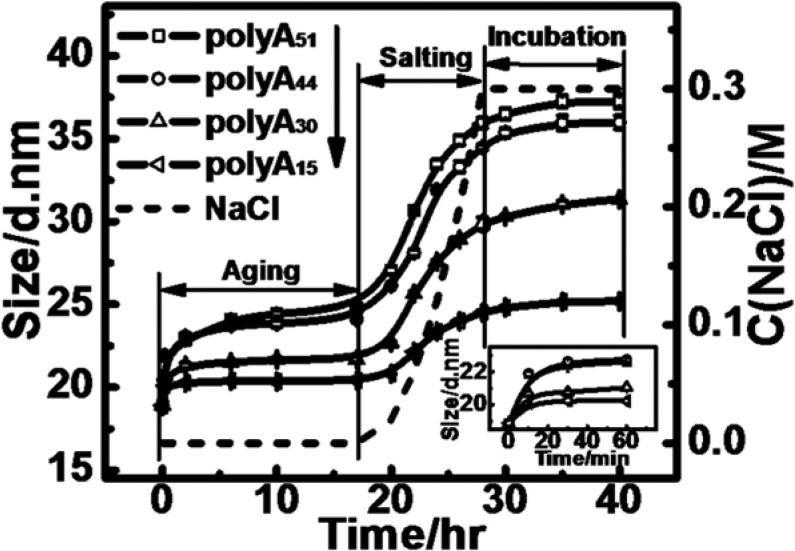
Dynamic light scattering (DLS) is a label free and completely noninvasive technique routinely used to analyze the hydrodynamic size (Dh) and size distribution of polymers, proteins, colloids, and nanoparticles in homogeneously dispersed solution and for the sensitive detection of the protein,30,31 DNA,32 and environmental pollutant.30,33−35 The technique is based on the Brownian motion of spherical particles in suspension that causes laser light to be scattered at greater angles and intensities for the larger particles. Analysis of these intensity fluctuations yields the translational diffusion coefficient and hence the Dh using the Stokes–Einstein relationship. DLS has been demonstrated to be a sensitive probe to directly measure the changes in particle size during functionalization of AuNPs with thiol-ssDNA and hybridization.19,28,36 Recently, DLS has been reported for the study of kinetic immobilization of protein and its conformation on AuNPs.37 DNA has homogeneous charge and relatively limited chemical and conformational complexity compared to proteins, providing the great opportunity to study the conformation of them on AuNPs by analyzing the Dh of the conjugates. In this study, for the first time, we use DLS as a sensitive and efficient probe to achieve the kinetic adsorption profile of linear DNA and aptamers on the surface of AuNPs in the typical three-step (aging, salting, and incubation) immobilization process invented by Mirkin (Figure 2 caption).4,38 Even though several more efficient immobilization protocols have recently been reported,39,40 the three-step process is still the most widely used protocol.
Figure 2.
Kinetic measurements of the Dh values of polyA/AuNP during the typical aging-salting preparation procedure. The molar ratios of polyA’s to AuNPs were all 500:1. The procedure includes the aging step (without adding NaCl, from 0 to 17 h), the salting step (stepwise adding 1 M NaCl phosphate buffer to gradually increase the concentration of NaCl up to 0.3 M, from 17 to 28 h), and the incubation step (without a further increase of NaCl concentration, from 28 to 40 h). The dotted line represents the NaCl concentration of the sample in the procedure. The inset figures showed the Dh of the conjugates in the first hour of the procedure. The errors were calculated from the three repeated measurements.
Experimental Section
Materials
Gold(III) chloride trihydrate (HAuCl4·3H2O), dithiothreitol (DTT), and triethylamine (TEA) were purchased from J&K Scientific LTD (Peking, China). All oligonucleotides (Table S-1) were synthesized and purified through HPLC by Sangon Biotech Co., Ltd. (Shanghai, China). NAP-5 columns (Sephadex G-25 Medium, DNA grade) were purchased from Pharmacia Biotech (GE Healthcare Bio-Sciences, Uppsala, Sweden). ZEN0117-disposable low volume cuvettes (100 μL) were purchased from Malvern Instruments Ltd. (Malvern, England). Millipore H2O purified with a Millipore ultrapure water system was used throughout the experiments. The bare AuNPs (13.0 ± 0.4 nm in diameter measured by transmission electron microscope, Figure S-1) were in-house prepared following the literature protocols.41 Through the immobilization process, the polydispersity of the DNA/AuNP conjugates was all in the range from 0.17 to 0.28, indicating their good quality and narrow distribution for the cumulants analysis.
DLS Measurements
The DLS measurements of the DNA/AuNPs were conducted using a Zetasizer Nano ZS90 (Malvern Instruments Ltd., England) equipped with a red (633 nm) laser and an avalanche photodiode detector (APD). A ZEN0117-disposable low volume cuvette (100 μL) was used as the sample container. The solution viscosity was set as 0.8872 cP, which is the dynamic viscosity of water at 25 °C. The solution refractive index was set as 1.330, which is the refractive index of water at 25 °C with the light wavelength at 633 nm. The medium used in this study is an aqueous solution and has a similar viscosity and refractive index to those for water (see CRC Handbook of Chemistry and Physics). Both the solution refractive index and the dynamic viscosity are required for the calculation of the hydrodynamic size of the particles. All experiments were performed in the water dispersant state at 25 °C with a 10 s equilibration time and 90° measurement angle. Each measurement was taken by conducting 20 runs, and each run took 10 s. The intensity weighted harmonic mean size, Z-average size, is used for the whole study due to its high reliability. The three repeated measurements for each sample were carried out to estimate the errors of the measurements. During the immobilization process of thiolated DNA on AuNPs, the concentration of AuNPs was gradually decreased during the salt adding step due to the stepwise addition of salt solution, commonly in the concentration range from the initial ∼5 to 3 nM. The concentration of AuNPs in this range has no significant effect on the values of the DLS measurements.
Results and Discussion
Kinetic DLS Measurements
The thiolated polyadenine (polyA) with varied lengths (polyA15, polyA30, polyA44, and polyA51, Table 1) has been chosen as an example to study the conformation of linear DNA on the surface of AuNPs. PolyA’s have been widely used as the spacers or the spacing block in DNA probes in the preparation of DNA/AuNP. The study of the conformation of polyA’s could also provide useful information for probe design. The four well-known aptamers (thrombin aptamer TBA44, TBA30, and cocaine aptamer CBA45, CBA51, Table 1) as the examples for secondary structure-rich DNA, were chosen to examine their conformation on the surface of AuNPs by directly comparing them to the polyA with the same length. In this study, the molar ratios between the thiolated DNA and AuNP were all 500:1 to ensure the good stability of the complex during the immobilization process and to achieve the high surface coverage of AuNPs (Figure S-2).
Table 1. Kinetic Parameters for Thiolated-polyA Adsorption.
| Lagergren-first-order
model |
pseudo-second-order
model |
||||||
|---|---|---|---|---|---|---|---|
| name | de/nm | de1/nm | Kf/h–1 | R2 | de2/nm | K′s/nm–1 h–1 | R2 |
| polyA15 | 1.5 | 0.3 | 0.563 | 0.907 | 1.5 | 5.371 | 0.998 |
| polyA30 | 2.8 | 1.1 | 0.518 | 0.993 | 2.8 | 1.171 | 0.999 |
| polyA44 | 5.2 | 1.8 | 0.169 | 0.963 | 5.2 | 0.536 | 0.998 |
| polyA51 | 6.0 | 3.0 | 0.196 | 0.991 | 6.0 | 0.260 | 0.996 |
The Dh increases of the four polyA/AuNP conjugates during the preparation process all follow a similar trend and include three stages, corresponding to the aging, salting, and incubation step, respectively (Figure 2). The overall Dh increase of polyA/AuNPs after the whole immobilization process was set as 100%. The 28.1 ± 4% and 90.6 ± 2% of the Dh increase was obtained after the aging and salting step, respectively. During the aging stage, the Dh increase included the two phases: the rapid increase in the first 20 min and the slow increase after that (Figure 1, inset). The longer polyA took a longer time to reach level-off than the shorter ones in the aging stage. For instance, for polyA15, 80% of the Dh increase during the aging step was observed after only 20 min incubation, and no further increase was observed after 2 h of incubation. In contrast, for polyA44 and polyA51, no saturation was observed even after 17 h of incubation.
Previous studies have shown that polyA containing consecutive adenines preferentially adsorb on Au with high affinity.42 Surprisingly, the aptamers showed almost the same adsorption kinetics in the aging step as polyA’s with the same length (Figure 3), implying that the base composition of DNA had no influence on the adsorption kinetics in the aging step. The results indicate that the linear DNA and aptamers should possess the same conformation during the aging step. Both for polyA’s and aptamers, as the NaCl concentration increased, the Dh of DNA/AuNP continuously increased, which was in good agreement with literature reports that the increased concentrations of Na+ decreased the static electronic repulsion between the negative surface charged AuNPs and the DNA, and thus more DNA were able to be immobilized on the AuNPs.43 Interestingly, a much smaller Dh increase of aptamer/AuNP in the salting and incubation step was observed compared to polyA/AuNP with the same length starting from a certain salt concentration, referred to as the critical salt concentration [Na+]c, suggesting that the conformation of the aptamers is significantly different from that of polyA’s when the salt concentration is higher than [Na+]c. Above [Na+]c, the aptamers may experience the formation of a compact secondary structure, resulting in difficulty in their conformation analysis. Therefore, the conformation of polyA’s in the aging step was first examined.
Figure 3.
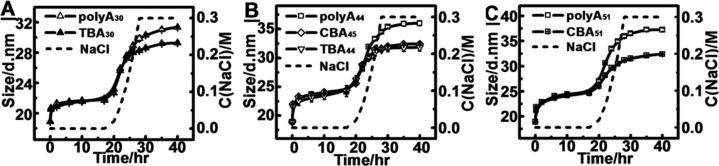
Direct comparisons of the Dh values of the polyA’s (polyA30, polyA44, and polyA51)/AuNP and aptamers (TBA30, TBA44, CBA45, CBA51)/AuNP in the preparation procedure. The dotted line represents the NaCl concentration in the procedure.
The Dh values of the polyA/AuNP provide valuable information on the conformational state of polyA’s. At the end of the aging step, the Dh of the conjugates increased 1.5, 2.8, 5.2, and 5.9 nm in the presence of polyA15, polyA30, polyA44, and polyA51, respectively, which were all significantly smaller than the estimated Dh at the stretched conformation (27.7, 40.6, 52.7, and 58.7 nm, respectively) but greater than the diameter of polyA (∼1 nm). The stretched length of polyA can be estimated as follows.23 The extension of the DNA comprised 0.92 nm, accounting for the thiol group at the 5′ end, which is linked by a carbohydrate spacer of six carbon atoms. In the case of stretched DNA, the length of single stranded DNA can be estimated by assuming a value of 0.43 nm per base. The estimated Dh of the polyA/AuNP at the stretched conformation is assumed to be the sum of the 13 nm diameter of the bare AuNP and 2 times the extension of the DNA molecules. The results suggested that the conformation of polyA’s with varied length at the end of the aging step was neither the wrap-around state nor the stretched conformation.
To get more information on the conformation state of the polyA’s, a direct comparison of the adsorption kinetics between the thiolated and nonthiolated polyA’s was conducted. It has been reported that the shorter DNA tend to adsorb on AuNPs faster than the longer ones.44−46 However, such a conclusion was experimentally obtained under the conditions where the concentration of DNA was quite low (in the low nM range) and the molar ratio between DNA and AuNP was very low.44,45 When DNA was at the large excess amount and at high concentrations like we used in this study, no kinetic adsorption preference of the shorter DNA was observed (Figure S-3). The adsorption kinetics of nonthiolated polyA’s was all quite fast and similar. The Dh’s of conjugates all reached the level-off within 20 min. Interestingly, regardless of the lengths of polyA’s, the level-off Dh increases were all around 1.0 nm, which is close to the diameter of polyA’s, suggesting that the nonthiolated polyA’s with varied length were all wrapped around the particles and there was no significant extension from the surface of AuNPs (Figure 1A). Similar results were also obtained by Cardenas et al.28
Kinetic Model of the Adsorption Process in the Aging Step Supports the DILOT Conformation
The clear difference in adsorption kinetics between the thiolated and nonthiolated polyA’s on AuNPs reflects their different binding mechanism. The latter involves a fast single step nonspecific adsorption, leading to the formation of a monolayer to substantially decrease the surface free energy of AuNPs. In contrast, the adsorption mechanism of the thiolated polyA’s on AuNPs involves a fast nonspecific adsorption and a slow specific adsorption. The nonspecific adsorption is the same as the adsorption of nonthiolated polyA, resulting in a rapid formation of a single oligonucleotide monolayer. The stronger thiol–Au interaction is also involved at the same time, resulting in a much greater Dh increase in the first 20 min compared to that of the nonthiolated polyA/AuNPs conjugates. As this monolayer approaches saturation, a much slower immobilization process that involves the rearrangement of the anchored strands and insertion of the new strands controls the kinetics. Very interestingly, the kinetic increases of the particle sizes were modeled accurately by the pseudo-second-order rate model as we have shown below, suggesting that DNA could have the statistically well-defined conformational evolution.
Specifically, there are two typical adsorption kinetic models on the liquid–solid interface, the Lagergren-first-order rate and pseudo second-order rate model.47 An adsorption process involving electron transfer is commonly well fit to the pseudo second-order rate model. Theoretically, the adsorption kinetics of thiolated DNA on AuNPs should fit the pseudo-second-order rate model better. If the DILOT model (Figure 1) is correct, every strand on the AuNP would reorganize its conformation and lift the wrap-around section away from the surface of AuNP with statistically the same distance as the adsorption of each strand. Therefore, the Dh increase would be proportional to the sorption capacity (or the amount of substance adsorbed) in a certain capacity range. The linear capacity range should be greater at the higher surface coverage since the contribution of every strand on AuNP on the Dh increase becomes smaller. Thus, the two kinetic models can be conveniently expressed in the changes of Dh over incubation time. The detailed derivation of the equations was described in the Supporting Information.
Based on eqs 8 and 9 as shown in the Supporting Information, curve fitting of the polyA adsorption kinetic data in the aging step was performed (Figure 4, Figure S-4), and the parameters in the models and regression coefficients (R2) for the two kinetic models were obtained (Table 1).47 The Lagergren-first-order rate constant Kf and de1 (the Dh increases caused by adsorption of DNA on AuNP at equilibrium) can be determined from the slope and intercept of the plot obtained by plotting log(de1 – dt) versus t (Figure S-4); the pseudo-second-order rate constant Ks′ and de2 (the Dh increases caused by adsorption of DNA on AuNP at equilibrium) can be determined from the intercept and slope of the plot obtained by plotting t/dt versus t (Figure 4A). The calculated de2 values of the pseudo-second-order rate equation are perfectly the same as the experimental de2 values. In contrast, the calculated de1 values of Lagergren-first-order rate equation are far away from the experimental values. The correlation coefficients (R2) for the pseudo-second-order rate model obtained for the studied DNA were all extremely high (above 0.996). Thus, the adsorption process in the aging step followed the pseudo-second-order kinetic model, which is in good agreement with the adsorption mechanism of the thiolated DNA where the rate-limiting step is chemical adsorption involving valency forces through sharing or exchange of electrons between the thiolated DNA and AuNPs.48 The Au–S interaction is much stronger than the nonspecific interaction between Au and the bases of DNA, and therefore no base differentiation on the adsorption kinetics in the aging step was observed (Figure 3). The almost perfect fitting of the Dh increase of polyA/AuNP conjugates as the function of incubation time in the pseudo-second-order equation supports our proposed DILOT conformation model.
Figure 4.
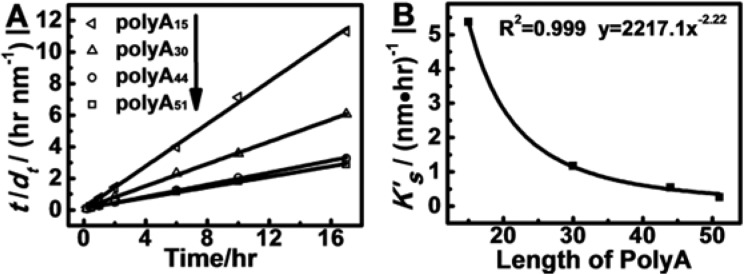
(A) Pseudo-second-order adsorption kinetics of thiolated polyA’s onto AuNPs in the aging step and (B) the low power exponential relationship between of the adsorption rate constant Ks and the length of the thiolated polyA’s.
The length of the thiolated polyA’s has a strong effect on the adsorption rate constant Ks′. As shown in Figure 4B, Ks′ shows a low power exponential function of the length of DNA (y = 2217x–2.32) with a correlation coefficient of 0.999. For example, the Ks′ of polyA15 is around 20 times greater than that of polyA51, suggesting a much faster adsorption rate of polyA15 than polyA51. Please remember that the preparation process is not a diffusion controlled process under the conditions we used here, and merely the size of polyA’s will not cause the decrease of Ks′. The results also well support the DILOT conformation since the longer DNA tends to adsorb on the surface of AuNPs with more binding sites and therefore with higher affinity, resulting in the slower rearrangement and insertion kinetics.
On the other hand, according to the DILOT model we hypothesized the proportional relationship between the Dh and the capacity of polyA on AuNPs in the equation derivation. As we expected, there was indeed a nice linear relationship (R2 = 0.996) between the Dh and the number of the FAM labeled polyA30 in the aging step (Figure S-5). The florescent labeled polyA30 was used to acquire the higher accuracy in capacity quantification. Interestingly, Alivisatos and Parak also reported the linear relationship between the number of DNA per particle and the effective diameters of DNA/AuNP conjugates at the low DNA capacities (up to seven strands per particle for 43 and 100 bases DNA).23,29 The results also well support the DILOT model.
DILOT Conformation also Works for the Salting and Incubation Step
From above, we demonstrated that the DILOT model can describe the conformation of linear DNA in the aging step very well. Now the question is if the DILOT model also works for the linear DNA in the salting and incubation step. To answer this question, we made a back of envelope calculation. Specifically, the final Dh’s of polyA15, polyA30, polyA44, and polyA51/AuNPs at the end of the preparation process in 10 mM phosphate buffer (PB)/0.3 M NaCl were 25.2 ± 0.1, 31.3 ± 0.1, 36.0 ± 0.4, and 37.6 ± 0.4 nm, respectively. To remove the salt effect on Dh, the conjugates were centrifuged and resuspended in 10 mM PB. The final Dh’s of them were 25.8 ± 0.1, 32.7 ± 0.1, 38.0 ± 0.1, and 41.9 ± 0.4 nm, respectively (Figure S-6). These values were all significantly smaller than the estimated diameters in the case of stretched DNA (27.7, 40.6, 52.7, and 58.7 nm, respectively), suggesting that the strands were still not fully stretched. Compared to the longer ones, the shorter polyA’s were more stretched. These data are in good agreement with the reported effective diameters derived from gel electrophoresis.23 In order to provide more conformation information on polyA’s, taking polyA30 as an example, we measured its surface capacity during the salting and incubation step. Interestingly, we found that the Dh’s in PB were in a linear relationship with the number of polyA’s per particle in the medium and high capacity range (28–65 and 65–125 strands per particle, R2 = 0.991 and 0.988, respectively), suggesting the conformation of DNA should still fit the DILOT model (Figure S-7). Exactly as we expect, the slopes of the curves gradually decrease as the surface capacity increases: 0.1779, 0.151, and 0.049 nm/strand, in the low, medium, and high capacity range, respectively, as shown in Figures S-5 and S-7. The linear capacity ranges also become greater at a higher surface coverage: 22–28.5, 28.5–65, and 65–125 strands per particle. These trends can all be well explained by the DILOT model. The addition of each strand on the Au surface requires the reorganization of all strands on AuNP and the lift-off of the wrapped-around section away from the surface of AuNPs with the statistically same length. Clearly, the lift-off length of every strand on AuNP on the Dh increase becomes smaller as the surface capacity increases, corresponding to the smaller curve slope and greater linear capacity range. In Figure S-7, we noticed another interesting phenomenon that the slope of the curve (0.151 nm/strand) in the medium capacity range is much greater than that in the high capacity range (0.049 nm/strand). It seems hard to understand. However, please note the significantly varied salt concentration in the salting and incubation step. It has been reported that the desorption rate of DNA on AuNPs increases as the salt concentration increases.44 With high salt, the DNA internal charges are screened to allow for more compact structures on the AuNP surface, reducing the number of contacting points and facilitating desorption. The increase of the desorption rate certainly favors the displacement of the wrapped-around section of DNA and causes the greater Dh increase per strand. As the surface capacity increases, the adsorbed length per DNA becomes shorter and shorter and the salt impact on the desorption rate becomes weaker and weaker. In addition, the DILOT conformation can also explain the effects of salt concentration, spacer composition, and sonication on the DNA loading on AuNPs. High salt concentration, a spacer with weak affinity to AuNPs, and sonication all can effectively weaken the inner wrapped-around section of DNA and favor the higher loading of DNA on AuNPs.43
As demonstrated above, we found that the DILOT model can be used to describe the conformation of linear DNA on the surface of AuNPs during the complete preparation procedure. The evolution of the conformation of linear DNA in the preparation process is depicted in Figure 1B. Thus, during the whole preparation process, the AuNPs should be always coated by the inner layer to maintain the lowest surface energy until the end of incubation. We further confirmed the existence of the inner layer even at the end of the incubation step by mixing the conjugates with 0.01 mM mecaptohexanol. The Dh of the conjugates increased from 32.3 to 35.3 nm after 30 min incubation, and the smaller mobility was also observed on the gel electrophoresis (Figure S-8). The results were in good agreement with the literature report.16 A detailed discussion can be found in the Supporting Information.
The Application of the DILOT Conformation
As the capacity increased, the extended tails of DNA became longer and longer as more and more of the DNA bases were away from the surface of AuNPs. Specifically, according to the DILOT conformation model, the base number (N) of the extended tail can be calculated using the following equation:
where Dh is the hydrodynamic size (nm) of the DNA/AuNP, DAu is the diameter (nm) of AuNP, and In is the thickness of the inner layer (0.5 nm) of the DNA/AuNP.
Thus, the base numbers of the extended tail are 13.7, 21.7, 27.9, and 32.4 bases for of polyA15, polyA30, polyA44, and polyA51/AuNPs, respectively. These results have implications for the probe design to achieve the effective hybridization and molecular recognition. For example, when AuNP is fully covered with DNA of 44 bases length as effective building blocks, the inner 16 bases are wrapped around the surface of Au and are not effective for hybridization. The longer probes need the longer spacer to avoid the blocking of the molecular recognition site on the surface of AuNPs.
Conformation of Aptamers on AuNPs
In case of aptamers, as shown in Figure 3, the conformational transition of aptamers can be divided into two stages during the whole preparation process: the low and the high salt concentration stages, respectively. In the low salt concentration stage, the kinetic curves of the Dh increases of aptamer/AuNP are almost completely overlapped with those of the ployA/AuNP with the same lengths, suggesting that the conformational transition of aptamers in this stage can be described by the DILOT model. However, when the salt concentration reaches the critical salt concentration [Na+]c, the kinetic curves of the aptamer/AuNP and polyA/AuNP separated from each other and the much smaller Dh increases of aptamer/AuNP conjugates than those of the polyA’s/AuNP conjugates were observed. The aptamers with the more negative of the free energy (ΔG) for their secondary structure formation have a lower [Na+]c (Figure 3). For example, CBA51/AuNP possesses the lowest [Na+]c among these four aptamer/AuNP conjugates due to the highest stability of the folded structure of CBA51. The results suggested that the folding of aptamers plays a significant role in surface immobilization.
The much smaller Dh decrease of aptamer/AuNP conjugates compared to that of polyA/AuNP conjugates is attributed to the folding of aptamers, but not the lesser surface capacity. We experimentally measured the capacity of polyA/AuNP and aptamer/AuNP conjugates by UV–vis measurements. As shown in Figure S-9, the capacities of aptamers were all much higher than those of the polyA’s with the same lengths. The results are quite understandable since the folding of aptamers causes less steric hindrance, easier strand displacement, and more unoccupied area on the surface of AuNPs compared to the linear DNA with the same lengths. Thus, the capacities of aptamers should be significantly higher than those of the linear DNA with the same lengths. The higher capacities of aptamers on AuNPs were also confirmed by their slower migration rates than those of polyA/AuNPs.23 The conformational effect on the capacity on AuNPs was also evidenced by others’ reports. For example, it was found that there were ∼180 adenosine aptamers (27 mer) on each AuNP, which was also significantly higher than linear DNA with a similar length.19 Adenosine aptamers can fold into a duplex conformation at a certain salt concentration and therefore significantly decrease the steric hindrance on surface of AuNPs. In addition, the different secondary structure of the aptamer could possess different steric hindrance on the surface of AuNPs and therefore affect the saturation coverage of them quite differently. For example, the two-dimensional Y shape conformation of cocaine aptamers (CBA45 and CBA51) showed a smaller steric hindrance than the three-dimensional G-quartette structure of thrombin aptamers (TBA30 and TBA44), resulting in their much higher probe densities. Moreover, the stability of the folded structure of aptamers also has an impact on the saturation coverage of them. For instance, the probe density of CBA51/AuNPs was even higher than that of CBA45/AuNPs.
Clearly, the DILOT model is not suitable to describe the conformation of aptamers when the salt concentration is higher than the [Na+]c. The inner layer may be partially or fully interrupted due to the involvement of bases in the formation of the secondary structure by base pairing, which may be attributed to the decreased stability of the conjugates, the increased nonspecific adsorption, and the failure of the conjugate preparation as reported in several works.20,49,50 These results have implications for effective preparation of aptamer/AuNP conjugates and their applications in molecular recognition. For example, it is necessary and critical to add the spacer at the immobilization end of the aptamer to keep the good stability of the aptamer/AuNP conjugates in the salting step and to make the aptamer available for molecular recognition. The spacer does not involve the folding of the aptamer and therefore can maintain the inner layer of the conjugates when the salt concentration is higher than the [Na+]c. In addition, the high capacity of aptamers on AuNPs may also hinder or even prevent the molecular recognition.
Conclusions
We conclude that the DNA on the surface of AuNPs always possesses the DILOT conformation after the initial formation of the inner layer when no folding of DNA is involved. The AuNPs are always coated by the inner layer to maintain the lowest surface energy until it is completely replaced by Au–S layer. As the capacity increased, the extended tails of DNA became longer and longer as more and more of the DNA bases were away from the surface of AuNPs. However, in the case of aptamers, when the salt concentration exceeds the [Na+]c, the aptamers on the surface of AuNPs start to partially fold into their secondary structures, and the DILOT conformation model does not work anymore.
The DILOT conformation model is clearly different from the random coiled conformation at the medium probe density proposed by other researchers. Even though the DILOT model was proposed using 13 nm diameter AuNPs as the model system, the model should be able to apply to other sized AuNPs since the surface interactions are similar. The linear DNA used in this study is polyA’s with the length from 15 to 51-mer. We believe that the longer or shorter ones should also follow a similar trend in their conformational changes on AuNPs. We demonstrated the strong impact of the folding of aptamers on their immobilization on AuNPs. The immobilization of molecular beacons or other secondary structure-rich DNA should be similar to that of aptamers. The results reported in this work have implications for effective hybridization, molecular recognition to the conjugates, and DNA-directed nanoparticle assembly. In addition, for the first time we demonstrated that DLS was a facile and powerful tool for the surface interaction study of DNA/AuNP systems. DLS could also be applied to other types of nanomaterials and in various kinetic studies on the surface of the nanoparticles such as enzymatic reaction kinetics, protein–DNA/RNA interactions, and so on.
Acknowledgments
This work was supported by National Natural Science Foundation (21305093, 20975108), National key scientific instrument and equipment development plan (2012YQ030111), Beijing City Talent Training Aid Program (2012D005016000004), Program for the Young Talents of Higher Learning Institutions in Beijing (CIT&TCD201304145), Special Fund of State Key Joint Laboratory of Environment Simulation and Pollution Control(13K03ESPCT), and Beijing City Board of Education Science and Technology Program (KM201210028020).
Supporting Information Available
The synthesis of gold nanoparticles, the kinetic DLS measurements during the DNA/AuNP complex preparation course, the quantification of the DNA capacity on AuNPs by UV–vis and fluorescent measurements, and derivation of the Lagergren-first-order rate and pseudo-second-order rate model as a function of Dh increase over incubation time. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Alivisatos A. P.; Johnsson K. P.; Peng X. G.; Wilson T. E.; Loweth C. J.; Bruchez M. P.; Schultz P. G. Nature 1996, 3826592609–611. [DOI] [PubMed] [Google Scholar]
- Mirkin C. A.; Letsinger R. L.; Mucic R. C.; Storhoff J. J. Nature 1996, 3826592607–609. [DOI] [PubMed] [Google Scholar]
- Rana S.; Bajaj A.; Mout R.; Rotello V. M. Adv. Drug Delivery Rev. 2012, 642200–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elghanian R.; Storhoff J. J.; Mucic R. C.; Letsinger R. L.; Mirkin C. A. Science 1997, 27753291078–1081. [DOI] [PubMed] [Google Scholar]
- Xie X.; Xu W.; Liu X. Acc. Chem. Res. 2012, 4591511–1520. [DOI] [PubMed] [Google Scholar]
- Wei-Yu C.; Yen-Chun S.; Chi-Lin L.; Arun Prakash P.; Huan-Tsung C.. DNA Functional Gold and Silver Nanomaterials for Bioanalysis. In Functional Nanoparticles for Bioanalysis, Nanomedicine, and Bioelectronic Devices Vol. 2; American Chemical Society: Washington, DC, 2012; Vol. 1113, pp 287–322. [Google Scholar]
- Saha K.; Agasti S. S.; Kim C.; Li X.; Rotello V. M. Chem. Rev. 2012, 11252739–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellington A. D.; Szostak J. W. Nature 1990, 3466287818–822. [DOI] [PubMed] [Google Scholar]
- Tuerk C.; Gold L. Science 1990, 2494968505–510. [DOI] [PubMed] [Google Scholar]
- Li D.; Song S.; Fan C. Acc. Chem. Res. 2010, 435631–641. [DOI] [PubMed] [Google Scholar]
- Famulok M.; Mayer G. Acc. Chem. Res. 2011, 44121349–1358. [DOI] [PubMed] [Google Scholar]
- Lou X. H.; Qian J. R.; Xiao Y.; Viel L.; Gerdon A. E.; Lagally E. T.; Atzberger P.; Tarasow T. M.; Heeger A. J.; Soh H. T. Proc. Natl. Acad. Sci. U. S. A. 2009, 10692989–2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakayama S.; Sintim H. O. J. Am. Chem. Soc. 2009, 1312910320–10333. [DOI] [PubMed] [Google Scholar]
- Xia F.; Zuo X.; Yang R.; Xiao Y.; Kang D.; Vallée-Bélisle A.; Gong X.; Yuen J. D.; Hsu B. B. Y.; Heeger A. J.; Plaxco K. W. Proc. Natl. Acad. Sci. U. S. A. 2010, 1072410837–10841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang E.; Satjapipat M.; Han S.; Zhou F. Langmuir 2001, 1741215–1224. [Google Scholar]
- Park S.; Brown K. A.; Hamad-Schifferli K. Nano Lett. 2004, 4101925–1929. [Google Scholar]
- Akamatsu K.; Kimura M.; Shibata Y.; Nakano S.-i.; Miyoshi D.; Nawafune H.; Sugimoto N. Nano Lett. 2006, 63491–495. [DOI] [PubMed] [Google Scholar]
- Wernette D. P.; Mead C.; Bohn P. W.; Lu Y. Langmuir 2007, 23189513–9521. [DOI] [PubMed] [Google Scholar]
- Zhao W.; Chiuman W.; Lam J. C. F.; McManus S. A.; Chen W.; Cui Y.; Pelton R.; Brook M. A.; Li Y. J. Am. Chem. Soc. 2008, 130113610–3618. [DOI] [PubMed] [Google Scholar]
- Song S.; Liang Z.; Zhang J.; Wang L.; Li G.; Fan C. Angew. Chem., Int. Ed. 2009, 48468670–8674. [DOI] [PubMed] [Google Scholar]
- Schessler H. M.; Karpovich D. S.; Blanchard G. J. J. Am. Chem. Soc. 1996, 118409645–9651. [Google Scholar]
- Li H. X.; Rothberg L. Proc. Natl. Acad. Sci. U. S. A. 2004, 1013914036–14039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parak W. J.; Pellegrino T.; Micheel C. M.; Gerion D.; Williams S. C.; Alivisatos A. P. Nano Lett. 2003, 3133–36. [Google Scholar]
- Herne T. M.; Tarlov M. J. J. Am. Chem. Soc. 1997, 119388916–8920. [Google Scholar]
- Cederquist K. B.; Keating C. D. ACS Nano 2009, 32256–260. [DOI] [PubMed] [Google Scholar]
- Hill H. D.; Millstone J. E.; Banholzer M. J.; Mirkin C. A. ACS Nano 2009, 32418–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kira A.; Kim H.; Yasuda K. Langmuir 2009, 2531285–1288. [DOI] [PubMed] [Google Scholar]
- Cardenas M.; Barauskas J.; Schillen K.; Brennan J. L.; Brust M.; Nylander T. Langmuir 2006, 2273294–3299. [DOI] [PubMed] [Google Scholar]
- Pellegrino T.; Sperling R. A.; Alivisatos A. P.; Parak W. J. J. Biomed. Biotechnol. 2007, 2007, 26796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X.; Dai Q.; Austin L.; Coutts J.; Knowles G.; Zou J.; Chen H.; Huo Q. J. Am. Chem. Soc. 2008, 13092780–2782. [DOI] [PubMed] [Google Scholar]
- Chun C.; Joo J.; Kwon D.; Kim C. S.; Cha H. J.; Chung M. S.; Jeon S. Chem. Commun. 2011, 473911047–11049. [DOI] [PubMed] [Google Scholar]
- Gao D.; Sheng Z.; Han H. Anal. Chim. Acta 2011, 6961–21–5. [DOI] [PubMed] [Google Scholar]
- Dai Q.; Liu X.; Coutts J.; Austin L.; Huo Q. J. Am. Chem. Soc. 2008, 130268138–8139. [DOI] [PubMed] [Google Scholar]
- Kalluri J. R.; Arbneshi T.; Khan S. A.; Neely A.; Candice P.; Varisli B.; Washington M.; McAfee S.; Robinson B.; Banerjee S.; Singh A. K.; Senapati D.; Ray P. C. Angew. Chem., Int. Ed. 2009, 48519668–9671. [DOI] [PubMed] [Google Scholar]
- Beqa L.; Singh A. K.; Khan S. A.; Senapati D.; Arumugam S. R.; Ray P. C. ACS Appl. Mater. Interfaces 2011, 33668–673. [DOI] [PubMed] [Google Scholar]
- Xu J.; Craig S. L. J. Am. Chem. Soc. 2005, 1273813227–13231. [DOI] [PubMed] [Google Scholar]
- Jans H.; Liu X.; Austin L.; Maes G.; Huo Q. Anal. Chem. 2009, 81229425–9432. [DOI] [PubMed] [Google Scholar]
- Storhoff J. J.; Elghanian R.; Mucic R. C.; Mirkin C. A.; Letsinger R. L. J. Am. Chem. Soc. 1998, 12091959–1964. [Google Scholar]
- Zu Y.; Gao Z. Anal. Chem. 2009, 81208523–8528. [DOI] [PubMed] [Google Scholar]
- Zhang X.; Servos M. R.; Liu J. J. Am. Chem. Soc. 2012, 134177266–7269. [DOI] [PubMed] [Google Scholar]
- Lou X.; Zhang Y. ACS Appl. Mater. Interfaces 2013, 5136276–6284. [DOI] [PubMed] [Google Scholar]
- Pei H.; Li F.; Wan Y.; Wei M.; Liu H.; Su Y.; Chen N.; Huang Q.; Fan C. J. Am. Chem. Soc. 2012, 1342911876–11879. [DOI] [PubMed] [Google Scholar]
- Hurst S. J.; Lytton-Jean A. K. R.; Mirkin C. A. Anal. Chem. 2006, 78248313–8318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X.; Servos M. R.; Liu J. Langmuir 2012, 2883896–3902. [DOI] [PubMed] [Google Scholar]
- Li H. X.; Rothberg L. J. J. Am. Chem. Soc. 2004, 1263510958–10961. [DOI] [PubMed] [Google Scholar]
- Zou R.; Lou X.; Ou H.; Zhang Y.; Wang W.; Yuan M.; Guan M.; Luo Z.; Liu Y. RSC Adv. 2012, 2114636–4638. [Google Scholar]
- Fu H.-Z.; Wang M.-H.; Ho Y.-S. J. Colloid Interface Sci. 2012, 379, 148–156. [DOI] [PubMed] [Google Scholar]
- Ho Y. S.; McKay G. Process Biochem. 1999, 345451–465. [Google Scholar]
- Li F.; Li J.; Wang C.; Zhang J.; Li X.-F.; Le X. C. Anal. Chem. 2011, 83176464–6467. [DOI] [PubMed] [Google Scholar]
- Wu Z.-S.; Lu H.; Liu X.; Hu R.; Zhou H.; Shen G.; Yu R.-Q. Anal. Chem. 2010, 8293890–3898. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.