Complex-Difference Constrained Compressed Sensing Reconstruction for Accelerated PRF Thermometry with Application to MRI Induced RF Heating

Abstract

Purpose

Introduce a novel compressed sensing reconstruction method to accelerate proton resonance frequency (PRF) shift temperature imaging for MRI induced radiofrequency (RF) heating evaluation.

Methods

A compressed sensing approach that exploits sparsity of the complex difference between post-heating and baseline images is proposed to accelerate PRF temperature mapping. The method exploits the intra- and inter-image correlations to promote sparsity and remove shared aliasing artifacts. Validations were performed on simulations and retrospectively undersampled data acquired in ex-vivo and in-vivo studies by comparing performance with previously proposed techniques.

Results

The proposed complex difference constrained compressed sensing reconstruction method improved the reconstruction of smooth and local PRF temperature change images compared to various available reconstruction methods in a simulation study, a retrospective study with heating of a human forearm in vivo, and a retrospective study with heating of a sample of beef ex vivo .

Conclusion

Complex difference based compressed sensing with utilization of a fully-sampled baseline image improves the reconstruction accuracy for accelerated PRF thermometry. It can be used to improve the volumetric coverage and temporal resolution in evaluation of RF heating due to MRI, and may help facilitate and validate temperature-based methods for safety assurance.

Introduction

In MRI, radiofrequency (RF) energy is applied to induce a detectable signal, while italso produces heating in biological tissues. To avoid adverse effects it is desirable to ensure that both the core body temperature and local temperature throughout the subject are carefully managed (1). Currently this is performed by monitoring the Specific energy Absorption Rate (SAR) averaged over the whole subject exposed to RF fields (whole-body SAR) and also estimating the maximum local SAR. Monitoring of the whole-body SAR can be accomplished fairly well with measurements of absorbed RF power and the mass of the subject (2). Estimates of maximum local SAR typically combine measures of power absorbed with a priori electric field distribution as calculated with standardized human models (3-5), which typically do not match the subject geometry perfectly, resulting in local SAR predictions that differ from reality (6-9).

With a variety of MRI techniques it is possible to achieve non-invasive measurement of temperature change (10). Among these methods, proton resonance frequency (PRF) shift thermography is often preferred for its high sensitivity and speed in tissues with high water content (11,12). PRF shift thermography is used routinely in monitoring of ablation procedures such as in MR-guided High Intensity Focused Ultrasound (MRgHIFU) (13), and has been used to evaluate small temperature changes due to MR-related RF heating in phantoms and in vivo (14-17).

Because PRF shift thermography has the potential to provide subject-specific information about RF heating and provides information more directly relevant to safety than current methods relying only on SAR, it is important to consider its potential utility in MR safety assurance. Although temperature increase due to MRI is expected to be a slower process than that due to ablation, the demands for high speed in assessing SAR-induced temperature increase may be greater than those in MRgHIFU for a variety of reasons. The sequence used to assess temperature increase must be interspersed with the imaging sequence being assessed without notably lengthening total imaging time. Also, unlike MRgHIFU, the location of peak heating is not likely to be known ahead of time, so it is necessary to cover a large volume of interest. All these must be accomplished while maintaining adequate sensitivity to much smaller temperature changes than ablation. Therefore, methods have been proposed recently to improve accelerated PRF thermography for potential real time RF safety feedback in phantoms and in vivo (18). A fast PRF imaging method could also improve the accuracy for 1) temperature based SAR quantification which has been used for transmit array safety testing (19) as well as to validate SAR simulation methods (20), and for 2) characterizing tissue thermal properties (21), which could in turn be used as calibration information for real-time temperature prediction (22).

Among many methods to accelerate PRF shift thermography and MRI in general, compressed sensing (CS) (23) is a promising, relatively new technique that exploits image compressibility/sparsity to reconstruct undersampled k-space data without notable loss of information. Successful application of CS requires image sparsity in a known space (e.g. finite differences, wavelets) and incoherence between the acquisition space and representation space. Incoherence between k-space and several sparsifying transforms can be accomplished by using variable-density random undersampling of k-space, where the low spatial frequencies are fully-sampled and the undersampling factor increases with distance from the center(23). Moreover, CS can be combined with parallel imaging to increase the acceleration rate by exploiting joint sparsity in the multicoil image ensemble (24-26). Conventional CS framework based on minimization of the sum of magnitude values, however, may be inefficient for PRF temperature imaging, in which the main contrast is the difference of the phase.

Among CS methods proposed for PRF thermography, a temporally constrained reconstruction (“TCR”) method has shown good accuracy for PRF temperature reconstruction (27-29), with the assumption of temporally smooth evolution of complex MR image values. This method has been demonstrated to achieve improved spatial and temporal resolution for MR-guided HIFU ablation (29). However, this method may not be the most effective in constraining the local and smooth temperature features, which can be important for modest and diffusive heating due to RF electromagnetic fields. Another reconstruction method for general phase contrast imaging was proposed by constraining the individual magnitude and phase (30). This method also did not constrain terms related to PRF-induced phase change and thus could not fully exploit the same important temperature features for MRI induced heating. These two methods also do not utilize the baseline image for the iterative reconstruction, which could provide additional useful information. Finally, another model-based method was proposed to directly reconstruct PRF phase maps for thermal ablation by exploiting directly the local temperature phase sparsity (31). This method is novel in that it does not reconstruct individual MR images related to PRF. However, it may also be not suitable for spatially diffuse RF heating applications.

Here, a novel complex difference constrained CS reconstruction method for tracking MRI induced RF heating using PRF thermometry is proposed. It exploits both the spatial and temporal local and smooth temperature change through the complex difference from a fully-sampled baseline image. The complex difference is shown to be a good approximation to PRF phase change, and with the use of a fully-sampled baseline image, the proposed method is shown to effectively exploit the inter- and intra- image correlations between the post-heating and baseline PRF images. The proposed method is tested in a variety of circumstances demonstrating its robustness for volumetric coverage and temporal consistency.

Theory

Conventional and Previously-Published Reconstruction Methods

Since the temperature distribution from MRI-induced RF heating varies relatively smoothly through space, in principle low-resolution sampling schemes could be used to accelerate imaging. However, because most anatomical images contain complex anatomical structures, low-resolution sampling would result in Gibbs-ringing artifacts, and volume averaging with regions of low water content, adversely affecting the PRF signal.

For PRF thermography and other phase contrast imaging methods, conventional CS can be implemented by separately reconstructing the undersampled k-space data of the baseline and post-heating images, as follows (23):

$${\min }_u\{{\alpha }_1\ast {\Vert u\Vert }_1+{\alpha }_2\ast \mathrm{TV}\left(u\right)\}s.t.Eu=v$$ (Eq. 1)

where u and v are the MR image and its corresponding k-space data for either the baseline or post-heating images, E the Fourier encoding operator, TV the spatial/temporal total variation function commonly used in CS (25). Throughout this report, $\mathrm{TV}\left(u\right)={\Vert {\nabla }_{x-y(-t)}u\Vert }_2^2$. The weighting coefficients, α₁ and α₂, are typically chosen as α₁ = α₂ = 1 in this study and will be discussed later.

By this method (“separated CS”), undersampling artifacts of the reconstructed PRF temperature change distribution can be partially removed. However, separated CS only exploits individual image correlations, not taking advantage of the strong correlations between images acquired before and after the temperature change. Moreover, the conventional formulation of CS exploits image sparsity by constraining the magnitude using an l₁-norm approach, while in phase-contrast imaging, the important information resides in the phase change, which calls for reevaluating the formulation of the conventional CS approach to exploit smoothness or sparsity in the phase images.

Because seperated CS is not applicable for a time series, TCR was proposed based on the temporal smoothness of the complex image values(27):

$${\min }_{u_i}\left\{{\mathrm{TV}}_{\text{temporal}}\left(u_i\right)\right\}\mathrm{s}.\mathrm{t}.\mathrm{E}{u}_i=v_i$$ (Eq. 2)

Here, u_i and v_i denote a time series of images and k-space data for PRF, that includes the baseline and post-heating acquisitions. The cost function used in this method does not exploit spatial temperature features which could further improve the reconstruction performance.

Proposed Complex Difference Constrained Compressed Sensing

A novel CS reconstruction method is proposed here based on three important facts that were not utilized in previously published methods. First, it is feasible with many PRF based applications to acquire a fully-sampled baseline image before a heating process has started. It is often the post-heating images (acquired during and after heating) that would benefit from rapid acquisition. Since mild temperature changes due to RF heating would result in minimal changes in image magnitude, and small changes in PRF phase (10), the post-heating image would be quite similar to the baseline image in both magnitude and phase overall, and thus knowledge of the baseline image could greatly facilitate the iterative reconstruction process. Second, temperature changes either due to diffuse RF heating or ablation should not only be temporally smooth but also spatially smooth with piecewise local variations in accordance with the bioheat equation (32) considering tissue types normally have similar thermal conductivities. Finally, PRF phase changes due to temperature elevation can be well-approximated by complex differences based on trigonometric principles, especially when the image magnitude and phase are generally close between baseline and post-heating images as discussed above. A CS reconstruction method designed with these novel features could result in better reconstruction accuracy than existing methods:

$$\underset{{\mathrm{u}}_{\mathrm{i}}}{\min }\{{\alpha }_1\ast {\Vert u_i-u_0\Vert }_1+{\alpha }_2\ast {\mathrm{TV}}_{spatial-temporal}(u_i-u_0)\}s.t.E(u_i-u_0)=v_i-v_{0i}$$ (Eq. 3)

Here, u_i are a series of post-heating images with their undersampled k-space data v_i, and u₀ is the fully-sampled baseline image with v_0i being the portion of the fully-sampled k-space data that shares the same k-space locations as v_i. For input of a time series of u_i, the TV operator performs an image-domain spatial-temporal finite complex difference operation (otherwise only the image-domain spatial finite complex difference would be performed). The l₁ and TV penalties enforce sparsity and smoothness of the complex difference approximated PRF phase changes to improve reconstruction accuracy. Unless otherwise specified, the weighting coefficients were chosen as α₁ = 1 and α₂ = 1 in this study, for equal importance of local and smooth features of the target temperature distribution to be reconstructed.

A nonlinear conjugate gradient (CG) algorithm (23) was employed to solve the minimization problem given in Eq. 3. The undersampled complex difference image {u_i′-u₀′} reconstructed by zero-filled fast Fourier transform (FFT) from undersampled k-space data {v_i-v_0i} was used as the initial guess. For each CG iteration, {u_i-u₀} is reconstructed from {v_i-v_0i} based on the minimization as in Eq. 4. After that, the output {u_i-u₀} is summed with u₀ to get u_i. Then, the k-space of the estimated u_i is updated with its already-collected data v_i. The resulting image domain data u_i is then used to calculate the initial guess for {u_i-u₀} for the next CG iteration. The number of CG iterations is set to 15 in this study which guaranteed convergence in all cases.

Methods

The proposed complex difference constrained CS method was evaluated in three scenarios: 1) a simulation study based on a modified Shepp-Logan phantom, 2) a retrospective undersampling study with heating of a human forearm in vivo to evaluate volumetric coverage, and 3) a retrospective undersampling study with heating of a large sample of beef ex vivo to evaluate temporal consistency. Both experiments were performed on a Siemens 3 Tesla Trio MRI system (Siemens AG, Health Sector, Erlangen, Germany). The human experiment was performed in compliance with institutional policies on human subject research and informed consent of the volunteer. Four oil phantoms were used in both experiments as references to remove unwanted gradient system phase drift by using polynomial fitting up to the first order (12,33,34). This phase drift correction was applied after all image reconstruction methods were performed. Fully sampled k-space data were acquired and retrospectively undersampled with variable-density Cartesian sampling patterns all generated based on published literature (23).

To evaluate the effect of the proposed reconstruction method, temperature root-mean-square error (RMSE) was calculated as

$$\mathrm{RMSE}=\frac{\sqrt{\Sigma (mask\ast {\mid ReconstructedTemperature-GoldStandardTemperature\mid }^2)}}{\Sigma (mask\ast {\mid GoldStandardTemperature\mid }^2)}\times 100\%$$

To evaluate both global and peak temperature accuracy, masks are generated respectively by thresholding the baseline anatomical image for global temperature accuracy so that the phase change in the air is not included, and thresholding the fully-sampled PRF temperature change image (for regions having temperature change larger than 60% of the highest temperature change) for peak temperature accuracy.

For temperature based assessment of RF heating, it is desired to collect PRF images more often when the temperature is increasing more rapidly. Assuming a temperature increase ΔT for every high-SAR sequence duration Δt_heating, with a PRF sequence with duration Δt_PRF applied (expecting Δt_PRF < < Δt_heating) in each cycle, we propose to define a temporal resolution as follow for the reported results.

$$\text{Temporal Resolution}=\frac{\Delta {\mathrm{t}}_{\mathrm{PRF}}}{\Delta {\mathrm{t}}_{\mathrm{heating}}}∕\frac{\Delta \mathrm{T}}{\Delta {\mathrm{t}}_{\mathrm{heating}}}=\frac{\Delta {\mathrm{t}}_{\mathrm{PRF}}}{\Delta \mathrm{T}}$$

Simulation Study

As the first demonstration, a smooth phase shift distribution was applied to the Shepp-Logan phantom to simulate heating. The distribution was designed and scaled to maximum temperature changes of 1 °C and 3 °C, corresponding to about 5 degrees and 15 degrees of PRF phase change between the baseline (u₀) and the post-heating (u) images respectively. Such relationships between temperature change and phase change is realistic for PRF thermography at 3T with a TE of 10 ms. The post-heating simulated image also had a 5% decrease in magnitude per degree of temperature increase (from u₀ to u) in the heated region-of-interest (ROI) to represent any possible T₁ increase due to heating (10). Complex noise corresponding to two different anatomic image SNR levels in the heated region (150 for 1 °C max temperature increase, and 50 for 3 °C max temperature increase), were added to the baseline and post-heating images to evaluate the proposed CS reconstruction method for different combinations of heating and anatomic image SNR levels. Thus the two cases share the same PRF SNR level, defined as the maximum temperature increase multiplied by anatomic SNR, as consistent with ref 10. A variable-density undersampling mask with R=4 reduction factor was applied to the k-space data. The undersampled baseline and post heating images were reconstructed with zero-filled FFT and are denoted as u₀′ and u′. For evaluation of the proposed method, a low resolution undersampling mask that shared the same undersampling ratio as the previous variable-density undersampling mask was also applied to the fully-sampled k-space data, and the reconstruction result from both low resolution zero-filled FFT and separated CS were compared to the proposed “Complex Difference” result. RMSEs in the heated ROI were calculated by comparing the reconstructed PRF temperature images against the fully-sampled gold standard with no noise added.

Retrospective Study on in vivo Human Forearm Heating

To evaluate volumetric coverage of the proposed complex difference constrained CS reconstruction method, a forearm of a human volunteer was heated using an in-house external RF coil inside an MRI system. This RF heating coil was a circular surface coil (8 cm diameter, matched to 50 Ω, tuned to 153 MHz to minimize possible coupling to transmit or receive coils). It was built to provide localized and controllable heating to ensure safety to the human volunteer while mimicking high-SAR heating to be monitored in practice. It was positioned against the ventral side of the forearm (Fig. 1) inside a transmit-receive extremity coil used for imaging. A frequency synthesizer (PTS 200, PTS, MA, USA) and a manually-adjustable RF power amplifier (LA200UELP, Kalmus, WA, USA) were used to heat the forearm for 2 minutes with 31.4 W power. The heating was monitored with PRF temperature imaging with fully-sampled Cartesian k-space datasets on 5 interleaved 2D slices acquired before and after the heating, with parameters 10 ms TE, 100 ms TR, 128 × 128 matrix size, 160 × 160 mm² FOV, 10 mm slice thickness, 10 mm spacing between the slices, 40° flip angle, and 1.5 kHz receiver BW, 4 averages for the baseline image, and 1 average for the post-heating image. The proposed reconstruction method was applied to the dataset retrospectively undersampled with the same undersampling trajectory for all slices (R=4) in different Cartesian directions (U-D: Up-Down, L-R: Left-Right), and the fully-sampled PRF temperature maps served as the gold standard.

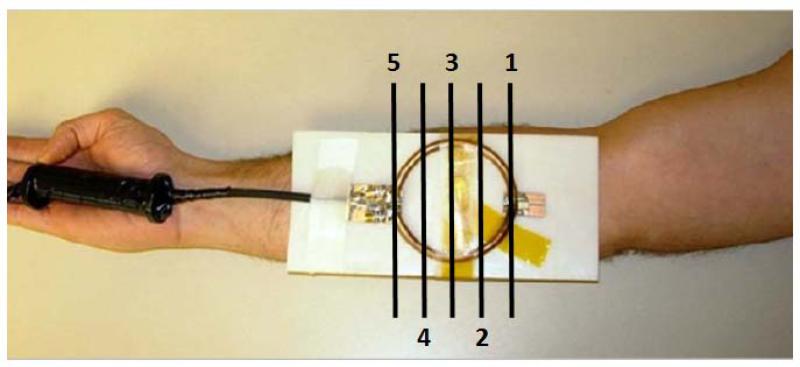
Figure 1.

RF heating coil placed against the forearm of a volunteer. The locations of five imaged slices are labeled with indexes and black lines.

Retrospective Study on ex vivo Beef Heating

To evaluate the temporal consistency of the proposed reconstruction method and to compare it with previously-published methods including “TCR” (27), a 6.8 kg beef roast was imaged for 12 time frames separated by 11 interspersed heating periods lasting one minute each. The first time frame served as the baseline image, and the remaining 11 frames were used to calculate 11 PRF temperature maps. The GRE imaging was performed with the MRI system body coil and 100 ms TR, 10 ms TE, 300 × 300 mm² FOV, 128 × 128 matrix size, 1 axial slice with 8 mm thickness, 40° flip angle, and 1.5 kHz receiver BW. The heating for each heating period was applied using the system body coil with 1 min of a modified turbo spin echo sequence (70° flip angle hard pulse as the refocusing pulses with 15% duty cycle). To ensure a gold standard with adequate PRF temperature SNR to be collected, the images were acquired with 2 averages (short term). The proposed reconstruction method was applied to half of each dataset (no averaging) undersampled to simulate an acceleration factor of R = 3, and compared to the fully-sampled data from 2 averages. To maximize temporal sparsity for the proposed method, different undersampling patterns (in the left-right direction) were generated to undersample the k-space data for each time frame. The undersampled k-space data for each timeframe was reconstructed in two ways: 1) based on data from the current and previous time frames (denoted as “Previous”, practical for MRI RF safety monitoring), and 2) based on data from all 12 frames (denoted as “All”, practical for temperature characterization). The proposed complex difference constrained CS method was compared to low resolution imaging, separated CS, and TCR (Eq. 2). The global RMSEs of time frames #2~#12 with different reconstruction methods were recorded. The reconstruction accuracy was also evaluated against a fiber optic temperature probe (AccuSens; OpSens, Quebec, Canada) inserted into the sample.

Finally, to demonstrate the effectiveness of each term in the proposed cost function in Eq. 4 and to further compare the proposed complex difference method with TCR, the undersampled beef dataset was reconstructed with variations of the proposed method and TCR (essentially setting α₁ and α₂ to either 1 or 0). For variations of TCR, l₁ and spatial TV of u_i were added to the cost function in Eq. 2:

$$\underset{{\mathrm{u}}_{\mathrm{i}}}{\min }\{{\alpha }_1\ast {\Vert u_i\Vert }_1+{\alpha }_2\ast {\mathrm{TV}}_{spatial-temporal}\left(u_i\right)\}s.t.E{u}_i=v_i$$ (Eq. 4)

Results

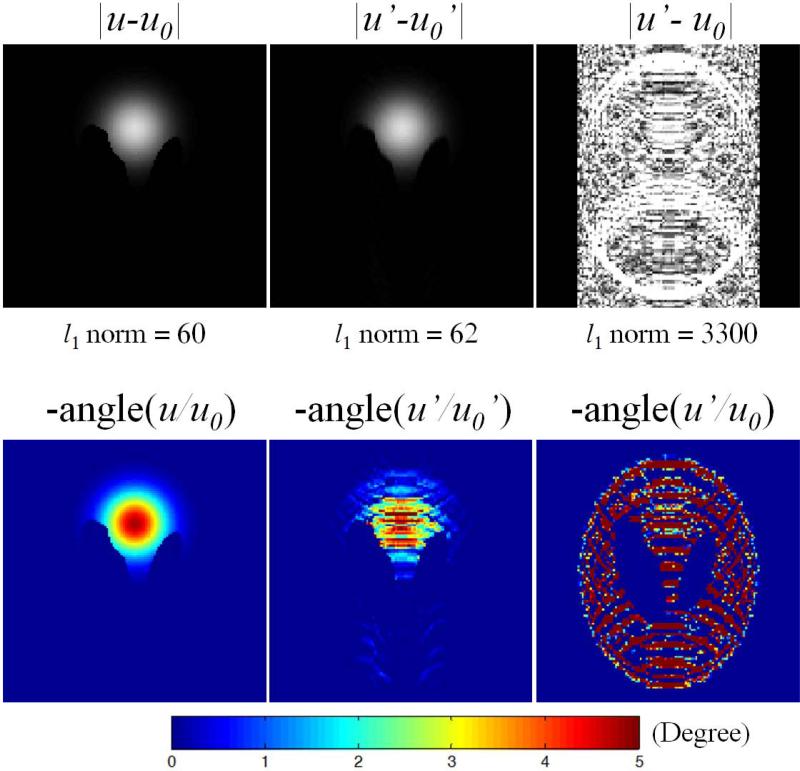
The results of the simulation study with a modified Shepp-Logan phantom are first shown in Fig. 2. The complex difference image {u-u₀} is sparser than the individual images (standard Shepp-Logan image, not shown), as expected due to the fact that temperature does not vary abruptly. Both complex magnitude and phase difference images (|u′-u₀′| and angle(u′/u₀′)) given by the subtraction of undersampled baseline (u₀′) from post-heating images (u′) contain less aliasing artifacts than would normally be expected from any individual undersampled magnitude or phase image (not shown). With the same data undersampling, the l₁ norm of complex difference increased by only 3% (from {u-u₀} to {u′-u₀′}), compared to a 15% increase for individual post-heating image u (not shown). Even though a fully-sampled baseline (u₀) is available, using the undersampled baseline (u₀′) rather than the fully-sampled baseline (u₀) in these subtraction operations also greatly improved the accuracy with a much smaller increase in l₁ norm, due to cancellation of aliasing artifacts from similar image features in the post-heating and baseline images. These important features demonstrate not only that l₁-minimization based CS method can be used to reconstruct the target complex difference based on k-space difference, but also that a complex difference based CS method should outperform individual image based CS method (such as separated CS) due to the smaller l₁ increase of complex difference than the individual post-heating image.

Figure 2.

Complex difference magnitude (top row) and phase difference (bottom row) of the baseline (u₀) and post-heating (u) images by simulation. Undersampled images are denoted with ′. The l₁ norms of each magnitude images are listed, with 3% increase from {u-u₀} to {u′-u₀′}, compared to 15% increase from u to u′ (not shown). All magnitude images are shown on the same color scale.

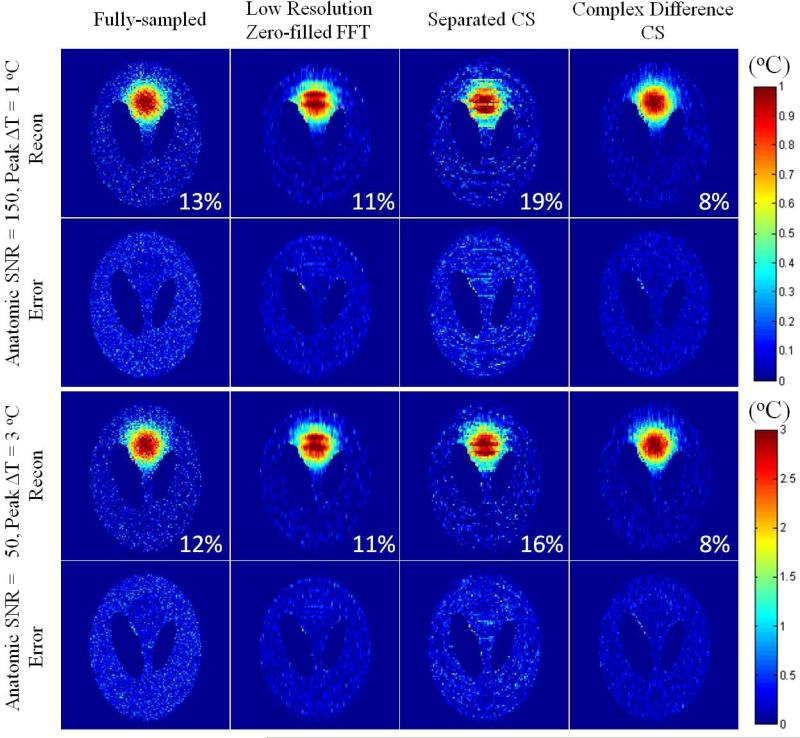
The effectiveness of the proposed reconstruction method on the simulation study is further demonstrated in Fig. 3. With different combinations of anatomic image SNR level and maximum temperature increase but the same PRF SNR, the proposed method showed very similar improvements in PRF image quality and RMSE over low resolution imaging with zero-filled FFT or separated CS.

Figure 3.

Reconstructed PRF images and corresponding spatial reconstruction errors with different combinations of max temperature increase and image SNRs (same PRF SNRs) and various reconstruction methods, with RMSEs in the heated ROI listed on the lower right of each reconstructed image.

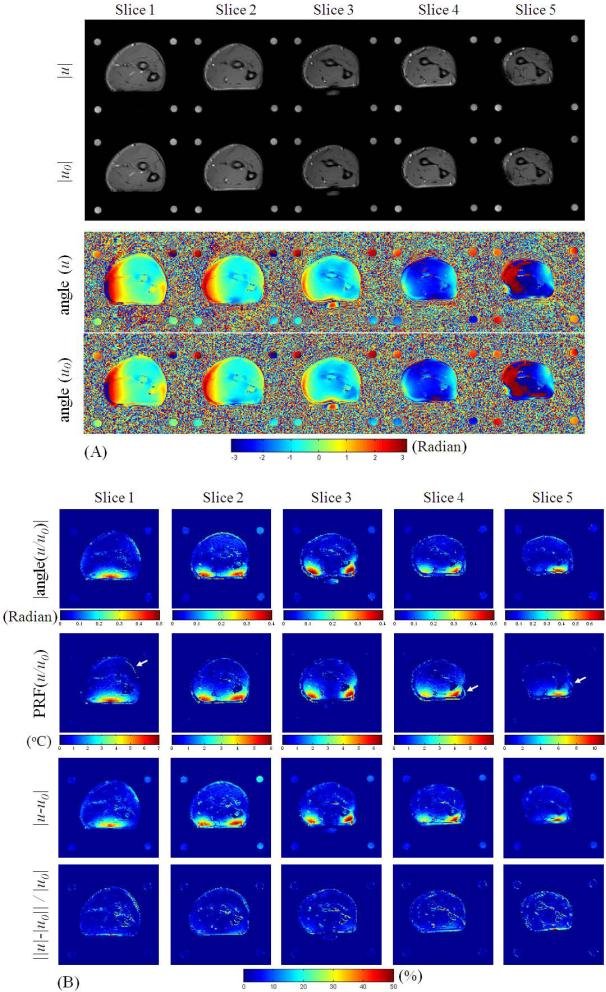
The results of the in vivo human forearm heating experiment are shown in Fig. 4 and Fig. 5. The fully-sampled magnitude and phase images of both baseline (u₀) and post-heating images (u) are first shown in Fig. 4(a), followed by absolute PRF phase change images (|angle(u/u₀)|), PRF temperature change images (PRF(u/u₀)), complex difference magnitude images (|u-u₀|), and the relative magnitude difference image (||u|-|u₀|| / |u₀|) as in Fig. 4(b). The complex difference magnitude images (|u-u₀|) show very similar smooth and local features as the absolute PRF phase change images (|angle(u/u₀)|) and PRF temperature change images (PRF(u/u₀)), illustrating that the proposed complex difference based CS method is able to constrain PRF temperature related features. The magnitude difference in percent ratio image shows that changes of image magnitudes can be found with the changes of in vivo temperature in this study. It should be noted that the anatomic SNR of the forearm in the post-heating image is about 55, and thus the peak PRF SNR of this study is generally smaller than 385.

Figure 4.

(a) Fully-sampled magnitude and phase of the post-heating and baseline images, and (b) their corresponding absolute phase change images, PRF temperature change images, complex difference magnitude images, and magnitude difference ratio images (in percent), all from the multi-slice in vivo forearm heating study. The slight-motion-induced mis-registration artifacts are denoted with white arrows.

Figure 5.

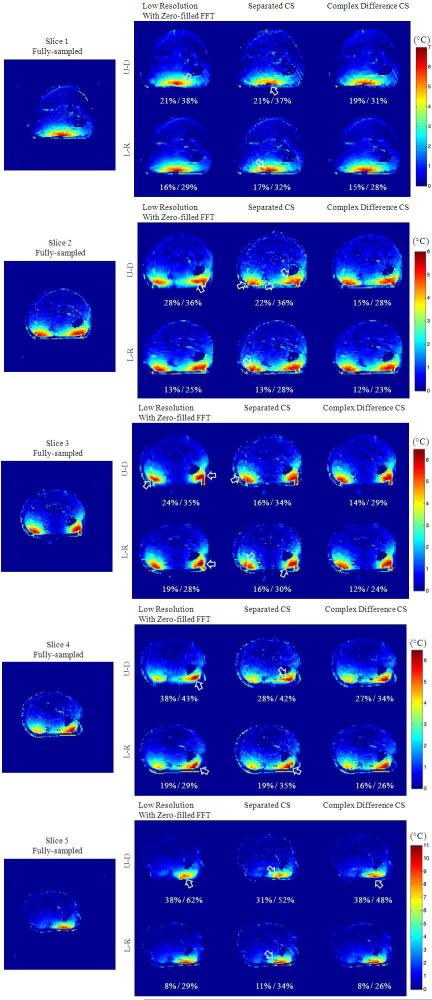
Reconstruction results from undersampled k-space dataset for in vivo human forearm heating. Results here demonstrate improved accuracy and volumetric robustness of the proposed method by using different undersampling directions (Left-Right and Up-Down) of the same Cartesian trajectory and different reconstruction methods on all five imaged slices. Visible differences from fully-sampled case are denoted with white arrows. The RMSEs are shown below each error images for peak temperature error and global temperature error (peak / global). These slices correspond to slices 1~5 in Fig. 4.

The robustness of the proposed method on different 2D imaging slices with a variety of temperature change patterns is demonstrated in Fig. 5. For almost all cases, the proposed method shows markedly improved temperature features (indicated with arrows) compared to low resolution with zero-filled FFT as well as separated CS. The temporal resolution would be improved from about 1.83 s/°C to 0.46 s/°C with R = 4 undersampling with the proposed method. The only exception found is with undersampling in the U-D direction for slice 5, where the proposed method is not as clearly advantageous. This is probably because the peak temperature increase was located at the skin, separated by PRF-insensitive fat from the muscle, and such local PRF phase change of the skin was severely corrupted by the fat when undersampled in the U-D direction. Therefore, care should be taken when using this method to monitor RF heating at the skin. However, equally poor performance was also found for separated CS and low resolution imaging which could also be affected by fat, and the proposed method shows overall better guarantee for accuracy of the proposed method over the other two methods.

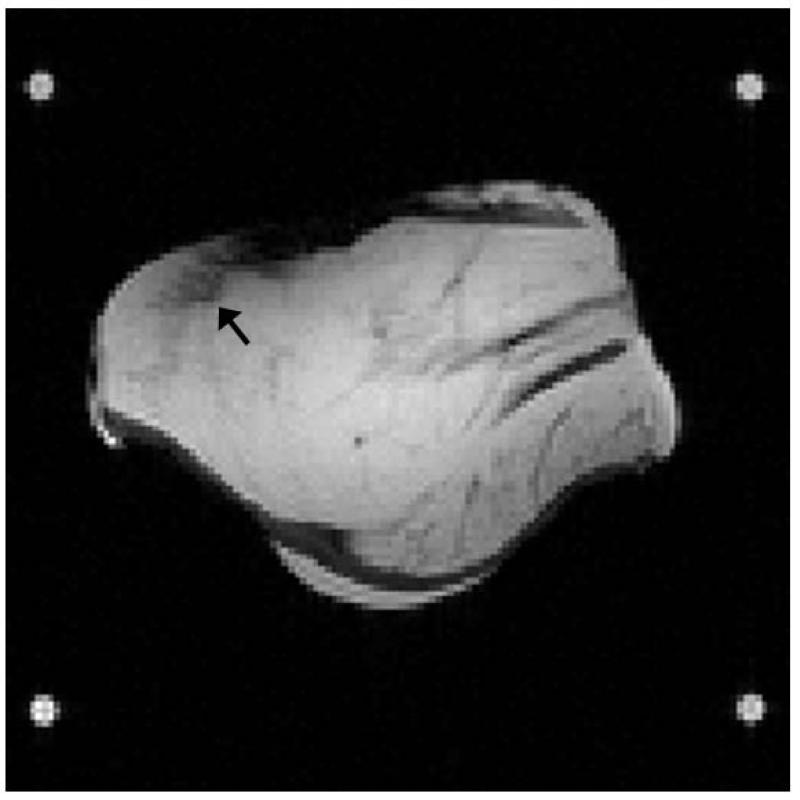
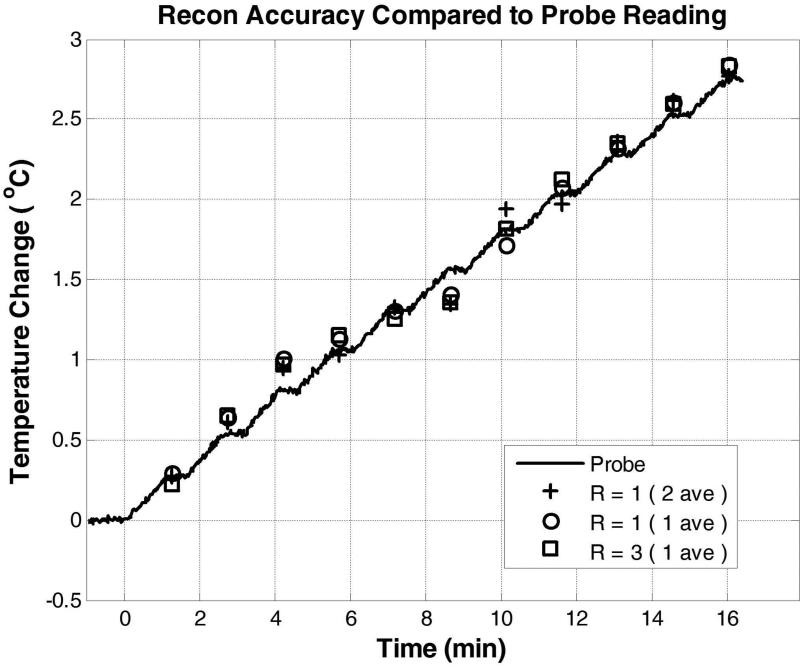
For the ex vivo beef heating study, the magnitude image is shown in Fig. 6 with the location of the inserted temperature probe. The reconstruction accuracy and robustness of the proposed method are demonstrated in Fig. 7 and Table 1. Generally, the proposed method achieved good accuracy for all frames of the dataset, demonstrating its potential usage in temperature monitoring and heating characterization due to RF pulses. As shown in Table 1, the result from the proposed reconstruction method is significantly better than other existing methods such as separated CS and TCR. These results show that, in practice, a lengthening of about 21% of original MR scan time due to additional PRF based RF heating monitoring would be reduced to about 7%, if this reconstruction method is used. The temporal resolution would be improved from about 1.83 s/°C to 0.6 s/°C with R=3 undersampling. It should be emphasized that the dataset was collected with the system body coil having limited anatomic SNR (about 40 for 1 average, and thus the peak PRF SNR of this dataset ranged from 60 of the 3^rd timeframe to 280 of the 7^th timeframe). The method should achieve better reconstruction accuracy when monitoring temperature increase with more closely-fitting receive coils. The temporal consistency is further validated with the temperature probe reading shown in Fig 8. Temperature measurement by fully-sampled PRF images achieved very good agreement with the temperature probe reading, especially at large temperature increase and PRF SNR. This validated the accuracy of our correction method for system phase drift to monitor subtle heating. The undersampled PRF temperature readings reconstructed with the proposed method achieved excellent fidelity with the fully-sampled PRF temperature readings, demonstrating again its robustness for temporal consistency.

Figure 6.

Anatomic image from the beef heating study. Black arrow shows the location where a fiber optic temperature probe was inserted.

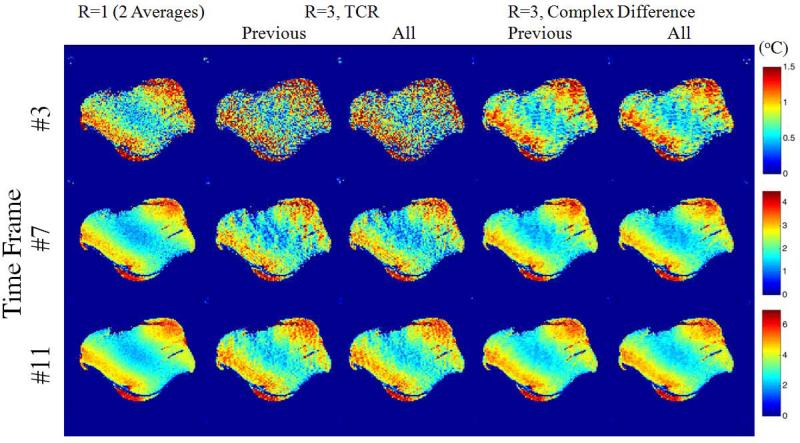
Figure 7.

Reconstructed PRF images with different reconstruction methods from the 12-frame time series. For TCR and Complex Difference, reconstructions using only current and previous time frames (denoted as “Previous”) and using all time frames (denoted as “All”) are reported.

Table 1.

Global RMSEs of the reconstructed PRF images of different time frames from the 12- frame time series. For TCR and Complex Difference, RMSEs for reconstructions using only current time frame (denoted as “Single”), current and previous time frames (denoted as “Previous”), and using all time frames (denoted as “All”) are reported.

Time Frame	R=1 (1 Average)	R=3, Low Resolution	R=3, Separated CS	R=3, TCR		R=3, Complex Difference
				Previous	All	Single	Previous	All
#2	43%	69%	92%	83%	93%	57%	57%	57%
#3	28%	47%	56%	61%	64%	41%	40%	40%
#4	21%	33%	42%	45%	48%	32%	30%	29%
#5	16%	30%	35%	38%	41%	26%	25%	23%
#6	13%	26%	27%	35%	35%	23%	22%	21%
#7	11%	26%	26%	33%	31%	21%	20%	19%
#8	10%	26%	23%	29%	28%	20%	18%	17%
#9	8.7%	24%	23%	26%	26%	20%	17%	16%
#10	7.5%	24%	23%	25%	23%	17%	16%	15%
#11	6.6%	24%	20%	23%	23%	18%	15%	14%
#12	6.5%	24%	19%	22%	22%	17%	14%	14%

Figure 8.

Evaluation of temporal consistency of the proposed reconstruction method by comparing temperature probe readings with PRF based temperature change values at the location of probe insertion reconstructed with fully-sampled data with 2 averages, fully-sampled data with 1 average, and undersampled data reconstructed by the proposed method with 1 average and R=3. Using the probe reading as the gold standard, the RMSEs of the three cases are respectively, 8.1%, 8.1%, and 7.8%.

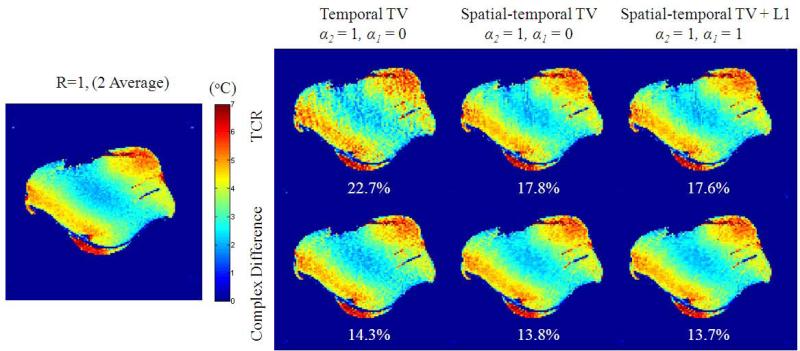
Finally, the proposed reconstruction method is compared with the TCR method on the beef dataset with their different variations, as shown in Fig. 9. These results show clear improvement in reconstruction accuracy of the proposed method compared to all variations of TCR. It should be noted, that because TV_temporal(u_i) = TV_temporal(u_i – u₀), the improvement in reconstruction accuracy in the left column demonstrates the effectiveness by using a fully-sampled baseline image to efficiently exploit sparsity between baseline and post-heating PRF images. From the left to the middle column, the effect of the proposed method in exploiting spatially smooth temperature features with the inclusion of the TV_spatial (u_i – u₀) term is clearly shown. Also, because the spatial temperature increase is predominantly smooth for this dataset, it is expected the inclusion of the complex difference l₁ term would yield little effect.

Figure 9.

Reconstructed temperature change maps and corresponding RMSE for variations of the proposed method and TCR from time frame 11.

Discussion

In this work, we propose, validate, and demonstrate a complex difference constrained CS reconstruction method, for mapping MRI-induced RF heating effects with PRF thermometry by reconstructing the PRF temperature change with constraints on the complex difference from a fully-sampled baseline image. The proposed formalism should provide improved acceleration in situations where the expected temperature is either smooth, local or a combination of both. The effectiveness of the proposed complex difference constrained method is demonstrated in a variety of cases by comparing it with classic and similar existing CS methods for both volumetric coverage and temporal consistency.

Although the TCR algorithm could also be viewed as constraining the complex difference (although only between adjacent time frames), there are major conceptual differences between the proposed formalisms and TCR. The formalism we propose utilizes a more direct relationship between “PRF temperature” (approximated by complex difference) and the collected k-space data. This encoding relationship has been demonstrated to be highly compressible and efficient in promoting sparsity (Fig 2). Utilization of complex difference based cost functions is also shown to be more capable in directly constraining the smooth and local features of the target temperature maps than TCR (Fig. 4, 7 and 9). Although |u-u₀| shows similar smooth and local features as the target PRF temperature map, it cannot be directly converted to the accurate PRF image, and therefore there is need to further reconstruct u, which becomes possible with the availability of the baseline image u₀. These important features together are shown to be effective for improving volumetric coverage and temporal resolution for temperature measurement. Fortuitously, the method is also expected to reduce off-resonance induced image distortion artifacts of fast EPI-based PRF thermometry methods (18) proposed to accomplish similar goals for temperature based RF safety assurance as our work.

It should be noted that although the proposed method is completely different in design principle compared to TCR, they share similar formalism and thus several aspects of the proposed complex difference constrained method not fully evaluated here can be expected to be very similar to TCR. These include determination for optimal number of CG iterations and optimal weighting coefficients for each terms of the cost function. However, these are general issues of the CS formalism (23), and we have tested the method with the same set of parameters and found them robust for all the datasets. Finally, it is expected that the proposed method can be combined with parallel imaging for further acceleration if large volumetric coverage is needed (24). Parallel imaging may also help decrease the scanning time of the baseline image.

It should also be pointed out that complex difference approximated PRF phase shift could be weighted by tissue anatomical features and RF coil field inhomogeneities, especially when the heating pattern is vastly diffusive, and a large RF coil is used for transmission or reception. Based on the ex vivo heating dataset, the proposed method still out-performed other existing methods. Although a phase difference constrained approach could potentially exploit smooth temperature features more uniquely without other anatomical or coil field weightings, direct constraint of PRF phase shift may be challenged by phase wrapping, non-linear relationship between phase and collected k-space data, and temperature related magnitude changes. We believe this work has laid out a good foundation to explore and compare possible phase difference constrained methods in the future.

Another potential limitation of the proposed method for temperature based RF heating evaluation is that it is based on conventional PRF implementation, which requires baseline images be collected, and would thus be generally sensitive to motion. However, for valuation of mild temperature changes due to MRI induced RF heating, baseline images are indispensible for phase drift correction. We have demonstrated the utility of this approach in realistic situations and saw no detrimental effects from slight motion (in vivo forearm heating) and the phase correction was shown to be successful over a long heating period (ex vivo beef heating). Application of the method to the torso may present challenges due to motion that warrants further investigation. Motion effects could perhaps be corrected by co-registration, or utilization of a library of baseline images collected from a full physiology cycle with the aid of triggering and navigation (35).

Conclusion

In this work, we propose a novel CS reconstruction method for PRF temperature mapping based on the complex difference between the post-heating and baseline images. Representation in complex difference space increases sparsity and removes shared aliasing artifacts, which enables higher accelerations than existing methods as demonstrated in simulations, ex vivo, and in vivo experiments. The method is quite general that its application may not be restricted to mild heating and could provide rapid temperature feedback in ensuring RF safety for high field MRI scanners.