Significance
The solvation free energy of a molecule includes the free energy required to remove solvent from what will become the molecular interior and the free energy gained from dispersive interactions between the solute and solvent. Traditionally, these free energies have been assumed to be proportional to the surface area of the molecule. However, we computed these free energies for a series of alkanes and four configurations of decaalanine and showed that although these free energies were linear in the surface area for each set of molecules, each atom’s contributions to these energies depended on correlations with its surrounding atoms. The atomic contributions to these energies were therefore not additive. This finding suggests that most current hydrophobic models are unsatisfactory.
Keywords: hydration, free energy of solvation
Abstract
Inserting an uncharged van der Waals (vdw) cavity into water disrupts the distribution of water and creates attractive dispersion interactions between the solvent and solute. This free-energy change is the hydrophobic solvation energy (ΔGvdw). Frequently, it is assumed to be linear in the solvent-accessible surface area, with a positive surface tension (γ) that is independent of the properties of the molecule. However, we found that γ for a set of alkanes differed from that for four configurations of decaalanine, and γ = −5 was negative for the decaalanines. These findings conflict with the notion that ΔGvdw favors smaller A. We broke ΔGvdw into the free energy required to exclude water from the vdw cavity (ΔGrep) and the free energy of forming the attractive interactions between the solute and solvent (ΔGatt) and found that γ < 0 for the decaalanines because −γatt > γrep and γatt < 0. Additionally, γatt and γrep for the alkanes differed from those for the decaalanines, implying that none of ΔGatt, ΔGrep, and ΔGvdw can be computed with a constant surface tension. We also showed that ΔGatt could not be computed from either the initial or final water distributions, implying that this quantity is more difficult to compute than is sometimes assumed. Finally, we showed that each atom’s contribution to γrep depended on multibody interactions with its surrounding atoms, implying that these contributions are not additive. These findings call into question some hydrophobic models.
Many techniques in computational biophysics require the computation of free-energy differences. However, directly computing these free-energy differences with quantum or classical molecular dynamics (MD) methods has proven challenging because doing so requires long simulation times. To make such computations more tractable, techniques have been developed based on the observation that these free-energy changes could be computed by combining estimates of the changes in vacuum, where they are usually easier to compute, with estimates of the solvation energies (ΔG) of the initial and final states (1, 2).
One common technique for computing ΔG is to break it into electrostatic (ΔGel) and hydrophobic (ΔGvdw) terms (3, 4). In this breakdown, ΔGvdw is the free energy required to place an uncharged van der Waals (vdw) cavity into solution, and ΔGel is the free energy of charging the cavity once it has been placed into solution. Several techniques, including the Poisson–Boltzmann equation (5), the generalized Born model (6), structured continuum approaches (7–9), and integral equation methods (10), have been developed to compute ΔGel. In the present study, we continue a study of ΔGvdw begun previously (11–13).
Many models have been constructed to compute ΔGvdw. The first of these models, and perhaps the most widespread, is
| [1] |
where γvdw is a positive constant independent of the properties of the molecule and b is the energy of solvating a point-like solute (2, 14–17). This model follows from assuming that ΔGvdw for microscopic cavities should scale with A in the same manner as for macroscopic cavities (18). Alternatively, several studies have pointed out that experimental measurements often are not consistent with Eq. 1 (19–27). These studies have argued that ΔGvdw should be split into purely repulsive (ΔGrep) and attractive (ΔGatt) parts:
| [2] |
Often, this breakdown follows that of Weeks et al. (19) and Chandler et al. (20). These studies usually then proceed to assume that ΔGrep is a linear function of A or the molecular volume (V),
| [3] |
| [4] |
| [5] |
where γrep and ρrep are positive constants independent of the properties of the molecule. Studies (28–31) have argued that ΔGrep should obey Eq. 3 for large solute molecules, Eq. 4 for small solutes, and Eq. 5 in a cross-over regime. Alternatively, one could construct other functional forms that would approach Eqs. 3 and 4 in the appropriate limits, such as
| [6] |
Some researchers (23, 24, 27) have then estimated ΔGatt by integrating over approximate solvent densities:
| [7] |
where this average was taken over , an approximate solvent distribution, and Uatt was the attractive dispersive interaction energy between the solute and solvent, as described in Materials and Methods.
In three previous studies, we obtained computational results that appeared to contradict some common expectations of ΔGvdw (11–13). For example, the idea that ΔGvdw drives the initial collapse during protein folding by opposing the formation of cavities in the solvent with an energy penalty that increases with A has frequently been discussed (2, 32, 33). However, in the first of our studies (11), where we computed ΔGvdw for a series of glycine peptides ranging in length from 1 to 5 monomers, we found that although ΔGvdw was linear in the number of monomers, as would be expected if it scaled with A, ΔGvdw was negative and decreased with the number of monomers, seemingly implying that γvdw was negative. In the second of our studies (12), we computed ΔGvdw for a set of decaalanine conformations and found that ΔGvdw was negative for these peptides as well. Finally, in the third study (13), we computed ΔGvdw for a series of alanine peptides ranging in length from 1 to 10 monomers, with the peptides either held in fixed, extended conformations or allowed to assume a normal distribution of conformations. We once again found that ΔGvdw was negative, and it decreased with the number of monomers when the peptides were held in extended conformations but increased with the number of monomers when the peptides were allowed to adopt a normal distribution of conformations.
To better understand these findings, here we computed with free-energy perturbation (FEP) (34, 35) not just ΔGvdw but also ΔGrep and ΔGatt for four conformations of decaalanine from a previous study (12) and a series of alkanes that has been examined in the literature (22). As discussed below, none of Eqs. 1 and 3–7 are consistent with our data. Each atom’s contributions to ΔGrep, ΔGatt, and ΔGvdw appear to depend on their chemical surroundings and the geometry of the molecular surface. We do not know of a theory that can explain the calculations presented here.
Results
In Table 1 ΔGrep, ΔGatt, and ΔGvdw are shown. As expected, ΔGrep and ΔGatt were highly correlated with A, and ΔGvdw was highly correlated with A for the decaalanine conformers. The significantly weaker correlation between ΔGvdw and A for the alkanes may be attributable to the small range of ΔGvdw for these molecules, about 2.0 kcal/mol. Estimates of γrep, γatt, and γvdw from least-squares fits between these energies and A are shown in Table 1, along with the Pearson’s correlation coefficients (R2) of these fits. Plots of ΔGrep, ΔGatt, and ΔGvdw against A are shown in SI Appendix, Figs. S2 and S3.
Table 1.
FEP estimates of ΔGrep, ΔGatt, and ΔGvdw and statistics of linear regressions between either ∂ΔGrep/∂xi or ∂ΔGatt/∂xi and ∂A/∂xi
| Molecule | A, Å2 | V, Å3 | ΔGrep | ΔGatt | ΔGvdw | Perturbative data | |||||
| R2 | R2 | ||||||||||
| Decaalanines | |||||||||||
| d | 1,510 | 3,084 | 94.22 | −71.05 | −71.49 | −86.58 | 23.17 | 46 | 0.83 | −19 | 0.43 |
| d1 | 1,172 | 2,670 | 79.49 | −54.91 | −50.57 | −68.46 | 24.58 | 44 | 0.84 | −21 | 0.25 |
| d2 | 1,267 | 2,797 | 83.77 | −59.76 | −55.02 | −73.96 | 23.01 | 44 | 0.82 | −21 | 0.29 |
| d3 | 1,424 | 2,994 | 90.47 | −67.10 | −60.28 | −83.32 | 23.37 | 42 | 0.81 | −28 | 0.30 |
| γ | 43 | −48 | −56 | −62 | −3 | ||||||
| R2 | 1.00 | 0.97 | 0.91 | 0.91 | 0.96 | ||||||
| Alkanes | |||||||||||
| Methane | 195 | 253 | 6.73 | −4.24 | −4.10 | −4.22 | 2.49 | 45 | 1.00 | −3 | 0.99 |
| Ethane | 236 | 331 | 9.33 | −6.76 | −6.47 | −6.84 | 2.57 | 47 | 0.99 | −5 | 0.84 |
| Propane | 272 | 403 | 11.64 | −8.97 | −8.60 | −9.19 | 2.67 | 50 | 0.97 | −8 | 0.85 |
| Butane | 305 | 471 | 14.10 | −11.02 | −10.56 | −11.37 | 3.08 | 52 | 0.96 | −10 | 0.77 |
| Pentane | 339 | 542 | 16.58 | −12.99 | −12.33 | −13.43 | 3.59 | 51 | 0.94 | −11 | 0.69 |
| Hexane | 371 | 609 | 18.52 | −14.97 | −14.25 | −15.67 | 3.55 | 51 | 0.95 | −11 | 0.66 |
| Isobutane | 301 | 467 | 13.82 | −10.87 | −10.40 | −11.20 | 2.95 | 53 | 0.97 | −11 | 0.85 |
| 2-Methylbutane | 330 | 530 | 16.35 | −12.73 | −12.16 | −13.23 | 3.62 | 53 | 0.95 | −13 | 0.72 |
| Neopentane | 323 | 521 | 14.93 | −12.56 | −10.85 | −10.83 | 2.37 | 57 | 0.98 | −17 | 0.90 |
| Cyclopentane | 308 | 483 | 14.34 | −12.43 | −10.86 | −10.71 | 1.91 | 51 | 0.91 | −12 | 0.68 |
| Cyclohexane | 331 | 537 | 16.16 | −14.13 | −12.15 | −12.11 | 2.03 | 49 | 0.89 | −14 | 0.54 |
| γ | 69 | −64 | −58 | −62 | 5 | ||||||
| R2 | 0.99 | 0.97 | 0.99 | 0.97 | 0.16 | ||||||
| ρ | 33 | −31 | −28 | −30 | 2 | ||||||
| R2 | 0.99 | 0.98 | 0.99 | 0.95 | 0.14 | * | |||||
All energies (ΔGrep, ΔGatt, , , and ΔGvdw) are in units of kcal/mol. All surface tensions (γ, , and ) are in units of cal/mol per Å2. All ρ are in units of cal/mol per Å3.
As a test of the convergence of ΔGrep and ΔGatt for the alkanes and ΔGrep for the decaalanines, we compared the estimates obtained from forward FEP to those obtained from backward FEP. To test the convergence of ΔGatt for the decaalanines, we computed estimates from simulations that were half as long. To compute ΔGvdw for the decaalanines, we combined ΔGrep computed with forward FEP with ΔGatt from the longer simulations. To compute ΔGvdw for the alkanes, we combined estimates of ΔGrep and ΔGatt obtained from forward FEP. The energies given by the presumably less accurate calculations differed by at most 0.57 kcal/mol from those given by the more accurate simulations. Additionally, our estimates of ∂ΔGrep/∂λ and ∂ΔGatt/∂λ varied smoothly with λ, indicating that our results were converged. Plots of ∂ΔGrep/∂λ and ∂ΔGatt/∂λ versus λ for one of the decaalanine conformations are shown in SI Appendix, Fig. S1, and the other estimates of ΔGrep, ΔGatt, and ΔGvdw are shown in SI Appendix, Table S1. The estimates of ΔGrep, ΔGatt, and ΔGvdw for the alkanes were in good agreement with results reported elsewhere (22).
In agreement with our previous studies (12, 13), γvdw < 0 for the decaalanines. By breaking ΔGvdw into ΔGrep and ΔGatt we saw that γvdw was negative because, although increasing the surface area led to increasingly unfavorable ΔGrep (γrep > 0), this energy penalty was more than offset by the increasingly favorable attractive interactions between the solute and solvent (γatt < 0, and −γatt > γrep.).
As shown in Table 1, γatt for the alkanes differed from that for the decaalanines. This finding is in agreement with previous studies that ΔGatt is not a simple function of A (19–27), and it implies that ΔGvdw ≡ ΔGatt + ΔGrep is also probably not a simple function of A. Attempting to estimate ΔGvdw with a single γvdw independent of the other properties of the molecule is probably not possible.
For the alkanes both linear response theory (LRT) and the single-step perturbation (SSP) methods yielded acceptable estimates of ΔGatt, and for the decaalanines LRT yielded estimates that were within 10 kcal/mol of the results given by FEP (1). However, SSP yielded clearly worse estimates of ΔGatt for the decaalanines, and both methods overestimated γatt for the decaalanines by more than 5 cal/mol per Å2. These findings imply that SSP may not give good estimates of ΔGatt for some systems. Instead, the change in the water distribution that occurs when the dispersive interactions are turned on would need to be taken into account. Additionally, the decaalanines examined here were smaller than many systems of interest in biophysical problems (e.g., globular proteins). Further work will be needed to determine whether these conclusions hold for larger biomolecules. Plots of and versus A are shown in SI Appendix, Fig. S2.
Table 1 also shows that γrep for the decaalanines differed significantly from γrep for the alkanes. This observation implies that even if a theory were created that could predict ΔGatt, estimating ΔGrep by assuming that it is linear in A with a surface tension that is independent of the properties of the molecule may not be possible.
Perturbative Derivative Calculations.
We used Eqs. 19 and 20 to investigate how small changes in atomic coordinates affect ΔGatt and ΔGrep, and we plotted the resulting derivatives against ∂A/∂xi. If ΔGrep and ΔGatt were simply linear functions of A, the slopes of the resulting least-squares lines would provide perturbative estimates, and , of γrep and γatt. Table 1 lists and for the molecules in this study, along with the R2 of the related least-squares lines. SI Appendix, Fig. S6 is a plot of ∂ΔGatt/∂xi versus ∂A/∂xi for the decaalanine conformations, and SI Appendix, Fig. S7 includes plots of ∂ΔGrep/∂xi and ∂ΔGatt/∂xi versus ∂A/∂xi for the alkanes.
The data in Table 1 show that for any of the systems in this study, and in general ∂ΔGatt/∂xi, with a few exceptions, was not strongly correlated with ∂A/∂xi. These findings may indicate that ΔGatt is not truly a simple linear function of A but instead must be computed with a more robust theory, as discussed in several previous studies (19–27).
To ensure that the estimates of ∂A/∂xi used to generate Table 1 were accurate, finite difference estimates of these derivatives were computed by moving each atom by 0.0001 A in each direction. The finite difference estimates of these derivatives were nearly identical to those given by PROGEOM (R2 > 0.99999, and the slopes of the least-squares lines were between 0.99 and 1.01). To check that ∂ΔGrep/∂xi and ∂ΔGatt/∂xi had converged, the estimates used to generate Table 1 were compared with estimates obtained by using only the first halves of the trajectories. The results from this second computation were nearly identical to those used to construct Table 1 (R2 > 0.99, with slopes between 0.96 and 1.03).
Additionally, for the alkanes (Table 1). In combination with the observation that γrep for the alkanes differed from that of the alkanes, this observation appears to imply that ΔGrep is not a simple linear function of A.
As can be seen in Table 1, for the decaalanines, but the correlation between ∂ΔGrep/∂xi and ∂A/∂xi (R2 ∼ 0.85) was weaker than that between ΔGrep and A (Table 1 and Fig. 1B). This weaker correlation could indicate that the good correlation between A and ΔGrep observed in Table 1 may be attributable to cancellations among small deviations from linearity. This observation may have implications for applications where the changes in ΔGrep arising from small perturbations of a structure, such as the rotation of a side chain or the addition or deletion of a few atoms, are estimated. Predicting such free-energy changes by simply assuming that changes in ΔGrep, ΔGatt, or ΔGvdw should be proportional to changes in A may not be accurate.
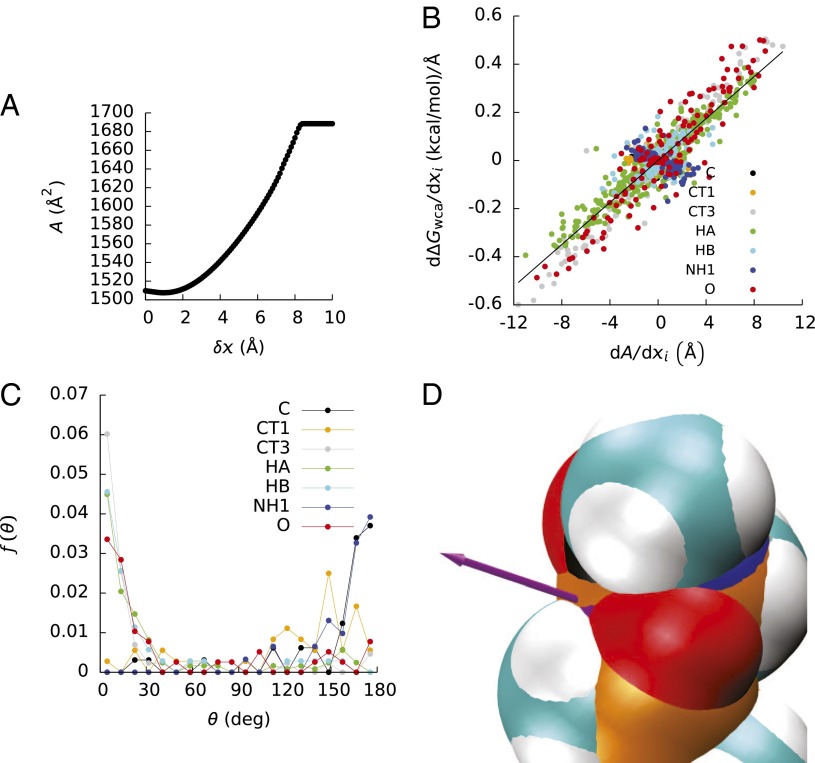
Fig. 1.
(A) Solvent-accessible surface area (A, a) of the decaalanine d as a function of the displacement (δx) of atom 15 along the vector (−∇iA) in which A, a would decrease as rapidly as possible. (B) Derivatives (∂ΔGrep/∂xi) of the repulsive component (ΔGrep of the energy required to create a vdw cavity with respect to the atomic coordinates (xi) as a function of the derivatives ∂A/∂xi for all atoms in the four decaalanines. The points are colored by the atom types in the CHARMM force field. (C) Probability densities (f) of the angle (θ) between ∇iA and ∇iΔGrep. (D) View of part of the solvent-accessible surface of the decaalanine d. The solvent-accessible surface area of atom 15 (a carbonyl carbon) is the small purple patch near the base of the purple arrow, which points in the direction of −∇iA for this atom. Atoms of type C (except for atom 15) are colored black, atoms of type CT1 are colored orange, atoms of type NH1 are colored dark blue, and all other atom types have the default coloring in the VMD molecular viewing program (36).
Fig. 1B shows that for four of the atom types in the decaalanines (CT3, HA, HB, and O, corresponding to the β-C and terminal carbons, the hydrogens that bind to the β-C, the hydrogens that bind to the α-C, and the backbone oxygens, respectively), ∂ΔGrep/∂xi is roughly linear in ∂A/∂xi, although the correlations between these two quantities are not perfect. However, for the atoms of type CT1 (α-C), no clear relationship between ∂ΔGrep/∂xi and ∂A/∂xi was seen, and for atom types NH1 (backbone nitrogen) and C (carbonyl carbon), ∂ΔGrep/∂xi actually appeared to decrease with increasing ∂A/∂xi. These findings are confirmed in Fig. 1C, where the probability densities (f) of the angles (θ) between the vectors ∇iA and ∇iΔGrep, where ∇i = (∂/∂xi, ∂/∂yi, ∂/∂zi) and (xi, yi, zi) were the coordinates of the center of atom i, are plotted as functions of θ. Although f(θ) was peaked at 0° for atom types CT3, HA, HB, and O, f(θ) was peaked at 180° for atom types NH1 and C, and f(θ) had no clear peak for atom type CT1.
Atom types CT3, HA, HB, and O all make up significant portions of the decaalanine solvent-accessible molecular surface (Fig. 1D), and they typically have a single, continuous solvent-accessible surface patch. Moving these atoms further into the solvent (thereby increasing ΔGrep) should also increase A. Conversely, although atoms of type CT1 have large solvent-accessible regions, these regions are broken up into several separate patches. Moving these atoms in one direction may increase the sizes of some of these patches while decreasing the sizes of others. This more complicated surface geometry probably explains why θ was not strongly peaked for the CT1 atoms. In contrast, atom types NH1 and C typically only have small patches of solvent-accessible surface. If such a patch lies at the bottom of a deep depression on the molecular surface, then moving the corresponding atom further into the solvent may increase its solvent-accessible surface area but may actually decrease A by burying solvent-accessible areas of neighboring atoms. An example of such an apparent anomaly is seen in Fig. 1D, where the solvent-accessible surface area of the carbonyl carbon of the second residue in one of the decaalanines (d) is shown, along with a vector pointing in the opposite direction of ∇iA. Moving this atom in this direction initially decreases A (Fig. 1A), but after moving this atom in this direction by about 1 A, further motion of the atom in this direction would increase A. Apparently, whether ΔGrep will increase and at what rate when an atom is moved depends not just on the change in A but on the arrangement of neighboring atoms and the local geometry of the molecular surface. In turn, because ΔGrep appears to depend on multibody interactions, the atomic contributions to ΔGrep do not appear to be additive.
Considering the Molecular Volume as a Confounding Variable.
As shown above, γrep for the decaalanines differed from that for the alkanes, , and for some atom types in the decaalanines ∂ΔGrep/∂xi was not linear in ∂A/∂xi. These observations imply that ΔGrep is not a function only of A, but at first glance they might appear to be consistent with the idea that ΔGrep is a function (f(A, V)) of A and V, approaching Eq. 3 for large molecules and Eq. 4 for small molecules, as has been widely discussed (28–31). However, for the systems presented here V is very nearly linear in A,
| [8] |
where α = 2.3 Å and c = −216 Å3 are fit constants, R2 = 0.998, and δ is a function of the coordinates of the atomic centers, defined by Eq. 8. Thus, the problem of fitting these data against models that contain both A and V, such as Eqs. 5 and 6, is not well-posed. However, we do feel that the results in this study, combined with Eq. 8, can be used to place constraints on a putative f(A, V).
Eq. 8 implies
| [9] |
Plots of ∂V/∂xi versus ∂A/∂xi yielded estimates of α = 2.0 for the alkanes, 2.2 for the decaalanines, and 2.1 when the two data sets were considered together. The R2 of the least-squares lines were 0.97, 0.75, and 0.84.
If ∂f/∂A, ∂f/∂V, and ∂δ/∂A do not change significantly for a data set and ΔGrep = f(A, V), then the slope of a plot of ΔGrep versus A will be
| [10] |
| [11] |
For the data in the present study, δ had no clear dependence on A.
Eq. 11, combined with the observations that γrep for the alkanes differed from that for the decaalanines and that δ has no clear dependence on A, leads us to conclude that if ΔGrep = f(A, V), then f(A, V) cannot be a linear function of some combination of A and V, as in Eq. 5, because then ∂f/∂A and ∂f/∂V would be equal in the two data sets and thus their γrep would be equal.
Next, note that
| [12] |
From Eqs. 11 and 12, we see that if ΔGrep = f(A, V) is simply a function of A and V, ∂f/∂A, ∂δ/∂A, and ∂f/∂V do not change much for a set of molecules, and Eq. 8 holds for that set of molecules, the least-squares line of a plot of ΔGrep versus A should have the same slope as one for a plot of ∂ΔGrep/∂xi versus ∂A/∂xi. However, for the alkanes, and for some of the atom types in the decaalanines ∂ΔGrep/∂xi was not even linear in ∂A/∂xi. We are therefore left with two possibilities: either ΔGrep cannot be written as a function of only A and V; or ∂f/∂A, ∂δ/∂A, and ∂f/∂V are not roughly constant for each of the two molecular sets examined here but vary in some way that allows the slopes of the two plots to be different but still maintain apparent linear relationships between ΔGrep and A, and ∂ΔGrep/∂xi and ∂A/∂xi.
Discussion
In this study, we computed the solvation free energy (ΔGvdw) of an uncharged vdw cavity into water by computing ΔGrep and ΔGatt for a series of alkanes and four configurations of decaalanine. As expected, ΔGatt and ΔGrep were linear in A for both the decaalanines and the alkanes, and ΔGvdw was linear in A for the decaalanines. Although the correlation between ΔGvdw and A was weak for the alkanes, this poor correlation could be attributable to insufficiently accurate estimates of ΔGrep and ΔGatt and the geometric contributions of the branched alkanes.
We found that γvdw < 0 for the decaalanines. This finding seems to indicate that whether ΔGvdw favors extended or compact conformations is system dependent. Repeating these calculations with larger and bulkier peptide side chains could provide insight into why such residues are usually buried in protein interiors. The current finding is, however, in agreement with our findings in earlier studies (11, 13) that ΔGvdw became increasingly negative as the number of monomers was increased for glycine and alanine peptides. By dividing ΔGvdw into ΔGrep and ΔGatt we found that γvdw < 0 for the decaalanines because, although increasing A increases the cost of excluding the water (γrep > 0), this cost is more than compensated for by the increased favorable dispersive interactions between the water and the peptide (γatt < 0, and −γatt > γrep).
Our analysis also allowed us to test the simple theories of hydrophobic solvation listed in the Introduction. Although ΔGvdw generally increased with A for the alkanes, γvdw < 0 for the decaalanines. In combination with the observation that both sets of systems provided different estimates of γrep and γatt, this finding may indicate that Eq. 1 is invalid because the proposed γvdw is not independent of the other properties of the molecule and the details of the correlations with solvent.
Eq. 3 also appears to be inconsistent with our results because the value of γrep obtained for the alkanes differed from that obtained for the decaalanines, also because for the alkanes, and finally because ∂ΔGrep/∂xi was not always linear in ∂A/∂xi. Indeed, for some atom types in the decaalanines ∂ΔGrep/∂xi was linear in ∂A/∂xi, but the slope of the least-squares line was negative. This finding is difficult to explain without taking into account the effects of multibody correlations with neighboring solute atoms, as described in Results. Although ΔGrep was linear in A for both the alkanes and decaalanines, the idea that ΔGrep can be computed for molecular-scale cavities with a single, universal surface tension is probably invalid.
Although these results demonstrate that ΔGrep is not simply a linear function of A (Eq. 3) for these molecules, they may at first glance appear to be consistent with the idea that ΔGrep is actually a function of both A and V (f(A, V)). However, as we discussed in Results, V was nearly linear in A for the systems in this study, so unambiguously fitting against models similar to those in Eqs. 5 and 6 was not a well-posed problem. Additionally, the linear dependence of V on A combined with the observations that γrep for the alkanes differed from that of the decaalanines, that for the alkanes, and that for some of the atom types in the decaalanines ∂ΔGrep/∂xi was not linear in ∂A/∂xi places strong constraints on the form of any such function f(A, V). In particular, models of the form in Eq. 5 are not consistent with these results.
Finally, our results indicate that even if ΔGrep were given, ΔGvdw might be difficult to compute because Eq. 7 cannot be used to compute ΔGatt for the decaalanines. Although SSP theory could predict ΔGatt for the alkanes, regardless of whether the initial or final water distributions were considered, it could not do so for the decaalanines. Instead, the change in water distributions between the initial and final states had to be considered.
In conclusion, we found that none of ΔGrep, ΔGatt, and ΔGvdw were simple functions of A and V over a range of alkanes and decaalanine conformers. Instead, these free energies appear to depend on multibody interactions with their neighboring atoms, the shape of the molecular interface, and on subtle changes in the water density surrounding the molecule when the attractive interactions are turned on. A successful hydrophobic theory will have to account for these interactions, and Eqs. 1 and 3–7 do not appear to be consistent with these findings.
Materials and Methods
All MD simulations were run with a modified version of NAMD (nanoscale molecular dynamics) 2.9 (37). SHAKE was used to constrain the hydrogens. All simulations used the TIP3P (transferable intermolecular potential 3 point) water model modified for use with the CHARMM (chemistry at Harvard macromolecular mechanics) force field (38, 39), a constant temperature of 300 K, a constant pressure of 1 atm, periodic boundary conditions, particle mesh Ewald for the electrostatics, and a 2-fs time step (37). All A, V, and their derivatives with respect to the atomic coordinates were computed with the ALPHASURF program in the PROGEOM package (40), modified to weight each atom by 1. The solvent-accessible surface as defined by Lee and Richards was used (41), with the vdw radii taken from the CHARMM 22 force field for alanine and from the parameters used by Gallicchio et al. for the alkanes (22). A probe radius of 1.7682 Å was used rather than the normal choice of 1.4 Å because it was the radius of the oxygen atom in the water model. This choice also led to slightly better correlations between ΔGrep and A.
Structure Preparation.
The decaalanine structures were taken from a previous study (12). The structures we used were identified in that study as extended (d), denatured 1 (d1), denatured 2 (d2), and denatured 3 (d3). The parameters for the decaalanines were taken from the CHARMM 22 force field (38), and the parameters for the alkanes were taken from a previous study (22). The atoms of the decaalanines were fixed during all simulations. The alkanes were created in ideal configurations and allowed to move freely during the calculations of ΔGrep and ΔGatt. For the simulations from which ∂ΔGrep/∂xi and ∂ΔGatt/∂xi were computed, the configurations of the alkanes were fixed in the configurations obtained after minimization and equilibration in the initial and final frames of the computation of ΔGatt. Because we were not concerned with electrostatics in these calculations, all simulations were run with uncharged solutes.
Free-Energy Definitions.
We defined ΔGrep as the free-energy difference between a system where the solute did not interact with the water and one where the interaction potential was given by the repulsive part of the Weeks–Chandler–Andersen decomposition (19, 20) of Uvdw:
| [13] |
where εij is the well depth and the location of the minimum of Uvdw. The energy difference between a system where the interaction potential between the solute and the water was Urep and a system where it was Uvdw then gave ΔGatt. This process can also be considered to be the addition of an attractive potential (Uatt ≡ Uvdw − Urep) to a system where the interaction energy between the solute and the solvent was Urep. We then defined ΔGvdw ≡ ΔGrep + ΔGatt. For this process of first creating the repulsive cavity and then turning on the attractive potential, ΔGatt, ΔGrep, and ΔGvdw are all well-defined.
Free-Energy Calculations.
We computed ΔGrep and ΔGatt by backward and forward FEP (34, 35). Although FEP estimates of solvation free energies converge more rapidly if they are performed by inserting the particle (42, 43), the differences between the results obtained with backward and forward FEP provide rough estimates of the errors in the calculations. In FEP a desired free-energy difference is computed by linking the initial and final states with a coupling parameter λ to create a λ-dependent potential (U(λ)), where U(0) is the interaction potential between the solute and the solvent in the initial state and U(1) is the interaction potential in the final state. For the computation of ΔGrep U(0) = 0, U(1) = Urep, and if then
| [14] |
For the computation of ΔGatt, U(0) = Urep, U(1) = Uvdw, and
| [15] |
For the computation of ΔGrep for the alkanes, λ-space was divided into 100 equally spaced windows. First, each configuration of decaalanine was placed in a water box and underwent 5,000 steps of minimization with the solute atoms fixed. These structures were then equilibrated at each λ-value. During this equilibration, the temperature of the solute was raised from 25 to 300 K in increments of 25 K with simulations of 2 ps at each temperature. Production simulations of 10 ps were run at each λ-value. Snapshots were taken every 0.2 ps, and these frames were used in the FEP calculations. For the computation of ΔGatt for the alkanes, λ-space was divided into 20 equally spaced windows, and equilibrated structures at each λ value were generated as before. Simulations of 200 ps were then run at each λ-value. Snapshots were taken every 2 ps.
For the computation of ΔGatt for the decaalanines, λ-space was divided into 20 equally spaced windows, and equilibrated structures were obtained at each λ-value as described above. Simulations of 10 ps were then run at each λ-value. Snapshots were taken every 0.2 ps, and these frames were used in the FEP. These simulations were then repeated but run for 20 ps at each λ-value to verify that the original simulations had converged. For the computation of ΔGrep for the decaalanines, λ-space was initially divided into 20 equally spaced windows, simulations of 1 ns were run at each λ-value, and snapshots were taken every 0.2 ps. To reach convergence, for any window in λ-space, if the estimate of the free-energy change across this window from forward FEP differed from that given by backward FEP by more than 1.0 kcal/mol divided by the total number of windows, the window was divided into two by inserting a new λ-value in between. This process was iterated until reasonable estimates were obtained. The final estimates of ΔGrep for d used 89 windows, d1 used 93 windows, d2 used 97 windows, and d3 used 115 windows.
LRT and SSP.
The LRT is an approximate method of computing free-energy changes between systems when the perturbing potential is small. In LRT, ΔGatt is estimated by
| [16] |
where the averages are taken over the ensembles defined by Urep and Uatt. If the relative probabilities of different configurations of the system do not change much between these two ensembles, then ΔGatt can be approximated by SSP either by
| [17] |
or
| [18] |
as has been attempted in several studies (23, 24, 27).
The simulations for the LRT and SSP calculations were obtained by running 1-ns simulations in the initial and final ensembles with the same conditions as used for the FEP calculations. Because the values of obtained from Eqs. 17 and 18 should be equal if the assumptions of SSP are valid, either equation could have been used to test the validity of SSP. The values quoted here were obtained from Eq. 18.
Free-Energy Derivatives.
In addition to computing ΔGrep and ΔGatt, we also computed their derivatives with respect to the atomic coordinates (xi). If ΔGrep and ΔGatt are linear functions of either A or V, then these derivatives will be proportional to either ∂A/∂xi or ∂V/∂xi. We computed ∂ΔGrep/∂xi by
| [19] |
where this average was taken in the ensemble defined by Urep. We used LRT to estimate ∂ΔGatt/∂xi:
| [20] |
These derivatives were computed from the same simulations used to compute the LRT and SSP estimates of ΔGatt.
Supplementary Material
Acknowledgments
We thank The Robert A. Welch Foundation (H-0037), the National Science Foundation (NSF) (CHE-1152876), and the National Institutes of Health (GM-037657) for partial support of this work. A portion of this work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant OCI-1053575. In particular, the calculations were performed on the machines at the Texas Advanced Computing Center and Kraken at Oak Ridge National Laboratory.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1406080111/-/DCSupplemental.
References
- 1.Babu CS, Tembe BL. The role of solvent models in stabilizing nonclassical ions. J Chem Sci. 1987;98(3):235–240. [Google Scholar]
- 2.Baldwin RL. Energetics of protein folding. J Mol Biol. 2007;371(2):283–301. doi: 10.1016/j.jmb.2007.05.078. [DOI] [PubMed] [Google Scholar]
- 3.Sharp KA, Honig B. Electrostatic interactions in macromolecules: Theory and applications. Annu Rev Biophys Biophys Chem. 1990;19:301–332. doi: 10.1146/annurev.bb.19.060190.001505. [DOI] [PubMed] [Google Scholar]
- 4.Cramer CJ, Truhlar DG. Implicit solvation models: Equilibria, structure, spectra, and dynamics. Chem Rev. 1999;99(8):2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 5.Grochowski P, Trylska J. Continuum molecular electrostatics, salt effects, and counterion binding—a review of the Poisson-Boltzmann theory and its modifications. Biopolymers. 2008;89(2):93–113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- 6.Bashford D, Case DA. Generalized Born models of macromolecular solvation effects. Annu Rev Phys Chem. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 7.Lounnas V, Pettitt BM, Phillips GN., Jr A global model of the protein-solvent interface. Biophys J. 1994;66(3 Pt 1):601–614. doi: 10.1016/s0006-3495(94)80835-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Makarov V, Pettitt BM, Feig M. Solvation and hydration of proteins and nucleic acids: A theoretical view of simulation and experiment. Acc Chem Res. 2002;35(6):376–384. doi: 10.1021/ar0100273. [DOI] [PubMed] [Google Scholar]
- 9.Lin B, Pettitt BM. Electrostatic solvation free energy of amino acid side chain analogs: Implications for the validity of electrostatic linear response in water. J Comput Chem. 2011;32(5):878–885. doi: 10.1002/jcc.21668. [DOI] [PubMed] [Google Scholar]
- 10.Truchon J-F, Pettitt BM, Labute P. A cavity corrected 3D-RISM functional for accurate solvation free energies. J Chem Theory Comput. 2014;10(3):934–941. doi: 10.1021/ct4009359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hu CY, Kokubo H, Lynch GC, Bolen DW, Pettitt BM. Backbone additivity in the transfer model of protein solvation. Protein Sci. 2010;19(5):1011–1022. doi: 10.1002/pro.378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kokubo H, Hu CY, Pettitt BM. Peptide conformational preferences in osmolyte solutions: Transfer free energies of decaalanine. J Am Chem Soc. 2011;133(6):1849–1858. doi: 10.1021/ja1078128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kokubo H, Harris RC, Asthagiri D, Pettitt BM. Solvation free energies of alanine peptides: The effect of flexibility. J Phys Chem B. 2013;117(51):16428–16435. doi: 10.1021/jp409693p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pierotti RA. A scaled particle theory of aqueous and nonaqueous solutions. Chem Rev. 1976;76(6):717–726. [Google Scholar]
- 15.Stillinger FH. Structure in aqueous solutions of nonpolar solutes from the standpoint of scaled-particle theory. J Solution Chem. 1973;2(2-3):141–158. [Google Scholar]
- 16.Sharp KA, Nicholls A, Fine RF, Honig B. Reconciling the magnitude of the microscopic and macroscopic hydrophobic effects. Science. 1991;252(5002):106–109. doi: 10.1126/science.2011744. [DOI] [PubMed] [Google Scholar]
- 17.Sitkoff D, Sharp KA, Honig B. Accurate calculation of hydration free energies using macroscopic solvent models. J Phys Chem. 1994;98(7):1978–1988. [Google Scholar]
- 18.Young T. An essay on the cohesion of fluids. Phil Trans R Soc. 1805;95:65–87. [Google Scholar]
- 19.Weeks JD, Chandler D, Andersen HC. Role of repulsive forces in determining the equilibrium structure of simple liquids. J Chem Phys. 1971;54(12):5237–5247. [Google Scholar]
- 20.Chandler D, Weeks JD, Andersen HC. Van der waals picture of liquids, solids, and phase transformations. Science. 1983;220(4599):787–794. doi: 10.1126/science.220.4599.787. [DOI] [PubMed] [Google Scholar]
- 21.Ashbaugh HS, Kaler EW, Paulaitis ME. A “universal” surface area correlation for molecular hydrophobic phenomena. J Am Chem Soc. 1999;121(39):9243–9244. [Google Scholar]
- 22.Gallicchio E, Kubo MM, Levy RM. Enthalpy-entropy and cavity decomposition of alkane hydration free energies: Numerical results and implications for theories of hydrophobic solvation. J Phys Chem B. 2000;104(26):6271–6285. [Google Scholar]
- 23.Gallicchio E, Zhang LY, Levy RM. The SGB/NP hydration free energy model based on the surface generalized Born solvent reaction field and novel nonpolar hydration free energy estimators. J Comput Chem. 2002;23(5):517–529. doi: 10.1002/jcc.10045. [DOI] [PubMed] [Google Scholar]
- 24.Zacharias M. Continuum solvent modeling of nonpolar solvation: Improvement by separating surface area dependent cavity and dispersion contributions. J Phys Chem A. 2003;107(26):3000–3004. [Google Scholar]
- 25.Choudhury N, Pettitt BM. On the mechanism of hydrophobic association of nanoscopic solutes. J Am Chem Soc. 2005;127(10):3556–3567. doi: 10.1021/ja0441817. [DOI] [PubMed] [Google Scholar]
- 26.Choudhury N, Pettitt BM. Local density profiles are coupled to solute size and attractive potential for nanoscopic hydrophobic solutes. Mol Simul. 2005;31(6-7):457–463. [Google Scholar]
- 27.Wagoner JA, Baker NA. Assessing implicit models for nonpolar mean solvation forces: The importance of dispersion and volume terms. Proc Natl Acad Sci USA. 2006;103(22):8331–8336. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lum K, Chandler D, Weeks JD. Hydrophobicity at small and large length scales. J Phys Chem B. 1999;103(22):4570–4577. [Google Scholar]
- 29.Huang DM, Chandler D. Temperature and length scale dependence of hydrophobic effects and their possible implications for protein folding. Proc Natl Acad Sci USA. 2000;97(15):8324–8327. doi: 10.1073/pnas.120176397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hummer G, Garde S, Garcıa AE, Pratt LR. New perspectives on hydrophobic effects. Chem Phys. 2000;258(2-3):349–370. [Google Scholar]
- 31.Rajamani S, Truskett TM, Garde S. Hydrophobic hydration from small to large lengthscales: Understanding and manipulating the crossover. Proc Natl Acad Sci USA. 2005;102(27):9475–9480. doi: 10.1073/pnas.0504089102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Meyer EE, Rosenberg KJ, Israelachvili J. Recent progress in understanding hydrophobic interactions. Proc Natl Acad Sci USA. 2006;103(43):15739–15746. doi: 10.1073/pnas.0606422103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ball P. Water as an active constituent in cell biology. Chem Rev. 2008;108(1):74–108. doi: 10.1021/cr068037a. [DOI] [PubMed] [Google Scholar]
- 34.Beveridge DL, DiCapua FM. Free energy via molecular simulation: Applications to chemical and biomolecular systems. Annu Rev Biophys Biophys Chem. 1989;18:431–492. doi: 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
- 35.Straatsma TP, McCammon JA. Computational alchemy. Annu Rev Phys Chem. 1992;43:407–435. [Google Scholar]
- 36.Humphrey W, Dalke A, Schulten K. VMD: Visual molecular dynamics. J Mol Graph. 1996;14(1):33–38, 27–28. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 37.Phillips JC, et al. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26(16):1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.MacKerell AD, Jr, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102(18):3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 39.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79(2):926–935. [Google Scholar]
- 40.Edelsbrunner H, Koehl P. The weighted-volume derivative of a space-filling diagram. Proc Natl Acad Sci USA. 2003;100(5):2203–2208. doi: 10.1073/pnas.0537830100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lee B, Richards FM. The interpretation of protein structures: Estimation of static accessibility. J Mol Biol. 1971;55(3):379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- 42.Pohorille A, Jarzynski C, Chipot C. Good practices in free-energy calculations. J Phys Chem B. 2010;114(32):10235–10253. doi: 10.1021/jp102971x. [DOI] [PubMed] [Google Scholar]
- 43.Levy RM, Gallicchio E. Computer simulations with explicit solvent: Recent progress in the thermodynamic decomposition of free energies and in modeling electrostatic effects. Annu Rev Phys Chem. 1998;49:531–567. doi: 10.1146/annurev.physchem.49.1.531. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.