Short- and long-term effects of unemployment on fertility

Significance

Fertility falls when unemployment rises, but there may be no long-run effect if women simply postpone childbearing. We analyze the effects of unemployment by following fixed cohorts of US-born women defined by their own state and year of birth. We find that a one percentage point increase in the unemployment rate experienced between the ages of 20 and 24 reduces the short-run fertility of women in this age range by six conceptions per 1,000 women. When these women are followed to age 40, a one percentage point increase in the unemployment rate experienced at 20 to 24 is associated with an overall loss of 14.2 conceptions. This larger long-term effect is driven largely by women who remain childless.

Abstract

Scholars have been examining the relationship between fertility and unemployment for more than a century. Most studies find that fertility falls with unemployment in the short run, but it is not known whether these negative effects persist, because women simply may postpone childbearing to better economic times. Using more than 140 million US birth records for the period 1975–2010, we analyze both the short- and long-run effects of unemployment on fertility. We follow fixed cohorts of US-born women defined by their own state and year of birth, and relate their fertility to the unemployment rate experienced by each cohort at different ages. We focus on conceptions that result in a live birth. We find that women in their early 20s are most affected by high unemployment rates in the short run and that the negative effects on fertility grow over time. A one percentage point increase in the average unemployment rate experienced between the ages of 20 and 24 reduces the short-run fertility of women in this age range by six conceptions per 1,000 women. When we follow these women to age 40, we find that a one percentage point increase in the unemployment rate experienced at ages 20–24 leads to an overall loss of 14.2 conceptions. This long-run effect is driven largely by women who remain childless and thus do not have either first births or higher-order births.

Demographers have been examining the effect of economic conditions on fertility for more than a century (1–10). Although some find that fertility is countercyclical (8–10), most studies find procyclical fertility; that is, fertility declines in times of rising unemployment (1–7). These fertility reductions may represent mere postponement of fertility to better times (a tempo effect) or persistent long-term effects on completed fertility, i.e., on the total number of children a woman ever bears (a quantum effect).

Measuring long-term effects requires the analyst to follow the fertility of fixed cohorts of women over time. Tracking cohorts is feasible at the aggregate level of an entire country, but there are few periods of high unemployment to exploit at this level of aggregation, and strong social trends in fertility that may overshadow long-term effects of past economic fluctuations (11–13). An analysis within countries—for example, at the state level—requires accounting for internal migration and immigration, both of which may be affected by economic conditions. For example, women giving birth to third children in California in 1995 may not be the same women who gave birth to second children in California in earlier years.

In this paper, we divide all births to US-born women over the past 35 y into cohorts defined by a mother’s own state and year of birth. Because these mother characteristics are constant over time, we can follow the fertility of these cohorts regardless of where in the United States women subsequently gave birth. This approach provides us with both annual and completed fertility rates at the state level that are not affected by women’s movements or by immigration.^†

Using these data, we first analyze short-run fertility responses to economic fluctuations at the national and state levels, and show that they are similar. We also investigate differences in fertility responses by age group. We then investigate the long-run effects of unemployment fluctuations experienced at various ages on women’s completed fertility and on the probability of remaining childless.

Our birth data come from the US Vital Statistics natality data, and include ∼140 million individual birth records for all births in the United States from 1975 and 2010. These records provide information about the state and date of the child’s birth, gestation length, the age of the mother, and the mother’s own state of birth. In our sample of all live births to US-born women over this period, we focus on the year of conception rather than on the year of birth, because economic conditions at the time of conception likely are more relevant to the decision to have a child. We also treat multiple births as a single conception (i.e., a single fertility choice). Thus, we are counting conceptions that resulted in a live birth. Cohorts are defined using the mother’s own state and year of birth. To obtain rates, we divide conception counts by population estimates that also are constructed at the level of women’s state and year of birth using data from the decennial US Census.

State-level unemployment rates are merged to cohorts’ conception rates at the annual level. Most of our estimates use the weighted average of the unemployment rates in all states in which a cohort gave birth in a given year, with the number of births in each state as weights. Because the number of cohort members giving birth in each state may not be in proportion to the number of cohort members living in each state, we use census data to check on the extent to which the spatial distribution of births reflects a cohort’s overall migration behavior.

Another issue is endogenous migration. Because prospective mothers might migrate to states with lower unemployment rates, using the actual locations of cohort members might cause fertility to appear more procyclical than it actually is. An alternative is to use the unemployment rate in the mother’s own state of birth, because most mothers remain in the state in which they were born. However, this estimate will not apply to mothers who have moved, so using it introduces some measurement error. Our preferred specifications use the unemployment rate in a mother’s own state of birth as an instrumental variable for the average unemployment rate in the states where their cohort gave birth at each age.^‡ However, our estimates are quite similar in all three specifications, as discussed further below. Our sample period covers five recessions that vary in strength and timing across states (SI Appendix, Fig. S1), providing us with a rich source of variation in unemployment.

Results

Restricting our analysis to conceptions between 1975 and 2009 to US-born mothers yields a sample of 111.9 million births, which resulted from 110.3 million conceptions (the difference is the result of multiples). Table 1 shows descriptive statistics for our study sample as well as for all births in the United States. The annual conception rate is expressed per 1,000 women aged 14–43, to be comparable to birth rates, which commonly are expressed per 1,000 women aged 15–44. The conception rate of 62.2 in our sample is somewhat lower than the overall US rate because of the relatively high fertility of immigrants. About one-third of US-born mothers give birth outside their own state of birth, indicating considerable internal migration. Our measure of completed fertility is the number of conceptions resulting in live births before age 40 per 1,000 women and averages 1,916. We also find that 18.44% of women are childless at age 40, i.e., they have not had any live births. These measures can be constructed only for US-born women because births to foreign-born women are not observed before immigration.

Table 1.

Descriptive statistics

Conception years 1975–2009	US-born women	All women
Births, n	111,880,471	135,995,642
Conceptions, n	110,339,005	134,172,249
Annual conception rate per 1,000 women aged 14–43	62.16	66.16
Age at conception, y	25.17	25.45
African American women, %	17.06	15.88
Women giving birth in own birth state, %	67.08	—
Conceptions before age 40 per 1,000 women, n	1,916	—
Women childless at age 40, %	18.44	—

“Conceptions” refers to conceptions resulting in live births. Births > conceptions because of births of multiples. Number of conceptions before age 40 and percent childless are calculated for cohorts 1961–1970. See Materials and Methods for definitions of fertility rates.

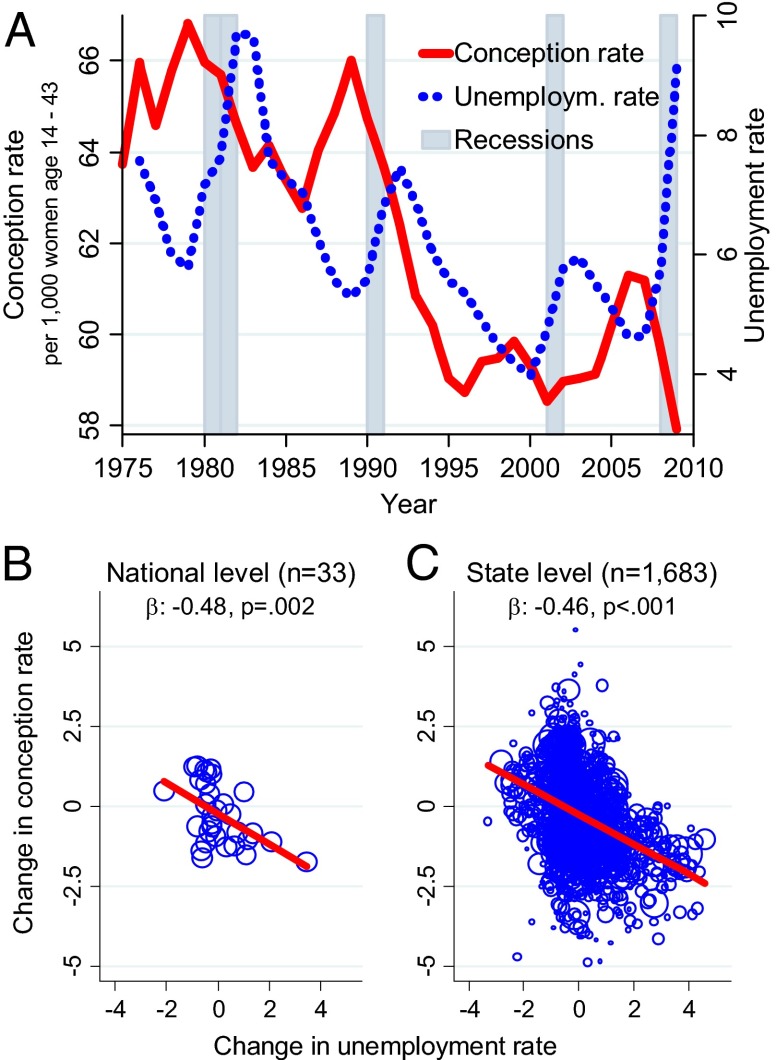
Fig. 1A shows the annual conception rate for US-born women and the overall unemployment rate. Shaded areas indicate recession periods. This figure shows that changes in the unemployment rate are negatively correlated with changes in the conception rate. For example, between 2008 and 2009, at the height of the Great Recession, the unemployment rate surged by 3.5 percentage points whereas the number of conceptions per 1,000 women decreased by 1.7.

Fig. 1.

Conception rates and unemployment rates at the national (A and B) and state (C) level. Conception rates are for US-born women only. “Conceptions” refer to conceptions resulting in live births. Straight lines in B and C are fitted using OLS. Observations are weighted by cohort size in C. Corresponding regression results are presented in SI Appendix, Table S1A. See Materials and Methods for the definition of conception and unemployment rates.

Fig. 1B uses the same data as Fig. 1A but plots annual changes in the conception rate against annual changes in the unemployment rate. The straight line is fitted using ordinary least squares (OLS). It has a slope of −0.48, which is statistically significant at the 1% level, indicating that a one percentage point increase in the national unemployment rate is associated with a fertility decrease of about 0.5 conceptions per 1,000 women. Plotting conception and unemployment rate changes at the state level in Fig. 1C yields a slope of −0.46 (P < 0.001). A similar effect also is observed within subperiods when focusing on the years around individual recessions (SI Appendix, Fig. S2).

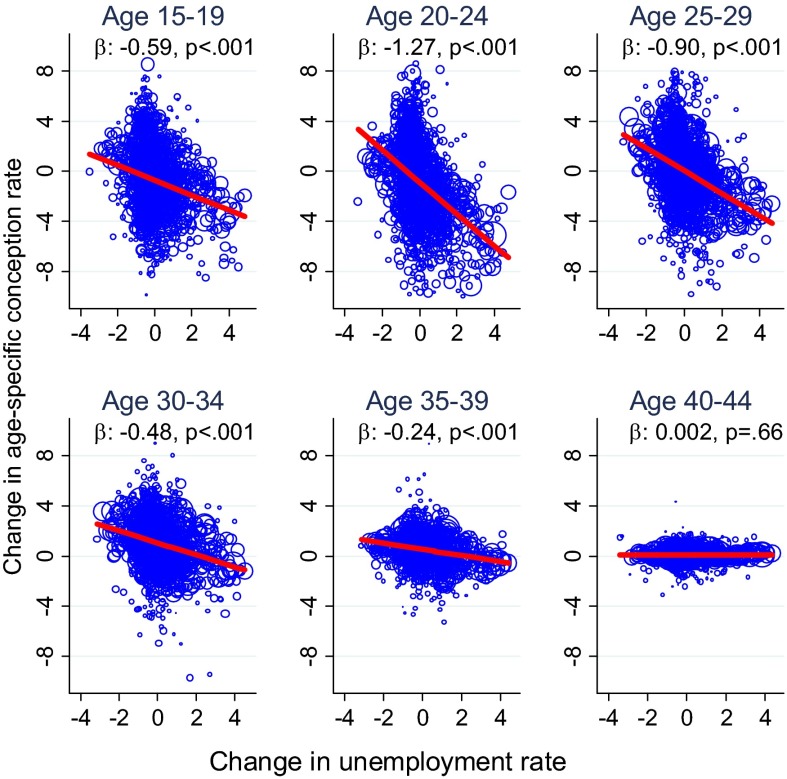
In Fig. 2, we repeat the state-level analysis separately for six age groups. The fertility response to changes in the unemployment rate is strongest for women 20–24 y of age. The negative effect in this age group is more than twice as large as the average effect across all age groups. With increasing age, the relationship becomes weaker, and it is virtually zero for women 40 and older. Models estimated in first differences are extremely transparent but not directly comparable to the long-run models we show later, which include indicators for each cohort of mothers. Therefore, we also estimate these models in levels with cohort-fixed effects and flexible time controls. These models yield very similar estimates (SI Appendix, Fig. S3 and SI Appendix, Table S2). The point estimate for the 20–24 age group is −1.20 in this specification, compared with −1.27 in first differences.

Fig. 2.

Short-term relationship between unemployment and conception rates at different ages. Straight lines are fitted using OLS. Observations are weighted by cohort size. Corresponding regression results and average fertility rates per age group are presented in SI Appendix, Table S1B. Further comments are as in Fig. 1.

Baseline fertility in the early 20s is high, with about 100 annual conceptions per 1,000 women (SI Appendix, Fig. S4). At the same time, these young women have almost 20 y of fertility ahead of them, so a temporary reduction in fertility might be compensated for by increasing fertility at later ages. The question of whether this postponement takes place cannot be investigated using data on annual conception rates. Instead, we need to look at completed fertility measures.

The first column of Table 2 shows the relationship between completed fertility per 1,000 women at age 40 and the unemployment rates that women have faced at different points in their fertile life cycle. The sample includes women born in 1961 through 1970 for whom we observe fertility up to age 40 (SI Appendix, Fig. S5). There is no significant effect of high unemployment before age 20 or after age 24. However, the average unemployment rate between age 20 and 24 has a statistically significant coefficient of −14.21 (P = 0.022), indicating that a one percentage point increase in the unemployment rate decreases the completed fertility rate at age 40 by about 14 conceptions per 1,000 women.

Table 2.

Long-run effect of the unemployment rate at different ages on completed fertility

	Conceptions resulting in live birth per 1,000 women before age:
Dependent variable	40 (col. 1)	35 (col. 2)	30 (col. 3)	25 (col. 4)	20 (col. 5)
Effect of average unemployment rate at ages:
15–19	−5.07	−4.83	−3.89	−9.65**	−7.37***
	(7.60)	(6.94)	(5.95)	(3.80)	(2.10)
20–24	−14.21**	−15.35**	−14.56***	−7.85*	0.65
	(6.02)	(5.84)	(5.56)	(4.16)	(2.30)
25–29	5.41	1.27	1.66
	(9.68)	(6.97)	(5.09)
30–34	−5.23	−4.44
	(16.30)	(16.03)
35–39	0.40
	(12.83)
N	510	510	510	510	510
Mean	1,916	1,770	1,416	900	362

Coefficients from OLS regressions of completed fertility on the average unemployment rate at different periods of women’s fertile life cycles are displayed. The data are aggregated by women’s state and year of birth. US-born women of cohorts born 1961–1970 are included. All regressions include indicator variables for women’s state and year of birth. The unemployment rate refers to the weighted average unemployment rate across states where women from the relevant cohort gave birth, with the number of births as weights. SEs are shown in parentheses and are clustered by state of birth. Observations are weighted by cohort size. Significance levels: *P < 0.1; **P < 0.5; ***P < 0.01.

Given a baseline of 1,916 conceptions resulting in a live birth prior to age 40, an effect of −14.21 is small in percentage terms (0.7%), as well as compared to the society-wide changes in fertility observed over the past century (12). Compared with the short-term estimates, however, this is a large effect. A one percentage point increase in the annual unemployment rate decreases the short-term fertility rate by 1.2 conceptions for those 20–24 y old. Multiplying this annual effect by 5 to make it comparable to effects of the 5-y average unemployment rate between ages 20 and 24 results in an overall short-term effect of −6.0. Thus, the long-term effect on completed fertility of −14.21 is more than twice as large as the short-term effect. In other words, among women aged 20–24, the initial negative effect of unemployment on conception accumulates over time rather than being fully compensated for by later conceptions.

Columns 2–5 of Table 2 show the estimated effects on completed fertility for the same cohorts of women as in column 1, but at earlier ages. The pattern of effects at ages 35 and 30 is very similar to the estimates in column 1, although the coefficient on the unemployment rate at ages 20–24 decreases slightly between column 2 and column 1, which suggests that there may be a small amount of “catch-up” but not enough to make up for the initial reduction in fertility. This pattern suggests that most of the long-term effect accumulates within the first 10 y after a young woman is exposed to high unemployment rates. At age 25, the effect of the age 20–24 unemployment rate is −7.8, which is only slightly larger than the corresponding short-term effect of −6.0. This comparison suggests that the accumulation of the long-term effect occurs largely between age 25 and age 30.

Columns 4 and 5 show that unemployment during a woman’s teen years also has a strong negative effect (of −9.6) on the number of conceptions resulting in a live birth up to age 25. However, this effect disappears at higher ages (although the point estimates remain negative), indicating that women largely make up for these fertility reductions in later years. Column 5 shows a model of completed fertility at age 20. Fertility at this age should not be affected by later unemployment, and column 5 shows that, in fact, it is not affected by the unemployment rate at ages 20–24.

The results in Table 2 are robust to alternative specifications of the unemployment rate. Using the unemployment rate in women’s own state of birth as an instrumental variable for the unemployment rate used above hardly affects the point estimates and leaves significance levels unchanged (SI Appendix, Table S3). Another alternative is to use the unemployment rate in a woman’s own state of birth not as an instrumental variable but as the regressor of interest. This substitution decreases the estimated effect size by about one-third (SI Appendix, Table S4), which is plausible given that one-third of mothers give birth outside their own state of birth, so the unemployment rate in these women’s state of birth is a noisy measure of the unemployment rate they actually experienced. Results also are robust to the exclusion of African American women (SI Appendix, Table S5), who have very distinct fertility patterns (SI Appendix, Fig. S6). The accumulated long-run effect also is observable when including more recent cohorts of women, who can be followed only to younger ages (SI Appendix, Table S6). Including more recent cohorts diversifies the time periods and economic conditions that feed into the unemployment rates at the different age intervals (SI Appendix, Fig. S5). The robustness of the estimates indicates that effects are not driven by economic conditions during one particular recessionary episode.

The strong and accumulating negative effects of the unemployment rate experienced in a woman’s early 20s on her completed fertility might be driven by women cutting back on higher-order births. Alternatively, some women who face high unemployment in their early 20s might end up not having children at all.

The effect of unemployment on the percent of childless women at various ages is investigated in Table 3, using the same specifications as in Table 2. The estimates in column 1 of Table 3 show a significant long-run effect of the unemployment rate experienced at ages 20–24 but not of unemployment rates experienced at other ages. The initial effect at age 25 in column 4 amounts to about half a percentage point. This effect accumulates to 0.68 at age 30 (column 3) and then decreases back to 0.51 at age 40, indicating some catch-up at higher ages. As for completed fertility, there is an effect of unemployment experienced during teen years on the fraction of childless women at ages 20 and 25, which disappears at higher ages. These long-run effects on childlessness are robust to the exclusion of African American women (SI Appendix, Table S7), and they are observed when including more recent cohorts (SI Appendix, Table S8).

Table 3.

Long-run effect of the unemployment rate at different ages on the percent of childless women

	Percent childless women at age:
Dependent variable	40 (col. 1)	35 (col. 2)	30 (col. 3)	25 (col. 4)	20 (col. 5)
Effect of average unemployment rate at ages:
15–19	0.34	0.33	0.21	0.50***	0.62***
	(0.25)	(0.24)	(0.23)	(0.17)	(0.11)
20–24	0.51**	0.55***	0.68***	0.48***	0.00
	(0.20)	(0.18)	(0.20)	(0.17)	(0.12)
25–29	−0.06	0.09	0.15
	(0.33)	(0.28)	(0.22)
30–34	0.27	0.20
	(0.54)	(0.53)
35–39	−0.01
	(0.46)
N	510	510	510	510	510
Mean	18.44	21.79	31.24	49.76	73.59

Coefficients from OLS regressions of the percent of childless women on the average unemployment rate at different periods of women’s fertile life cycles are displayed. See notes under Table 2 for further comments. Significance levels: *P < 0.1; **P < 0.5; ***P < 0.01.

The coefficient of 0.51 (P = 0.015) in column 1 implies that a one percentage point increase in the average unemployment rate at ages 20–24 is associated with about five additional childless women per 1,000 at age 40. Under the assumption that absent high unemployment these women would have had the average number of conceptions, this estimate of 0.51 implies a strong and accumulating effect on completed fertility. In our data, there are, on average, 2.35 conceptions among women who reach age 40 with at least one child (1.916/[1 − 0.1844]). Thus, 5.1 fewer women with children per 1,000 yields about 12 fewer conceptions per 1,000 before age 40. This accumulating effect explains almost the entire estimated effect on completed fertility (of −14.21) shown in column 1 of Table 2.^§

Discussion

Whether temporary fertility reductions reflect mere postponement or lead to permanent reductions in completed fertility has been a central question in demographic research (16, 17). In a seminal contribution, Bongaarts and Feeney (17) develop a tempo-adjusted total fertility rate that accounts for reductions in observed fertility caused by shifts in maternal age. If, for example, women began to delay first births but went on to have the same number of children, there would be a temporary decline in fertility that would not affect completed fertility. However, to analyze the actual long-term effects of observed short-run fertility reductions on completed fertility, it is necessary to follow affected cohorts over their fertile life cycle (18, 19).^¶ Our cohort-based approach achieves this goal, following women at the state-of-birth level over time so that we can relate their completed fertility to the unemployment rates they faced at different points in their fertile life cycle.

The completed fertility measures we construct using the Vital Statistics natality data are very similar to the standard estimates the US Census Bureau publishes biannually based on surveys of nationally representative samples (SI Appendix, Fig. S7).^‖ However, unlike the estimates from survey data, the Vital Statistics data provide us with mothers’ state of birth, which allows us to follow cohorts over time. At the same time, the statistical power derived from including the universe of US births allows for a precise analysis at the level of these individual birth cohorts. Further, in the data we see the states in which women in each cohort give birth at different ages, information used to infer the actual unemployment rates that each cohort experienced.

A possible issue is that because not every woman in a cohort gives birth in every year, using women who give birth to track the cohort might impart some bias. In census years, it is possible to obtain the location of each cohort and to compare the distribution of locations for all women in the cohort with the distribution of locations of women from the cohort who give birth. This comparison suggests that the spatial distribution of women who give birth is a good proxy for a cohort’s overall migration behavior (SI Appendix, Fig. S8). Hence, we can relate completed fertility to the unemployment rates that a cohort actually faced at different ages.

A second issue is that we observe only conceptions that result in live births. It is possible that the number of live births falls with unemployment because more women seek abortions or suffer pregnancy losses rather than solely because fewer women conceive. Thus, our results pertain to the cyclicality of conceptions resulting in live births rather than to the universe of all conceptions.

Our analysis shows a robust negative short-term response of fertility to changes in the unemployment rate. This procyclical effect on fertility is visible in the national US time series data. The short-term estimates are very similar whether they are estimated at the state or the national level and are strongest for women aged 20–24. Cohorts of women who face high unemployment rates during their early 20s do not just postpone fertility but have fewer children in both the short and long term, suggesting that the negative effect accumulates over time.

The observed short- and long-term impacts of unemployment on fertility also might have compositional effects on maternal characteristics such as maternal age or race. Postponing births would imply an increase in average maternal age at conception in affected cohorts. When we examine average maternal age over all conceptions up to age 40, we do not find any significant effect of the unemployment rate at ages 20–24 (SI Appendix, Table S9, column 1), and we do find a significant positive effect (0.05; P < 0.01) of the unemployment rate experienced at ages 15–19. We also find a significant negative effect of the unemployment rate at ages 15–19 on the percent of African American mothers (−0.84; P = 0.01; SI Appendix, Table S9, column 2), perhaps because the fertility response at that age range is more persistent for this racial subgroup.

These long-run effects on the composition of mothers might have an impact on health at birth. The offspring of mothers who faced high unemployment between ages 15 and 29 are significantly less likely to be low birth weight (SI Appendix, Table S9, column 3). However, this effect on health at birth disappears when we control for the fraction of African American mothers (column 5), indicating that the health effect is in fact driven by the change in the composition of mothers.

What economic mechanisms drive the short- and long-term fertility responses to recessions? The standard economic theory of fertility (20) assumes that children are “normal goods,” that is, that fertility increases with income. However, higher female wages also make children more expensive, because childbearing and rearing have costs in terms of foregone income. Recent empirical studies (21–24) support these opposing theoretical mechanisms.

Recessions are known to affect male employment more than female employment (25), suggesting they may have effects on household income that are greater than the effects on female earning opportunities. The reduction in income in turn might explain lower fertility during recessions. The short-term fertility response to the recent Great Recession (SI Appendix, Fig. S2) was unusually large, which is in keeping with the fact that initially it had a very large effect on male employment (26). In terms of long-run effects it is known that young adults, and especially young men, entering the labor market during recessions suffer strong and persistent reductions in their lifetime income (27, 28). These long-term income losses among men entering the labor market during recessions may make them less attractive matches for women in the same cohorts.**

Using data from the American Community Survey, we find that a one percentage point increase in the average unemployment rate at ages 20–24 raises the fraction of women never married prior to age 40 by about half a percentage point (P = 0.01; SI Appendix, Table S10). This estimate is similar to the estimated long-run effect on the fraction of childless women, and it is in line with a literature that finds a persistent negative effect of unemployment on marriage rates (30). We do not find significant effects on women’s educational attainment; if young women facing a recession obtained more education than otherwise, then this might have been an independent factor decreasing fertility (SI Appendix, Table S10, column 2).

A useful benchmark to assess the magnitude of the estimated long-term effects on completed fertility is provided by Black et al. (21), who studied the coal boom in the 1970s as a “natural experiment” that increased male workers’ incomes in coal regions. They found that the coal boom increased the completed fertility of affected cohorts by 3% while incomes were permanently increased by 6%. Our estimates suggest that a one percentage point increase in the average unemployment rate decreases completed fertility by 0.7%, whereas the long-run income effect of a one percentage point unemployment rate increase for young male workers has been estimated to be around 1.5% (27). Hence, our estimates are close to the elasticity of 0.5 reported in Black et al. (21).

The estimated long-term response of −14.21 conceptions per 1,000 women aged 20–24 facing a one percentage point increase in the unemployment rate is sizeable. Given that there are about 9.2 million US-born women aged 20–24 currently living in the United States, our estimates suggest that the increase of 3.22 percentage points in the 5-y unemployment rate experienced during the Great Recession will result in a long-term loss of 420,957 conceptions (and 426,850 live births) among affected cohorts, a 2.4% decrease in completed fertility. This long-term effect on fertility is driven largely by women who remain childless. The estimates imply that of the women aged 20–24 at the start of the Great Recession, an additional 151,082 will remain childless at age 40 (an 8.9% increase in the rate of childlessness).^†† We find it remarkable that changes in macroeconomic conditions in young adulthood have such a profound effect on an individual woman's future life.

Materials and Methods

Birth Data.

We include birth records from the 50 US states and the District of Columbia, provided by the Centers for Disease Control (31). Birth records report birth dates by year and month of birth, whereas gestation is reported in weeks. We start with all conceptions that resulted in a live birth and calculate the year of conception by subtracting the rounded number of gestation months (gestation weeks*7/30.5) from the birth date. Of these observations, 0.49% had missing values for gestation. Missing values for gestation length are imputed by using linear regression with indicators of mothers’ age and birth year. Results remain unchanged if we simply replace missing values by 40 wk of gestation. We exclude conceptions in 1974 and 2010 because for these years, only late and early conceptions are observed, respectively. We assume that conceptions occur in the same state where the birth is observed. Multiple births are counted as one conception. Maternal age at conception is proxied by maternal age at birth minus one, and mothers’ year of birth is calculated subtracting age at conception from the conception year. For notational convenience, conceptions before age 14 are counted as occurring at age 14. This affects 0.3% of the sample. We divide conceptions into cohorts defined by mothers' state of birth (s*) and year of birth (y*). Birth records report birth order, which allows us to identify first conceptions. We subtract the number of first births ever observed in a cohort from the overall number of women in a cohort to measure the number of childless women.

Population Estimates.

The number of women in each cohort comes from the decennial US Census for 1970, 1980, 1990, and 2000 and from the American Community Survey 2010 (the 2010 US Census was not yet available at the time of this writing), provided by the Integrated Public Use Microdata Series (IPUMS) (32). These data contain women’s state of birth and their age. Female mortality is low in the fertile age range, and there is no apparent negative trend in cohort size across census waves. Therefore, we combine the information from all census waves that cover a cohort in the fertile age range (14–44 y) and use the average cohort size across waves as the population estimate. For example, the size of the 1955 birth cohort is calculated as the average cohort size across the census waves 1970, 1980, and 1990. We use single race recodes for multirace responses in 2000 and 2010 provided by IPUMS.

Fertility Rates.

The cohort-specific annual conception rate (CR) is calculated as

$$C{R}_{s*,y*,t}=\frac{C_{s*,y*,t}}{cohortsiz{e}_{s*,y*}}*\mathrm{1,000},$$

where C_s*,y*,t is the number of conceptions (resulting in a live birth) in calendar year t of a cohort born in state s* and year y*. Cohortsize_s*,y* is the number of women in cohort s*, y*, estimated from the decennial census (see above). Calendar year and birth year determine age, hence CR_s*,y*,t = CR_s*,age,t with age = t − y*. The CR can be aggregated to the state (CR_s*,t) or national (CR_t) level.

The completed conception rate (CCR) at age 40 refers to the number of conceptions resulting in a live birth that occurred in a cohort before age 40 per 1,000 women in that cohort:

$$CC{R}_{s*,y*,40}=\frac{{\displaystyle {\sum }_{a=14}^{39}{C}_{s*,y*,a}}}{cohortsiz{e}_{s*,y*}}*\mathrm{1,000},$$

where C_s*,y*,a is the number of conceptions resulting in a live birth in cohort s*, y* at age a, i.e., in calendar year t = y* + a.

The percent of childless women at age 40 is calculated by subtracting the number of first conceptions resulting in a live birth in a cohort before age 40 from the overall number of women per cohort:

$$CLES{S}_{s*,y*,40}=\frac{cohortsiz{e}_{s*,y*}-{\displaystyle \sum _{a=14}^{39}First{C}_{s*,y*,a}}}{cohortsiz{e}_{s*,y*}}*100,$$

where FirstC_s*,y*,a is the number of first conceptions of cohort s*, y* at age a, i.e., in calendar year t = y* + a.

Unemployment Rates.

State-level unemployment rates are obtained from the Bureau of Labor Statistics and are available starting in 1976 (33). In every year, we assign to the cohort s*, y* the weighted average unemployment rate across the states in which women of the cohort s*, y* conceive, with the number of conceptions as weights:

$$U_{s*,y*,t}=\frac{{\displaystyle \sum _{s=1}^{51}\left(U_{s,t}{C}_{s*,y*,t}^s\right)}}{C_{s*,y*,t}}.$$

C_s*,y*,t is the overall number of conceptions resulting in a live birth occurring in year t among cohort s*, y*.C^s_s*,y*,t is the same cohort’s number of conceptions occurring in state s. U_s,t is the unemployment rate in state s in year t. For example, in a cohort of women born in New York in 1960 and delivering in 1981, 10% might have given birth in New Jersey whereas 90% might have given birth in New York (these numbers are purely illustrative). In this case, we would assign the unemployment rate 0.1*U_NJ + 0.9*U_NY to this cohort and year. We also use the unemployment rate from the woman’s own state of birth and child’s year of conception in some specifications, as discussed above.

Methods.

The short-term effects of the unemployment rate on fertility are illustrated in Figs. 1 B and C and 2 by plotting changes in the annual conception rate against changes in the annual unemployment rate. In these figures, we fit regression lines corresponding to regression Eqs. 1–3 below. Eq. 4 shows a level specification comparable to the long-term effect model:

• $$\text{First differences (national aggregation)}:\mathrm{\Delta }C{R}_t=\alpha +\beta *\mathrm{\Delta }{U}_t+{\epsilon }_t$$ [1]
• $$\text{First differences (state aggregation)}:\mathrm{\Delta }C{R}_{s*,t}=\alpha +\beta *\mathrm{\Delta }{U}_{s*,t}+{\epsilon }_{s*,t}$$ [2]
• $$\text{First differences (age groups)}:\mathrm{\Delta }C{R}_{s*,A,t}=\alpha +\beta *\mathrm{\Delta }{U}_{s*,A,t}+{\epsilon }_{s*,A,t}$$ [3]
• $$\text{Levels}:C{R}_{s*,a,t}=\alpha +\beta *U_{s*,a,t}+{\delta }_{s*}+{\theta }_{y*}+{\omega }_a+{\tau }_{1}T+{\tau }_2{T}^2+{\tau }_3{T}^3+{\epsilon }_{s*,a,t}.$$ [4]

Here, Δ refers to annual changes and CR_s*,a,t is the annual conception rate of women born in state s* who are of age a in year t. CR_t, CR_s*,t, and CR_s*,A,t are conception rates aggregated to the national, state, and age-group levels, respectively. δ_s*, θ_y*, and ω_a are state, cohort, and age indicators (“fixed effects”), respectively. T is a time trend. Observations are weighted by the number of women in each group in year t. SEs are clustered at the state level. First differences absorb a linear time trend at the national level, as well as time constant differences between states in Eq. 2 and time constant differences between state-specific age groups in Eq. 3.

Long-term effects of the unemployment rate at different points in women’s fertile life cycles on completed fertility at age 40 are estimated by

$$CC{R}_{s*,y*,40}=\alpha +{\beta }_1{\overline{U\left(15to19\right)}}_{s*,y*}+{\beta }_2{\overline{U\left(20to24\right)}}_{s*,y*}+{\beta }_3{\overline{U\left(25to29\right)}}_{s*,y*}$$

$$+{\beta }_4{\overline{U\left(30to34\right)}}_{s*,y*}+{\beta }_5{\overline{U\left(35to39\right)}}_{s*,y*}+{\delta }_{s*}+{\theta }_{y*}+{\epsilon }_{s*,y*,40},$$

where $\overline{U\left(15to19\right)}$_s*,y* is the average unemployment rate that cohort s*, y* faced at ages 15–19 and the other unemployment rate variables are defined similarly. The θ_y* are cohort indicators, which absorb nationwide differences between birth cohorts, such as the trend toward later childbearing shown in SI Appendix, Fig. S4. The δ_s* are state indicators, which absorb time constant differences between states, such as permanent differences in the unemployment and the fertility rate that are not driven by temporary economic fluctuations. Observations are weighted by cohort size and SEs clustered at the state level. We use the same specification to estimate long-term effects on childlessness, maternal composition, health at birth and marriage rates.