Single-spin stochastic optical reconstruction microscopy

Significance

Mastering nanoscopic quantum systems promises applications in quantum information processing (QIP) and nanoscale metrology. However, the spatial density of individually addressable systems is not only limited by their size, but rather by the scale needed for control and readout. This affects upscaling of QIP devices and limits nanoscale sensors to be scanning probe devices with serial data acquisition. Here, we simultaneously apply parallel nanoscale microscopy and spin resonance methods on ensembles of optically addressable spins. The latter have been applied as qubits and nanoscale quantum sensors on the single level. In contrast, our method allows parallel individual addressing inside ensembles of qubits/sensors with nanometer distances. This promises a vast speedup for sensing applications compared with scanning probe methods.

Abstract

We experimentally demonstrate precision addressing of single-quantum emitters by combined optical microscopy and spin resonance techniques. To this end, we use nitrogen vacancy (NV) color centers in diamond confined within a few ten nanometers as individually resolvable quantum systems. By developing a stochastic optical reconstruction microscopy (STORM) technique for NV centers, we are able to simultaneously perform sub–diffraction-limit imaging and optically detected spin resonance (ODMR) measurements on NV spins. This allows the assignment of spin resonance spectra to individual NV center locations with nanometer-scale resolution and thus further improves spatial discrimination. For example, we resolved formerly indistinguishable emitters by their spectra. Furthermore, ODMR spectra contain metrology information allowing for sub–diffraction-limit sensing of, for instance, magnetic or electric fields with inherently parallel data acquisition. As an example, we have detected nuclear spins with nanometer-scale precision. Finally, we give prospects of how this technique can evolve into a fully parallel quantum sensor for nanometer resolution imaging of delocalized quantum correlations.

Stochastic reconstruction microscopy (STORM) techniques have led to a wealth of applications in fluorescence imaging (1–3); for example, few ten-nanometers 3D spatial resolution (lateral 20 nm, axial 50 nm) has been achieved in cellular imaging. So far, STORM fluorophores have been used as markers to achieve nanoscale microscopy of specific targets (4). Here, we present a spin-based approach that promises to combine sub–diffraction-limit imaging via STORM and simultaneous sensing of various physical quantities.

As a prominent multipurpose probe and highly photostable single emitter, we use the nitrogen vacancy (NV) spin defect in diamond. It can be applied for nanometer-scale scanning magnetometry (5–8) as well as magnetic imaging (9–14) (e.g., for imaging spin distributions, magnetic particles or organisms, or device intrinsic fields), the measurement of electric fields, and diamond lattice strain (15–18) (e.g., for imaging elementary charges or charge distributions, or for imaging strain fields induced by mechanical action on the diamond surface). Very recently, precise temperature measurements (19, 20) even in living cells (21) have been demonstrated.

During the last decades, a variety of methods have been invented to circumvent the diffraction limit in farfield optical microscopy. One approach reduces the spatial region within a laser focus from which optical response of a single emitter is possible by exploiting optical nonlinearities. Examples are stimulated emission depletion (STED) and ground-state depletion (GSD) microscopy (22, 23). Another approach tailors the timing of optical response of several emitters from within a diffraction-limited spot to distinguish them in the time domain. One example is stochastic optical reconstruction microscopy (24–26). This latter technique is intrinsically parallel as it uses a CCD array for imaging and is therefore particularly suited for high-throughput imaging.

STED and GSD microscopy, which are both scanning techniques, have been recently implemented for NV centers in diamond (27, 28) with resolutions down to a few nanometers (29). In addition, localization-based superresolution microscopy has been shown with NV centers in nanodiamonds (30).

Here, we experimentally demonstrate STORM for NV centers in diamond as a new optical superresolution technique with wide-field parallel image acquisition for NV centers in bulk diamond. Our technique is based on recently gained profound knowledge about statistical charge state switching of single NV centers (31), and its scalability relies on the homogeneity of this charge state dynamics for NV centers in bulk diamond. Furthermore, we combine optical superresolution microscopy with high–spectral-resolution optically detected magnetic resonance (ODMR). On the one hand, we use the latter technique to assign magnetic resonance data to nanometer-scale locations, which is important for qubit or metrology applications (9–11, 32). On the other hand, different magnetic resonance fingerprints of closely spaced NV centers are used to further increase the already obtained superresolution, as demonstrated in refs. 32 and 33, which is important for emitter localization in imaging applications.

Results

Relevant Key Features of NV Centers in Diamond.

The negatively charged NV center in diamond is an optically active emitter with an electronic spin in its ground state (Fig. 1B) with favorable coherence properties (34, 35). The NV’s special properties allow for optical detection of single centers and the optical initialization and readout of its electronic spin. The latter is used for metrology (5, 15, 20, 36, 37) and quantum information processing (32, 38–41) applications. More specifically, the NV center in diamond is a point defect in the diamond lattice consisting of a substitutional nitrogen atom next to a carbon vacancy. It appears mainly in two different charge states, NV⁻ and the neutral NV⁰ (31) (Fig. 1B). Upon illumination in a wide spectral range (≈500…637 nm), fluorescence indicating the charge state can be invoked. The spectral excitation windows as well as the fluorescence spectra for NV⁰ are slightly blue shifted with respect to NV⁻, exhibiting a zero-phonon line at ≈575 and ≈637 nm, respectively, accompanied by phonon sidebands (31).

Fig. 1.

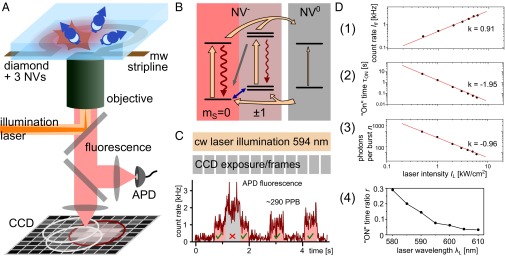
The NV center in diamond and the experimental setup. (A) Experimental setup (Materials and Methods, Experimental Setup). In this illustration, one of three NV centers in the focal spot is in the negative charge state (On), and the others are neutral (Off). An exemplary CCD image with marked PSFs is sketched. (B) Simplified energy level scheme for neutral and negatively charged NV center. Laser-induced rates are shown as orange arrows and luminescence is shown as wavy lines. The line widths symbolize strengths of the transitions. The NV spin polarization rate is sketched as gray arrow, and mw-induced spin transitions are shown as blue double arrow. (C) Upper part displays the STORM measurement scheme for NV centers (Results, STORM with NV Centers in Diamond). Laser illumination is applied continuously and CCD imaging is performed with a fixed frame rate. The lower part shows an exemplary fluorescence time trace recorded with an APD. Lowest count level indicates that all NV defects are in the Off state. Two distinguishable higher fluorescence levels correspond to one and two NV centers in the On state. (D, 1) Laser intensity dependence of single NV center fluorescence count rates $\mathrm{\Gamma }$. (2) Laser intensity dependence of NV⁻ charge state lifetime ${\tau }_{\text{on}}$ (i.e., On time). (3) Laser intensity dependence of average photons per burst n. (4) The NV⁻ charge state fraction [i.e., $r={\tau }_{\text{on}}/\left({\tau }_{\text{on}}+{\tau }_{\text{off}}\right)$] for excitation wavelengths between 580 and 610 nm.

Recently, frequent switching between NV⁻ and NV⁰ charge states has been demonstrated and can be detected via the presence and absence of fluorescence, respectively (31, 42). This stochastic fluorescence switching (i.e., visible bursts of fluorescence from single NV centers; Fig. 1C) is exploited in our work for STORM. By adjusting illumination intensity $I_{\text{L}}$ and wavelength ${\lambda }_{\text{L}}$, we can tune parameters such as fluorescence burst length ${\tau }_{\text{on}}$, photons per burst n, and the “On”-time fraction $r={\tau }_{\text{on}}/\left({\tau }_{\text{on}}+{\tau }_{\text{off}}\right)$ of the emitter (Fig. 1 C and D and Materials and Methods). As an example, for a single NV center and I_L ∼ 1 kW/cm² of ${\lambda }_{\text{L}}=594$-nm illumination light, ${\tau }_{\text{on}}\sim 2$-s–long bursts of $n\sim 600$ photons become visible separated by ${\tau }_{\text{off}}\sim 18$ s of background fluorescence.

The demonstrated optically induced charge state dynamics and fluorescence response are homogeneous for all NV centers in bulk diamond. This is a valuable property for a scalable parallel superresolution microscopy technique.

STORM with NV Centers in Diamond.

We demonstrate STORM on three NV centers within a diffraction-limited spot. In Fig. 2A, we compare the resulting images from conventional (Left) and STORM (Center) imaging. For conventional imaging, we illuminate emitters with 532-nm laser light at saturating power levels (i.e., with laser intensity I_L ≈ 200 kW/cm²) resulting in a CCD image exhibiting a single fluorescent spot. For STORM imaging, in contrast, we apply 594-nm laser light with intensities on the order of I_L ≈ 1 kW/cm² (i.e., far below saturation), finally yielding a reconstructed image showing three distinct NV emitters.

Fig. 2.

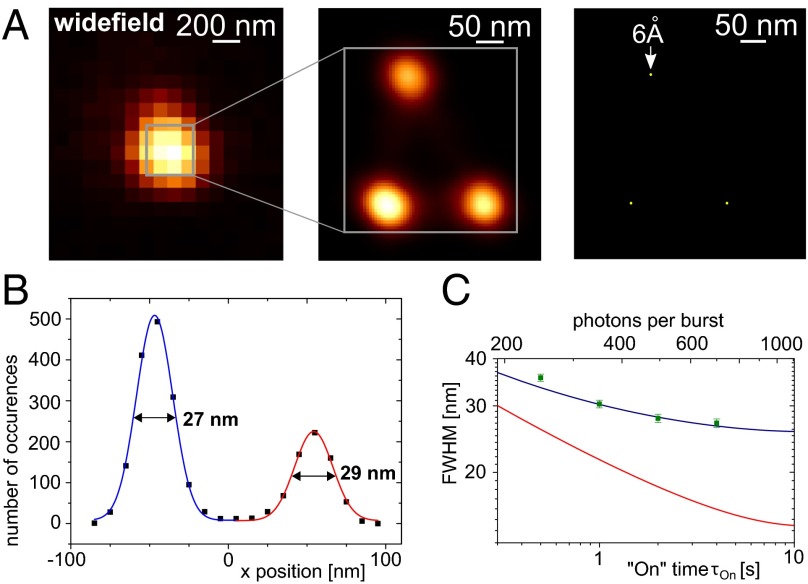
Sub–diffraction-limit imaging of NV centers by STORM. (A) From Left to Right: Diffraction-limited CCD image of three unresolved NV centers. STORM image of the formerly unresolved centers shows three distinct location distributions. Emitter localization accuracy is further reduced due to multiple photon bursts per NV. The STORM settings were 1-s average On time and on average 350 photons per burst. (B) One-dimensional line scan through a STORM image. The emitter location distribution (x coordinate) resolves two NV defects with FWHM = 27 and 29 nm, respectively. Here, the average On time was 4 s. (C) Resolution as a function of the On time or the number of photons per burst, respectively. Green squares are measurement data, and the blue curve is a fit according to Eqs. 1 and 2, considering the changing number of signal and background photons with increasing On time. The red curve shows the theoretical resolution, when the contribution caused by sample drift is neglected.

When switching to the low-intensity 594-nm laser light for STORM, we start seeing distinguishable fluorescence photon bursts (Fig. 1C) either on a single-photon–counting module [avalanche photo diode (APD)] or a CCD camera.

For STORM imaging, we record CCD images at a constant rate. As the “On”–“Off” switching of fluorescence happens stochastically, it is therefore not synchronized with the CCD frames. We set the exposure time of the CCD camera to the average On-time ${\tau }_{\text{on}}$ of the emitters. As our emitters do not bleach, we can record many bursts per NV center. Finally, the asynchronous switching of the emitters necessitates postprocessing of the data (Materials and Methods).

The idea of STORM is to assign all photons $n_i$ of a single, localized burst i on the CCD to a single yet-unknown emitter. To this end, all photons $n_i$ are used to calculate an average center location $\left[x_i,y_i\right]$ with a reduced location uncertainty ${\sigma }_{x/y,i}$ compared with the diffraction limit ${\sigma }_{\lambda ,i}$. The improved uncertainty scales approximately as ${\sigma }_{x/y,i}\propto {\sigma }_{\lambda ,i}/\sqrt{n_i}$ (Materials and Methods). Eventually, summing up Gaussian location distributions with parameters $\left[x_i,y_i\right]$ and ${\sigma }_{x/y,i}$ for all photon bursts yields Fig. 2A, Center, where three individual emitters are clearly distinguishable. The FWHM of the location distribution is 27 nm (Fig. 2B) and in the absence of drift is projected to be ≈14 nm (Fig. 2C and Materials and Methods). In the end, each obtained emitter location corresponds to a particular, distinguishable subset of distributions (each of the three spots in Fig. 2A, Center). These distributions can be used to further improve the localization accuracy of that particular emitter to 6 Å in the present case (Fig. 2A, Right, and Materials and Methods).

Sub–Diffraction-Limit Magnetic Resonance.

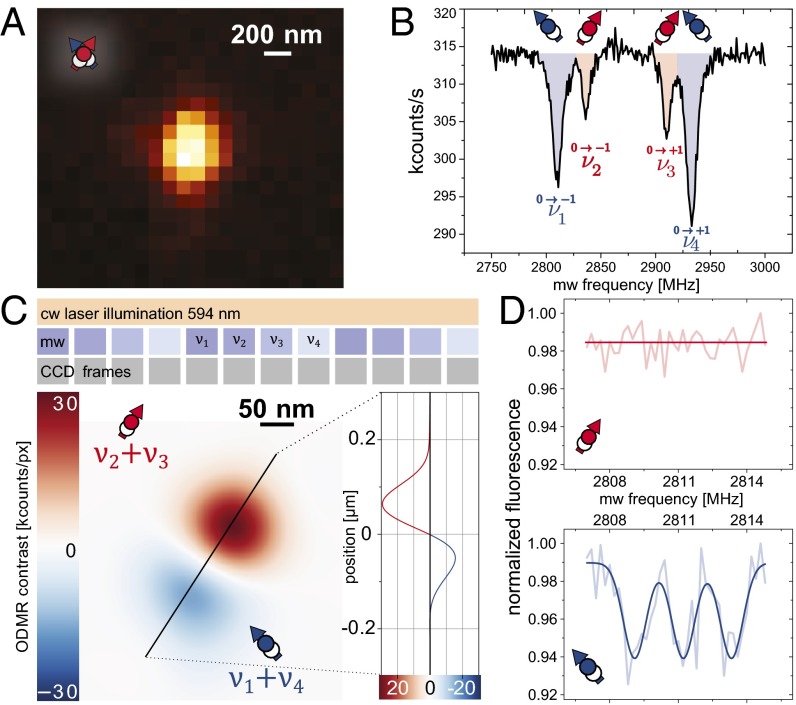
As the photon count rate during fluorescence bursts of STORM imaging does depend on the electron spin state, tagging of photons by the NV spin state is feasible. An exemplary conventional ODMR spectrum (Materials and Methods) of two spatially unresolved NV centers (Fig. 3A) is shown in Fig. 3B where the outer spectral lines (${\nu }_1,{\nu }_4$) belong to one NV and the inner resonances (${\nu }_2,{\nu }_3$) to the other one. Using conventional ODMR, however, no assignment of spatial to spectral information is possible. In contrast, STORM in conjunction with ODMR (STORM-ODMR) allows tagging the spatial location of NV centers with spectral information to achieve said assignment (Fig. 3C). We apply the latter assignment to two distinct tasks. On the one hand, NV spin spectral information is vital for metrology (e.g., nuclear spin detection) where STORM-ODMR enables nanoscale metrology. On the other hand, different spectral information of two NV centers, unresolved by bare STORM, eventually leads to their discrimination by STORM-ODMR.

Fig. 3.

Nanoscale magnetic field sensing with NV defects. (A) Diffraction-limited microscopy image of two NV centers with different crystallographic orientations (Inset sketch). (B) Conventional cw ODMR of NV pair exhibiting two pairs of resonance lines. Addressing of individual spins is possible due to different NV orientation but assignment to a location is missing. (C, Upper) STORM-ODMR measurement sequence (Results, Sub–Diffraction-Limit Magnetic Resonance). The average NV On time was 1 s. (Lower) STORM-ODMR image (Results, Sub–Diffraction-Limit Magnetic Resonance). The zero crossing (line scan) between both centers will even appear for mutual distances below STORM resolution. (D) High-resolution STORM-ODMR spectra assigned to individual NV centers. The mw frequencies are centered around ${\nu }_1$. Thus, only the blue NV shows a resonance.

To apply STORM-ODMR, we perform STORM as described while simultaneously applying microwave (mw) radiation and switching its frequency repeatedly from ${\nu }_1$ through ${\nu }_4$ synchronously to the CCD frames. The resulting image is shown in Fig. 3C. Here, we have added up all location distributions of photon bursts for mw frequencies ${\nu }_{\mathrm{1,4}}$ and subtracted those for ${\nu }_{\mathrm{2,3}}$. As a result, we see a red (positive) and a blue (negative) distribution of locations, belonging to the NV with resonances ${\nu }_{\mathrm{2,3}}$ and the one with resonances ${\nu }_{\mathrm{1,4}}$, respectively. Both distributions are separated by a zero crossing (line scan in Fig. 3C). Please note that this zero crossing will occur for every distance of the two emitters even if they are closer than the STORM resolution ${\sigma }_{x/y,i}$. This shows that ODMR can be used to enhance the STORM resolution (Materials and Methods) similar to diffraction-limited microscopy like demonstrated in refs. 7, 32, 33, and 43.

Further on, we show that localization is not only sensitive to the electron but also to nuclear spin states. Using high–spectral-resolution magnetic resonance enables to reveal hyperfine coupling to proximal nuclear spins. To this end, we reduce the mw power to avoid a related broadening of the ODMR resonance lines, and thus to exploit the small electron spin relaxation rate. The latter is mainly limited by the ¹³C nuclear spin bath (35). We demonstrate high spectral resolution by sampling the frequency range around resonance position ${\nu }_1$ obtained in the previous ODMR measurement. Consequently, we are able to assign a partial high-resolution ODMR spectrum to each individual NV center (Fig. 3D). As expected, one NV center shows ODMR resonances in this spectral window, whereas the other one does not. In the corresponding spectrum, we can resolve the hyperfine coupling to the adjacent ¹⁴N nuclear spin. The summed-up contrast of the STORM-ODMR spectrum of $18\hspace{0.17em}\text{\%}$ is comparable to that of conventional ODMR spectra on NV centers (i.e., ≈30%). To further discriminate individual, proximal bath spins, dynamical decoupling sequences need to be applied (44).

From the resonance lines’ slopes and contrasts in the STORM-ODMR spectrum in Fig. 3D, we estimate the magnetic field sensitivity for a single NV spin to be $\delta B\approx 190\hspace{0.17em}\mathrm{\mu }\text{T}/\sqrt{\text{Hz}}$. The sensitivity depends on the number of NV centers per focal spot N (in this case, $N=2$). Combined with the advantage of parallel imaging, we are able to measure the magnetic field at all accessible centers in many focal spots simultaneously (Materials and Methods).

Discussion

Summarizing, we demonstrated the first optical superresolution imaging technique with parallel data acquisition for NV centers in bulk diamond. Additionally, we were able to combine superresolution imaging with spin resonance techniques. Due to the homogeneity of the exploited properties among NV centers in bulk diamond, our method is intrinsically scalable to a vast number of color centers simultaneously.

Regarding the optical superresolution imaging of NV centers, we developed a dedicated STORM technique, achieving a FWHM resolution of single emitters of 27 nm and a localization accuracy of 6 Å. As our emitters inherently do not bleach or move with respect to the diamond itself, it is a potential calibration sample for STORM microscopes or a fixed background reference for experiments on otherwise moving objects of study. Furthermore, there is no need for high intensity or even pulsed lasers as illumination source, which makes our method extremely valuable for biological experiments in vivo or any other light- or temperature-sensitive measurements.

Regarding nanometer-scale spin resonance, we combined STORM with ODMR to demonstrate NV electron spin readout with a spatial resolution far below the diffraction limit. Apart from assigning individual spin resonance spectra to nanometer-separated NV centers, we have also applied STORM-ODMR in reversed way. Namely, we have further improved spatial resolution of the bare STORM imaging technique by tagging and thereby identifying photons of yet-unresolved emitters. STORM-ODMR is therefore particularly valuable for applications of diamond as a “microscope sensor slide.” In such a device, dense ensembles of NV centers (i.e., distances of ∼10 nm) are placed close (∼1 nm) to the diamond surface and can then detect physical quantities (e.g., magnetic and electric fields or nuclear spin concentrations) originating from samples just outside of the diamond (9–14, 45, 46). A particularly interesting application is parallel nanoscale magnetic resonance imaging (nano-MRI) as opposed to scanning probe nano-MRI (47, 48) or parallel diffraction limited MRI (49). Apart from detecting signals from outside the diamond sample, STORM-ODMR can also be applied for parallel nanoscale NV spin characterization, which can reveal individual couplings among proximal, now optically resolvable centers (32, 50).

Another application of STORM with NV centers could be fluorescent nanodiamonds used as bio markers. At the current time, application of our STORM technique to nanodiamonds is challenging due to the large inhomogeneity of NV and nanodiamond properties. For example, fluorescence intensities, charge state ratios, as well as timescales and spectral response of charge state dynamics differ greatly among different NV centers and nanodiamonds. The latter observation was attributed to electron tunneling and differing Fermi levels among nanodiamonds in ref. 30. Nevertheless, in ref. 30, a similar charge state switching mechanism was used to superresolve NV centers.

Beyond our proof-of-principle experiments, there is room for further improvement. With the reduction of sample drift and the increase of photon collection efficiency, a FWHM resolution below ≈10 nm is achievable in the short term. In the longer term, control of the Fermi level, diamond doping, and surface preparation (51, 52) might allow for a wider range of possible illumination intensities and wavelengths and thus higher acquisition speeds and a tailored degree of parallelism. Furthermore, we have sketched a road toward a fully parallel 2D quantum sensor array with nanometer-scale resolution. Some of its features would be, for example, large area parallel magnetic field sensing, which outperforms scanning techniques by orders of magnitude (Materials and Methods), or the direct imaging of spatially distributed quantum correlations on length scales down to nanometers.

Materials and Methods

Experimental Setup.

The setup can be divided into two main parts, which are the optical microscope to address single NV centers and the spin manipulation equipment consisting of mw sources and static magnetic fields (Fig. 1A). The microscope is capable of both wide-field CCD imaging and scanning confocal imaging. For illumination, we use lasers with wavelengths 532 and 594 nm, which can be both switched on the order of nanoseconds and which are intensity controlled. To detect fluorescence only from negatively charged NV centers, an optical long-pass filter with a cutoff wavelength of 650 nm is used. For adjusting the electron spin energy eigenstates and the respective transition frequencies, we place and orient permanent magnets accordingly. Microwave radiation for spin manipulation is guided via copper wires close to the NV centers.

For confocal imaging a collimated beam is sent into a 1.35 N.A. oil-immersion objective (apochromatic, plan corrected objective with a field of view of nominally more than 400 μm). The fluorescence light is collected by the same objective and finally focused onto a pinhole for spatial filtering and then onto a single-photon–counting APD (Fig. 1). A 3D piezostage with nanometer precision is used to move the objective across the diamond sample. For CCD imaging, the piezoscanner is fixed and additional lenses can be flipped into the beam path to focus the illumination laser onto the back focal plane of the objective, which leads to wide-field illumination. In that case, the fluorescence light is guided onto the pixel array of an electron multiplying CCD camera (iXon Ultra 897; Andor Technology). The magnification is set such that $100$ nm in the focal plane corresponds to one pixel on the CCD (Fig. 1A). We have not corrected the CCD images for aberrations because the effects are expected to be negligible.

We use commercial diamond samples of type IIa, grown by chemical vapor deposition, which contain as grown and artificially created NV centers. The latter were created by N⁺ ion implantation with a kinetic energy of ≈10 keV, which leads to an average depth of ≈10 nm. The as-grown NV centers used in this work had a depth of up to ≈2 μm.

NV Charge State Switching for STORM.

For illumination with ${\lambda }_{\text{L}}$ = 594-nm light and intensities $I_{\text{L}}$ far below saturating levels, the NV center fluorescence level exhibits sudden jumps that can be attributed to charge state switching from NV⁻ to NV⁰ induced by two-photon ionization (Fig. 1C) (31, 42). This behavior can be characterized and controlled as follows. The average On and Off times, ${\tau }_{\text{on}}$ and ${\tau }_{\text{off}}$, of fluorescence bursts and background fluorescence, respectively, are inversely proportional to $I_{\text{L}}^2$ (${\tau }_{\text{on}},{\tau }_{\text{off}}\propto I_{\text{L}}^{-2}$). In addition, the fluorescence count rate $\mathrm{\Gamma }$ during a burst is directly proportional to $I_{\text{L}}$ ($\mathrm{\Gamma }\propto I_{\text{L}}$). Consequently, the average number of photons per burst n is proportional to the square root of ${\tau }_{\text{on}}$ and inversely proportional to $I_{\text{L}}$ ($n\propto \sqrt{{\tau }_{\text{on}}},\hspace{0.17em}n\propto I_{\text{L}}^{-1}$; Fig. 1D). The ratio of ${\tau }_{\text{on}}$ and ${\tau }_{\text{off}}$ can be altered by tuning the illumination wavelength (Fig. 1D). For 594-nm illumination light, the ${\tau }_{\text{on}}$ fraction is $r\approx 0.1$, and it decreases for longer wavelengths.

STORM.

During STORM imaging, we continuously record CCD images at a constant rate while the On–Off switching of fluorescence happens stochastically. This necessitates postprocessing of the data, which is divided into two steps. First, we select frames with just a single active emitter by setting upper and lower thresholds for the photon number. Thus, we discard empty frames or those with two or more active emitters. In a second step, we check for lateral asymmetries in the fitted point spread function (PSF) of all remaining frames as an additional sign for more than one active emitter.

For the remaining frames, a 2D Gaussian function is fitted to frame number i, which yields a center location $\left[x_i\left(n_i\right),y_i\left(n_i\right)\right]$, the number of photons $n_i$ and the width ${\sigma }_{\lambda ,i}$ of the PSF. Please note that the Gaussian function is just an approximation of the real PSF. The width ${\sigma }_{\lambda ,i}$ of the fitted PSF allows the determination of the relative axial location of the emitter with respect to the focal plane. In our case, however, all emitters are in the same focal plane. As the number of photons contributing to the center location is $n_i$, the expected SD of that location should scale as ${\sigma }_{x/y,i}\propto {\sigma }_{\lambda ,i}/\sqrt{n_i}$. Sensor pixelation and background noise, however, affect the SD like the following (53):

$${\sigma }_{x/y,i}^2=\frac{{\sigma }_{\lambda ,i}^2}{n_i}+\frac{a^2/12}{n_i}+\frac{8\pi {\sigma }_{\lambda ,i}^4{b}^2}{a^2\cdot n_i^2},$$ [1]

where a = 100 nm is the pixel size of the images and $b\left(t\right)\approx 1+0.3\hspace{0.17em}{\text{s}}^{-1}\cdot t$ accounts for background photons per pixel in dependence of exposure time t. In our STORM technique, the average number of photons $n_i$ increases with the square root of the burst length/exposure time t, where the burst length is altered by the illumination intensity. Hence, we expect an optimal time for minimal SD ${\sigma }_{x/y,i}^2$ according to Eq. 1 (Fig. 2C).

With a set of locations $\left[x_i,y_i\right]$ and SDs ${\sigma }_{x/y,i}$ for each valid CCD frame we construct a new emitter location distribution $p\left(x,y\right)={\displaystyle {\sum }_i\left(1/2\pi {\sigma }_{x/y,i}^2\right)\exp \left(-\left({\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2\right)/2{\sigma }_{x/y,i}^2\right)}$ by adding up 2D Gaussians with the respective parameters and unit weight. Fig. 2 B and C shows the resulting superresolution image with typical FWHM of the location distributions of ≈28 nm.

For on average ≈700 photons per burst and average burst lengths of 4 s, these location distributions are broader than what is expected from Eq. 1. This is due to sample drift during the accumulation of CCD frames, which leads to additional broadening when all bursts are summed up. Thus, the overall SDs of the emitter locations can be estimated as follows:

$${\sigma }_{x/y}^2={\sigma }_{x/y,i}^2+{\sigma }_{\text{drift}}^2,$$ [2]

where we have evaluated the drift to be ${\sigma }_{\text{drift}}\approx 10$ nm.

As the achieved SD ${\sigma }_{x/y}\approx 28$ nm is smaller than the average distance between the emitters, we are able to recognize single distinct location distributions for individual NV centers. Thus, we can compute the localization accuracy ${\widehat{\sigma }}_{x/y}={\sigma }_{x/y}/\sqrt{M}$, where we ideally gain an additional factor of $1/\sqrt{M}$, where M is the number of detected bursts for an individual NV center (Fig. 2B). With an average number of bursts per NV of ≈2,000, we achieve a localization accuracy of ${\widehat{\sigma }}_{x/y}$ = 6 Å.

The shown resolution in Fig. 2C was achieved under optimal conditions (i.e., optimal laser intensity) with respect to SD ${\sigma }_{x/y}$ of location distributions. The optimum of ${\sigma }_{x/y}$ arises from an increase of $n\propto \sqrt{{\tau }_{\text{on}}}$ for decreasing laser intensity (i.e., increasing exposure time ${\tau }_{\text{on}}$) on the one hand and an increase in background noise $b\propto {\tau }_{\text{on}}$ on the other hand (Eq. 1). For laser powers below the optimum value, b will become the leading term resulting in worsening resolution. In Fig. 2C, the FWHM of the location distribution is presented for different average burst durations (i.e., different laser powers). The theoretical estimation is in agreement with these values. We like to stress that the current resolution is mainly limited by sample drift. Accordingly, we estimate FWHM in the absence of sample drift to be ≈14 nm.

Sub–Diffraction-Limit Magnetic Resonance.

At first, conventional ODMR is performed on two NV centers within one diffraction-limited spot. To this end, 532-nm laser light (with intensities saturating the optical transition of the NV centers) and mw radiation (capable of spin transition rates of ≈10 MHz) are continuously on, the mw frequency is swept, and the corresponding fluorescence is recorded. The laser pumps the NV spin into projection $m_S$ = 0, whereas resonant mw radiation induces transitions $m_S=0\leftrightarrow \pm 1$ (Fig. 1B). As the Zeeman interaction splits the $m_S=\pm 1$ levels, there are usually two different resonances. Away from spin resonance, the spin state is $m_S=0$, and accordingly a high rate of fluorescence photons is obtained. Upon resonance conditions, the levels $m_S=\pm 1$ become populated and the fluorescence decreases. Although both NV centers are exposed to the same external magnetic field, by chance their symmetry axes lie along different directions of $\langle 111\rangle$ in the diamond lattice resulting in crystal fields with different directions (5). Thus, the vectorial sum of external and crystal field is different for both NV centers and thus are their ODMR resonance lines.

Fig. 3C demonstrates mw enhancement of STORM resolution. The zero crossing of the line scan in Fig. 3C will be visible for any distance d between two NV centers. However, the depth of the minimum and maximum will approximately decrease proportional to d. Thus, to achieve a unit signal-to-noise ratio, the number of accumulated photons for decreasing d goes as $1/d^2$ or inverse measurement time squared. In other words, the resolution increases further as square root of the photon number.

For high–spectral-resolution magnetic resonance, we have reduced mw power to avoid power broadening of the resonance lines and we have sampled the resonance line ${\nu }_1$ in small frequency steps. For each valid CCD frame, we noted the corresponding mw frequency. As in the previous measurement, one NV shows a resonance around ${\nu }_1$ and the other one does not. Apparently, the line width is drastically reduced and the hyperfine interaction of 2.2 MHz to the nitrogen nuclear spin with total nuclear spin $I=1$ is visible. The current line width limit is set by the ¹³C nuclear spin bath (35).

From the high-resolution STORM-ODMR, we can calculate the magnetic field sensitivity. Therefore, we can take into account all three hyperfine lines ($m_I=-1,\hspace{0.17em}0,\hspace{0.17em}1$) because they would be shifted commonly upon a change in magnetic field. For the sensitivity, we arrive at $\delta B={\left({\displaystyle {\sum }_{m_I=-\mathrm{1..1}}{\frac{d\mathrm{\Gamma }}{d\nu }|}_{\max }}\right)}^{-1}{\sigma }_{\mathrm{\Gamma }}\frac{2\pi }{{\gamma }_e}\sqrt{T}$, where $d\mathrm{\Gamma }/d{\nu }_{\text{max}}$ is the maximum slope at each hyperfine line, ${\sigma }_{\mathrm{\Gamma }}$ is the SD of the data from the fit, ${\gamma }_e$ is the gyromagnetic ratio of the electron spin, and T is the total measurement time. Finally, the achieved sensitivity is $\delta B\approx 190\hspace{0.17em}\mathrm{\mu }\text{T}/\sqrt{\text{Hz}}$. This value is four times higher than what is expected for bare photon shot noise limitations. We attribute this mismatch to the postprocessing of the CCD frames and fluctuating laser intensity.

The sensitivity is dependent on the actual number of emitters in one focal spot N and is estimated in the following. In our case, the sensitivity was evaluated for two emitters. The probability to detect the signal of a single emitter within a single CCD frame increases less than linear with N (up to $N\approx 1/r$) and decreases for higher emitter densities. The On-time fraction r can be altered by changing the illumination wavelength (Fig. 1D). The probability of a charge state change of any emitter within a single frame increases with N. To keep the probability constant, we have to decrease the laser intensity by a factor of $1/\sqrt{N}$, which changes the single center sensitivity by a factor of $\approx N^{1/4}$. In our case, increasing the density of emitters to $N=1/r=10$ should change the sensitivity by a factor of ≈2.4.

The magnetic field sensitivity for conventional single NV experiments is better because of the higher fluorescence count rate. Under similar conditions (i.e., same ODMR line width), an ideal single NV experiment (shot noise limited) might yield $\approx 180\hspace{0.17em}\text{nT}/\sqrt{\text{Hz}}$ (54). Consequently, the conventional sensing technique is ∼10⁶ times faster for a single NV center. However, when scanning many NV centers in parallel and with nanometer spatial resolution this will eventually pay off. For example, with a field of view of 100 × 100 μm² and CCD with 1,024 × 1,024 pixels, we can resolve and consequently measure the local magnetic field of ≈10⁷ NV centers simultaneously given a FWHM spatial resolution of ≈30 nm. A scanning superresolution technique like STED ideally might achieve the mentioned sensitivity of $\delta B\approx 180\hspace{0.17em}\text{nT}/\sqrt{\text{Hz}}$. However, as the number of NV centers in our example is ${10}^7$, its overall speed is still one order of magnitude slower than our STORM-ODMR method. With foreseeable improvements, the speed of STORM-ODMR can be increased by many orders of magnitude (see below).

Summarizing, the signals of emitters from separate focal spots add up in a parallel fashion, whereas signals from within the same focal spot are diminished due to the decrease in sensitivity, as explained above.

STORM-ODMR Prospects.

Our technique of using STORM in conjunction with ODMR on NV centers can be used for building very powerful quantum sensors. The latter exploits the sensitivity of the NV center’s spin transition on quantities like magnetic and electric fields, strain, or temperature. For the first time (to our knowledge), a truly parallel quantum sensor array with nanometer-scale “pixel” size can be envisioned. Some of its features would be, for example, large area parallel magnetic field sensing or the direct imaging of spatially distributed quantum correlations on length scales down to nanometers.

Taking into account current NV diamond properties, we are going to estimate the achievable sensitivity of a potential NV sensor based on STORM-ODMR. With respect to magnetic field sensitivity, it is optimal to have the smallest possible ODMR line width. For full benefit with continuous-wave (cw) laser illumination, the optical excitation rate must be similar to the spin decoherence rate. In our demonstrated nanoscale ODMR, the line width was limited to ≈1 MHz by the diamond nuclear spin bath (35). For comparison, the optical excitation rate was ∼1 kHz. Thus, a potential reduction of the ODMR line width down to the order of the optical excitation rate (as demonstrated in ref. 35) would yield a linear sensitivity enhancement of three orders of magnitude. For further improvement in sensitivity, both optical excitation rate and magnetic resonance line width would have to be decreased equally and the sensitivity improvement would then scale as the square root of the rate reduction (54).

In addition to rather incoherent cw ODMR techniques, also pulsed schemes are applicable. These allow for a higher versatility owing to coherent spin control (17, 20, 34, 45). To this end, laser and mw control of the spins are interleaved (34) to prevent optical excitation during coherent spin operations.

Summarizing, STORM-ODMR enables the same measurement possibilities as demonstrated for single NV centers with the benefit of an increased spatial resolution and highly parallel control and readout, however, with a lower fluorescence count rate per emitter. The latter drawback can be mitigated in ultrahigh-sensitivity metrology applications where spin transitions with homogeneous line widths of ∼1 kHz are exploited (34). In these cases, average fluorescence count rates for conventional single NV measurements and STORM-ODMR measurements approach the order of emitter On and Off time ratio, which is $r\approx 10$ in our experiment. Thus, conventional measurements would be ∼10 times faster for a single NV center. Eventually, parallel STORM-ODMR measurements on as few as ∼10 NV nanoprobes would perform equally well as conventional serial measurements on ∼10 single NV centers. With a 100 × 100-μm² area, 60-mW laser power, a FWHM resolution of 14 nm, and a corresponding NV density, parallel measurements would be up to ${10}^6$ times faster than serial superresolution measurements.

The currently sketched sensor array does not operate fully parallel, which means NV centers within the same focal spot are read out in serial. To take an instant snapshot of the whole sensor array with nanometer resolution, nuclear spins can be used as nonvolatile memory (55, 56). To this end, all NV center probes sense at the same time (9), their results are stored on their individual proximal nuclear spins [e.g., ¹⁴N (55)], which are then read out via STORM-ODMR. This way, even delocalized quantum correlations can be monitored.