Heritability of White Matter Fiber Tract Shapes: A HARDI Study of 198 Twins

Abstract

Genetic analysis of diffusion tensor images (DTI) shows great promise in revealing specific genetic variants that affect brain integrity and connectivity. Most genetic studies of DTI analyze voxel-based diffusivity indices in the image space (such as 3D maps of fractional anisotropy) and overlook tract geometry. Here we propose an automated workflow to cluster fibers using a white matter probabilistic atlas and perform genetic analysis on the shape characteristics of fiber tracts. We apply our approach to large study of 4-Tesla high angular resolution diffusion imaging (HARDI) data from 198 healthy, young adult twins (age: 20–30). Illustrative results show heritability for the shapes of several major tracts, as color-coded maps.

1 Introduction

The relationship between genetics, brain structure, and function has long been debated in medicine, sociology, education, and neuroscience. How is the brain influenced by nature (genetics) and nurture (environment)?

Most studies of genetic influences on brain structure use T1-weighted anatomical MRI, which lacks information on white matter fiber tracts in the brain. For two decades, diffusion tensor magnetic resonance imaging (DT-MRI [1]) has been increasingly used to study pathology and connectivity of white matter pathways. DT-MRI provides directional information on water diffusion in brain tissue. Fractional anisotropy (FA), as a measure of microstructural directionality, tends to be higher when fiber tracts are more directionally coherent. Recent genetic analyses of DT-MRI show moderately high heritability for several diffusivity measures including the FA [2], which is widely considered to be a measure of fiber integrity. Structural equation models and heritability analyses have also been extended to handle the full diffusion tensor [3], and orientation density functions that represent the diffusion process [4]. Significant proportions of the population variability in FA are due to genetic factors. Heritability is detected in several white matter areas, such as the corpus callosum, internal capsule, along others, in voxel-wise FA maps [2].

The major disadvantage of voxel-based analysis of FA is that tract geometry is overlooked. FA maps do not provide information on the geometric characteristics of tract, making it hard to assess genetic effects on their shapes. Brouwer et al. [5] assessed genetic and environmental influences on fiber tracts in children by constructing average fiber bundles from manually defined regions of interest; even so, manual seeding of tracts makes it hard to analyze a large dataset, and limits the coverage to a few tracts.

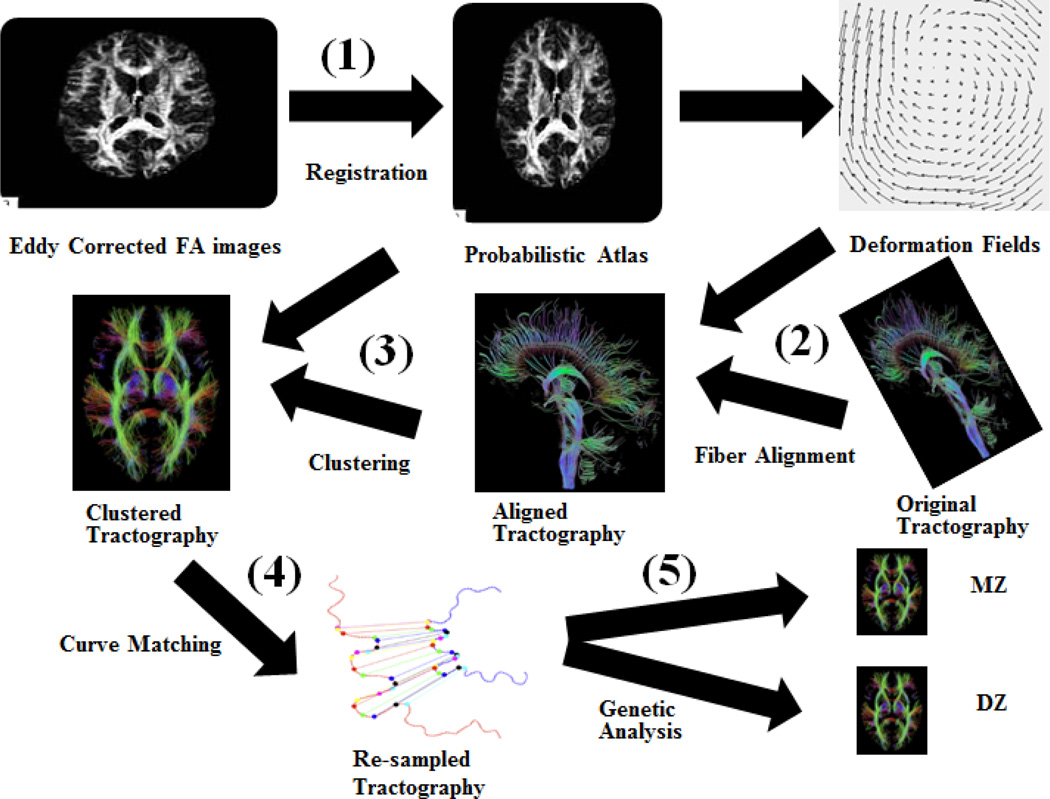
Here we introduce an automated workflow to (1) cluster the results of whole-brain high angular resolution diffusion imaging (HARDI) tractography into anatomically meaningful tracts, and (2) discover genetic contributions to tract shape characteristics, assessing their heritability. It is important to know if a fiber property is heritable; if so, it can be used in the search for specific variants on the genome that contribute to the wiring of the brain. To cluster fibers from whole-brain tractography across a large population, we used a white matter probabilistic atlas, to which all subjects’ brain images were non-linearly aligned. Fibers reconstructed from streamline tractography were warped to the same atlas space by applying the deformation fields from the registration step. Clustering was performed based on the probabilistic atlas. Once each tract was extracted, a curve matching method was implemented to find corresponding points on each fiber belonging to that tract across the population. For each tract, shape dispersion measures were analyzed using a statistical model of heritability. A flow chart is shown in Fig. 1. We conducted a large population study with this workflow, as detailed next.

Fig. 1.

Flow chart of the image processing steps: (1) Each subject’s FA image was nonlinearly registered to the atlas. (2) The resulting deformation fields were applied to the extracted fibers to warp them into the atlas space. (3) Fibers were clustered based on their locations in the atlas. (4) With shaped-based curve matching, we interpolated the points on the fibers corresponding to those on the mean curve of the tract. (5) Genetic analysis was performed on the defined shape metrics.

2 Methods

2.1 Subjects and Image Acquisition

Participating in this study were 198 healthy young adult twins (mean age: 23.2+/−2.1SD) from 99 families in Australia. All twins were right-handed. No subjects had any major medical condition or psychiatric illness. All subjects were evaluated to exclude any pathology known to affect brain structure. Diffusion imaging was available in 99 complete pairs – 62 monozygotic pairs (21 male-only pairs) and 37 same-sex dizygotic twin pairs (12 male-only pairs).

Compared to DT-MRI, HARDI [6] allows the use of a complex diffusion model. In fiber tractography, this can allow more accurate reconstruction of fibers that mix and cross, and more sophisticated definitions of diffusion anisotropy when multiple fiber orientations are present in a voxel [7]. HARDI images were acquired with a 4T Bruker Medspec MRI scanner, using single-shot echo planar imaging with parameters: TR/TE = 6090/91.7ms, 23cm FOV, and a 128×128 acquisition matrix. Each 3D volume consisted of 55 2-mm axial slices, with no gap, and 1.79×1.79mm² in-plane resolution. 105 image volumes were acquired per subject: 11 with no diffusion sensitization, i.e., T₂-weighted b₀ images, and 94 diffusion-weighted images (b = 1159 s/mm²).

2.2 Fiber Tractography

The raw HARDI images were corrected for eddy-current induced distortions with FSL [8]. To perform whole-brain tractography, we used the Diffusion Toolkit [9], a software package that uses a streamline algorithm to reconstruct fiber paths. The software applied the Fiber Assignment by Continuous Tracking (FACT)-like method [10] but was based on the HARDI data model that each voxel has multiple principal diffusion directions. We performed whole-brain tractography, with the maximum fiber turning angle set to 35° per voxel.

2.3 Image Registration

Eddy-current corrected diffusion images were skull-stripped using the FSL tool, BET, to facilitate registration. Each subject’s fractional anisotropy (FA) map was generated from the 105 diffusion volumes with FSL. Registration was performed on the FA images. The target image was a single-subject FA map in the ICBM-152 space called the “Type II Eve Atlas” [11]. This atlas FA image was 181×217×181, with 1mm isotropic resolution.

Subjects’ FA images were first linearly aligned to the atlas with FLIRT in FSL [12], via a 12-parameter affine registration, with mutual information as the cost function, and trilinear interpolation. To improve alignment, all linearly registered FA images were elastically registered to the atlas using inverse-consistent elastic registration [13]. This step used mutual information as a cost function to optimize an elastic deformation using the spectral method (Fast Fourier Transform). The resulting three 64×64×64 resolution deformation fields (x-, y-, and z-direction, respectively) were used to align all subjects’ FA images to the atlas coordinate space.

2.4 Fiber Alignment

Fibers generated in Section 2.2 were aligned to the same coordinate space by applying the affine transformation and deformation fields from the elastic registration in Section 2.3. Jin et al. [14] previously verified that nonlinear alignment improves analysis of tract data.

2.5 Fiber Clustering

We excluded any fibers with arc lengths <6.5cm, leaving ~15,000 fibers per subject for clustering. This number of fibers was sufficient to represent the cortico-spinal tract and other major white matter structures.

Clustering was based on a spatial probability map of white matter tracts in the atlas, for 47 major tracts [15]. For each fiber in the subject’s brain, we matched every point on the fiber to the nearest neighboring voxel to apply information in the probabilistic map. We defined “the fiber probability” of being a particular tract as the mean of the probabilities of the voxels, associated with the corresponding fiber points, which belong to this particular tract in the probabilistic map. Whether a fiber belonged to a particular tract depended on the following 3 criteria: (1) the fiber probability was largest for that particular tract among all tracts; (2) the fiber probability of being this particular tract was at least 0.2; (3) at least 70% of points on the fiber fell into this particular tract.

2.6 Curve Matching

Although many other choices are possible, we used shape dispersion measures to define tract shape. For a given tract, we first calculated the mean curve for the set of fibers in that tract; we then registered all the fibers in the tract to this mean curve; next, we calculated the mean and standard deviation of the distances from the corresponding points on each fiber inside this tract to those on the mean curve.

To compute each tract’s average shape, we used a representation proposed in Joshi et al. [16][17]. This representation used a square-root velocity function to represent open curves. Given a unit-length curve β: [0,1] → R³, its shape is represented by a function q: [0,1] → R³ such that $\mathrm{q}=\dot{\beta }/\sqrt{\dot{\beta }}$, where β̇ represents the derivative of β. Therefore, a fiber curve in the native space is transported to its shape in the space of all q functions that assume this square-root velocity form. An important ingredient for computing the mean shape is the establishment of geodesics between shapes. A geodesic is a shortest path between two points in a space. The mean curve for a fiber tract is the one minimizing the sum of the squared pairwise geodesic distances to all individual fibers of that bundle.

To compute corresponding points across the subjects, first, for any individual tract, a mean curve based on the sampled points was calculated for each subject; then, a population mean curve was generated with the information on those individual mean curves for each subject; in turn, the parameterization of the population mean curve was projected back onto the individual mean curve; finally, every fiber that belonged to this tract for each subject was re-sampled, based on the re-sampled individual mean curve.

2.7 Genetic Analysis

Monozygotic (MZ) twins share 100% of their genetic variants whereas dizygotic (DZ) twins share, on average 50%, of their genes. A simple and widely-used estimate of heritability, in twin studies, assesses how much the intra-class correlation for MZ twin pairs (r_MZ) exceeds the DZ twin correlation (r_DZ). Falconer’s heritability statistic [18] is defined as h²=2(r_MZ−r_DZ). It estimates the proportion of the overall variance that is due to genetic differences among individuals. Here, the measures we chose in Section 2.6 (the mean and the standard deviation of the distances from the points on each fiber to the corresponding points on the mean curve) were used to calculate intra-class correlations r_MZ and r_DZ. When h²=0, there is no evidence of a genetic effect; h²=1 implies all of the variance is due to genetic factors.

3 Results

3.1 Clustering

Fig. 2 shows clustering results (top, front, and side views) in a representative subject. Major tracts, distinguished in color, include the cortico-spinal tracts, thalamo-cortical tracts to primary motor and frontal areas, multiple sectors of the corpus callosum, the cingulum, and the superior and inferior longitudinal fasciculi.

Fig. 2.

A representative clustering result for 4-Tesla 105-gradient HARDI data from one individual subject, showing major white matter tracts. Top, front, and side views are shown.

Fig. 3 shows clustering results for several tracts in four different subjects (no twin pairs). Despite some individual variations, the overall tract shapes are consistent across the population. The tracts are the left cortico-spinal tract (inferior-superior orientation) in yellow, the callosal genu (left-right orientation) in red, and the left cingulum (posterior-anterior orientation) in green.

Fig. 3.

The left cortico-spinal tracts for 4 different subjects (not members of the same twin pair) are shown in yellow. The tract running through the callosal genu is shown in red, and the left cingulum tract is shown in green.

3.2 Genetic Analyses

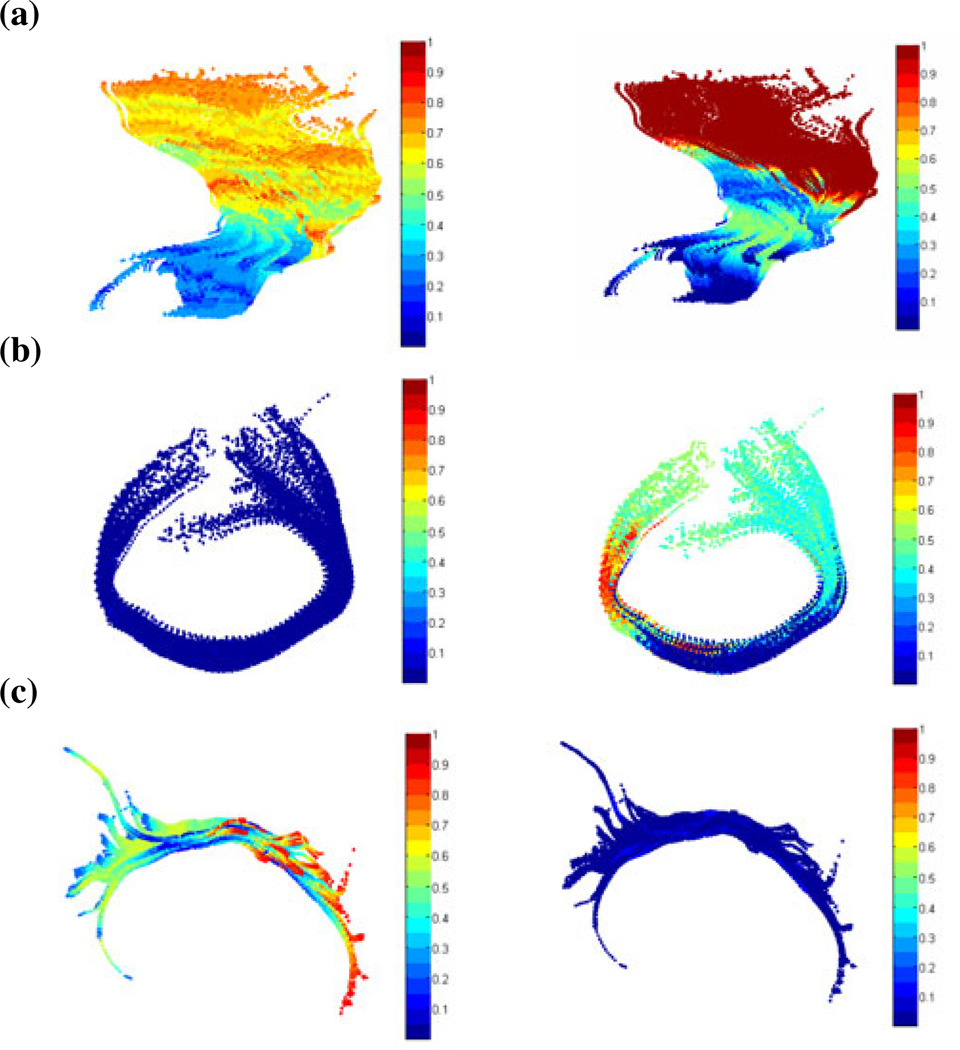
Fig. 4 shows color maps of Falconer’s heritability statistic, based on the mean and the standard deviation of distances between individual fibers and the mean curve for a particular tract (as in Section 2.6). The mean distance is related to the thickness of a tract. The left panel of each figure shows the mean and the right panel shows the standard deviation. Fig. 4(a), 4(b), and 4(c) show the left corti-cospinal tract, the callosal genu, and the left cingulum bundle.

Fig. 4.

Color maps show Falconer’s heritability statistic for (a) the mean distances (left) and the standard deviations of distances (right) of the left corticospinal tract; (b) the mean distances (left) and the standard deviations of distances (right) of the tract that runs through the callosal genu; (c) the mean distances (left) and the standard deviations of distances (right) of the left cingulum tract.

In Fig. 4(a), greater heritability is detected near the cortex, perhaps because the overall variability across subjects is greater there. Minimal genetic influence is detected for the mean distances in the callosal genu in Fig. 4(b), but there is some influence on the standard deviation of distances. An opposite trend is found for the left cingulum tract in Fig. 4(c). These maps are exploratory, and the patterns will be verifiable when larger cohorts of subjects are available.

4 Conclusion

Here we proposed an automated framework for genetic analysis of clustered fiber tracts in a large population. We focused on geometric properties of the tracts, such as their local thickness (which is related to the mean distance of fibers to a central curve), and their dispersion. These features were heritable, and therefore may offer promising targets to screen for specific genetic polymorphisms that influence tract geometry.

As this was a large, multi-subject study, nonlinear registration of HARDI was used to better align fibers prior to atlas-based clustering. We have found that atlas based clustering can give more anatomically interpretable tracts than spectral approaches that use geometric information about the fibers themselves, but combining both types of information may offer additional benefits in the future.

The tract shape measures we defined are basic, intuitive parameters that may not fully represent the characteristics of tract geometry. More sophisticated measures will be defined, in future, to more fully characterize tract shapes, and how they interrelate. In addition, as the sample size increases, we will fit more complex structural equation models to separate genetic (A), shared environmental (C), and unique environmental (E) components of the variance.

This is a high-throughput workflow, and avoids the inefficiency of manually seeded approaches. It may expedite the discovery and replication of specific genetic polymorphisms associated with tract characteristics.