The stability of cylindrin β-barrel amyloid oligomer models – a molecular dynamics study

Abstract

Small soluble amyloid oligomers are believed to play a significant role in the pathology of amyloid diseases. Recently, the atomic structure of a toxic oligomer formed by an 11 residue and its tandem repeat was found to have an out-off register antiparallel β-strands in the shape of a β-barrel. In the present article we investigate the effect of mutations in the hydrophobic cores on the structure and dynamic of the β-barrels using all atom multiple molecular dynamics simulations with an explicit solvent. Extending previous experiments with molecular dynamics simulations we systematically test how stability and formation of cylindrin depends on the interplay between hydrophobicity and steric effects of the core residues. We find that strong hydrophobic interactions between geometrically fitting residues keep the strands (both in register and out-off-register interface) in close proximity, which in turn stabilizes the side-chain and main-chain hydrogen bonds, and the salt bridges on the outer surface along the weak out-of-register interface. Our simulations also indicate presence of water molecules in the hydrophobic interior of the cylindrin β-barrel.

Introduction

Amyloid formation is implicated in the pathology of over 20 human diseases including Alzheimer’s, Parkinson diseases, type 2 diabetes and cataract^1,2. There is increasing evidence that the main cause of amyloid cellular toxicity^1,3 are soluble oligomers. While amyloid fibrils themselves exhibit little toxicity ⁴ and are built out of highly ordered parallel or antiparallel in-register β-sheets with a dry steric zipper interface between sheets ^5,1, these toxic amyloid oligomers are unstable, rich in β-sheet structure, display polymorphic properties and react with oligomer recognizing antibody^6,7. Because of the potential health applications there is considerable interest in the structure of these toxic oligomers and the process by that they form and/or convert to fibrils. However, these transient structures and processes are difficult to probe in experiments; and until recently there did not exist a plausible model for these oligomers and their growths.

Recently, Eisenberg’s team has resolved the atomic structure of cylindrin from αB–crystalline. Cylindrin is a toxic oligomer built out of six identical 11-residue peptides that form out-of-register antiparallel β-strands in the shape of a barrel⁸, instead of the in-register β-strands typically observed in amyloid fibril structures. Based on cell toxicity studies they have proposed that the out-of-register β-barrel of cylindrin is a structural motif shared by the various toxic amyloid oligomers^{4, 8}, and that cylindrin therefore can serve as a model for the toxic oligomers implicated in Alzheimer’s and other diseases. This hypothesis explains, for instance, why amyloid oligomers can interact with lipid membranes by forming ion pores that lead to ion leakage resulting in cell death ³. The Eisenberg hypothesis is supported by recent experiments of Pan et al. ⁹ who have found β-barrels of tetrameric Aβ_1–40 peptides arranged in antiparallel β-turn-β motifs similar to the X-ray structures of cylindrins^8,4. Supporting evidence comes also from a computational study by Liu C et al⁴ who could demonstrate that the C terminal of Aβ_1-42 is indeed capable of forming a cylindrin-like oligomer with high non polar surface⁴. Hence, short peptides oligomer such as cylindrin can provide models for the process by that amyloid oligomers assemble, and therefore allow one to probe the factors that contribute to their assembly and stability. The latter question is the topic of the present paper.

The 11-residue segments from αB–crystalline and its tandem repeat form in solution hexamers and trimers, where six β–strands arrange in a cylindrical barrel⁸ (Figure 1), built from three identical anti-parallel in-register pairs with strong interfaces and three out-off-register antiparallel pairs. The in registers pairs of strands form more main chain hydrogen bond than the out-off-register pairs. The interior of the cylinder is devoid of water and consists of three pairs of hydrophobic contacts between valine residues in the top and the bottom of the cylindrin with a total of six hydrophobic contacts. Substitution of Val4 residues with Trp in the tandem repeat of the 11-residue segment from αB–crystalline disrupt the formation of the cylindrin structure due to steric clash of the buried residues ⁸ and leads to reduced cell toxicity. On the other hand, replacement of Val2 with Leu leads to a stable cylindrical barrel. These previous results suggest that formation and stability of the cylindrins depend on the interplay between hydrophobicity and van der Waals volume of the side chains inside the cylindrin^8,4.

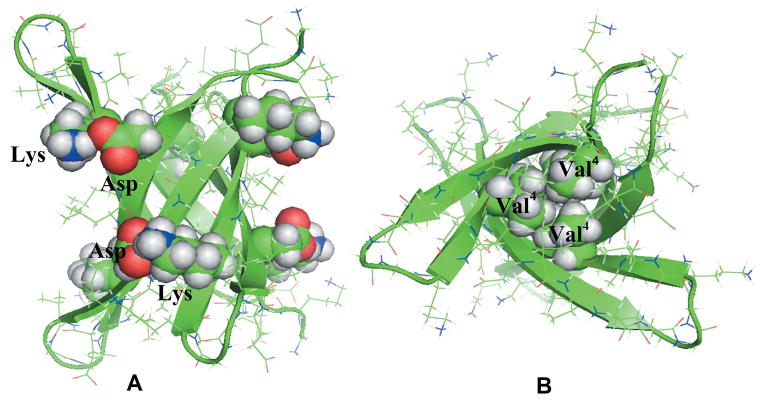
Figure 1.

Residues involved in the salt bridge interactions (A) and hydrophobic interactions (B) are labeled and shown in sphere in the initial structure of the tandem repeat cylindrin.

We hypothesize that increasing hydrophobicity with slight or no increase in side chain size would stabilize the cylindrin while decreasing the size and hydrophobicity would reduce the stability. On the other hand, bulky side chains in the center of the dry inner hydrophobic core would lead to steric clashes and therefore are not compatible with out-off-register packing of the cylindrin. In order to test this hypothesis we have mutated in this in-silico study systematically the Val4 and Val8 residues in the tandem repeat and single chain cylindrin (Table I), as contacts formed by the hydrophobic valine residues contacts are believed to be important during the early stages of the β-barrel cylinders formation⁸.

Table I.

Summary of simulation conditions for the wild type and mutants of tandem repeat cylindrin, the single chain cylindrin and steric-zipper fibril models. Mutations are marked with red color and bold font. The postfix –TR marks tandem repeats, -SZ steric zipper.

Models	Peptide sequence	Strand organization	Pdb code	Simulated time, ns	Temp. (K)
Tandem repeat cylindrin
WT-TR	GKVKVLGDVIEVGGKVKVLGDVIEV	3 (hairpins), anti-parallel	—	300 ns (3), 50 ns (2)	310
V2L-TR		3 (hairpins), anti-parallel	3SGR	300 ns (3), 50ns (2)	310
V4AV8A-TR		3 (hairpins), anti-parallel	—	300 ns (3), 50 ns (2)	310
V4GV8G-TR		3 (hairpins), anti-parallel	—	300 ns (3), 50 ns (2)	310
VTL-TR		3 (hairpins), anti-parallel	—	300 ns (3), 50 ns (2)	310
Single chain cylindrin
WT	KVKVLGDVIEV	6 strands, anti-parallel	3SGO	300 ns (3),	310
V2L		6 strands, anti-parallel	3SGP	300 ns (3	310
V4AV8A		6 strands, anti-parallel	–	300 ns (3)	310
V4GV8G		6 strands, anti-parallel	–	300 ns (3)	310
V4LV8L		6 strands, anti-parallel	–	300 ns (3)	310
Steric-zipper fibril models (Sheet 2, strands 6)
WT-SZ	KVKVLGDVIEV	Anti-parallel, strand-sheet	Ref (6)	50 ns (2)	310
V2L-SZ		Anti-parallel, strand-sheet	-	50 ns (2)	310
V4AV8A-SZ		Anti-parallel, strand-sheet	-	50 ns (2)	310
V4GV8G-SZ		Anti-parallel, strand-sheet	-	50 ns (2)	310
VTL-SZ		Anti-parallel, strand-sheet	-	50 ns (2)	310

Previous experimental work of the Eisenberg group has studied only the effect of single mutations of Val2 on the stability of the β-barrel⁸. In the present paper, we extend this investigation by exploring systematically in silico the effect of mutations that replace valine by residues with different hydrophobicity and size of side chains. Unlike in the previous work we investigate the effect of double mutations on tandem repeat, the single chain cylindrin and the steric zipper fibril models. Examining a broad set of double mutations of valine to leucine (larger hydrophobicity and side chain size), valine to alanine or glycine (lower hydrophobicity and side chain size), we probe how the cylindrin depends on: 1) hydrophobicity of the side chains in the hydrophobic core, 2) size of side chain in the hydrophobic core, 3) the dependency of the hydrogen bond and salt bridge interaction stability on the hydrophobic contacts in the out-off-register interface, 4) the effect of additional glycine residues in the hydrophobic core on the stability of the β-barrel cylinders. For this purpose, we have performed molecular dynamic simulations of various the β-barrel models as listed in Table I. We simulate both tandem repeat and single chain cylindrin models, as the three double glycine linkers and the additional N-terminal glycine in the tandem repeat may influence its stability. Simulating both tandem repeats and their related steric zipper fibril models for wild type and all mutants, we compare also the difference in the assembly energies of the fibril and β-barrel tandem repeat cylinders. This complements a pervious study that compared the assembly energies of the wild type single chain cylindrin and its steric zipper fibril model⁸. Systematically probing the role of the hydrophobic core motif and salt bridges in the assembly and stability of the cylindrin β-barrel our study derives rules that can be helpful for designing inhibitors molecules ¹⁰ or for designing amyloid based materials¹¹. Our simulations also support a commonly assumed mechanism for cell toxicity of the amyloid oligomers as they reveal the presence of water molecules in the hydrophobic interior of the cylindrin β-barrel.

Material and methods

The x-ray derived atomic structures of the tandem repeat cylindrin (PDB Code 3SGR), single chain cylindrin (PDB Codes 3SGO and 3SGP) are reported by Eisenberg group ⁸. The coordinates of steric zipper fibril model of the amyloid peptides KVKVLGDVIEV is kindly provided by Eisenberg group⁸.

Computational Mutation

The experimental tandem repeats and single chain cylindrin models are used as the starting structure to generate hydrophobic core mutants as listed in Table I. Starting configurations of the mutants are built from the wild type by replacing the side chains of the targeted residues with alanine, glycine and leucine using the VMD software¹². The mutants are obtained from wild type coordinates by replacing the side chains of the targeted residues, but without changing the backbone conformations and side-chain orientations. The structure of the designed mutants is first minimized for 500 steps using the steepest decent algorithm with the backbone of the protein restrained before being subjected to the system setup and the production simulation described below.

Molecular dynamics simulations

Simulations of structure and dynamics of large biomolecules require accurate and reliable force fields (FF) that are able to reproduce the behavior of the peptides¹³. A common choice for exploring amyloid peptide aggregation ^13,14 and β-barrel proteins in explicit water ^15,16 is the AMBER ff99SB force field ¹⁷, used also in this study. We run three independent molecular dynamics simulations of 300 ns for the wild type and each of the V4GV8G, V4AV8A, V4LV8L and VTL mutant β-barrel cylindrins models (see Table I). For these simulations we use the GROMACS program version 4.5.3 ¹⁸ and a time step of 2 fs. Hydrogen atoms are added using the pdb2gmx module of the GROMACS suite. The starting configurations of all proteins are set in the center of a cubical box where the distance between the solute and the edge of the box is at least 12 Å. Periodic boundary conditions are employed, and electrostatic interactions calculated with the PME algorithm ^19,20. Hydrogen atoms are constrained using the LINCS ²¹ algorithm, and for water the Settle algorithm is used ²². The temperature of 310 K is kept constant by the Parrinello-Donadio-Bussialgorithm²³ (τ = 0.1 fs) and pressure with the Parrinello-Rahman algorithm ²⁴ (τ = 1 fs) at 1 bar. The Parrinello-Donadio-Bussi thermostat is similar to Berendsen coupling but the stochastic term ensures that a proper canonical ensemble is generated ^23,25. The solvated start configuration is first energy minimized using the steepest descent method, followed by conjugate gradient. Afterwards, the system is equilibrated in two steps of 500ps, the first step in an NVT ensemble and the second phase in an NPT ensemble at 1 bar. After equilibrization, 300 ns of trajectories are analyzed for each system to examine the structural changes of the oligomers aggregates with time. Data are saved at 4.0 ps intervals for further analysis. For each system, three independent simulations with different initial velocity distributions are performed to test for thermalization and to guarantee at least three independent sets of measurements.

The temperature of 310 K is chosen as a compromise between preserving the experimental observed stability of the amyloid fibrils ²⁶ and the desire to enhance sampling by raising temperature ^27,28. The molecular dynamics trajectories are analyzed using the tool set of the GROMACS package. Especially, we monitor conformational changes and stability of the β-barrel models through the time evolution of the root means square deviations of the Cα atoms (RMSD), root-mean-square fluctuation (RMSF), radius of gyration, distance between the strands, pore diameter, fraction of native contacts, persistence of the Asp-Lys salt-bridges, hydrophobic contacts and hydrogen bonds. Structural changes are visualized using PyMOL²⁹.

Free energy calculations

The free energy of cylindrin tandem repeats is estimated with the MM-PBSA methodology as implemented in AMBER11³⁰ and compared with that of the steric-zipper fibril models. For the purpose of these MM-PBSA free energy calculations we simulate two independent 50ns trajectories for each of the cylindrin tandem repeats and two runs of equal length for each of the steric-zipper fibril models (Table I). These simulations rely on the AMBER11³¹ software package, using again the all atom AMBER99SB¹⁷ force field. The molecules are solvated in a periodic water box of TIP3P molecules, and carefully equilibrated before the production run²⁷.

Results and discussion

Structural stability comparison

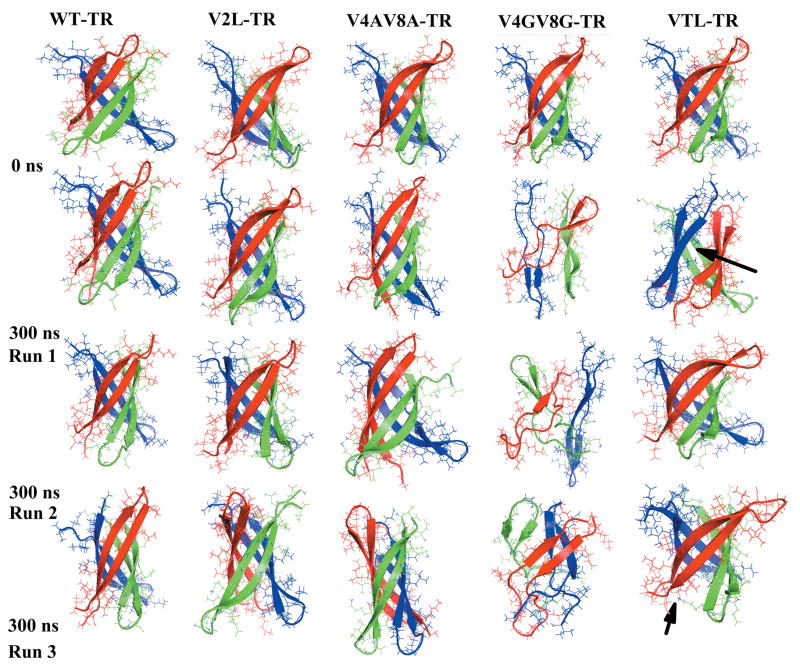
The stability and flexibility of the β-barrels is described in terms of root mean-squared deviation (RMSD), radius of gyration (Rg), pore diameter, and inter-strand distances. The Cα root mean-squared deviation (RMSD) provides a measure for the protein drift from the initial X-ray-derived conformation (the reference structure) and therefore monitors the structural changes during the run. This quantity differs strongly between the various systems, with the smallest RMSD values observed for the wild-type and V2L mutants, and the largest values seen for the double Glycine mutants (Table II). The average <RMSD> of the wild type and V2L mutant of both the tandem repeats and the single chain cylindrin are small: less than 1.80 Å. In contrast, the<RMSD> of the double mutants (V4GV8G, V4AV8A and VTL) are within the range of 2.69 to 5.74 Å, and therefore much larger. These large RMSD values of V4GV8G and V4AV8A mutants indicate substantial structural changes in these mutants and instability of these mutants. Visual inspection of the structures shows that the initial β-barrels structure is retained in all the three trajectories of the wild type and V2L mutant of both the tandem repeat and the single chain cylindrin (Figure 2 and 1S). On the other hand, the initial β-barrels structure is lost in the V4GV8G mutant trajectories, and in the other mutants the β-barrels structures are unstable (Figure 2 and 1S). The collapse of β-barrel structure in Glycine mutants is likely due to high flexibility of glycine and the smaller hydrophobic interaction in the inner dry interface compared to the wild-type (Figure 2 and 1S)

Table II.

Average Cα RMSD (Å), Rg (Å), inner pore diameter (Å) and inter-stand distances (Å) of the wild type and mutants of tandem repeat cylindrin, the single chain cylindrin.

Type of Analysis	Run	Models of tandem repeat cylindrin					Models of single chain cylindrin
		WT-TR	V2L-TR	V4AV8A-TR	V4GV8G-TR	VTL-TR	WT	V2L	V4AV8A	V4GV8G	V4LV8L
Cα RMSD (Å)	1	1.72	1.52	3.03	5.06	2.84	2.27	1.51	2.96	4.13	2.86
	2	1.63	1.46	3.04	6.96	3.16	1.33	1.08	2.97	5.10	2.49
	3	2.06	1.53	3.31	5.19	2.99	1.68	1.46	3.271	5.09	2.71
Mean value ±SD§		1.81±0.2	1.50±0.3	3.13±0.4	5.74±0.8	2.99±0.5	1.76±0.3	1.35±0.3	3.07±0.3	4.62±0.9	2.69±0.4
Rg (Å)	1	12.33	12.23	12.15	12.01	12.52	11.70	11.68	11.59	11.65	12.10
	2	12.35	12.22	12.19	12.41	12.21	11.92	11.73	11.70	11.79	11.61
	3	12.37	12.22	12.17	11.81	12.18	11.77	11.75	11.74	11.65	12.04
Mean value ±SD		12.35±0.1	12.22±0.1	12.17±0.1	12.08±0.3	12.31±0.3	11.79	11.72±0.1	11.68±0.1	11.72±0.3	11.91±0.2
Pore diameter (Å)	1	11.84	12.24	12.05	14.85	13.34	11.63	11.66	11.68	8.94	12.58
	2	12.02	12.14	12.60	7.98	13.36	11.58	12.16	12.60	16.84	13.61
	3	11.72	12.31	13.13	13.35	13.24	11.96	12.17	13.13	12.90	13.70
Mean value ±SD		11.86±0.5	12.22±0.5	12.59±1.3	12.06±2.1	13.31±0.6	11.72±0.5	11.99±0.6	12.59±1.3	12.89±1.8	13.30±0.9
In register ISD *	1	3.72	3.77	3.95	6.24	3.77	3.67	3.72	3.88	4.65	3.89
	2	3.74	3.77	3.94	7.45	3.75	3.64	3.77	3.91	5.46	3.77
	3	3.66	3.77	3.95	5.35	3.76	3.72	3.73	4.05	5.06	3.89
Mean value ±SD		3.71±0.1	3.77±0.1	3.94±0.2	6.34±0.9	3.76±0.1	3.70±0.1	3.74±0.1	3.95±0.2	5.44±0.7	3.85±0.2
Out-off -register**	1	4.84	5.08	4.61	5.99	6.87	4.76	4.93	4.62	6.08	7.41
	2	4.89	5.09	4.60	6.99	6.40	4.74	5.11	4.59	6.12	6.26
	3	4.77	5.08	4.60	6.28	6.54	4.87	5.01	4.63	6.10±0.80	7.38
Mean value ±SD		4.83±0.2	5.08±0.3	4.61±0.1	6.43±1.0	6.60±0.6	4.81±0.1	5.01±0.4	4.61±0.2	6.19±0.8	7.02±0.5

^§Mean values and standard deviation (SD) are calculated from the three values obtained by averaging over the 300 ns of each of the three independent runs of each model

^*In register inter-strand distance,

^**out-off-register inter-strand distance

Figure 2.

Snapshots of wild type and mutants of tandem repeat cylindrin at the beginning and end of 300 ns simulation.

In order to evaluate the compactness of the studied protein, we have estimated the size of a protein by its radius of gyration and the diameter of the inner pore. The average radii of gyration (Rg), suggest that the overall compactness of the β-barrels does not change significantly during the wild type and V2L mutant simulations of both the tandem repeat and the single chain cylindrin. This indicates that their native protein structures are stable (Table II). In contrast, the average Rg values for V4GV8Gmutants are 12.08±0.3 Å and 11.68±0.1 Å for the final structures of tandem repeat and the single chain cylindrin, indicating that these mutants have collapsed (Table II, Figure 2 and 1S).

Monitoring the diameter of the pore within the β-barrel allows one to quantify the extent of conformational re-arrangement of the β-barrel. On average, the pore in the micro crystal structure is narrowest near the center i.e. away from the mouth of the β-barrel. In the x-ray structure ⁸, the pore diameter at this point is 12 Å. The pores are wider in the mutants than in the wild type when valine in the hydrophobic core is mutated to leucine and alanine (Table II). The wild type and other mutants retain the initial inner β-barrel (around 12 Å, Table II) while the β-barrels exhibit major conformational alterations in the glycine mutants.

The β-barrel cylinders have two kinds of contacts along the strand-to-strand interface: in register interfaces have strong contacts, and out-off-register interfaces have weak⁸ contacts. The strong interface for the tandem repeat is between strands 1 and 2, strands 3 and 4, and strands 5 and 6. The weak interfaces involve the contacts between strands 1 and 4, strands 2 and 6, and strands 3 and 5. In the single chain cylindrin the strong interface is between strands 1 and 3, strands 2 and 5, and strands 4 and 6. The weak interface involves the contacts between strands 1 and 4, strands 2 and 3, and strands 5 and 6. The inter-strand distances are measured as an averaged distances between the mass centers of two adjacent β-strands. The average in register and out-off-registers interface distances for wild type and mutants are shown in Table II. The average out-off- register interface inter-strand distance for wild type (both WT and WT-TR), and V2L (V2L-TR) mutants are about 5 Å. In contrast, the out-off-register interface inter-strand distance for the VTL and V4GV8Gmutants of both the tandem repeat and single chain cylindrin are more than 1.5 Å larger than the wild type, indicating that there is a loss of inter strand contacts along the weak interface. In the case of the glycine mutants this loss of the out-off-register interface is due to an increase in the flexibility of the β-strand region that reduces the contact between strands. In the case of the double leucine mutant the increase in the inter-strand-out-off-register interface is due to the expansion of the inner hydrophobic region as needed to accommodate the side chain of leucine, which is larger than the one of valine found in the wild type (see Figure 2 and 1S). All of the β-barrels structures except the glycine double mutants have an average in-register inter-stand distance of about 3.8Å suggesting strong contacts along these interfaces (Table II). However, in the V4GV8G mutants the average in-register inter-stand distance is 6.3±0.9 Å and 5.4±0.7 Å for the tandem repeat and single chain cylindrin respectively. Hence, the instability of the glycine mutant is due to the loss of both in register and out-off-register contacts while in mutants such as V2L, V4AV8A it is due to the loss of the inter-strand contacts along the out-off-register interface (Table II).

Native contacts and RMSF

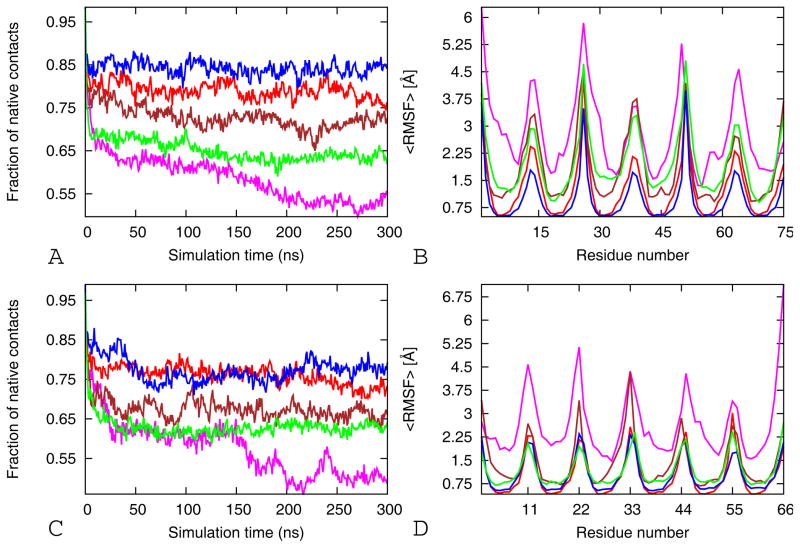
In order to study further the driving force for the stability of β-barrels, the fractions of native contacts are calculated. We define a side chain contact by the condition that the distance between the center of mass of two side chains is 6.5Å. Our reference structure is the energy-minimized crystal structure. Figure 3A and C show that stable systems (WT, WT-TR, V2L and V2L-TR) maintain at least 75% of their native contacts, whereas unstable systems (V4GV8G) lost 45% of the native contacts after 100 ns. The V2L tandem repeat and single chain cylindrin models loss about 35 % of the native contacts after 50 ns. The double alanine mutant tandem repeat and single chain models loss about 30% of the native contacts after 50 ns. The correlation between the stability of the oligomers and the number of native contacts suggests that the inter-strand interactions along the interfaces are important for stabilizing the oligomers (Table II).

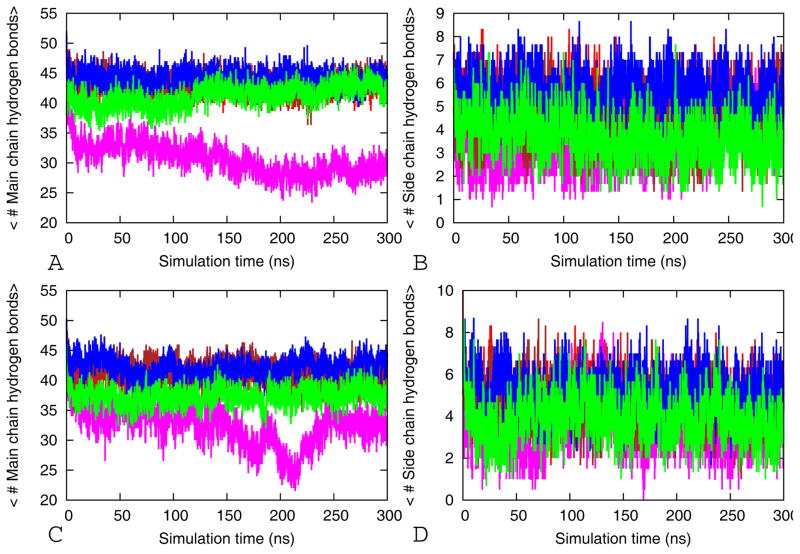
Figure 3.

The fraction of native contacts and average backbone RMS fluctuations (RMSF) per residue as function of time. The average fraction of native contacts (A) and the average RMSF (B) of the tandem repeat cylindrin simulations. Red for wild-type (WT-TR), magenta for V4GV8G-TR, brown for V4AV8A-TR, blue V2L-TR, and green for VTL-TR. The average fraction of native contacts (C) and the average RMSF (D) of the single chain cylindrin simulations. Red for wild-type (WT), magenta for V4GV8G, brown for V4AV8A, blue V2L-TR, and green for VTL. The results are calculated by using the three 300 ns trajectories for each model.

The flexibility of the β-barrels can be described also in terms of the root mean square fluctuations (RMSFs), which reflect the mobility of a certain residue around its mean position. The RMSF values of Cα atoms are displayed in Figure 3B and D. The most flexible residues for the wild type and mutants are located in the N-terminal and C terminal regions and in the loops connecting the β-strands in the tandem repeats (Figure 2). This is because the side chains of these residues point radially outward from the protein and are exposed to solvent, preventing stiffening. The WT-TR and V2L-TR tandem repeats have little flexibility and are nearly super imposable. However all the other mutants have larger RMSFs than the wild type, with the largest RMSF being observed in the double glycine mutants (Figure 3). The residues involved in the hydrophobic interactions on the interface of both along the in registered and out-off-registered strands interface show a little fluctuation. Mutations to less hydrophobic residues (Ala and Gly) and to larger and more hydrophobic residue (Leu) within this region results in a considerably higher value of RMSF emphasizing the role of hydrophobic interaction in stabilization of the β-barrel models (Figure 3B and D).

The differences in RMSF, Rg, RMSD, inter-stand distances, pore diameter and native contacts of the various β–barrel molds are consistent with the stability of the models when inspected visually (Figures 2 and 1S). The replacement of the leucine for valine at position 2 (V2L-TR and V2L) leads to a β-barrel structure that is identical with the wild type in both the tandem repeat and single chain cylindrin. In the wild type, the overall cylindrical shape of the β-barrel is maintained throughout the 300 ns trajectories. In all other mutants we find loss of structural stability, largest in the glycine mutants.

Effect of Cα-Cα hydrophobic contacts

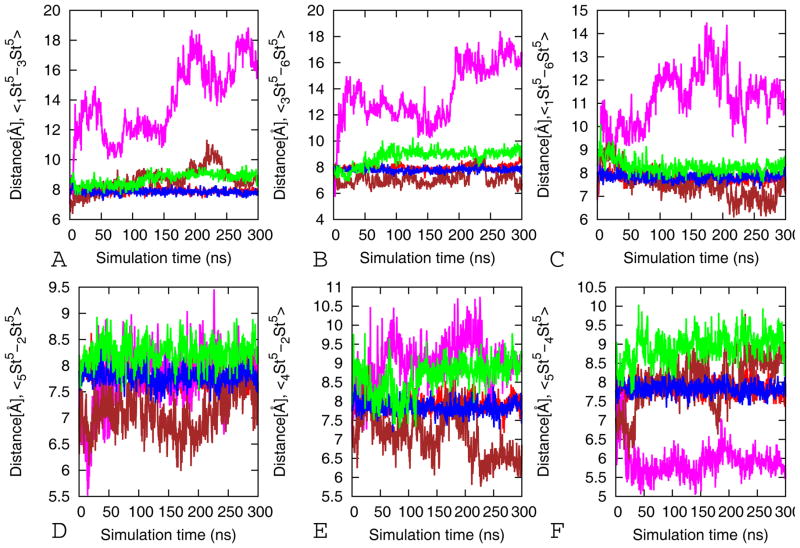
The stability of the beta barrel structure depends on both hydrophobicity and size (and flexibility) of the side chain in the inner core of the system. An increase in side chain size of residues in the dry inner core of the cylindrin will reduce its stability, as the pore size has to increase to avoid steric clashes. The resulting expansion of the pore changes the distance and orientation between strands in the out-off-register interface reducing the number of salt bridge and hydrogen bonds. On the other hand, increasing the number of tiny and flexible glycine residues in the hydrophobic core of the strands reduces its rigidity and makes the mutant unstable (Figure 4). The structurally stable wild type and its V2L mutant model retained an average Cα-Cα of about 8 Å (the Cα-Cα distance in the experimental microcrystal structure between adjacent valines in the inner hydrophobic core is 8 Å) between the neighboring Val4 residues through the simulation. This indicates that the hydrophobic contacts between adjacent valines are intact while there is an increase in the Cα-Cα distance along the out-off-register and in registers interfaces in VTL-TR, V4LV8L V4GV8G and V4GV8G. In the VTL-TR and V4LV8L the average Cα-Cα distances are above 8 Å and vary with 8 to 10 Å indicating the strands along the interfaces are moving apart (Figure 4). The alanine double mutants (V4AV8A-TR and V4AV8A) have average Cα-Cα distances below 7 Å along the two contacts indicating they are close to each other due to the reduced size of the side chain. Simulations of the mutants (V4AV8A-TR, V4AV8A, V4GV8G-TR, and V4GV8G) show that substitution of Val-4, Val-8 by a shorter Ala or Gly residue disrupts the dry interior steric zipper between two neighboring strands. The substituted Ala and Gly residues do not have the strong van der Waals interactions with its neighboring strands, leading to destabilization of the oligomers. Hence, the correct geometrical matching of the side chains via inter-strand interactions is another important factor in determining the stability of oligomers³².

Figure 4.

Hydrophobic contacts Cα-Cα distances between the pair of residue 4 from each strand (St) in the dry interior of tandem repeat cylindrin as function of time. Red for wild-type (WT-TR), magenta for V4GV8G-TR, brown for V4AV8A-TR, blue V2L-TR, and green for VTL-TR. Shown are the averages over three independent 300 ns trajectories. For each model, the standard deviations are calculated from the three values obtained by averaging over each of the 300 ns trajectories.

Role of hydrogen bonds

Main chain peptide hydrogen bonds and side chain hydrogen bonds are the main forces that stabilize amyloid fibril and β-barrel cylinders structures ^4,5,8,13. Hence, the change in the number of hydrogen bonds along a molecular dynamics trajectory is a measure for the stability of the β-barrels models. The mean number of inter-stand backbone hydrogen bonds and side chain hydrogen bonds are presented in Figure 5. In the in register interface there are only main chain hydrogen bonds while the out-off-register interface includes side chain and main hydrogen bonds. Hydrogen bonds are calculated using the g_hbond module available in Gromacs. A hydrogen bond is assigned if the distance between donor D and acceptor A is ≤3.5 Å and the angle D–H-A was smaller than 30.0°. The average number of main chain and side chain hydrogen bonds of wild-type and V2L mutants and V4AV8A of both tandem repeat and the single chain cylindrin are higher than that from the V4GV8G and VTL mutants (Figure 5). Especially, the stable models (WT-TR, WT, V2L-TR and V2L) have a larger number of side chain hydrogen bonds. These are responsible for retaining the initial micro crystal structure in physiological environment (Figure 5). As also supported by our above geometric stability analysis (RMSF, RMSD etc.), we conclude that the stability of the short peptide oligomers depends also on the number of side chain and main chain hydrogen bonds. Because of its high stability, the hydrogen bond network in collaboration with the hydrophobic interactions inhibits the dissociation of the stands and keeps the β-barrel cylinders structure intact.

Figure 5.

Average numbers of main chain hydrogen bonds and side chain-side chain as function of time. For tandem repeat cylindrin, the average main chain hydrogen bonds are shown in (A) and side chain-side chain in (B). Red for wild-type (WT-TR), magenta for V4GV8G-TR, brown for V4AV8A-TR, blue V2L-TR, and green for VTL-TR. For single chain cylindrin, the average main chain hydrogen bonds are displayed in (C) and side chain-side chain in (D). Red for wild-type (WT), magenta for V4GV8G, brown for V4AV8A, blue V2L-TR, and green for VTL. The results are the averages of three independent 300ns trajectories. Here, a stands for strand number and b for residue number in _aSt^b-_aSt^b designation of the Cα-Cα distance of the hydrophobic core residues Val⁵ of the wild type tandem repeat and mutants.

Role of the salt bridge interactions

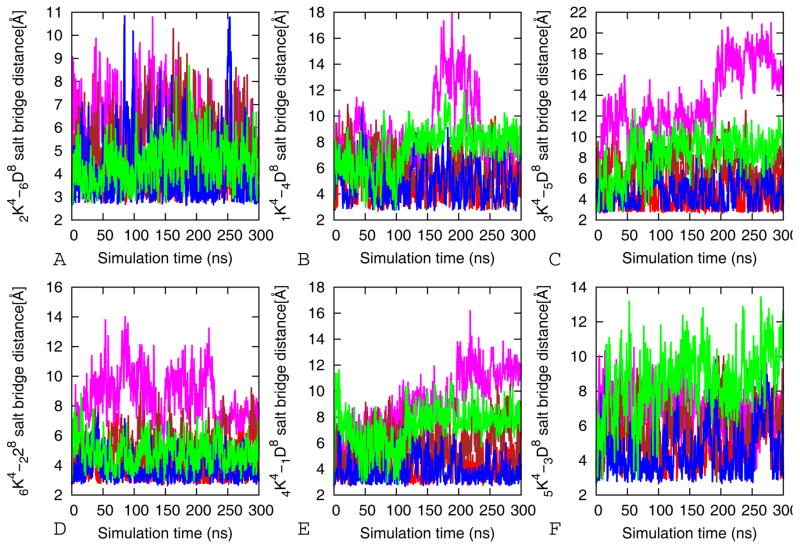
The anti-parallel orientation of strands in the β-barrel cylinders models allows for close contact between positively charged Lys and negatively charged Glu side chains of the C- and N termini of neighboring molecules in the out-off-register interface. These salt bridges contribute to the stabilities of the β-barrel oligomers. We perform a time dependent analysis of the salt bridges to determine its influence on the stability of β-barrel peptide oligomer models. The salt bridge distance is calculated as the averaged distance N atom of the NH₃⁺ in Lys to the C=O bonds carboxyl group of Glu. Direct salt bridges are assumed to be around 4.3 Å, whereas indirect or water-mediated salt bridges have a distance between 4.3 and 7.0 Å ^{33, 34}. The stability of Lys-Asp contact of the β-barrel oligomers is analyzed and the results are shown in Figure 6 and Figure 3S. Six salt bridges are present in both the tandem repeat and single chain cylindrin, and the distances between any pair of oppositely charged residues range from 3.3 to 7.0 Å (except for VTL-TR, VTL, V4GV8G-TR and V4GV8G). Unlike the wild type and V2L the remaining mutants with reduced structural stability have salt bridges that are flexible with distances larger than 7 Å (Figure 6 and 3S). The Asp and Lys residues, involved in salt bridge formation, are solvent exposed due to their location close to the C and N terminal flexible regions. Hence, they are unlikely to be of structural importance without the strong hydrophobic interactions that keep them in close proximity (Figure 5 and 2S). In conclusion, our simulation reveal that hydrophobic residues with stabile geometrically fitting side chains in the dry inner core stabilize the tandem repeat and single chain cylindrin models due to an increase in the number of hydrophobic contacts that in turn anchor the side chain and main chain hydrogen bonds, and salt bridges on the outer surface.

Figure 6.

Comparison of the average salt bridge interactions distances between Lys (K) and Asp (D) along the 300 ns simulation of the wild-type and its mutants of tandem repeat cylindrin along the three out of register interfaces. Red for wild-type (WT-TR), magenta for V4GV8G-TR, brown for V4AV8A-TR, blue V2L-TR, and green for VTL-TR. The results are the average of three independent 300 ns simulations of each system. Here, a stands for strand number and b for residue number in _aK^b- _aD^b designation of the salt bridge distance of the wild type tandem repeat cylindrin and mutants.

Free energy of tandem repeat cylindrins and steric-zipper fibril models

In general, methods such as free energy perturbation are superior over the MM-PBSA approach discussed in the method part, and therefore should be used despite that they are computationally much more costly (as they require extensive sampling of conformations). However, the Eisenberg group⁴ has shown that for cylindrin and fibril models MM-PBSA leads to a ranking of models that is in agreement with the one obtained from free energy perturbation. For this reason, we use the less costly MM-PBSA approach in our study. The calculated energetic stabilities of the various tandem repeat cylindrin models relative to the fibrils are shown in Table III. The individual energy terms contributing to the enthalpy are listed for each tandem repeats cylindrin and steric-zipper fibril models model as an average over both trajectories. Two thousand equally spaced snapshots are generated from the two 50 ns MD trajectories and all water molecules are removed before the MM-PBSA calculations. Coordinates are extracted by using MMPBSA.py script in AMBER11. The MM-PBSA single trajectory approach implemented in Amber11 is used to calculate the binding energy. The same approach has been used recently to study the thermodynamics of amyloidogenic peptides ^{35,36,28,37,27,13,38}. Solute entropic contributions have not been calculated since they can only be crudely estimated by normal mode analysis and their contribution to the total energy difference is small compared to the term resulting from conformational changes in amyloid peptides ^38,8. Hence, although the MM-PBSA calculations may overestimate the absolute binding free energy due to these missing terms and underestimate the de-solvation free energy, they give a reasonable qualitative estimate on the relative binding free energy as long as similar systems are compared^39,40. In our study, the investigated steric-zipper fibril models have in all cases lower free energy than the tandem repeat cylindrin models (Table III). The V2L, and wild type tandem repeats and their fibril forms are energetically more stable than the unstable models (V4AV8A-TR, V4AV8A-SZ, V4GV8G-TR compared with V4GV8G-SZ; and VTL-TR compared with VTL-SZ). However, even in the case of the most stable cylindrin (WT-TR, WT-SZ, V2L-TR), the free energy of the corresponding steric-zipper fibril model (V2L-SZ) is lower by more than 30 Kcal/mol, qualitatively similar to previous⁴ studies of the wild type. Given such large values, our results provide additional evidence that the out-off-register cylindrin structure is off pathway in the process of fibril formation.

Table III.

Calculated free energy and standard deviations calculated with MM-PBSA with its components (Kcal/mol) for the tandem repeats cylindrins and the steric-zipper fibril models

MM-PBSA binding energy components of the different tandem repeat cylindrins amyloid
System	ΔEvdw	ΔEele	ΔGPB	ΔGSA	ΔGsolv	ΔGbinding
WT-TR	−70.06† (0.1)‡	−469.67(10.9)	473.43(9.7)	−7.72(0.1)	465.71(9.6)	−74.03(1.4)
V2L-TR	−80.09(0.2)	−500.61(16.9)	501.94(15.6)	−8.34(0.1)	493.59(15.8)	−87.10(1.3)
V4AV8A-TR	−69.36(1.9)	−499.05(65.8)	502.15(60.9)	−8.43(0.5)	493.72(60.4)	−74.69(7.3)
V4GV8G-TR	−86.45(9.3)	−495.73(65.2)	522.81(70.3)	−9.94(0.9)	512.86(69.3)	−69.31(5.3)
VTL-TR	−78.85(1.9)	−429.72(35.3)	441.59(37.9)	−8.39(0.3)	433.20(38.2)	−75.37(4.8)
MM-PBSA binding energy components of doublelayer (SH2-ST6) steric-zipper fibril models
System	ΔEvdw	ΔEele	ΔGPB	ΔGSA	ΔGsolv	ΔGbinding	ΔΔG§
WT-SZ	−127.29(1.7)	−266.89(3.6)	294.59(7.6)	−12.69(0.1)	281.91(7.5)	−112.27(2.2)	−38.27
V2L-SZ	−124.72(2.5)	−354.23(36.7)	371.56(31.6)	−12.81(0.2)	358.74(31.8)	−120.21(2.4)	−31.11
V4AV8-SZ	−117.14(9.8)	−352.87(38.5)	380.08(42.9)	−11.83(0.1)	368.25(42.9)	−101.76(5.4)	−27.06
V4GV8G-SZ	−105.55(1.3)	−534.37(78.2)	558.37(78.2)	−12.53(0.4)	545.84(78.5)	−94.64(1.2)	−25.32
VTL-SZ	−139.72(4.3)	−323.53(24.6)	353.31(20.2)	−13.35(0.2)	339.96(20.4)	−123.29(0.1)	−47.86

ΔE_ele, non-solvent electrostatic potential energy; ΔG_PB, electrostatic contributions to the solvation free energy calculated with Poisson-Boltzmann equation; G_SA, nonpolar contributions to solvation free energy; ΔE_vdw, van der Waals potential energy; and ΔG_binding, calculated bindingΔG_solv are the polar, nonpolar and total solvation energies. Data are shown as mean with the standard deviation (SD) in brackets. ΔG_binding = ΔE_vdw + ΔE_ele + ΔG_sol; ΔG_sol = ΔG_PB + ΔG_SA.

^†Mean values are calculated from the two trajectories for each model resulting from two independent simulations.

^‡The standard deviation (SD) therefore describes the deviation between the two independent simulations.

ΔΔG^§(the difference in binding free energy between the tandem repeat cylindrins amyloid and steric-zipper fibril models. The negative values indicates the steric zippers are more stable than the corresponding tandem repeat cylindrins)

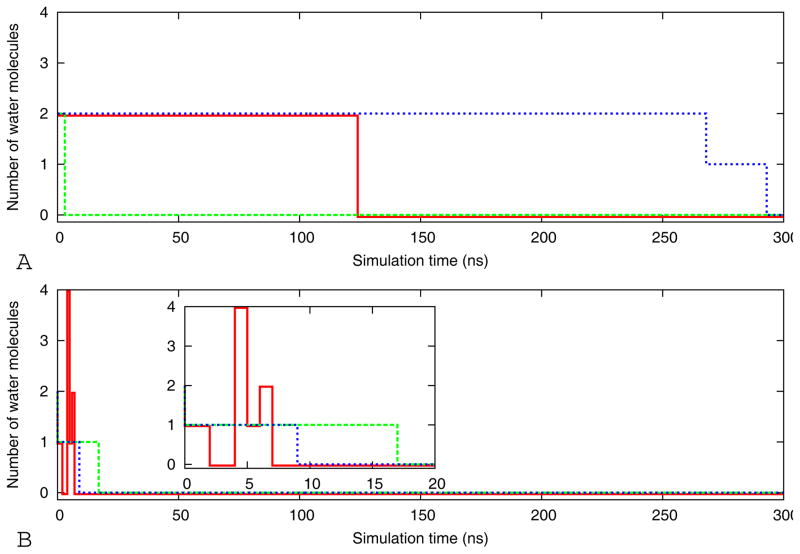
A likely cause for the toxicity of amyloids oligomers is the sequestration or mis-location of other proteins ^41,42 and the interactions of the oligomers with cell membranes that compromise the integrity of lipid membranes^43,42. The underlying mechanisms are only poorly understood⁴⁴. Membrane disruption could be caused through the formation of trans-membrane oligomeric pore. ³ Another possibility is that the hydrophobic oligomers increase membrane conductance and permeability to charged species by spreading the lipid head groups apart and consequently thinning the bilayer and lowering the permeability barrier⁴⁵. In the case of the β-barrel cylindrin, it seems plausible that their toxicity is due to their potential to act as pores in the cell membrane through which water molecules and ions can penetrate into the cell. In our molecular dynamics simulations the initial structures of the cylindrins do not enclose water molecules, but water can penetrate the interior of the β-barrel during the filling of the periodic box with water. In Figure 7 we show for the three independent trajectories of the tandem repeat models WT-TR and V2L-TR (two systems for which membrane leakage experimental data are available⁸) the number of water molecules in the interior of the β-barrel as function of time. Clearly, water molecules can enter the hydrophobic pore (see Figure 8), and for the wild type tandem repeat are observed in the interior over the time scale of up to 250ns, while they are pushed out of the interior of the V2L-TR mutants within the first 20ns. This is consistent with the experiments by the Eisenberg group, which show stronger leakage for the V2L-TR mutant than for the wild type WT-TR. However, in order to establish the mechanism of cylindrin cell toxicity, our simulations, revealing for the first time the presence of water within a model for toxic amyloid oligomers, need to be extended to computational studies of the cylindrin aggregation in the presence of lipid membranes. Such simulations are now in preparation.

Figure 7.

Number of water molecules in the interior central hydrophobic region of the cylindrin pore as a function of time for the three independent simulations (red, blue and green, respectively) of WT-TR (A) and V2L-TR(B)

Figure 8.

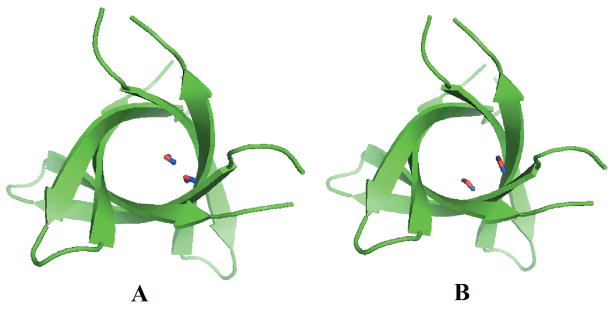
Snapshots of the tandem repeat β-barrel models with water molecules in the interior for WT-TR (A) and V2L-TR(B).

Conclusion

The cylindrin structure of αB–crystalline has been proposed as a structural motif that is common in all toxic amyloid oligomers. In the present paper we extend previous experimental investigations by exploring in silico the factors that determine the stability of the cylindrin structure. For this purpose, we have simulated the wild type and various single and double point mutants. Molecular dynamics simulations demonstrate that substitution of Val-4 and Val-8 by shorter and less hydrophobic Ala residues, or flexible Gly residues, disrupts the dry interior steric zipper between two neighboring strands. This is because the substitution of Val with Ala or Gly reduces van der Waals interactions between strands that stabilize the wild type oligomers. As a result, the Gly mutants (and to a lesser extend also the Ala mutants) become visibly disordered. In contrast, the single point mutation of Val2 to Leu (leading to a slight increase in hydrophobicity and size of side chain) does not alter the stability of the cylindrin structure. However, in the double Val to Leu mutants the pore size has to increase in order to avoid steric clashes. The expansion of the pore in turn reduces the number of hydrophobic contacts, hydrogen bonds and salt bridge, therefore reducing the stability of these mutants.

Our analysis suggests that the interaction between hydrophobic residues of a size that fit into the dry inner core are the main factor that stabilizes the tandem repeat and single chain cylindrin models. This is because the cylindrin geometry leads to a larger number of hydrophobic contacts that in turn stabilize the side chain and main chain hydrogen bonds, and the salt bridges on the outer surface along the weak out-off-register interface. As the Asp and Lys residues, involved in salt bridge formation, are solvent exposed, they are unlikely to be of structural importance without strong hydrophobic interactions that keep them in close proximity.

The relative stabilities of the mutants and wild types have been ranked based on the binding energy using a MM-PBSA-based analysis, and are found to be in agreement with pervious computational and experimental observation^8,4. The difference in the free energy between the fibril models and the corresponding β-barrel cylindrin indicate that the fibril models are more stable than the β-barrel by more than 10 Kcal/mol. These large values add evidence to the idea that the β-barrel model from B–crystalline is off the pathway to the fibril formation⁸, although due to limitations of available computing resources we did not explore directly the oligomerization process. A complete description of the oligomer assembly will require further simulations using efficient sampling methods and coarse-grained models that we are now setting up. Another extension of the presented work is simulations of cylindrin aggregation in the presence of lipid membranes since we could demonstrate the presence of water molecules in the hydrophobic interior of the cylindrin β-barrels. Such simulations therefore would probe directly the mechanism of cell toxicity of an amyloid oligomer. However, already our present results have demonstrated that molecular dynamics simulations can identify the factors that determine the stability of β-barrel amyloid oligomers. They confirm the role of computational modeling as a tool that can complement the expensive and time-consuming in vitro experiments on amyloid oligomers assembly and stability.

Supplementary Material

Supplemental Figure 1. Figure S1.

Snapshots of wild type and mutants of single chain cylindrin at the beginning and end of 300 ns simulation.

Supplemental Figure 2. Figure S2.

Change in the hydrophobic contacts Cα-Cα distances between the pair of residue 4 from each strand in the dry interior of single chain cylindrin. Red for wild-type (WT-TR), magenta for V4GV8G, brown for V4AV8A, blue V2L, and green for VTL. The results are the averages of three independent 300 ns trajectories. Here, a stands for strand number and b for residue number in _aSt^b-_aSt^b designation of the Cα-Cα distance of the hydrophobic core residues Val⁴ in the wild type single chain cylindrin and mutants.

Supplemental Figure 3. Figure S3.

Comparison of the average salt bridge interactions distances between Lysn and Asp along the 300 ns simulation of the wild-type and its mutants of single chain cylindrin along the three out of register interfaces. Red for wild-type (WT-TR), magenta for V4GV8G, brown for V4AV8A, blue V2L, and green for VTL. The results are the average of three independent 300 ns simulations of each system. Here, a stands for strand number and b for residue number in _aK^b- _aD^b designation of the salt bridge distance of the wild type single chain cylindrin and mutants