Pixel-based absorption correction for dual-tracer fluorescence imaging of receptor binding potential

Abstract

Ratiometric approaches to quantifying molecular concentrations have been used for decades in microscopy, but have rarely been exploited in vivo until recently. One dual-tracer approach can utilize an untargeted reference tracer to account for non-specific uptake of a receptor-targeted tracer, and ultimately estimate receptor binding potential quantitatively. However, interpretation of the relative dynamic distribution kinetics is confounded by differences in local tissue absorption at the wavelengths used for each tracer. This study simulated the influence of absorption on fluorescence emission intensity and depth sensitivity at typical near-infrared fluorophore wavelength bands near 700 and 800 nm in mouse skin in order to correct for these tissue optical differences in signal detection. Changes in blood volume [1-3%] and hemoglobin oxygen saturation [0-100%] were demonstrated to introduce substantial distortions to receptor binding estimates (error > 30%), whereas sampled depth was relatively insensitive to wavelength (error < 6%). In response, a pixel-by-pixel normalization of tracer inputs immediately post-injection was found to account for spatial heterogeneities in local absorption properties. Application of the pixel-based normalization method to an in vivo imaging study demonstrated significant improvement, as compared with a reference tissue normalization approach.

1. Introduction

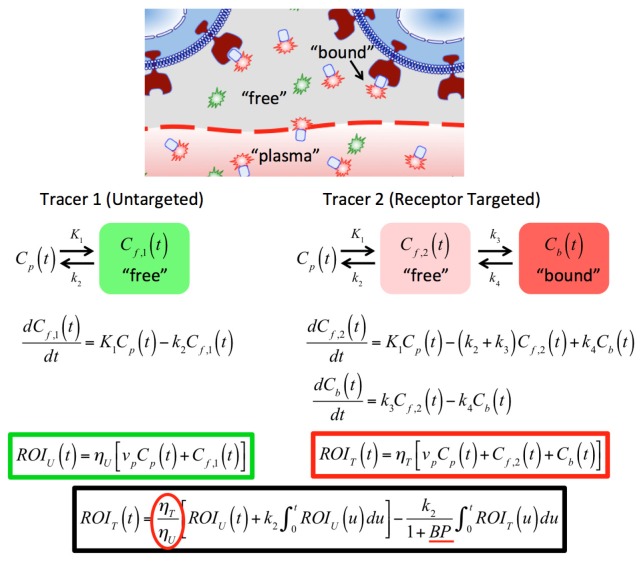
Approaches to quantitate the concentration of available molecular receptors in tissues of interest in vivo have the potential to guide the development of targeted cancer therapeutics [1]. Conventional molecular imaging can be complicated by multiple factors that can influence extravasation, retention, and clearance of a targeted imaging agent within a tissue – including perfusion volume, vascular permeability, lymphatic flow, receptor-binding, and non-specific binding [2, 3] – making it intractable to quantify receptor binding or concentration. A variety of ratiometric imaging methods (such as ratioing fluorescence at two wavelengths: one sensitive to binding and one not) have been used extensively in fluorescence assays and microscopy to provide more quantitative information about targeted molecular expression [4]; however, they have been explored sparingly for in vivo studies owing to tissue optical property differences at different wavelengths of light, which can be difficult to account for. Recently, our group has reported on a dual-tracer approach to quantify binding potential [BP: a metric that is equivalent to the affinity of the tracer to the target, multiplied by the receptor concentration [5]]. The approach involves the simultaneous administration and imaging of ‘targeted’ and ‘untargeted’ compounds [6]. Figure 1 presents the detailed mathematics of the kinetics governing BP, using a linearized version [7] of Lammertsma and Hume’s simplified reference tissue model [8], as applied to dual-tracer kinetics [9]. Note that the reference tissue models require tracer-receptor binding be less than 10% of saturation (for first order rate constants), that the bound and free states of the targeted tracer are in rapid equilibrium, and that the ratio of K₁/k₂ (rate constants of extravasation and tissue efflux, respectively: Fig. 1) be equivalent between target and reference curves [8]. For application of these models to the dual-tracer methodology, the arterial input functions of the two tracers also need to be equivalent [9], or any difference needs to be accounted for [10]. The models developed in the cited articles assume the targeted and reference signals are of equivalent scale. For simple planar fluorescent imaging applications of this dual-tracer approach, optical property differences at the wavelengths of fluorescence excitation and detection of the two tracers must be accounted for (represented as ${\eta }_T$ and ${\eta }_U$ for the targeted and untargeted tracers, respectively). In this study, the effects of blood volume and oxygenation on optical property differences between two common near-infrared fluorescent imaging bands are investigated, and two potential methods of correcting for these optical property differences are evaluated: a reference tissue-based approach and a pixel-based approach.

Fig. 1.

In vivo dual-tracer compartment model for cell-surface receptors. ROI_T(t) and ROI_U(t) represent the measured uptake curves of the targeted and untargeted tracers, respectively, in any region of interest, as a function of time, t; η_T and η_U are the imaging system detection efficiencies for the targeted and untargeted tracers (see text for details); K₁ and k₂ are the rates of exchange of the tracers from the blood concentration (C_p) to the interstitial space (C_f,2 for the targeted tracer and C_f,1 for the untargeted tracer) and back, respectively; and k₃ and k₄ are the rates of association and dissociation of the targeted tracer to its receptor in a bound state (C_b), respectively. The fraction plasma volume in the tissue is represented by v_p. The red circled fraction in the black bordered equation is the parameter attained by the pixel-by-pixel or reference tissue normalization approaches explored in this study. The BP, underlined in red, is known as the “binding potential” and is the key parameter of interest: it is equivalent to k₃/k₄ and proportional to the receptor concentration by the tracer affinity.

Normalization of the fluorescence emission intensities from the two tracers (represented by the ratio of ${\eta }_T/{\eta }_U$) accounts for variations in excitation intensities $\left(\varphi \right)$, detector spectral sensitivity $\left(K\right)$, tracer quantum yield $\left(Q\right)$, and attenuation as a function of background optical properties $f({\mu }_t)$, some of which can vary spatially in $\left(x,y\right)$. Therefore, for fluorescence imaging of each tracer $i\in \left[T,U\right]$, which designates targeted and untargeted, respectively, the product of these factors yields ${\eta }_i(x,y)={\varphi }_i(x,y)K_i(x,y)Q_{i}f({\mu }_{t,i}(x,y))$. While device specific quantities (i.e. ${\varphi }_i,K_i$) can be accounted for by accurate system calibration, the role of optical properties may persist. The origin of ${\mu }_{t,i}$ differences for the targeted and untargeted tracers are attributable to excitation and emission pairings that are located at different wavelengths. It is known that the local absorption coefficient $\left[{\mu }_a(x,y)\right]$ at a pixel in a wide field image is strongly dependent on the local hemodynamic parameters (e.g. blood volume, hemoglobin saturation) and that variations in these parameters can alter the attenuation of light remitted by each tracer differently; i.e. observed changes in fluorescence may be attributable to variations in tracer concentrations or absorption coefficient. Additionally, tracer-specific background ${\mu }_a$ values may result in different volumes or depths of sensitivity for the collected fluorescence of each tracer, and such a depth mismatch would violate an assumption that both tracers have been sampled from the same tissue volume in vivo. Regional differences in ${\mu }_a$can be mitigated using images of the excitation fields sampled by custom designed imaging setups to implement the Born normalization [11]; however, many commercially available small animal imaging systems that are optimized to sample dual fluorescent targets do not explicitly sample the excitation field.

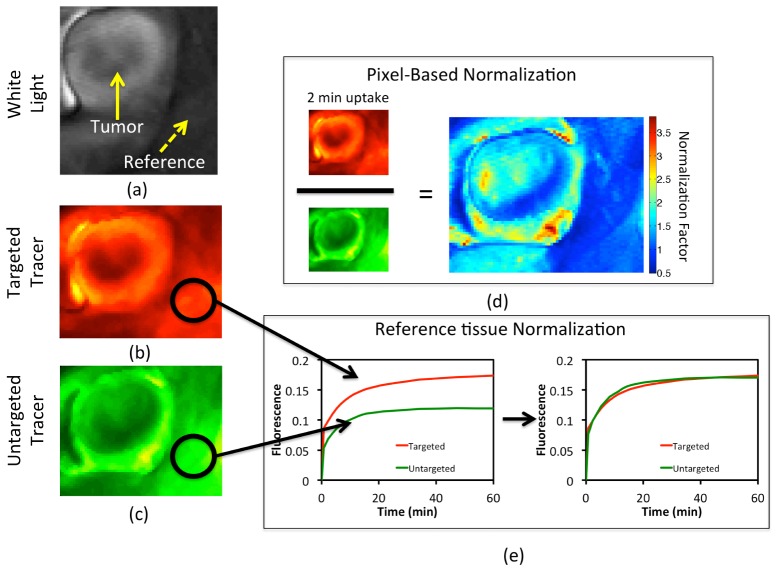
This study considers two methods to normalize measured fluorescence images; Fig. 2 shows the use of these two methods on representative in vivo measurements on a mouse model. The first method was the reference tissue approach, which was based on the assumption that the uptake of the targeted and untargeted tracers should be the same in a tissue devoid of receptor; any discrepancy in tracer-specific fluorescence remission is measured by dividing the average uptake of the targeted tracer in the reference tissue by the average uptake of the untargeted tracer. All untargeted tracer uptake images are then corrected by scaling by this one normalization factor (Fig. 2(e)). The second approach was a pixel-based normalization, wherein the uptake of the targeted and untargeted tracers is assumed to be equivalent within the first 2 min after tracer injection in all tissues. Pixel-by-pixel based normalization is then carried out by taking the dot-quotient of the targeted uptake image and the untargeted uptake image at 2 min and then dot-multiplying all images by this normalization factor map (Fig. 2(d)).

Fig. 2.

A gray-scale white light image of an exposed subcutaneous xenograph glioma tumor grown on the left flank of an athymic mouse is depicted in (a). Targeted and untargeted tracer uptakes at 2 min after tracer injection are presented in (b) and (c), respectively. The pixel-based normalization approach, wherein all untargeted tracer images are scaled by a normalization factor map that is determined by dividing, pixel-by-pixel, the uptake images of the targeted and untargeted tracers at 2-min post-injection, is depicted in (d). The reference tissue-based normalization approach, wherein all untargeted tracer images are scaled by a single normalization factor determined by the ratio of the uptakes of the targeted and untargeted tracers in a region devoid of receptor is depicted in (e).

This study utilizes Monte Carlo simulations of planar fluorescence imaging of two targeted tracers to characterize the influence of physiologically-relevant optical property variations on estimates of binding potential. Simulations are used to characterize the sensitivity of sampled intensity and the depth of fluorescence origin for a pair of widely used tracers that absorb in the 700 nm and 800 nm, respectively. Two methods for correcting fluorescence used to estimate binding potential for distortions due to optical properties are then used to analyze spatially resolved simulated data for validation, and then applied to measurements made in mice in vivo to show the impact on estimated biological binding potential.

2. Methods

Monte Carlo simulations of fluorescence imaging of binding potential

A Monte Carlo model was used to simulate the planar fluorescence imaging of dual tracers in mouse skin using previously validated code [12]. The model assumes that two tracers are localized within a cylindrical inclusion (radius = 2 mm, height = 2 mm), akin to assessment of molecular expression in either a subsurface tumor or lymph node. The inclusion was oriented with the top face normal to the air/medium boundary of a larger surrounding phantom (x,y-dimensions of 20 mm, z-dimension of 20 mm) and placed at selected subsurface depths [0.25,0.5,1.0] mm. Figure 3(a) shows a schematic of the simulated measurement geometry. The simulated source emitted wide-field illumination normal to the x-y phantom interface. The detector was approximated as a lens focused on the surface of the phantom and collected all photons that remitted from the imaged surface. The optical properties of the sampled medium and inclusion were matched, with the ${\mu }_a$constructed by specifying a basis set of chromophores that included oxygenated and deoxygenated hemoglobin and a background absorption contribution [13], with spectral profiles of background absorption shown in Fig. 3(b). Simulations were performed with permutations of blood volume fractions (BVF)s of [1–3]% and hemoglobin saturations (Sat) of [0, 50, 100]%. The background reduced scattering coefficient $\left({\mu }_s^{\prime }\right)$ was specified as ${\mu }_s^{\prime }={\left(\lambda /800nm\right)}^{-1.2}$, expressed in units of $\left[m{m}^{-1}\right]$, with a spectrally constant anisotropy = 0.8 and the index of refraction of the medium set to 1.38. These properties approximated those commonly found in skin [14]. These simulations considered tracers with excitation and emission properties selected to mimic IRDye-700DX (IR700) and IRDye-800CW (IR800) dyes (LI-COR Biosciences, Lincoln, NE), with the absorption and normalized emission spectra for both shown in Fig. 3(c); these dyes are at a common wavelength of fluorophore emission in the near-infrared range [15]. Simulated measurements excited IR700 and IR800 at 685 and 785 nm, respectively, and collected spectrally-resolved fluorescence photons that remitted across the imaged phantom surface. For each measured phantom, the total integrated fluorescence intensity for each tracer was summed across the imaged surface and normalized to the mean of all simulations. A post-processing algorithm estimated fluorescence in response to a time-dependent change in tracer concentration by scaling collected photons for each tracer by the concentration as specified in Fig. 3(d). Specifically, the targeted tracer uptake curve was simulated using the analytical solution to the two-tissue compartment model shown on the right hand side of Fig. 1 [16]. The untargeted tracer was simulated using the analytical solution to the one-tissue compartment model shown on the left hand side of Fig. 1 [17]. Values of K₁ and k₂ used for both the targeted and untargeted tracer curve simulations were chosen based on values measured for a 3.0-kDa imaging agent to match the size of the targeted tracer employed in the animal experiments (~7 kDa): the values were K₁ = 0.013 min⁻¹ and k₂ = 0.13 min⁻¹ [18]. The disassociation binding rate constant k₄ is equivalent to koff in enzyme kinetic nomenclature and was measured by Zhou et al. to be approximately 0.1 min⁻¹ for EGF bound to EGFR [19] - native EGF was the targeting moiety used in the animal experiments in this study. Then with binding potentials (k₃/ k₄) roughly equivalent to 2 for a typical EGFR overexpressing tumor line (U251: see Animal experiments), k₃ was by association assumed to be equal to 0.2 min⁻¹. A typical arterial input function was taken from a prior study looking at fluorescence in blood samples using the same tracers employed in the animal experiments in the current study [20]. Targeted tracer uptake curves were simulated based on the equation in Fig. 1 using the untargeted tracer as input and assuming the same k₂ and specifying the BP. Resulting fluorescence vs. time data were analyzed using a linearized solution to the Equation set shown in Fig. 1, as in [7, 21], returning estimates of binding potential, $\widehat{BP}$. Simulations also returned the depth of origin for collected fluorescence photons, which were used to generate depth sensitivity histograms for each tracer and a weighted sampled depth as in [22]. Each simulation initialized 10⁸ excitation photons, with emission sampled at 10 discrete wavelengths within the tracer specific emission waveband. In all, fluorescence spectra for 2 tracers were measured in phantoms with 9 background ${\mu }_a$ values with fluorescence inclusions located at 3 depths, resulting in 54 simulated spectra, each of which were used to estimate a fluorescence intensity at 60 time points.

Fig. 3.

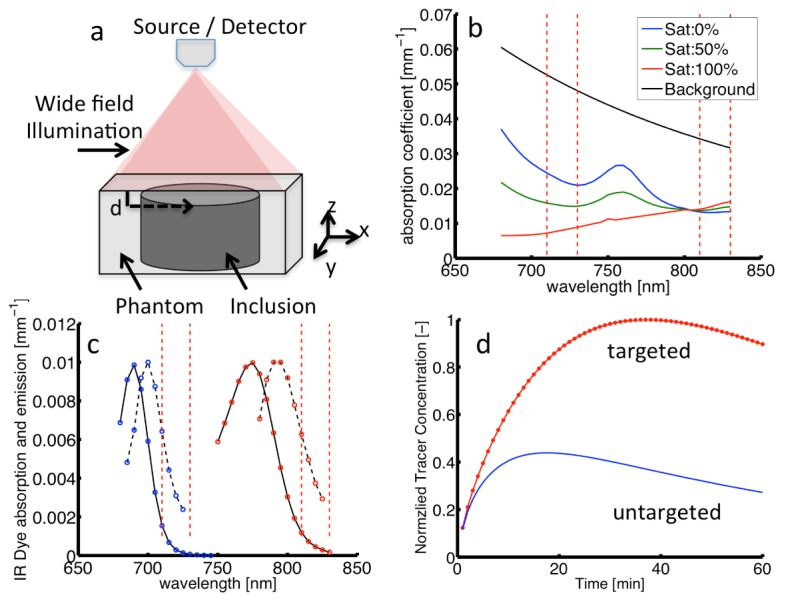
a) Schematic of simulated measurement geometry. b) Absorption spectra for 2% blood volume at selected saturations and background absorption. c) Absorption (solid) and emission (dashed) spectra for dual tracers (i.e. IR700 and IR800). Vertical dashed lines in both panels represent integrated waveband for fluorescence intensity. d) Time-dependent concentrations of targeted and untargeted tracers for binding potential = 1.7.

Additional simulations were performed to mimic spatially-resolved fluorescence imaging of a medium that contains absorbing inclusions. These simulations considered a semi-infinite medium, with a 30x30 mm field of view with background absorption specified by BVF = 2%, Sat = 70%. The medium contained two absorbing inclusions with a radius of 5 mm. The first inclusion was centered at (x,y) coordinates of (19.25,19.25) mm and contained [BVF = 25%, Sat = 50%], while the second was centered at (11.25,11.25) mm and contained [BVF = 100%, Sat = 0%]. A fluorescence inclusion with radius of 10 mm centered at the (15,15) mm with the top face positioned at the air/medium interface was placed in the medium. An x-y view of the geometry with inclusions is shown in Fig. 5(a). Within the volume of the phantom surrounding the inclusion, the concentration of both IR700 and IR800 were specified by the ‘untargeted’ curve in Fig. 3(d). Within the fluorescence inclusion the concentration dynamics of IR800 were specified by the ‘targeted’ curve in Fig. 3(d). Simulations tracked all fluorescent emission photons that transmitted from the imaged phantom surface and for each photon returned the wavelength, the location of origin from within the phantom, and the location of remission from the phantom surface. Fluorescence images were produced by discretizing the location of remission on the surface of the medium into a 2-D (x,y) grid with bin dimensions of 0.5 mm and integrating the collected spectra over the tracer-specific wavebands. A post-processing algorithm estimated time-dependent emission maps by weighting the photons collected at each pixel by the concentration of the tracer at the location of origin; these data were used to simulate fluorescence maps at 1 min time intervals for 60 min. Binding potential maps were calculated at each pixel in the image using a linearized simplified reference tissue approach (Fig. 1) [7, 21], using both reference- and pixel-based normalization procedures to determine the normalization factor, η_T/η_U.

Experimental measurements of binding potential in a mouse model

Three 6-week-old male severe combined immunodeficient (SCID) mice were implanted with 10⁶ U251 human glioma cells (from Dr. Israel at Dartmouth College) subcutaneously in the left flank, explained in more detail in a previous study [22]. Once the tumors grew to a diameter of approximately 5 mm, the mice were anesthetized with an intra-peritoneal injection of ketamine-xylazine (100 mg/kg:10 mg/kg) and a small section of skin was excised to expose the tumor. The mice were then affixed, tumor-side-down, to a standard glass microscopy slide and placed in a two-fluorescence-wavelength, Odyssey imaging system (LI-COR Biosciences). The mice were injected intravenously in the tail vein with 1 nanomole of both IRDye-800CW-EGF [an epidermal growth factor (EGFR) targeted tracer (LI-COR Biosciences)] and IRDye-700DX (LI-COR Biosciences). Fluorescence from each tracer was imaged repeatedly in the tumor and surrounding tissue at 2-min intervals for up to 60 min. Location of the tumor was clear on pre-injection autofluorescence images taken with the odyssey scanner at 700 nm [20]. We used this image to select tumor and reference regions. Binding potential maps were calculated using a linearized simplified reference tissue approach (Fig. 1) [7, 21], using both reference- and pixel-based normalization procedures to determine η_T/η_U.

3. Results

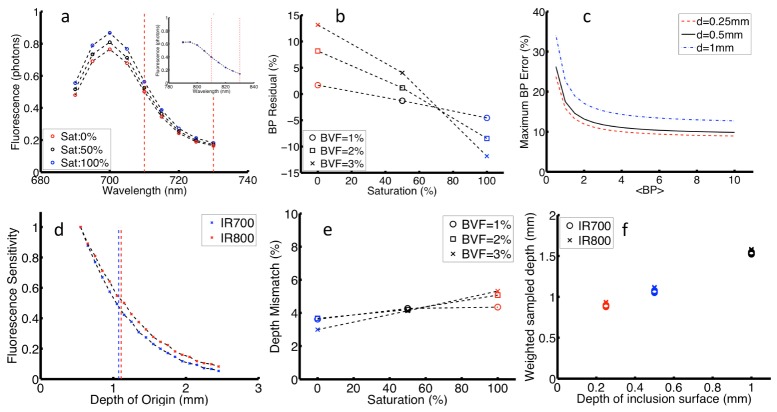
Figure 4(a) shows a representative fluorescence remission spectrum for both tracers for different Sat values [0, 50, 100] % at constant BVF = 2%. These spectra show that differences in physiological parameters introduce differences in the remission intensity collected for each tracer; these differences are clearly visible for IR700, but not for IR800. The equation set in Fig. 1 was applied to simulated fluorescence emission profiles, and residuals between known ($\langle BP\rangle$) and estimated ($\widehat{BP}$) values of BP were given as, $100\%\frac{\widehat{BP}-\langle BP\rangle }{\langle BP\rangle }$; these errors represent absorption-dependent variations in $\widehat{BP}$. Figure 4(b) shows error in $\widehat{BP}$ plotted vs. Sat for different BVF; these data were calculated for $\langle BP\rangle$ = 1.7. The data show that estimates of binding potential are more sensitive to variations in Sat (with a maximum error of 26%) than in BVF (11%). This observation can be explained by considering the different influence these parameters have on the ${\mu }_a$ spectrum: changes in Sat introduce a spectrally dependent change to ${\mu }_a$_, while changes in BVF introduce a linear shift across the full ${\mu }_a$ spectrum. Absorption-based error in BP was also assessed for different inclusion depths and $\langle BP\rangle$ values; the summary of the combined variations is shown in Fig. 4(c). Binding potential error increased with inclusion depth, which is expected as attenuation increases with path length. BP error also increased for smaller $\langle BP\rangle$ values, which can be understood by considering that as the binding-dependent difference in fluorescence emission decreases, absorption-based distortions have a more substantial influence on $\widehat{BP}$.

Fig. 4.

a) IR700 emission spectra for various Sat (inset for IR800); b) Error in BP vs. Sat; c) Maximum error in BP vs. expected BP for various inclusion depths; d) Depth sensitivity for both tracers for BVF = 2% and Sat = 100%; e) Tracer depth mismatch vs. Sat; f) Mean sampling depth vs. inclusion depth. In b and e markers indicate BVF and colors indicate Sat.

Figure 4(d) shows representative depth sensitivity profiles for fluorescence intensity collected for both tracers measured for simulated the physiological case of Sat = 100%, BVF = 2%; these profiles displayed near matching sampling depth for both tracers. Figure 4(e) shows the difference between the depths of origin for both tracers (expressed as a %) vs. Sat for selected BVF values. Here, the depths are exceptionally well matched, with error of <6% for all cases. In Fig. 3(f) the sampled vs. inclusion depth shows a simple linear increase, with no observable spread among tracer data points for all ${\mu }_a$ combinations. These data validate a key assumption that both tracers are sampled within matching tissue volumes.

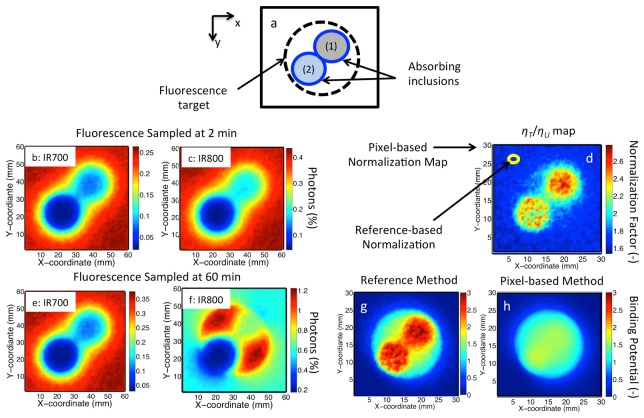
Figure 5 shows the application of the normalization methods to spatially-resolved simulated measurements of a turbid medium containing absorbing inclusions. Figure 5(a) shows the phantom geometry, with two absorbing and one fluorescence inclusion. Figure 5(b) and 5(c) show raw emission intensities for the fluorescence collected for both IR700 and IR800. Here the fluorescence emission results from near-uniform distribution of both tracers throughout the model geometry, but these images show substantial distortion due to background absorption by both inclusions. Taking a ratio of the images in Fig. 5(b) and 5(c) yielded a pixel-based calibration map of ${\eta }_T/{\eta }_U$, which is shown in Fig. 5(d). Reference tracer estimation of ${\eta }_T/{\eta }_U$was by selecting a 1 mm² region centered at x = 5, y = 25 mm, a location away from the heterogeneities. Figure 5(e) and 5(f) show fluorescence images for both IR700 and IR800 sampled at 60 min; these data show similar a distribution pattern for the untargeted tracer, but a substantial increase in fluorescence of the targeted tracer (IR800) is observed in the center of the image over the fluorescence inclusion. Figure 5(g) and 5(h) show images of spatially-resolved maps of binding potential estimates for the non-uniform fluorescence distributions as returned by the reference tissue and pixel-based normalization methods, respectively. The true binding potential value in each map is $\langle BP\rangle =1.7$. The image obtained from the reference tracer method shows clear distortions in the estimates of BP both in and around the fluorescence inclusion for the reference model (with the mean error of $<35\pm 20\%$), while the pixel-based model recovers the embedded fluorescence inclusion with clear demarcation and substantially reduced distortions (with mean error of $<6\pm 3\%$). These results validate the use of pixel-based normalization procedure to account for spatially-resolved differences in background absorption.

Fig. 5.

a) Model geometry of a turbid medium containing two absorption inclusions (1) BVF = 25%, Sat = 50% and (2) BVF = 100%, Sat = 0%. b) and c) Show simulated fluorescence images with of IR700 and IR800 at 2 min, respectively. d) Shows the pixel-based normalization map. e) and f) Show simulated images of both tracers at 60 min. g) and h) Show binding potential maps for images in the presence of the absorption inclusions as estimated by both the reference tracer method and pixel-by-pixel normalization method, respectively.

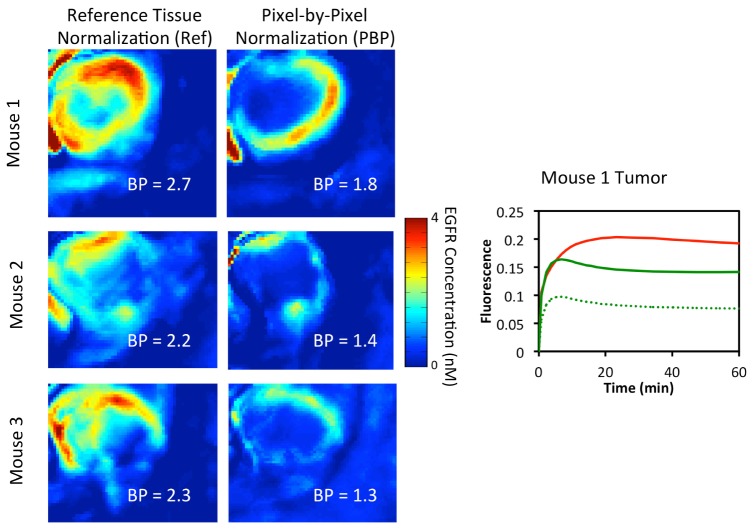
Figure 6 shows the application of these approaches to estimating binding potential in a murine subcutaneous tumor model. Normalization of the images to determine ${\eta }_T/{\eta }_U$ was performed using images obtained at early time points (i.e. 2 min following simulations tracer injections), a time point when both tracers are expected to share matching perfusion-based kinetics. Figure 6 columns 1 and 2 show EGFR receptor concentration (e.g. BP) estimated by the reference- and pixel-based normalization procedures, respectively. The changes in normalization procedure yielded a different bulk BP estimate of EGFR concentration in the tumor (yielding a 38 ± 5% decrease in BP). Also interesting is that the estimated maps show differences in the spatial distribution of BP, differences that are not recovered by a linear scaling operator. Instead these spatial differences are presumably attributable to differences in the local ${\mu }_a$ (between pixels), which introduced a spatial distortion factor in the reference tissue map; this distortion can be seen in the normalization factor map for Mouse 1 in Fig. 2(d) and is removed through self-normalization using the pixel-based method. Inspection of the dynamic fluorescence vs. time profiles in Fig. 1(e) shows that the reference-based approach yields appropriately matched profiles for both tracers in normal tissue at all time points. However, the data in Fig. 6 (far right) show that the pixel-based approach yields an improved match for both tracers at early times. While these in vivo data do not provide definitive confirmation of the local tracer concentrations, this approach assumes that tracer distribution at these time points is dominated by plasma-based kinetics, and as a result, the distribution for both tracers is similar. These results suggest the pixel-based normalization procedure removes the influence of absorption-based differences in BP calculations.

Fig. 6.

Binding potential maps calculated using the reference tissue-based normalization (first column of images) and the pixel-based normalization approach (second column of images) are presented for 3 athymic mice with subcutaneous xenograph glioma tumors. The binding potential (BP) measured in each case within the tumor is displayed on the figure. For reference, the white-light image for Mouse 1 is depicted in Fig. 1(a). On the far right, the average targeted tracer uptake (red curve) in the tumor is presented along with the untargeted tracer uptake after normalization by the reference tissue-based approach (dotted green curve), and by the pixel-based approach (solid green curve).

4. Discussion

This study investigates fluorescence normalization approaches necessary to quantitatively image receptor binding potential in vivo using a dual tracer method. The approaches employ the administration of two fluorescent tracers, one ‘targeted’ to a specific receptor (e.g. EGFR) and the other ‘untargeted’. Previous work has shown that interpretation of fluorescence images of both tracers could be used to quantitate the binding potential, which is a surrogate-metric for the concentration of a receptor in tissue in vivo [5]. The dual-tracer approach involves the optical sampling of two tracers that absorb and emit at different wavelengths; therefore, variability in biological chromophores (e.g. oxy- and deoxy-hemoglobin) can introduce differential distortions in the remission intensity of the two tracers. This study utilized simulations to mimic wide field fluorescence imaging of two dyes commonly used in the NIR (i.e. IRDye-700DX and IRDye-800CW) over a wide range of vascular physiological parameters, including blood volume fractions in the range of [1–3]% and hemoglobin saturations in the range [0-100%]%. Substantial distortion in the absolute estimates of binding potential (BP) in response to changes in background absorption was observed (with >30% error observed in BP); however the fluorescence sampled for both tracers originated in similar depths over the parameter space. These results suggested that proper normalization of fluorescence images is required to correct for distortions introduced by spatial-variations in absorption. These results motivated the comparison of two basis approaches to obtain the normalization factor ${\eta }_T/{\eta }_U$: (1) determination within a reference location in ‘normal’ tissue (devoid of targeted receptor), which is then applied to all pixels in the image field, or (2) a pixel-by-pixel basis. Simulation of spatially-resolved fluorescence imaging in the presence of strong absorption inclusions showed the influence that differences in vascular density, or even extreme situations such as blood pooling, known to occur in tumors [23], which have substantial influence on fluorescence remission can be corrected for using a pixel-based normalization approach. Prospective application of these two methods to in vivo data showed substantial differences between the references tissue model and pixel-by-pixel normalization estimates of receptor distribution within human xenograft tumors grown in mice.

Ideally, the pixel-by-pixel normalization should be carried out on data points collected as soon after the injection as possible, when the arrivals of the targeted and untargeted tracers to the tissue are predominantly based on delivery (blood flow and vascular leakage, i.e., K₁ based). At these early time-points, any discrepancy between measured targeted and untargeted tracer concentration should predominantly be associated with detection efficiency differences and/or optical property differences for the different wavelengths at which the tracers are detected. At later time-points, the delivery of the targeted tracer will become increasingly dependent on binding to the targeted receptor, and will therefore begin to separate (be retained in the tissue to a greater extant) from the untargeted tracer. Note: if there is no receptor present in the tissue of interest, the targeted and untargeted tracers should remain at equivalent levels.

Expanding on the curve simulations describe in the Monte Carlo Methods, an additional set of targeted tracer uptake curves were created for binding potentials (BPs) of 0 to 5. For all statistical analyses, 1% of peak signal noise (larger than the highest noise per pixel in the animal experiments) was added to the data and analyses were repeated with random noise addition for 100 iterations. The data was assumed to be collected at 1-min intervals beginning at 1 min post-injection. The optimal time window for data normalization was explored by normalizing the targeted tracer curves to the untargeted tracer untargeted tracer curves at 1 min, 1:2 min, 1:5 min, and 1:10 min post-injection, after the targeted tracer was randomly scaled by a number between 0.5 and 2 to simulate variability in optical properties (Fig. 7). As demonstrated, the optimal mean estimation of BP was achieved when the normalization was carried out at the 1 min interval, with BP underestimates of just over 5%. However, the variance in these estimates was substantial (approximately 15% of the mean), owing to poor noise stability with averaging on one time-point. The best standard deviation of ~2% of the mean was achieved for the 1:10 min normalization because of the preferable noise characteristics of averaging over 10 measurements; however, this normalization window extended well into the “binding window” (when binding accounts for a significant percentage of targeted tracer uptake) resulting in a mean underestimation in BP of approximately 60%. Qualitatively, the best tradeoff between accuracy and precision was observed for the 1:2 min normalization with a mean error of approximately 10 ± 10%. This was the same window used in the pixel-by-pixel normalization in all other studies in this work. It should be noted that with higher temporal resolution and better signal-to-noise characteristics, BP estimates could be improved by carrying out the normalizations at as earlier a time-point as possible.

Fig. 7.

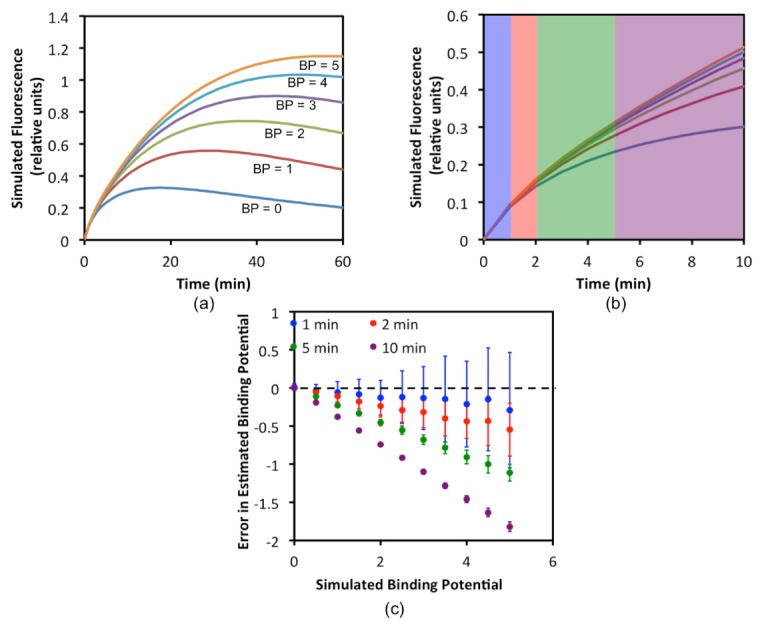
Simulation study results to determine the optimal time-window in which to normalize targeted and untargeted tracer uptake curves to correct for optical property and detection efficiency mismatch between tracers. In (a), the various simulated targeted tracer uptake curves based on binding potentials (BP) between 0 and 5 are presented over 60 min. In (b), the same curves in (a) are re-plotted for just the first 10 min of uptake. The shaded regions demonstrate the ranges over which the 1-min (blue), 2-min (red), 5-min (green), and 10-min (purple) normalizations were carried out. The results of these normalizations and their affects on BP estimation are presented in (c) in the form of a Bland-Altman.

The pixel-based normalization approach characterized in this study makes images of receptor concentration insensitive to spatial-variations in background absorption without the need for a light-transport model based correction, which is a focus of many groups and typically requires multispectral imaging systems [14, 24, 25]. It should be noted that while the proposed normalization method cannot account for dynamic variations in ${\mu }_a$ that may occur during tracer monitoring, the anticipated spatial variation in ${\mu }_a$ between different regions in the sampled field of view is expected to dominate dynamic changes to ${\mu }_a$ that may occur within a single pixel. While demonstrated in a specific application, this early time-point, pixel-by-pixel normalization approach could allow ex vivo ratiometric microscopy approaches to be translated to in vivo applications, allowing users to account for uneven-distribution of the tracer excitation, detection sensitivity, and tissue attenuation of tracer signal, as long as the imaging system has linear detection in both channels.