FPscope: a field-portable high-resolution microscope using a cellphone lens

Abstract

The large consumer market has made cellphone lens modules available at low-cost and in high-quality. In a conventional cellphone camera, the lens module is used to demagnify the scene onto the image plane of the camera, where image sensor is located. In this work, we report a 3D-printed high-resolution Fourier ptychographic microscope, termed FPscope, which uses a cellphone lens in a reverse manner. In our platform, we replace the image sensor with sample specimens, and use the cellphone lens to project the magnified image to the detector. To supersede the diffraction limit of the lens module, we use an LED array to illuminate the sample from different incident angles and synthesize the acquired images using the Fourier ptychographic algorithm. As a demonstration, we use the reported platform to acquire high-resolution images of resolution target and biological specimens, with a maximum synthetic numerical aperture (NA) of 0.5. We also show that, the depth-of-focus of the reported platform is about 0.1 mm, orders of magnitude longer than that of a conventional microscope objective with a similar NA. The reported platform may enable healthcare accesses in low-resource settings. It can also be used to demonstrate the concept of computational optics for educational purposes.

1. Introduction

Optical microscopy pervades almost all aspects of modern bioscience and clinical applications. To achieve high-resolution microscopic imaging, a precise and expensive objective lens is typically needed for collecting light over a large angle. In recent years, there has been an increasing interest in developing portable microscope platforms that would benefit remote clinics or be used in resource-limited environments [1–8]. Lensless microscopy is a good example of this direction. It has been shown that, sub-micron resolution can be achieved using various lensless imaging techniques, such as optofluidic microscopy [1, 3], digital in-line holography [2, 5], and contact imaging microscopy [4]. Applications of these techniques range from malaria parasite screening, single cell tracking, to real-time cell culture monitoring and etc. While these techniques have been successfully demonstrated, they are limited to a relatively small range of samples. Optofluidic microscopy requires the sample to flow across a microfluidic channel. It works well for dispersible samples such as blood, fluid cell cultures, and other suspensions of cells or organisms, but is incompatible with adherent samples or samples on glass slides. Digital in-line holographic microscopy records interference intensity distribution of a target under coherent light illumination. Confined object support constraint is typically needed in the recovery process, and thus, this approach may not be suited for confluent samples such as pathology slides. The contact imaging approach requires the sample placed at close proximity to the sensing surface, and thus, cannot handle conventional microscope glass slides. While other lens-based portable setups exist [6–8], their performance are largely limited by the employed optics.

Here we report our effort on the development of a portable high-resolution microscope platform, termed FPscope, using the Fourier ptychography (FP) approach [9, 10]. FP is a recently developed computational imaging procedure that synthesizes a number of variably illuminated, low-resolution intensity images in Fourier space to produce a high-resolution complex sample image. The FP algorithm combines the concepts of synthetic aperture [11–13] and phase retrieval [14] by alternatively imposing the constraints in the spatial and Fourier domains. FP is different from the conventional coherent diffraction imaging [15] in two aspects: 1) raw image is captured in the spatial domain, and 2) aperture scanning is performed in the Fourier domain. By capturing images in the spatial domain, FP reduces the requirements of spatial coherence and detector’s dynamic range. By scanning the aperture in the Fourier domain, FP is able to recover an image with a resolution much higher than the limit of the employed lens. The final achievable resolution of FP is determined by the largest incident angle of the illumination wave, and thus, it is possible to achieve both high-resolution and wide field-of-view by using a low-NA lens. We also note that, FP is different from the structured illumination microscopy [16, 17] in two aspects: 1) FP uses angle-varied plane waves for sample illumination; it is a coherent imaging method and not suited for fluorescence imaging. 2) The recovery process of FP is based on an iterative phase retrieval process and it is different from the linear inversion of the structured illumination technique. In FP, lens aberration can be digitally corrected by introducing a complex pupil function in the recovery process [18, 19]. Recently, we have also extended the FP procedure to multiplexed imaging [20], 3D holographic imaging [21], and super-resolution macroscopic imaging beyond the diffraction limit [21].

This paper is structured as follows: in section 2, we will discuss the system design of the FPscope. In section 3, we will characterize the imaging performance using a USAF resolution target. In section 4, we will demonstrate the use of the FPscope for imaging biological samples. Finally, we will summarize the results and discuss the future directions.

2. System design of the FPscope

The core component of the FPscope is a cellphone lens. The large consumer market has made cellphone lens modules available at low-cost and in high-quality. There are several unique advantages of cell phone lenses: 1) they are highly-corrected and cost-effective, 2) they are compact and light-weight, and 3) they have a relatively large field-of-view. For a conventional cellphone camera, the lens module is used to demagnify the scene onto the image plane of the camera, where the image sensor is located. In the FPscope, we use the cellphone lens module (Nokia 808) in a reverse manner; we replace the image sensor with sample specimen and use the cellphone lens to project the magnified image onto a low-cost CCD camera (DMM 31AU03, The Imaging Source). The magnification factor can be tuned by adjusting the distance between the sample and the cellphone lens. In our design, the magnification factor was chosen to be 4.5, satisfying the Nyquist sampling requirement. We note that the configuration shown in Fig. 1(a) is not new. We have demonstrated the same configuration (using a lens in the reverse manner and projecting the magnified image onto the detector) for gigapixel imaging [22]. However, the use of a cellphone lens in conjugation with the FP algorithm would enable a cost-effective solution for field-portable microscopy imaging.

Fig. 1.

System design of FPscope. (a) A cellphone lens is used in a reverse manner. The magnified sample image is projected onto a CCD sensor. An 8 by 8 LED matrix is used for sample illumination. (b) The assembled FPscope connected to a computer.

To supersede the diffraction limit of the lens module, we used an 8 by 8 LED array for sample illumination. Each LED element of the array illuminates the sample from an oblique incident angle, and the corresponding image is acquired using the cellphone lens with a 0.15 NA. The acquired 64 images are then synthesized in Fourier space using the Fourier ptychographic algorithm. The final synthetic NA is determined by the largest incident angle of LED illumination, and it can be adjusted by changing the distance between the LED array and the sample. In our design, the distance between the LED array and the sample is chosen to be ~10 cm, corresponding to a maximum synthetic NA of 0.5. We also note that if the illumination is placed too close to the sample, there won’t be enough Fourier spectrum overlapping between two adjacent LEDs [23]. The spectrum overlapping (data redundancy) is important for a successful FP reconstruction.

We designed a 3D manual stage to move the sample in the x-y plane and to adjust the focal position. Most of the components in our design were produced using a Makerbot 3D printer. The components were assembled with springs and screws. Figure 1(b) shows the FPscope connected to a computer. Figure 2 shows the assembly process of the FPscope. Figure 2(a) show the cellphone lens mount in front of the CCD camera. Figure 2(b) shows the x-y stage and the slide holder assembly. Figure 2(c) shows the z stage assembly. The final assembled FPscope is shown in Fig. 2(d). The dimensions of the FPscope are 8 x 8 x 16 cm. The mass of the platform is about 250 grams, most of which is from the CCD camera.

Fig. 2.

The assembling process of the FPscope. (a) A Nokia cellphone lens is fitted in to a plastic case. The case is assembled onto a CCD camera. (b) The assembling of the x-y stage and the slide holder. (c) The assembling of the z stage. (d) The final assembled FPscope.

3. System characterization of the FPscope

We characterized the system resolution performance by imaging a USAF target. In this experiment, we captured 64 low-resolution images and used them to recover a high-resolution image using the FP algorithm. The recovery process switches between the spatial and Fourier domains. In the spatial domain, the acquired low-resolution images are used to constrain the amplitude of the solution. In the Fourier domain, the coherent transfer function (i.e., the pupil function) of the cellphone lens is used as a support constraint for the solution. This support constraint is digitally panned across Fourier space to reflect the angle-varied illuminations of the 8 by 8 LED array. In the FPscope platform, we also need to know the relative position between the LED array and the camera. One can carefully measure the position of the LED array or use a post-processing optimization step to find out the position of the LED array. The detailed FP recovery procedure and calibration process can be found in [18, 19].

Figure 3(a) shows the raw image captured by the cellphone lens; the NA was measured to be ~0.15. Figure 3(b) shows the recovered image, and the maximum synthetic NA was, as expected, about 0.5. We can clearly resolve the feature in group 9, element 3, where line-width is 0.78 µm (632 nm illumination). Another advantage of the FPscope is the capability of incorporating pupil correction in the recovery process. By introducing a defocused pupil function, we can digitally tune the focal position along the optical axis. Figure 4 demonstrates the digital refocusing capability of the FPscope. In this experiment, we used a precise mechanical stage to move sample to + 50 µm and −50 µm defocused positions, as shown in Fig. 4(b1) and 4(c1). Figure 4(b2) and 4(c2) show the recovered high-resolution images. We can see that, the depth-of-focus of the FPscope is longer than 0.1 mm without trading off resolution. This much depth-of-focus is orders of magnitude longer than that of conventional microscope objective lens with a similar NA. Therefore, the FPscope is significantly less prone to sample misalignment.

Fig. 3.

Resolution characterization of the FPscope. (a) One of the 64 low-resolution raw images captured using the cellphone lens. (b) The FP recovered image, where feature of group 9, element 3 can be clearly resolved.

Fig. 4.

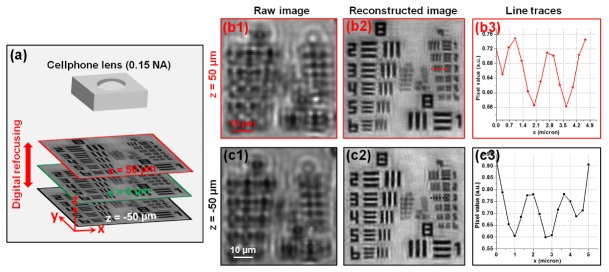
(a) Depth-of-focus characterization of the FPscope. One of the low-resolution raw images captured at (b1) z = 50 µm and (c1) z = −50 µm. (b2-b3), (c2-c3) The FP reconstructions by introducing defocused pupil functions at the recovery process. The depth-of-focus is orders of magnitude longer than that of conventional microscope objective lens with a similar NA.

4. Demonstration of the FPscope with biological samples

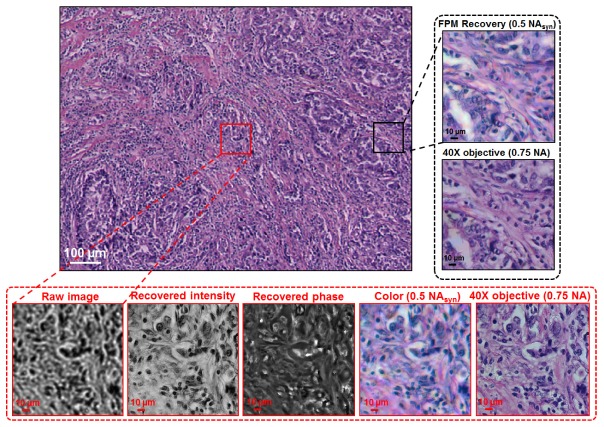
We also used the FPscope to image biological samples. In the first experiment, we used a blood smear as our sample. Figure 5(a) shows the low-resolution raw image of the blood smear. Figure 5(b1)-5(b2) show the recovered intensity and phase images of the sample. We also recovered the color image of the sample by combining the FP constructions from R/G/B illuminations. Figure 5(c) shows the image captured with a 40X, 0.75 NA objective.

Fig. 5.

(a) Raw image of a blood smear (0.15 NA). (b) FP recovered intensity image, phase, and color image. The maximum synthetic NA is 0.5. (c) The image captured using a conventional microscope with a 40X, 0.75 NA objective lens.

In the second experiment, we used a pathology slide as our sample (human adenocarcinoma of breast section, Carolina). The full field-of-view is about 1.1 mm by 0.8 mm, as shown in Fig. 6. The corresponding computational time is about 50 seconds in MATLAB using a personal computer with an i7 qual-core CPU. High-resolution views are provided for two regions, one at the central field-of-view, and the other one at the edge. We used 4 FP iterations to recover the images. Images captured with a conventional microscope with a 0.75 NA objective lens are also provided for comparison.

Fig. 6.

Demonstration of the FPscope using a pathology slide. The full field-of-view is about 1.1 mm by 0.8 mm. The maximum synthetic NA is 0.5. Images captured using conventional microscope with a 0.75 NA objective lens are also shown for comparison.

5. Discussion and conclusion

In summary, we have reported a compact, lightweight, low-cost, and high-resolution microscope platform that we termed FPscope. There are several advantages of the reported platform: 1) the resolution of the reported platform is determined by the largest incident angle of the illumination, not the NA of the cellphone lens and, therefore, we are able to eliminate the traditional reliance on a high-NA lens. 2) Aberrations of the cellphone lens are compensated by the complex pupil function introduced to the FPscope. We have demonstrated the use of a second order defocused pupil function to extend the depth-of-focus beyond the physical limit of the lens. 3) The rich literature on FP can be integrated into the reported framework. For example, the pupil correction scheme [19] and the adaptive system correction scheme [18] in FP can be integrated into the reported framework for factoring out system uncertainties, such the position of the sample, the intensity of the LED array, the position of the LED array and etc. The sparsely sampled FP scheme [23] can be used in the reported framework to bypass the pixel aliasing problem. The information multiplexing scheme can also be used in the FPscope to perform multispectral imaging [20].

We note that, the current FPscope requires the use of a powerful laptop for image reconstruction. However, with the rapid development of mobile hardware, we envision that smart phone applications can be developed for FP image processing. As a reference point, the computational power of smart phone CPU is currently about 10 times lower than that of a desktop. Finally, we reiterate that the use of a lens in a reverse manner is not a new idea. It has been demonstrated in our previous work on gigapixel imaging [22]. However, the use of a reversed cellphone lens in conjunction with the FP algorithm enables a cost-effective solution for field-portable microscopy imaging, which may allow healthcare access in resource-limited environments. FPscope can also be used to demonstrate the concept of computational optics for educational purposes.