Abstract
This study investigates the hypothesis that structured light reflectance imaging with high spatial frequency patterns can be used to quantitatively map the anisotropic scattering phase function distribution in turbid media. Monte Carlo simulations were used in part to establish a semi-empirical model of demodulated reflectance () in terms of dimensionless scattering and , a metric of the first two moments of the distribution. Experiments completed in tissue-simulating phantoms showed that simultaneous analysis of spectra sampled at multiple in the frequency range [0.05-0.5] allowed accurate estimation of both in the relevant tissue range [0.4-1.8] , and in the range [1.4-1.75]. Pilot measurements of a healthy volunteer exhibited -based contrast between scar tissue and surrounding normal skin, which was not as apparent in wide field diffuse imaging. These results represent the first wide-field maps to quantify sub-diffuse scattering parameters, which are sensitive to sub-microscopic tissue structures and composition, and therefore, offer potential for fast diagnostic imaging of ultrastructure on a size scale that is relevant to surgical applications.
OCIS codes: (170.3660) Light propagation in tissues; (170.3880) Medical and biological imaging; (170.6510) Spectroscopy, tissue diagnostics; (170.7050) Turbid media; (290.0290) Scattering
1. Introduction
Light scattering in biological tissue is a complex process that occurs as photons traverse index of refraction mismatches along their propagation path. The index mismatches are associated with tissue morphology (e.g. cytoskeletal arrangement) and cellular ultrastructure (e.g. size and shape of nucleus, mitochondria, other cytoplasmic organelles). Measurements of scattering remission spectra have shown sensitivity to sub-cellular morphological changes in biological tissue [1–8]; these observations support the use of scattering as an endogenous and label-free contrast mechanism to differentiate between tissue types [8, 9]. Scattering spectroscopy has important clinical implications for the diagnosis of cancers [10–14], and for the assessment of surgical margins to guide tumor resections [15–17].
While scatter remission spectra are sensitive to biological structure and morphology, the biological information that is encoded in collected spectra is dependent on the light transport regime that is sampled. Scattering interactions between photons and tissue can be described by a basic set of parameters including the frequency of scattering events, given by the scattering coefficient , the probability of scattering angles, defined by the scattering phase function, and the average scatter direction, given by the first moment of the distribution as . Photons that have experienced many scattering events within turbid media have lost the orientation to their original direction of travel and are considered diffuse [18]. Diffuse remission is insensitive to the direction of individual scattering events, and can be modeled with a diffusion approximation to the radiation transport equation, which introduces the reduced scattering coefficient to combine the effects of scatter frequency and directionality into a single lumped parameter [19]. Diffusion theory is generally applicable to light that remits one or two mean scattering lengths, i.e. 1-2, from the source location, which in biological tissue is approximately 1-2 mm. Previous studies correlated diffuse measurements of with the size distribution of scattering centers in bulk tissue [20], providing a noninvasive characterization of biological tissue structure; however, these measurements are averaged over a large tissue volume and are insensitive to changes in local tissue microstructure. Localized measurements of scatter remission have been developed to interrogate small tissue volumes of interest [6, 21, 22]. When near the source, they collect a population of photons that have experienced few scattering events, making the signal sensitive to the direction of individual scattering events [23–25]; light in this transport regime is termed sub-diffuse. Model-based interpretation of sub-diffuse remission spectra requires both and a parameter that describes the phase-function-dependent probability of large-angle backscatter events which are likely to be collected during reflectance measurements [26–28]. For forward-directed scattering media, such as in biological tissue, the relative probability of large backscattering events is proportional to the weighted ratio of the 1st and 2nd Legendre moments of, given by and, as [24]. Approaches that have quantitated sub-diffusion scattering parameters in biological tissue have classically been limited to the sampling of small volumes, usually sub-mm [29, 30]. Imaging of localized scatter has been achieved by mechanically scanning a fiber optic [6], and results suggest that contextual interpretation of heterogeneous spatial-variations in scatter remission may discriminate between tissue types and potentially guide clinical decisions [15]. However, these approaches can be time-intensive and studies published to date did not interpret the signal in terms of underlying scattering properties. This paper investigates the hypothesis that structured light imaging can be used to sample a sub-diffuse reflectance signal in a wide-field acquisition geometry and quantitate scattering properties relevant to anisotropic transport.
Guidance of clinical decisions (e.g. during surgery) often requires fast assessment of large areas of tissue; this requirement has limited the translation and adoption of localized quantitative spectroscopic approaches within the clinical theatre. Recently, spatial frequency domain imaging (SFDI) has been demonstrated as a method to provide quantitative spatial maps of and the absorption coefficient in turbid media, with fast image acquisitions over a wide field of view [31–33]. The method applies structured light to illuminate the surface of a medium with sinusoidal intensity patterns at various spatial frequencies . The collected signal is demodulated and optical properties are estimated from diffusion theory [32]. The diffuse analysis invokes two important assumptions: (1) scatter dominates absorption such that, and (2) the maximum collected is limited to 0.25 to 0.33 (where for the non-absorbing case), a range of frequencies that limits the sampling of photons which experience few scattering events. The first assumption was addressed by Erickson et. al [34] who presented a Monte Carlo look up table to analyze SFDI signals in highly absorbing tissues. To date, no study has directly addressed the second assumption and quantitatively analyzed sub-diffuse remission collected from structured illumination imaging, although related work published by Konecky et. al [35], considered rotation of the incident illumination pattern to identify directional preferences for scatter within a wide field of view. This unique illumination pattern was characterized as a special case of diffuse light collection that was sensitive to the anisotropic orientation of scatterers on the order of the transport length in the sampled medium, but did not yield estimates of quantitative scattering parameters. Here, we consider structured illumination imaging patterns with high spatial frequencies (i.e.>0.33) to sample reflectance in the sub-diffuse light transport regime and provide an analysis to extract wide field quantitative maps of sub-diffusion scattering parameters that are sensitive to meso/micro-scale tissue structure, e.g. and .
In this study, wide-field imaging of a localized and sub-diffuse scatter signal is achieved by proper selection of the sampled which determines the sensitivity to depth within the medium and allows dynamic selection of the sampled transport regime (i.e. diffuse or sub-diffuse). Low frequency patterns (~0) approximate a uniform wide-field illumination, and the resulting signal is dominated by diffusely scattered light that has travelled a wide range of depths prior to remission. As is increased, the incident pattern is preserved at shallower depths, localizing the signal towards the surface; this principle serves as the basis for depth-resolved tomography via SFDI [31], and more recently for direct sampling of scatter originating from the superficial tissue surface by using a single high frequency image [36]. Additionally, at high frequencies (>0.33) the demodulated reflectance should contain substantial contributions from sub-diffuse photons. The present study utilizes Monte Carlo simulations and experiments to characterize the sensitivity of demodulated reflectance, , to the form of over a wide range of scattering properties and sampled spatial frequencies. A model-based approach is developed to simultaneously analyze sampled at multiple to estimate maps of and quantitatively. The approach is validated in optical phantoms and then used prospectively in vivo to illustrate differences in observed parameters between scar tissue and normal surrounding skin in a healthy volunteer.
2. Methods
2.1 Structured illumination imaging device
A commercially available SFDI device (Modulated Imaging Inc., Irvine, CA, USA), shown schematically in Fig. 1, was used in the present study. The light source was a projector coupled to four LED light sources with wavelengths centered about [658, 730, 850, 970] nm. The system sampled a range of = [0-0.5] at intervals of 0.05 ; higher values were observed to fall below the noise floor. Collection of specular reflection from the surface of the sample was limited by the use of cross-polarizers and orienting the source projector at an angle relative to the detector. The structured light illumination patterns were sinusoids of the form:
| (1) |
with phase offsets of for . The demodulated reflectance image was calculated from the set of intensity images as
| (2) |
at each pixel in the sampled field whereas the spatially variant DC amplitude was computed from
| (3) |
The calibrated demodulated reflectance was formed from the ratio of demodulated intensity measured on a sample to the same data recorded from a siloxane titanium dioxide reflectance standard [17] with known optical properties multiplied by an absolute calibration coefficient informed by Monte Carlo simulations :
Fig. 1.
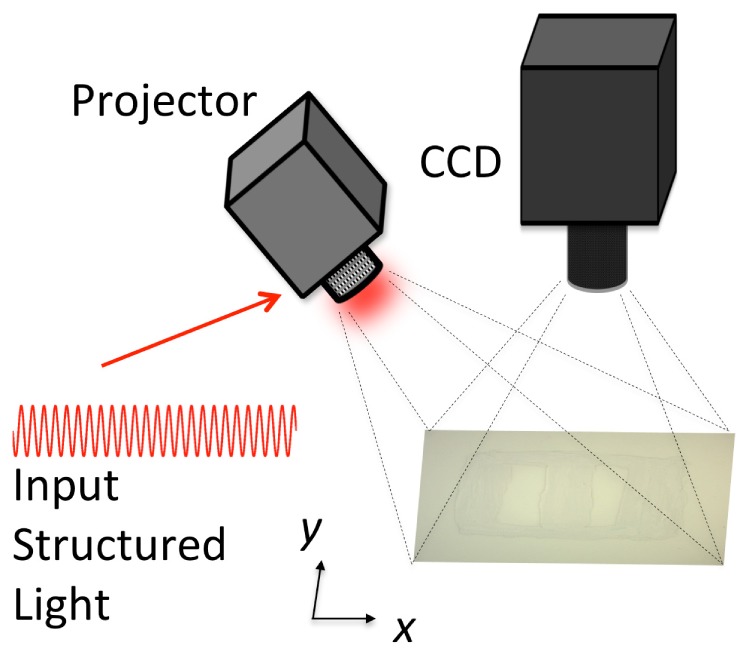
Schematic of measurement setup for structured light imaging.
| (4) |
2.2 Monte Carlo model of structured light imaging
This study utilized a customized version of CUDA-accelerated Monte Carlo code that has been described in detail previously [37]. The model geometry was constructed to mimic a point-source incident on the air interface of a semi-infinite turbid medium with thickness of 100 cm and a maximal radial distance of 20 cm from the source location. The index of refraction of the medium and air were specified as = 1.37 and = 1.0, respectively. Both source and detector were oriented normal to the medium/air interface with numerical apertures specified as NA = 0.15. Photons that scattered within the medium and remitted across the medium/air interface within the cone of acceptance for the detector were collected. The simulation returned the radial distance between incidence and remission , which was discretely binned with a spacing of 0.1 mm.
Simulations were performed over a wide range of scattering parameters. The modified Henyey-Greenstein form of was selected to allow independent modification of and [38]. Optical properties were specified to simulate a range of = [0.3, 0.5, 1, 3, 5, 10] mm−1 for 18 unique phase combinations of = [0.75, 0.85, 0.95] and = [1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9]; in each simulation was selected to return the appropriate for a specified . In all, 108 independent simulations were performed, each initializing 108 photons.
To convert the spatially resolved MC outputs of to spatial-frequency resolved reflectance, , a 1-D Hankel Transform was performed as in [32]:
| (5) |
where is the zeroth-order Bessel function of the first kind. This transformation was used to estimate for 50 spatial frequencies over the range [0-2.0] mm−1. Equation (5) was applied to all MC simulated measurements to yield 5400 combinations of .
2.3 Semi-empirical model of demodulated reflectance
Monte Carlo simulations of were used to inform the development of a semi-empirical model expressed as a function of,, and. The model structure follows from previously published expressions of single fiber reflectance intensity [28, 38–40], and is based on the idea that exhibits a -specific proportionality vs. dimensionless scattering given as the product of :
| (6) |
where the fitted parameters include , which represents the collection efficiency of the detector, and , for , which are fitted coefficients used to capture the dynamics in demodulated reflectance observed in response to changes in and . Model coefficients were estimated by minimizing the difference between simulated and model-estimated values of demodulated reflectance using the lsqnonlin subroutine in Matlab, where the 95% confidence intervals were determined for each fitted parameter using the Matlab nlparci subroutine [41].
2.4 Model-inversion of to estimate and
Equation (6) provides an accurate forward model to describe in terms of and . However, estimation of the scattering properties from a single is complicated by the coupled influence of both variables at each sampled wavelength, resulting in an underdetermined inversion problem. Building on previous work [38], the inversion process can be successfully achieved by analyzing sampled over multiple length scales (i.e. ). Estimation of is performed by specifying a wavelength-dependent model for , which has been shown to follow a power-law in biological tissue in the visible to near-infrared region for <500 nm [42] given as with fitted parameters . The spectral characteristics of in biological tissue are not well understood, and few studies have reported on them [8, 29, 43, 44]; hence, is estimated independently at each sampled wavelength. Thus, for the SFDI device utilized in this study, which sampled reflectance at four wavelengths per spectrum, the inversion approach estimated six parameters (i.e. two for to define and four to define at each of the four wavelengths).
The present study presents a detailed example of the inversion algorithm that is employed on a spectrum representative of a ‘simulated phantom’ constructed from Monte Carlo data with 3% noise. The example case mimics the experimental device with sampled in the range [658-970] nm with = [1.2-0.8] mm−1 and = [1.7-1.4]. Deployment of this inversion method to analyze experimental measurements involved fitting of on a pixel-by-pixel basis within the field of view. Experimental data were analyzed with a custom Matlab fitting algorithm operating on 4 compute cores in parallel, and a representative image required 15 minutes on average to estimate and for all pixels within the sampled field of view along with the 95% confidence intervals for the fitted parameters. The accuracy of model estimates was evaluated in terms of the mean residual between the estimates and their known values.
2.5 Structured light imaging of tissue-simulating phantoms and a healthy volunteer
Liquid phantoms were prepared by diluting amounts of Intralipid 20% (Frenius-Kabi, Bad Homburg, Germany) with phosphate buffered saline. Phantoms were prepared in volumes of 7 mL with dilutions yielding lipid percentages in the set: [0.6, 0.8, 1.0, 1.2, 1.4, 1.6] %. This dilution set produced = [0.4-1.8] mm−1 and = [1.4-1.75] in the [658-970] nm wavelength range as defined previously by Michaels et. al [45]. Structured light images were acquired with the phantoms arranged on a black tray where the diameter of each sampled phantom was 25 mm within the full field of view [140 mm x 114 mm]. Images were generated for all phantoms in a single field of view with an exposure time that was automatically adjusted for each sampled wavelength, and each intensity was corrected for differences in exposure time. Images of phantoms were analyzed using Eq. (6) fit to Monte Carlo simulations were selected to mimic phase functions observed in Intralipid (i.e. four phase functions with = [0.4, 0.6, 0.5, 0.7] and = [1.4, 1.5, 1.6, 1.7]) [45]. Images were thresholded to identify regions of the liquid phantoms from the black background. Model fitting was performed using Eq. (6) to estimate and on a pixel-by-pixel basis.
Structured light imaging was also performed on the skin of a healthy volunteer. The imaged field of view included scar tissue from a previous superficial injury that had since healed. Color photographs of the sampled area were also taken. The skin measurements were analyzed using Eq. (6) from the full set of Monte Carlo simulations (i.e. all 18 phase functions), and reflectance maps were analyzed on a pixel-by-pixel basis.
3. Results
3.1 Characterization of the sensitivity of structured illumination imaging to sub-diffuse scattering parameters
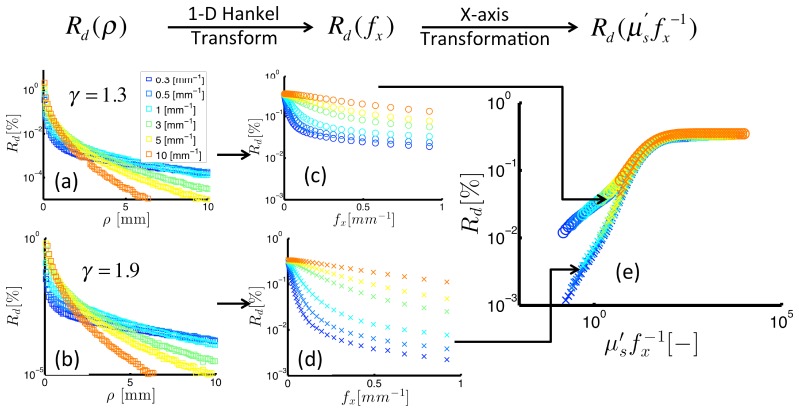
Figure 2 shows demodulated reflectance intensity expressed vs. distance, (left column), spatial frequency, (middle column), and dimensionless scattering, (right column). Data in the top and bottom rows present remission intensities for different , with the backscatter probability higher in the top relative to in the bottom row (defined by = 1.3 and = 1.9, respectively). The left column of Fig. 2 shows returned by Monte Carlo simulations; these data exhibit an exponential decay in intensity as the distance increases from the source, with the rates of decay dependent on as shown for = [0.4-10] mm−1. A 1-D Hankel transform was used to convert to , as shown in transition to from the left to the middle column. The data suggests two distinct trends: (1) increases in response to increases in , and (2) increases in response to decreases in . Closer inspection reveals a coupled dependence of on and , with a 10-fold increase in from 0.5 to 5 mm−1 at constant = 0.1 mm−1 yielding a 6-fold increase in ; the same change in reflectance is introduced by a 10-fold decrease in from 0.05 to 0.5 mm−1 at constant = 1.0 mm−1. The right hand panel of Fig. 2 expresses vs. and indicates how and interchangeably affect . The dimensionless representation of the data also shows distinct transport regimes that depend on the magnitude of. For high values (i.e. >10), is insensitive to with no observable differences in for different. The rationale for this observation is that these photons have experienced many scattering events and are completely insensitive to the direction of any individual scattering event. For low values (i.e. <10), has a -dependent slope vs. . Here, phase functions that specify a higher probability of backscatter yield higher remitted reflectance intensity for the same dimensionless scattering value. For example, at = 1, experiences a 4-fold increase between = 1.9 and = 1.3. These data provide an example of the profound influence that both and have on remittance sampled in the sub-diffuse transport regime.
Fig. 2.
Reflectance intensity expressed on various scales: spatial (left), spatial frequency (middle), dimensionless scattering (right). The top and bottom panels show reflectance for different scattering phase functions (as noted by the -values). The right panel presents the -specific relationship between reflectance and dimensionless scattering.
3.2 Semi-empirical model of
Monte Carlo simulations returned for a wide range of = [0.3-10] mm−1, g = [0.75-0.95], = [1.3-1.9] and = [0-1] mm−1. These results were used to fit the semi-empirical model of given in Eq. (6). Figure 3(a) shows both simulated data points (symbols) and model predictions (black lines) vs. . The model captures the important dynamics of the vs. relationship, including a -dependent slope for low , and a saturating -independent value at high . These model fits were obtained by estimating the coefficients as , , , , . The confidence intervals for the fitted parameters are small compared to their respective estimates, confirming the appropriateness of the selected parameter set. The resulting estimates of showed high quality fits to from the MC simulations with a mean residual of and a Pearson Correlation coefficient of 0.998. Figure 3(b) presents the model estimates vs. MC simulated, which indicate the high quality of the fits across multiple orders of magnitude.
Fig. 3.
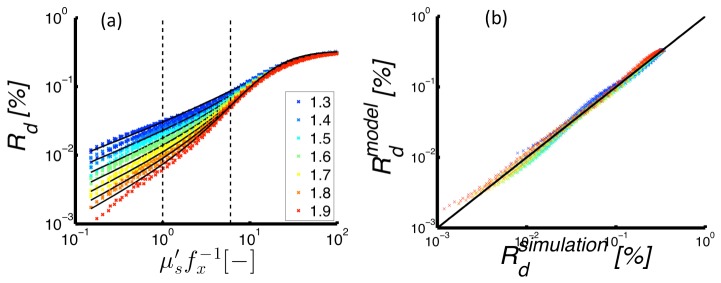
(Left) Reflectance intensity vs. dimensionless scattering as simulated by Monte Carlo models (markers) and predicted by the semi-empirical model (lines). Here, different colors indicate different -values of the scattering phase function. (Right) Simulated vs. model-estimated reflectance with the line of unity slope included for visualization of the linearity of the relationship.
3.3 Model inversion of measured to estimate and
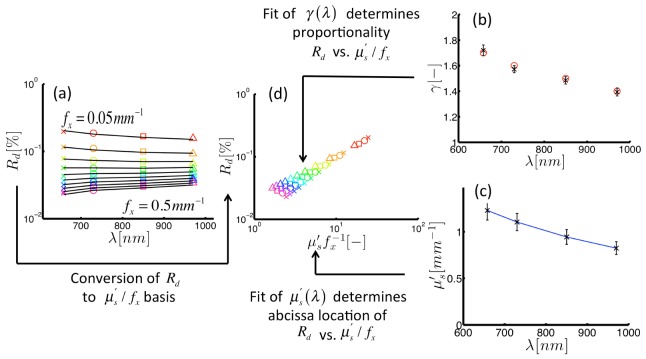
The forward-model given in Eq. (6) was used in an inversion algorithm to extract estimates of and from measurements of sampled at multiple. Figure 4 shows an example of these results within a simulated optical phantom with assembled from the Monte Carlo data (with 3% noise added). This example phantom specifies in units of mm, and a wavelength-dependent decrease in in the range [1.7-1.4], the spectral profiles of which are displayed in Figs. 4(b) and 4(c), respectively. Figure 4(a) displays where marker colors indicate the sampled = [0.05-0.5] mm−1 and marker shapes define each = [658-970] nm. These data suggest that the wavelength-dependent remission slope is different for different values. Figure 4(d) shows the vs. relationship with a wavelength-dependent slope that depends on . The annotations in Fig. 4 reveal the interconnected flow of information within the fitting procedure for , which interprets both the -dependent differences at each sampled , and -dependent differences at each sampled . Simultaneous fitting of the data in Fig. 4(a) accurately recovers () and () over the sampled wavelength range. These results provide the theoretical proof that sampled at multiple can be used to break the similarity relationship betweenand .
Fig. 4.
Inversion of demodulated reflectance model using simulated data. (a) Demodulated reflectance spectra sampled at multiple spatial frequencies (color markers) from a medium with background scattering properties, and , specified with the color markers in (b) and (c), respectively. (d) Reflectance from spectra in panel (a) plotted vs. dimensionless scattering clearly showing a -specific slope. Here, different symbols indicate wavelength, and colors define spatial frequency. The inversion algorithm returns a fitted estimate of reflectance (shown as black lines in (a)) and estimates optical properties (shown by black markers in (b) and (c)).
3.4 Experimental validation of sub-diffuse scattering imaging in optical phantoms
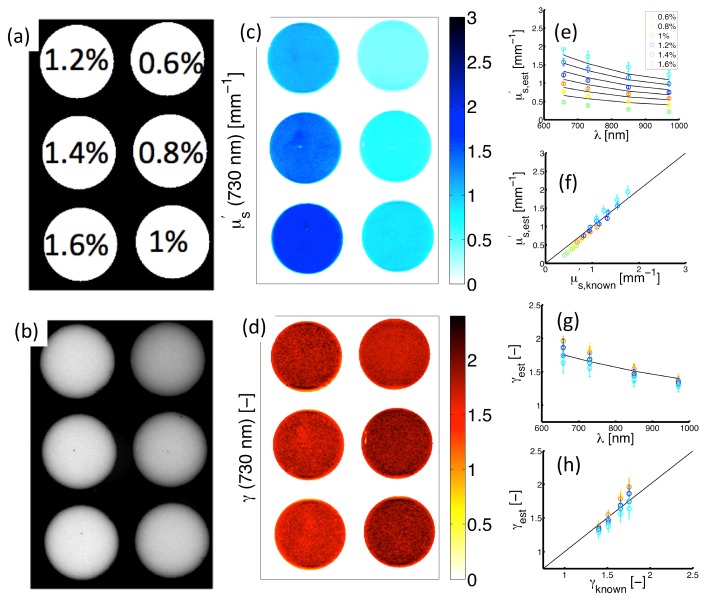
Figure 5(a) shows experimental measurements of Intralipid-based optical phantoms containing a range of lipid percentages = [0.6-1.6]% within the field of view. Figure 5(b) presents a wide-field monochromatic reflectance image ( at ) having increased remission intensity associated with increased lipid percentage. Figure 5(c) contains a map of estimates in the imaged phantoms. These data show proportionality between and the lipid percentage, which is expected because an increase in the lipid volume fraction increases the number of scatterers within the turbid medium, and in turn the remitted reflectance. Figure 5(e) shows spectra for both model-estimated (symbols) and known (lines) values; these spectra were evaluated from remission at the center of each imaged phantom. Figure (f) suggests good agreement exists between estimated and known over the full range of = [0.4-1.8] mm−1 with ; the black line with a slope of unity is included for visualization of the quality of the linear relationship. Figure 5(d) shows an image of estimates in each of the phantoms. Because is an implicit scattering parameter, the true value of is unchanged between the different volume fractions of lipid, with in all phantoms within the image. Model estimates accurately predict this invariance with the average in the six phantoms yielding . Figure 5(g) contains spectra for both model-estimates (symbols) and known values (lines). Figure 5(f) indicates good agreement for the values of = [1.4-1.75] investigated over the measured wavelength range with . The data in Fig. 5 validate the ability of model-based analysis of structured light to image spectral-variations accurately in sub-diffuse scattering parameters within a wide field of view.
Fig. 5.
Experimental measurements of structured light in Intralipid phantoms. (a) Sampled lipid volume fractions. (b) Diffuse intensity map (). (c) and (d) show spatially-resolved estimates of and at 730 nm. (e) Spectrally resolved in each phantom. (f) Corresponding estimates vs. known values. (g) spectra in each phantom. (h) Corresponding estimates vs. known values.
3.5 Preliminary in vivo imaging of a superficial scar
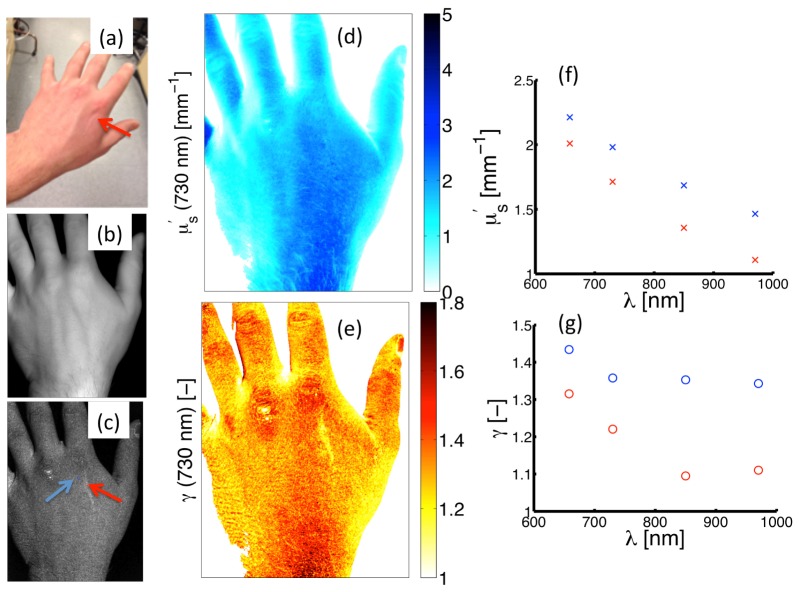
Structured light imaging was performed on a healthy volunteer who had a superficial scar located on the posterior side of the left hand near the distal end of the second metacarpal bone, as shown in Fig. 6(a). Figures 6(b) and 6(c) present diffuse () and high frequency () images of demodulated reflectance intensity. The scar is distinguished by a bright area of contrast on the high frequency image in 6(c) and is highlighted by the red arrow; this contrast is absent in the diffuse image in 6(b). Figures 6(d) and 6(e) show spatial maps of and at 730 nm, respectively. Spectral descriptions of both parameters are provided in Figs. 6(f) and 6(g), with these spectra originating from point locations denoted by arrows: blue (indicating normal skin) and red (indicating the scar). The map of does not provide obvious contrast between the superficial scar and surrounding normal tissue. However, substantial contrast is observed in between normal and scar tissue both in the spatial map and spectral profiles, with a maximum difference of at 850 nm. These data suggest that imaging of sub-diffuse scattering parameters may provide endogenous contrast to differentiate between tissue types, even when tissues appear similarly under diffuse optical sampling.
Fig. 6.
Measurement of the scar on the hand of a healthy volunteer. (a) Color photograph. (b) and (c) shows a reflectance remission intensity maps for low () and high () spatial frequencies, respectively. (d) and (e) show spatial maps of and at 730 nm. (f) and (g) showand spectra evaluated at point locations within the scar (red markers) and normal skin (blue markers), with the measurement locations shown by the red and blue arrows in (c).
4. Discussion and conclusions
This study investigated the use of structured light to image scattering properties quantitatively in turbid media that are relevant to anisotropic transport in the sub-diffusion regime. Monte Carlo simulated data were used to develop a semi-empirical model of demodulated reflectance,, in terms of dimensionless scattering expressed as , and , a descriptive metric of the backscatter probability defined by . Model-based estimation of both and was achieved by simultaneously fitting sampled at multiple. This approach was experimentally validated in Intralipid phantoms, and provided accurate estimation of sub-diffuse scattering properties over the range: = [0.4-1.8] mm−1 and = [1.4-1.75]. These data offer a unique multi-dimensional tissue assessment in terms of spatial as well as spectral variations in multiple scattering parameters. Pilot imaging results from a superficial scar on a healthy volunteer returned maps of that provided clear spatial demarcation between the scar and surrounding normal skin. While this preliminary in vivo image did not provide definitive confirmation of the differences in tissue structure between the sampled scar and normal skin, scar tissue is widely appreciated to contain differences in collagen composition relative to normal skin [46, 47], and this difference is attributed to be the source of the observed -based contrast associated with the location and shape of the scar in the image.
Structured light imaging samples scatter remission from turbid media in an epi-collection geometry in which the detection area overlaps the area that is illuminated with the sinusoidal pattern. This configuration enables collection of both diffuse photons that have scattered many times, and sub-diffuse photons that have anisotropically scattered only a few times. By placing an upper limit on the sampled spatial frequency of <0.33 the signal inherently contains more diffuse photons and limits the sensitivity of reflectance to [32]. Using the data in Fig. 3, it is possible to estimate the error introduced into the classical SFDI measurement of a turbid medium that is caused by lack of prior knowledge of the phase function. Assuming measurements of a purely scattering medium with with = would correspond to , a dimensionless scattering value that shows substantial sensitivity to can be found with a 42% variation about the median for in the range [1.3-1.9]. Sampling the same medium at a lower maximum spatial frequency = would correspond to and reduce the -associated variability in to 20%. This calculation considers a wide range of -values, and the -based distortions in biological tissue are likely to be less than these limits. These data support the concept that with proper selection of , analysis using diffusion theory is appropriate. The data also show the substantial influence that has on sampled above these limits. In the low dimensionless scattering region (<6), the demodulated reflectance can become dominated by the sub-diffuse signal, and substantial variations in remission intensity can be caused by either changes in the number of scatters or changes in the scattering phase function. For example, at = 1 a 4-fold difference in is observed between = 1.3 and = 1.9. This difference in equates to a change in by a factor of 4 for = 1.9, or conversely, a change in by a factor of 11 for = 1.3. Thus, these data suggest that diffuse analysis of SFDI may require careful selection of , especially in weakly-scattering media in order to avoid -based errors in obtained by diffusion theory.
The approach developed in this paper allows estimation of and from spectra that are sampled in a scatter-dominated turbid medium. A key component of the method is that sampling of at multiple values identifies a -specific vs. proportionality, and this analysis assumes that background absorbers do not attenuate the reflectance remission intensity. Reflectance sampled at high spatial frequency patterns is insensitive to a wide range of background absorption (i.e. ) [32]; however, reflectance sampled at lower spatial frequency patterns is sensitive to absorption. Simulations were performed to estimate the influence of background absorption on the remission spectra in tissue-simulating phantoms. A phantom composed of 99% water and 1% lipid is expected to have a maximum absorption at 970 nm of ; a factor that is 3 to 30-fold greater than the at the other sampled wavelengths. This maxima corresponds to a ratio of ~20, and when sampled at absorption only introduces a 10% decrease in (data not shown). Previous work has shown that sub-diffuse scattering parameters can be estimated in the presence of strong absorbers by utilizing a model to estimate reflectance remission in the absence of absorption [39, 40], a calculation that is informed by a basis set of chromophores, the specific absorption coefficients of the chromophores, and a model-based estimate of the photon path length within the medium [48, 49]. In the present study the experimental device only samples four wavelengths, and does not provide adequate spectral information to fit both the scattering and absorption properties. Future investigations will consider optimization of the structured illumination design sample sets of wavelengths and spatial frequencies necessary to estimate scattering properties in the presence of strong biological absorbers.
It is also worth noting that the sub-diffusive imaging approach developed in the current study was tested and validated in homogenous optical media and then applied to heterogeneous tissue. The appropriateness of this transition is based on the principle that the sampled scatterers are relatively constant within the areas defined by the (local) spatial frequencies used in the illumination. Future investigations will consider the influence that structural heterogeneities (e.g. layered tissue) may have on the sub-diffuse parameter estimates.
The present study represents a proof-of-principle that structured light imaging can be used to map spatial variations in sub-diffuse scattering parameters quantitatively. While previous studies have achieved independent estimation of and metrics of the such as , they have been limited to microscopic fields of view (i.e. sub-mm length scale) [8, 12, 29, 43]. The structured illumination imaging approach described here has three important benefits for imaging of scatter-based contrast in tissue: (1) the scatter properties are localized to the superficial tissue, (2) the sampled field of view is large (i.e. on the scale of tens of cm), and (3) measurement of remission at multiple spatial frequencies can be used to break the similarity relationship between scatter frequency and directionality. Independent assessment of spatial variations of multiple spectroscopically resolved parameters may provide a multi-dimensional basis for characterizing differences between tissue types.
Acknowledgments
Funding for this project has been provided by National Institutes of Health grants K25 CA164248 (SCK), R01 CA109558 (BWP, DMM, JTE), DOC/NIST: 60NANB13D210 (SCK, BWP, DMM) and a Canadian Institutes of Health Fellowship (JTE). The authors would also like to thank Dr. Jeeseong C. Hwang for helpful discussions.
References and links
- 1.Boustany N. N., Kuo S. C., Thakor N. V., “Optical scatter imaging: subcellular morphometry in situ with Fourier filtering,” Opt. Lett. 26(14), 1063–1065 (2001). 10.1364/OL.26.001063 [DOI] [PubMed] [Google Scholar]
- 2.Wax A., Yang C., Backman V., Badizadegan K., Boone C. W., Dasari R. R., Feld M. S., “Cellular organization and substructure measured using angle-resolved low-coherence interferometry,” Biophys. J. 82(4), 2256–2264 (2002). 10.1016/S0006-3495(02)75571-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schuele G., Vitkin E., Huie P., O’Connell-Rodwell C., Palanker D., Perelman L. T., “Optical spectroscopy noninvasively monitors response of organelles to cellular stress,” J. Biomed. Opt. 10(5), 051404 (2005). 10.1117/1.2075207 [DOI] [PubMed] [Google Scholar]
- 4.Liu Y., Li X., Kim Y. L., Backman V., “Elastic backscattering spectroscopic microscopy,” Opt. Lett. 30(18), 2445–2447 (2005). 10.1364/OL.30.002445 [DOI] [PubMed] [Google Scholar]
- 5.Kim Y. L., Liu Y., Wali R. K., Roy H. K., Backman V., “Low-coherent backscattering spectroscopy for tissue characterization,” Appl. Opt. 44(3), 366–377 (2005). 10.1364/AO.44.000366 [DOI] [PubMed] [Google Scholar]
- 6.Krishnaswamy V., Hoopes P. J., Samkoe K. S., O’Hara J. A., Hasan T., Pogue B. W., “Quantitative imaging of scattering changes associated with epithelial proliferation, necrosis, and fibrosis in tumors using microsampling reflectance spectroscopy,” J. Biomed. Opt. 14(1), 014004 (2009). 10.1117/1.3065540 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Subramanian H., Pradhan P., Liu Y., Capoglu I. R., Rogers J. D., Roy H. K., Brand R. E., Backman V., “Partial-wave microscopic spectroscopy detects subwavelength refractive index fluctuations: an application to cancer diagnosis,” Opt. Lett. 34(4), 518–520 (2009). 10.1364/OL.34.000518 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.van Leeuwen-van Zaane F., Gamm U. A., van Driel P. B. A. A., Snoeks T. J. A., de Bruijn H. S., van der Ploeg-van den Heuvel A., Mol I. M., Löwik C. W. G. M., Sterenborg H. J. C. M., Amelink A., Robinson D. J., “In vivo quantification of the scattering properties of tissue using multi-diameter single fiber reflectance spectroscopy,” Biomed. Opt. Express 4(5), 696–708 (2013). 10.1364/BOE.4.000696 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Boustany N. N., Boppart S. A., Backman V., “Microscopic Imaging and Spectroscopy with Scattered Light,” Annu. Rev. Biomed. Eng. 12(1), 285–314 (2010). 10.1146/annurev-bioeng-061008-124811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Backman V., Roy H. K., “Optical spectroscopic markers of cancer,” Dis. Markers 25(6), 279 (2008). 10.1155/2008/561471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wax A., Zhu Y. Z., Terry N. G., Chen X. X. L., Gebhart S. C., Brown W. J., “Label-Free Nuclear Morphology Measurements of Dysplasia in the Egda Rat Model Using Angle-Resolved Low Coherence Interferometry,” Gastroenterology 136, A122 (2009). [Google Scholar]
- 12.Yi J., Radosevich A. J., Stypula-Cyrus Y., Mutyal N. N., Azarin S. M., Horcher E., Goldberg M. J., Bianchi L. K., Bajaj S., Roy H. K., Backman V., “Spatially resolved optical and ultrastructural properties of colorectal and pancreatic field carcinogenesis observed by inverse spectroscopic optical coherence tomography,” J. Biomed. Opt. 19(3), 036013 (2014). 10.1117/1.JBO.19.3.036013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu Y., Uttam S., Alexandrov S., Bista R. K., “Investigation of nanoscale structural alterations of cell nucleus as an early sign of cancer,” BMC Biophys 7(1), 1 (2014). 10.1186/2046-1682-7-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Patel M., Gomes A., Ruderman S., Hardee D., Crespo S., Raimondo M., Woodward T., Backman V., Roy H., Wallace M., “Polarization gating spectroscopy of normal-appearing duodenal mucosa to detect pancreatic cancer,” in press Gastrointest. Endosc. (2014). [DOI] [PMC free article] [PubMed]
- 15.Laughney A. M., Krishnaswamy V., Rizzo E. J., Schwab M. C., Barth R. J., Pogue B. W., Paulsen K. D., Wells W. A., “Scatter spectroscopic imaging distinguishes between breast pathologies in tissues relevant to surgical margin assessment,” Clin. Cancer Res. 18(22), 6315–6325 (2012). 10.1158/1078-0432.CCR-12-0136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Laughney A. M., Krishnaswamy V., Rizzo E. J., Schwab M. C., Barth R. J., Jr, Cuccia D. J., Tromberg B. J., Paulsen K. D., Pogue B. W., Wells W. A., “Spectral discrimination of breast pathologies in situ using spatial frequency domain imaging,” Breast Cancer Res. 15(4), R61 (2013). 10.1186/bcr3455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Laughney A. M., Krishnaswamy V., Rice T. B., Cuccia D. J., Barth R. J., Tromberg B. J., Paulsen K. D., Pogue B. W., Wells W. A., “System analysis of spatial frequency domain imaging for quantitative mapping of surgically resected breast tissues,” J. Biomed. Opt. 18(3), 036012 (2013). 10.1117/1.JBO.18.3.036012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jacques S. L., Pogue B. W., “Tutorial on diffuse light transport,” J. Biomed. Opt. 13(4), 041302 (2008). 10.1117/1.2967535 [DOI] [PubMed] [Google Scholar]
- 19.Farrell T. J., Patterson M. S., Wilson B., “A Diffusion Theory Model of Spatially Resolved, Steady-State Diffuse Reflectance for the Noninvasive Determination of Tissue Optical Properties In Vivo,” Med. Phys. 19(4), 879–888 (1992). 10.1118/1.596777 [DOI] [PubMed] [Google Scholar]
- 20.Bartek M., Wang X., Wells W., Paulsen K. D., Pogue B. W., “Estimation of subcellular particle size histograms with electron microscopy for prediction of optical scattering in breast tissue,” J. Biomed. Opt. 11(6), 064007 (2006). 10.1117/1.2398903 [DOI] [PubMed] [Google Scholar]
- 21.Amelink A., Bard M. P., Burgers S. A., Sterenborg H. J., “Single-scattering spectroscopy for the endoscopic analysis of particle size in superficial layers of turbid media,” Appl. Opt. 42(19), 4095–4101 (2003). 10.1364/AO.42.004095 [DOI] [PubMed] [Google Scholar]
- 22.Reif R., A’Amar O., Bigio I. J., “Analytical model of light reflectance for extraction of the optical properties in small volumes of turbid media,” Appl. Opt. 46(29), 7317–7328 (2007). 10.1364/AO.46.007317 [DOI] [PubMed] [Google Scholar]
- 23.Mourant J. R., Boyer J., Hielscher A. H., Bigio I. J., “Influence of the scattering phase function on light transport measurements in turbid media performed with small source-detector separations,” Opt. Lett. 21(7), 546–548 (1996). 10.1364/OL.21.000546 [DOI] [PubMed] [Google Scholar]
- 24.Bevilacqua F., Depeursinge C., “Monte Carlo study of diffuse reflectance at source-detector separations close to one transport mean free path,” J. Opt. Soc. Am. A 16(12), 2935–2945 (1999). 10.1364/JOSAA.16.002935 [DOI] [Google Scholar]
- 25.Kanick S. C., Krishnaswamy V., Gamm U. A., Sterenborg H. J., Robinson D. J., Amelink A., Pogue B. W., “Scattering phase function spectrum makes reflectance spectrum measured from Intralipid phantoms and tissue sensitive to the device detection geometry,” Biomed. Opt. Express 3(5), 1086–1100 (2012). 10.1364/BOE.3.001086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vitkin E., Turzhitsky V., Qiu L., Guo L. Y., Itzkan I., Hanlon E. B., Perelman L. T., “Photon diffusion near the point-of-entry in anisotropically scattering turbid media,” Nat. Commun. 2, 587 (2011). 10.1038/ncomms1599 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gomes A. J., Backman V., “Analytical light reflectance models for overlapping illumination and collection area geometries,” Appl. Opt. 51(33), 8013–8021 (2012). 10.1364/AO.51.008013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kanick S. C., Gamm U. A., Schouten M., Sterenborg H. J., Robinson D. J., Amelink A., “Measurement of the reduced scattering coefficient of turbid media using single fiber reflectance spectroscopy: fiber diameter and phase function dependence,” Biomed. Opt. Express 2(6), 1687–1702 (2011). 10.1364/BOE.2.001687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Thueler P., Charvet I., Bevilacqua F., St Ghislain M., Ory G., Marquet P., Meda P., Vermeulen B., Depeursinge C., “In vivo endoscopic tissue diagnostics based on spectroscopic absorption, scattering, and phase function properties,” J. Biomed. Opt. 8(3), 495–503 (2003). 10.1117/1.1578494 [DOI] [PubMed] [Google Scholar]
- 30.Gomes A. J., Ruderman S., DelaCruz M., Wali R. K., Roy H. K., Backman V., “In vivo measurement of the shape of the tissue-refractive-index correlation function and its application to detection of colorectal field carcinogenesis,” J. Biomed. Opt. 17(4), 047005 (2012). 10.1117/1.JBO.17.4.047005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cuccia D. J., Bevilacqua F., Durkin A. J., Tromberg B. J., “Modulated imaging: quantitative analysis and tomography of turbid media in the spatial-frequency domain,” Opt. Lett. 30(11), 1354–1356 (2005). 10.1364/OL.30.001354 [DOI] [PubMed] [Google Scholar]
- 32.Cuccia D. J., Bevilacqua F., Durkin A. J., Ayers F. R., Tromberg B. J., “Quantitation and mapping of tissue optical properties using modulated imaging,” J. Biomed. Opt. 14(2), 024012 (2009). 10.1117/1.3088140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gioux S., Mazhar A., Lee B. T., Lin S. J., Tobias A. M., Cuccia D. J., Stockdale A., Oketokoun R., Ashitate Y., Kelly E., Weinmann M., Durr N. J., Moffitt L. A., Durkin A. J., Tromberg B. J., Frangioni J. V., “First-in-human pilot study of a spatial frequency domain oxygenation imaging system,” J. Biomed. Opt. 16(8), 086015 (2011). 10.1117/1.3614566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Erickson T. A., Mazhar A., Cuccia D., Durkin A. J., Tunnell J. W., “Lookup-table method for imaging optical properties with structured illumination beyond the diffusion theory regime,” J. Biomed. Opt. 15(3), 036013 (2010). 10.1117/1.3431728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Konecky S. D., Rice T., Durkin A. J., Tromberg B. J., “Imaging scattering orientation with spatial frequency domain imaging,” J. Biomed. Opt. 16(12), 126001 (2011). 10.1117/1.3657823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Krishnaswamy V., Elliott J. T., McClatchy D. M., 3rd, Barth R. J., Jr, Wells W. A., Pogue B. W., Paulsen K. D., “Structured light scatteroscopy,” J. Biomed. Opt. 19(7), 070504 (2014). 10.1117/1.JBO.19.7.070504 [DOI] [PubMed] [Google Scholar]
- 37.Calabro K. W., Aizenberg E., Bigio I. J., “Improved empirical models for extraction of tissue optical properties from reflectance spectra,” Proc. SPIE 8230, 82300H (2012). 10.1117/12.906753 [DOI] [Google Scholar]
- 38.Kanick S. C., Gamm U. A., Sterenborg H. J., Robinson D. J., Amelink A., “Method to quantitatively estimate wavelength-dependent scattering properties from multidiameter single fiber reflectance spectra measured in a turbid medium,” Opt. Lett. 36(15), 2997–2999 (2011). 10.1364/OL.36.002997 [DOI] [PubMed] [Google Scholar]
- 39.Gamm U. A., Kanick S. C., Sterenborg H. J., Robinson D. J., Amelink A., “Measurement of tissue scattering properties using multi-diameter single fiber reflectance spectroscopy: in silico sensitivity analysis,” Biomed. Opt. Express 2(11), 3150–3166 (2011). 10.1364/BOE.2.003150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gamm U. A., Kanick S. C., Sterenborg H. J., Robinson D. J., Amelink A., “Quantification of the reduced scattering coefficient and phase-function-dependent parameter γ of turbid media using multidiameter single fiber reflectance spectroscopy: experimental validation,” Opt. Lett. 37(11), 1838–1840 (2012). 10.1364/OL.37.001838 [DOI] [PubMed] [Google Scholar]
- 41.Amelink A., Robinson D. J., Sterenborg H. J., “Confidence intervals on fit parameters derived from optical reflectance spectroscopy measurements,” J. Biomed. Opt. 13(5), 054044 (2008). 10.1117/1.2982523 [DOI] [PubMed] [Google Scholar]
- 42.Jacques S. L., “Optical properties of biological tissues: a review,” Phys. Med. Biol. 58(11), R37–R61 (2013). 10.1088/0031-9155/58/11/R37 [DOI] [PubMed] [Google Scholar]
- 43.Bevilacqua F., Piguet D., Marquet P., Gross J. D., Tromberg B. J., Depeursinge C., “In vivo local determination of tissue optical properties: applications to human brain,” Appl. Opt. 38(22), 4939–4950 (1999). 10.1364/AO.38.004939 [DOI] [PubMed] [Google Scholar]
- 44.U. A. Gamm, M. Heijblom, D. Piras, F. M. Van den Engh, S. Manohar, W. Steenbergen, H. J. C. M. Sterenborg, D. J. Robinson, and A. Amelink, “In vivo determination of scattering properties of healthy and malignant breast tissue by use of multi-diameter-single fiber reflectance spectroscopy (MDSFR),” Biomedical Applications of Light Scattering Vii. 8592, (2013). [Google Scholar]
- 45.Michels R., Foschum F., Kienle A., “Optical properties of fat emulsions,” Opt. Express 16(8), 5907–5925 (2008). 10.1364/OE.16.005907 [DOI] [PubMed] [Google Scholar]
- 46.Epstein F. H., Singer A. J., Clark R. A. F., “Mechanisms of disease - Cutaneous wound healing,” N. Engl. J. Med. 341(10), 738–746 (1999). [DOI] [PubMed] [Google Scholar]
- 47.van Zuijlen P. P. M., Ruurda J. J. B., van Veen H. A., van Marle J., van Trier A. J. M., Groenevelt F., Kreis R. W., Middelkoop E., “Collagen morphology in human skin and scar tissue: no adaptations in response to mechanical loading at joints,” Burns 29(5), 423–431 (2003). 10.1016/S0305-4179(03)00052-4 [DOI] [PubMed] [Google Scholar]
- 48.Kanick S. C., Robinson D. J., Sterenborg H. J., Amelink A., “Monte Carlo analysis of single fiber reflectance spectroscopy: photon path length and sampling depth,” Phys. Med. Biol. 54(22), 6991–7008 (2009). 10.1088/0031-9155/54/22/016 [DOI] [PubMed] [Google Scholar]
- 49.Kanick S. C., Robinson D. J., Sterenborg H. J., Amelink A., “Method to quantitate absorption coefficients from single fiber reflectance spectra without knowledge of the scattering properties,” Opt. Lett. 36(15), 2791–2793 (2011). 10.1364/OL.36.002791 [DOI] [PubMed] [Google Scholar]