Automated identification of basal cell carcinoma by polarization-sensitive optical coherence tomography

Abstract

We report an automated classifier to detect the presence of basal cell carcinoma in images of mouse skin tissue samples acquired by polarization-sensitive optical coherence tomography (PS-OCT). The sensitivity and specificity of the classifier based on combined information of the scattering intensity and birefringence properties of the samples are significantly higher than when intensity or birefringence information are used alone. The combined information offers a sensitivity of 94.4% and specificity of 92.5%, compared to 78.2% and 82.2% for intensity-only information and 85.5% and 87.9% for birefringence-only information. These results demonstrate that analysis of the combination of complementary optical information obtained by PS-OCT has great potential for accurate skin cancer diagnosis.

1. Introduction

Skin cancer, the most common form of cancer in the Western world, accounts for billions in annual healthcare costs [1–3]. In the United States alone, roughly one million people develop skin cancer each year [4,5]. Because the expertise needed to clinically diagnose skin cancer can be costly and difficult to obtain in the absence of access to specialized medical care, reliable, automated and non-invasive diagnostic methods are needed to expedite and facilitate diagnosis in the clinic and to provide new options for medical care in poorly resourced regions.

Optical coherence tomography (OCT) is an established tool for biomedical research that has been used in many clinical applications to perform high-resolution, cross-sectional imaging of subsurface structures. Several studies have suggested that OCT can perform non-invasive diagnosis of skin cancer, particularly because it is able to visualize sub-dermal features associated with the first appearance of skin cancer [6–11]. For example, Jørgensen et al. demonstrated a machine learning-based method to diagnose and classify skin cancer with OCT [6]. While their OCT system revealed structural information derived from differences in scattering intensity for cancerous versus healthy tissue, OCT-based scattering contrast in their and others’ work had limited power to discriminate skin cancer, leading to a sensitivity and specificity below 80% [10, 12–15].

It is well known that the development of skin cancer alters the distribution and alignment of collagen, resulting in a change in the birefringence of skin [10, 16–19]. Birefringence provides orthogonal optical information to scattering; hence, a discriminator that combines birefringence and structural information should achieve higher accuracy than one using structural information alone. For example, Wang et al. recently introduced a logistic prediction model to measure the birefringence of ovarian tissue using polarization-sensitive (PS-) OCT and achieved a sensitivity of 100% for diagnosing ovarian cancer [20]. Cross-polarized OCT, a variant of PS-OCT, has also yielded improvements of >12% in the specificity and sensitivity of diagnosing bladder cancer compared to using standard OCT alone [21]. Several groups have demonstrated that PS-OCT is capable of visualizing birefringence in skin, but these works stop short of using this information to quantitatively assess birefringence changes associated with skin cancer [22–25]. Conversely, Strasswimmer et al. used PS-OCT to show that the slope of the phase retardation as a function of depth is a biomarker for skin cancer [8], but their method to measure this parameter requires that the lateral range and depth of the tumor or suspected tumor tissue be manually determined in advance, which is not practical for early stages of skin cancer. Hence, while it is clear that PS-OCT is promising for the detection of skin cancer, there remains a need for automated methods to detect the presence of cancerous tissue in the collected images.

In this study, we used PS-OCT to simultaneously acquire intensity and birefringence images of samples of healthy and cancerous mouse skin ex vivo. We then developed a support-vector-machine (SVM)-based classifier to automatically identify images presenting with basal cell carcinoma (BCC), the most frequently occurring form of skin cancer. The presence of BCC in the images is determinable based on features extracted from their morphological (backscattering intensity) and birefringence (phase retardation) properties. Using the combined information from intensity and phase retardation, our automated classifier significantly outperforms previous works examining skin cancer based on OCT alone and achieves a sensitivity and specificity of 94.4% and 92.5%, respectively. These successful results suggest that PS-OCT is a strong candidate for robust, automated diagnosis of skin cancer.

2. Experimental methods

2.1. Sample preparation

Our dataset contained two types of BCC samples: endogenous and allograft BCCs. We generated endogenous BCC samples from Ptch +/− K14CreER2 tg, p53 fl/fl mice as described elsewhere but including some slight adjustments [26]. To create endogenous tumors, mice were injected with 100 μL of tamoxifen for three consecutive days at six weeks of age and exposed to 4 Gy of ionizing radiation at eight weeks of age. When visible BCCs developed (around six to eight months of age), samples from the cancerous regions (indicated by a papule 5–7 mm in length) and/or normal, tumor-free regions of the mouse (“normal skin”) were collected. To generate allograft BCCs, we created a cell suspension of the endogenous BCCs generated from the Ptch +/− K14CreER2 tg, p53 fl/fl mice and mixed it with Matrigel in a 1:1 ratio. A small volume (100 μL) of this mixture (totaling around 2,000,000 cells) was injected into each of two distinct sites on the dorsal surface of immunocompromised NOD/SCID mice, and the tumors were allowed to grow. When visible BCCs developed (around four to six weeks post injection), the same set of samples was collected. All mice were housed in the animal facility at the Children’s Hospital Oakland Research Instituted (CHORI) and monitored based on the guidelines set by their IACUC. All samples were harvested from the mice within two hours of the intended imaging time, immersed in a test tube containing 10% Dulbecco’s modified Eagle’s medium solution and surrounded by ice for transport to the imaging setup.

2.2. Imaging protocol

Prior to imaging the samples, residual mouse hair was removed by shaving. We applied a small amount of 0.9% sodium chloride onto the surface of the tissue to avoid air-drying. Samples were then imaged with a home-built, free-space spectral-domain PS-OCT system (λ = 840 nm, FWHM = 40 nm). The configuration of the system is similar to that described elsewhere [27,28]. The axial and lateral resolutions and sensitivity of the system were measured to be 9.0 μm, 20 μm and 96 dB, respectively, with 1.9 mW illuminating the sample at an A-line rate of 20 kHz. Sets of 16 B-scans (each comprising 1024 A-scans) spanning 5.6 mm were acquired through repeated scanning of the same region to enhance the image signal-to-noise ratio (SNR) and to restrain speckle noise (through averaging).

The sample was illuminated with circularly polarized light. The intensity and phase retardation (birefringence) were obtained with standard equations: that is, by calculating the quadratic sum and ratio of the signal amplitude of the two orthogonally polarized detection channels [27, 28]. The final intensity and retardation images were calculated from averaged B-scans.

2.3. Comparison of PS-OCT and histology images

To validate whether our samples correlated with histological classifications of BCC or healthy tissue, we also took histology images of some of our samples after PS-OCT imaging. The B-scan planes imaged by PS-OCT were marked with insoluble ink; the samples were then immersed in formalin solution and processed for histology. Histological images collected by microscopy were manually registered to PS-OCT images from the same tissue slices.

3. Algorithm development

Development of the classifier proceeded in several steps. First, we observed the collected intensity and retardation images in an attempt to extract visible trends apparent in images known to contain healthy or BCC tissue (see Sec. 3.1). We then devised a method to automatically identify the surface of the skin and segment a region of interest (see Sec. 3.2) for calculating quantitative parameters (see Sec. 3.3) to describe the relevant features. Finally, we employed a supervised learning method to construct the classifier and tested its performance on the samples.

3.1. Feature selection and classification

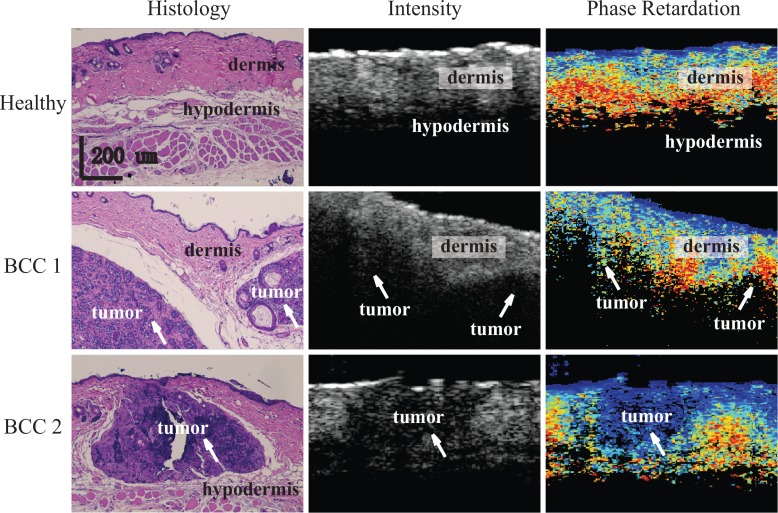
Figure 1 shows representative comparison images of the histology and OCT datasets. The top row shows images obtained from healthy mouse skin, and images in the middle and bottom rows were acquired from two types of BCCs samples, allograft and endogenous, respectively, each with different tumor sizes. The following observations regarding visual features of the OCT intensity and retardation images that correlate with structural features evident in the histology were useful to guide the selection of parameters for the classifier: 1) Across all samples, we identified the epidermal layer as a very thin, hyper-reflective layer near the skin surface, while the dermis was a relatively thicker layer beneath it. 2) The pixels in the intensity images of tumorous regions, which are marked by white arrows in Fig. 1, as well as those in hypodermis tissue, which mainly contain fat and muscle, appeared as regions of low scattering. This is possibly due to the high absorption of light in tumors and hypodermis tissue. 3) There often appeared a visible interface between either dermis and hypodermis or dermis and tumor in intensity OCT images. 4) In phase retardation images, we could clearly observe a trend of increasing retardation with penetration depth in dermis, indicating the existence of birefringence; in contrast, tumorous regions were marked by a constant phase retardation, consistent with the expectation that the development of tumor would reduce birefringence in tissue by distorting the alignment of the collagen. 5) As seen in images in the middle row of Fig. 1 and as observed in some other samples (not shown), we found that the presence of a tumor can cause thinning of the surrounding dermis layer. This thinning usually resulted in an increased amount of birefringence in the dermis.

Fig. 1.

Representative histological (left column), intensity (middle column), and phase retardation (right column) images obtained from the same or similar locations in healthy (top row), endogenous BCC (top row), and allograft BCC (bottom row) mouse skin tissue. White arrows indicate location of tumors. The scale bars are applicable to all images.

3.2. Region of interest selection

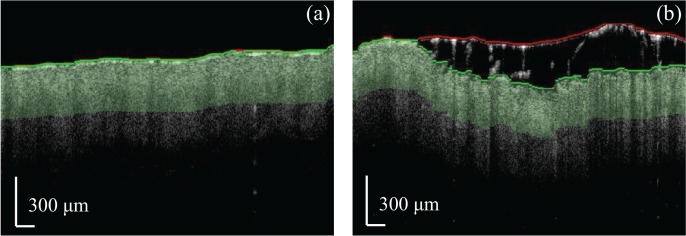
The effect of scattering in biological tissue leads to a decrease in SNR in deeper layers of skin, which ultimately limits the reliability of data in these regions [29–31]. Hence, we restricted our calculation of parameters based on image features to a shallow region of interest (ROI) just beneath the skin surface. The liquid drop added to the surface during the imaging protocol complicated the surface extraction procedure due to the presence of an additional, thick layer of water and occasional trapping of mouse hair. Thus, our procedure to identify the true surface of the skin was as follows: 1) We identified a “first surface,” which could either be the true skin surface or a boundary between water and fur, by solving for the path with the minimum cost when traversing the image from the leftmost to the rightmost A-line. The cost function was defined as in [32]. 2) We performed a second segmentation by carrying out another minimum-cost path search over the region comprising the first surface and the 100-pixel sub-area below it. If the second segmentation yielded a “second surface” that was within three pixels of the top of this sub-area, we considered the first surface as the skin/air boundary; otherwise, the second surface was considered the true skin surface. Figure 2 shows two representative images in which the first surface is denoted in red, and the second surface is denoted in green. Note how the presence of the water droplet and residual fur in Fig. 2(b) leads to a stark difference in position between the first and second surfaces, whereas the two surfaces are nearly overlapped in Fig. 2(a). Finally, the ROIs were selected to comprise the first 100 pixels (320 μm) beneath the true skin surface, represented in Fig. 2 as light green areas.

Fig. 2.

Surface segmentation and ROI selection for intensity images. The red and green curves represent the first and second (true) skin surface segmentations, respectively.

3.3. Classifier parameter selection

Based on our initial observation and comparison between histological and PS-OCT images, we established six global and seven local parameters to populate our classifier model (Table 1). The parameters were representative of features that could distinguish tumor and healthy samples based on the intensity and retardation information present in the ROI of the PS-OCT images. Global parameters were obtained by analysis of all data in the ROI of the intensity or phase retardation image, while local parameters were extracted from smaller datasets obtained by selecting A-lines within a moving lateral window 1/16^th the width of the whole image (5.6 mm). Thus, the moving window aggregated information from 64 A-lines at a time. The length of this window was chosen based on the observed widths of the tumors in the images and the need to reduce speckle contrast.

Table 1.

List of global and local intensity and birefringence parameters used in the classifier.

Intensity	Global	1	Gint : Average slope of the intensity of the averaged A-line.
		2	Th: Estimated mean thickness of the dermal layer.
	Local	3	Max(Δgi(x)): Maximum difference in the attenuation coefficient between the first 30 and last 30 pixels in the averaged A-line across all sub-images.
		4	Min(Δgi(x)): Minimum difference in the attenuation coefficient between the first 30 and last 30 pixels in the averaged A-line across all sub-images.
		5	std(Δgi(x)): Standard deviation of the difference in attenuation coefficient between the first 30 and last 30 pixels in the averaged A-line across all sub-images.
Birefringence	Global	6	std(ΔR(x)): Standard deviation of the difference in the mean retardation between the first and second set of 50 pixels in the ROI.
		7	r0.1: Percentage of lines in the first 50 pixels having a mean retardation at least 0.1 radians lower than in the second 50 pixels.
		8	r0.2: Percentage of lines in the first 50 pixels having a mean retardation at least 0.2 radians lower than in the second 50 pixels.
		9	r0.3: Percentage of lines in the first 50 pixels having a mean retardation at least 0.3 radians lower than in the second 50 pixels.
	Local	10	Min(gr(x)): Minimum slope of the retardation across all local sub-images. Max(gr(x)): Maximum slope of the retardation across all local sub-images.
		11
		12	Min(Resr(x)): Minimum residual of the linear regression for retardation as a function of depth in all local sub-images.
		13	Max(Resr(x)): Maximum residual of the linear regression for retardation as a function of depth in all local sub-images.

The global intensity parameters were based on an averaged A-line, I_ave(z), generated by averaging ROI-sized segments of all A-lines within each intensity image on a logarithmic scale. Figure 3 shows a representative intensity image and its associated averaged A-line. The global attenuation of the sample was evaluated using the slope parameter G_int, which was extracted from a linear regression fit to the averaged A-line (red, dashed line). The starting point of the linear regression was D_fit, the depth located three pixels below the location of the peak intensity. This depth was chosen to avoid potential fluctuations of the peak near the surface and is indicated by the vertical, black dashed line in Fig. 3(b).

Fig. 3.

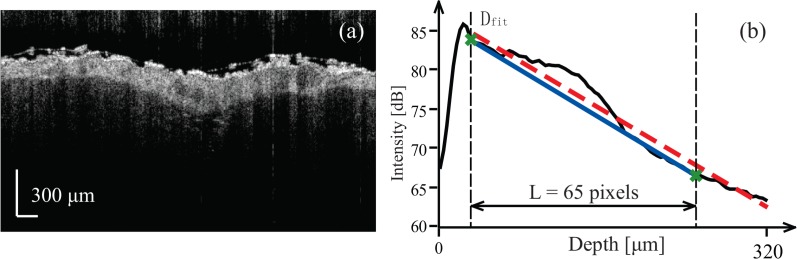
Description of global intensity parameters. (a) An intensity image of mouse skin. (b) Averaged intensity A-line versus depth and visual guides to calculate parameters of interest. The black curve is averaged intensity A-line. The leftmost black, vertical dashed line indicates the starting position of the linear regression (red, dashed line), while the green line connects the starting point of the linear regression to the point 65 pixels below it and is used to calculate the thickness of the dermis layer.

Since both tumor and hypodermis exhibited lower scattering (i.e., higher intensity extinction coefficient) than the adjacent dermal layer, the bottom boundary of the dermis was marked by a convex pattern in the averaged A-scan. The thickness of dermis layer, Th, was roughly estimated by finding the thickness of this convex pattern. We connected the point D_fit to a point 65 pixels (208 μm) below it to create a ramp function, Ramp(z), shown as the blue solid line in Fig. 3(b). The thickness of the dermis was roughly determined to be the depth-weighted center of mass of the difference between I_ave(z) and Ramp(z):

$$\mathit{Th}=\frac{{\sum }_{z=D_{\mathit{fit}}}^{D_{\mathit{fit}}+L}z\cdot f\left(I_{\mathit{ave}}(z)-\mathit{Ramp}(z)\right)}{{\sum }_{z=D_{\mathit{fit}}}^{D_{\mathit{fit}}+L}f\left(I_{\mathit{ave}}(z)-\mathit{Ramp}(z)\right)},$$ (1)

where the function f (x) considers only positive values of its argument. That is:

$$f(x)=\{\begin{array}{cc}x,& x>0\\ 0,& \mathit{otherwise}\end{array}.$$ (2)

Local intensity parameters were calculated along moving windows comprising the 64-A-line ROIs. For each window, we generated an averaged A-line as was done to extract the global parameters. Then, we implemented two linear regressions: one each along the first 30 and last 30 points in the averaged A-line. The difference in slope between these two regressions represented a change in the attenuation coefficient or scattering properties as a function of depth within the window. The difference in slope was calculated for all local windows, and the maximum, minimum, and standard deviation of this value were chosen as representative parameters to describe the local properties of the intensity images.

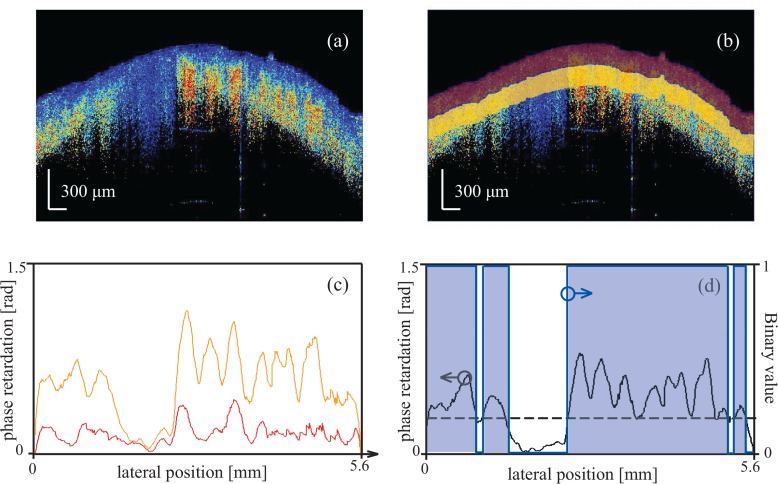
As seen in Fig. 1, images containing tumors exhibit regions of skin showing loss of birefringence, which manifest as little to no change in the phase retardation as a function of depth. Hence, to evaluate the presence of such a change, we divided the 100-pixel ROI below the surface into two sub-ROIs comprising the first and second group of 50 pixels (160 μm) beneath the surface, shown as red and yellow areas in Fig. 4(b). Then, we averaged the phase retardation obtained for all pixels within a given sub-ROI. Representative curves showing the mean retardation for each A-line of the two sub-ROIs are shown in Fig. 4(c). The change in mean phase retardation between the two sub-ROIs was calculated as:

$$\mathrm{\Delta }R=\frac{1}{50}\sum _{i=51}^{100}R(x,i)-\frac{1}{50}\sum _{i=1}^{50}R(x,i),$$ (3)

where R(x,i) denotes the retardation value obtained at lateral position x and depth associated with the i-th pixel in the ROI. A representative curve is shown in black in Fig. 4(d). We calculated the standard deviation of ΔR(x) to evaluate its fluctuation, which describes the lateral variation in birefringence. We then converted ΔR(x) to a binary value, using as a threshold the dashed line shown in Fig. 4(d). The percentage of A-lines for which ΔR(x) was higher than the threshold was calculated as:

$$r_{\mathit{threshold}}=\frac{1}{50}\sum _{z=1}^{N}H(\mathrm{\Delta }R(x)-\mathit{threshold}),$$ (4)

where N is the number of the A-lines in each B-scan image, and H(•) is the Heaviside step function. In our case, we selected thresholds of 0.1, 0.2, and 0.3 radians to describe three parameters: r_0.1, r_0.2, and r_0.3. These parameters directly reflected the percentage of A-lines having a change in birefringence above a specified level.

Fig. 4.

Description of global retardation parameters. (a) Phase retardation image of a mouse skin sample. (b) The red and yellow regions are the two sub-ROIs comprising the first and second 50 pixels below the surface. (c) The red and yellow curves show the mean retardation in each lateral line in the red and yellow areas, respectively. (d) The black curve is the difference between the red and yellow curves in (c), and the blue line is the binary signal created based on the threshold indicated by the black dashed line.

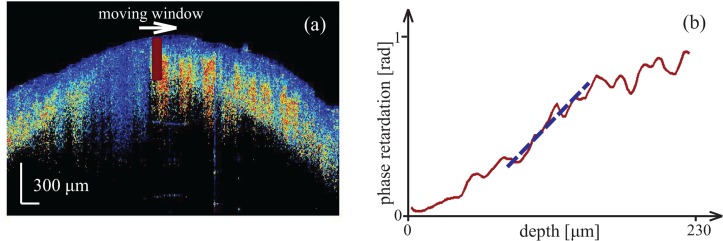
As with the local intensity parameters, local retardation parameters were calculated from data within a moving window along the ROI of the phase retardation images (Fig. 5(a)). For a given window, we generated an averaged retardation A-line by averaging the phase retardation along the lateral direction. We then implemented a linear regression of length 30 pixels (96 μm) for the averaged retardation A-line. The range for fitting was chosen to be that possessing the minimum residual among all possible 30-pixel-wide linear regressions along the averaged A-line, as shown in Fig 5(b). In this way, the obtained retardation slope was that having the best linearity. After performing this linear regression across all sub-images, the maximum and minimum of the retardation slope g_r(x), as well as the maximum and minimum of the fit residual Res_r(x), were retained as parameters to characterize local features in each phase retardation image.

Fig. 5.

Description of local retardation parameters. (a) The red box identifies a representative moving window in a retardation image. (b) A linear regression for the retardation curve was fit over the 30-pixel range having the lowest residual in a linear fit.

3.4. Classifier testing

We used a support-vector machine (i.e., a supervised learning method) with a “linear” kernel to classify 124 PS-OCT measurements (each measurement comprising separate intensity and birefringence images, yielding 248 images total) obtained from 32 BCC skin samples and 107 PS-OCT measurements obtained from 28 healthy samples of healthy tissue. A parameter vector comprising the values for all local and global parameters was created for each PS-OCT measurement.

Typically, “leave-one-out” cross-validation is an effective method to test classifiers with small sample populations [7, 33, 34]. In our case, our image dataset included multiple B-scans from different regions of the same tissue sample. Although we expected to obtain different features from each image of a given tissue sample due to the very different morphologies that each presented, we recognized the potential for high correlation between their parameter vectors. Thus, to minimize this effect on our results, we employed a “leave-one-sample-out” strategy to test our classifier. Hence, when testing one image, all other images acquired from the same sample were excluded from the training data. Meanwhile, the remaining images were tested on a database similar to the standard “leave-one-out” method.

4. Results and discussion

All BCC images involved in this study were taken from 14 samples with tumors excised from two transgenic mice (endogenous BCCs) and 18 samples with tumors obtained from three treated mice (allograft BCCs). The average sample area was ∼2 cm². Normal skin samples were taken from either surrounding normal regions on mice with BCC or from normal mice. In total we obtained 124 BCC and 107 normal B-scans from all mouse skin samples.

We observed that variability in the axial position of the tumor between different samples led to noticeable variations in the structural and birefringent properties of the dermal layer. This fact can make it difficult to describe the features of skin cancer using parametric methods alone. In practice, it can also be difficult for those with a limited understanding of how to interpret OCT intensity and birefringence images to visually distinguish images of cancerous tissue from normal tissue. In contrast, an SVM-based classifier can automatically distinguish between normal and BCC tissue based on the parameter vector associated with the measurement. After testing all images in our database using the “leave-one-sample-out” method, we found only 8 out of 107 normal skin measurements and 7 out of 124 BCC skin measurements were misclassified. Hence, the calculated specificity and sensitivity are 92.5% and 94.4%, respectively, yielding an overall accuracy of 93.5% (Table 2). These values are significantly higher than those obtained using intensity or birefringence information alone: the specificity and sensitivity of a version of our SVM-based classifier based solely on intensity parameters were respectively 82.2% and 78.2%, which is comparable to that achieved using conventional OCT reported in literature; a classifier we generated based on phase retardation parameters alone did slightly better, at 85.0% and 87.9%. The same trends are also observed in positive prediction value (PPV) and negative prediction value (NPV), which are important parameters to describe the performance of a diagnostic test.

Table 2.

Summary of classifier results using different subsets of parameters.

	Sensitivity	Specificity	PPV	NPV	Accuracy
Intensity	78.2%	82.2%	83.6%	76.5%	80.1%
Birefringence	87.9 %	85.0%	87.2 %	85.8%	86.6%
Both	94.4%	92.5%	93.6 %	93.4%	93.5%

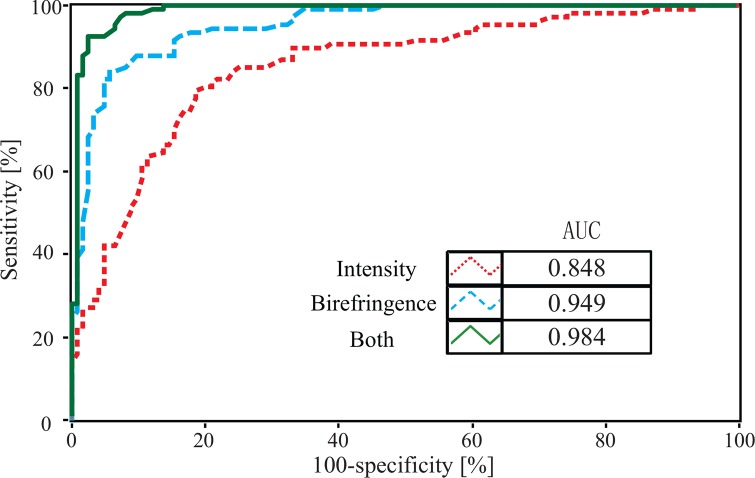
We used the data to generate a receiver-operator curve (ROC), shown in Fig. 6, which further supports that a classifier based on a combination of intensity and phase retardation (PR) information provides much better performance than one using intensity or birefringence information alone. The area under the curve (AUC) was 0.984 in the case of the combined parameters.

Fig. 6.

ROCs of different classifiers based on using intensity-only, birefringence-only or intensity and birefringence parameters.

To better understand what factors may have led to wrong classifications, we performed a manual review of the images. In one instance, we found the classification accuracy of the images obtained from three “normal” samples scanned on the same day was extremely low: only 9 of 15 measurements were correctly classified as normal, while the other 6 were classified as diseased. Figure 7 shows an intensity and retardation image from the misclassified image set. The red arrow denotes a location that simultaneously exhibits low scattering and low retardation, which is suggestive of no birefringence and, therefore, the presence of tumor. Given that the diagnosis of these specific samples as “normal” was made based on clinician assessment, rather than histological confirmation, it is possible that this region represents a small, sub-surface tumor that was not visible to the clinician during excision. Hence, a likely explanation of the misclassification is human error. Indeed, a version of our classifier tested by removing the data collected on this particular day yielded improved classifier results, with a sensitivity of 96.8% and a specificity of 95.7%. For this test we excluded the 15 questionable measurement datasets obtained on this one day but kept the remaining 124 BCC and 94 normal datasets that were obtained from other days.

Fig. 7.

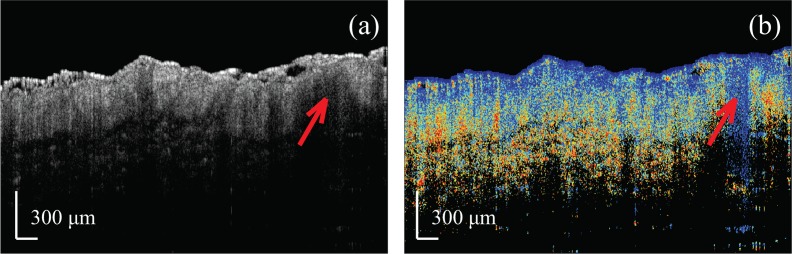
Example PS-OCT images of a misclassified “normal sample.” The red arrow denotes a location showing BCC-like features.

We also tested our classifier using the standard “leave-one-out” validation procedure. The achieved sensitivity and specificity were respectively 98.4% and 95.3%, both higher than that in our “leave-one-sample-out” validation method. These “improvements” might be caused by the correlation between training and testing data, as we expected in Sec. 3.4. Hence, this justifies our decision use “leave-one-sample-out” validation in order to avoid overestimating the performance on the classifier. On the other hand, these improved results may also suggest that we can further enhance the accuracy of our classifier by increasing the number of samples used in the training data.

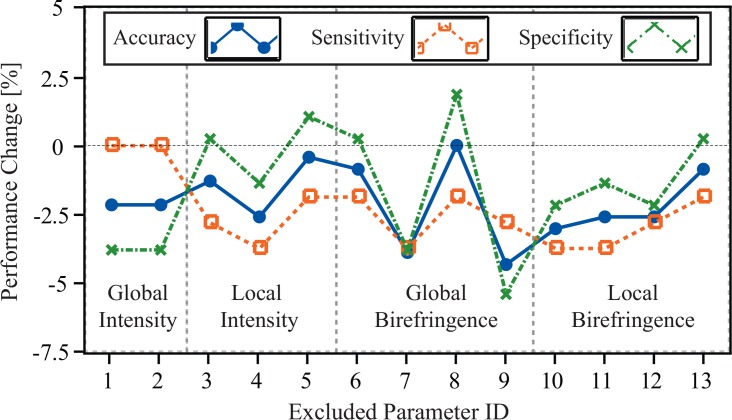
It is known that overfitting, which may cause drops in sensitivity and specificity, occurs when too many features are selected for SVM-based classification. Our final classifier itself comprises a subset of the total number of parameters we initially developed to perform this analysis (13 vs. 45). To check the performance of the final parameter selection as well as to better understand the importance of each individual parameter in our classifier, we evaluated our work by using a “leave-one-parameter-out” validation procedure. For this, we trained 13 classifiers comprising 12 parameters each. These classifiers were then tested by the same method discussed in Sec. 3.4. The sensitivity, specificity, and accuracy changes of each classifier are shown in Fig. 8.

Fig. 8.

Performance changes in accuracy, sensitivity, and specificity of classifiers excluding a given proposed parameter. The excluded parameter ID corresponds to numbers shown in the third column of Tab. 1.

The results indicate that excluding any of the parameters from our proposed classifier leads to a decrease in both sensitivity and overall accuracy, while specificity slightly increased in some cases. This suggests that our classifier does not suffer from overfitting. Moreover, we observed that the accuracy dropped the most when excluding the parameters corresponding to r_0.1 and r_0.3. This suggests that these two parameters provided stronger contrast between healthy and BCC groups than other parameters. Notably, these parameters are both related to birefringence information, supporting the importance of PS-OCT for this application over standard OCT-based methods that use intensity information alone.

5. Conclusion

This work is a pilot study of automated skin cancer diagnosis of mouse models using local and global parameters associated with the intensity and retardation images generated by PS-OCT. The SVM classifier we developed successfully discriminated normal and BCC samples with a sensitivity and specificity of 94.4% and 92.5%, respectively. This performance is much higher than that of other machine-learning methods to diagnose skin cancer that rely solely information about backscattering intensity obtained by conventional OCT. Our results indicate that analysis of both intensity and birefringence images significantly improve machine learning-based classifiers for skin cancer detection. This study also validates the serious potential of PS-OCT for clinical skin cancer diagnosis. In the future, we aim to apply this technique to human skin samples.