Fluorescent correlation spectroscopy measurements with adaptive optics in the intercellular space of spheroids

Abstract

In this study we demonstrate the use of adaptive optics to correct the biasing effects of optical aberrations when measuring the dynamics of molecules diffusing between cells in multicellular spheroids. Our results indicate that, on average, adaptive optics leads to a reduction of the 3D size of the point spread function that is statistically significant in terms of measured number of molecules and diffusion time. The sensorless approach, which uses the molecular brightness as optimization metric, is validated in a complex, highly heterogeneous, biological environment. This work paves the way towards the design of accurate diffusion measurements of molecules in thick biological specimens.

1. Introduction

Multicellular spheroids are model systems used to study tumor development as well as their interactions with the surrounding environment in a well-controlled manner [1]. Spheroids were first used for drug screening and they now also appear as a good compromise between over simplified 2D cultures and in vivo tumors to address fundamental questions, i.e. cellular auto organization inside the tumor, as well as the invasion, and the crosstalk between a tumor and its microenvironment [2]. Limited diffusion establishes a radial gradient of species (oxygen, nutrients, growth factors …) within the spheroids and is related to its internal architecture. In particular, cell population becomes heterogeneous as the spheroid grows, as a result of a local difference in proliferation, gene and protein expression, and differentiation [2]. A spheroid is characterized by the fact that cells divide mostly where they are well fed and oxygenated (at the surface) and die in the core of the tumor [3]. The intercellular space contains various molecules from the culture media, and in particular proteins that are differentially expressed according to their position from the center of the spheroid. Among them, the extracellular matrix (ECM), mostly constituted of large fibers, plays a major role in the organization of cells as a tissue. Monitoring the diffusion of molecules through the extracellular matrix, at different locations inside the spheroid is therefore of major relevance to understand the link between the permeability of the ECM and the mechanical properties of the spheroid.

Fluorescent correlation spectroscopy (FCS) measures the mobility of fluorescent molecules at the scale of the confocal point spread function (PSF) [4–6]. It can be used to monitor the mechanical changes in the medium that surrounds a cell, like the secretion of collagen by fibroblasts [7–9], and is potentially well suited to assess the building of the extracellular matrix in time and space within a spheroid. FCS is therefore complementary to the quantitative imaging of collagen fibers with second harmonic generation [10].

FCS gives better results if the observation volume is small and therefore requires the use of dedicated high numerical aperture objectives which are associated to an extreme sensitivity to optical aberrations [11,12]. We previously demonstrated that FCS is biased by optical aberrations at the level of a single living cell [13] and developed a confocal microscope equipped with adaptive optics (AO). In this paper, we demonstrate the use of the same system to perform FCS measurement in the intercellular space of spheroids, which are dense and heterogeneous materials inducing optical aberrations and light scattering. The comparison of pairs of FCS measurements (prior and after aberration correction) demonstrates the relevance of adaptive optics for FCS measurements at moderate depth (30 μm on average) in a complex biological system.

2. Materials and methods

2.1 Spheroid culture and staining

Spheroids were prepared with colon carcinoma cells (CT26) following a cushion agarose protocol [1]. Briefly, cells are seeded on a 4% agarose gel cushion in multiwell plates for 3 days for complete assembly of the spheroids. Cells were cultured in Dulbecco’s modified medium (DMEM, Life Technologies) supplemented with 10% fetal bovine serum (Life Technologies) and antibiotic-antimitotic at 37°C with 5% CO2. Spheroids were stained overnight prior to measurements, by adding 100nM Sulforhodamine-B (SRB) molecules to the cell culture medium. Since SRB is hydrophilic, it mostly stays in the intercellular space. After a few hours (3 to 24), the fluorescent molecules have homogeneously diffused inside the spheroids and are confined in the intercellular space during the time scale of the experiment. Before the measurements, the spheroids are washed several times to remove the auto-fluorescent molecules brought by the culture medium (phenol red). They are then observed at the bottom of a multiple chamber coverslip (Nunc Labtek I).

2.2 Optical setup

We use a custom-built confocal microscope, which we already described in a previous letter [13]. The optical layout is shown in Fig. 1. In brief, it couples a high-speed 97 actuator ALPAO deformable mirror (DM) to the exit pupil of a high numerical water objective (1.2 numerical aperture, 63 × Zeiss apochromat) to correct the supposedly equal aberrations of the illumination and detection beams (laser light at 561 nm and fluorescence in the 600-700 nm range respectively). The system was designed for optimal detection in aberration free conditions: the laser beam fills entirely the pupil of the objective; the detector is a single photon counting avalanche photodiode coupled to the system by a 50 µm multimode fiber and has the size of the Airy disk of the illumination PSF. The shape of the DM is parameterized with a combination of 8 Zernike modes (pairs of astigmatisms, comas and trefoils, plus the two lowest order spherical aberrations) and is driven by the optimization of 4-second measurements of the molecular brightness, a metric that quantifies the signal to noise ratio of FCS measurements [13,14]. The optimization procedure takes 200 seconds (3 measurements of 4 seconds, per Zernike mode ( × 8), per cycle of correction ( × 2)). Theoretical modeling of the photon budget and measurement characteristics predict that in principle this duration can be largely reduced at a minor cost of correction efficiency [15]. The power of the laser beam was maintained at 25 μW in the sample. It was found by inspection of the photon count time series that the photobleaching of SRB at this laser power was negligible.

Fig. 1.

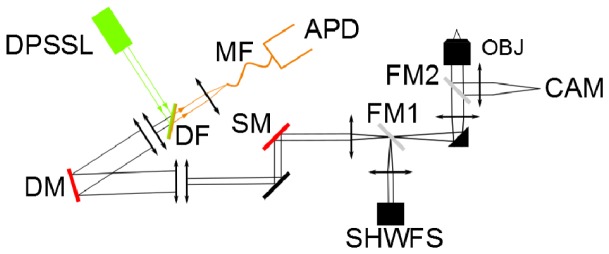
The optical layout. DPSSL: 561 nm diode-pumped solid state laser (Cobolt); DM: 97 actuator deformable mirror (ALPAO); OBJ: 63 × /1.2 water immersed microscope objective (Zeiss); SM: 3 mm X/Y galvanometric mirrors (Cambridge Technology); APD: single photon counting avalanche photodiode (Perkin Elmer); MF: 50 μm multimode fiber; DF: 600 nm long-pass dichroic filter (Chroma); SHWFS: 32 × 32 Shack-Hartmann wavefront sensor for DM calibration (ALPAO); CAM: wide field camera; FM1: flip mirror for DM calibration with SHWFS; FM2: flip mirror for transmission microscopy.

3. Measurements

Prior to measurements, the DM is flattened in a closed-loop scheme using an ALPAO Shack-Hartmann wavefront sensor (SHWFS) and its sensitivity to control commands is calibrated in terms of Zernike aberrations. Then we perform AO corrections and FCS measurements using a 15 nM fluorescent solution of SRB deposited in one of the 8 chambers of the coverslip that we later use for FCS measurements in spheroids. The optimized set of Zernike modes that corrects for the system aberrations is stored and used as the default mirror commands for the in-vivo measurements. After a 4-hour experiment, we typically measure a very modest drop of 2-5% of the molecular brightness in the same reference aqueous solution, which indicates a very good stability of the AO set-up. This observation validates the fact that the aberrations corrected during the experiments were introduced by the spheroids and were not due to a drift of the optical system.

The confocal imaging capability of the microscope was used to precisely target the intercellular region of the spheroids, where the SRB molecules have diffused, for FCS measurement. We found that neighboring cells are separated by a 2 μm free space (respectively 2 and 5 times the axial and radial extent of the confocal PSF, which we measured with 100 nm fluorescent beads). The low concentration of SRB molecules was favorable to FCS measurements, at the cost of low signal to noise when imaging. The photon count rate was typically around 30 kHz in the intercellular space. It therefore requires a 1-ms pixel dwell time for imaging with a signal to noise of 5. We show in Fig. 2 a 512 × 512 pixels image of the spheroid with a 0.2 μm resolution at around 20 μm depth, recorded over a 4-min exposition. We typically use smaller field of view (5 × 5 to 20 × 20 µm) to precisely define the location of the FCS measurements.

Fig. 2.

Example of a 100 × 100 μm² confocal image of a spheroid at 20 μm depth. The fluorescence signal mainly originates from SRB molecules located in the extracellular matrix, between the cells. Hot spots, probably corresponding to aggregates of molecules, were avoided when performing FCS measurements.

We have compared the impact of aberration corrections on 50 pairs of FCS measurements (before/after AO correction), which were obtained on 13 spheroids. The normalized autocorrelation functions (ACFs) $G(\tau )={\langle F(t)F(t+\tau )\rangle /\langle F(t)\rangle }^2$ are obtained by applying a multiple-τ algorithm to 12 s time series of the fluorescence photon count rate F(t). Most of the time, we observed that the ACFs could not be properly fitted by assuming that a unique species diffuses with a well-defined diffusion constant. Therefore, we performed two separate methods to analyze the ACF curves. The first method is a model-free analysis, where the mean number of molecules inside the observation volume is calculated from the amplitude of the ACF at zero lag, $\overline{N}$ = 1/G(0), using the very general assumption that the number of molecules, N, follows Poisson statistics. In practice, the value of G(0) is computed from the mean value of G(τ) over the interval 3-10 μs, to reduce the contributions of measurement noise and fast processes such as transition to triplet states. The diffusion time was then estimated as the lag τ_1/2 that corresponds to a 50% decay of the ACF. The second method consists in fitting the ACF curves with the effective model of anomalous diffusion, often invoked for molecules diffusing in crowded environment [8,9]. In this case, the ACF takes the analytical form:

$$G(\tau )=\frac{{\overline{N}}_A}{\left[1+{\left(\tau /{\tau }_A\right)}^{\alpha }\right]{\left[1+\frac{1}{S^2}{\left(\tau /{\tau }_A\right)}^{\alpha }\right]}^{1/2}}$$ (1)

α is the anomalous parameter that is equal to 1 in case of normal diffusion. To gain in fit robustness, we limited the algorithm to the optimization of ${\overline{N}}_A$ (mean number of molecules for the anomalous model), α and τ_A (the anomalous diffusion time). The shape parameter S that describes the anisotropy of the FCS observation volume was fixed to its value estimated in fluorescent solution (S = 5), because the S/N of measurements in living specimens is not high enough to properly adjust S. The fits were performed over the interval of lags [20 μs – 10 ms]. Shorter lags were ignored to remove the influence of the transition to the triplet state, while longer lags were disregarded to reduce the influence of photobleaching and spatial drifts of the sample that influence long time behavior of the ACFs.

Strictly speaking, FCS does not make it possible to measure the PSF, but gives access to some properties of the PSF. More precisely, the number of molecules is proportional to the observation volume, which is defined by a ratio of 3D integrals of the PSF, while the diffusion time is proportional to the squared transverse radius of the PSF [11]. Therefore, FCS measurements are a means to quantify the spatial extension of the PSF.

4. Results

The main results of the analysis of the ACF curves are summarized in Table 1. AO sharpens the focus of the microscope, therefore maintaining the observation volume close to the diffraction limit. It decreases the measured mean number of molecules by 27% for the model-free analysis (N) and 24% for the anomalous diffusion model (N_A). AO does not reduce the relative variability in the measurements of the number of molecules, which remains around 50% for the two analysis methods (standard errors/mean in Table 1).

Table 1. Impact of AO corrections on the photon count rate and on the FCS parameters (mean ± std). Numbers in parenthesis give the relative variability (std/mean) of the measured quantities. Data are averaged over 50 pairs of measurements, which were acquired in 13 different spheroids.

	Photon count rate F (kHz)	Model-free analysis		Anomalous diffusion model
		Number of molecules N	Diffusion time τ1/2 (μs)	Number of molecules NA	Diffusion time τA (μs)	Anomalous parameter α
Before AO	33 ± 14	5.2 ± 2.9 (56%)	67 ± 15 (22%)	3.8 ± 2.1 (55%)	37 ± 17 (46%)	0.80 ± 0.14 (18%)
After AO	36 ± 15	3.8 ± 1.8 (47%)	61 ± 13 (21%)	2.9 ± 1.5 (52%)	32 ± 11 (34%)	0.83 ± 0.12 (14%)

We found a 9% and 14% decrease of the diffusion time for the model-free (τ_1/2) and anomalous model (τ_A), respectively. The variability of τ_A is notably reduced by AO (46% to 32%). This observation does not hold for τ_1/2.

Paired t-test analyses of the numbers of molecules and diffusion times show, for both models, that all the differences (before vs after AO) are significant at the 0.01 level. In addition, the brightness, or photon count rate per molecule (F/N), increases from 6.3 kHz before AO to 9.5 kHz after AO.

The impact of AO on the measurement of the anomalous parameter α is small and its estimation has a smaller variability than the other FCS parameters (around 15% of the mean value).

The average RMS amplitude of corrected sample-induced aberrations was 49 ± 30 nm for the 8 corrected modes.

5. Discussion

5.1 Effects of AO on FCS measurements

AO reduces on average the observation volume (i.e. the 3D extension of the PSF). This can be seen in Table 1, both in terms of number of molecules and diffusion time. To clarify this point, it is relevant to plot the gain brought by AO for each kind of measurement (number of molecules, diffusion time and fluorescence photon count rate) as a function of the root mean square (RMS) amplitude of the aberrations corrected by the DM at the end of the optimization process. We calculated 3 figures of merit that should in principle be larger than 1 if the observation volume is sharpened after AO: N^bef/N^aft (reduction of the number of molecules), τ_1/2^bef/τ_1/2^aft (reduction of the characteristic time spent by the molecules in the observation volume) and F^aft/F^bef (increase of the photon count rate). These data are plotted in Fig. 3, as a function of the RMS amplitude of the aberration (black curves). They are compared to reference figures of merit obtained with SRB molecules freely diffusing in pure water. In the fluorescent solution, Zernike modes (astigmatism, coma, and spherical aberration) are separately introduced by the DM, so that the “after AO” measurement is obtained with the DM correcting the system aberration, while the “before AO” were obtained with a Zernike mode at a given RMS amplitude added to the system correction. The reference figures of merit shown in Fig. 3 were obtained with a SRB solution at a concentration of 10 nM, but according to our experience represent a large range (concentration and species) of freely diffusing molecules in solution. They show the relevance of the aberration corrections in our experiment with spheroids. For the three quantities measured in spheroids (number of molecules, diffusion time and photon count rate), the AO benefit correlates with the RMS amplitude of aberrations. The number of molecules is more significantly reduced by AO correction than the diffusion time. This observation illustrates the fact that the diffusion time only scales as the radial waist of the PSF, while the number of molecules scales as its volume [11], which is confirmed by the data in the fluorescent solution. These data also show that the impact of aberrations does not only depend on the RMS amplitude, but also on the type (mode) of aberration. For instance, in comparison with other modes, spherical aberration mostly extends the PSF along the optical axis and has therefore much less impact on the measured diffusion time than on the number of molecules.

Fig. 3.

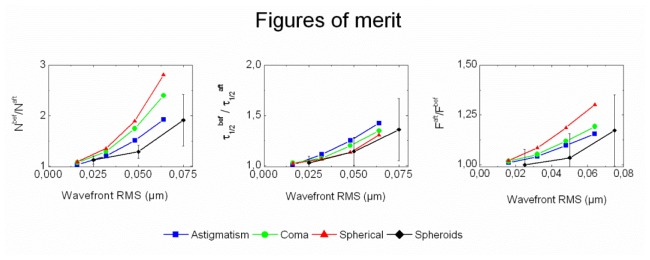
AO benefits as a function of the RMS amplitude of aberration corrected by the DM. The figures of merit correspond to ratios of parameters N, τ_1/2 and F, measured before and after AO corrections, averaged over the entire data set obtained on spheroids (black curves, with error bars). For clarity, data obtained on spheroids were uniformly binned over 3 intervals of RMS values. Superimposed curves are the equivalent data obtained with SRB freely diffusing in water, with controlled aberrations introduced by the DM (blue: astigmatism, green: coma, and red: spherical aberration).

For a given RMS amplitude, the benefit of AO in spheroids is not as high as one would expect from the measurements in solution. This is due to the noise on the estimated mode amplitudes that prevents from reaching the optimal brightness. The ratio η between the real gain and the gain expected from the overall amplitude applied to the DM can be related to the residual RMS = ${\displaystyle {\sum }_{i=1}^M{a}_i{}^2=}$ Mν² after correction, where ν is the noise (standard deviation) of each mode, supposed to be equal for any of the M modes. Assuming that η scales like the confocal Strehl ratio [12], a factor $\eta =e^{-2M{\left(2\pi \nu /\lambda \right)}^2}$ is expected. Our measurements in spheroids have been performed with a brightness of 6 kHz/molecule. Previous experiments with our system have shown that this brightness leads to a residual error of ν = 10 nm per mode [15]. Therefore, we expect η = 0.8 for M = 8 modes at λ = 561 nm wavelength. The data of Fig. 3 can be used to quantify the correction accuracy with spheroids and show that the largest discrepancy between the AO gain in solution and in spheroids is on average 0.6, suggesting the presence of additional sources of noise in living specimen. The noise rejection of our AO system could be optimized by choosing a more advanced search algorithm to gain robustness in complex and heterogeneous media (in particular, the intercellular space is only 2-5 times wider than the PSF, which can lead to a loss of signal during the AO correction).

There is still an important variability in the FCS estimation of number of molecules and diffusion time. However, AO reduce the relative variability of the anomalous diffusion time τ_a (46% to 34%). This observation suggests that the sharpening of the PSF improves the fit of the anomalous diffusion model, which uses an implicit assumption of 3D Gaussian PSF. The remaining variability of the FCS parameters may reflect the heterogeneity of the molecular confinement in the ECM. We have used for the experiments described in this paper a small and soluble fluorescent molecule (SRB, MW = 560 Da), which diffuses more freely than macromolecules. We estimated a value of the anomalous parameter that corresponds to a regime of subdiffusion (α < 1), a result comparable with data of Alexa 488 (MW = 570 Da) measured in solutions of hyaluronic acid, one of the more important components of the ECM [16].

5.2 Effects of AO on imaging

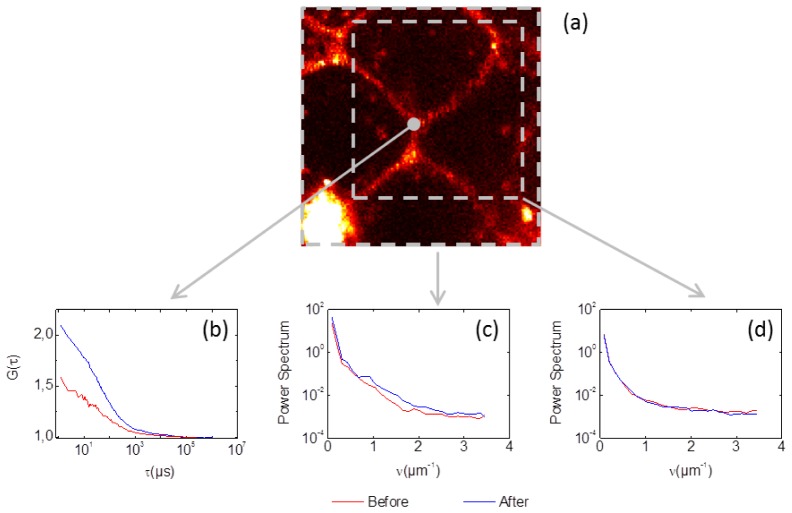
The impact of optical aberrations depends on the structure of the object and it is well known that the low contrasted image of an extended object will only be marginally affected by the typical aberrations in a microscope [17]. In this study, we found that the images (like the one shown in Fig. 2) were marginally affected by optical aberrations. Images for which the AO benefit was not negligible correspond to aggregates of non-diffusing SRB molecules, which were not relevant in our study. For example, we show in Fig. 4 how the presence of a very bright fluorescent aggregate makes the image quality sensitive to aberrations (here probably a dead cell, at the bottom left of Fig. 4(a). Figure 4(c) shows the gain brought by AO correction on the power spectrum of the entire image (especially in the 1-2 μm⁻¹ range). In comparison, the AO correction has no visible impact on the sub-image, delimited by the dashed box in Fig. 4(a), which does not contain the fluorescent aggregate, though the ACF shown in Fig. 4(b) and measured at the center of the sub-image is significantly improved. As far as optical aberrations are concerned, a major feature of FCS measurement is its local sensitivity to the detection volume sharpness and not to the magnitude of the fluorescence signal (i.e. the photon count rate).

Fig. 4.

Comparison of the effects of AO, before (red) and after (blue) one AO cycle performed at one single point. (a) The 25 × 25 μm confocal image. (b) ACF curves obtained at the center of the image. (c) Radially averaged power spectrum of the entire image. (d) Radially averaged power spectrum computed over a reduced field of view (grey sub-box). The optimized mirror shape had a 75 nm RMS amplitude.

5.3 Impact of light scattering on FCS measurements

Our data confirm the sensitivity of FCS measurements to optical aberrations, which we previously demonstrated in fluorescent solutions [12,13]. Within the limited small focusing depths that were investigated inside the spheroids (up to 60 µm), we did not find a significant correlation between the RMS amplitude of aberrations and the focusing depth.

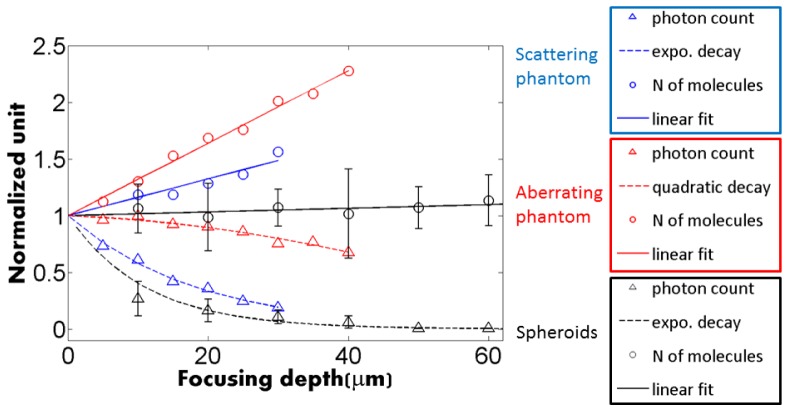
Figure 5 show the variation of N and photon count rate, without AO, as a function of the imaging depth. In spheroids, N (black circles) is fairly independent of the imaging depth, thus confirming that our corrections do not depend on depth, while the photon count rate (black triangle) follows an exponential decay typical for a scattering medium, with a characteristic damping length of 34 μm. The data obtained in spheroids are compared with FCS measurements of SRB molecules diffusing in an aberrating phantom (mix of water glycerol with a n = 1.42 refractive index) and in a scattering phantom (20% Intralipid). Clearly, the trend in spheroids strongly differs from the one observed with the aberrating phantom, which drastically biases FCS measurements (N and τ) without much loss of photons. In contrast the trend in spheroids is similar to the one observed with a scattering phantom, where N increases more slowly with the imaging depth, while the photon count rate strongly decreases. The relative insensitivity of FCS measurements to scattering was pointed out by Zustiak et al. [18], which accounts for the stability of the number of molecules measured at different depths in the spheroids. Spheroids are highly scattering media and the loss of photons prevents us from getting good signal to noise ratio for FCS measurements deeper than 50 µm approximately.

Fig. 5.

Comparison of the depth dependence of FCS measurements in spheroids (black, with error bars) and two phantoms in which SRB molecules freely diffuse. Blue: scattering phantom (10 nM SRB in 20% intralipid), which shows the same trend as the spheroid measurements: exponential decay of the photon count rate, and slower increase of the number of molecules. Red: aberrating phantom (10 nM SRB in water-glycerol mix of refractive index 1.4), which shows the sharp increase of the number of molecules, and the slower decay of the photon count rate.

6. Conclusion

Our approach of sensorless AO is extremely sensitive to the presence of small aberrations (around λ/10 RMS on average), yet significant for many modern approaches of microscopy at the molecular level, such as those based on fluorescence fluctuation microscopy. Following a previous demonstration with single cells [13], we applied our approach to a multi-cellular specimen. The non-flat topography of the spheroid was found to create optical aberrations at shallow depth (< 60 μm). These aberrations were significant for FCS, yet hardly perceptible on the confocal images. The correction of 8 Zernike modes improves both the signal to noise and the reliability of FCS measurements. It significantly sharpens the 3D PSF, which results, on average, in a significant improvement of the measured FCS parameters (24% and 14%, for the number of molecules and diffusion times using the anomalous diffusion model). Despite AO corrections, the variability of the measured FCS parameters in the extra-cellular matrix suggests a strong heterogeneity of the state of the extra-cellular matrix. Photon scattering prevents us from investigating deeper into the spheroids, yet it did not alter significantly the accuracy of FCS measurements. Obtaining quantitative measurements of the diffusion of molecules over the entire spheroid remains an instrumental challenge. Combining our FCS-based AO system with a longer wavelength to minimize scattering should yield a powerful optical tool for quantitative measurements in the extracellular matrix and the understanding of the biophysics of spheroids.