Intercellular delay regulates the collective period of repressively coupled gene regulatory oscillator networks

Abstract

Most biological rhythms are generated by a population of cellular oscillators coupled through intercellular signaling. Recent experimental evidence shows that the collective period may differ significantly from the autonomous period in the presence of intercellular delays. The phenomenon has been investigated using delay-coupled phase oscillators, but the proposed phase model contains no direct biological mechanism, which may weaken the model's reliability in unraveling biophysical principles. Based on a published gene regulatory oscillator model, we analyze the collective period of delay-coupled biological oscillators using the multivariable harmonic balance technique. We prove that, in contradiction to the common intuition that the collective period increases linearly with the coupling delay, the collective period turns out to be a periodic function of the intercellular delay. More surprisingly, the collective period may even decrease with the intercellular delay when the delay resides in certain regions. The collective period is given in a closed-form in terms of biochemical reaction constants and thus provides biological insights as well as guidance in synthetic-biological-oscillator design. Simulation results are given based on a segmentation clock model to confirm the theoretical predictions.

I. Introduction

Rhythms are fundamental to biological activities. With periods ranging from seconds in glycolytic oscillations to years in reproduction, these rhythms are among the most conspicuous properties of living systems [1], [2]. Underlying biological rhythms are networks of interacting cellular oscillators. These cellular oscillators can synchronize rhythms with a certain collective period, yet it remains an exciting challenge to understand the mechanism of how collective oscillation period arises from autonomous cellular oscillations.

Although it has been generally believed that the collective period is determined by the average of cell-autonomous periods, it is recently reported that in the presence of intercellular delays the collective period will be greatly altered from the averaged autonomous periods. This has been experimentally substantiated for coupled semiconductor lasers [3] and in the zebrafish segmentation clock [4]. This phenomenon is of fundamental importance in the study of biological rhythms, given the prevalence of time delays in biological interactions. One source of delay is a threshold effect, i.e., the concentration of an effector must exceed or fall below a certain value before the affected value is altered [5]. Both nonlinear chemical reaction kinetics and hysteresis can act like thresholds, even when the threshold values are not sharp. Secondly, there are known delays in transcription and translation associated with mRNA and protein processing in the nucleus and cytoplasm, respectively [6]. Finally, there are delays in the transport of intermediates between cellular compartments [6].

Based on phase oscillators, the authors in [3], [4], [7], [8] studied the collective period of delay-coupled oscillators. However, the phase oscillator model may be too phenomenological to reveal underlying principles, because it contains no direct biological mechanism for the cellular clock. In this paper, we analyze the influence of intercellular delay on the collective period using a gene regulatory biophysical clock model. To our knowledge, no analytical results have been reported on the collective period of delay-coupled mechanism-based gene regulatory oscillators to date. In our study, we use an oscillator model in which oscillations are induced by the direct autorepression of a gene by its own protein product. Biological rhythms as diverse as cell-cycles in bacterial [9], segmentation clocks in vertebrates [10], and circadian rhythms in mammals [11] depend heavily on autorepression. Following the same principles, we model the intercellular interaction as co-repression based on the fact that mutual repression between a pair of oscillators comprises a positive feedback loop between the oscillators, which has been reported to synchronize various biological oscillators [12]. This model is also inspired by the fact that intercellular repression is widespread in sensory pyramidal neurons [13], visual thalamus [14], and insulin secretion [15], to name a few examples.

We use the multivariable harmonic balance (MHB) technique to analyze the collective period of delay-coupled gene regulatory oscillator networks. The MHB technique, although approximate, has been shown to be reliable for the analysis of biochemical oscillating systems [16], [17], and can provide an effective way to characterize the frequency, amplitude, and phase of coupled oscillators [16], [18], [19], [20]. Due to multi-cellular structure, the solution to harmonic balance equations is very difficult to obtain. Here we circumvent the problem by restricting our attention to solutions corresponding to synchronized oscillations since we are interested in the collective period. The main contributions are as follows: 1) the collective period of delay-coupled gene regulatory oscillators is derived in terms of biochemical parameters, which gives insights into the basic mechanism of biological oscillations; 2) it is proven that the collective period is a periodic function of the intercellular delay in contrast to the linear function assumed in the existing literature (e.g., [10]); and 3) the region in which the collective period is larger/smaller than the autonomous period (oscillation period of isolated oscillators) and, the region in which the collective period increases/decreases with the intercellular delay are given explicitly.

II. Model description

We adopt the well-established Hill-type auto-repression model of cellular oscillators [10], [21]:

$$\{\begin{array}{c}\frac{dm\left(t\right)}{dt}=f\left(p(t-T_m)\right)-cm\left(t\right),f\left(p\right)=\frac{k}{1+p^{\nu }∕p_0^{\nu }}\hfill \\ \frac{dp\left(t\right)}{dt}=am(t-T_p)-bp\left(t\right)\hfill \end{array}\phantom{\}}$$ (1)

where m(t) ≥ 0 is the instantaneous concentration of a mRNA which codes for a protein with instantaneous concentration p(t) ≥ 0. The protein acts as a repressor. The constants a > 0 and b, c > 0 denote production and decay rates, respectively. T_m > 0 denotes the time delay between the initiation of transcription and the arrival of the mature mRNA molecule in the cytoplasm. T_p > 0 denotes the time delay between the initiation of translation and the emergence of a complete functional protein molecule. f(p) is the rate of production of new mRNA molecules, and the constants k and p₀ represent the action of an inhibitory protein that acts as a dimer. ν is the Hill coefficient, which describes the cooperativity of end product repression.

We use co-repression to establish the intercellular signaling [12]. This is based on the facts that 1) mutual repression between a pair of biological oscillators constitutes a positive feedback loop coupling between the oscillators, which is regarded as the most prevalent induction scheme of synchronization in homogeneous biological oscillators [12]; and 2) intercellular repression is widespread in gene regulatory networks [22]. The i^th oscillator's dynamics is described by:

$$\{\begin{array}{c}\frac{d{m}_i\left(t\right)}{dt}=g(p_i(t-T_m),m_{{\mathbb{N}}_{\stackrel{‒}{i}}})(t-\tau )-c{m}_i\left(i\right),\hfill \\ \frac{d{p}_i\left(t\right)}{dt}=a{m}_i(t-T_p)-b{p}_i\left(t\right),i=1,2,\dots ,N\hfill \end{array}\phantom{\}}$$ (2)

where $g(p_i\left(t\right),m_{{\mathbb{N}}_{\stackrel{‒}{i}}}\left(t\right))=\frac{k}{1+\frac{p_i^{\nu }\left(t\right)}{p_0^{\nu }}+{\sum }_{j\in {\mathbb{N}}_{\stackrel{‒}{i}}}\frac{m_j^{\nu }\left(t\right)}{m_0^{\nu }}}$ and ${\mathbb{N}}_{\stackrel{‒}{i}}$ denotes index set {j = 1, 2, . . . , N, j ≠ i} and $m_{{\mathbb{N}}_{\stackrel{‒}{i}}}=\{m_{j_1},m_{j_2},\cdots ,m_{j_{N-1}}\mid j_k\in {\mathbb{N}}_{\stackrel{‒}{i}}\}$; m₀ is a constant; τ is the time delay in intercellular interaction. Since $g(p_i,m_{{\mathbb{N}}_{\stackrel{‒}{i}}})$ is a decreasing function of m_j(j ≠ i), the intercellular coupling between oscillator i and oscillator j is repressive.

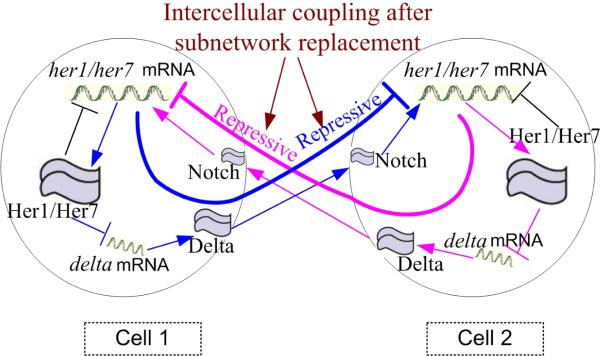
Remark 1: It is worth noting that the intercellular signaling can be a complex cascade composed of many intermediate molecules. For example, in the zebrafish segmentation clock, the intercellular signaling is a cascade [10]: her1/her7 mRNA in cell 1 → Her1/Her7 in cell 1 ⊣ delta mRNA in cell 1 → Delta in cell 1 → Notch in cell 2 → her1/her7 mRNA in cell 2, where “→” denotes activation and “⊣” denotes repression (cf. Fig. 1). In this case, by using the subnetwork replacement technique [23], the interaction cascade can be replaced with “her1/her7 mRNA in cell 1 ⊣ her1/her7 mRNA in cell 2” without changing the qualitative characteristics of intercellular interaction [23]. Given this, (2) can be used to model many biochemical oscillator networks such as the insulin secreting pancreatic islets [12], ovulation regulation networks [12], and neural stem cell maintenance networks [24], to name a few.

Fig. 1.

Modeling the intercellular coupling in the segmentation clock [10]. Utilizing the subnetwork replacement technique [23], the cascade (the thin blue/pink arrows/bars) can be replaced with the repressive interaction (the thick blue/pink bar ⊣.

III. The collective period

To facilitate analysis, we recast (2) in a matrix form:

$$\{\begin{array}{c}\frac{dM\left(t\right)}{dt}=G(P(t-T_m),M(t-\tau ))-cM\left(t\right)\hfill \\ \frac{dP\left(t\right)}{dt}=aM(t-T_p)-bP\left(t\right)\hfill \end{array}\phantom{\}}$$ (3)

where M(t) = [m₁(t) m₂(t) . . . m_N(t) ]^T, P(t) = [p₁(t) p₂(t) . . . p_N(t) ]^T, and $G(P\left(t\right),M\left(t\right))={\left[g(p_1\left(t\right),m_{{\mathbb{N}}_{\stackrel{‒}{1}}}\left(t\right))g(p_2\left(t\right),m_{{\mathbb{N}}_{\stackrel{‒}{2}}}\left(t\right))\dots g(p_N\left(t\right),m_{{\mathbb{N}}_{\stackrel{‒}{N}}}\left(t\right))\right]}^T$.

The most biologically significant property of (1) is that it can have oscillating solutions, which is the focus of this paper. (Note that the HMB technique does not give a necessary and sufficient condition for such solutions [19], [20].) It is noteworthy that although the period of a single cellular oscillator has been studied [16], [17], no analytical results exist addressing the collective period of repressively coupled gene regulatory oscillators. Building upon our recent study on delay-free coupled Goodwin oscillators [25], we propose to study delay-coupled oscillators using the MHB technique [18], [26]. Since multi-cellular structure leads to high-dimensional harmonic balance equations, it is very difficult to derive the solution. Here we are interested in the collective period, so we restrict our attention to solutions corresponding to synchronized oscillations, which gives a way to solve the problem. The definition of synchronized oscillation is provided below. We assume that the parameters are chosen such that synchronized solution exists.

Definition 1: (2) is synchronized if $\underset{t\to +\infty }{\lim }\mid m_i\left(t\right)-m_j\left(t\right)\mid =0$ and $\underset{t\to +\infty }{\lim }\mid p_i\left(t\right)-p_j\left(t\right)\mid =0$ for all 1 ≤ i, j ≤ N.

Theorem 1: Using harmonic balance technique, m_i(t) and p_i(t) can be approximated by (14) and (15) respectively, and the collective period of (2) (when synchronized) can be obtained as $T=\frac{2\pi }{w}$, where w is the minimum positive solution to

$$\frac{\frac{(b+c)w}{(N-1)}+\xi (b\sin w\tau -w\cos w\tau )}{\frac{(bc+w^2)}{(N-1)}+\xi (-b\cos w\tau -w\sin w\tau )}=-\tan \left((T_m+T_p)w\right)$$ (4)

and

$$\begin{array}{cc}\hfill \xi =& \frac{(bc-w^2)\cos \left((T_m+T_p)w\right)-(b-c)w\sin \left((T_m+T_p)w\right)}{\kappa +(N-1)(f_1\left(w\right)+f_2\left(w\right))}\hfill \\ \hfill f_1\left(w\right)=& (w\sin w\tau +b\cos w\tau )\cos \left((T_m+T_p)w\right),\hfill \\ \hfill f_2\left(w\right)=& (b\sin w\tau -w\cos w\tau )\sin \left((T_m+T_p)w\right)\hfill \end{array}$$ (5)

In (5), κ denotes the ratio between the Fourier coefficients of $g(p_i,m_{{\mathbb{N}}_{\stackrel{‒}{i}}})$ with respect to p_i and $m_j(j\in {\mathbb{N}}_{\stackrel{‒}{i}})$, respectively (Due to the structure of $g(p_i,m_{{\mathbb{N}}_{\stackrel{‒}{i}}})$, κ is independent of i and j). The value of κ (which is not needed in the analysis in this paper) can be calculated numerically [27].

The proof is given in the appendix.

Remark 2: Although the collective period of coupled oscillators has been studied based on the simple phase model in [3], [4], [7], [8], [28], to our knowledge, no analytical result exists addressing the collective period of delay-coupled gene regulatory oscillators.

From the proof of Theorem 1, one gets that the influence of intercellular coupling is represented by ξ. So by setting ξ = 0, one gets the autonomous period of a single gene regulatory oscillator, which is the same as the existing result in [17]:

Corollary 1: The autonomous period of gene regulatory oscillator (1) can be obtained as

$$T_A=2\pi ∕w_A$$ (6)

where w_A is the minimum positive solution to

$$\frac{(b+c)w_A}{bc-w^2}=-\tan \left((T_m+T_p)w_A\right)$$ (7)

Proof: The corollary can be easily obtained by setting ξ in (4) to 0.

IV. The influence of intercellular delay on the collective period

Although the system of equations in (4) and (5) cannot be solved analytically, it can be used to analyze the influence of intercellular delay τ on the collective period T:

Theorem 2: Define $Q\left(x\right)=(\frac{x}{2}+\frac{\text{arctan}\frac{w_A}{b}}{2\pi })T_A$, then when the network in (2) is synchronized, the relationship between collective period T and intercellular delay τ is as follows:

1. when τ satisfies

   $$\tau =T_m+T_p+Q\left(k\right),k=0,1,2,\dots ,$$ (8)

   T is identical to the autonomous period T_A in (6);
2. when τ satisfies

   $$T_m+T_p+Q\left(k\right)<\tau <T_m+T_p+Q(k+1),$$ (9)

   for some k = 2n–1, (n = 0, 1, 2, . . .), then T is smaller than the autonomous period T_A;
3. when τ satisfies

   $$T_m+T_p+Q\left(k\right)<\tau <T_m+T_p+Q(k+1),$$ (10)

   for some k = 2n, (n = 0, 1, 2, . . .), then T is larger than the autonomous period T_A;

Moreover,

1. when τ resides in the following region,

   $$T_m+T_p+Q(2k-0.5)<\tau <T_m+T_p+Q(2k+0.5)$$ (11)

   for some k = 0, 1, 2, . . ., then T increases with τ;
2. when τ resides in the following region,

   $$T_m+T_p+Q(2k-1.5)<\tau <T_m+T_p+Q(2k-0.5),$$ (12)

   for some k = 0, 1, 2, . . ., then T decreases with τ;

The proof is given in the appendix.

Remark 3: Theorem 2 is consistent with the simulation results in [29], which show that depending on its magnitude, intercellular delay can both increase and decrease the collective oscillation period of stellate cell networks. It is also reminiscent of the simulation results in [30], which show that the intercellular delay periodically regulates the collective period of inter-coupled Hodgkin-Huxley neurons. From a mathematical point of view, periodic regulation is also reasonable since any intercellular delay τ has the same effect as τ + nT (n = 1, 2, . . .) due to the periodic oscillation (repetition) of m_i(t). Therefore, periodic regulation of the collective period by intercellular delay may be a general rule of delay coupled biochemical oscillator networks, and the results obtained in this paper can provide insights into biological oscillator network behavior understanding as well as guidance in synthetic biological oscillator network design.

V. Application to a segmentation clock model

We apply the obtained results to the segmentation clock model proposed in [10], [31]. The segmentation clock is a population of coupled cellular gene regulatory oscillators in the embryo that drive the sequential subdivision of the presomitic mesoderm into multicellular blocks termed somites. In [10], Lewis formulated each cellular oscillator of the zebrafish segmentation clock as a feedback loop in which Her1 or Her7 protein directly binds to the regulatory DNA of its own gene to inhibit transcription. Let m_i(t) and p_i(t) be the concentrations of her1/her7 mRNA and the corresponding protein in the ith (i = 1, 2, . . . , N) cell at time t, then the dynamics of p_i(t) and m_i(t) in an isolated cell are governed by (1) with parameters given as follows [10]: b = c = 0.231, a = 4.5 protein molecules per mRNA molecule per minute, k = 33 molecules per diploid cell per minute, ν = 2, and p₀ = 40 molecules. Lewis modeled the intercellular coupling pathway from cell i to cell j as her1/her7 mRNA in cell i → Her1/Her7 in cell i ⊣ delta mRNA in cell i → Delta in cell i → Notch in cell j → her1/her7 mRNA in cell j. According to Remark 1, the intercellular signaling reduces to her1/her7 mRNA in cell i ⊣ her1/her7 in cell j. So the interaction between any two oscillators is mutual repressive and the dynamics of the oscillator network can be formulated by (2).

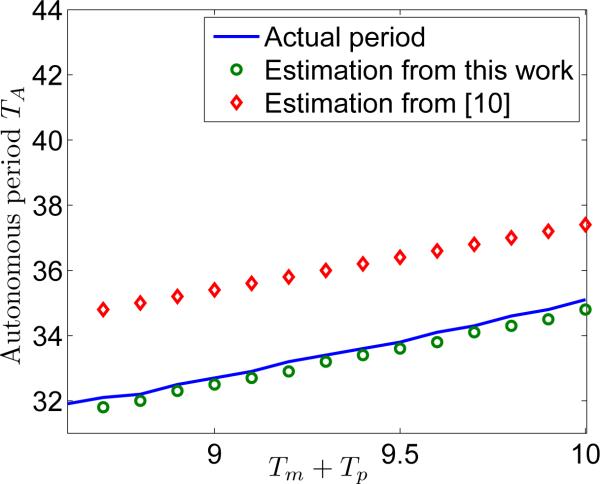
Reference [10] gives an analytic approximation of the autonomous oscillation period, i.e.,

$$T=2(T_m+T_p+\frac{1}{b}+\frac{1}{c})$$ (13)

thus, we can compare it with our results in (7). The comparison under different values of T_m + T_p is given in Fig. 2, where it can be seen that our result is more accurate.

Fig. 2.

Comparison of estimated autonomous period with [10]. The actual period is calculated from direct numerical simulation of the model in [10].

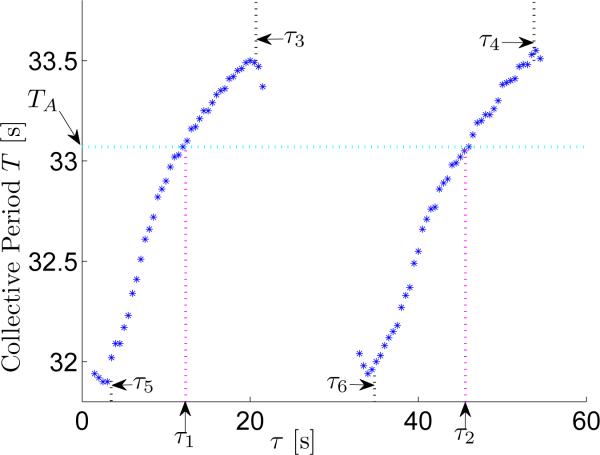
Next we show that our analytical prediction is consistent with numerical simulation of the network of gene regulatory oscillators. We set N = 9 and m₀ identical to p₀, i.e., 40 molecules. We fixed T_m and T_p to 7.1s and 1.7s, respectively, which gives an autonomous oscillation period T_A = 33.07s. The results of simulating the network under different intercellular delays, τ, are given in Fig. 3. The collective period is represented by blue asterisks (when 0 < τ < 1.5 and 21.5 < τ < 33, the network did not synchronize, so there is no collective period under these delays). We can see that at $\tau ={\tau }_1=T_m+T_p+\frac{\varphi }{2\pi }{T}_A$ and $\tau ={\tau }_2=T_m+T_p+(\frac{\varphi }{2\pi }+1)T_A$ where $\varphi =\arctan \frac{w_A}{b}$, the collective period is identical to the autonomous period. This verifies Theorem 2, which predicts that if the network can be synchronized and the intercellular delay is expressed by $T_m+T_p+(\frac{\varphi }{2\pi }+\frac{k}{2})T_A$ for k = 0, 1, 2, . . ., then the collective period will be identical to T_A. From the figure, we can also see that when $\tau <{\tau }_1=T_m+T_p+\frac{\varphi }{2\pi }{T}_A$ or $T_m+T_p+(\frac{\varphi }{2\pi }+\frac{1}{2})T_A<\tau <{\tau }_2=T_m+T_p+(\frac{\varphi }{2\pi }+1)T_A$, the collective period is smaller than T_A, and otherwise it is larger than the autonomous period T_A, which is also consistent with the statement in Theorem 2. Furthermore, the results in Fig. 3 also roughly follow the monotonicity property prediction in Theorem 2, which states that when $0<\tau <{\tau }_5=T_m+T_p+(\frac{\varphi }{2\pi }-\frac{1}{4})T_A$ and $T_m+T_p+(\frac{\varphi }{2\pi }+\frac{1}{4})T_A={\tau }_3<\tau <{\tau }_6=T_m+T_p+(\frac{\varphi }{2\pi }+\frac{3}{4})T_A$, the collective period decreases with τ, otherwise the collective period increases with τ (Note that since the prediction is based on the assumption that all oscillators are synchronized, there is a small prediction error when delay τ gets close to the non-synchronizable regions).

Fig. 3.

Verification using a segmentation clock model described in [10].

VI. Discussion

The collective period of coupled biological oscillators are attracting increased attention as more experimental evidence shows that it can differ significantly from the autonomous period. Existing analytical results are based on sinusoidally delay-coupled phase oscillators, which may be too phenomenological to reveal underlying mechanisms. In fact, from the numerical results in Fig. 3, it can be seen that the variation of the collective period with the intercellular delay is quite different from a sinusoidal curve, which further substantiates the necessity of non-phase model based studies. However, to our knowledge, there are no existing analytical results addressing the collective period of delay-coupled oscillators based on biophysical regulatory models. Using a gene regulator oscillator model of the cellular oscillation in the segmentation clock, we study the collective period of delay-coupled cellular oscillators using the multivariable harmonic balance technique. Due to the multiple oscillator structure, the harmonic balance equations are very difficult to solve. We circumvent the problem by ignoring solutions corresponding to unsynchronized oscillations, which are not relevant to our study, but will greatly facilitate the analysis.

When there is an intercellular delay, we prove that the collective period is a periodic function of the intercellular delay. This argues against the existing assumption that the collective period increases linearly with the intercellular delay. More surprisingly, we prove that the collective period may even decrease with the intercellular delay when the delay resides in certain regions. The results are confirmed by numerical simulations on a published gene regulatory oscillator network model of the segmentation clock. The results are given in a closed-form expression in terms of the biochemical reaction constants and thus provide biological insight as well as guidance in synthetic-biological-oscillator design.

Appendix: Harmonic balance investigation

The dynamics of the coupled gene regulatory oscillators in (3) can be transformed into the frequency domain as shown in Fig. 4.

Fig. 4.

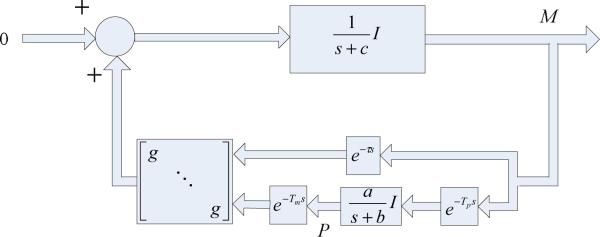
Schematic diagram of the frequency domain formulation of (3). P(s) and M(s) are the respective element-wise Laplace transform of P(t) and M(t) in (3).

According to the harmonic balance technique [26], since $\frac{1}{s+c}$ and $\frac{a}{s+b}$ in Fig. 4 are low pass filters, the higher order harmonics of oscillations in the closed-loop system in Fig. 4 can be safely neglected. Thus the wave forms of m_i(t) and p_i(t) can be approximated by their zero-order and first-order harmonic components [26]:

$$m_i\left(t\right)=x_i+y_i\sin (wt+{\phi }_i),i=1,2,\dots ,N$$ (14)

$$p_i\left(t\right)={\alpha }_i+{\beta }_1\sin (wt+{\varphi }_i),i=1,2,\dots ,N$$ (15)

where α_i, x_i and β_i, y_i denote the amplitudes of the zero-order and first-order harmonics, respectively, and w and ϕ_i, φ_i denote the oscillation frequency and the phases, respectively.

Again, because the higher order harmonics of oscillations in the closed-loop system can be safely neglected, g(•) in (2) can be approximated legitimately by its describing functions based on multivariable Fourier analysis [27]:

$$g(p_i\left(t\right),m_{{\mathbb{N}}_{\stackrel{‒}{i}}}\left(t\right))\approx {\vartheta }_i+{\eta }_i{\beta }_i\sin (wt+{\varphi }_i)+\sum _{j\in {\mathbb{N}}_{\stackrel{‒}{i}}}{\xi }_{i,j}{y}_i\sin (wt+{\phi }_i)$$ (16)

where ${\mathbb{N}}_{\stackrel{‒}{i}}$ denotes the index set {j = 1, 2, . . . , N, j ≠ i} and

$${\vartheta }_i=\frac{1}{{\left(2\pi \right)}^N}{\int }_{-\pi }^{\pi }\cdots {\int }_{-\pi }^{\pi }g(p_i\left(t_i\right),m_{{\mathbb{N}}_{\stackrel{‒}{i}}}\left(t_{{\mathbb{N}}_{\stackrel{‒}{i}}}\right))d{t}_1\dots d{t}_N$$ (17)

$${\eta }_i=\frac{1}{{\pi }^N{\beta }_i}{\int }_{-\pi }^{\pi }\cdots {\int }_{-\pi }^{\pi }g(p_i\left(t_i\right),m_{{\mathbb{N}}_{\stackrel{‒}{i}}}\left(t_{{\mathbb{N}}_{\stackrel{‒}{i}}}\right))\sin \left(t_i\right)d{t}_1\dots d{t}_N$$ (18)

$${\xi }_{i,j}=\frac{1}{{\pi }^N{y}_i}{\int }_{-\pi }^{\pi }\cdots {\int }_{-\pi }^{\pi }g(p_i\left(t_i\right),m_{{\mathbb{N}}_{\stackrel{‒}{i}}}\left(t_{{\mathbb{N}}_{\stackrel{‒}{i}}}\right))\sin \left(t_j\right)d{t}_1\dots d{t}_N$$ (19)

The describing function η_i and ξ_i,j are the gains of g(•) when the inputs are two sinusoids of amplitudes β_i and y_j, respectively, and the output is approximated by the first-order harmonic [26], [27]. Combining (2) and (16) one gets that ξ_i,j denotes oscillator j's influence on oscillator i, namely, the influence of intercellular coupling.

Based on the harmonic balance technique [26], p_i(t) (i = 1, 2, . . . , N) in Fig. 4 must satisfy:

$$\left(e^{-T_{m}jw}{\rm Y}-\frac{jw+b}{a}{e}^{T_{p}jw}((jw+c)I-e^{-\tau jw}A)\right)P=0$$ (20)

where

$$\begin{array}{cc}\hfill {\rm Y}=& \mathrm{diag}\{{\eta }_1,{\eta }_2,\dots ,{\eta }_N\},\hfill \\ \hfill A=& \left[\begin{array}{ccccc}\hfill 0\hfill & \hfill {\xi }_{1,2}\hfill & \hfill {\xi }_{1,3}\hfill & \hfill \cdots \hfill & \hfill {\xi }_{1,N}\hfill \\ \hfill {\xi }_{2,1}\hfill & \hfill 0\hfill & \hfill {\xi }_{2,3}\hfill & \hfill \cdots \hfill & \hfill {\xi }_{2,N}\hfill \\ \hfill {\xi }_{3,1}\hfill & \hfill {\xi }_{3,2}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\xi }_{3,N}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\xi }_{N,1}\hfill & \hfill {\xi }_{N,2}\hfill & \hfill \cdots \hfill & \hfill {\xi }_{N,N-1}\hfill & \hfill 0\hfill \end{array}\right]\hfill \end{array}$$ (21)

In its present form, analytical treatment of equation (20) is very difficult. However, considering that we are interested in the collective period, we can restrict our attention to solutions that describe synchronized oscillations of the oscillator network. This provides a clue to simplify the dynamics: synchrony indicates that the phases of each oscillator ϕ_i and φ_i (i = 1, 2, . . . , N) are identical, respectively.

A. Proof of Theorem 1

Given that the cellular oscillators are homogeneous and the coupling is symmetric, the amplitudes of all oscillators β_i and y_i (i = 1, 2, . . . , N) are respectively identical, too. Since ξ_i,j and η_i are determined by β_i and y_i, we further have ξ_1,2 = . . . = ξ_1,N = . . . = ξ_N–1,N = ξ and η₁ = η₂ = . . . = η_N = η. Using these properties, we can reduce (20) to:

$$(\eta I-H\left(jw\right))P=0$$ (22)

where

$$\begin{array}{cc}\hfill H\left(jw\right)=& \frac{jw+b}{a}{e}^{(T_m+T_p)jw}(jwI+cI-A{e}^{-\tau jw}),\hfill \\ \hfill A=& \xi (1\times 1^T-I),1={[1,1,\dots ,1]}^{\mathbf{T}}\hfill \end{array}$$ (23)

It can be verified that H(jw) has two eigenvalues:

$${\delta }_1=(jw+c-\xi (N-1)e^{-\tau jw})\frac{jw+b}{a}{e}^{(T_m+T_p)jw}$$ (24)

of multiplicity 1 and

$${\delta }_2=(jw+c+\xi e^{-\tau jw})\frac{jw+b}{a}{e}^{(T_m+T_p)jw}$$ (25)

of multiplicity N – 1, and only δ₁ corresponds to eigenvectors with identical elements.

As analyzed above, when the network is synchronized, P and M are vectors of identical elements. Thus we have

$$\eta ={\delta }_1=(jw+c-\xi (N-1)e^{-\tau jw})\frac{jw+b}{a}{e}^{(T_m+T_p)jw}$$ (26)

According to (18), η is real, thus the item on the right hand side of (26) must be real, i.e., its imaginary part is zero.

Since $(jw+c-\xi (N-1)e^{-\tau jw})\frac{(jw+b)}{a}{e}^{(T_m+T_P)jw}$ can be rewritten as

$$\frac{1}{a}((bc+w^2)-\xi (N-1)w\sin w\tau -\xi (N-1)b\cos w\tau +j((b+c)w+\xi (N-1)b\sin w\tau -\xi (N-1)w\cos w\tau ))\times (\cos w(T_m+T_p)+j\sin w(T_m+T_p))$$

it follows that the imaginary part of the right hand side of (26) is zero given that (4) is satisfied. Denote the ratio between the Fourier coefficients of $g(p_i,m_{{\mathbb{N}}_{\stackrel{‒}{i}}})$ with respect to p_i and m_j $(j\in {\mathbb{N}}_{\stackrel{‒}{i}})$ respectively as κ (Note that due to the structure of $g(p_i,m_{{\mathbb{N}}_{\stackrel{‒}{i}}})$, κ is independent of i and j, and its exact value—which is not needed in the analysis in this paper—can be calculated numerically [27]), (5) is obtained from the equality of both sides of (26). Hence the theorem is proven.

B. Proof of Theorem 2

When the oscillator network is synchronized, the collective period is determined by (4), which can be rewritten as

$$(b+c)w\cos w(T_m+T_p)+(N-1)\xi b\sin w\tau \cos w(T_m+T_p)-(N-1)\xi w\cos w\tau \cos w(T_m+T_p)+(bc-w^2)\sin w(T_m+T_p)-(N-1)\xi b\cos w\tau \sin w(T_m+T_p)-(N-1)\xi w\sin w\tau \sin w(T_m+T_p)=0$$ (27)

From trigonometric addition formulas, (27) is equivalent to

$$(b+c)w\cos w(T_m+T_p)-(N-1)\xi b\sin w(T_m+T_p-\tau )-(N-1)\xi w\cos w(T_m+T_p-\tau )+(bc-w^2)\sin w(T_m+T_p)=0$$ (28)

Eqn. (28) can be further transformed into

$$(b+c)w-(w^2-bc)\tan w(T_m+T_p)=(N-1)\frac{\xi w\cos w(T_m+T_p-\tau )+\xi b\sin w(T_m+T_p-\tau )}{\cos w(T_m+T_p)}$$ (29)

Setting

$$g\left(w\right)=(b+c)w-(w^2-bc)\tan w(T_m+T_p)$$ (30)

and using the linear combination rule of sine and cosine, we can recast (29) into

$$g\left(w\right)=(N-1)\frac{\xi \sqrt{w^2+b^2}\sin (w(T_m+T_p-\tau )+\varphi )}{\cos w(T_m+T_p)}$$ (31)

where $\left(\frac{w}{b}\right)$.

It can be easily verified that g(w_A) = 0. So we have

$$\{\begin{array}{c}\sin (w(T_m+T_p-\tau )+\varphi )=0\hfill \\ g\left(w\right)=0\hfill \end{array}\phantom{\}}\Rightarrow \{\begin{array}{c}w(T_m+T_p-\tau )+\varphi =k\pi ,k=0,1,2,\dots ,\hfill \\ w=w_A\hfill \end{array}\phantom{\}}$$ (32)

Therefore, when (8) holds, the collective period T is the same as the autonomous period T_A.

Since w is the minimal positive value satisfying (7) and (4) from the harmonic balance technique [26], one can verify that $w\in (\frac{\pi }{2(T_m+T_p)},\Omega )$ where $\Omega \triangleq \min \{\frac{\pi }{T_m+T_p},\sqrt{bc}\}$. This is because when $w\in (0,\frac{\pi }{2(T_m+T_p)})$ the respective two sides of (7) and (4) have different signs—excluding the possibility of solutions, whereas when $w\in (\frac{\pi }{2(T_m+T_p)},\Omega )$, the respective two sides of (7) and (4) can be verified to have an intersection via trend analysis. (Note that: ① ξ < 0 holds since g(•) decreases with m_i(t) and hence has a negative describing function [16], [27]; ② $\sqrt{bc}>\frac{\pi }{2(T_m+T_p)}$ holds due to the fact that the half lives of molecules, $\frac{\ln 2}{b}$ and $\frac{\ln 2}{c}$, need to be much smaller than T_m + T_p to guarantee sustained oscillations [32], [33].) Therefore, we have tan w(T_m + T_p) < 0 and bc–w² > 0. Hence g(w) in (30) satisfies g(w) > 0 if and only if w > w_A holds, and g(w) satisfies g(w) < 0 if and only if w < w_A holds. Therefore, from (31), we have w > w_A when sin(w(T_m+T_p–τ)+ϕ) > 0 is satisfied, and we have w < w_A when sin(w(T_m + T_p – τ) + ϕ) < 0 is satisfied (notice that cos w(T_m+T_p) < 0 for $w\in (\frac{\pi }{2(T_m+T_p)},\Omega )$ and ξ < 0). Using the properties of sinusoidal functions, we have w > w_A when τ satisfies (9) for k = 2n – 1 (n = 0, 1, 2, . . .), and w < w_A when τ satisfies (10) for k = 2n (n = 0, 1, 2, . . .).

Next we proceed to prove that when τ satisfies (11), the collective period T increases with τ, and when τ satisfies (12), the collective period decreases with τ.

It can be verified that g(w) is an increasing function of w for $w\in (\frac{\pi }{2(T_m+T_p)},\Omega )$. Given that ξ < 0 and cos w(T_m+T_p) < 0 when $w\in (\frac{\pi }{2(T_m+T_p)},\Omega )$, the right hand side of (31) increases with sin(w(T_m+T_p – τ)+ϕ), which is a decreasing function of τ when τ satisfies (11). So w is a decreasing function of τ when τ satisfies (11). Similarly, we can prove that the right hand side of (31) increases with sin(w(T_m + T_p – τ) + ϕ), which is an increasing function of τ when τ satisfies (12). So w is an increasing function of τ when τ satisfies (12). Recall that T is equal to $\frac{1}{w}$ and hence is a decreasing function of w, we have the second part of Theorem 2.