A Simple and Fast Approach for Predicting ¹H and ¹³C Chemical Shifts: Toward Chemical Shift-Guided Simulations of RNA

Abstract

We introduce a simple and fast approach for predicting RNA chemical shifts from interatomic distances that performs with an accuracy similar to existing predictors and enables the first chemical shift-restrained simulations of RNA to be carried out. Our analysis demonstrates that the applied restraints can effectively guide conformational sampling toward regions of space that are more consistent with chemical shifts than the initial coordinates used for the simulations. As such, our approach should be widely applicable in mapping the conformational landscape of RNAs via chemical shift-guided molecular dynamics simulations. The simplicity and demonstrated sensitivity to three-dimensional structure should also allow our method to be used in chemical shift-based RNA structure prediction, validation, and refinement.

Introduction

The recent realization of the important role played by ribonucleic acids (RNAs) in regulating cellular processes^1,2 has resulted in significant interest in characterizing the structure of these molecules at atomic resolution. However, RNAs possess significant conformational flexibility, which complicates structure determination via X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy. From a biophysical standpoint, this conformational flexibility has significant mechanistic implications on RNA function. For instance, in the context of molecular recognition, a number of RNAs, most notably the HIV-1 trans-activating response (TAR) element RNA, bind ligands via a conformational capture mechanism in which the ligand-free RNA samples a number of distinct “bound-like” states.³⁻⁶ In the case of HIV-1 TAR, the conformations of the RNA in complex with a number of ligands closely resemble some of the conformations sampled in the ligand-free state.^6,7 As such, instead of a static RNA structure, an ensemble representation that captures the entire range of accessible conformations, along with their associated population weights, is needed.

In principle, molecular dynamics (MD) simulations can be used to map the landscape of any biomolecule in a thermodynamically rigorous manner. However, the force fields used to simulate the dynamics of biomolecules in MD simulations are imperfect. This is particularly true for RNA force fields, which, due to the protein-centric view that has been prevalent up to this point, have been the subject of less development than their protein counterparts. The use of experimentally guided simulations has emerged as an alternative to the often tedious and time-consuming reparameterizations of force fields. In these guided simulation approaches, the force field is augmented with a biasing term that ensures that the system being simulated matches some experimental observable(s).⁸⁻¹² The use of experimentally guided simulations to accurately map the conformational landscape of proteins is now well-established.¹³⁻²⁰

Of particular interest are approaches that use NMR chemical shifts to guide MD simulations of biomolecules. Chemical shifts have emerged as an attractive source of structural information due to the fact that, in addition to being readily accessible and being the most precisely measured NMR observable, they exhibit exquisite sensitivity to structure.²¹⁻²⁶ Advances in site-specific labeling techniques²⁷⁻³⁰ and automated assignments approaches³¹⁻³⁵ means that chemical shifts are, and will continue to become, increasingly accessible, not only for the small RNAs (<40 nt) typically studied using NMR, but for larger and more complex RNAs as well.^30,36

A prerequisite for the use of chemical shifts-guided simulations to map the conformational landscape of a biomolecule is the availability of structure-based approaches that allow chemical shifts to be predicted from the three-dimensional (3D) coordinates of the molecule. In this regard, empirical methods have been shown to be of great utility. In the case of proteins, a plethora of such empirical structure-based chemical shift predictors have been developed.³⁷⁻⁴² In contrast, only a few such methods exist for RNA. Two of these methods, SHIFTS⁴³ and NUCHEMICS,⁴⁴ predict nonexchangeable ¹H chemical shifts, while the recently described RAMSEY⁴⁵ is capable of predicting both nonexchangeable ¹H and protonated ¹³C chemical shifts. In principle, the ability to predict both ¹H and ¹³C chemical shifts makes RAMSEY an ideal predictor to be used in chemical shifts-guided simulations. However, RAMSEY, which was developed using the random forest approach, is a “black box” predictor, which automatically precludes its direct incorporation into MD simulations because no closed-form analytical solution can be obtained.

As a first step toward using chemical shifts to guide MD simulations of RNA, we report on the development of LARMOR^D (LARMOR for the Larmor frequency (ω) and D for distance), a simple distance-dependent chemical shift predictor that allows chemical shifts to be easily incorporated into molecular simulations of RNA. In what follows we: (i) describe the model and the approach used to parametrize LARMOR^D; (ii) assess the accuracy of LARMOR^D; (iii) demonstrate the sensitivity of LARMOR^D predicted chemical shifts to RNA 3D-structure; and (iv) apply LARMOR^D enabled chemical-shift guided MD simulations (CS-MD) to a model RNA system. Collectively, our results indicate that in addition to its simplicity and speed, LARMOR^D is accurate, sensitive to RNA 3D structure, and enables effective biasing restraints to be derived from experimental NMR chemical shifts.

Methods and Material

The Chemical Shift-Structure Database

To generate LARMOR^D, we compiled a training set consisting of RNAs for which NMR structures were available via the Protein Data Bank (PDB: http://www.pdb.org) and chemical shifts were available via either the Biological Magnetic Resonance Bank (BMRB: http://www.bmrb.wisc.edu/) or the literature (Supporting Information, Table S1). Excluded from the database were RNAs: (i) that were known and verified to contain systematic ¹³C referencing errors;^45,46 (ii) whose corresponding chemical shifts were assigned at temperatures <290 K; (iii) that were bound to small molecules and/or proteins; and (iv) that contained modified residues. In total, the compiled chemical shift-structure training set contained data from 35 RNAs. In addition to the training set, a testing set was compiled. The testing set consists of chemical shifts and structures for 28 RNAs, 17 of which were known and verified to contain ¹³C referencing errors (Supporting Information, Table S2). The testing set served two purposes: (i) it allowed us to test whether the LARMOR^D predictors, specifically, the ¹³C predictors, were accurate enough to detect known systematic referencing errors, and (ii) after correcting for identified systematic referencing errors, it allowed us to independently assess the accuracy of both¹H and ¹³C chemical shift predictors. For both data sets, we carried out outlier analysis by examining the distributions of reported chemical shifts for each unique nucleus (i.e., each unique combination of ¹H and ¹³C nuclei and residue types). Outliers were identified as entries that were greater than the median by more than three standard deviations (i.e., the 3σ rule). The outliers comprised <1% of the combined data set and, for completeness, the entries identified as outliers are listed in Supporting Information, Table S3. The final training set (excluding outliers) contained 5505 and 2924 ¹H and ¹³C chemical shifts, respectively, and the testing set (excluding outliers) contained 5520 and 3745 ¹H and ¹³C chemical shifts, respectively.

For each RNA entry in the training and testing sets, the interatomic distances, r_ij (see eq 1), that were to be used to predict chemical shifts were extracted from the NMR bundle of the corresponding RNA using the following approach. First, to generate a representative model, the member of the NMR bundle that was closest (i.e., had smallest structural root-mean-square deviation (RMSD)) to the average structure of the bundle was selected and then briefly minimized using the steepest-descent gradient method. For every nucleus for which ¹H or ¹³C chemical shifts were available, the distance between that nucleus and all heavy atoms were measured from the coordinates of the representative model. All distances were determined using the MDAnalysis⁴⁷ python module.

Distance-Based Chemical Shift Prediction Model

In our model, the chemical shift, δ_i^pred, for a given RNA nucleus i, is expressed as a function of interatomic distances,^40,41 that is:

1

Here, δ_i^ref is the reference chemical shift for nucleus i, N is the total number of heavy atoms in the RNA, r_ij is the interatomic distance between atoms i and j, and α_ij is a parameter that depends on the atom type of i, and the atom and residue type associated with j (Figure 1). For each nonexchangeable ¹H (H1′, H2′, H3′, H4′, H5′, H5″, H2, H5, H6, H8) and protonated ¹³C (C1′, C2′, C3′, C4′, C5′, C2, C5, C6, C8) nucleus, the set {α_ij} that minimized the objective function χ², which quantifies the error between measured and predicted chemical shifts, was determined using a genetic algorithm (GA) optimization approach. Here,

2

where δ_i^meas and w_i are the measured chemical shift and weighting factor, respectively, and for a given nucleus i. The summation runs over the set of N_CS chemical shifts in the training set. All GA optimizations were carried out with a population size of 10, and the number of evolution cycles was set to 4000 using the Pyevolve python module.⁴⁸ Each GA optimization was initialized with {α_ij} = 0∀j (i.e., for some nucleus i, δ_i = δ_i^ref (eq 1)) and w_i = 1∀i throughout the optimization. Using these GA settings, all optimizations were converged, and the fitted errors ((χ²)^1/2) were near the expected ranges; for protons and carbons, the average (χ²)^1/2 was ∼0.19 and 1.09 ppm, respectively. By comparison RAMSEY has prediction errors of ∼0.16 and 0.90 ppm for protons and carbons, respectively.⁴⁵

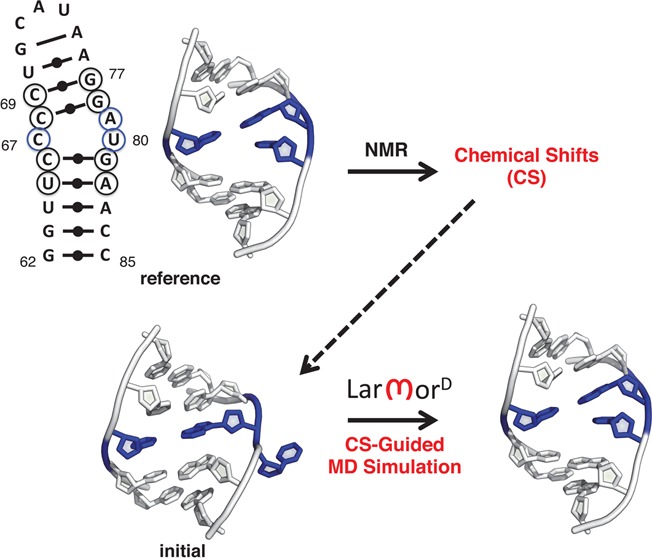
Figure 1.

Illustration of the approach used to predict RNA chemical shifts. For a given nucleus (red sphere), chemical shifts are predicted as a function of the distances between that nucleus and all heavy atoms in the RNA (cyan lines; eq 1).

Chemical Shift-Guided MD Simulation

To carry out chemical shift-guided MD simulations (CS-MD), LARMOR^D was implemented into the CHARMM macromolecular mechanics package.⁴⁹ CS-MD simulations were then carried out using the hybrid energy approach⁵⁰ in which the total energy associated with a conformer X, E(X), is given by

3

Here, E_CHARMM(X) and β are the CHARMM force-field energy of X and 1/k_BT (k_B = Boltzmann constant), respectively, and χ² is the expression noted above (see eq 2). In this case, however, the weighting factors (w_i) were used to account for the differential accuracy of the predictors. Specifically,

4

where MAE_i is the estimated mean absolute error between measured and LARMOR^D predicted chemical shifts for the nucleus type associated with i. Here the MAE_i were estimated using the testing set. In addition to accounting for the differential accuracy of the predictors, w_i scales the error such that nuclei with different dynamic ranges can contribute similarly to the χ² (for example ¹H and ¹³C nuclei). The hybrid energy with a log-harmonic restraint term was introduced by Habeck et al. and is a Bayesian-inspired marginal hybrid energy⁵¹ that has the special feature that it does not include a “force constant” scaling factor for the restraint term–in typical hybrid energy schemes, an ad hoc force constant that scales the contribution of the restraint term relative to the physical energy (here E_CHARMM(X)) must be specified.

As a proof of concept, chemical shift-guided MD (CS-MD) simulations were carried out on the U6 intramolecular stem-loop (ISL) RNA.⁵² In solution, the U6 ISL RNA exists in different conformational states at pH 5.7 and at 7.0. At pH 5.7, U80 is extrahelical, whereas at pH 7.0 it is intrahelical (Figure 3B). CS-MD simulations of the U6 ISL were initiated from the pH 5.7 conformation (model 1; PDB: 1SYZ(53)), and measured chemical shifts assigned at pH 7.0 (BMRB: 5371⁵⁴) were used to guide the simulations using eq 3. As a control, conventional unrestrained MD simulations were also carried.

Figure 3.

Assessing accuracy of LARMOR^D: (A) Bar plots of the mean absolute error (MAE) between measured and (gray) LARMOR^D and (light gray) RAMSEY predicted ¹H (left) and ¹³C (right) chemical shifts. (B) Bar plots of the Pearson correlation coefficient (R) between measured and LARMOR^D and RAMSEY predicted ¹H (left) and ¹³C (right) chemical shifts. Results are shown for RNAs in the testing set.

To prepare for simulations, model 1 from PDBID: 1SYZ was solvated in a 67 Å cubic box of TIP3 waters.⁵⁵ The system was then charge neutralized with sodium counterions and relaxed with 100 steepest-descent, followed by 1000 adopted basis Newton–Raphson minimization steps. Prior to production runs, the RNA was heated from 250 to 325 K over 20 ps. During this phase the heavy atoms of the RNA were harmonically restrained using a force constant of 2.0 kcal/mol/Å. Production runs were then initiated from the resulting systems. For each independent simulation, the heating phase was initiated with different velocities by supplying distinct random number seeds. For both CS-MD and MD simulations, 10 independent production runs were carried, each 2 ns long and simulated in the NPT ensemble (325 K and 1 atm). All simulations were carried out using the CHARMM36⁵⁶ nucleic acid force field. SHAKE was used to constrain hydrogen-containing bonds.⁵⁷ The van der Waals potential was truncated using a switching function between 10 and 12 Å. Long-range electrostatics was calculated using particle-mesh Ewald (PME) with a fourth-order B-spline used for interpolation.⁵⁸

Results and Discussion

For chemical shifts to be incorporated as structural restraints that guide MD simulations, the method used to predict chemical shifts from 3D coordinates must be (i) fast, (ii) accurate, and (iii) sensitive to RNA 3D structure. By design, LARMOR^D’s simple dependence on interatomic distances guarantees that it can rapidly predict chemical shifts for 3D coordinates, and indeed, profiling of its predictions confirms this (Supporting Information, Table S4). We therefore focus our assessment of LARMOR^D on its accuracy and then its sensitivity to RNA 3D structure.

LARMOR^D Can Detect Referencing Errors in ¹³C Data Sets

Before assessing the accuracy of individual LARMOR^D 1H and ¹³C chemical shift predictors, we investigated whether (i) ¹³C chemical shifts data set with known referencing errors could be detected and (ii) reliable estimates for the magnitude of these errors could be determined using LARMOR^D. Unlike many other experimental observables, NMR chemical shifts are relative measurements. As such, any data set of chemical shifts is susceptible to issues related to inconsistent referencing, which complicates the establishment of reliable structure–chemical shifts relationship.⁵⁹

In the case of proteins it was found that a significant number of data sets deposited in the BMRB contained ¹³C and ¹⁵N referencing errors.^59,60 Wishart and co-workers have addressed this using a structure-based approach in which a predictor, trained on chemical shift data known to be correctly and consistently referenced, is used to predict chemical shifts for a target protein from its solved X-ray or NMR structure. Systematic errors can be identified by comparing the predicted chemical shifts to the measured chemical shifts.⁶⁰

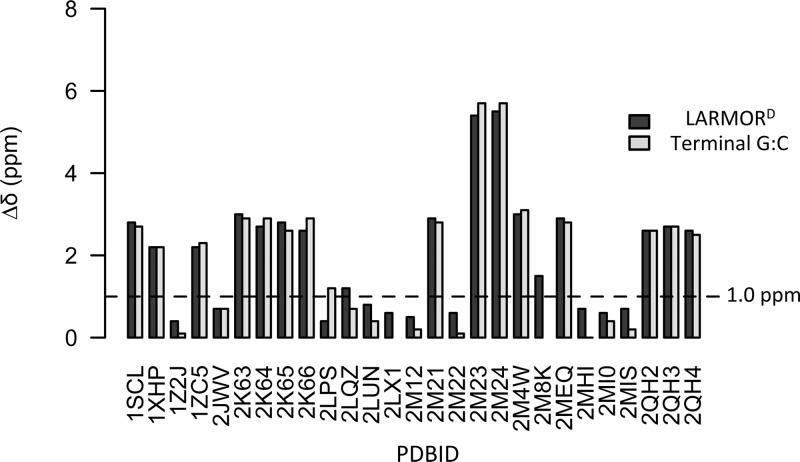
Similar to those of proteins, RNA chemical shifts, in particular ¹³C chemical shifts, are known to also contain referencing errors. Aeschbacher et al. recently described an approach that utilizes the chemical shift signatures of terminal G-C base pair to detect referencing errors.⁴⁶ Application of their approach indicated that a number of the entries in our testing set contained systematic referencing errors (Δδ_GC).

To test whether LARMOR^D can detect referencing errors, it was used to predict ¹³C chemical shifts for each RNA in the testing set, and then the absolute median error between measured and predicted chemical shifts was determined and used as an estimate of the systematic error (Δδ_pred). As shown in Figure 2, 17 of the 27 entries in testing set that contained ¹³C shifts exhibited large systematic error (i.e., Δδ_pred >1.0 ppm). Remarkably, Δδ_pred were in excellent agreement with Δδ_GC suggesting that LARMOR^D was not only able to identify referencing errors in ¹³C chemical shift data sets but was also able to provide reliable estimates of the magnitude of these errors. Immediately, LARMOR^D could be incorporated into an automated procedure that allows referencing errors in RNA chemical shifts to be detected, corrected, and then made available to the scientific community via a secondary database, as has been done for proteins.⁶⁰

Figure 2.

Detecting chemical shift referencing errors using LARMOR^D: comparison between LARMOR^D predicted referencing errors and those estimated using the approach of Aeschbacher et al., in which the chemical shift signature of the terminal G:C base pair is compared to expected values for correctly referenced chemical shifts. Results are shown for RNAs (identified by the PDBIDs) in the testing set.

Despite Its Simplicity, LARMOR^D Accurately Predicts Chemical Shifts

Given the simple model used by LARMOR^D, a critical question is how accurate are the predicted chemical shifts. We answered this question for individual¹H and ¹³C nuclei by calculating the mean absolute error (MAE) and the Pearson correlation coefficient (R) between experimentally measured and LARMOR^D predicted chemical shifts in the testing set. Prior to assessing their accuracy, ¹³C chemical shifts were re-referenced where necessary. The MAE for ¹H nuclei ranged between 0.09 and 0.24 ppm, with a mean of 0.15 ppm. For ¹³C the range was 0.53 and 1.09 ppm, and the mean was 0.81 ppm (Figure 3B). By comparison, RAMSEY⁴⁵ exhibited MAE that ranged between 0.08 and 0.18 ppm (mean of 0.14 ppm) for ¹H and between 0.57 and 1.14 ppm (mean of 0.83 ppm) for ¹³C (Figure 3B). The accuracy for LARMOR^D is therefore similar to RAMSEY. A similar picture emerged when examining R—for ¹H and ¹³C, the mean value was 0.51 and 0.57, respectively, for LARMOR^D, compared to 0.59 and 0.53, respectively, for RAMSEY (Figure 3C).

In general, RAMSEY appears to predict ¹H chemical shifts with slightly greater accuracy than LARMOR^D. Because ¹H chemical shifts are known to be more highly sensitive to ring-current effects, we investigated whether accounting for ring-current effects when predicting ¹H chemical shifts would result in more accurate predictions. For ¹H nuclei, we generated a set of new predictors by repeating the parametrization (see eq 1), but this time including an additional ring-current term (calculated using the Johnson–Bovey model⁶¹) in eq 1. For these predictors, however, we did not observe any noticeable improvements in the accuracy (data not shown). Direct comparison with SHIFTS and NUCHEMICS, two empirical predictors capable of also predicting ¹H chemical shifts, revealed LARMOR^D to be more accurate. SHIFTS and NUCHEMICS predict chemical shifts with an MAE of 0.37 and 0.21 ppm, and an R of 0.38 and 0.46, respectively, as compared to 0.15 ppm and 0.51, respectively, for LARMOR^D (Supporting Information, Table S5). Together, these results suggest that without explicitly accounting for hydrogen bonding, base–base stacking, ring current, magnetic anisotropies, and bond polarization effects, the simple distance-based approach used here is sufficient to enable LARMOR^D predictions of both ¹H and ¹³C chemical shifts with good accuracy relative to the currently available empirical structure-based approaches.

LARMOR^D Predicted Chemical Shifts Are Sensitive to RNA 3D Structure

For chemical shifts to be used to guide MD simulations, it is essential that the predictor used to back-predict chemical shifts from atomic models is sensitive to RNA structure. To assess its sensitivity to 3D structure, LARMOR^D was used to predict the chemical shifts for each model in a conformational pool that contained 8000 putative models of the sarcin–ricin loop (SRL) RNA.⁶² These models were generated from its sequence using the RNA structure prediction software MCSYM⁶³ and correspond to structures consistent with the nine lowest-energy secondary structures as predicted by the program MC-fold.^49,63 In Figure 4 the six models with the lowest error between measured and LARMOR^D predicted chemical shifts are overlaid with the X-ray structure. As can been seen the low-error models are in excellent agreement with the solved structure. Further, we found that 24 of the 30 models with the lowest chemical shift error had an RMSD < 2.0 Å. These results indicate that LARMOR^D predicted ¹H and ¹³C chemical shifts are indeed sensitive to RNA 3D structure. LARMOR^D should therefore be useful in the context of chemical shift-guided MD simulations. Additionally, the demonstrated sensitivity to RNA 3D structure strongly suggests that LARMOR^D can be employed in RNA structure prediction either as a postprocessing structural filter to identify representative models (as was demonstrated for SRL RNA here) or to construct a penalty term to guide conformational exploration in structure prediction approaches à la CS-Rosetta-RNA.²⁶

Figure 4.

Assessing the ability of LARMOR^D chemicals shifts to resolve 3D structure of the SRL RNA: MCSYM was used to predict the structure of the sarcin–ricin loop (SRL) from sequence. The MCSYM conformational pool contained 8000 models. After using LARMOR^D to predict chemical shifts for each model in the MCSYM conformational pool, models with the lowest chemical shift errors were identified. This figure shows the cartoon overlays comparing the X-ray structure (PDB: 430D; white) of SRL RNA with the six MCSYM models that exhibited lowest error between measured and LARMOR^D predicted chemical shifts (blue).

LARMOR^D Predicted Chemical Shifts Effectively Guides MD Simulations of RNA

As the focus of this work was the development of a chemical shifts predictor that enabled NMR chemical shifts to be easily incorporated into molecular simulations of RNA, we conclude our study by implementing the LARMOR^D-based chemical shifts restraint functionality into the CHARMM macromolecular mechanics package⁴⁹ and then carrying out chemical shift-restrained MD (CS-MD) simulations on a model system. Specifically, CS-MD simulations were carried out on the U6 intramolecular stem-loop (ISL) RNA⁵² (Figure 5A,B). At pH 5.7, the U80 base of U6 ISL is in an extrahelical position, whereas at pH 7.0, U80 is intrahelical (Figure 5B). Base flipping is ubiquitous in RNA structural dynamics and in many cases acts as a switching mechanism between conformational states of an RNA.⁶⁴⁻⁶⁷ Together with its relatively small size (27 nt), this makes the U6 ISL an excellent benchmark system for our CS-MD simulation approach.

Figure 5.

LARMOR^D enabled chemical shifts guided simulations of the U6 ISL RNA: (A) Secondary structure of the U6 intramolecular stem-loop (ISL) RNA. Residues C67, A79, and U80 are highlighted in blue. Residues 65–69 and 76–82, which makes up the conformationally active region, are circled. (B) Cartoon representation of the U6 ISL at pH 5.7 (model 1; PDB: 1SYZ) and pH 7.0 (model 1; PDB: 1SY4). Only the conformationally active region is shown in the cartoons. (C) RMSD distribution over the set of 10 CS-MD (black) and MD (red) trajectories. RMSDs were calculated relative to the pH 7.5. From each of the 10 CS-MD and 10 MD trajectories, the model with the lowest RMSD was extracted; shown are the five models with the lowest RMSD extracted from the (D) CS-MD and (E) MD trajectories.

Starting from the pH 5.7 coordinates (PDB: 1SYZ;⁵³ model 1), we carried out CS-MD simulations using reference chemical shifts assigned at pH 7.0 (BMRB: 5371⁵⁴). If the chemical shifts restraints are effective then, in comparison to the unrestrained simulation, the conformations along the trajectory of the CS-MD simulation should more closely resemble the intrahelically stacked pH 7.0 conformation; this despite the fact that the simulations were initiated from the extrahelical pH 5.0 conformation.

We found that in the case of the CS-MD simulations, the distribution of RMSDs relative to the pH 7.0 structure was shifted toward lower RMSD values than in the control MD simulations (Figure 5C; Supporting Information, Figure S1). This indicates that the chemical shifts restraint, constructed using chemical shifts assigned at pH 7.0, was effective in guiding sampling away from the initial pH 5.7 conformation (Figure 5B; left) toward the pH 7.0 (Figure 5B; right). Five out of the 10 CS-MD simulations sampled conformations with RMSDs < 1.8 Å, compared to only one for the control simulations (Figure 5D,E and Supporting Information, Figures S1 and S2). Similarly, three out of the 10 CS-MD simulations were able to sample conformations within ∼1.3 Å of the flipped in and stacked state, while the unrestrained simulations were limited to RMSDs > 1.7 Å (Figure 5D; Supporting Information, Figure S1). These results demonstrate that the LARMOR^D chemical shift restraints are able to effectively guide conformational sampling of U6 ISL, allowing chemical shifts to be used within the context minimally biased¹² and/or maximum entropy-based¹¹ approaches to map the conformational landscape of RNA.

In addition to opening up the possibility of using chemical shifts to map the conformational landscape of RNAs,⁶⁸ chemical shift-guided simulations may be of utility in carrying explicit solvent MD-based refinement of NMR structures. Conventional NMR structure determination is typically carried out without explicitly accounting for solvent effects (i.e., carried out in vacuo) and using ad hoc treatment of nonbonded interactions. Indeed, previous work has shown that structure refinement using an accurate force field, while explicitly accounting for solvent, resulted in structures that are sometimes in better agreement with the original NMR data than the structures solved using conventional in vacuo approaches.⁶⁹

To facilitate the use of LARMOR^D, the parameters and the source code implementing the predictor is made freely available to academics (see the link shown in the Supporting Information byline). In addition, the LARMOR^D-based chemical shifts restraint module will be available in CHARMM.

Though RNA was the focus of the current work, the implementation of LARMOR^D in the stand-alone predictor and CHARMM follows a general design approach, so that in principle they can be used for any molecular assembly, for example, proteins, nucleic acids (NA), protein–protein, protein–NA, and NA–NA complexes, provided, of course, that the appropriate parameters are available, which is a component of ongoing work.

Conclusion

In summary, we have developed LARMOR^D, a simple, fast, and accurate method for predicting nonexchangeable ¹H and protonated ¹³C RNA chemical shifts based only on interatomic distances. We showed that LARMOR^D was capable of resolving RNA 3D structure, and more importantly for this study, we demonstrated that LARMOR^D-based chemical shifts restraints were effective in guiding conformational sampling during CS-MD simulations. Future work will focus on developing and validating robust CS-MD simulations protocols that will allow chemical shifts to be used to map the conformational landscape of RNAs, as well as protocols for using chemical shifts to refine NMR structures of RNAs. In addition, we will also explore more fully combining LARMOR^D with current state-of-the-art prediction approaches to aid in RNA structure prediction. This application would be particularly useful in cases where chemical shifts are the only high-quality structural data available–as is the case for transiently populated “invisible” states of RNAs that can now be detected using chemical shifts relaxation dispersion experiments.^70,71

Supporting Information Available

Tables S1–S8: (S1) training set; (S2) testing set; (S3) chemical shift entries identified as outliers; (S4) LARMOR^D execution times. (S5) Comparison between the accuracy of LARMOR^D 1H predictors to SHIFTS and NUCHEMICS; (S6) Reference chemical shifts used in eq 1. (S7) Accuracy of preliminary imino ¹H and ¹⁵N chemical shift predictors; and (S8) Comparison between measured and predicted chemical shifts for U6 ISL RNA. Figures S1 and S2: (S1) RMSD time series for CS-MD and MD simulations of the U6 ISL RNA; and (S2) Effective chemical shifts error time series for CS-MD and MD simulations of the U6 ISL RNA. Movie 1: (S1) Movie of a CS-guided MD trajectory of U6 ISL RNA. Data S1: (S1) The optimized LARMOR^D parameters. This material is available free of charge via the Internet at http://pubs.acs.org. The source for LARMOR^D is available at: http://brooks.chem.lsa.umich.edu/software. The LARMOR^D module implementing the predictor and the chemical shift biasing restraint will also be made available in CHARMM.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States