Image Analysis and Length Estimation of Biomolecules Using AFM

Abstract

There are many examples of problems in pattern analysis for which it is often possible to obtain systematic characterizations, if in addition a small number of useful features or parameters of the image are known a priori or can be estimated reasonably well. Often, the relevant features of a particular pattern analysis problem are easy to enumerate, as when statistical structures of the patterns are well understood from the knowledge of the domain. We study a problem from molecular image analysis, where such a domain-dependent understanding may be lacking to some degree and the features must be inferred via machine-learning techniques. In this paper, we propose a rigorous, fully automated technique for this problem. We are motivated by an application of atomic force microscopy (AFM) image processing needed to solve a central problem in molecular biology, aimed at obtaining the complete transcription profile of a single cell, a snapshot that shows which genes are being expressed and to what degree. Reed et al. (“Single molecule transcription profiling with AFM,” Nanotechnology, vol. 18, no. 4, 2007) showed that the transcription profiling problem reduces to making high-precision measurements of biomolecule backbone lengths, correct to within 20–25 bp (6–7.5 nm). Here, we present an image processing and length estimation pipeline using AFM that comes close to achieving these measurement tolerances. In particular, we develop a biased length estimator on trained coefficients of a simple linear regression model, biweighted by a Beaton–Tukey function, whose feature universe is constrained by James–Stein shrinkage to avoid overfitting. In terms of extensibility and addressing the model selection problem, this formulation subsumes the models we studied.

I. Introduction

There are many examples of problems in pattern analysis for which it is often possible to obtain systematic characterizations, if in addition a small number of useful features or parameters of the image are known a priori or can be estimated reasonably well. Examples of such feature-based analysis of patterns occur in human speech [1], genomic data analysis [2], face recognition [3], etc. Often the relevant features of a particular pattern analysis problem are easy to enumerate, as when statistical structures of the patterns are well understood from the knowledge of the domain. We study a problem from molecular image analysis, where such a domain-dependent understanding may be lacking to some degree and the features must be inferred via machine-learning techniques. Similar techniques are beginning to appear in natural image processing [4], [5], neural connectomics analysis [6], population genomics [7], etc., but have not been explored in the area of molecular image analysis, which poses very specific problems of its own. In this paper, we propose a rigorous, fully automated technique for this problem. In particular, we address several computational questions related to the problem: namely, how can one use standard image processing approaches to get an initial estimate of the length of a dsDNA from its atomic force microscopy (AFM) image and characterize the residual errors? how can one discover a parsimonious set of features that can explain the residue and improve the length estimate? how can one automatically learn the contributions from a well-chosen subset of features using a training set of calibrating molecules, which may be assumed to contain a large number of “good” examples but possibly corrupted with a few false positives?

We are motivated by an application of image processing needed to solve a central problem in molecular biology, aimed at obtaining the complete transcription profile of a single cell, a snapshot that shows which genes are being expressed and to what degree. Seen in series as a movie, these snapshots would give direct, specific observation of the cell's regulation behavior. Taking a snapshot amounts to correctly classifying the cell's ∼300 000 mRNA molecules into ∼30 000 species, and keeping accurate count of each species. The cell's transcription profile may be affected by low abundances (1–5 copies) of certain mRNAs; thus, a sufficiently sensitive technique must be employed. A natural choice is to use AFM to perform single-molecule analysis. Reed et al. [8] developed such an analysis that classifies each mRNA by the following three steps: 1) synthesize a complementary DNA (cDNA) copy of each mature mRNA, 2) multiply cleave the cDNAs with a restriction enzyme, and 3) construct each cDNA classification label from ratios of the lengths of its resulting fragments. Thus, they showed the transcription profiling problem reduces to making high-precision measurements of cDNA backbone lengths—correct to within 20–25 bp (6–7.5 nm).

Thus, the solution of the image-processing algorithm needs to be particularly accurate, significantly more than the one that has been demonstrated with previous approaches, and must do so over a wider range of DNA sizes. The approach must be fully automated, and yet be competitive against the manual or semimanual approaches that currently outperform computers. The yield from the automatic analysis must be close to perfect; otherwise, the low-copy-number gene expressions will be miscounted. Finally, it has to be compatible with the chemistry and the sensing physics; in other words, the molecules need to be elongated on a sticky uneven surface, may not be fully stretched, may entangle with other molecules, etc. Similarly, AFM may generate multidimensional information (e.g., a magnitude and a phase), may use a wide variety of scanning strategies, may use parallel scanning with an array of probes, may operate in real time to accommodate low latency and high throughput, etc. None of the previous work that we discuss below addresses these issues.

A. Related Work

For more than a decade, researchers have investigated the problem of how to accurately measure DNA contour length by computer analysis of AFM images. This study falls into three broad categories: manual methods, where human operators hand-draw piecewise linear backbones over objects extracted from the image background¹; semiautomated methods [9] that involve human interaction with image processing and object segmentation algorithms; and automated methods [10]–[18] that perform their analysis and measurement unsupervised. For reasons of speed and reproducibility, we focused our investigation on automated methods.

The problem breaks down into two steps: image processing and length estimation. Image processing takes as input an AFM image of high resolution (say, 1024 × 1024 pixels representing a microscopic area of 1000 × 1000 nm) and outputs a set of 1-D, eight-connected pixel paths in a transformed image that form the discrete representation of the continuous molecule backbone contours. Length estimation assigns to these backbones numerical values that purport to measure the true end-to-end length of the molecules.

All of the automated processing methods employ a pipeline of image processing steps. In common are steps that remove noise, extract foreground objects, iteratively erode each 2-D object into a joined 1-D line structure (tree), and finally, prune each tree's branches from its trunk—the backbone contour to be measured next. The erosion (alternatively called thinning or skeletonizing) algorithms employed are surveyed in [19]. Some of the automated methods [10], [11], [15]–[18] insert a step after erosion that uses a line-continuity heuristic to decide whether to recover tip pixels that were eliminated during the erosion step. In his masters thesis (2007), S. Cirrone innovated the last, tree-pruning step by transforming it from a strict image processing problem to a graph optimization one, where instead of eliminating branch pixels until the trunk is encountered, the tree is represented as a graph. In this scheme, a node is a pixel at the point of path bifurcation or path termination; an edge is a pixel path whose weight is given by a linear combination of two types of distance, determined by the relative orientations of consecutive pixel pairs: unit distance for horizontal and vertical, √2 for diagonal; the longest path traversal through this graph represents the trunk, or molecule backbone in this application.

For nearly 50 years, since Freeman's pioneering works in the image analysis of chain-encoded planar curves [20], the study of contour digitization has received much attention. Namely, what is the most accurate estimator of the end-to-end length of an arbitrary continuous contour that underlies its discrete representation as a 1-D pixel path? The literature contains numerous estimators and frameworks to evaluate their relative performance [21]–[29]. All of the automated processing methods mentioned earlier employ a pipeline of length estimation steps chosen from this set of estimators. These pipelines' approaches vary from those that simply traverse the chain code to yield a linear combination of unit and √2 distances [10]–[12] to those that use one of a variety of parametric estimators [13], [15]–[18] to one that takes a signal processing approach based on fast-Fourier transformation followed by the Gaussian filtering and normalization [14].

A related focus of investigation involves estimating the intrinsic curvature of DNA from AFM images [30], [31]. Intrinsic curvature of DNA is a function of the nucleotide sequence, independent of dynamic components of curvature brought on by thermal agitation. This study may eventually improve DNA backbone contour length estimates by inputting accurate estimates of curvature to a length estimator that models the DNA contour as a sequence of straight lines and circular arcs [23], [25], [29].

B. Our Approach

We first process the AFM images in a manner typical to the literature: filter the image to extract binary features from background, erode the binary features into 1-D backbone trees, and then prune the trees to extract the backbones. For this last step, we employ the graph-based method used by Cirrone, specified earlier. The sum of the straight line segments in this backbone gives its first length estimate L_LS. Then, we fit each backbone pixel path with a sequence of cubic splines, one for each five-pixel subpath, where the last pixel of a given subpath is the first pixel of the next (i.e., all subpaths share one extremity pixel). A tailing subpath 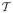having p < 5 pixels is handled by fitting a cubic spline to the subpath formed by prepending to 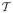the prior 5 — p pixels, then counting the spline's length from its closest approach to the first and last pixels in 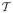. The resulting summed length of the cubic splines gives the second backbone length estimate L_CS.

We correct L_CS by a linear combination of five features, given below. The true length ℒ is thus modeled as L_CS plus a linear combination of the feature terms plus an error term ε where the feature term coefficients derive from an overdetermined system of linear equations obtained from a set of calibrating molecules of known length. We assume ε ∼ N (0, σ²) represents a Gaussian noise, thus satisfying the Gauss–Markov condition.

Our system implements a meta-approach to the problem of feature-based length estimation. Any number of image-based features may be incorporated into our simple linear model in an easily extensible way, giving rise to backbone length estimates whose error is not necessarily constrained by geometric lower bounds in terms of, for example, pixel density [21], [22], [25] or multigrid convergence [26], [28]. In this way, our approach subsumes the length estimation formulations comprised in small, fixed sets of backbone chain code parameters cited earlier.

Each image-based feature provides limited predictive power for backbone contour length. But integrated into a properly chosen model, with each feature contributing according to its demonstrated informativeness during training, in principle, the collective result should be superior to any rendered by strict subsets, provided there is no overfitting. Moreover, aside from computational complexity considerations, there should be no bound on the number of features one applies to the problem.

Our motivation for using the simple machine learning approach of linear regression is manifold.

1. It is easy to implement: off-the-shelf libraries are robust, optimized, and have undergone rigorous testing and debugging.

2. It is easy to interpret: coefficients are comparatively meaningful as feature weights.

3. It is easy to extend: it can support an arbitrary number of image features.

4. The Gauss–Markov theorem guarantees that among all “linear” unbiased estimators, ordinary least squares (OLS) estimates have the smallest variance, and thus, OLS is a best linear unbiased estimator (BLUE).

5. The mathematical form of linear regression (Na⃗ = l⃗) naturally admits two refinements, aimed at reducing systematic and modeling error, respectively:

   1. empirical Beaton–Tukey biweighting, to address statistical significance: each weight acts on the corresponding row of N, the q × k feature matrix (q calibration molecules by k image features).
   2. James–Stein shrinkage, to address overfitting by reducing feature dimensionality: shrinkage uses the mean of each column of N to derive a shrinkage factor that acts on the corresponding feature coefficient in a⃗; features that are noisy (arising from systematic error) or dependent (arising from modeling error) are thus eliminated.

In sum, the training process is supervised learning that is based on a set of examples and counter examples and the universe of features. Since our method is entirely automated, it lends itself to high-throughput applications.

II. Methods

Our application, called AFM Explorer, implements an image processing and a length estimation pipeline. Details of these are given in the “Methods” section of the Supplementary Materials, but we give a brief synopsis here.

The image processing pipeline has four phases: filter, erode, select, and remove. The original 24-bit RGB image from the AFM is filtered through a series of stages into a binary image where the molecules are represented as white blobs against a black background. Each blob is eroded down to a set of candidate 1-D molecular backbones, an eight-connected pixel tree graph structure. This structure is examined and the longest path in the tree is selected to represent the molecular backbone contour. Finally, backbones that stray close to the image boundary are removed since these represent molecules at the edge of the viewing area that will likely introduce truncated fragments.

The length estimation pipeline first makes an initial and secondary estimation of the backbone contour length, then performs four phases upon the secondary estimation: train, weight, shrink, and apply. We first estimate the length of the backbone contour b⃗ by stringing together straight line segments joining each pixel pair along b⃗ and call this estimate L_LS (b⃗). We next estimate the length of b⃗ by stringing together cubic splines, each fitting a set of five contiguous pixels, and call this estimate L_CS (b⃗).

When the application runs in train mode, we extract six features from each backbone b⃗: the number of horizontal pixel pairs n_horz; the number of vertical pixel pairs n_vert; the number of diagonal pixel pairs n_diag; the number of pixel triples arranged as perpendiculars n_perp; the coefficient of variation for height n_htcv; and the coefficient of variation for thickness n_tkcv These together with L_CS(b⃗) form the data of a possibly overdetermined linear system. We assume the images used to train represent a polydisperse set of molecules having known theoretical length ℒ. We train a linear regression model on q ≥ 6 calibrating molecule backbones b⃗ having known theoretical length ℒ, using values from these six features: {n_horz, n_vert, n_diag, n_perp, n_htcv, n_tkcv}, giving Na⃗ = l⃗, where N is the q × 6 feature matrix, a⃗ is the correction coefficient six-vector to solve for, and l⃗ is the length estimate error q-vector […, (ℒ − L_CS(b⃗_i)), …], where i = 1,…, q. The model has the analytic solution a⃗ = (N^TN)⁻¹ N^Tl⃗. This gives a trained estimator L′_T as computed in the apply phase below.

This formulation of ℒ′_T assumes all fragments that have equal weight, owing to their equivalent validity as observations. However, such an assumption may be challenged on the grounds that upon taking into consideration the difference between the empirically measured null distribution and the actual shape of the distribution in L_CS measurements, certain observations appear to be false positives, and others false negatives—a notion that we address in the weight mode by using robust regression, namely, the Beaton–Tukey formulation [32], implemented by MATLAB's robustfit command (with default parameters). This gives a weighted trained estimator ℒ′_W as computed in the apply phase below.

In our modeling of estimation error above, one or more features in training may introduce too much variance (systematic error) or dependence (model error). We would like our model to have an extensible and adaptive structure, where any number of features may be used, and proceed with confidence, knowing that noisy or dependent features will have a contribution to the estimate that shrinks to zero. In shrink mode, the application applies the James–Stein shrinkage algorithm [33] to the correction coefficients a⃗ without applying the resulting backbone contour length estimator to test data—the task of apply mode.

When the application is in apply mode, the model correction coefficients are locked—they are unadjusted from training—and are loaded from disk. Then, each b⃗ obtains its final estimate, ℒ′ ∈ {ℒ′_T, ℒ′_W}, from the correction function, C(b⃗) = a₁n_horz(b⃗) + a₂n_vert(b⃗) + a₃n_diag(b⃗) + a₄n_perp(b⃗) + a₅n_htcv(b⃗) + a₆n_tkcv (b⃗), and is given by ℒ′(b⃗) = L_CS(b⃗) + C(b⃗).

We presently discuss the experimental results of our model's performance, and related factors, on a large set of training and test images.

III. Experiments and Results

A prototype version of AFM Explorer reported L_LS for all existing fragments in the image. Comparing these preliminary, automatically computed values with the length estimates of hand-drawn backbones (Supplementary Fig. 2) gave us reason to believe that while an image processing pipeline can bring us close to the apparent length of DNAs and RNAs, more would be required. Namely, bridging the gap between apparent and true length would first require using a better length estimator (e.g., L_CS), and then from that modeling the systematic error intrinsic to the problem.

A. Experiments

Our experiments used four datasets, summarized in Table I. They consist of the following.

Table I. Training and Test Data Sets Used in Experiments.

Data Set	Images	Fragments	τ (nm) (bp)
Train	17	1,865	74.9	139.6	223.0	351.8	453.1	583.8
			227.0	423.0	675.8	1066.1	1373.0	1769.1
Test A	20	3,415	33.0	66.0	99.0	132.0	165.0	170.6	198.0	231.0	264.0	297.0	330.0	396.0	500.6
			100.0	200.0	300.0	400.0	500.0	517.0	600.0	700.0	800.0	900.0	1000.0	1200.0	1517.0
Test B	9	646	135.3	258.7	492.4
			410.0	783.9	1492.1
Test C	14	1,292	265.0	299.0	475.6	588.1
			803.0	906.1	1441.2	1782.1

Each data set's label, number of images, number of admissible fragments and theoretical lengths of fragments τ is given, both in nanometers (upper row) and in base pairs (lower row).

1. Train data: 17 images comprising a set of 1865 cDNA fragments having known theoretical lengths {74.9, 139.6, 223.0, 351.8, 453.1, 583.8 } nm.

2. Test A data: 20 images comprising a set of 3415 cDNA fragments having unknown theoretical lengths {33.0, 66.0, 99.0, 132.0, 165.0, 170.6, 198.0, 231.0, 264.0, 297.0, 330.0, 396.0, 500.6} nm.

3. Test B data: 9 images comprising a set of 646 cDNA fragments having unknown theoretical lengths {135.3, 258.7, 492.4} nm.

4. Test C data: 14 images comprising a set of 1292 cDNA fragments having unknown theoretical lengths {265.0, 299.0, 444.2, 588.1 } nm.

Note that “known” fragment lengths were provided to the length estimation algorithm for training the linear estimator; these were provided exactly as the set given earlier, not as molecular labels (i.e., so the algorithm would know the L_CS values would be comprised of a mixture of six distributions centered at those six values). The algorithm was blind to “unknown” fragment lengths (known to the experimenter) for testing. Let us reiterate that unlike our preliminary experiment illustrated in Supplementary Fig. 2, these experiments used unlabeled data. That is, none of the molecules in the train or test data were labeled with their respective theoretical lengths.

Upon acquiring L_CS and the six-feature vector n⃗ for each of the 1865 Train backbones, we trained our linear regression model by solving for the six feature correction coefficients a⃗. We created a histogram of the cubic spline L_CS values for the training data (Supplementary Fig. 3).

B. Results

The cubic spline L_CS and estimated length after weighted training ℒ′_W results for Test A, Test B, and Test C are summarized in Table II. In all AFM data, after image processing, there are a large number of short noisy objects. The noise is a combination of electronic and vibration signal noise in the AFM system (very low in our experimental system), and real particles or small bumps on the surface generated by the sample preparation (present in our experimental system)—in general, these are never as long as even the smallest DNA molecules which we are interested in measuring.

Table II. Experimental Results.

	Length (nm)			Error (nm)		Length (bp)			Error (bp)		Error (%)
Test	LCS	${ℒ}_W^{\prime }$	τ	LCS	${ℒ}_W^{\prime }$	LCS	${ℒ}_W^{\prime }$	τ	LCS	${ℒ}_W^{\prime }$	LCS	${ℒ}_W^{\prime }$
A	68.87	67.69	66.00	2.87	1.69	208.70	205.12	200.00	8.70	5.12	4.35	2.56
A	102.67	101.19	99.00	3.67	2.19	311.12	306.64	300.00	11.12	6.64	3.71	2.21
A	137.87	135.09	132.00	5.87	3.09	417.79	409.36	400.00	17.79	9.36	4.45	2.34
A	174.47	171.59	167.80	6.67	3.79	528.70	519.97	508.48	20.21	11.48	3.98	2.26
A	239.27	238.49	231.00	8.27	7.49	725.06	722.70	700.00	25.06	22.70	3.58	3.24
A	274.77	271.19	264.00	10.77	7.19	832.64	821.79	800.00	32.64	21.79	4.08	2.72
A	305.27	299.79	297.00	8.27	2.79	925.06	908.45	900.00	25.06	8.45	2.79	0.94
A	341.57	333.29	330.00	11.57	3.29	1035.06	1009.97	1000.00	35.06	9.97	3.51	1.00
B	140.70	138.79	135.30	5.40	3.49	426.36	420.58	410.00	16.36	10.58	3.99	2.58
B	269.00	262.69	258.70	10.30	3.99	815.15	796.03	783.94	31.21	12.09	3.98	1.54
B	509.70	493.79	492.40	17.30	1.39	1544.55	1496.33	1492.12	52.42	4.21	3.51	0.28
C	271.74	265.75	265.00	6.74	0.75	823.45	805.30	803.03	20.42	2.27	2.54	0.28
C	310.44	301.65	299.00	11.44	2.65	940.73	914.09	906.06	34.67	8.03	3.83	0.89
C	489.44	469.95	475.60	13.84	5.65	1483.15	1424.09	1441.21	41.94	17.12	2.91	1.19
C	606.64	590.65	588.10	18.54	2.55	1838.30	1789.85	1782.12	56.18	7.73	3.15	0.43

Rows are divided into three groups, corresponding to Tests A, B, and C, indicated by the first column. Columns are then divided into five groups, corresponding to lengths measured in nanometers (cubic spline length L_CS, estimated length after weighted training ${ℒ}_W^{\prime }$, and theoretical length τ), errors measured in nanometers (|τ – L_CS| and $|\tau -{ℒ}_W^{\prime }|$, respectively), lengths measured in base pairs (cubic spline length L_CS, estimated length after weighted training ${ℒ}_W^{\prime }$, and theoretical length τ), errors measured in base pairs (|τ − L_CS| and $|\tau -{ℒ}_W^{\prime }|$, respectively), and errors measured in the percentage of corresponding theoretical fragment length ( $\frac{|\tau -L_{\text{CS}}|}{\tau }$. 100 and $\frac{|\tau -{ℒ}_W^{\prime }|}{\tau }$. 100, respectively). Results from the “Length (nm)” columns are plotted in Supplementary Fig. 7. Results from the “Error (%)” columns are plotted in Supplementary Fig. 8.

For each Test A, B, and C, we created two histograms, corresponding to algorithmic output of L_CS and ${ℒ}_W^{\prime }$ (Supplementary Figs. 4–6, respectively). We applied a smooth function fit of the histogram data, using MATLAB's ksdensity function with kernel width 5, to obtain a set of peaks. The locations of these peaks give our estimation of the theoretical fragment lengths in each test Images were processed using the 0.97 $\frac{\text{nm}}{\text{pixel}}$ conversion factor.

Measured (L_CS and ${ℒ}_W^{\prime }$) versus theoretical lengths for the 15 distinct cDNA fragment lengths in Tests A, B, and C are shown in Supplementary Fig. 7. Their respective percentage errors ( $\frac{|\tau -L_{\text{CS}}|}{\tau }$. 100 and $\frac{|\tau -{ℒ}_W^{\prime }|}{\tau }$. 100, given in Table II) are shown in Supplementary Fig. 8.

We would like to highlight some of our observations and decisions regarding our experiments and error analyses.

1. Test A, τ = {198.0} nm: No peak was detected using our chosen smoothing settings; thus, it is a false negative and we did not report this error in Table II.

2. Test A, τ = {165.0, 170.6{ nm: The peak finding detected only one of the two peaks because these were so close together; thus, we used their arithmetic mean (μ = 167.8 nm) as the “known” theoretical value for the sake of reporting the corresponding errors in Table II.

3. Test A, τ = {396.0, 500.6} nm: The abundances of these two species are too low to be meaningful; thus, we did not report these errors in Table II. This is an inherent property of the sample, not our experimental method: Test A is a 100 bp sizing ladder used for size standards in gel electrophoresis; by design the shorter species have higher abundance, not an artifact of sample preparation or data processing.

4. Test C, τ = {444.2} nm: Peaks were detected at L_CS = 489.44 and ${ℒ}_W^{\prime }=469.95$, giving respective errors of: 45.24 and 25.75 nm (10.19% and 5.80%)—obvious outlier errors. Since the original sequence provided for the plasmid by the vendor did not reconcile with our measurements, we decided to investigate further. It turns out that the plasmid we used had a modification that was not documented; thus, the detected peaks represented a true unknown. This can happen in cases where the plasmid is obtained from a large collection (as ours was) and the vendor's quality control is not 100% effective. We obtained the sequence of the plasmid ourselves and discovered the correct theoretical length is 475.60 nm instead of 444.20 nm. The corrected theoretical length is reported in Table I, and the corrected error values are reported in Table II and Supplementary Figs. 7 and 8.

5. Test C: We observed a large number of objects measured for 200 nm and shorter. These are not real molecules measured incorrectly but are rather upstream image processing artifacts from the background thresholding step. (While we could improve this thresholding in theory, we feel it is not central to the thrust of this paper or the feature-based error correction we are investigating.) The large number of these short, noisy artifacts give all of our Test C distributions (for L_LS, L_CS, and ${ℒ}_W^{\prime }$) a heavy left tail. We want to make it clear that the errors we report are estimates of systematic error and are not affected by the artifacts.

Moreover, we do not estimate and report dispersion in our length measurements in the test data. If we wanted to drive this down, we could simply increase the sample size N, and the standard deviation would decrease proportionally to $\frac{1}{\sqrt{N}}$. Instead, we calculate bias in our L_CS and ${ℒ}_W^{\prime }$ length estimators, which is a systematic error that persists across sample sizes. Hence, for each theoretical length (for each type of molecule we know is in the test set), we compute L_CS and ${ℒ}_W^{\prime }$ errors (estimator bias) as described earlier: the distance between the theoretical length and the closest detected peak in the smooth function fit over the distribution of length measurements.

IV. Discussion

In the problem described in this paper, there are two principal sources of error: bias from the method of estimation (the extrinsic factors), and systematic error (the intrinsic factors) that come from chemistry experimental error, and AFM operation and measurement error. We have given a BLUE estimator for molecular backbone contour length, namely, the piecewise cubic spline fitting measure L_CS But, this estimator gets us only part way to the answer, since systematic error underlies all such measurements. We improved on L_CS by training a linear regression model to estimate the systematic error and thereby correct L_CS, yielding a superior estimator ${ℒ}_T^{\prime }$. By weighting the linear regression training based on computed Beaton–Tukey biweights, we created another estimator ${ℒ}_W^{\prime }$ that further improves performance. These estimators were trained on the aforementioned six features. James–Stein shrinkage analysis gave almost undetectable improvement, suggesting the six features were neither noisy nor dependent (Supplementary Table I). One consequence of such a design is an inherent adaptability and extensibility: a researcher may compose any number and arrangement of features into the estimation. We believe our approach will help ameliorate the model selection problem in this context.

A. Comparison With Other Studies

In the following discussion, we define: the known theoretical length of a given molecular fragment to be τ; the best reported length estimator in a given study to be ℒ; the error in nm for a given measurement with respect to a given τ to be |τ − ℒ | and the error percentage for the given measurement with respect to given to τ to be $\frac{|\tau -ℒ|}{\tau }$. 100.

Among the automated methods studied, Fang et al. [12] have published the most comprehensive work on this issue to date, where they achieved an error percentage in the range [1.67, 10.67]% for 13 distinct theoretical lengths of fragments in the length range [30.00, 750.00] nm. Sanchez-Sevilla et al. [14] reported error percentage in the range [0.56, 1.46]% for two distinct theoretical lengths of fragments in the length range [206.00, 355.00] nm. More impressively, Ficarra et al. [18] described a method that achieved better sizing, reporting error percentage in the range [0.31, 1.18]% for two distinct theoretical lengths of fragments in the length range [633.40, 1098.00]. We report error percentage in the range [0.28, 3.24] % for 15 distinct theoretical lengths of fragments in the length range [66.00, 588.10] nm. We present all comparative results in Supplementary Table II and Supplementary Fig. 9, where for our study we define ℒ to be ${ℒ}_W^{\prime }$.

We should note the trends that are evident in Supplementary Fig. 9. Viewed as a function of fragment length, error percentage: increases for Fang, et al. [12] inside a wide dispersion of N = 16 data points; decreases for Sanchez-Sevilla et al. [14] inside a dispersion of N = 2 data points; increases for Ficarra, et al. [18] inside a dispersion of N = 3 data points; and decreases for our results inside a narrow dispersion of N = 15 data points. Our trend gives us reason to believe that our estimation method would yield accurate (< 1 error percentage) length measurements for molecular fragments larger than 600 nm. While our results do not strictly speaking outperform those reported by Sanchez-Sevilla et al. [14] and Ficarra et al. [18], we believe our results achieve nearly the same length measurement accuracy through a novel supervisory learning approach that benefits from empirical-Bayesian statistical insights. We should also note that we (and Fang et al. [12]) tested our approach more comprehensively than did Sanchez-Sevilla et al. [14] and Ficarra et al. [18] (i.e., more fragments, wider range of sizes, etc.)

The other studies we found took the image processing aspect of the problem to the limit. The approach taken by Ficarra et al. [18] is a good example. These studies also use simple length correction methods to address the errors that pixel quantization imposes upon the smooth and continuous molecular backbone contours whose lengths are to be estimated. Regarding systematic error estimation, all these studies use an image processing step to thin 2-D objects into 1-D eight-connected pixel paths, and some approaches reclaim pixels at the ends, while others argue that this is unfounded. This is as far as they go to address the tip convolution problem, discussed below; they assume the dilation effects are symmetric and uniform, while this may not be the case. And none of these studies address the problem of thermal drift, discussed in the “Unique Aspects of AFM” section of the Supplementary Materials.

We give a meta-approach to the problem of backbone contour length estimation that learns to characterize the systematic error from the data, namely, image features whose values depend on the lengths of backbone contours. In our current AFM system, thermal drift is negligible over the time scale for one molecule to be imaged (a few seconds).

One may use such an approach to address the extended problem of distinguishing DNA fragments using length estimation. While fragment distinction is beyond the scope of this paper, we analyze the feasibility of using a coding scheme to do this in [8] and we make this the center of our discussion in [34].

V. Summary and Conclusion

The approach developed in this paper builds upon the concept of “supervised learning,” a widely used methodology in machine learning with applications to systems biology and internet tools. In this methodology, a supervisor trains a machine learning algorithm to select a model by looking for significant features from large corpora of correct examples. In this way, we attempt to learn various subtle features in the data and how these features are related to systematic error; these models are then used to rectify the systematic errors. However, if the supervisor is imperfect, and allows some number of false positive examples, then these outliers can confound the machine learning algorithm, as it attempts to compensate for the presumed systematic errors even when there is no relationship between the perceived errors in these false positive examples and the extracted features. The resulting process would then lead to an undesirable bias in the statistical estimation. The solution to these problems would require either manual marking of the correct examples or some form of outlier detection and robust estimation process. Our approach involves a weighted scheme, in which a weight is assigned to each training example, and corresponds to the probability that the putative training example belongs to a particular theoretical length. We built an empirical method for assigning weight around the Beaton–Tukey biweighting algorithm. In this scheme, the statistical estimator algorithm was suitably modified to minimize a weighted sum-of-square error. Afterward, James–Stein shrinkage provides a means of constraining the universe of features to retain those that informatively describe molecular backbone length correction.

Biographies

Andrew Sundstrom (M'97) received the B.A. degree in computer science from Cornell University, Ithaca, NY, in 1993, and the M.S. degree in computer science from the Courant Institute of Mathematical Sciences, New York University, New York, NY, in 2008, where he is currently working toward the Ph.D. degree in computational biology, being co-advised by Prof. Bud Mishra (Courant Institute of Mathematical Sciences) and Prof. Dafna Bar-Sagi (NYU Langone Medical Center).

While pursuing graduate studies, he was a Scientific Informatics Developer at Cold Spring Harbor Laboratory in 2009 and a Research Scientist at the Courant Institute of Mathematical Sciences, from 2007 to 2008. Prior to this, he was an Associate at Morgan Stanley from 1998 to 2007, a Research Associate at the IBM Thomas J. Watson Research Center from 1996 to 1998, a Member of Scientific Staff at Nortel Networks from 1994 to 1996, and a Member of Research Staff at Prime Factors, Inc. in 1992. His research interests include using single-molecule approaches to characterize dynamic cellular processes, and using computational approaches to model evolutionary, developmental, and cancer biology.

Mr. Sundstrom is a member of the ACM, AAAS, and NYAS.

Silvio Cirrone was born in Catania, Italy, in 1985. He received the B.S. and M.S. degrees in computer science engineering from the University of Catania, Catania, Italy, in 2007 and 2010, respectively.

In 2006, he was a Production Operator at the ST Microelectronics, Catania, Italy. In 2007, he was a Resarcher at the Courant Institute of Mathematical Sciences, New York University. In 2009, he was a Resarcher at the Innovation and Design Technology Department, Malardalen University, Vasteras, Sweden. In 2010, he moved to the Accenture Technology Consulting in Turin, Italy, where he is currently a Consultant working in FIAT projects for automotive.

Salvatore Paxia was born in Catania, Italy, in 1969. He received the M.S. degree in electrical engineering from the University of Catania, Catania, Italy, in 1993, and the Ph.D. degree in computer science from the Courant Institute of Mathematical Sciences, New York University, New York, NY, in 2003.

From 1999 to 2003, he was a Research Scientist at the New York University Center for Advanced Technology, and from 2003 to 2008, he was a Senior Research Scientist in the Bioinformatics Group, Courant Institute of Mathematical Sciences. In 2008, he moved to the Blackstone Group in New York, NY, where he is currently a Managing Director in the Hedge Funds Solutions Group.

Carlin Hsueh, photograph and biography not available at the time of publication.

Rachel Kjolby, photograph and biography not available at the time of publication.

James K. Gimzewski, photograph and biography not available at the time of publication.

Jason Reed, photograph and biography not available at the time of publication.

Bud Mishra (M'93–SM'98–F'09) received an ISc degree from Utkal University, Bhubaneswar, Orissa, India, in 1975, and a B.Tech. degree in electronics and communication engineering from the Indian Institute of Technology Kharagpur, Kharagpur, India, in 1980, and the M.S. and Ph.D. degrees in computer science from Carnegie-Mellon University, Pittsburgh, PA, from 1983 to 1985.

He is currently a Professor of computer science and mathematics at New York University (NYU) Courant Institute of Mathematical Sciences and a Professor of cell biology at NYU School of Medicine, in New York, NY. He founded the NYU/Courant Bioinformatics Group, a multidisciplinary group working on research at the interface of computer science, applied mathematics, biology, biomedicine and bio/nanotechnologies. From 2001 to 2004, he was a Professor at the Watson School of Biological Sciences, Cold Spring Harbor Lab, Long Island, NY; currently he is a QB visiting scholar at Cold Spring Harbor Lab. He is an author of a textbook on algorithmic algebra and more than two hundred archived publications. He also holds Adjunct Professorship at the Tata Institute of Fundamental Research, Mumbai, India.

Dr. Mishra is a Fellow of ACM and AAAS, a Distinguished Alumnus of IIT-Kharagpur, and an NYSTAR Distinguished Professor.