Abstract
We directly measure the dynamics of the HIV trans-activation response (TAR)–DNA hairpin with multiple loops using single-molecule Förster resonance energy transfer (smFRET) methods. Multiple FRET states are identified that correspond to intermediate melting states of the hairpin. The stability of each intermediate state is calculated from the smFRET data. The results indicate that hairpin unfolding obeys a “fraying and peeling” mechanism, and evidence for the collapse of the ends of the hairpin during folding is observed. These results suggest a possible biological function for hairpin loops serving as additional fraying centers to increase unfolding rates in otherwise stable systems. The experimental and analytical approaches developed in this article provide useful tools for studying the mechanism of multistate DNA hairpin dynamics and of other general systems with multiple parallel pathways of chemical reactions.
Introduction
The melting and annealing of DNA hairpins are essential in many biological processes such as replication, transcription, recombination, gene expression, and DNA transposition for both prokaryotic and eukaryotic systems.1,2 Furthermore, hairpins with multiple loops are known to play specific roles in viral replication.3 An important example is the human immunodeficiency virus-1 (HIV-1) trans-activation response region (TAR) hairpin.1,4 The TAR sequence is remarkably well conserved among HIV isolates, indicating a strong selection pressure to maintain its structure.5 Thus, the TAR hairpin is of therapeutic interest.6−9 The TAR–RNA hairpin and its complement, TAR–DNA hairpin, are involved in several crucial steps in the viral life cycle.10−12 The TAR hairpin has four bulges, which have been found to be critical to the biological function of the TAR sequence because they determine the hairpin unfolding/folding dynamics.5,13−15 As a general topic, understanding hairpin dynamics is further motivated by the advent of therapeutics with aptamers, which are small RNA and DNA molecules that often form single or multiloop hairpin conformations.16,17
In order to understand the molecular-scale dynamics of DNA/RNA hairpins, hairpins have been studied using technologies such as temperature-jump,18,19 optical trap,20 single-molecule fluorescence resonance energy transfer (smFRET),21−26 and combinations of spectroscopic techniques.2,27−31 However, these hairpin structures usually have one single loop connecting a stem region of several base pairs (Figure 1a). It is generally understood that the unfolding/folding rates of such simple DNA hairpins are dependent on the binding energy of the hairpin, the diffusion rate of the two ends of the stem followed by nucleation, and the propagation of base pairing.30,32−35 This process yields folding times that range from milliseconds to microseconds, depending on the sequence length and base composition.22,27 smFRET is particularly suited to this study due to its wide applications in studying the single-molecule dynamics of nucleic acids.36−38
Figure 1.
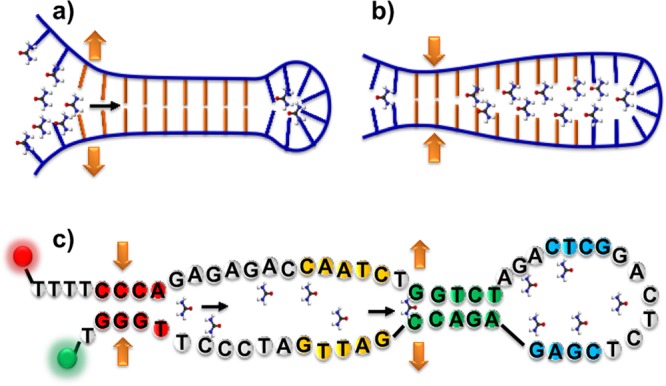
Schematic of proposed examples of unfolding/folding routes of (a, b) model DNA hairpins and (c) the TAR–DNA hairpin with two dyes Cy3 and Cy5 labeled to the ends. Urea molecules within the solution are shown, and the double helix is not shown for easier demonstration.
For DNA melting (unfolding), a “fraying and peeling mechanism” has been predicted,39,40 and for annealing (folding) a “collapsing mechanism” has been proposed.41 Molecular dynamics simulations of the unfolding of short double-stranded DNA have suggested that DNA is opened via untwisting and then peeling.39 This rapid “fraying” at the end of the helix has been experimentally observed for simple model DNA molecules.42 This mechanism suggests that the unfolding of the DNA helix starts from one end of the stem and progresses dynamically to the other end of the DNA, similar to unzipping a zipper (Figure 1a). During the folding process of DNA hairpins, end-to-end contact (collapse) has been observed using temperature-jump measurements.41 This mechanism suggests that the unfolded DNA stalks are extremely flexible and end to end closing is common (Figure 1b).35 This flexibility is consistent with the molecular dynamics simulations where multiple intermediate states and trap states have been observed.39 It remains an open question as to whether the general conclusions discussed above can be extended to describe the dynamics of more complex biologically relevant DNA hairpins that include loops and bulges.
We hypothesize that a possible biological function for a hairpin loop/bulge is to serve as an additional fraying center to increase unfolding rates in otherwise stable systems. This has been explained thermodynamically using a free energy penalty in hairpin pairing, and the effect of the bulges on folding/unfolding dynamics of the hairpin has been predicted.43 However, it has been difficult to experimentally measure the stability of intermediate states for complicated structures because of the coexistence of multiple states. In this article, we carried out single-molecule FRET experiments to study the complex dynamics of HIV TAR–DNA hairpin. In order to tune the lifetime of the TAR–DNA folding/unfolding dynamics to our measuring time scale, we introduced two additives, urea and poly(ethylene glycol) (PEG), to the buffer solution. After the smFRET data were obtained, we performed a state analysis algorithm and derived a statistical analysis model to calculate the stabilities of the intermediate states.
Experimental Section
Sample Preparation
Purified and labeled single-stranded DNA (ssDNA) TAR and a mutant with the bulges removed (Figure 2) were acquired from TriLink Biotechnologies. The ssDNAs were modified with functional groups: biotin was used for surface immobilization; Cy3-amidite was directly coupled to the 5′ end and Cy5-succinimidyl ester was coupled to a C6 amino linker at the 3′ end of the DNA; dT spacers were designed at the end of the sequences to reduce unwanted photophysical effects. The ssDNAs were immobilized on glass substrates using the biotin–streptavidin interaction. Briefly, plasma cleaned glass coverslips were functionalized with aminosilane (Vectabond,Vector Laboratories). The slides were then grafted in a aqueous solution of 25% (m/m, mass fraction) methoxypoly(ethylene glycol) 5000 propionic acid N-succinimidyl ester (>80%, Sigma-Aldrich), 0.25% (m/m) SUNBRIGHT BI-050TS (Biotin-PEG-COO-MAL, Mw 5000, NOF Corporation, Japan), and 0.8% (m/m) NaHCO3 (Sigma-Aldrich). Custom HybriWell chambers (Grace Bio-Labs) which had a volume of ∼15 μL, secure seal spacers (Grace Bio-Labs), tube connectors (Grace Bio-Labs), and Teflon tubing (Western Analytical Products) were used to construct a flow chamber that was attached to each biotin-PEGylated slide.44 The biotin-PEGylated slide was incubated with 2 mg mL–1 streptavidin (Invitrogen) in 25 mM HEPES (Sigma-Aldrich) and 40 mM NaCl (Sigma) buffer solution for 10 min followed by DNA (200 pM) adsorption for 20 min. Before the DNAs were attached to the streptavidin-labeled substrates, the DNA samples were denatured at 80 °C in buffer solution for 2.5 min and annealed at 60 °C for 2.5 min, and then 2 mM MgCl2 (Ambion) was added and the solution was reannealed at 0 °C for 5 min to homogenize the samples.
Figure 2.
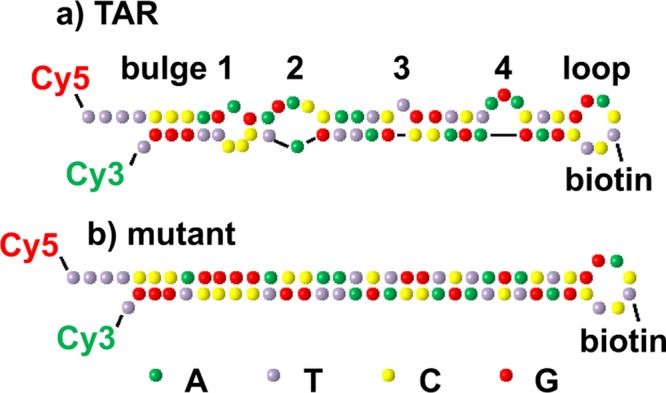
Structures of the DNA hairpins used in the smFRET studies. Predicted secondary structure of the (a) TAR–DNA with four bulges and a loop and (b) TAR–DNA mutant with the bulges removed. Cy3 and Cy5 were used as the donor and acceptor dye molecules which were coupled to the 5′-dT and 3′-dT of the DNA, respectively. The DNAs were attached to the surface via a biotin linker attached to a -dT in the hairpin loop region.
FRET Measurements
Single-molecule images were acquired by a home-built sample scanning confocal microscope based on a Zeiss Axiovert 200 microscope. Raster scanning of the sample coverslip was achieved by a closed-loop xyz piezo stage (P-517.3CL; Physik Instrumente) with 100 × 100 × 20 μm travel range and a minimum resolution of ∼1 nm (SPM 1000; RHK Technology). A 532 nm diode-pumped solid-state laser (Coherent, Compass 315M-100 SL) was used as the excitation source. The light was expanded to overfill the back aperture of a Fluar 100× 1.3 NA oil immersion microscope objective lens (Carl Zeiss, GmbH) which focused the laser light to a spot with a full width at half-maximum (fwhm) beam radius and height of ∼125 nm and ∼1 μm, respectively. The intensity of the laser was controlled with a neutral density filter to be ∼4 μW before the objective, yielding an estimated total power density at the sample of ∼800 W cm–2. The fluorescence signal was collected and refocused by the same objective and was separated from the excitation light using a dichroic mirror (z532rdc; Chroma Technology). Scattered laser light was removed by the use of notch and emission long-pass filters (NHPF-532.0, Kaiser Optical; ET585 and ET685, Chroma Technology). The refocused signal was then further separated by a beam splitter (Chroma 640 DCXR) into donor emission and acceptor emission fluorescence and then finally directed to two avalanche photodiodes detectors (SPCM-AQR-15; PerkinElmer).
The smFRET experiments were carried out at room temperature (20 ± 1 °C). Into the flow cell, a buffer solution was flowed at 1 μL min–1 for the duration of the measurements. The HEPES buffer solution containing an oxygen-scavenging system to extend the lifetime of the fluorophores was used in all experiments, and was prepared according to an established protocol:45 3% (w/w) β-d-(+)-glucose (Sigma-Aldrich), 0.1 mg mL–1 of glucose oxidase (Sigma), 0.02 mg mL–1 of catalase (Sigma-Aldrich), 40 mM NaCl, 25 mM HEPES buffer, and saturated Trolox solution (6-hydroxy-2,5,7,8-tetramethylchroman-2-carboxylic acid; Sigma-Aldrich). In addition, cosolute 2 mM MgCl2, urea (Sigma-Aldrich) and/or PEG-6000 (Sigma-Aldrich) were added to the solution from stock solutions of 10 M urea and 60% PEG respectively when needed.
SmFRET Analysis
All analysis programs were written in MATLAB (R2009b) except for the hidden-Markov models (HMMs) analysis methods for FRET efficiency trajectories, which were provided by the HaMMy GUI (http://bio.physics.uiuc.edu/HaMMy.html, accessed 09/2013)46 and vbFRET (http://vbfret.sourceforge.net, accessed 09/2013).47 The emission intensity trajectories were collected at 1 ms resolution and later binned to 10 ms time steps to improve signal-to-noise ratio. The corrected fluorescence signal trajectories were used directly to calculate the FRET efficiency (EFRET), as the fraction of the fluorescence signal of the acceptor dye over the total signal of acceptor dye and the donor dye:17,48,49
| 1 |
where Iacceptor and Idonor correspond respectively to Cy5 and Cy3 fluorescence intensity with background and crosstalk correction and blinking removed.17,48,49 The fitting processes and algorithms can be found in the original literature.46−52 Briefly, trajectories of all the molecules are combined into a single data file without further modification, and then the file is fed to the two software packages for fitting. During the fitting, the number of states is varied and the other fitting parameters are kept at the software defaults.
Simulation of Wormlike Chain (WLC) Model
The average FRET efficiency, ⟨E⟩, within any long-enough bin time is calculated with WLC:53,54
| 2 |
where r is a unitless value representing the end-to-end distance R over the maximum possible distance L of the ends-labeled polymer; R0 is the constant Förster radius; and p(r) is the probability factor:
| 3 |
where A is a normalization constant:
| 4 |
and t is related to another constant called persistence length Lp, a basic mechanical property quantifying the stiffness of a polymer: t = L/Lp.
The established WLC model can be applied to our smFRET data of TAR–DNA. The maximum possible length of the ssDNA L = 0.63N nm, where N is the number of unpaired nucleotides (nt) between the two ends with 0.63 nm/nt length.53 The Förster radius R0 for Cy3–Cy5 dye has been measured to be ∼6 nm when attached to DNA.53,55 The persistence length of TAR–DNA in urea is estimated from comparing the histogram of smFRET data and simulated FRET values.
The smFRET values are simulated with Metropolis Monte Carlo simulations of the time trajectory of the end-to-end distance R.53,56 In every time step (10 ps), R is allowed to randomly walk between 0 and L with a Gaussian distributed distance step centered at 0.55 nm and a standard deviation 0.2 nm according to the above probability function (representing a 1D diffusion coefficient of ∼1.5 × 10–4 cm2 s–1 = (0.55 nm)2/2/0.01 ns).53 At each step, the donor will be excited at a probability of 1/5 ns–1, ∼5 times slower than its fluorescence decay rate. If the donor is excited, then it has a decay lifetime of τD ∼ 1 ns into donor fluorescence or (R/R0)6τD into a nonexcited acceptor molecule. If the acceptor is excited, it has a fluorescence decay lifetime 1.3 ns as measured (1.3 ± 0.1 ns, see Supporting Information). The total simulation time for each number of nucleotide is 1 ms. The FRET efficiency is the fraction of the number of steps of acceptor emission over sum of the steps of acceptor emission and donor emission.
Results and Discussion
Photophysics of the Dye Molecules
Blinking and bleaching of the dyes, as well as the dye–DNA interaction, were confirmed to have little influence on our smFRET measurements of the hairpin dynamics. We labeled the two ends of the DNA hairpin with Cy3 and Cy5 and immobilized the hairpin on PEGylated glass slides via biotin–streptavidin interaction, as shown in Figure 2. One potential issue with smFRET experiments is that the photophysical stability of the dyes can change depending on the solution as well as the dye–DNA interaction. These conditions can affect the quantum yields of the dyes and thus affect the FRET efficiency between the donor dye and the acceptor dye.57 When covalently attached to DNA, cyanine dyes are well-known to bend and attach to DNA basepairs with hydrophobic interactions, varying the dyes’ quantum yields via conformational confinement and charge transfer.58 The average quantum yields of the dyes are dependent on the DNA sequences they are attached to;57,59,60 however, the variation of single-dye quantum yield is not observed during our smFRET measurement, probably because the above-mentioned dynamics are too fast to be observed on the time scale of milliseconds to seconds common for single-molecule measurements. As each of our smFRET data points is calculated from the total photon counts of the two dyes during 10 ms, the variations at shorter time scale are time-averaged. Stable photon counts with shot noise were observed for the smFRET time trajectory of the bulge-removed mutant DNA hairpin in HEPES buffer solution (Figure 3a), for which no unfolding dynamics are expected at room temperature and a stable FRET value is expected. This stability of photon counts (representing the quantum yield) confirms that any dye–DNA interactions are (1) minimal and (2) faster than the dynamics measured in our experiments. The single-step bleaching profile confirms that we are measuring single-molecule events. The stability of the dyes are also observed in the presence of different cosolutes (Figure 3b–d), which is consistent with the unchanged lifetimes of the dyes under the different solutions (see Supporting Information for time-resolved fluorescence data). This stability of smFRET at the millisecond time scale is consistent with other smFRET studies of DNA hairpins labeled with the same two dyes.53,61,62
Figure 3.
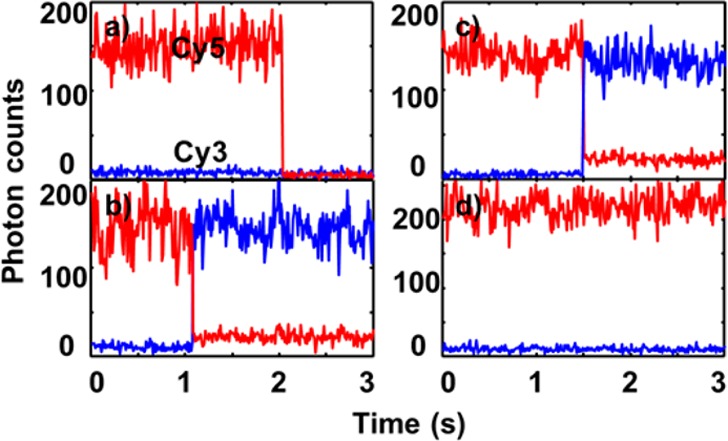
Representative photon trajectories show stable photon counts of Cy3 and Cy5 attached to the ends of mutant DNA hairpin in (a) HEPES buffer with 2 mM Mg2+, (b) HEPES buffer with 2 mM Mg2+ and 24% PEG, (c) HEPES buffer with 2 mM Mg2+ and 6 M urea, and (d) HEPES buffer with 6 M urea (full trajectory shown in the Supporting Information). These are raw data for typical molecules binned at 10 ms with bleaching of either dye shown as the transition point of the signals. The FRET histograms of over 50 molecules/each are shown in Figure 4a–d, respectively.
Tuning the Folding/Unfolding Lifetime
Two challenges arise when measuring the dynamics of the TAR–DNA hairpins: the equilibrium lies strongly toward the folded state of the hairpin, and some of the kinetic processes are too fast to be observed by our millisecond time resolution. On the basis of the dynamics established from model hairpins,22,27 we calculate that the folded-state and unfolded-state lifetimes of the states of TAR–DNA hairpin are at ∼1 ms and ∼10 μs, respectively (see Supporting Information). These values indicate that, at equilibrium, the TAR–DNA hairpin effectively remains folded at room temperature, with brief explorations of the unfolded state that are too fast to be resolved with typical smFRET experiments carried out at the 1–100 ms time scale. Therefore, our ability to characterize even two-state folding kinetics of the hairpin is limited by the fast folding rate (or unstable unfolded state). In the retroviral replication process, the unfolding/folding dynamics are altered by the nucleocapsid (NC) protein,63,64 which destabilizes the two break points near the open end of the TAR hairpin and allows for the characterization of the protein-induced hairpin unfolding/folding dynamics of the outermost bulge by smFRET, which has a minimum time resolution at ∼1 ms level.45,62,64−66 In order to understand the mechanism of multiloop hairpin unfolding/folding dynamics, alternative methods were pursued to shift the equilibrium toward the unfolded states and to slow down the dynamics to our experimental time resolution.
To this effect, we introduced two additives, poly(ethylene glycol) (PEG) and urea, to the buffer solution. It is well-known that crowding agents such as PEG, sucrose, and glycerol increase the viscosity of aqueous solutions,67−69 and studies have shown that PEG solutes can destabilize DNA at small weight values of PEG70,71 but do not significantly affect the stability of DNA if the PEG is larger than 1 kDa.72,73 Thus, PEG-6000 is used in this study. Urea, a commonly used destabilizer of DNA and proteins, was used to induce helix unfolding and to shift the hairpin folding equilibrium away from the folded state at room temperature.21,24,74 Although a general consensus on the biological relevance of urea as a denaturant has not been reached, there has been recent evidence in support of urea to perturb conformational changes of nucleic acids and proteins.74 This conclusion is consistent with the successful application of urea in studying human telomerase RNA pseudoknot folding/unfolding dynamics using smFRET.24
The smFRET efficiency distribution of the TAR-DNA hairpin is broadened when PEG-6000 is added to the buffer solution (Figure 4f), as the standard deviation increases to 0.12 FRET efficiency compared to 0.02 in HEPES buffer. Under the same conditions, the standard deviation of the bulge-removed mutant only slightly increases to 0.04 (Figure 4b). We confirmed that PEG-6000 has negligible effects on the time-averaged secondary structure of DNA and the dye’s photophysical response using circular dichroism (CD) and fluorescence anisotropy decay measurements for both the standard TAR–DNA and the mutant construct in the presence and absence of PEG (see Supporting Information). Therefore, we consider PEG-6000 a suitable crowding agent to slow down the dynamics of the TAR–DNA and mutant constructs and that the broadening of the smFRET distributions depicted in Figure 4 can be attributed primarily to conformational broadening.
Figure 4.
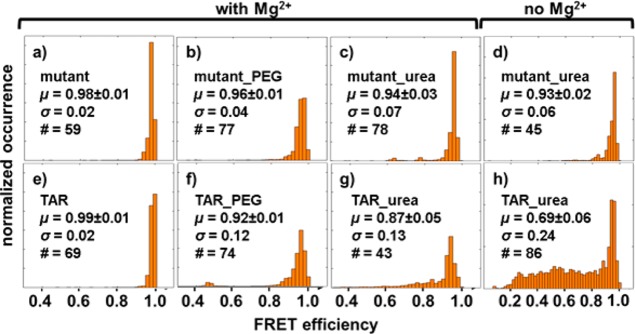
Global ensemble histogram of the mutant and TAR–DNA in (a, e) HEPES buffer with 2 mM Mg2+; (b, f) HEPES buffer with 2 mM Mg2+ and 24% PEG; (c, g) HEPES buffer with 2 mM Mg2+ and 6 M urea; (d, h) HEPES buffer with 6 M urea. The total counts of the histograms are normalized to unity. Insets show the mean FRET efficiency, μ, (error is the standard deviation of three independent measurements) representing the average conformational structure of the DNA; the standard deviation, σ, of the histogram that represents the variation of the FRET distribution and thus the range of conformations; and the number of single molecules measured for each sample, #.
Further analysis of the distribution of the FRET efficiencies of the two DNA hairpins in PEG solution suggests that the unfolding of the hairpins by thermoagitation, known as “fraying”,42 stops after each loop, as long as there are sufficient base pairs between loops to provide a barrier to further unfolding. We compared the distribution of the FRET efficiencies (Figure 4) with previous reported distributions of end-labeled TAR–DNA.45,62,64 The FRET efficiency distribution of TAR–DNA is consistent with the hairpin unfolding to the second bulge from the opening (Figure 2, bulge 2). This is expected because only two base pairs connect bulges 1 and 2 in TAR–DNA, making it the weakest of the bulge connecting sections. This behavior has also been observed previously in the presence of NC proteins.45,62,64
By analyzing the dwell times for transitions between the two observed smFRET states of TAR–DNA with 24% PEG, as identified by HaMMy, we can confirm that the addition of PEG slows down the unfolding/folding dynamics of the TAR–DNA hairpin. The unfolded-state and folded-state lifetimes of the TAR–DNA hairpin are 142 and 353 ms, respectively (Supporting Information Figure S6), and are slower by 3 orders and 1 order of magnitude, respectively, when in the presence of PEG, shifting them well within the resolvable time frame of smFRET observations. Slowing down the fraying dynamics, however, does not allow us access to all of the possible open hairpin states. Thus further perturbation is required to accomplish this goal.
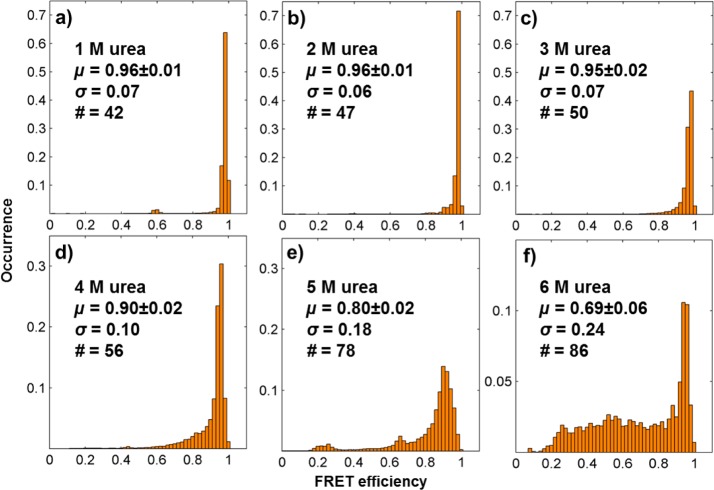
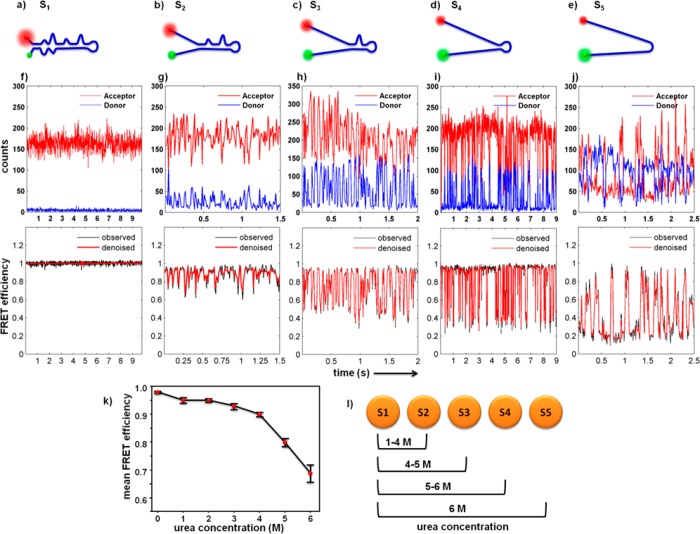
By tuning the concentration of a denaturant, urea, we can shift the TAR–DNA hairpin equilibrium to more opened states to observe each of the distinct loop unfolding/folding transitions. The ensemble smFRET histograms for each condition are included in Figure 5, and short pieces of smFRET trajectories for each condition are shown in Figure 6. The trajectories in Figure 6 shift to more open states as the urea concentration is increased, referred to as S1, S2, S3, S4, and S5. Because fluorescence measurements have suggested that the photophysical properties of the dyes are not changed by the presence of urea (see Supporting Information), the primary explanation for the broadening of the FRET distribution of the FRET efficiencies in Figure 5 is urea-induced hairpin unfolding. Single-molecule time trajectories (Figure 6) suggest that the broadening is due to transitions among newly observable FRET states. In the presence of 1 and 2 M urea, the FRET efficiency distributions of the DNA hairpin (Figure 5a,b) are almost the same as the distributions of those with no urea (Figure 4), and thus only one state is observed in the time trajectories (Figure 6f). When the urea concentration increases to around 3 M, the FRET efficiency distribution (Figure 5c) becomes more broad and tails toward a FRET efficiency value of 0.8, in the direction of the state between 0.6 and 0.8 observed in the single-molecule FRET time trajectories (Figure 6g). More states are observed at successively higher urea concentrations (Figures 5d,e and 6h,i), until, in the presence of 6 M urea (Figures 5f and 6j), all states become observable, including those with FRET efficiencies at ∼0.4 and ∼0.2. Qualitatively, the smFRET data change the ensemble steady-state view of urea denaturation of DNA to a more dynamic picture. The ability of urea to control the equilibrium of the TAR–DNA hairpins is more obvious in the average values of the ensemble FRET efficiency (Figure 6k). Just like the results one would get from ensemble measurements, urea reduces the average FRET values. At the single-molecule level, however, the larger the urea concentration, the longer the dwell times of more opened states (Figure 6l).
Figure 5.
Insets indicate the different concentrations of urea, the mean FRET efficiency (μ), the standard deviation (σ) of the FRET efficiency, and the number of molecules measured (#).
Figure 6.
Proposed structures and smFRET trajectories with their FRET efficiencies showing five different states of TAR–DNA in its folded form S1 (a, f), 0–2 M urea (scheme showing as an example structure of the state); S2 (b, g), 3 M urea; S3 (c, h), 4 M urea; S4 (d, i), 5 M urea; and unfolded hairpin form S5 (e, j), 6 M urea in the absence of Mg2+ (full trajectories shown in the Supporting Information). (k) The mean FRET efficiency as a function of urea concentration represents the denaturing (unfolding) of the DNA. Error bars are standard deviation of three measurements, >20 molecules for each urea concentration at different days for three different samples. Relatively small error bars indicate that the number of molecules is large enough to represent ensemble average. (l) Number of states observed under our specific experimental conditions.
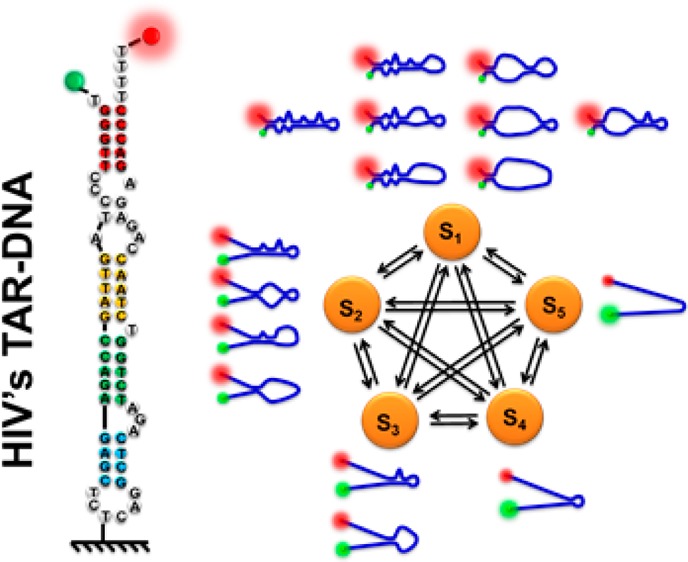
According to Figures 4–6, as well as previous studies on smFRET of TAR–DNA,45,64 we assigned the FRET efficiency 1.0–0.9 to state S1 of TAR–DNA; ∼0.8 to state S2; ∼0.6 to state S3; ∼0.4 to state S4; and 0.3–0.0 to the completely unfolded state S5, all associated with opening through the sequential bulge regions. The assignment is consistent with our hypothesis that a hairpin with four bulges and a loop should yield five resolvable states (Figure 7).
Figure 7.
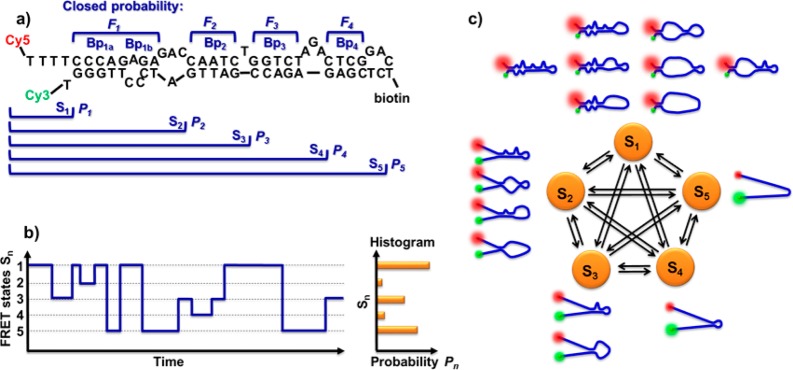
(a) Scheme of the breaking points of TAR–DNA. The four breaking points (Bpn) define five states Sn, and each state has probability of Pn to be observed in smFRET experiments. Each breaking point has a closed probability Fn. Bp1a and Bp1b are jointed together as has been discussed earlier in the main text. (b) Scheme of smFRET trajectory with random transitions between states. The histogram summarizes the random trajectory with the bars representing the probabilities of observing the states. (c) Scheme of the microstates and the transitions between the five FRET states.
Because the states are defined by the bulges that are connected with the breaking points (Bpn) (Figure 7a), quantitatively, the equilibrium constant of each breaking point can be calculated from the probabilities of the states (Figure 7b). According to the ergodic principle, the probability of each state measured at the single-molecule level represents its concentration in ensemble experiments. State S1 represents the eight microstates that have Bp1 closed but can have Bp2–4 either opened or closed (Figure 7c); state S2 contains four microstates; state S3 has two microstates; and states S4 and S5 have only the one microstate. As such, a statistical approach is proposed to obtain the equilibrium constants Kclosed,n from the probabilities of the five FRET states:
| 5 |
The equilibrium constant is defined by closed probability Fn: Kclosed,n = Fn/(1 – Fn), and the free energy can be calculated via ΔGn = –RT ln Kclosed,n, where R is gas constant and T is temperature. The measured probability of each state can be expressed as a function of Fn, and the following expressions can be written:
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
Therefore, Fn can be calculated from the measured state probabilities Pn, and ΔGn can be calculated from Fn.
In order to obtain the probabilities of the states Pn under 6 M urea when all the states are observed, the hidden Markov model (HMM)26,46,50−52,75 and the wormlike chain (WLC) model53 were used to analyze and refine the FRET states of TAR–DNA in the next two sections. The rate constants of the transitions among different FRET states are extractable from the time trajectories, but the process is complicated by measurement noise, state-blur induced by fast transitions within each binned time, variation among molecules, the breakdown of ergodicity for individual molecules, and the complexity of the transitions among the five states. Many methods have been developed to analyze or assist in the analysis of these kinds of complicated time trajectories including the widely used HMM,46,48,50−52,75−79 which has recently been successfully used to analyze very complicated hairpin smFRET data.26
Using HHM To Obtain the Probabilities of the Five States
First we use HMM to fit the trajectories for FRET states and extract the dwell-time distributions of the different states using two HMM packages HaMMy and vbFRET.46−52 Both packages are well-established programs that use the HMM principle but implement it differently, with HaMMy using maximum likelihood (ML) and vbFRET using maximum evidence (ME) as a measurement of the goodness of fit. The ML and ME scores increase with the number of states and does not reach the maximum even at 10 states (Figure 8a). This is expected because noise and state-blur caused by the fast dynamics among the states make the data better fitted with more parameters, which is consistent with the analysis results of simulated traces with five preset states, designed to have similar noise levels and fast dynamics on the order of the bin time. The five states identified by HaMMy are 0.92, 0.76, 0.57, 0.42, and 0.33 and by vbFRET are 0.94, 0.89, 0.74, 0.54, and 0.37.
Figure 8.
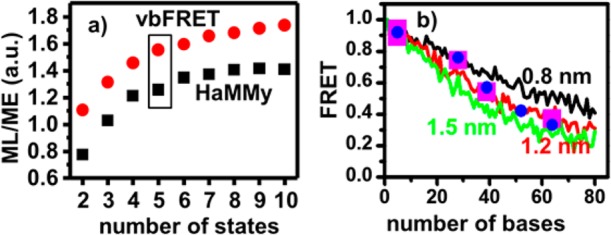
(a) Fitting probability as a function of number of states with HaMMy (maximum likelihood, ML) and vbFRET (Maximum evidence, ME). Five-state is picked based on the hairpin unfolding model explained in the text. (b) Average FRET efficiencies vs the number of unpaired bases between the donor dye and the acceptor dye predicted by wormlike chain model assuming 0.8, 1.2, and 1.5 nm persistence length of the ssDNA. The curves represent the simulated data (see Experimental Section). The blue dots are the states identified by HaMMy, and the magenta squares are the states identified by vbFRET where the first two points are combined together.
The fitting results from both packages are compared to the simulation results of wormlike chain (WLC) model to check which result is more consistent with our model of the hairpin dynamics. WLC model is a theory that can be used to explain the average separation distance of the two ends of a polymer chain under fast diffusion, where the most important parameter is the persistence length of the polymer that characterizes the softness of the polymer chain.53,54 We are particularly interested in this model because smFRET of Cy3- and Cy5-labeled ssDNA has been used to measure the persistence lengths of ssDNA under specific solutions; thus, all parameters except for the persistence length have been established in the literature.53 Because the persistence length varies with salt conditions, and is affected by pH value and urea, too,53,80,81 different persistence lengths are used to simulate the FRET curves vs the number of the bases between the two ends of the unfolded hairpin (Figure 8b). From these curves, the five states identified by HaMMy follow the trend well, while the five states identified from vbFRET follow the trend only if the first two states are combined together. As such, the results from HaMMy are adapted for further analysis in this case.
The probabilities of each state are obtained from the fitted time trajectories. The time trajectories and the five-state HaMMy result are shown in Figure 9a. The distributions of these states are further extracted from the fitted data (Figure 9b). When the states are assigned to each molecule, some “inactive” molecules turn out to stay only in a single state during the entire observation period. These molecules might stay fixed due to the strong molecule–substrate interaction25,82,83 and are thus not counted for the statistical distribution of the states to reduce the effect of immobilization. The dwell times of the first state and the last state of each molecule are also excluded from the histogram to remove the edge effect. After these treatment, the probabilities for the five states 0.92, 0.76, 0.57, 0.42, and 0.33 are 0.09, 0.27, 0.33, 0.20, and 0.11, respectively.
Figure 9.
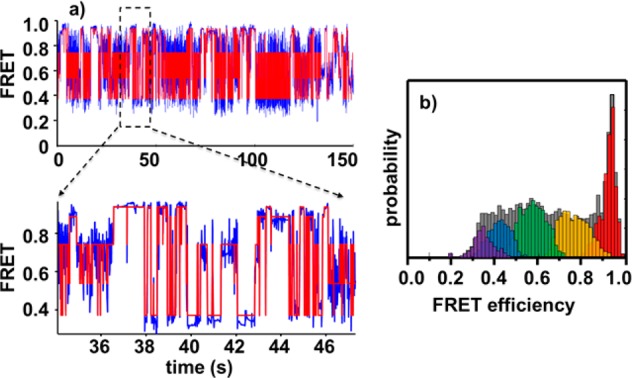
(a) Summary of the smFRET time trajectories of TAR–DNA under 6 M urea. The blue line is the binned data, and the red line is the fitted result from HaMMy at five states. (b) FRET distributions of the five states identified by HaMMy.
Free Energy of Each Break Point under 6 M Urea
Equations 6–10 can be used to calculate the free energy change of each Bpn that is independent of other breaking points and the microstates, although the overall free energy of all the Bpn should be 0. Our calculations produce the probability of the TAR–DNA hairpin staying folded F1 = 0.09, F2 = 0.30, F3 = 0.52, and F4 = 0.65. The equilibrium constant Kclosed,n = Fn/(1 – Fn) yields Kclosed,1 = 0.10, Kclosed,2 = 0.42, Kclosed,3 = 1.1, and Kclosed,4 = 1.8 for the four Bpn. As such, the free energies, ΔGn= −RT ln(Kclosed,n), for the base pairs in the presence of 6 M urea are 5.6, 2.1, −0.15, and –1.5 kJ mol–1 for the four breaking points at 20 °C with 6 M urea. The order of the free energies is not consistent with the order of the hybridization energy (Supporting Information Figure S2) or the number of hydrogen bonds 14, 10, 13, and 11 for Bp1 to Bp4, respectively, but rather suggests that in addition to the hydrogen binding strength (enthalpy control), the closer a base pair is to the anchoring point at the end loop, the easier it is for it to remain hydrogen bonded (entropy control).
Conclusion
In summary, our experimental observations are consistent with the hypothesis that the bulges are the fraying centers of hairpin folding/unfolding. In addition, we developed an approach to extract the equilibrium constants of the folding/unfolding of each breaking point to estimate its relative stability. Experimentally, we have successfully demonstrated the method to slow down the dynamics and to open more conformational states for the zipped hairpin by using PEG and urea as cosolutes. The quantitative data analysis is consistent with our model; however, our data analysis is based on the assumptions and models, which will certainly affect the results if they are further optimized. In addition, because the noise and the fast transitions blur our binned data, the existing methods have difficulties to fit the states without specifying the number of states. Thus, we are developing new methods hopefully to analyze the data more objectively or even in a model-free fashion. The results of this study support a “fraying and peeling” mechanism for the unfolding and “collapse” mechanism for the folding of DNA hairpins. Our quantitative analysis of the free energy of each breaking point suggests that the stability of the paired region is a function of both the pairing sequence and its distances to the anchoring/loop positions. The method developed in this paper will be very useful to study the mechanism for the inhibition of the HIV’s TAR–DNA transcription with short DNA oligomers or RNA aptamer and for studying other systems, such as TAR–RNA hairpin, with multiple interconverting states that might be otherwise unresolvable.
Acknowledgments
C.F.L. thanks the support from Welch Foundation (C-1787), the National Science Foundation (CBET-1133965 and CHE-1151647), and the National Institutes of Health (GM94246-01A1). We thank Prof. Stephan Link, Dr. Wei-Shun Chang, and the whole Link research group for helpful discussions. We also thank PicoQuant, Germany, for the kind loan of their FluoTime 300 instrument.
Supporting Information Available
Additional experimental methods, labeling strategy, theoretical calculation of folding/unfolding lifetimes for the DNA hairpin loops, photophysics of Cy3 and Cy5, full time trajectories, and TAR–DNA dynamics under PEG. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Present Address
J.C.: Department of Chemistry and Biochemistry, Ohio University, Athens, OH 45701.
Author Present Address
N.K.P.: Department of Biotechnology, IIET, Invertis University, Bareilly 243123, India.
Author Contributions
J.C. and N.K.P. contributed equally.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Watts J. M.; Dang K. K.; Gorelick R. J.; Leonard C. W.; Bess J. W. Jr.; Swanstrom R.; Burch C. L.; Weeks K. M. Architecture and Secondary Structure of an Entire HIV-1 RNA Genome. Nature 2009, 460, 711–716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy A. K.; Guhathakurta A.; Kleckner N.; Haniford D. B. Tn10 Transposition via a DNA Hairpin Intermediate. Cell 1998, 95, 125–134. [DOI] [PubMed] [Google Scholar]
- Enemark E. J.; Joshua-Tor L. Mechanism of DNA Translocation in a Replicative Hexameric Helicase. Nature 2006, 442, 270–275. [DOI] [PubMed] [Google Scholar]
- Feng S.; Holland E. C. HIV-1 tat Trans-activation Requires the Loop Sequence within tar. Nature 1988, 334, 165–167. [DOI] [PubMed] [Google Scholar]
- Rounseville M.; Kumar A. Binding of a Host Cell Nuclear Protein to the Stem Region of Human Immunodeficiency Virus Type 1 Trans-Activation-Responsive RNA. J. Virol. 1992, 66, 1688–1694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Upert G.; Di Giorgio A.; Upadhyay A.; Manvar D.; Pandey N.; Pandey V. N.; Patino N. Inhibition of HIV Replication by Cyclic and Hairpin PNAs Targeting the HIV-1 TAR RNA Loop. J. Nucleic Acids 2012, 2012, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LaFemina R. L.Antiviral Research: Strategies in Antiviral Drug Discovery; ASM Press: Washington, DC, 2009. [Google Scholar]
- Landes C. F.; Zeng Y.; Liu H.-W.; Musier-Forsyth K.; Barbara P. F. Single-Molecule Study of the Inhibition of HIV-1 Transactivation Response Region DNA/DNA Annealing by Argininamide. J. Am. Chem. Soc. 2007, 129, 10181–10188. [DOI] [PubMed] [Google Scholar]
- Lee Y.; Hyun S.; Kim H. J.; Yu J. Amphiphilic Helical Peptides Containing Two Acridine Moieties Display Picomolar Affinity toward HIV-1 RRE and TAR. Angew. Chem. 2007, 120, 140–143. [DOI] [PubMed] [Google Scholar]; Angew. Chem., Int. Ed. 2007, 47, 134 - 137.
- Das A. T.; Klaver B.; Berkhout B. The 5′ and 3′ TAR Elements of Human Immunodeficiency Virus Exert Effects at Several Points in the Virus Life Cycle. J. Virol. 1998, 72, 9217–9223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berkhout B.; Vastenhouw N. L.; Klasens B. I.; Huthoff H. Structural Features in the HIV-1 Repeat Region Facilitate Strand Transfer During Reverse Transcription. RNA 2001, 7, 1097–1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vo M. N.; Barany G.; Rouzina I.; Musier-Forsyth K. HIV-1 Nucleocapsid Protein Switches the Pathway of Transactivation Response Element RNA/DNA Annealing from Loop-loop “Kissing” to “Zipper”. J. Mol. Biol. 2009, 386, 789–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S.; Delling U.; Chen C.; Rosen C.; Sonenberg N. A Bulge Structure in HIV-1 TAR RNA is Required for Tat Binding and Tat-Mediated Trans-activation. Genes Dev. 1990, 4, 1365–1373. [DOI] [PubMed] [Google Scholar]
- Harrich D.; Mavankal G.; Mette-Snider A.; Gaynor R. B. Human Immunodeficiency Virus Type 1 TAR Element Revertant Viruses Define RNA Structures Required for Efficient Viral Gene Expression and Replication. J. Virol. 1995, 69, 4906–4913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanciault C.; Champoux J. J. Effects of Unpaired Nucleotides within HIV-1 Genomic Secondary Structures on Pausing and Strand Transfer. J. Biol. Chem. 2005, 280, 2413–2423. [DOI] [PubMed] [Google Scholar]
- Lu C.-H.; Yang H.-H.; Zhu C.-L.; Chen X.; Chen G.-N. A Graphene Platform for Sensing Biomolecules. Angew. Chem. 2009, 121, 4879–4881. [DOI] [PubMed] [Google Scholar]; Angew. Chem., Int. Ed. 2009, 48, 4785 - 4787. [DOI] [PubMed]
- Taylor N. J.; Darugar Q.; Kourentzi K.; Willson R. C.; Landes C. F. Dynamics of an Anti-VEGF DNA Aptamer: a Single-Molecule Study. Biochem. Biophys. Res. Commun. 2008, 373, 213–218. [DOI] [PubMed] [Google Scholar]
- Ansari A.; Kuznetsov S. V.; Shen Y. Configurational Diffusion down a Folding Funnel Describes the Dynamics of DNA Hairpins. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 7771–7776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuznetsov S. V.; Ren C. C.; Woodson S. A.; Ansari A. Loop Dependence of the Stability and Dynamics of Nucleic Acid Hairpins. Nucleic Acids Res. 2008, 36, 1098–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodside M. T.; Behnke-Parks W. M.; Larizadeh K.; Travers K.; Herschlag D.; Block S. M. Nanomechanical Measurements of the Sequence-Dependent Folding Landscapes of Single Nucleic Acid Hairpins. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 6190–6195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deniz A. A.; Dahan M.; Grunwell J. R.; Ha T.; Faulhaber A. E.; Chemla D. S.; Weiss S.; Schultz P. G. Single-Pair Fluorescence Resonance Energy Transfer on Freely Diffusing Molecules: Observation of Förster distance Dependence and Subpopulations. Proc. Natl. Acad. Sci. U. S. A. 1999, 96, 3670–3675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grunwell J. R.; Glass J. L.; Lacoste T. D.; Deniz A. A.; Chemla D. S.; Schultz P. G. Monitoring the Conformational Fluctuations of DNA Hairpins using Single-pair Fluorescence Resonance Energy Transfer. J. Am. Chem. Soc. 2001, 123, 4295–4303. [DOI] [PubMed] [Google Scholar]
- Kim J.; Doose S.; Neuweiler H.; Sauer M. The Initial Step of DNA Hairpin Folding: a Kinetic Analysis Using Fluorescence Correlation Spectroscopy. Nucleic Acids Res. 2006, 34, 2516–2527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmstrom E. D.; Nesbitt D. J. Single-Molecule Fluorescence Resonance Energy Transfer Studies of the Human Telomerase RNA Pseudoknot: Temperature-/Urea-Dependent Folding Kinetics and Thermodynamics. J. Phys. Chem. B 2014, 118, 3853–3863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kastantin M.; Schwartz D. K. DNA Hairpin Stabilization on a Hydrophobic Surface. Small 2013, 9, 933–941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller B. G.; Kobitski A.; Jäschke A.; Nienhaus G. U.; Noé F. Complex RNA Folding Kinetics Revealed by Single-Molecule FRET and Hidden Markov Models. J. Am. Chem. Soc. 2014, 136, 4534–4543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonnet G.; Krichevsky O.; Libchaber A. Kinetics of Conformational Fluctuations in DNA Hairpin-loops. Proc. Natl. Acad. Sci. U. S. A. 1998, 95, 8602–8606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung J.; Ihly R.; Scott E.; Yu M.; Van Orden A. Probing the Complete Folding Trajectory of a DNA Hairpin Using Dual Beam Fluorescence Fluctuation Spectroscopy. J. Phys. Chem. B 2008, 112, 127–133. [DOI] [PubMed] [Google Scholar]
- Wallace M. I.; Ying L.; Balasubramanian S.; Klenerman D. Non-Arrhenius Kinetics for the Loop Closure of a DNA Hairpin. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 5584–5589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace M. I.; Ying L.; Balasubramanian S.; Klenerman D. FRET Fluctuation Spectroscopy: Exploring the Conformational Dynamics of a DNA Hairpin Loop. J. Phys. Chem. B 2000, 104, 11551–11555. [Google Scholar]
- Long X.; Parks J. W.; Bagshaw C. R.; Stone M. D. Mechanical Unfolding of Human Telomere G-Quadruplex DNA Probed by Integrated Fluorescence and Magnetic Tweezers Spectroscopy. Nucleic Acids Res. 2013, 41, 2746–2755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin Y.; Zhao X. S. Kinetics and Dynamics of DNA Hybridization. Acc. Chem. Res. 2011, 44, 1172–1181. [DOI] [PubMed] [Google Scholar]
- Ying L.; Wallace M. I.; Klenerman D. Two-State Model of Conformational Fluctuation in a DNA Hairpin-loop. Chem. Phys. Lett. 2001, 334, 145–150. [Google Scholar]
- Jung J.; Van Orden A. A Three-state Mechanism for DNA Hairpin Folding Characterized by Multiparameter Fluorescence Fluctuation Spectroscopy. J. Am. Chem. Soc. 2006, 128, 1240–1249. [DOI] [PubMed] [Google Scholar]
- Kuznetsov S. V.; Ansari A. A Kinetic Zipper Model with Intrachain Interactions Applied to Nucleic Acid Hairpin Folding Kinetics. Biophys. J. 2012, 102, 101–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preus S.; Wilhelmsson L. M. Advances in Quantitative FRET-Based Methods for Studying Nucleic Acids. ChemBioChem 2012, 13, 1990–2001. [DOI] [PubMed] [Google Scholar]
- Zhuang X.; Bartley L. E.; Babcock H. P.; Russell R.; Ha T.; Herschlag D.; Chu S. A Single-Molecule Study of RNA Catalysis and Folding. Science 2000, 288, 2048–2051. [DOI] [PubMed] [Google Scholar]
- Liu S.; Abbondanzieri E. A.; Rausch J. W.; Grice S. F. J. L.; Zhuang X. Slide into Action: Dynamic Shuttling of HIV Reverse Transcriptase on Nucleic Acid Substrates. Science 2008, 322, 1092–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong K.-Y.; Pettitt B. M. The Pathway of Oligomeric DNA Melting Investigated by Molecular Dynamics Simulations. Biophys. J. 2008, 95, 5618–5626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez A.; Luque F. J.; Orozco M. Frontiers in Molecular Dynamics Simulations of DNA. Acc. Chem. Res. 2012, 45, 196–205. [DOI] [PubMed] [Google Scholar]
- Ma H.; Wan C.; Wu A.; Zewail A. H. DNA Folding and Melting Observed in Real Time Redefine the Energy Landscape. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 712–716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andreatta D.; Sen S.; Perez Lustres J. L.; Kovalenko S. A.; Ernsting N. P.; Murphy C. J.; Coleman R. S.; Berg M. A. Ultrafast Dynamics in DNA: “Fraying” at the End of the Helix. J. Am. Chem. Soc. 2006, 128, 6885–6892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SantaLucia J.; Hicks D. The Thermodynamics of Dna Structural Motifs. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 415–440. [DOI] [PubMed] [Google Scholar]
- Karam P.; Ngo A. T.; Rouiller I.; Cosa G. Unraveling Electronic Energy Transfer in Single Conjugated Polyelectrolytes Encapsulated in Lipid Vesicles. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 17480–17485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darugar Q.; Kim H.; Gorelick R. J.; Landes C. Human T-Cell Lymphotropic Virus Type 1 Nucleocapsid Protein-induced Structural Changes in Transactivation Response DNA Hairpin Measured by Single-Molecule Fluorescence Resonance Energy Transfer. J. Virol. 2008, 82, 12164–12171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKinney S. A.; Joo C.; Ha T. Analysis of Single-Molecule FRET Trajectories Using Hidden Markov Modeling. Biophys. J. 2006, 91, 1941–1951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bronson J. E.; Fei J.; Hofman J. M.; Gonzalez R. L. Jr.; Wiggins C. H. Learning Rates and States from Biophysical Time Series: A Bayesian Approach to Model Selection and Single-Molecule FRET Data. Biophys. J. 2009, 97, 3196–3205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor N. J.; Makarov D. E.; Landes C. F. Denoising Single-Molecule FRET Trajectories with Wavelets and Bayesian Inference. Biophys. J. 2010, 98, 164–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landes C. F.; Rambhadran A.; Taylor J. N.; Salatan F.; Jayaraman V. Structural Landscape of Isolated Agonist-binding Domains from Single AMPA Receptors. Nat. Chem. Biol. 2011, 7, 168–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrec M.; Levy R. M.; Talaga D. S. Direct Determination of Kinetic Rates from Single-Molecule Photon Arrival Trajectories Using Hidden Markov Models. J. Phys. Chem. A 2003, 107, 7454–7464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talaga D. S. Markov Processes in Single Molecule Fluorescence. Curr. Opin. Colloid Interface Sci. 2007, 12, 285–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanco M.; Walter N. G. Analysis of Complex Single-Molecule FRET Time Trajectories. Methods Enzymol. 2010, 472, 153–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy M. C.; Rasnik I.; Cheng W.; Lohman T. M.; Ha T. Probing Single-Stranded DNA Conformational Flexibility Using Fluorescence Spectroscopy. Biophys. J. 2004, 86, 2530–2537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thirumalai D.; Ha B. Y.. Statistical Mechanics of Semiflexible Chains. In Theoretical and Mathematical Models in Polymer Research; Grosberg A., Ed.; Academic Press: San Diego, CA, 1998; pp 1–35. [Google Scholar]
- Iqbal A.; Arslan S.; Okumus B.; Wilson T. J.; Giraud G.; Norman D. G.; Ha T.; Lilley D. M. J. Orientation Dependence in Fluorescent Energy Transfer Between Cy3 and Cy5 Terminally Attached to Double-Stranded Nucleic Acids. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 11176–11181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metropolis N.; Rosenbluth A. W.; Rosenbluth M. N.; Teller A. H.; Tell E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar]
- Sanborn M. E.; Connolly B. K.; Gurunathan K.; Levitus M. Fluorescence Properties and Photophysics of the Sulfoindocyanine Cy3 Linked Covalently to DNA. J. Phys. Chem. B 2007, 111, 11064–11074. [DOI] [PubMed] [Google Scholar]
- Ha T.; Tinnefeld P. Photophysics of Fluorescent Probes for Single-Molecule Biophysics and Super-resolution Imaging. Annu. Rev. Phys. Chem. 2012, 63, 595–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey B. J.; Perez C.; Levitus M. DNA Sequence-Dependent Enhancement of Cy3 Fluorescence. Photochem. Photobiol. Sci. 2009, 8, 1105–1110. [DOI] [PubMed] [Google Scholar]
- Agbavwe C.; Somoza M. M. Sequence-Dependent Fluorescence of Cyanine Dyes on Microarrays. PLoS One 2011, 6, e22177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsukanov R.; Tomov T. E.; Masoud R.; Drory H.; Plavner N.; Liber M.; Nir E. Detailed Study of DNA Hairpin Dynamics Using Single-Molecule Fluorescence Assisted by DNA Origami. J. Phys. Chem. B 2013, 117, 11932–11942. [DOI] [PubMed] [Google Scholar]
- Cosa G.; Zeng Y.; Liu H. W.; Landes C. F.; Makarov D. E.; Musier-Forsyth K.; Barbara P. F. Evidence for Non-Two-State Kinetics in the Nucleocapsid Protein Chaperoned Opening of DNA Hairpins. J. Phys. Chem. B 2006, 110, 2419–2426. [DOI] [PubMed] [Google Scholar]
- Levin J. G.; Guo J.; Rouzina I.; Musier–Forsyth K.; Kivie M. Nucleic Acid Chaperone Activity of HIV-1 Nucleocapsid Protein: Critical Role in Reverse Transcription and Molecular Mechanism. Prog. Nucleic Acid Res. Mol. Biol. 2005, 80, 217–286. [DOI] [PubMed] [Google Scholar]
- Cosa G.; Harbron E. J.; Zeng Y.; Liu H.-W.; O Connor D. B.; Eta-Hosokawa C.; Musier-Forsyth K.; Barbara P. F. Secondary Structure and Secondary Structure Dynamics of DNA Hairpins Complexed with HIV-1 NC Protein. Biophys. J. 2004, 87, 2759–2767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vo M. N.; Barany G.; Rouzina I.; Musier-Forsyth K. Mechanistic Studies of Mini-TAR RNA/DNA Annealing in the Absence and Presence of HIV-1 Nucleocapsid Protein. J. Mol. Biol. 2006, 363, 244–261. [DOI] [PubMed] [Google Scholar]
- Liu H. W.; Cosa G.; Landes C. F.; Zeng Y.; Kovaleski B. J.; Mullen D. G.; Barany G.; Musier-Forsyth K.; Barbara P. F. Single-Molecule FRET Studies of Important Intermediates in the Nucleocapsid-Protein-Chaperoned Minus-Strand Transfer Step in HIV-1 Reverse Transcription. Biophys. J. 2005, 89, 3470–3479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uzawa T.; Cheng R. R.; Cash K. J.; Makarov D. E.; Plaxco K. W. The Length and Viscosity Dependence of End-to-end Collision Rates in Single-Stranded DNA. Biophys. J. 2009, 97, 205–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng R. R.; Uzawa T.; Plaxco K. W.; Makarov D. E. The Rate of Intramolecular Loop Formation in DNA and Polypeptides: the Absence of the Diffusion-Controlled Limit and Fractional Power-Law Viscosity Dependence. J. Phys. Chem. B 2009, 113, 14026–14034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ansari A.; Kuznetsov S. V. Is Hairpin Formation in Single-Stranded Polynucleotide Diffusion-Controlled?. J. Phys. Chem. B 2005, 109, 12982–12989. [DOI] [PubMed] [Google Scholar]
- Lambert D.; Draper D. E. Effects of Osmolytes on RNA Secondary and Tertiary Structure Stabilities and RNA-Mg2+ Interactions. J. Mol. Biol. 2007, 370, 993–1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blose J. M.; Pabit S. A.; Meisburger S. P.; Li L.; Jones C. D.; Pollack L. Effects of a Protecting Osmolyte on the Ion Atmosphere Surrounding DNA Duplexes. Biochemistry 2011, 50, 8540–8547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spink C. H.; Garbett N.; Chaires J. B. Enthalpies of DNA Melting in the Presence of Osmolytes. Biophys. Chem. 2007, 126, 176–185. [DOI] [PubMed] [Google Scholar]
- Nakano S.; Wu L.; Oka H.; Karimata H. T.; Kirihata T.; Sato Y.; Fujii S.; Sakai H.; Kuwahara M.; Sawai H.; Sugimoto N. Conformation and the Sodium Ion Condensation on DNA and RNA Structures in the Presence of a Neutral Cosolute as a Mimic of the Intracellular Media. Mol. Biosyst. 2008, 4, 579–588. [DOI] [PubMed] [Google Scholar]
- Guinn E. J.; Schwinefus J. J.; Cha H. K.; McDevitt J. L.; Merker W. E.; Ritzer R.; Muth G. W.; Engelsgjerd S. W.; Mangold K. E.; Thompson P. J.; Kerins M. J.; Record M. T. Quantifying Functional Group Interactions That Determine Urea Effects on Nucleic Acid Helix Formation. J. Am. Chem. Soc. 2013, 135, 5828–5838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabiner L.; Juang B. An Introduction to Hidden Markov Models. ASSP Mag., IEEE 1986, 3, 4–16. [Google Scholar]
- Gilks W. R.; Richardson S.; Spiegelhalter D. J.. Markov Chain Monte Carlo in Practice; CRC Press: Boca Raton, FL, 1996; Vol. 2. [Google Scholar]
- Li C.-B.; Yang H.; Komatsuzaki T. Multiscale Complex Network of Protein Conformational Fluctuations in Single-molecule Time Series. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 536–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- König S. L. B.; Hadzic M.; Fiorini E.; Börner R.; Kowerko D.; Blanckenhorn W. U.; Sigel R. K. O. BOBA FRET: Bootstrap-Based Analysis of Single-Molecule FRET Data. PLoS One 2013, 8, e84157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sultana T.; Takagi H.; Morimatsu M.; Teramoto H.; Li C.-B.; Sako Y.; Komatsuzaki T. Non-Markovian Properties and Multiscale Hidden Markovian Network Buried in Single Molecule Time Series. J. Chem. Phys. 2013, 139, 245101. [DOI] [PubMed] [Google Scholar]
- Liang X.; Kuhn H.; Frank-Kamenetskii M. D. Monitoring Single-Stranded DNA Secondary Structure Formation by Determining the Topological State of DNA Catenanes. Biophys. J. 2006, 90, 2877–2889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh D. B.; Saleh O. A. Salt Species-dependent Electrostatic Effects on ssDNA Elasticity. Macromolecules 2011, 44, 2328–2333. [Google Scholar]
- Rasnik I.; McKinney S. A.; Ha T. Surfaces and Orientations: Much to FRET about?. Acc. Chem. Res. 2005, 38, 542–548. [DOI] [PubMed] [Google Scholar]
- Kastantin M.; Schwartz D. K. Connecting Rare DNA Conformations and Surface Dynamics Using Single-Molecule Resonance Energy Transfer. ACS Nano 2011, 5, 9861–9869. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.