Quantitative Analysis of Cardiac Tissue Including Fibroblasts Using Three-Dimensional Confocal Microscopy and Image Reconstruction: Towards a Basis for Electrophysiological Modeling

Abstract

Electrophysiological modeling of cardiac tissue is commonly based on functional and structural properties measured in experiments. Our knowledge of these properties is incomplete, in particular their remodeling in disease. Here, we introduce a methodology for quantitative tissue characterization based on fluorescent labeling, 3-D scanning confocal microscopy, image processing and reconstruction of tissue micro-structure at sub-micrometer resolution. We applied this methodology to normal rabbit ventricular tissue and tissue from hearts with myocardial infarction. Our analysis revealed that the volume fraction of fibroblasts increased from 4.83 ± 0.42% (mean ± standard deviation) in normal tissue up to 6.51 ± 0.38% in myocardium from infarcted hearts. The myocyte volume fraction decreased from 76.20 ± 9.89% in normal to 73.48 ± 8.02% adjacent to the infarct. Numerical field calculations on 3-D reconstructions of the extracellular space yielded an extracellular longitudinal conductivity of 0.264 ± 0.082 S/m with an anisotropy ratio of 2.095 ± 1.11 in normal tissue. Adjacent to the infarct, the longitudinal conductivity increased up to 0.400 ± 0.051 S/m, but the anisotropy ratio decreased to 1.295 ± 0.09. Our study indicates an increased density of gap junctions proximal to both fibroblasts and myocytes in infarcted versus normal tissue, supporting previous hypotheses of electrical coupling of fibroblasts and myocytes in infarcted hearts. We suggest that the presented methodology provides an important contribution to modeling normal and diseased tissue. Applications of the methodology include the clinical characterization of disease-associated remodeling.

I. Introduction

CONFOCAL microscopy has the capability to image the 3-D structure of biological tissues with sub-micrometer resolution [1], [2]. It is commonly applied to fluorescently labeled preparations, which allows identification of tissue compartments and cell types [3]. A variety of quantitative methods have been developed to analyze and characterize fluorescence images of normal and diseased tissues.

This work aims at establishing high resolution confocal imaging and quantitative image analysis as a basis for computational modeling of electrophysiology of normal and diseased cardiac tissue. In the past, various approaches have been developed to model the electrophysiology of normal and diseased heart tissue [4], [5], [6]. Most approaches are based on spatial discretization at sub-millimeter resolution followed by assignment of electrical and electrophysiological properties to the discrete regions [7]. For instance, the bidomain model is commonly based on finite element or finite difference meshes with locally defined intra- and extracellular electrical conductivity tensors [4]. These conductivity tensors reflect the distribution of various types of cells in the tissue, their intercellular coupling and the extracellular space. In cardiac tissue, myocytes occupy most of the volume. They underlie activation and synchronization of contraction by electrical signaling. Fibroblasts are the most numerous cells in cardiac tissue [8]. They form a complex network within the connective tissue matrix [9], [10]. Fibroblasts play an important role in the maintenance of the extracellular matrix and healing processes. Other cell populations like endothelial cells or smooth muscle cells are comparably small [11].

It is well established that cardiac myocytes are electrically coupled by gap junction channels of low resistance. In ventricular tissue, primarily the gap junction proteins Connexin-43 (Cx43) and Cx45 were found. In a prior study on rat ventricular tissue, we investigated the spatial distribution of Cx43 in myocytes by 3-D confocal microscopy and fluorescent labeling [12]. The study confirmed that Cx43 is primarily located at the ends of cells. Additionally, the study revealed that Cx43 distributions in myocytes are highly variable and asymmetric. Cx40 was found in vascular endothelium in sheep ventricular normal and infarcted tissue as well as in fibroblasts of rabbit sino-atrial node [13], [14].

The nature of electrical coupling of fibroblasts in cardiac tissue remains controversially discussed. Evidence for myocyte-fibroblast coupling in tissue was provided for the sino-atrial node by confocal microscopy and scrape-loading of Lucifer Yellow [13]. In vitro electrophysiological studies demonstrated electrical coupling between myocytes and fibroblasts as well as in-between fibroblasts in culture [15], [16]. Two-dimensional confocal microscopy studies indicated electrical myocyte-fibroblast coupling in infarcted hearts [14]. During myocardial infarction (MI) and ischemia, the amount and distribution of gap junctions proteins varied significantly, depending on the region in the heart and the infarct age. Fibroblasts were found to express mainly Cx45 in early stages and Cx43 in later stages of MI [14].

These studies suggest a possible influence of fibroblasts on cardiac electrophysiology in vivo beyond acting as passive electrical insulators and creating collagenous septa. Several computational studies have been performed to investigate the possible influence on electrophysiology [17]–[23]. The studies suggested significant effects in the case of fibroblast-myocyte coupling with low resistance. However, most modeling parameters such as the degree of electrical coupling between myocytes and fibroblasts as well as the volume fractions of myocytes, fibroblasts and extracellular space were based on estimation. An exception is the computational modeling study of Zlochiver et al. [24], which is based on optical mapping of cells in cultures. This study showed far-ranging influence of fibroblasts on myocyte electrophysiology in tissue culture. The extent to which this occurs in vivo remains unknown.

In this study, we aim at providing a micro-structural basis for certain parameters needed for modeling of cardiac tissue electrophysiology. We introduce methodology for quantitative characterization of the micro-structure of cardiac tissue at sub-micrometer resolution focusing on the extracellular space, the arrangement of myocytes and fibroblasts, and distribution of gap junction channels. The methodology is based on fluorescent labeling, 3-D scanning confocal microscopy and digital image processing. Crucial components were 3-D reconstructions of the extracellular space, which were derived from labeling and imaging of constituents of the extracellular matrix with wheat germ agglutinin (WGA). We applied our methodology to preparations of normal rabbit ventricular tissue and tissue next to the scar from infarcted hearts. From the obtained reconstructions we derived parameters, for example cell volume fractions and spatial relationships of Cx43 intensities to myocytes and fibroblasts, that are important input for computational modeling studies. Furthermore, we describe an approach to apply reconstructions of the extracellular space for measurement of extracellular conductivity tensors using numerical methods for calculation of electrical fields.

II. Methods

A. Preparation of Cardiac Tissue

We obtained cardiac tissue from adult New Zealand White rabbits (2.5 kg). The animals were anesthetized with an intravenous administration of sodium pentobarbital (50 mg/ml). The heart was excised quickly and the aorta cannulated. The heart was retrograde perfused with a Ca²⁺-free HEPES-buffered saline solution containing (in mmol/l): 4.4 KCl, 128 NaCl, 5 MgCl2, 1 CaCl2, 22 dextrose, 24 HEPES, 20 Taurine, 5 Creatinine, 0.5 Na-pyruvate (pH 7.2 with NaOH). After 15 min we used a Ca²⁺-free HEPES-buffered saline solution containing 2% of paraformaldehyde (PFA). Finally the heart was removed and submerged in that solution for an additional 20 min, and stored at 4 °C in phosphate buffered saline (PBS) with 30% sucrose and 0.05% azide. This procedure was performed with two groups of animals, a normal group (normal) and an MI group. The MI was caused by ligation of the circumflex artery as described elsewhere [25].

Biopsies with a diameter of 5 mm were obtained through the left ventricular wall as described in [12]. To prevent tissue damage during freezing for subsequent cryosectioning, the biopsies were placed in a 30% sucrose solution for 3–14 d. Biopsies were frozen in tissue-freezing medium (Triangle Biomedical Sciences, Durham, NC, USA) at −24 °C. Using a cryostat, the biopsies were sectioned in slices of 80 – 100 μm immediately after freezing. Sections were obtained parallel to the epicardial surface through the entire thickness of the ventricular wall. This study characterizes only mid-myocardial sections. Biopsies from two normal hearts were considered. In the MI group, biopsies were taken from four regions in one heart, differing in their distance to the scar: Region 1 (directly adjacent to the scar, biopsy center approximately 3 mm from the scar), region 2 (approximately 10 mm from the scar), region 3 (approximately 15 mm from the scar), and region 4 (approximately 20 mm from the scar). The distance was measured epicardially between the border of scar and the center of the biopsy. The MI had an age of 19 d.

B. Fluorescent Labeling

Combinations of up to four fluorescent labels were used to image the arrangement of structures and proteins in cardiac tissue. All incubations for labeling were conducted on a laboratory platform rocker at room temperature (Thermo Fisher Scientific, Waltham, MA, USA). Between incubation steps, samples were rinsed three to five times with PBS for 15 min per rinse. Primary and secondary antibody incubations were for 12 and 6 h, respectively. Constituents of the extracellular matrix were labelled by incubating with WGA conjugated to Alexa Fluor 488, 555, or 633 (Invitrogen, Carlsbad, CA, USA) at a concentration of 40 μ g/ml. After labeling with WGA, tissue samples were permeabilized with 0.5% Triton-X for 1 h. Nuclei were labeled with 4',6-diamidino-2-phenylindole (DAPI) in a 1:500 dilution. The proteins Cx43 and Cx45, vimentin, N-Cadherin (NC) and α-smooth muscle actin (α SMA) were labeled with antibodies. Cx43 was labeled with mouse monoclonal GJA1 IgM or IgG1 anti-Cx43 (Abcam, Cambridge, U.K.) in a 1:100 dilution, followed by goat anti-mouse IgM or IgG1, respectively, conjugated to Alexa Fluor 488, 555, or 633 (Invitrogen) in the same dilution. Similarly, Cx45 was labeled with mouse monoclonal GJA7 IgG1 anti-Cx45 (Abcam) in a 1:100 dilution, followed by goat anti-mouse IgG1 conjugated to Alexa Fluor 488, 555 or 633 (Invitrogen) in the same dilution. Mouse monoclonal IgG1 anti-vimentin (Sigma, St. Louis, MO, USA) conjugated to Cy3 (555 nm) was used in a 1:20 dilution to label the cytoskeleton of fibroblasts. NC is a glycoprotein that mediates calcium-dependent adhesion of cells [26]. For its staining, we used a 1:25 dilution of mouse monoclonal anti-N-Cadherin IgG1 (Abcam) and goat anti-mouse IgG1 conjugated to Alexa Fluor 488, 555, or 633 (Invitrogen) in a 1:100 dilution. αSMA is present in smooth muscle cells, especially in myofibroblasts and endothelial cells [27]. We applied mouse monoclonal IgG2a α-smooth muscle anti-actin (Sigma) in a 1:200 dilution in combination with goat anti-mouse IgG2a conjugated to Alexa Fluor 488, 555, or 633 (Invitrogen) in the same dilution. Samples were stored at 4°C PBS until imaging.

C. Confocal Imaging and Image Data Processing

Confocal microscopic imaging was performed using a Zeiss LSM 5 Duo (Zeiss, Jena, Germany) equipped with a 40x oil immersion lens (numerical aperture 1.3) or a 63x oil immersion lens (numerical aperture 1.4). In some experiments, tissue samples were imaged with a Nikon AR1 (Nikon, Melville, NY, USA) equipped with a 40x oil-immersion lens (numerical aperture 1.3). The imaging setup has been described before [12]. Tissue sections were placed on a glass slide and surrounded by Fluoromont-G (Electron Microscopy Science, Hatfield, PA, USA) to reduce mismatches of the refractive index of glass, tissue and fluid. A coverslip was placed on top. The x-axis of the image stacks was aligned with myocyte orientation via visual inspection and adjustment of the scanning direction. Three-dimensional image stacks were acquired with a typical size of 1024 × 768 × 200 voxels. With the 40x lens, the voxel size was 0.2μm × 0.2μm × 0.2 μm in x-, y-, and z-direction. When imaging with the 63x lens, the voxel size was 0.1 μm × 0.1 μm × 0.1 μm ×, respectively. These resolutions were maintained throughout image processing and analyses, except for the computation of the extracellular conductivity. The z-axis was parallel to the laser beam direction. For all imaging with the Zeiss LSM 5 Duo, a multi-track protocol was applied for quasi-simultaneous slice-wise imaging of two to four labels. For all imaging with the Nikon AR1, the labels were imaged simultaneously using bandpass filters for light emission. The dwell time per voxel was typically μs.

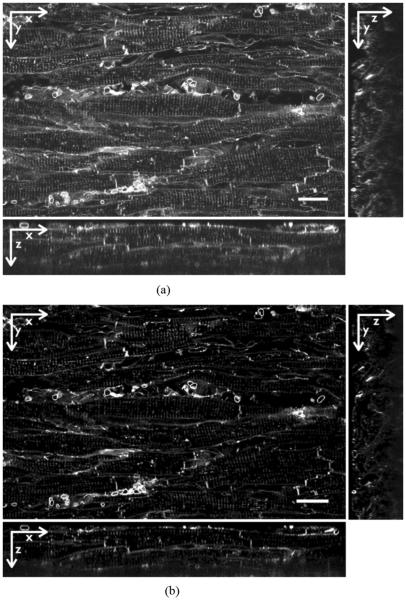
Image stacks were corrected for background signals and depth-dependent attenuation as previously described [12]. The Richardson–Lucy algorithm based on measured point spread functions (PSFs) was applied to deconvolve the image stacks. Fig. 1 shows the WGA images from a 3-D stack (a) before and (b) after processing.

Fig. 1.

(a) Raw and (b) processed images from 3-D stack of WGA labeled ventricular tissue from rabbit with MI. After processing the background signal is repressed. The image stack was deconvolved and corrected for depth-dependent attenuation. Scale bars: 20 μm.

We inspected image stacks for cross-reactions of antibodies or overlap of two emission spectra (bleed-through) causing cross-talk. A general description of the imaging process including cross-talk is based on the assumption that dye concentrations are linearly related to measured signal intensities [28]

$$\left[\begin{array}{c}\hfill I_1\hfill \\ \hfill I_2\hfill \\ \hfill I_3\hfill \\ \hfill I_4\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill w_{11}\hfill & \hfill w_{12}\hfill & \hfill w_{13}\hfill & \hfill w_{14}\hfill \\ \hfill w_{21}\hfill & \hfill w_{22}\hfill & \hfill w_{23}\hfill & \hfill w_{24}\hfill \\ \hfill w_{31}\hfill & \hfill w_{32}\hfill & \hfill w_{33}\hfill & \hfill w_{34}\hfill \\ \hfill w_{41}\hfill & \hfill w_{42}\hfill & \hfill w_{43}\hfill & \hfill w_{44}\hfill \end{array}\right]\left[\begin{array}{c}\hfill C_1\hfill \\ \hfill C_2\hfill \\ \hfill C_3\hfill \\ \hfill C_4\hfill \end{array}\right]+\left[\begin{array}{c}\hfill B_1\hfill \\ \hfill B_2\hfill \\ \hfill B_3\hfill \\ \hfill B_4\hfill \end{array}\right]$$ (1)

where I_i refers to the detected signal intensity of channel i, C_i to the dye concentration, B_i to the background signal and w_ij to the transformation matrix. Cross-talk is characterized by nondiagonal values in this matrix.

Our inspection revealed cross-talk between the Cx and vimentin signal in some image stacks. In case of cross-talk from only one channel to a second channel and subtracted background signal, the imaging process can be simplified to

$$\left[\begin{array}{c}\hfill I_1\hfill \\ \hfill I_2\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill w_{11}\hfill & \hfill 0\hfill \\ \hfill w_{21}\hfill & \hfill w_{22}\hfill \end{array}\right]\left[\begin{array}{c}\hfill C_1\hfill \\ \hfill C_2\hfill \end{array}\right]=\left[\begin{array}{c}\hfill w_{11}{C}_1\hfill \\ \hfill w_{21}{C}_1+w_{22}{C}_2\hfill \end{array}\right]$$ (2)

and all other channels are linearly dependent only on the concentration of the referring dye. Cross-talk can be corrected by multiplying the measured intensities with the inverse transformation matrix, leading to the original dye concentrations plus a background signal. However, diagonal values of the transformation matrix only scale the linear dependency of the measured signal strength of the belonging dye concentration and are therefore not relevant. The correction process merely involves subtraction of the cross-talk in the second channel

$$\left[\begin{array}{c}\hfill I_{1,\text{corr}}\hfill \\ \hfill I_{2,\text{corr}}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill I_1\hfill \\ \hfill I_2\hfill \end{array}\right]-\left[\begin{array}{c}\hfill 0\hfill \\ \hfill w_{21}{C}_1\hfill \end{array}\right]=\left[\begin{array}{c}\hfill I_1\hfill \\ \hfill I_2\hfill \end{array}\right]-\left[\begin{array}{c}\hfill 0\hfill \\ \hfill \frac{w_{21}}{w_{11}}{I}_1\hfill \end{array}\right]$$ (3)

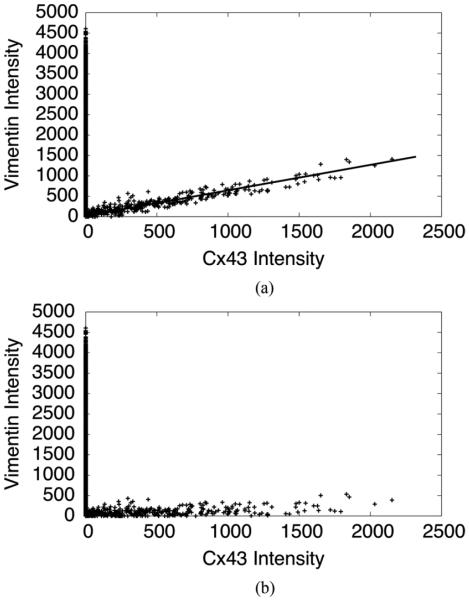
with the corrected intensities I_1,corr and I_2,corr. Estimation of the transformation matrix was thus reduced to the detection of w₂₁/w₁₁. In a scatter plot with the intensities of channel 1 and 2, the cross-talk line was visible as skewed scatter, showing a fraction of the intensity in channel 1 proportional to the intensity in channel 2. As the coefficient of this proportional relationship, w₂₁/w₁₁ is the slope of the scatter line. Fig. 2 shows the scatter plot in an example of bleed-through from the Cx43 associated channel to the vimentin associated channel (a) before and (b) after cross-talk correction. Its slope w₂₁/w₁₁ was extracted via a linear fit. In this example, the value for w₂₁/w₁₁ was approximately 0.6.

Fig. 2.

(a) Scatter plot of Cx and vimentin intensity values before cross-talk correction. The cross-talk relationship is clearly visible. In this case, its slope, defining the parameter w₂₁/w₁₁, is approximately 0.6. (b) Scatter plot of Cx and vimentin intensity values after cross-talk correction.

For subsequent analyses, we cropped image stacks to remove empty spaces. These spaces were typically close to the glass slide and at borders of tissue sections.

D. Quantitative Analysis

1) Calculation of Volume Fractions

For calculation of volume fractions of myocytes, fibroblasts and extracellular space, the preprocessed image stacks (described above) of WGA, vimentin and DAPI were segmented using a thresholding approach. The threshold was in general set to the mode of the intensity distribution plus one standard deviation. The thresholded WGA image stack served for reconstruction of the extracellular space. The intracellular space of fibroblasts was segmented by processing and thresholding of the vimentin and DAPI signals. A median filter was applied to the preprocessed vimentin images to reduce noise. To eliminate openings in the interior of fibroblasts, we applied a morphological closing operator. For this, we first employed a dilation operator (6-neighborhood, 10 iterations). Then, we identified nuclei of fibroblasts. To distinguish those from nuclei of other cells, we calculated the colocalization of the dilated vimentin image segmented by thresholding with the threshold-segmented DAPI signal. The observed distribution is referred to as segmented fibroblast-associated DAPI signal. Afterwards, we applied an erosion operator (6-neighborhood, 10 iterations) to the dilated vimentin image. This image was segmented using the threshold described above. Fibroblast distribution was defined as the union of segmented vimentin signal and segmented fibroblast-associated DAPI signal. To calculate the volume fractions, we counted identified voxels and divided them by the overall number of voxels. We assumed that cardiac tissue is composed only of fibroblasts, myocytes and extracellular space. We calculated the volume fraction of myocytes V_myo as

$$V_{\text{myo}}=1-V_{\text{fibro}}-V_e$$ (4)

with V_fibro and V_e referring to the volume fractions of fibroblasts and extracellular space, respectively.

2) Computation of Extracellular Conductivity

Based on the WGA image intensity I_WGA, we computed conductivity tensors of the extracellular space. Image stacks of I_WGA in normal and infarcted tissue were sampled at a resolution of 800 nm in each direction to reduce the large data volume and allow for efficient computation of electrical fields. As described above, we calculated a threshold intensity of WGA t_WGA as the mode plus one standard deviation. Voxels with intensities equal to or above t_WGA were related to 2 S/m, which is a common value for the conductivity of extracellular fluid [29], [30]. An estimation based on the chemical composition of the fluid leads to a similar value [29]. Intensity values of the WGA signal less than t_WGA were related to a conductivity σ_e proportional to I_WGA

$${\sigma }_e=2\frac{S}{m}\frac{I_{WGA}}{t_{WGA}}\text{for}{I}_{WGA}<t_{WGA}$$ (5)

$${\sigma }_e=2\frac{S}{m}\text{for}{I}_{WGA}\ge t_{WGA}.$$ (6)

For this computation, we modeled electrodes by setting two planes on opposite sides of the image stack to a conductivity of 200 S/m. On these electrodes, Dirichlet boundary conditions were defined by setting a constant electrical potential. The finite element method (FEM) was used to solve Poisson's equation for stationary electrical fields for the given boundary conditions. The homogenized conductivity of the extracellular space σ_E,dir for a given direction dir was defined as

$${\sigma }_{E,\text{dir}}=\frac{J_{\text{dir}}}{E_{\text{dir}}}.$$ (7)

The scalar J_dir refers to the current density through one plane parallel to the electrodes, the scalar E_dir to the applied electrical field strength. For each image stack, we calculated the scalar conductivity in the direction along the myocytes (longitudinally) and in two orthogonal directions (transversely), allowing us to define an extracellular conductivity tensor. The described approach to calculate σ_e is based on the assumption that no current passes through the cell interior.

In a homogeneous image stack with a local conductivity of 2 S/m at each point, we calculated a total conductivity of 2.01 S/m. This test supported reliability of our approach.

3) Measurement of Cx43 Intensity and Its Relationship to Fibroblasts and Myocytes

Using the vimentin segment Ω_fibro and the WGA segment Ω_e, we identified the myocyte space (Ω_myo) as the union of all voxels that were neither in Ω_fibro nor in Ω_e. For each image stack we summed Cx43 intensities for specific ranges of distances to Ω_myo and Ω_fibro. The summed Cx43 intensities in these distance ranges were divided by the total Cx43 intensity in the respective image stack. Finally, we calculated the fraction of Cx43 intensity within Ω_fibro(C_fibro).

III. Results

A. Confocal Imaging and Image Reconstruction

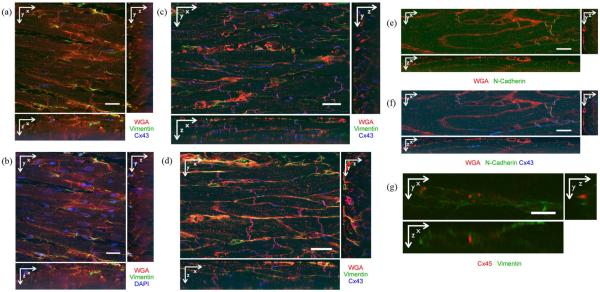
We applied our approach to normal and infarcted fixed rabbit ventricular tissue. Cross sections of typical processed image stacks for different fluorescent labelings are shown in Fig. 3. The image data involved up to four labels per tissue preparation. We show at most three different labels per image stack, making additive RGB images possible. The colors that we used do not refer to excitation or emission wavelengths.

Fig. 3.

Cross sections of 3-D image stacks. (a) Normal tissue labeled with WGA (red), anti-Cx43 (blue), and anti-vimentin (green). Myocytes were regularly aligned. Cx43 was mainly found at ends of myocytes, but also on their sides. (b) Normal tissue labeled with WGA (red), DAPI (blue), and anti-vimentin (green). Nuclei were found in myocytes, fibroblasts and other cells. (c) Infarcted tissue from region 1 labeled with WGA (red), anti-Cx43 (blue), and anti-vimentin (green). Myocyte structure was irregular. Cx43 was found at the sides of myocytes. (d) Infarcted tissue from region 4 labeled with WGA (red), anti-Cx43 (blue), and anti-vimentin (green). Myocyte structure appears irregular. Cx43 was present mainly at the ends of myocytes. (e) Normal tissue labeled with WGA (red) and anti-NC (green). NC was found at ends of myocytes and on their sides. (f) Same image stack as in (e), but including Cx43 labeling. Cx43 and NC signals were overlapping and adjacent. (g) Infarcted tissue in region 2 labeled with anti-Cx45 (red) and anti-vimentin (green). Occasionally, Cx45 and vimentin signals were proximal. Scale bars: (a)–(f) μm; (g) 10 μm.

Fig. 3(a) shows tissue from normal rabbit myocardium labeled with WGA, anti-Cx43, and anti-vimentin. As reported previously [12], [13], WGA signal was primarily associated with the sarcolemma and extracellular space. Myocytes were aligned and had a regular shape. Cx43 was found at the ends of myocytes, but also on their lateral sides, indicating the presence of gap junctions. Anti-vimentin labels the cytoskeleton of fibroblasts and endothelial cells. Fibroblasts were visible as thin, elongated cells, arranged in the clefts between myocytes. The same image region is shown in Fig. 3(b) including WGA, DAPI, and anti-vimentin. Nuclei were identified by the DAPI signal. They were found in myocytes, fibroblasts, and in other cell types. Similar to Fig. 3(a), a labeling with WGA, anti-Cx43, and anti-vimentin was conducted in infarcted tissue. Cross sections from image stacks in region 1 and 4 are shown in Fig. 3(c) and (d), respectively. Characteristic differences to normal tissue were revealed, mainly in region 1. Myocyte micro-structure and shape appeared irregular. Cx43 was found at lateral sides of the myocytes. In region 1, fibroblasts appeared to be thicker than in normal tissue.

Cx43 was, compared to Cx45, considerably more abundant in all our image stacks. Thus we concentrated our assessment on the distribution of Cx43. In an attempt to support our Cx43 labeling, we performed additional labeling with anti-NC. NC is responsible for adhesion of cells [26] and thus provides mechanically stable environments for gap junctions. Previous studies demonstrated colocalization of Cx43 and NC [32], [33]. Fig. 3(e) shows WGA and NC in normal tissue. NC was found at ends of myocytes, but plaques of NC were also visible on lateral sarcolemma. In Fig. 3(f), Cx43 image data were added to the visualization. Cx43 was located in regions close to NC. We calculated Mander's coefficient k₁, described in an earlier publication [34], for the overlap of NC with Cx43 intensity. We observed a value of k₁ = 0.979 in normal tissue. In infarcted tissue, we did not carry out a labeling with both anti-Cx43 and anti-NC. Nevertheless, in image stacks with NC in infarcted tissue, plaques of NC on the lateral myocytes membranes were clearly visible (data not shown). These findings supported our hypothesis that there is specific gap junction labeling on lateral membranes even in myocytes from infarcted tissue.

To characterize Cx45 distributions, we labeled normal and infarcted tissue with WGA, anti-Cx45 and anti-vimentin. In normal tissue, Cx45 was insignificant (data not shown). In all regions of the infarcted tissue, Cx45 was marginal versus Cx43. However, we occasionally found clusters of Cx45 signal adjacent to regions with vimentin signal [Fig. 3(g)]

To differentiate fibroblasts and myofibroblasts, we performed labeling that included anti-αSMA. This labeling has been demonstrated for myofibroblasts and smooth muscle cells such as endothelial cells, but not for fibroblasts [27]. We did not detect myofibroblasts in significant quantities in any of our image stacks (data not shown). Blood vessels were clearly marked by the αSMA antibody.

B. Quantitative Analysis

1) Calculation of Volume Fractions

Table I summarizes the calculated volume fractions of fibroblasts, extracellular space, and myocytes, respectively. V_fibro was smaller in normal tissue than in regions 1, 2, and 3 in MI. Region 4 had almost the same V_fibro as normal tissue. V_e was lower in normal tissue than in tissue from region 1, but both values exhibited a high standard deviation. V_e increased with decreasing distance to the scar in MI tissue. V_myo was larger in normal tissue than in region 1. In MI tissue we found a decreasing V_myo with decreasing distance to the scar.

TABLE I.

Measured Volume Fractions of Fibroblasts, Extracellular Space, and Myocytes

Tissue	Vfibro (%)	Ve (%)	Vmyo (%)
Normal	4.83±0.42 (n=4)	18.97±9.47 (n=12)	76.20±9.89
Region 1	5.12±0.55 (n=4)	21.40 ±7.47 (n=4)	73.48±8.02
Region 2	6.05±0.46 (n=4)	17.12±1.74 (n=4)	76.83±2.20
Region 3	6.51 ±0.38 (n=4)	14.73±2.37 (n=4)	78.76±2.75
Region 4	4.87±0.76 (n=6)	14.37±1.20 (n=5)	80.76±1.96

2) Computation of Extracellular Conductivity

The calculated extracellular conductivities are listed in Table II. For each image stack, the conductivity was calculated in three directions: longitudinally (σ_e,long, x-direction) and transversally (σ_e,trans1, y-direction, and σ_e,trans2, z-direction). As previously mentioned, the x-direction is aligned with the myocyte orientation, and the z-direction is transmural. Compared to normal tissue, σ^e,long in infarcted tissue was increased in region 2 and slightly increased in regions 3 and 4. With some exceptions in the second transversal direction, σ_e,trans1 and σ_e,trans2 increased in infarcted tissue. In comparison to normal tissue the anisotropy ratio σe,long/σe,trans1 was smaller in all regions of infarcted tissue. In most regions of infarcted tissue the anisotropy ratio σe,long/σe,trans2 was higher than in normal tissue.

TABLE II.

Calculated Extracellular Conductivity in the Longitudinal Direction (σ_e,long) and Both Transversal Directions (σ_e,trans1 and σ_e,trans2)

Tissue	σe,long (S/m)	σe,trans1 (S/m)	σe,trans2 (S/m)	$\frac{{\sigma }_{e,\mathit{long}}}{{\sigma }_{e,\mathit{trans}1}}$	$\frac{{\sigma }_{e,\mathit{long}}}{{\sigma }_{e,\mathit{trans}2}}$
Normal (n=4)	0.264±0.082	0.126±0.056	0.217±0.073	2.095±1.11	1.217±0.06
Region 1 (n=2)	0.264±0.029	0.172±0.029	0.200±0.031	1.535±0.09	1.320±0.06
Region 2 (n=4)	0.400±0.051	0.309±0.061	0.291±0.116	1.295±0.09	1.37±0.31
Region 3 (n=4)	0.284±0.022	0.174±0.027	0.269±0.111	1.632±0.15	1.056±0.29
Region 4 (n=4)	0.284±0.075	0.169±0.065	0.187±0.065	1.681±0.32	1.519±0.19

3) Measurement of Cx43 Intensity and Its Relationship to Fibroblasts and Myocytes

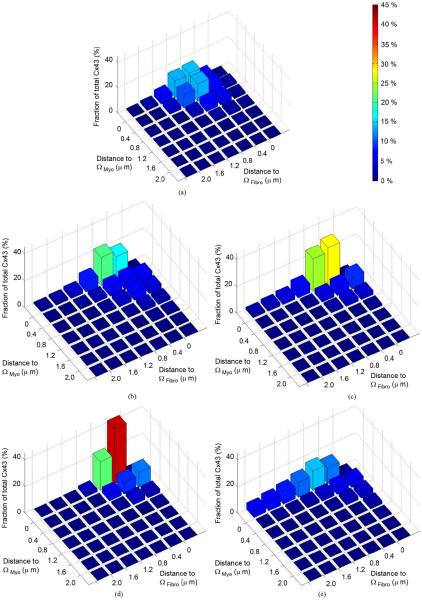
Fig. 4 presents the distribution of normalized Cx43 intensity in specific distances to Ω_myo and Ω_fibro. In normal tissue [Fig. 4(a)], the majority of Cx43 intensity is within or proximal to Ω_myo. Here, most Cx43 intensity is remote to Ω_fibro. In comparison, MI regions 1–4 [Fig. 4(b)–(e)] show increased Cx43 intensity within and proximal to Ω_fibro. In regions 1, 2, and 3, most Cx43 intensity is either near Ω_myo and remote from Ω_fibro or close to both spaces. Cx43 intensity proximal to Ω_fibro and remote from Ω_myo is marginal. Region 4 shows characteristics similar to normal tissue, but exhibits a higher fraction of Cx43 close to both spaces.

Fig. 4.

Fractions of Cx43 intensity in certain distances to Ω_myo and Ω_fibro in (a) normal and (b)–(e) region 1–4 of MI tissue. Color indicates the height of the bars and thus the fraction of Cx43 intensity.

In Table III, we list the fraction of Cx43 intensity within Ω_fibro, C_fibro, for the different regions. In regions 1, 2, and 3 of MI hearts, C_fibro was increased versus normal tissue. In particular, in C_fibro region 3 was increased by 172% versus normal tissue. In region 4, C^fibro is at similar levels as in normal tissue.

TABLE III.

C_fibro for Normal and Infarcted Tissue

Tissue	Cfibro (%)
Normal	2.96±1.09 (n=4)
Region 1	3.86±1.32 (n=2)
Region 2	6.86±0.60 (n=3)
Region 3	8.06±0.62 (n=3)
Region 4	3.53±3.21 (n=3)

IV. Discussion and Conclusion

We developed an approach for quantitative characterization of cardiac tissue, based on high-resolution scanning confocal microscopy, image reconstruction and analysis. The approach relies on computational methods for processing of high-volume multi-dimensional image data. We applied the approach to tissues from normal and MI hearts to reconstruct tissue micro-structure. We analyzed and quantified remodeling in MI and normal tissue at sub-micrometer resolution. Our aim was to derive structural parameters that are relevant for computational modeling of electrophysiology of cardiac tissue including fibroblasts.

Our approach is complementing previously developed approaches to create image-based models of cardiac structure and electrophysiology at sub-millimeter to microscopic scale [7], [35], [36]. Commonly, the developed structural models comprised larger volumes of the cardiac tissue than our models and the structural models were applied for mono- and bidomain simulations of cardiac conduction.

The developed techniques for measurement of volume fractions of myocytes, fibroblasts, and the extracellular space as well as the electrical conductivity of the extracellular space are novel. Table IV summarizes results of various studies on the volume fractions of myocytes, fibroblasts and extracellular space.

TABLE IV.

Comparison of Measured Volume Fractions in Normal and Infarcted Tissue to Other Studies. Tissues Were From Ventricle of Rabbit if not Specified Otherwise. Volume Fractions Were in % (Mean ± Standard Deviation) if not Specified Otherwise

Parameter	This study	Different Study
Ve (normal)	18.97±9.47	19.2±0.05* (rat) [37]
		21.3±0.05* (rat) [37]
		24.6±0.60* [38]
		0.29±0.05 ml/mg [39]
		0.30±0.05 ml/mg [39]
Vmyo (normal)	76.20±9.89	75.4 [38]
		79.7±4.7 [40]
Vfibro (normal)	4.83±0.42	5–6 (c. t, human) [10]
		1.9 (papillary, rat) [41]
Vfibro (MI)	5.12±0.55 (Region 1)	18.1±0.9 (3d) [14]
	6.05±0.46 (Region 2)	14.5±0.8 (12d) [14]
	6.51±0.38 (Region 3)	8.0±0.7 (30d) [14]
	4.87±0.76 (Region 4)

c. t: connective tissue, d: infarct age in days,

^*data presented as mean ± standard error.

Previous measurements of V_e were based on radioactive tracers and analysis of microscopic images. Polimeni [37] measured V_e in rat ventricle using [³⁵S] sulfate as a tracer and, alternatively, morphometric analysis of histological images. Results with the two methods were not significantly different. Frank and Langer [38] used a similar combination of tracers and analysis of electron-microscopic images to measure V_e in rabbit ventricular myocardium. Their definition of extracellular space comprised the spaces filled with fluid and glycocalyx, collagen, blood vessels cavities, endothelial cells and cells of connective tissue. The contribution of endothelial cells and cells of connective tissue to V_e was 3.6 ± 0.07% (mean ± standard error) and 1.5 ± 0.16%, respectively. Bridge et al. [39] labeled the extracellular space in ventricular myocardium of rabbit with ⁵⁸Co-ethylenediaminetetraacetic acid and [¹⁴C] sucrose and measured the fluid volume per weight of myocardium.

Our measurements of V_e are in close agreement with the measurements of Polimeni as well as of Frank and Langer after deduction of the contribution of endothelial cells and cells of connective tissue. However, our measurements of V_e were based on labeling with WGA conjugated fluorophores, confocal microscopic imaging, and digital image processing. WGA is an established marker of glyococonjugates in the extracellular matrix [31], [42]. Glycoconjugates are abundant in the glycocalyx on the surface and in the periphery of cell membranes. Also, glycoconjugates are associated with collagen strands [43], which form a dense network and are underlying mechanical coupling of myocytes to contiguous myocytes and capillaries [44]. Thus, at the molecular level WGA labeling does not provide direct information on the spatial extent of extracellular space, but outlines its constituents and borders provided by cell membranes. Confocal microscopy, however, is not able to spatially resolve the distribution of WGA in the extracellular space, for instance, to discriminate between the glycocalyx and glycoconjugates associated with collagen strands. Instead, confocal microscopy produces a blurred image due to the finite resolution of the imaging system. Fig. 3 presents examples of WGA images indicating that our approach is able to provide information on extracellular space at the microscopic scale. The approach is based on the assumption that gaps in WGA labeling in the extracellular space are closed by blurring of the image system. This assumption was invalid at tissue surfaces, which exhibited clefts caused by the cryosectioning. Our measurement approach required removal of these regions by cropping of the image stacks.

Our measurements of V_e exhibit a high standard deviation. We suggest that a major reason for the high standard deviation is the small volume of our tissue preparations and local heterogeneity of tissue. Causes for local heterogeneity include the variable distribution of blood vessels and laminar architecture of tissue [35], [45].

The measured V_myo in normal tissue in this study agrees well with the results of Frank and Langer assuming that V_myo = 100%−V_e with V_e as described above. Also, the measured V_myo is close to our previous measurements on isolated ventricular tissue from rabbit using a dextran-conjugated fluorophore for labeling of the extracellular space [40]. In the present study, our calculation of V_myo was based on measurements of V_e and V_fibro and is therefore dependent on errors in those measurements. We neglected structures other than myocytes, fibroblasts and extracellular space, which might lead to an overestimation of V_myo.

Data on V_fibro are rare in literature and difficult to reconcile with our measurement. Camelliti et al. estimated the volume fraction of connective tissue in normal adult human myocardium as 5%–6% [10]. Since connective tissue also involves other components, this value overestimates V_fibro. Anversa et al. measurement of V_fibro was based on analysis of electron-microscopic images from papillary muscle of rat [41]. The measured V_fibro is ~ 40% of the V_fibro determined in our study on normal rabbit ventricular myocardium.

Increased values of V_fibro were found after MI in sheep heart [14]. This is in agreement with our study on rabbit hearts after 19 d of MI. However, we observed only a slight increase of V_fibro in MI tissues. Moreover, we did not find myofibroblasts in our tissue preparations from infarcted hearts. Those had been suggested by other studies [46], [47]. However, the development and density of myofibroblasts might change with the region in the MI heart and the age of the MI. Furthermore, we did not find significant amounts of Cx45 in normal tissue, similar to Teunissen et al. in human, rat and mouse tissue [48]. Camelliti et al. found increased Cx45 in sheep tissue after infarction [14].

A focus of our study was on measurement of σ_e and its anisotropy. The anisotropy is a major determinant of epicardial potential distribution in simulations [53]. Table V summarizes different experimental and computational studies on conductivity of the extracellular space in normal tissue. Measurements of σ_e are sparse and exhibit high variability, which might reflect differences of species and tissues. Also, differences might be related to the experimental preparation, the level of perfusion and the model for interpretation [29]. Clerc [49] measured conduction in calf right ventricular trabeculae and used a cable model of electrical conduction for calculation of σ_e. The studies of Roberts et al. [50], [51] were performed on canine subepicardial myocardium. Different modeling approaches have been developed to compute σ_e, [29], [52]. The computational models are based on idealized geometrical models at sub-cellular scale [29], [52]. Our results are within the range of previously reported results from measurements and modeling studies. In this comparison, only the anisotropy based on the longitudinal and the first transversal conductivity was considered.

TABLE V.

Extracellular Conductivities in Experimental and Modeling Studies

Reference	σe,long (S/m)	σe,trans (S/m)	$\frac{{\sigma }_{e,\mathit{long}}}{{\sigma }_{e,\mathit{trans}}}$
Clerc* [49]	0.62	0.24	2.58
Roberts* [50]	0.22	0.13	1.69
Roberts* [51]	0.12	0.08	1.50
Stinstra [29]	0.21	0.06	3.50
Hand [52]	0.300	0.156	1.923
This Study	0.264	0.126	2.095

^*experimental study.

Our approach relies on a realistic description of the extracellular domain and can therefore be viewed as an extension and refinement of previous computational approaches. We recognize that our approach for the computation of σ_e has several limitations. As a first approximation, we assumed a truncated linear relationship between the WGA signal, the volume of extracellular space and its local conductivity. Thresholds t_WGA for truncation were calculated independently for each image stack based on histogram analysis. Other types of relationships might be more appropriate for this derivation. Calculation of σ_e is based on image stacks with reduced resolution, which might remove important detail. Also, the ion composition of the extracellular fluid might change during infarction, leading to a different local and macroscopic σ_e. However, changes in the ion composition do not affect our calculation of anisotropy ratios. While our computations of extracellular space are in agreement with previously published studies, our approach has not been validated by comparison to volume markers, such as dextran conjugated fluorophores, and direct electrical measurements. Difficulties with the approach are associated with reduced resolution of confocal imaging systems along the laser beam direction and depth-dependent attenuation. We attempted to account for these issues using deconvolution and attenuation correction, respectively. A further difficulty was the small extension of our image stacks in z-direction. Thus, the stacks included only a small number of cell layers, which complicated the reliable computation of the macroscopic conductivity.

Our approach for quantification of the 3-D distribution of gap junctions in relation to fibroblasts and myocytes is novel. We used 3-D reconstructions to assess the intercellular coupling in normal tissue and tissue from infarcted hearts. Our data suggest differences in intercellular coupling in MI versus normal tissue. We interpret elevated Cx43 intensity within or proximal to Ω_myo and Ω_fibro as a sign for coupling between myocytes and fibroblasts. In MI tissue, especially in regions 1, 2, and 3, we found an increased fractional Cx43 intensity within or proximal of both spaces, which indicates heterocellular coupling. Marginal Cx43 intensity was found within Ω_fibro and distant to Ω_myo indicating sparse or absent homocellular coupling of fibroblasts. Our results do not support hypotheses of considerable coupling of fibroblasts to other fibroblasts and myocytes in normal ventricular tissue. However, we cannot exclude the possibility that even in normal tissue fibroblasts are to some extent coupled by Cx43. Cx occurrence in fibroblasts is dependent on the species [54]. A study of isolated murine fibroblasts suggested expression of both Cx43 and Cx45 [55]. Since Cx45 is rare in our samples, our data indicate primarily fibroblast coupling via Cx43.

We suggest that our approach provides an improved basis for computational modeling of fibroblast-myocyte interactions in diseased tissue by providing quantitative data on the tissue remodeling. In particular, the developed approach has important clinical relevance. Remodeling in MI, especially of gap junctions, is associated with an increased risk of potentially fatal arrhythmia [56]. It has been hypothesized that the increased risk is due to coupling of fibroblasts to myocytes and dependent on the coupling strength [20]. Structural remodeling of myocytes, fibroblasts and extracellular spaces underlies alteration of electrical conductivity in MI tissue and thus affects fundamental mechanisms of arrhythmogenesis and maintenance of arrhythmia.

We discussed limitations of image resolution in our previous work [12], [40]. Structures with dimensions below the image resolution cannot be resolved. For instance, confocal microscopy cannot resolve individual gap junction channels, but only give evidence for the amount of Cx.

The study applied PFA-fixed tissue, which can cause shrinkage of cells and extracellular space. Levels of shrinkage were not measured, but could influence our measurements. In a previous study on rat tissue using a similar protocol as in this study, we were not able to detect significant shrinkage of cardiac myocytes [12].

Only tissues from two normal and one MI heart with an MI age of 19 d have been analyzed. Only four different regions in the infarcted heart were studied. However, the focus of this study was to introduce methodology. For a statistical analysis, a larger number of preparations at various MI ages and at various locations in the infarcted heart has to be considered. Furthermore, we did not consider the scar region in our analyses. Fibroblasts have been suggested previously to transmit electrical signals through the scar [57] and might therefore play important roles for the initiation of arrhythmia. In a computational model of MI hearts [58], the scar core alone did not increase vulnerability to electric shocks, whereas it did in the presence of a peri-infarct zone, highlighting the importance of the tissue surrounding the scar. We suggest that our approach can be applied to further characterize scar cores and scar transition zones.

Limitations were related to antibodies available for identifying proteins and cells in rabbit tissue. We applied a method for correction of crosstalk in the case of multi-labeling in confocal microscopy, caused by bleed-through, cross-talk or cross-reactions of antibodies. Similar approaches will be important when applying multiple labeling under impeded conditions as in rabbit tissue, where the various antibodies raised in rabbit cannot be easily used. Anti-vimentin labels both the cytoskeleton of fibroblasts, endothelial cells and other very small populations of cells in the heart. In our study, the amount of fibroblasts therefore might be overestimated. However, a labeling with anti-αSMA showed only insignificant amounts of smooth muscle cells.

Labeling of the protein Cx40 was not performed in this study. Thus we cannot draw conclusions on the potential significance of Cx40 for electrical coupling in MI tissue.

The focus of our study was on micro-structure only and we did not measure functional properties, e.g., intercellular conductances. The existence of Cx on cell membranes merely provides evidence for the possibility of intercellular electrical coupling [12]. For instance, lateral plaques of Cx43 might not indicate intercellular electrical coupling. However, labeling with NC indicated that the detected Cx is located in a mechanically stable environment, an important requirement for function. In culture, a rise of Cx43 in fibroblasts from MI hearts has been shown to be associated with increased functional coupling of those [59]. Moreover, the conductance of gap junctions can change in disease, for instance in MI [60]. In this case, the Cx intensity alone is not sufficient for estimating conductance.