Spatial panel analyses of alcohol outlets and motor vehicle crashes in California: 1999–2008

Abstract

Although past research has linked alcohol outlet density to higher rates of drinking and many related social problems, there is conflicting evidence of density’s association with traffic crashes. An abundance of local alcohol outlets simultaneously encourages drinking and reduces driving distances required to obtain alcohol, leading to an indeterminate expected impact on alcohol-involved crash risk. This study separately investigates the effects of outlet density on (1) the risk of injury crashes relative to population and (2) the likelihood that any given crash is alcohol-involved, as indicated by police reports and single-vehicle nighttime status of crashes. Alcohol outlet density effects are estimated using Bayesian misalignment Poisson analyses of all California ZIP codes over the years 1999–2008. These misalignment models allow panel analysis of ZIP-code data despite frequent redefinition of postal-code boundaries, while also controlling for overdispersion and the effects of spatial autocorrelation. Because models control for overall retail density, estimated alcohol-outlet associations represent the extra effect of retail establishments selling alcohol. The results indicate a number of statistically well-supported associations between retail density and crash behavior, but the implied effects on crash risks are relatively small. Alcohol-serving restaurants have a greater impact on overall crash risks than on the likelihood that those crashes involve alcohol, whereas bars primarily affect the odds that crashes are alcohol-involved. Off-premise outlet density is negatively associated with risks of both crashes and alcohol involvement, while the presence of a tribal casino in a ZIP code is linked to higher odds of police-reported drinking involvement. Alcohol outlets in a given area are found to influence crash risks both locally and in adjacent ZIP codes, and significant spatial autocorrelation also suggests important relationships across geographical units. These results suggest that each type of alcohol outlet can have differing impacts on risks of crashing as well as the alcohol involvement of those crashes.

1. Introduction

Alcohol-related traffic crashes are a major problem in the United States, resulting in more than 10,000 fatalities in 2010 and imposing annual costs of $37 billion (NHTSA, 2012). Although alcohol involvement rates among traffic crashes declined sharply during the 1980s and early 1990s, drinking has consistently been associated with roughly one third of crash fatalities since 1995 (IIHS, 2005, 2011). One strategy for reducing alcohol-involved traffic crashes is to impose limitations on the physical availability of alcohol, which many studies indicate can reduce drinking and related problems (reviewed in Gruenewald, 2011). Limiting alcohol outlets in an area is theorized to increase the convenience cost of obtaining beverages and thus reduce alcohol demand and drinking-related problems (Chaloupka et al., 1998). Some authors have argued that reductions in alcohol availability may be less effective at reducing motor vehicle crashes than other drinking problems because increased driving distances to obtain alcohol may outweigh any reduction in average drinking (McCarthy, 2003; Lapham et al., 1998; Gary et al., 2003; Gruenewald et al., 2002).

1.1. Prior empirical research

Previous studies have produced inconsistent findings regarding the relationship between alcohol availability in an area and the local risks of alcohol-involved crashes. A majority of analyses have suggested a positive relationship between alcohol availability and crash risks, particularly for bar density (Scribner et al., 1994; Jewell and Brown, 1995; Gruenewald et al., 1996; Escobedo and Ortiz, 2002; McCarthy, 2003, 2005; Farmer et al., 2005; Treno et al., 2007). Cotti and Walker (2010) found vehicle crash risks to be positively related to the presence of tribal casinos, which typically include beverage service and tend to draw more customers than do typical alcohol outlets. Other studies, however, have estimated a negative relationship between alcohol availability and crashes (McCarthy, 2003 for off-premise density; Baughman et al., 2001; Treno et al., 2007 for restaurant density).

Past studies take varying approaches to measuring the impacts of alcohol availability on crashes, and these will affect the interpretation of their results. Several studies examine only the effect of categorical legal bans on alcohol sales within a jurisdiction (e.g., dry counties; Baughman et al., 2001; Gary et al., 2003), providing less guidance about adding outlets in the majority of areas that allow alcohol sales. Other analyses measure continuous outlet-density effects at the county level (Jewell and Brown, 1995; Kelleher et al., 1996), but alcohol retail concentrations averaged across such large geographic areas may not accurately reflect ease of access at the local level. This lack of geographic resolution potentially biases effect estimates toward zero. Other studies have measured outlet density effects on crashes in California at finer spatial resolution such as cities (Scribner et al., 1994; McCarthy, 2003; Farmer et al., 2005) or postal codes with stable populations (Treno et al., 2007). The smaller spatial units allow these analyses to measure outlet density more accurately, but their restricted geographic samples (excluding rural areas or regions with rapid population growth) may not be representative of the entire state.

1.2. Spatial scale

The spatial scale of the hypothesized relationship between alcohol outlet density and crashes is not clear. Customers may drive a long or short distance to obtain alcohol. Large geographic areas such as counties are more likely to contain both the outlet and the crash location, but the county-wide outlet density may not reflect the local accessibility of alcohol to any given resident. Outlet density measures will be more relevant in smaller spatial units such as cities or postal codes, but at this scale customers are more likely to cross into nearby areas to obtain alcohol. Some previous studies have included both local and adjacent-area outlet density measures in order to allow for such cross-border effects (Jewell and Brown, 1995; Treno et al., 2007).

1.3. Biased statistical tests

Standard regression methods assume that model residuals are independent across all observations, and a failure of this independence can bias analyses toward finding significant effects. This assumption of independence is generally violated in spatial data, where neighboring areas tend to be similar in ways that cannot be completely explained by model covariates. Gruenewald et al. (1996) and Treno et al. (2007) found a high degree of spatial autocorrelation in their analyses relating traffic crashes to alcohol outlet densities and used statistical methods to control for it. Other analyses in this literature have failed to account for spatial auto-correlation, however, and may therefore be substantially biased.

1.4. Study outline

The goal of this study is to provide improved estimates of the relationship between alcohol outlet density and injury crashes. It analyzes a panel data set for the State of California that is larger and more spatially-resolved than has been used in prior studies, with over 1600 statewide ZIP codes over the years 1999–2008 (n = 16,712). Because high outlet density has been hypothesized to increase drinking but possibly reduce driving distances, we separately assess the impacts of alcohol availability on population crash risks and the likelihood that those crashes are alcohol-involved. Unlike most prior studies, these analyses measure the effects of various types of alcohol outlets while controlling for general retail density, helping to differentiate the effect of a bars or liquor stores from establishments that do not sell alcohol. These outlet density relationships with injury crashes are estimated both within a geographical area and between adjacent ZIP codes. These models are designed to investigate two hypotheses: (1) greater numbers of injury crashes relative to population will occur in association with greater densities of retail establishments in general (which attract traffic into an area) and of alcohol establishments in particular and (2) greater proportions of injury crashes will be alcohol related in areas with greater densities of bars. The second hypothesis is tested using crashes in two alcohol-related categories: those for which police noted a driver who had been drinking (HBD, which has shown high validity as a measure of impaired driving; McCarty et al., 2009), and single-vehicle nighttime (SVN) collisions (a common impaired-driving surrogate that has been shown to be highly alcohol-involved; Voas et al., 2009). All models control for the effects of local demographic and economic characteristics as well as residual spatial autocorrelation.

2. Material and methods

We collected data on motor vehicle crashes, alcohol retail outlets, and other variables throughout California for the years 1999–2008. Although crashes and alcohol outlets are located at specific points, they were aggregated to the ZIP code level for purposes of these analyses. ZIP codes have high geographic resolution in urban areas and are the finest available level of resolution for some archival data sets. These units entail significant disadvantages, however, as they do not align closely with community or political boundaries and the number of units as well as individual boundaries change over time.

2.1. ZIP code definitions

ZIP codes are collections of routes, defined by the US Postal Service to expedite the delivery of mail, and as such are frequently altered to meet postal needs. Statewide counts of ZIP codes increased from 1645 to 1693 during the study period. Geographic Data Technologies (and successors TeleAtlas and TomTom) create regularly updated ZIP code polygon files based on postal route data and interpolating on topology and roadway connectivity to ensure complete polygon coverage of the state (annual files obtained from Claritas, Inc., 2002, and ESRI, 2010). ZIP codes defined strictly for post office boxes or for a single building were merged into surrounding polygons to create a working ZIP code polygon file for each year. Geocoded data such as crash locations and alcohol outlet addresses were then aggregated to these year-specific polygon files.

2.2. Injury crash data

Individual-level data on traffic crashes within California for the years 1999–2008 were obtained from the California Highway Patrol’s (CHP) Statewide Integrated Traffic Records System (SWITRS). This system combines crash data from all local law-enforcement jurisdictions in the state. Only crashes involving an injury or death were selected for these analyses because property damage only crash data is inconsistently collected. State law requires that all crashes involving any injury or death be reported to the CHP, either directly or via local police agencies (California Vehicle Code Section 20008). The SWITRS crash data is widely used in the literature (Scribner et al., 1994; McCarthy, 2003; Treno et al., 2007). Supplementary analyses including property-damage-only crashes produced similar results (not shown). Crash locations were geocoded to ZIP codes in three phases. First, nearly 100% of SWITRS records listing highway post-miles were geocoded by the University of California’s Safe Transportation Resource and Education Center (SafeTREC). Second, other crash locations were geocoded to StreetMap USA (ESRI, 2010) street segments within each of California’s 58 counties in order to facilitate automatic geocoding. Third, crash locations not geocoded in prior steps were checked to see whether the SWITRS-reported crash city corresponded to a single ZIP code in a given year, in which case all crashes were assigned to that ZIP code. In all, 94.6% of SWITRS crash records were successfully geocoded to the ZIP code level. The models below analyze three outcome measures: the ZIP-code-by-year counts of all injury crashes, and the counts of alcohol-involved crashes as indicated by had been drinking (HBD) or single-vehicle nighttime (SVN, occurring between 8 PM and 4 AM) status. Supplementary analyses of crashes involving a charge of driving under the influence (DUI) had very similar results to those for HBD (not shown).

2.3. Alcohol and general retail outlet data

Three types of retail alcohol outlets were measured within the state of California. These included off-premise establishments (license types 20 and 21), restaurants (license types 41 and 47) and bars/pubs (license types 23, 40, 42, 48, 61 and 75). Active license records as of January of each year were obtained from the California Department of Alcohol Beverage Control (ABC) and geocoded to the premise address listed for each record. The three types of outlets were kept separate in analyses, as the direction and strength of associations between outlet types were hypothesized to differ. For example, visits to bars are more likely to involve drinking than are visits to alcohol-serving restaurants, and beverages purchased at off-premise outlets may not be consumed when the store is visited. Outlet density variables were defined as hundreds of outlets per square mile, with the units chosen to produce regression parameters with a reasonably large size for presentation purposes.

The regressions also include an equivalent density of all retail outlets in order to differentiate the impacts of alcohol outlets from that of other retail establishments, which may influence crashes via their impact on driving. Counts of retail outlets, defined as NAICS sectors 44–45 for retail trade plus sector 72 for accommodations and food services, were obtained from ZIP Code Business Patterns (U.S. Bureau of the Census, 2011). Because this general-retail density measure includes alcohol outlets, regression parameters for the alcohol-density variables should be interpreted as the additional impact of the specified premise type relative to that of a generic retail establishment. Since tribal casinos tend to serve alcohol and draw large numbers of customers from a wide catchment area, the models also include an indicator variable for whether each ZIP code in a given year contained one or more of the 58 casinos that have been allowed to operate in the state (California Gambling Control Commission, 2010). Spatially-lagged versions of each outlet density measure were calculated as the unweighted average density of the specified retail type among all ZIP codes that share a border with the ZIP code in question.

2.4. Transportation variables

The models contain an indicator variable for whether a ZIP code is served by a class 1 or 2 highway (ESRI, 2010). A single yes/no variable was chosen because a given stretch of roadway may share multiple designations (e.g., a state highway number and a Federal highway designation), which could lead to duplicatation in counting of the number of such routes. Although crash risks may also be affected by vehicle miles traveled, speed limits, precipitation and local road conditions (Keay and Simmonds, 2005; Ahmed et al., 2011), no consistent data sources were available across these years at the ZIP code level.

2.5. Census-based data

Estimates of annual ZIP-code-level demographic data were collected from the Sourcebook America (ESRI, 2009). Variables used included proportions of population that were male, racially white or black (with all others as the excluded group), of Hispanic ethnicity, and within four age groups (20–24, 25–44, 45–64, and 65+); population density (categorized by quintiles to reduce impact of extreme outliers); average household size; and inflation-adjusted median household income (year 2007 dollars times 10,000). ZIP codes without values for total population were assigned a minimal population value of 5. Census-based rate variables were missing in 2.9% of ZIP-code observations, with most of these being for “synthetic” ZIP codes (unpopulated areas such as national forests that are not covered by postal delivery service but could contain crashes and therefore must be included to assure statewide coverage); these were assigned the California state average for the year.

2.6. ZIP code instability measure

The analysis model described below assumes that ZIP code boundary shifts are not causally related to crash risks. This assumption was tested using an estimate of the geographic instability of a ZIP code’s population due to changes in the ZIP code boundaries between the current and prior year. This measure is calculated based on the year 2000 Census Block population whose centroids fall within a given year’s ZIP code boundaries. It measures the percentage of year-2000 block populations within the current ZIP code definition that would not have fallen within the boundaries of the best-matched ZIP code from the prior year.

3. Theory/calculation

3.1. Bayesian spatial models

ZIP code crash counts are analyzed using a class of Bayesian Poisson models that corrects for both large outlying risk in low-population areas as well as the effects of unexplained spatial autocorrelation (Besag et al., 1991; Bernardinelli et al., 1995; Carlin and Louis, 2000). The former problem is likely to be important in rural ZIP codes where even a single injury crash could result in very high local rates per resident. Spatial autocorrelation may be especially problematic for modeling motor vehicle crash risks. One reason is a lack of consistent panel data to control for regional factors such weather patterns. A second reason is that drinkers may cross multiple ZIP codes to access alcohol, particularly in urban areas, and the effects of these longer trips will not be captured by the adjacent-area outlet density measures. These problems violate the assumptions of standard regression analyses and can lead to biased results in uncorrected models. Bayesian methods developed for small area analysis and disease mapping address both of these issues by providing precise model-based estimates of local rates utilizing both local and neighboring observations. Conditional Autoregressive (CAR) random effects account for spatial autocorrelation and reduce the influence of outlying local rates by allowing each spatial area to “borrow strength” from its neighbors (Waller and Gotway, 2004). Bayesian hierarchical models extend this framework to examine relative risks of problems over both space and time. These approaches typically include CAR random effects that account for certain geographic areas having consistently higher or lower problem risks than others, plus an additional random effect that models residual variation in risks that is not spatially autocorrelated (Carlin and Louis, 2000). These Poisson models can effectively control for over-dispersion as well. Lord et al. (2005) suggest that the assumptions of zero-inflated count models are not well-matched to crash data, but that hierarchical Bayesian methods can effectively account for “excess” zero counts that often occur in small areas with high crash risk. Aguero-Valverde and Jovanis (2006) demonstrated that Bayesian CAR Poisson models provide comparable fit to negative-binomial specifications for crash risks in a panel of Pennsylvania counties, preferring the former analyses which control for spatial autocorrelation.

3.2. ZIP code misalignment model

Typical Bayesian hierarchical models assume that geographic units are consistent across time, which is not the case for ZIP codes. Zhu et al. (2011) introduced a spatial misalignment variant of these models that allows the use of ZIP-code data for longitudinal analysis despite changes in these geographic units. This misalignment approach allows for spatial autocorrelation of errors within each year’s unique ZIP code map to be modeled as a separate CAR random effect for each time period’s specific spatial adjacencies. The CAR random effects are assumed to have mean zero and share a common standard deviation. The model also allows for a separate random effect that is not spatially autocorrelated.

3.3. Model specification

Given that the outcome measures are the counts of injury crashes (total, HBD, or SVN) in a given ZIP code and time period, a Poisson regression model is used:

$$Y_{i,t}\mid {\mu }_{i,t}\sim \mathrm{Poisson}(E_{i,t}\exp ({\mu }_{i,t}))$$ (1)

where Y_i,t represents the count of injury crashes in ZIP code i during year t and E_i,t denotes the expected number of the injury crashes. For the total crash analyses, this expectation assumes that crashes are distributed in direct proportion to ZIP code population. Hence exp(μ_i,t) may be interpreted as the relative injury-crash risk of residing in spatial unit i at time t: regions with exp(μ_i,t) > 1 will have greater crash counts than expected based on their population, and regions with exp(μ_i,t) < 1 will have fewer than expected. For the analyses of HBD and SVN crashes, the expectation E_i,t assumes that statewide crashes in these alcohol-related categories are distributed in direct proportion to total injury crashes in each ZIP code. In these cases exp(μ_i,t) can be interpreted as the relative risk that an injury crash occurring in spatial unit i at time t will be designated as HBD or SVN.

Following standard generalized linear models, the log-relative risk, μ_i,t, is modeled linearly as:

$${\mu }_{i,t}=\alpha +X_{i,t}^{\prime }\beta +{\theta }_{i,t}+{\varphi }_{i,t}$$ (2)

This is a linear combination of fixed covariate effects and random effects which may take account of spatial and/or temporal correlation. Parameter α is an intercept that controls for the statewide level of injury crash risk that is not explained by other covariates. Preliminary analyses included year-specific intercepts, but these did not identify a clear pattern of temporal change and were subsequently dropped from the models. Matrix X′_i,t contains space-and time-specific covariates and β is a vector of fixed-effects estimates of the impacts of those covariates. θ_i,t and φ_i,t denote the pair of random effects capturing spatially unstructured heterogeneity and CAR spatial dependence, respectively. Models were estimated using WinBUGS 1.4.3 software (Lunn et al., 2000). Uninformed priors were specified for all fixed and random effects. Models were allowed to burn-in for 40,000 (HBD and SVN crashes) to 200,000 (total injury crashes) Markov Chain Monte Carlo (MCMC) iterations, which were sufficient for all parameter estimates to stabilize and converge between two chains with different initial values. Posterior estimates were then sampled for an additional 40,000 iterations within each MCMC chain to provide model results. Traces of MCMC iterations demonstrated good convergence for all parameters.

4. Results

4.1. Data description

Table 1 presents descriptive statistics for the outcome measures and explanatory variables included in the analyses. The average ZIP code had nearly 112 injury crashes in a given year, of which 12 were specifically noted by a police officer as HBD and 7 were categorized as SVN. The average ZIP code has outlet densities per square mile of 0.8 for bars, 4.7 for alcohol-serving restaurants, 2.7 for off-premise outlets, and 24.6 for total retail establishments. Mean densities are not weighted by the area of each ZIP code, making the average more representative of the numerous dense urban ZIP codes than of the fewer rural ZIP codes that make up most of the state’s land area. The spatial lags of the retail variables tend to have similar means to the local versions of the variables, but they can differ considerably because geographically-small neighbors are weighted equally to large ones. Over 64% of ZIP codes are served by at least one major (class 1 or 2) highway, and the average ZIP code shares 99.2% of its year-2000 Census block population with its best-matched prior-year ZIP code.

Table 1.

Descriptive statistics for model variables

Variable	Mean	S.D.	Min	Max
Outcome measures
Injury crash count	111.803	120.432	0.000	935.000
E(injury crashes) vs. populationa	111.803	112.099	0.022	607.313
HBD injury crash count	12.085	12.876	0.000	96.000
E(HBD injury crashes) vs. injury crashesb	12.086	12.976	0.010	98.523
SVN injury crash count	7.083	7.327	0.000	60.000
E(SVN injury crashes) vs. injury crashesb	7.084	7.629	0.010	54.251
Retail variables
Local bars/pub density (100s/sq. mile)	0.008	0.037	0.000	0.880
Spatial lag bars (100s/sq. mile)c	0.008	0.028	0.000	0.415
Local restaurant density (100s/sq. mile)	0.047	0.201	0.000	4.583
Spatial lag restaurants (100s/sq. mile)c	0.044	0.163	0.000	2.968
Local off-premise density (100s/sq. mile)	0.027	0.071	0.000	1.456
Spatial lag off-premise (100s/sq. mile)c	0.027	0.063	0.000	0.968
Local any-casinos dummy	0.016	0.124	0.000	1.000
Spatial lag casino dummyc	0.019	0.072	0.000	1.000
Local total retail density (100s/sq. mile)	0.246	0.980	0.000	22.639
Spatial lag total retail (100s/sq. mile)c	0.470	1.513	0.000	27.789
Other covariates
Real HH income ($10,000s)	5.728	2.831	0.010	60.203
Average HH size	2.790	0.609	1.000	8.000
Proportion White	0.680	0.207	−0.133	1.200
Proportion Black	0.047	0.085	−0.106	0.884
Proportion Hispanic	0.264	0.218	−0.133	1.167
Proportion male	0.507	0.053	0.000	1.000
Proportion aged 20–24	0.070	0.058	0.000	1.000
Proportion aged 25–44	0.281	0.075	0.000	1.000
Proportion aged 45–64	0.248	0.080	0.000	1.000
Proportion aged 65+	0.124	0.068	0.000	1.001
Population density 2nd quintile	0.196	0.397	0.000	1.000
Population density 3rd quintile	0.200	0.400	0.000	1.000
Population density 4th quintile	0.200	0.400	0.000	1.000
Population density 5th quintile	0.200	0.400	0.000	1.000
Any class 1 or 2 Hwy dummy	0.643	0.479	0.000	1.000
Percent ZIP code instabilityd	0.794	4.059	0.000	63.325

Data for California ZIP codes from 1999 through 2008, combine n = 16,712. Yearly ZIP code counts ranged from 1645 in 1999 to 1693 in 2008.

^aExposure computed assuming observed study-wide total injury crashes are proportional to population.

^bExposure computed assuming observed study-wide HBD or SVN injury crashes proportional to total crashes.

^cSpatial lag is unweighted average value among all adjacent ZIP codes.

^dPercent of year-2000 census block populations in current ZIP code boundaries not in best-matched prior year ZIP code.

4.2. Local outlet density effects

Table 2 presents the results for Bayesian ZIP-code misalignment models that control for local densities of retail outlets but not those in adjacent geographical units. The left set of columns present the analysis of risks of total injury crashes relative to what would be expected based on ZIP code population alone. The center and right sets of columns present the analyses of risks of HBD and SVN injury crashes relative to what would be expected based on local counts of all injury crashes. The raw coefficients from these Poisson models are log relative rates from the posterior distribution, and for ease of interpretation all values have been exponentiated in the table to represent relative rates. Relative rates greater than 1 indicate that higher values of the explanatory variable are associated with higher crash risks, while relative rates below 1 suggest an inverse association between the explanatory variable and the crash risk. The median relative rate from each model’s sampled MCMC iterations represents the expected value for each effect. This median relative rate is followed in parentheses by a credible interval indicating a range of values that is expected to contain the true relative rate with 95% probability (a Bayesian concept analogous to standard confidence intervals). The lower relative rate in this credible interval identifies the 2.5th percentile of MCMC iterations from the posterior distribution, while the higher number corresponds to the 97.5th percentile. If the entire credible interval for an explanatory variable is above 1.0, this suggests that there is a well-supported finding that the variable is positively associated with crash risk, while a credible interval entirely below 1.0 suggests a well-supported negative relationship. Each well-supported finding is noted in the tables.

Table 2.

Relative risks associated with ZIP code characteristics, among total injury crashes and crash types.

Variable	Total injury crashes (relative to total population) median (95% C.I.)	Had been drinking crashes (relative to all injury crashes) median (95% C.I.)	Single-vehicle night crashes (relative to all injury crashes) median (95% C.I.)
Bar/pub density (100s/sq. mile)	0.707 (0.357, 1.437)	2.050 (1.419, 2.960)a	2.133 (1.092, 4.196)a
Restaurant density (100s/sq. mile)	2.157 (1.800, 2.629)a	1.064 (0.954, 1.190)	0.981 (0.803, 1.202)
Off-prem. density (100s/sq. mile)	0.329 (0.205, 0.478)a	0.871 (0.717, 1.073)	0.180 (0.126, 0.260)a
Any casinos (dummy variable)	0.982 (0.887, 1.086)	1.055 (1.008, 1.106)a	0.980 (0.925, 1.039)
Total retail density (100s/sq. mile)	1.088 (1.059, 1.124)a	0.947 (0.930, 0.965)a	0.916 (0.882, 0.949)a
Real HH income ($10,000s)	0.985 (0.977, 0.995)a	0.972 (0.968, 0.977)a	1.002 (0.997, 1.008)
Average HH size	0.833 (0.802, 0.856)a	1.129 (1.095, 1.153)a	1.144 (1.115, 1.172)a
Proportion White	0.727 (0.639, 0.834)a	1.704 (1.589, 1.830)a	1.379 (1.279, 1.500)a
Proportion Black	2.183 (1.689, 2.789)a	1.381 (1.244, 1.543)a	1.432 (1.251, 1.642)a
Proportion Hispanic	2.440 (2.047, 2.850)a	1.534 (1.446, 1.632)a	0.943 (0.867, 1.025)
Proportion Male	0.066 (0.053, 0.086)a	2.153 (1.699, 2.592)a	4.238 (3.300, 5.478)a
Proportion aged 20–24	52.910 (37.626, 83.739)a	0.489 (0.367, 0.654)a	0.530 (0.392, 0.727)a
Proportion aged 25–44	22.092 (15.997, 31.852)a	0.906 (0.701, 1.156)	0.615 (0.491, 0.785)a
Proportion aged 45–64	7.616 (5.872, 10.930)a	2.668 (2.059, 3.303)a	2.505 (1.989, 3.187)a
Proportion aged 65+	7.603 (5.634, 10.631)a	0.872 (0.682, 1.095)	0.819 (0.668, 1.042)
Pop. density quintile 2 dummy	0.259 (0.247, 0.272)a	1.115 (1.080, 1.152)a	0.880 (0.849, 0.912)a
Pop. density quintile 3 dummy	0.145 (0.137, 0.154)a	1.007 (0.973, 1.043)	0.626 (0.602, 0.650)a
Pop. density quintile 4 dummy	0.096 (0.091, 0.103)a	0.902 (0.869, 0.938)a	0.485 (0.465, 0.506)a
Pop. density quintile 5 dummy	0.070 (0.066, 0.077)a	0.886 (0.852, 0.926)a	0.413 (0.392, 0.433)a
Any class 1 or 2 highway dummy	1.639 (1.593, 1.698)a	0.905 (0.891, 0.919)a	1.095 (1.072, 1.119)a
Percent ZIP code instability	1.006 (1.002, 1.009)a	1.001 (0.999, 1.004)	1.005 (1.002, 1.008)a
Intercept	4.232 (3.797, 5.092)a	0.364 (0.317, 0.498)a	0.497 (0.418, 0.556)a
SD (CAR random effect)	0.708 (0.682, 0.731)	0.224 (0.211, 0.235)	0.217 (0.202, 0.233)
SD (non-CAR random effect)	0.644 (0.629, 0.657)	0.098 (0.079, 0.113)	0.202 (0.187, 0.216)
CAR proportion of error variance	0.548 (0.521, 0.572)	0.841 (0.782, 0.896)	0.535 (0.471, 0.602)
Moran’s I for CAR random effect	0.434 (Z = 28.097)	0.774 (Z = 50.075)	0.451 (Z = 29.227)
Deviance (−2a LogLikelihood)	111,210	74,539	67,309

Notes: Posterior results are from Bayesian space-time Poisson analyses of 1600+ California ZIP codes over the years 1999–2008 (total n = 16,712). Each Poisson model included an exposure variable with coefficient restricted to one, calculated on the assumption that outcome counts study-wide are distributed in exact proportion to population (total crash model) or to total crashes (HBD and SVN crashes models). Raw Poisson coefficients and credible intervals have been exponentiated and are thus interpretable as relative risks.

^aWell-supported effects (those for which the 95% credible interval does not include a relative risk of one).

The results fail to identify a well-supported relationship between bar/pub density and the population rate of injury crashes, but suggest that an abundance of bars is positively associated with the likelihood that those crashes are categorized as alcohol-related (HBD or SVN). The models suggest that restaurant density is positively associated with injury crash risks, but not related to the odds that a given crash is alcohol involved. Off premise outlet density appears to be associated with lower population rates of injury crashes as well as reduced chances that a crash is SVN. The presence of casinos is unrelated to crash risks, but appear positively associated with the odds that crashes are labeled as HBD. An area’s density of all retail establishments is associated with higher crash risks but lower risks of those crashes being alcohol-related.

There are a number of notable effects among the demographic and economic covariates. Income is negatively associated with injury crash risks and the likelihood that crashes are categorized as HBD. ZIP codes with larger average households and higher proportions of whites and males tend to have lower risks of crashing but greater odds that those crashes will be in the alcohol-related categories. The proportion black is positively related to risks of both crashes and alcohol-involvement, whereas areas with high Hispanic concentrations tend to have higher risks of crashing and of the crashes being HBD. Crash risks tend to be most elevated in areas with high proportions of younger adults (particularly ages 20–24), but alcohol involvement of those crashes is highest among middle-aged adults. Both crash risks and the probability of alcohol involvement decline with increasing population density. The presence of major (class 1 or 2) highways is positively associated with crash rates relative to population and the chances of crashes being SVN, but reduces the odds that crashes are labeled as HBD. Areas with larger changes in ZIP code definitions tend to have slightly elevated risks of crashes and of those crashes being SVN.

The bottom section of Table 2 presents statistics on the random effects allowing for residual variation that is or is not spatially auto-correlated. In each model the CAR spatial random effect explains more variance than does the non-spatial effect. The spatial share of variance is 54% for the analyses of crash risk and the chance that crashes are SVN, whereas the spatial random effect accounts for 84% of unexplained variance in the HBD model. There is a strongly positive and highly-significant spatial autocorrelation among each model’s CAR random effects, with Moran’s I statistics of 0.43 for total injury crashes, 0.77 for HBD, and 0.45 in the SVN analysis. Fig. 1 presents statewide maps showing the quintiles of these spatially correlated random effects for each model, representing regional differences in risk beyond that explained by the models’ covariates. These maps are for the 2008 ZIP codes, but the spatial patterns in earlier years are similar for each model. The highest (darkest) quintile for the crash random effect has relative risks at least 2.8 times higher than the lowest quintiles, while the equivalent ratios are 1.35 for HBD and 1.22 for the SVN spatial random effect. The spatial residual risks for crashes relative to population are notably elevated in two east-west bands, one in Northern California between the San Francisco Bay Area and the Reno/Lake Tahoe area, and the other in Southern California between the Los Angeles region and Las Vegas. These same areas tend to have relatively lower risks that crashes are alcohol related.

Fig. 1.

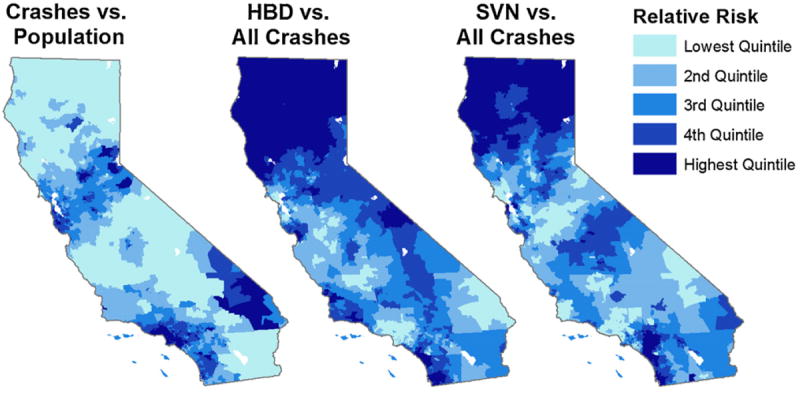
Comparing residual spatial variation across models: quintiles for 2008 CAR random effects. Legend: Posteriors of CAR random effects are for the models without spatially-lagged outlets effects as shown in Table 2. The maps would be very similar using the analyses that include spatially-lagged outlet effects (Table 3). The lighter shade represents the 20% of ZIP codes with the lowest spatial risk not explained by covariates, while the darker shade represents the highest 20% in terms of residual spatial risk. The residual spatial risk for the highest quintile of ZIP codes is at least 2.8 times that of the lowest quintile in the analysis of injury crashes relative to population. The highest quintile’s residual spatial risk is at least 35% higher than the lowest quintile for HBD crashes relative to all injury crashes, and at least 22% higher for SVN crashes relative to all injury crashes.

4.3. Models with adjacent-area outlet effects

Table 3 presents selected results from a second set of Bayesian analyses that is identical to those presented in Table 2, but introduces additional covariates for average retail densities and presence of casinos in adjacent ZIP codes. Results for non-retail covariates are not shown in this table because they are extremely similar to those presented in the prior table. As in Table 2, there is no well-supported relationship between overall crash risk and bar density. A positive relationship between local bar density and risk of crashes being labeled HBD remains, but no well-supported effect for bars in adjacent ZIP codes. The opposite pattern holds for the likelihood that a crash is SVN, with the model finding no effect for local bar density but a positive association with bars in neighboring areas. Local crash risks are found to be positively related to local restaurant density but negatively associated with restaurants in neighboring ZIP codes. Adjacent-area restaurant density is found to be positively related to the risk that a crash is labeled as HBD but negatively associated with the odds of being SVN. Local off-premise outlet density is negatively related to risks both of crashing and of those crashes being SVN, but adjacent-area off-premise density is associated with higher risks of both crashing and of the crashes being HBD. The presence of casinos within the local ZIP code is estimated to be unrelated to crash risks but positively associated with the odds that those crashes are HBD, whereas the presence of casinos in adjacent communities is related to higher population rates of crashes. High levels of general retail in a community and adjacent areas both predict higher risks of crashes among local populations while reducing the likelihood that those crashes will be alcohol-involved.

Table 3.

Relative risks associated with local and adjacent outlets, among total injury crashes and crash types.

Variablea	Total injury crashes (vs. total population) median (95% C.I.)	Had been drinking crashes (vs. all injury crashes) median (95% C.I.)	Single-vehicle night crashes (vs. all injury crashes) median (95% C.I.)
Local bar/pub density (100s/sq. mile)	0.714 (0.364, 1.330)	1.876 (1.292, 2.745)*	1.633 (0.797, 3.219)
Spatial lag bar/pub density (100s/sq. mile)	2.326 (0.324, 20.499)	0.742 (0.332, 1.740)	44.541 (11.819, 167.553)*
Local restaurant density (100s/sq. mile)	1.705 (1.426, 2.049)*	1.068 (0.951, 1.196)	1.055 (0.859, 1.334)
Spatial lag restaurant density (100s/sq. mile)	0.112 (0.066, 0.143)*	1.331 (1.099, 1.644)*	0.589 (0.431, 0.802)*
Local off-premise density (100s/sq. mile)	0.281 (0.200, 0.428)*	0.864 (0.696, 1.074)	0.128 (0.089, 0.184)*
Spatial lag off-premise density (100s/sq. mile)	9.584 (3.601, 26.91)*	1.924 (1.174, 3.082)*	1.218 (0.642, 2.267)
Local casinos (dummy variable)	1.004 (0.905, 1.114)	1.057 (1.009, 1.107)*	0.980 (0.924, 1.040)
Spatial lag casinos (proportion of neighbors)	1.330 (1.042, 1.698)*	1.085 (0.964, 1.223)	1.014 (0.880, 1.169)
Local total retail density (100s/sq. mile)	1.107 (1.079, 1.143)*	0.953 (0.936, 0.970)*	0.916 (0.878, 0.952)*
Spatial lag retail density (100s/sq. mile)	1.211 (1.169, 1.252)*	0.952 (0.933, 0.970)*	0.997 (0.970, 1.026)
Deviance (−2* logLikelihood)	111,260	74,520	67,310

These results are from an equivalent model to that presented in Table 2, except that separate variables are entered for the mean outlet densities among adjacent ZIP codes. Results for non-retail variables are not reproduced here because they are extremely similar to those in Table 2.

5. Discussion

The empirical literature is divided regarding the relationship between alcohol outlet densities and alcohol-involved traffic crashes. The lack of agreement may arise because a high density of alcohol outlets logically implies both increased alcohol consumption and reduced driving distances, resulting in indeterminate predictions for risk of alcohol-involved crashes. The analyses presented here separately investigated the relationship of alcohol availability and injury crashes from the relationship of alcohol availability to the probability that an injury crash was alcohol-involved. Further, we used officers’ assessments of whether drivers had been drinking (HBD) as well as a traditional alcohol surrogate, single vehicle night time crash (SVN). Each model controlled for the effects of general retail density so that the estimates for alcohol outlet densities can be interpreted as the extra risk due to a retailer selling alcohol.

5.1. Retail density and crash risks

Hypothesis 1 predicted that greater numbers of injury crashes relative to population would occur in association with greater density of retail establishments in general and of alcohol establishments in particular. As expected, the results indicate that local crash rates were positively related to overall retail densities both within a given ZIP code and in adjacent areas. The results were somewhat mixed, however, regarding whether alcohol outlets had additional positively associations with crash risks than accounted for by their role as general retail outlets. The density of bars and pubs was not found to have a well-supported association beyond that of general retail, while the well-supported estimates for restaurants and off-premise outlets were in opposite directions and both differed in direction between local and adjacent-unit effects. The presence of a casino had a well-supported impact on crashes in surrounding ZIP codes but not locally.

5.2. Bar density and alcohol involvement

Hypothesis 2 predicted that greater proportions of injury crashes will be alcohol related in areas with greater densities of bars due to the greater capacity for alcohol consumption. The results in Table 2 support this hypothesis, indicating that local bar density was positively related to the likelihood that a crash falls into each of the alcohol-involved categories, had-been-drinking and single-vehicle-nighttime. Table 3 suggests that the positive bar density effect operated locally for the risk of HBD, but primarily affected neighboring ZIP codes for SVN. Densities of other alcohol outlets were less clearly related to alcohol-involvement. ZIP codes with casinos exhibited slightly elevated risks that an injury crash would be categorized as had-been-drinking, even after allowing for the effects of alcohol licenses held by these gambling establishments, supporting prior evidence that casinos are positively associated with traffic fatalities (Cotti and Walker, 2010). General retail density was related to lower risks of crashes being alcohol-related in both the local and adjacent ZIP codes.

5.3. Outlet effects are relatively small

Although the statistical model and large data set used here had considerable power to identify well-supported impacts of outlet densities, it should be noted that these physical availability differences were not associated with large variation in relative risks. Table 4 presents simulated percentage changes in crashes and alcohol-involvement risks associated with a one percent increase of each type of outlet density in every ZIP code, calculated from the median relative rate estimates presented in Table 3. Although many of the outlet effects were well supported by the regression results (displayed in bold in the table), in no instance does a 1% outlet density increase lead to even a 0.1% change in estimated risks for crashes or alcohol-involvement. Thus the high statistical power of these models allows us to reject both the absence of outlet density effects and the hypothesis that these impacts are particularly large.

Table 4.

Average change in relative risk for a 1% rise in outlet densities.

Outlet type	Total crashes relative to population	HBD crashes relative to total crashes	SVN crashes relative to total crashes
Bar/pub density
Local	−0.003%	0.005%	0.004%
Spatially lagged	0.007%	−0.002%	0.030%
Restaurant density
Local	0.025%	0.003%	0.002%
Spatially lagged	−0.095%	0.013%	−0.023%
Off-premise density
Local	−0.035%	−0.004%	−0.056%
Spatially lagged	0.061%	0.018%	0.005%
Total retail density
Local	0.025%	−0.012%	−0.022%
Spatially Lagged	0.045%	−0.011%	−0.001%

Note: this table simulates the average change in predicted crash or alcohol-involvement risks if every ZIP code had one percent more establishments of the specified outlet type than it actually had in each year. This simulation is based on posterior effect estimates from Table 3. Changes for well-supported outlet density effects are shown in bold.

The spatial aspects of these results provide some insights for investigating the relationships between outlet densities and motor vehicle crash risks. The local and adjacent-unit outlet density effects shown in Tables 2 and 3 suggest that the spatial dynamics of motor vehicle crashes extend beyond the size of a typical ZIP code. In some cases the effects of local and adjacent outlet densities are in the same direction, in which case their combined effect might be considerably larger than predicted by a model that does not allow for spatially-lagged outlet effects. For example, an increase of 100 total retail establishments per square mile (an extremely large proportional increase) across all ZIP codes would be expected to raise population crash rates by 8.8% according to Table 2, but its combined local and adjacent-unit effect from Table 3 imply a 34.1% rise in crash risks (calculated by multiplying the local relative rate of 1.107 times the adjacent relative rate of 1.211). In cases in which the local and adjacent outlet effects are in opposite directions, however, accounting for spatially-lagged densities can reduce the expected outlet-density effect or even change its direction. For example, Table 2 suggests that an increase of 100 restaurants per square mile would be associated with a 116% increase in population crash rates, whereas multiplying the local and adjacent-ZIP relative rates from Table 3 suggests a decrease in crash risk of nearly 81%. These examples indicate that predictions regarding motor vehicle crashes can be quite sensitive to the scale of geographic units as well as to whether models allow for spatially-lagged outlet density effects.

5.4. Residual spatial patterns

The large and highly-significant spatial autocorrelations in these models provide additional evidence of crash risks extending beyond ZIP-code boundaries. The positive autocorrelations, ranging from approximately 0.45 in the crash and SVN analyses to 0.77 in the HBD analysis, suggest that crash risks tend to be similar between adjacent ZIP codes even after accounting for local characteristics. These conditional autoregressive random effects made it possible to identify specific geographic patterns in risk that are not explained by other covariates, in particular noting elevated population crash rates near two of California’s largest east-west transportation corridors (San Francisco to Reno via Sacramento in the north, Los Angeles to Las Vegas in the south; left panel of Fig. 1). The elevated crash risks within these major metropolitan areas may be due to commuting, while the high risks between these pairs of cities might reflect long-distance traffic along these major east-west transportation corridors (I-80 and Highway 50 in the north, I-15 and I-40 in the south) being very high relative to the small local populations. These spatial random effects had to be estimated separately for each year due to changes in ZIP code boundaries, but their stable geographic patterns across years suggests that the CAR models are identifying time-invariant geographic differences that are not explained by model covariates. The ability to map otherwise unexplained spatial patterns has considerable potential for identifying local population or transportation-network characteristics that are associated with elevated risks of alcohol-involved traffic crashes.

5.5. Limitations and future directions

This study has several important limitations. (1) Alcohol license data from January will not perfectly reflect outlet densities for crashes at other times of year, potentially biasing effect estimates toward finding no association. (2) Outlet density effects could be biased by the lack of important transportation variables available at the ZIP code level data across the ten years studied. For example, areas with high retail densities would presumably have low traffic speeds, but this could not be explicitly controlled due to the lack of an appropriate speed-limit covariate. (3) The spatial units of analysis do not necessarily match the scale of the underlying activity. ZIP codes tend to be physically compact in urban areas but extremely large in rural places. Although city dwellers may easily visit alcohol outlets across many ZIP codes, rural residents may have to drive long distances to reach establishments within their home ZIP code. (4) The measure of spatial connections between units may be inappropriate. The current study uses simple adjacency to calculate spatially-lagged outlet densities. An alternative approach might inversely weight outlet densities by their distance or driving times from a given geographic unit, but this would involve significant computational difficulty. (5) The large spatial autocorrelations and substantive spatial lag effects presented above suggest that the characteristic scale of traffic crashes is larger on average than zip code areas, and particularly so in urban areas and (6) the combination of local and spatially-lagged outlet density effects with strongly-positive spatial autoregressive effects would suggest that the total impacts of alcohol outlets may be much greater than has been estimated here (LeSage and Pace, 2009).

Future studies could address many of these concerns by exploring data and analytical assumptions that better reflect local conditions and travel patterns. More highly-resolved geographic units could better account for local road conditions such as traffic flow, congestion and vehicle speed. The use of high-resolution spatial units increases the likelihood that any vehicle trip will cross multiple geographic units, suggesting the usefulness of defining spatial connectedness by more than simple adjacency. One possibility might define the degree of connectedness between areas based on the how well they are linked by the road network. Another might allow each neighborhood’s alcohol availability to be defined not only by outlet densities within itself and nearby communities, but also by retail availability in a highly-connected downtown area.

6. Conclusions

This research suggests that local retail densities are positively associated with the population risks of motor vehicle crashes resulting in injury. These analyses provide additional evidence that various types of alcohol outlets have effects on risks beyond those of non-alcohol retailers. Although these ZIP-code level models have identified statistically well-supported associations between alcohol outlet densities and injury crash rates, the estimated effect sizes are too small to recommend physical availability reductions as a powerful policy to reduce traffic injuries. Future studies using higher-resolution geographic units and better controls for travel patterns and road conditions may offer improved ability to estimate these effects.