Low-rank and Sparse Matrix Decomposition for Accelerated Dynamic MRI with Separation of Background and Dynamic Components

Abstract

Purpose

To apply the low-rank plus sparse (L+S) matrix decomposition model to reconstruct undersampled dynamic MRI as a superposition of background and dynamic components in various problems of clinical interest.

Theory and Methods

The L+S model is natural to represent dynamic MRI data. Incoherence between k−t space (acquisition) and the singular vectors of L and the sparse domain of S is required to reconstruct undersampled data. Incoherence between L and S is required for robust separation of background and dynamic components. Multicoil L+S reconstruction is formulated using a convex optimization approach, where the nuclear-norm is used to enforce low-rank in L and the l₁-norm to enforce sparsity in S. Feasibility of the L+S reconstruction was tested in several dynamic MRI experiments with true acceleration including cardiac perfusion, cardiac cine, time-resolved angiography, abdominal and breast perfusion using Cartesian and radial sampling.

Results

The L+S model increased compressibility of dynamic MRI data and thus enabled high acceleration factors. The inherent background separation improved background suppression performance compared to conventional data subtraction, which is sensitive to motion.

Conclusion

The high acceleration and background separation enabled by L+S promises to enhance spatial and temporal resolution and to enable background suppression without the need of subtraction or modeling.

Introduction

The application of compressed sensing (CS) to increase imaging speed and efficiency in MRI demonstrated great potential to overcome some of the major limitations in terms of spatial and temporal resolution, volumetric coverage and sensitivity to motion. CS exploits the fact that an image is sparse in some appropriate basis to reconstruct undersampled data without loss of information (1–3). Successful application of CS requires image sparsity and incoherence between the acquisition space and representation space. MRI presents favorable conditions for the application of CS, since (a) medical images are naturally compressible by using appropriate sparsifying transforms, such as wavelets, finite differences, learned dictionaries (4) and many others, and (b) MRI data are acquired in the spatial frequency domain (k-space) rather than in the image domain, which facilitates the generation of incoherent aliasing artifacts via random undersampling of Cartesian k-space or the use of non-Cartesian k-space trajectories. Image reconstruction is performed by enforcing sparsity in the solution, subject to data consistency constraints. A key advantage for MRI is that CS can be combined with parallel imaging to further increase imaging speed by exploiting joint sparsity in the multicoil image ensemble rather than in each coil separately (5–8). Dynamic MRI is particularly well suited for the application of CS, due to extensive spatiotemporal correlations that result in sparser representations than would be obtained by exploiting spatial correlations alone.

Low-rank matrix completion extends the idea of compressed sensing to matrices, enabling recovery of missing or corrupted entries of a matrix under low-rank and incoherence conditions (9). In a similar fashion to sparse signals/images, which only have few large coefficients, low-rank matrices, which only have a few large singular values, depend upon a smaller number of degrees of freedom and undersampling becomes possible. Low-rank matrix completion from what seems to be incomplete information is performed by minimizing the nuclear-norm of the matrix (sum of singular values), which is the analog of the l₁-norm for signal vectors (sum of absolute values) (10). Low-rank matrix completion has been applied to dynamic MRI by considering each temporal frame as a column of a space-time matrix, where the spatiotemporal correlations produce a low-rank matrix (11,12). Local k-space correlations in a multicoil data set have been exploited to perform calibrationless parallel imaging reconstruction via low-rank matrix completion (13).

The combination of compressed sensing and low-rank matrix completion represents an attractive proposition for further increases in imaging speed. In dynamic MRI, previous work on this combination proposed finding a solution that is both low-rank and sparse (14,15). A different model suggested decomposing a data matrix as a superposition of a low-rank component (L) and a sparse component (S) (16,17). Whereas topics in graphical modeling motivate the L+S decomposition in (17), the aim in (16) is to use the L+S decomposition to perform robust principal component analysis (RPCA); that is to say, to recover the principal components of a data matrix with missing or corrupted entries. RPCA improves the performance of classical PCA in the presence of sparse outliers, which are captured in the sparse component S. RPCA, or equivalently the L+S decomposition, has been successfully applied to computer vision, where it enables separation of the background from the foreground in a video sequence (16), to image alignment (18), and to image reconstruction in 4DCT with reduced numbers of projections (19).

The L+S decomposition is natural for dynamic imaging, where L can model the temporally correlated background and S can model the dynamic information that lies on top of the background. Early work on the application of L+S to dynamic MRI has been reported by Gao et al., initially for the reconstruction of retrospectively undersampled cardiac cine datasets (20) and more recently for the reconstruction of an accelerated series of diffusion-weighted images (21). In parallel to Gao's latest work, we have developed a L+S reconstruction approach for accelerated dynamic contrast-enhanced imaging, which was tested on prospectively undersampled data sets (22,23).

Here we extend this preliminary work to present L+S reconstruction of various accelerated dynamic MRI datasets of clinical interest, and to introduce novel applications, such as separation of contrast enhancement from background and automated background suppression without the need of subtraction or modeling. We also demonstrate the superior compressibility of the L+S model compared to using a sparse or low-rank model only, which is the empirical basis that supports improved performance of the L+S method. Reconstruction of highly-accelerated dynamic MRI data corresponding to cardiac perfusion, cardiac cine, time-resolved peripheral angiography, abdominal and breast perfusion using Cartesian and golden-angle radial sampling are presented to show feasibility and general applicability of the L+S method. This work extends our conference publications (22,23) to present compressibility analysis for the L+S model, convergence analysis of the reconstruction algorithm, application to patient studies and detailed discussion about the pros and cons of the proposed method¹. Matlab code that reproduces some of the examples presented in this work is available at cai2r.net/resources/software/ls-reconstruction-matlab-code

Theory

L+S matrix decomposition

The L+S approach aims to decompose a matrix M as a superposition of a low-rank matrix L (few non-zero singular values) and a sparse matrix S (few non-zero entries). The decomposition is unique and the problem is well posed if the low-rank component is not sparse, and, vice versa, if the sparse component does not have low rank (16,17). We refer to this condition as incoherence between L and S. For example, these conditions are guaranteed if the singular vectors of L are not sparse and if the nonvanishing entries of S occur at random locations (16).

The L+S decomposition is performed by solving the following convex optimization problem:

$$\text{min}{\Vert L\Vert }_{*}+\lambda {\Vert S\Vert }_{1}s.t.M=L+S,$$ (1)

where ‖L‖_* is the nuclear norm or sum of singular values of the matrix L, ‖S‖₁ is the l₁-norm or sum of absolute values of the entries of S and λ is a tuning parameter that balances the contribution of the l₁-norm term relative to the nuclear norm term.

L+S representation of dynamic MRI

In analogy to video sequences and following the work of Gao et al. (20), dynamic MRI can be inherently represented as a superposition of a background component, which is slowly changing over time, and a dynamic component, which is rapidly changing over time. The background component corresponds to the highly correlated information among frames. The dynamic component captures the innovation introduced in each frame, which can be assumed to be sparse or transform-sparse since substantial differences between consecutive frames are usually limited to comparatively small numbers of voxels. Our hypothesis is that the L+S decomposition can represent dynamic MRI data more efficiently than a low-rank or sparse model alone, or than a model in which both constraints are enforced simultaneously.

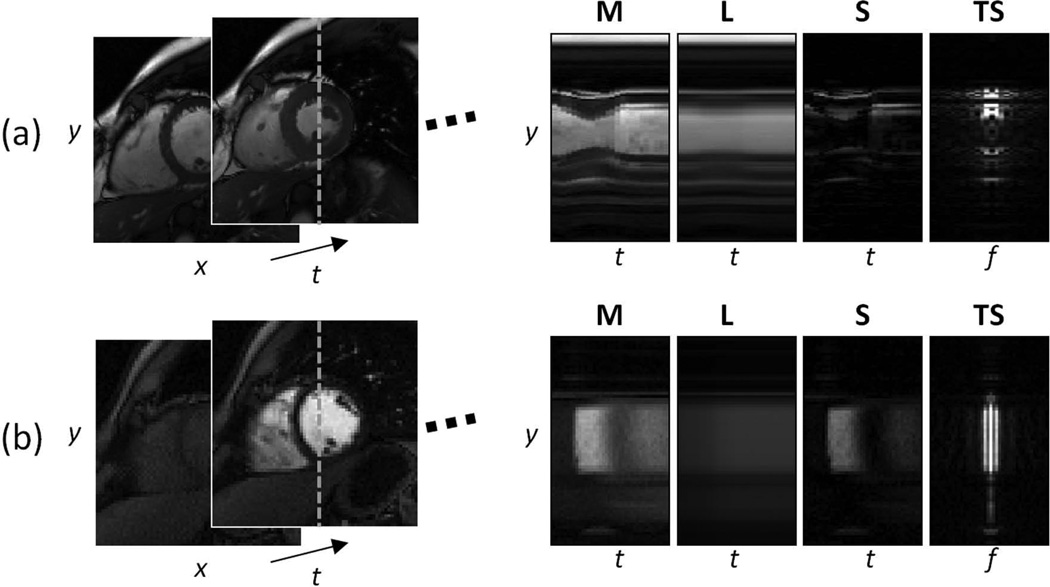
The time-series of images in a dynamic MRI data set is converted to a matrix M, where each column is a temporal frame, in order to apply the L+S decomposition approach. Figure 1 shows the L+S decomposition of cardiac cine and perfusion data sets, where L captures the correlated background between frames and S captures the dynamic information (heart motion for cine and contrast-enhancement for perfusion). Note that the L component is not constant over time, but is rather slowly changing among frames, which differs from just taking a temporal average. In fact, for the case of cardiac cine, the L component includes periodic motion in the background, since it is highly correlated among frames.

Figure 1.

L+S decomposition of fully-sampled 2D cardiac cine (a) and perfusion (b) data sets corresponding to the central × location. The low-rank component L captures the correlated background among temporal frames and the sparse component S the remaining dynamic information (heart motion for cine and contrast-enhancement for perfusion). The L component is not static, but is rather slowly changing over time and contains the most correlated component of the cardiac motion (a) and contrast enhancement (b). The rightmost column shows the sparse component S in y−f space (Fourier transform along the columns), which shows increased sparsity compared to the original y−t domain.

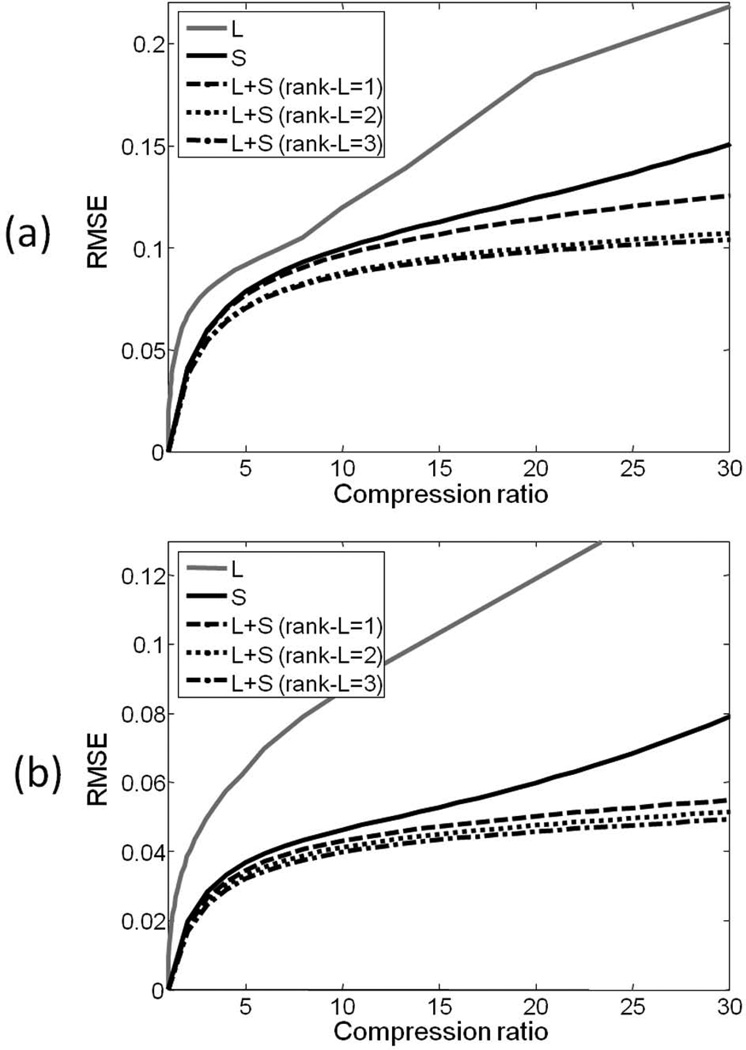
Another important feature is that the S component has sparser representation than the original matrix M, since the background has been suppressed. This gain in sparsity is already obvious in the original y−t space, but it is more pronounced in an appropriate transform domain where dynamic MRI is usually sparse, such as the temporal frequency domain (y−f) that results from applying a Fourier transform along the columns of S (rightmost column of Figure 1). This increase in sparsity given by the background separation will in principle enable higher acceleration factors, since fewer coefficients need to be recovered, if the load to represent the low-rank component is lower. In order to test this hypothesis, the compressibility of dynamic MRI data using L, S and L+S models were compared quantitatively on the cardiac cine and perfusion data sets mentioned above. Rate-distortion curves were computed using the root mean square error (RMSE) as distortion metric (Figure 2). Data compression using the low-rank (L) model was performed by truncating the SVD representation of the dynamic image series. Data compression using the sparse (S) model was performed by discarding low-value coefficients in the transform domain according to the target compression ratio, i.e. only the top n/C coefficients were used to represent the image, where n is the total number of coefficients and C is the target compression ratio. Data compression using the L+S model was performed by assuming a fixed low-rank approximation, e.g. rank(L) = 1, 2 or 3, which was subtracted from the original matrix M to get S. S was then transformed to the sparse domain and coefficients were discarded according to the target compression rate and the number of coefficients to represent the L component, e.g. the top n/C-n_L coefficients were used to represent S, with n_L coefficients used to represent L. n_L is given by rank(L)×(n_s + n_t − rank(L)), where n_s is the number of spatial points and n_t is the number of temporal points. The rate-distortion curves in Figure 2 clearly show the advantages of the L+S model in representing dynamic MRI images with fewer degrees of freedom, which will lead to higher undersampling factors.

Figure 2.

Root mean square error (RMSE) vs. compression ration curves for fully-sampled (a) cardiac cine and (b) cardiac perfusion data sets using low-rank (L), sparsity in the temporal Fourier domain (S) and low-rank + sparsity in the temporal Fourier domain (L+S). For the L+S model, compression ratios were computed by fixing the rank of the L component to 1, 2 or 3. The L+S model presents lower compression errors than the L or S models, particularly at higher compression ratios. This gain in compressibility is expected to increase the undersampling capability of L+S reconstruction compared to low-rank approximations or conventional compressed sensing(sparsity only).

Incoherence requirements

L+S reconstruction of undersampled dynamic MRI data involves three different types of incoherence:

• Incoherence between the acquisition space (k−t) and the representation space of the low-rank component (L)

• Incoherence between the acquisition space (k−t) and the representation space of the sparse component (S)

• Incoherence between L and S spaces, as defined earlier.

The first two types of incoherence are required to remove aliasing artifacts and the last one is required for separation of background and dynamic components. The standard k−t undersampling scheme used for compressed sensing dynamic MRI, which consists of different variable-density k-space undersampling patterns selected in a random fashion for each time point, can be used to meet the requirement for the first two types of incoherence. Note that in this sampling scheme, low spatial frequencies are usually fully-sampled and the undersampling factor increases as we move away from the center of k-space. First, high incoherence between k−t space and L is achieved since the column space of L cannot be approximated by a randomly selected subset of high spatial frequency Fourier modes and the row-space of L cannot be approximated by a randomly selected subset of temporal delta functions. Second, if a temporal Fourier transform is used, incoherence between k−t space and x−f space is maximal, due to their Fourier relationship. This analysis also holds for non-Cartesian k-space trajectories, where undersampling only affects the high spatial frequencies even if a regular undersampling scheme is used. The third type of incoherence is independent of the sampling pattern and depend only on the sparsifying transform used in the reconstruction.

L+S reconstruction of undersampled dynamic MRI

The L+S decomposition given in Eq. (1) was modified to reconstruct undersampled dynamic MRI as follows:

$$\text{min}{\Vert L\Vert }_{*}+\lambda {\Vert TS\Vert }_{1}s.t.E(L+S)=d,$$ (2)

where T is a sparsifying transform for S, E is the encoding or acquisition operator and d is the undersampled k−t data. L and S are defined as space-time matrices, where each column is a temporal frame, and d is defined as a stretched-out single column vector. We assume that the dynamic component S has a sparse representation in some known basis T (e.g., temporal frequency domain), hence the idea of minimizing ‖TS‖₁ and not ‖S‖₁ itself. Note that E is a general linear operator that maps a matrix to a vector. For a single-coil acquisition, the encoding operator E performs a frame-by-frame undersampled spatial Fourier transform. For acquisition with multiple receiver coils, E is given by the frame-by-frame multicoil encoding operator, which performs a multiplication by coil sensitivities followed by an undersampled Fourier transform, as described in the iterative SENSE algorithm (24). In this work, we focus on the multicoil reconstruction case, which enforces joint multicoil low-rank and sparsity and thus improves the performance as was demonstrated previously for the combination of compressed sensing and parallel imaging (7).

A version of Eq. (2) using regularization rather than strict constraints can be formulated as follows:

$$\underset{L,S}{\text{min}}\frac{1}{2}{\Vert E(L+S)-d\Vert }_2^2+{\lambda }_L{\Vert L\Vert }_{*}+{\lambda }_S{\Vert TS\Vert }_1,$$ (3)

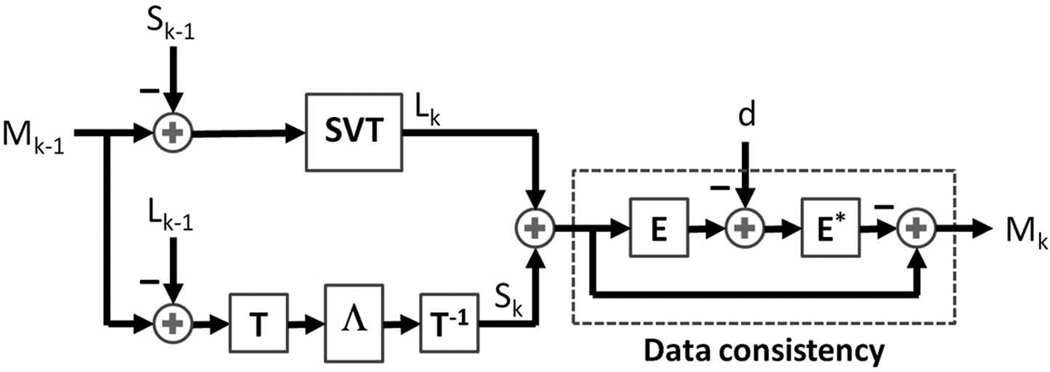
where the parameters λ_L and λ_S trade off data consistency versus the complexity of the solution given by the sum of the nuclear and l₁ norms. In this work, we solve the optimization problem in Eq. (3) using iterative soft-thresholding of the singular values of L and of the entries of TS. We define the soft-thresholding or shrinkage operator as ${\mathrm{\Lambda }}_{\mathrm{\lambda }}(x)=\frac{x}{|x|}\text{max}(|x|-\lambda ,0)$, in which x is a complex number and the threshold λ is real valued. We extend this to matrices by applying the shrinkage operation to each entry. Next, we define the singular value thresholding (SVT) by SVT_λ (M) = UΛ_λ (Σ)V^H, where M = UΣV^H is any singular value decomposition of M. Table 1 and Figure 3 summarize the proposed L+S reconstruction algorithm, where at the k-th iteration the SVT operator is applied to M_k−1−S_k−1, then the shrinkage operator is applied to M_k−1−L_k−1 and the new M_k is obtained by enforcing data consistency, where the aliasing artifacts corresponding to the residual in k-space E^* (E(L_k + S_k − d)) are subtracted from L_k+S_k. Here E^* refers to the adjoint operator of E, which maps a vector to a matrix. The algorithm iterates until the relative change in the solution is less than 10⁻⁵, namely, until ‖L_k + S_k − (L_k−1 + S_k−1)‖₂ ≤ 10⁻⁵ ‖L_k−1 + S_k−1‖₂.

Table 1.

L+S reconstruction algorithm for undersampled dynamic MRI

L+S using iterative soft-thresholding
input:
d: multicoil undersampled k−t data
E: space-time multicoil encoding operator
T: sparsifying transform
λL: singular-value threshold
λS: sparsity threshold
initialize: M0 = E*d, S0 = 0
while not converged do
% L: singular-value soft-thresholding
Lk = SVTλL (Mk−1 − Sk−1)
% S: soft-thresholding in the T domain
Sk = T−1(ΛλS (T(Mk−1 − Lk−1)))
% Data consistency: subtract residual
Mk = Lk + Sk − E*(E(Lk + Sk) − d)
end while
output: L, S

Figure 3.

Sequence of operations for the k-th iteration of the L+S reconstruction algorithm (see also Table 1). First, a singular value thresholding (SVT) is applied to M_k−1−S_k−1 to get L_k; second, the soft-thresholding (ST) operator is applied to M_k−1−L_k−1 in the T domain to get S_k; and third, data consistency is enforced to update the intermediate solution M_k, where the aliasing artifacts corresponding to the residual in k-space E^*(E(L_k+S_k)−d) are subtracted from L_k+S_k. The forward encoding operator E receives a space-time matrix as input and outputs a multicoil k-space representation and the adjoint encoding operator E^* performs the reverse operation as described in the iterative SENSE technique.

This algorithm represents a combination of singular value thresholding used for matrix completion (10) and iterative soft-thresholding used for sparse reconstruction (25). Its convergence properties can be analyzed by considering the algorithm as a particular instance of the proximal gradient method for solving a general convex problem of the form:

$$\text{min}g(x)+h(x).$$ (4)

Here, g is convex and smooth (the quadratic term in Eq. (3)), h is convex but not necessarily smooth (the sum of the nuclear and l₁ norms in Eq. (3)). The proximal gradient method takes the form:

$$x_k={\mathit{\text{prox}}}_h(x_{k-1}-t_k\nabla g(x_{k-1})),$$ (5)

where t_k is a sequence of step sizes and prox_his the proximity function for h:

$${\mathit{\text{prox}}}_h(y)=\text{arg}\underset{x}{\text{min}}\frac{1}{2}{\Vert y-x\Vert }_2^2+h(x).$$ (6)

When h(x) represents the nuclear-norm, the proximity function may be shown to be equivalent to soft-thresholding of the singular values, and when h(x) represents the l₁-norm, the proximity function is given by soft-thresholding of the coefficients. Using a constant step size t, the proximal gradient method for Eq. (3) becomes:

$$L_k=SV{T}_{{\lambda }_L}(L_{k-1}-t{E}^{*}(E(L_{k-1}+S_{k-1})-d))S_k=T^{-1}\left[{\mathrm{\Lambda }}_{{\lambda }_S}\right(T[S_{k-1}-t{E}^{*}(E(L_{k-1}+S_{k-1})-d)]\left)\right].$$ (7)

This is equivalent to the iterations given in Table 1 with the proviso that we set t=1. Note that the cost function is $f\left(\right[\begin{array}{c}\hfill L\hfill \\ \hfill S\hfill \end{array}\left]\right)$ and not f(L+S), so the gradient of the cost function is the stack of the gradient with respect to L and the gradient with respect to S. Given the convex and smooth function g as follows:

$$g\left(\right[\begin{array}{c}\hfill L\hfill \\ \hfill S\hfill \end{array}\left]\right)={\Vert [\begin{array}{cc}\hfill E\hfill & \hfill E\hfill \end{array}]\left[\begin{array}{c}\hfill L\hfill \\ \hfill S\hfill \end{array}\right]-d\Vert }^2,$$ (8)

general theory (26,27) asserts that the iterates in Eq. (7) will eventually minimize the value of the objective in Eq. (3) if:

$$t<\frac{2}{{\Vert [\begin{array}{cc}\hfill E\hfill & \hfill E\hfill \end{array}]\Vert }^2}=\frac{1}{{\Vert E\Vert }^2}=\frac{1}{{\lambda }_{\text{max}}(E^{*}E)},$$ (9)

where ‖E‖ is the spectral norm of E or, in other words, the largest singular value of E (and ‖E‖² is therefore the largest singular value of E^* E). When t=1, this reduces to ‖E‖² < 1. In our setup, the linear operator E is given by the multiplication of Fourier encoding elements and coil sensitivities. Normalizing the encoding operator E by dividing the Fourier encoding elements by $\sqrt{n}$, where n is the number of pixels in the image, and the coil sensitivities by their maximum value, gives ‖E‖² = 1 for the fully-sampled case and ‖E‖² < 1 for the undersampled case.

Methods

The feasibility of the proposed L+S reconstruction was first tested using retrospective undersampling of fully-sampled data, which enables comparison reconstruction results with the fully-sampled reference. We compared the performance of the L+S reconstruction against compressed sensing using a temporal sparsifying transform (CS) and against joint low-rank and sparsity constraints (L&S²). The latter approach was implemented for comparison purposes only using the following optimization problem:

$$\underset{L,S}{\text{min}}\frac{1}{2}{\Vert EM-d\Vert }_2^2+{\lambda }_L{\Vert M\Vert }_{*}+{\lambda }_S{\Vert TM\Vert }_1.$$ (9)

In a second step, the L+S reconstruction method was validated on prospectively accelerated acquisitions with k−t undersampling patterns for Cartesian and radial MRI.

Image reconstruction

Image reconstruction was performed in Matlab (The MathWorks, Natick, MA). L+S reconstruction was implemented using the algorithm described in Table 1 and Figure 3. The multicoil encoding operator E was implemented using FFT for the Cartesian case and NUFFT (28) for the non-Cartesian case following the method used in the iterative SENSE algorithm (24). Coil sensitivity maps were computed from the temporal average of the accelerated data using the adaptive coil combination technique (29). The singular value thresholding step in Table 1 requires computing the singular value decomposition of a matrix of size n_s × n_t, where n_s is the number of pixels in each temporal frame and n_t is the number of time points. Since n_t is relatively small, this is not prohibitive and can be performed very rapidly.

The regularization parameters λ_L and λ_S were selected by comparing reconstruction performance for a range of values. For datasets with retrospective acceleration, reconstruction performance was evaluated using the root mean square error (RMSE) and for datasets with true acceleration, qualitative assessment in terms of residual aliasing artifacts and temporal fidelity was employed. The datasets were normalized by the maximum absolute value in the x-y-t domain in order to enable the utilization of the same regularization parameters for different acquisitions of similar characteristics.

For comparison purposes, standard CS reconstruction was implemented by enforcing sparsity directly on the full matrix M, which is equivalent to the k−t SPARSE-SENSE method (7). L&S reconstruction was implemented by simultaneously enforcing low-rank and sparsity constraints directly on the full matrix M. This approach enabled fair comparison, since the same optimization algorithm was used in all cases and only the manner in which the constraints are enforced was modified. Regularization parameters for CS and L&S were selected by comparing reconstruction performance for several parameter values. As for L+S parameter selection, CS and L&S reconstruction performance was compared using RMSE for experiments with retrospective acceleration and qualitative assessment of residual aliasing and temporal fidelity for experiments with true acceleration.

Simulated undersampling of fully-sampled Cartesian cardiac perfusion data

Data were acquired in a healthy adult volunteer with a modified TurboFLASH pulse sequence on a whole-body 3T scanner (Tim Trio, Siemens Healthcare, Erlangen, Germany) using a 12-element matrix coil array. A fully-sampled perfusion image acquisition was performed in a mid-ventricular short-axis location at mid diastole (trigger-delay=400ms) with an image matrix size of 128 × 128 and 40 temporal frames. Relevant imaging parameters include: FOV=320×320mm², slice-thickness=8mm, spatial resolution=3.2×3.2mm², and temporal resolution=307ms. Fully-sampled Cartesian data were retrospectively undersampled by a factor of 10 using a different variable-density random undersampling pattern along k_y for each time point (k_y−t undersampling) and reconstructed using CS, L&S and L+S methods with a temporal Fourier transform serving as sparsifying transform. Quantitative image quality assessment was performed using the metrics of RMSE and structural similarity index (SSIM) (30), with the fully-sampled reconstruction used as a reference. RMSE values are reported as percentages after normalizing by the l₂-norm of the fully-sampled reconstruction.

Simulated undersampling of fully-sampled Cartesian cardiac cine data

2D cardiac cine imaging was performed in a healthy adult volunteer using the same MR scanner as in the previous perfusion study. Fully-sampled data were acquired using a 256×256 matrix size (FOV = 320×320 mm²) and 24 temporal frames and retrospectively undersampled by a factor of 8 using a k_y−t variable-density random undersampling scheme. Image reconstruction was performed using multicoil CS, L&S and L+S methods with a temporal Fourier transform serving as sparsifying transform. Quantitative image quality assessment was performed using RMSE and SSIM metrics as described in the cardiac perfusion example.

Cardiac perfusion with prospective 8-fold acceleration on a patient

2D first-pass cardiac perfusion data with 8-fold k_y−t acceleration was acquired on a patient with known coronary artery disease using the pulse sequence described in (7). Relevant imaging parameters were as follows: image matrix size = 192×192, temporal frames = 40, spatial resolution=1.67×1.67mm² and temporal resolution = 60ms. Image reconstruction was performed using CS and L+S methods with a temporal Fourier transform using the same regularization parameters from the cardiac perfusion study with simulated acceleration. Signal intensity time courses were computed using manually drawn ROIs according to the 6-sector model of the myocardial wall defined by the American Heart Association (AHA).

Accelerated time-resolved peripheral MR angiography

Contrast-enhanced time-resolved 3D MR angiography of the lower extremities was performed in a healthy adult volunteer using an accelerated TWIST (Time-resolved angiography WIth Stochastic Trajectories) pulse sequence (31) on a 1.5T scanner (Avanto, Siemens Healthcare, Erlangen, Germany) equipped with a 12-element peripheral coil array. TWIST samples the center of k-space at the Nyquist rate and undersamples the periphery using a pseudo-random pattern, which is suitable to obtain sufficient incoherence for the L+S approach. Relevant imaging parameters were as follows: FOV = 500×375×115 mm³, acquisition matrix size = 512×230×42, number of frames = 10. An acceleration factor of 7.3 was used to achieve a temporal resolution of 6.4 seconds for each 3D image set. Image reconstruction was performed using the L+S approach without a sparsifying transform, since angiograms are already sparse in the image domain. For comparison purposes, a CS reconstruction which employed data subtraction was performed. The reference for data subtraction was acquired before the dynamic acquisition with 2-fold parallel imaging acceleration. After reconstructing the reference in k-space using GRAPPA (32), complex data subtraction was performed in k-space and the resulting time-series was reconstructed using CS with no sparsifying transform.

Free-breathing accelerated abdominal DCE-MRI with golden-angle radial sampling

Contrast-enhanced abdominal MRI data were acquired on a healthy volunteer during free breathing using a 3D stack-of-stars (radial sampling for k_y−k_x and Cartesian sampling for k_z) FLASH pulse sequence with a golden-angle acquisition scheme (33) on a whole-body 3T scanner (MAGNETOM Verio, Siemens Healthcare, Erlangen, Germany) equipped with a 12-element receiver coil array. Relevant imaging parameters include: FOV = 380×380mm², number of points for each radial spoke = 384, slice thickness = 3mm. 600 spokes were continuously acquired for each of 30 slices during free-breathing, to cover the entire liver (total acquisition time was 77 seconds). Golden-angle radial sampling (34) is well-suited for compressed sensing due to the presence of significant spatial and temporal incoherence given by the different k-space trajectory used to acquire each spoke. A time-series of incoherently undersampled frames with uniform coverage of k-space can be formed by grouping a Fibonacci number of consecutive spokes (35). 8 consecutive spokes were employed to form each temporal frame, resulting in a temporal resolution of 0.94 sec, which corresponds to an acceleration rate of 48 when compared to the Cartesian case with the same image matrix size. The reconstructed 4D image matrix size was 384×384×30×75 with a spatial resolution of 1×1×3mm³. Image reconstruction was performed using CS and L+S methods with temporal finite differences serving as sparsifying transform.

Free-breathing accelerated breast DCE-MRI with golden-angle radial sampling

Free-breathing breast DCE-MRI was performed on a patient referred for MRI-guided biopsy scans on a whole-body 3T scanner (MAGNETOM TimTrio, Siemens AG, Erlangen, Germany) equipped with a 7-element breast coil array (InVivo Corporation, Gainesville, FL). The same pulse sequence as for the liver case was employed for data acquisition. Relevant imaging parameters include: FOV= 280×280mm², number of points for each radial spoke = 256, slice thickness = 4mm. CS and L+S reconstructions were performed by grouping 21 consecutive spokes to form each temporal frame with temporal resolution = 2.6 seconds/volume and the reconstructed 4D image matrix size was 256×256×35×108. When compared to the Cartesian case with the same matrix size, the acceleration factor was 12.2.

Results

Simulated undersampling of fully-sampled Cartesian cardiac perfusion data

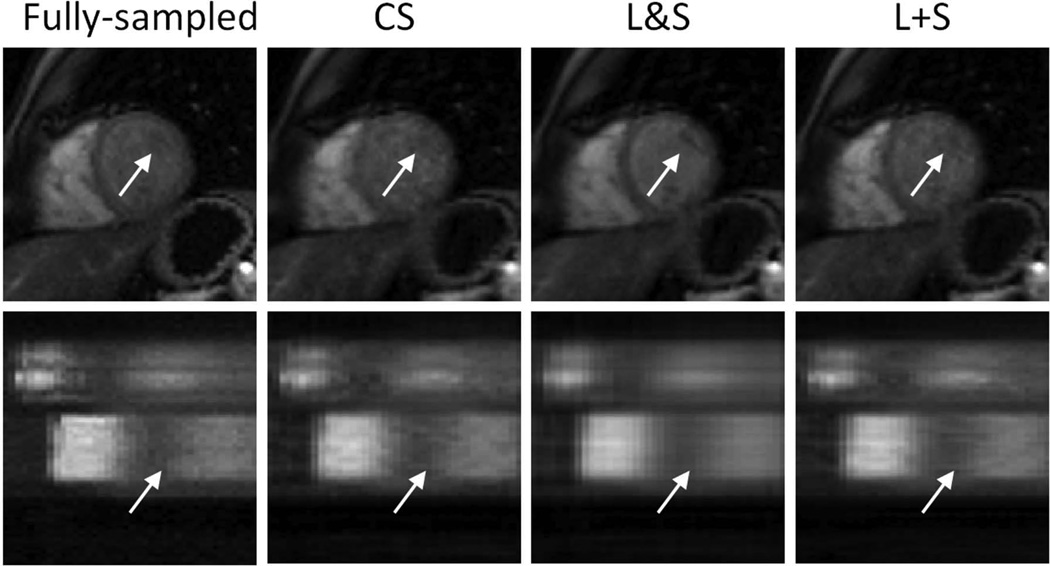
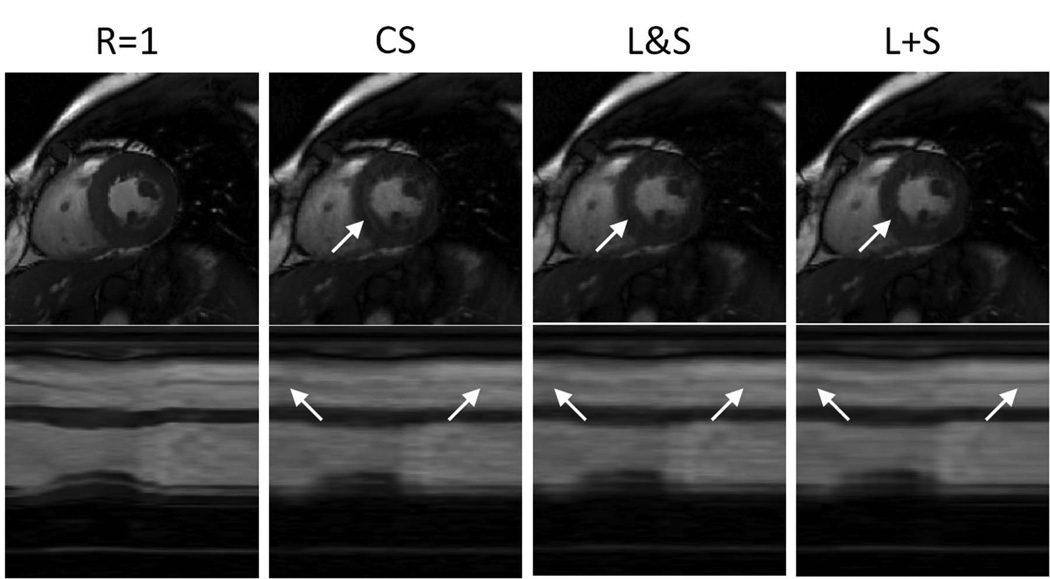
Figure S1.a (supplementary material) shows the effect of the regularization parameters λ_L and λ_S on the L+S reconstruction. High values of λ_L, which would correspond to removing an essentially static background, and very low values of λ_L, which would correspond to including substantial dynamic information in the L component, both increase the RMSE and lead to reduced performance. λ_L= 0.01 and λ_S = 0.01 presented the lowest RMSE. L+S reconstruction presented lower residual aliasing artifacts than CS and better temporal fidelity than L&S (Figure 4 and Video 1). The L&S may in certain respects look cleaner than the L+S images, but note that the left ventricle has a different contrast and the papillary muscles have a different shape than in the fully-sampled case (see arrows in Figure 4 - top row). The x−t plots show more temporal smoothing in the L&S reconstruction than in the L+S reconstruction (Figure 4 - bottom row). These qualitative findings are corroborated by the RMSE and SSIM values in Table S1 (supplementary material).

Figure 4.

Myocardial-wall-enhancement-phase images and x−t plots corresponding to reconstruction of cardiac perfusion data with retrospective 10-fold undersampling using compressed sensing (CS), simultaneous low-rank and sparsity constraints (L&S) and L+S decomposition (L+S). L+S presents lower residual aliasing artifacts than CS, and improved temporal fidelity as compared with L&S (arrows indicate temporal blurring artifacts in the L&S reconstruction).

Simulated undersampling of fully-sampled Cartesian cardiac cine data

As expected, the optimal regularization parameters for the L+S reconstruction of undersampled cardiac cine are different than the ones from cardiac perfusion, due to differences in dynamic information content (cardiac motion vs. contrast-enhancement) (Figure S1.b - supplementary material). λ_L= 0.0025 and λ_S = 0.00125 presented the lowest RMSE and temporal blurring artifacts. The L+S approach yields lower RMSE and higher SSIM than both CS and L&S (Table S1 - supplementary material). CS introduced temporal blurring artifacts, particularly at systolic phases where the heart is contracted and the myocardial wall is prone to signal leakage from other frames (Figure 5 and Video 2 show a bright ring in the myocardial wall for CS). Both, L&S and L+S, can significantly remove these artifacts, but L+S offers an improved estimation of the original cine image, as depicted by better preservation of fine structures in the x−t plots and reduced residual aliasing artifacts.

Figure 5.

Systolic-phase images and x−t plots corresponding to reconstruction of cardiac cine data with simulated 8-fold undersampling using compressed sensing (CS), simultaneous low-rank and sparsity constraints (L&S) and L+S decomposition (L+S). CS reconstruction presents temporal blurring artifacts (e.g. the ring in the myocardial wall indicated by the white arrow), which are effectively removed by both L&S and L+S reconstructions. However, L+S presents higher temporal fidelity (fine structures indicated by the arrows in the x−t plots) and lower residual aliasing artifacts.

Cardiac perfusion with prospective 8-fold acceleration on a patient

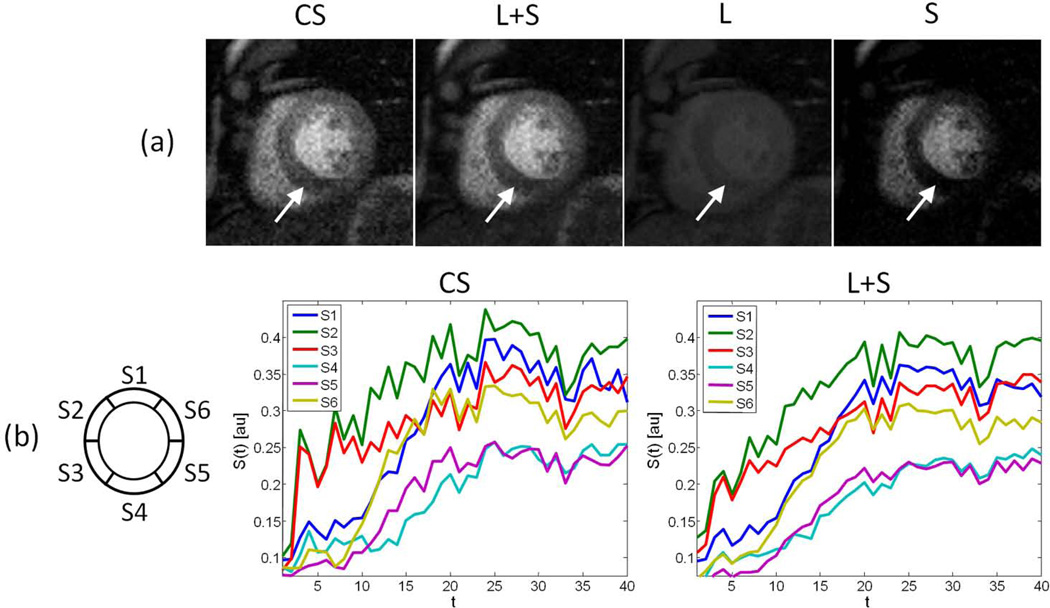
L+S presented lower residual aliasing artifacts than CS, which resulted in lower fluctuations in the SI curves (Figure 6 and Video 3). Both CS and L+S SI curves clearly show perfusion defects in sectors 4 and 5, which is in agreement with the static images. However, stronger temporal fluctuations in the CS reconstruction can pose challenges for accurate quantification. The regularization parameter for CS reconstruction was selected to provide similar temporal fidelity as in the L+S reconstruction, at the expense of increasing residual aliasing artifacts. One can also increase the regularization parameter to reduce aliasing artifacts, but with the adverse effect of introducing temporal blurring. The L+S approach offers improved performance in reducing aliasing artifacts without degrading temporal fidelity. In addition to improving the reconstruction quality compared to standard CS, L+S improved the visualization of the perfusion defect in the S component, where the background has been suppressed and improved contrast is observed between the healthy portion of the myocardium and the lesion. This capability may be useful to identify lesions that are difficult to visualize in the original image.

Figure 6.

(a) Myocardial-wall-enhancement-phase images and (b) signal intensity (SI) time-course for the six sectors defined in the American Heart Association model of the myocardium, resulting from reconstruction of the 8-fold accelerated cardiac perfusion scan performed on a patient with coronary artery disease using compressed sensing (CS) and L+S decomposition (L+S). The images and SI curves show a perfusion defect in sectors 4 and 5. Besides improving overall image quality and reducing temporal fluctuations in the SI time-course, the L+S approach improves the visualization of the perfusion defect (white arrow) in the sparse component S, where the background has been suppressed.

Accelerated time-resolved peripheral MR angiography

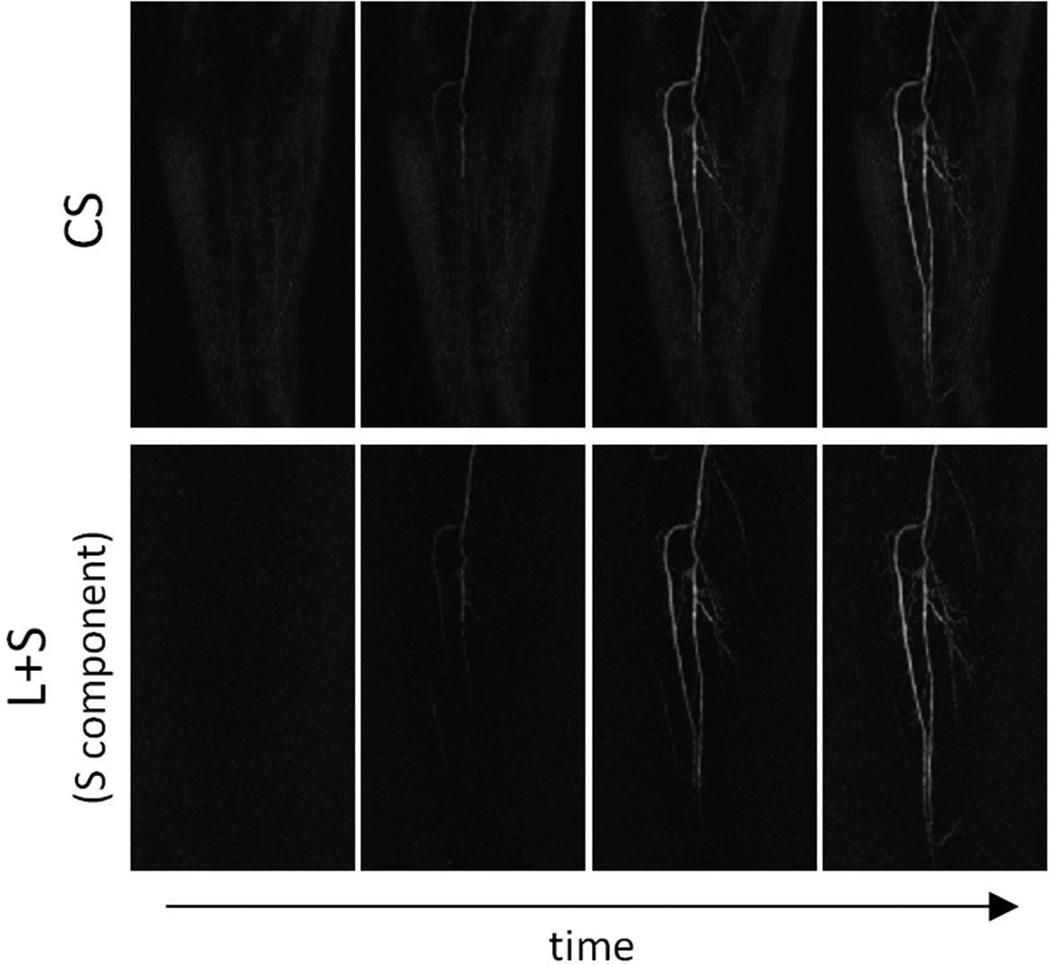
The L+S approach automatically separates the non-enhanced background from the enhanced vessels without the need of subtraction or modeling. At the same time, the S component provides angiograms with improved image quality as compared with CS reconstruction with raw data subtraction (Figure 7 and Video 4). CS reconstruction results in incomplete background suppression, which might be due, in part, to inconsistencies between the time-series of contrast-enhanced images and the reference used for subtraction.

Figure 7.

Maximum intensity projection (MIP) maps corresponding to CS and L+S reconstructions of the 7.3-fold accelerated time-resolved peripheral MR angiography data for three different contrast-enhancement phases. CS reconstruction employed raw data subtraction using a reference acquired before contrast injection. The L+S approach automatically separated the non-enhanced background from the enhanced vessels without the need of subtraction, and the S component presented improved angiograms compared to CS with data subtraction. In particular, small vessels are better visualized in the S component of the L+S reconstruction than in CS.

Free-breathing accelerated abdominal DCE-MRI with golden-angle radial sampling

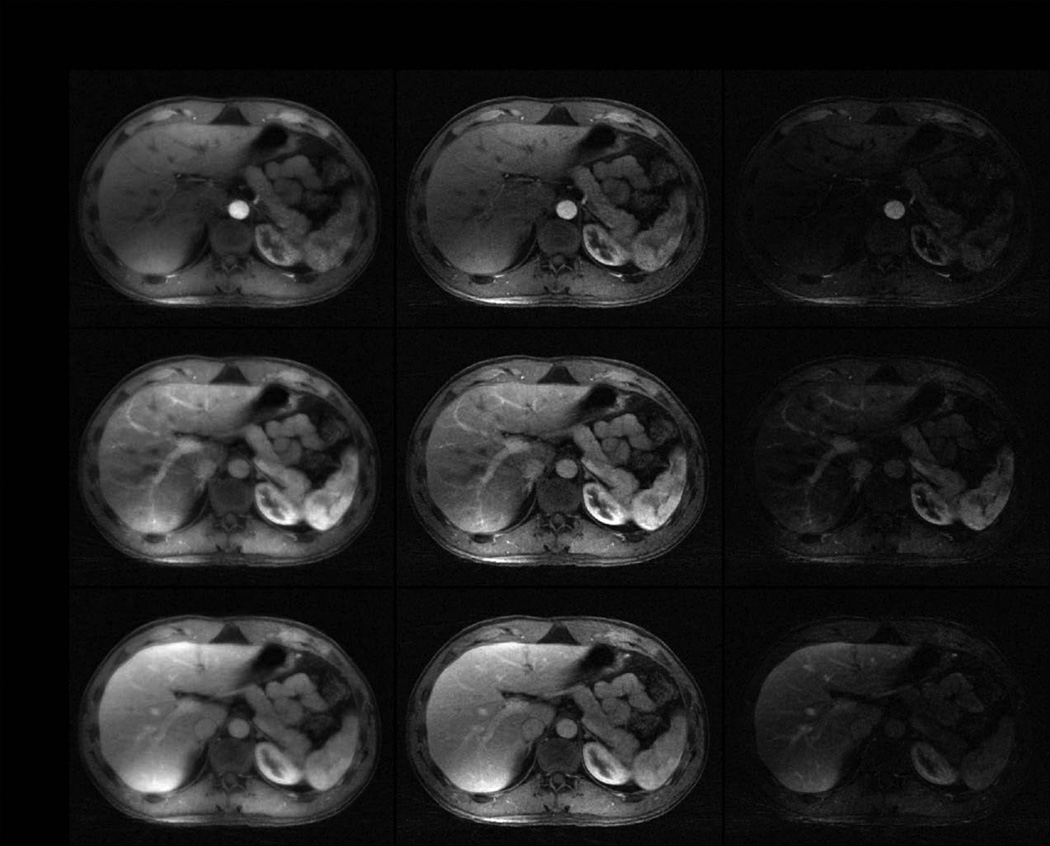
Figure 8 and Video 5 shows one representative slice of reconstructed 4D contrast-enhanced abdominal images corresponding to aorta, portal vein and liver enhancement phases. L+S presents improved reconstruction performance compared to CS as indicated by better depiction of small structures which appear fuzzy in the CS reconstruction. Moreover, the intrinsic background suppression improves the visualization of contrast enhancement in the S component, which might be useful for detection of regions with low enhancement that are otherwise submerged in the background.

Figure 8.

CS and L+S reconstruction of 4D dynamic contrast-enhanced abdominal data acquired with golden-angle radial sampling (8 spokes / frame, undersampling factor = 48, temporal resolution = 0.94 seconds per 3D volume) corresponding to a representative slice and three contrast-enhancement phases (aorta, portal vein, liver). L+S compares favorably to CS, and the S component (right column), in which the background has been suppressed, offers improved visualization of contrast-enhancement.

Free-breathing accelerated breast DCE-MRI with golden-angle radial sampling

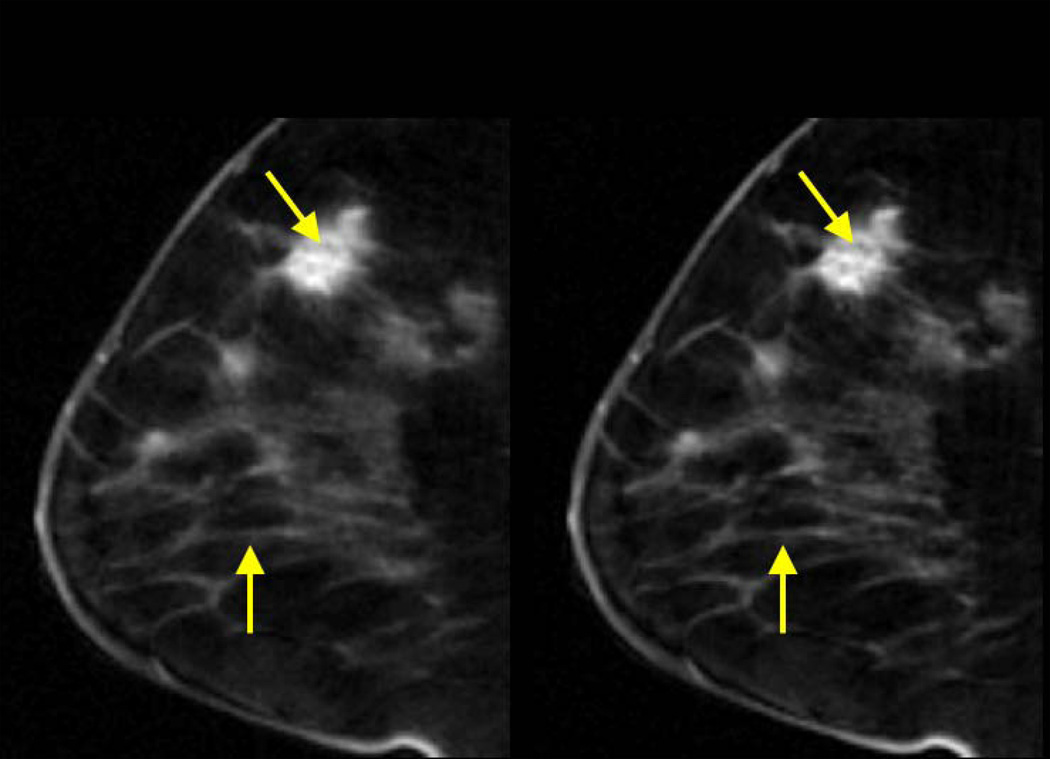
L+S reconstruction of dynamic contrast-enhanced breast data improves the visualization of fine structures within the breast lesion as compared to CS – a capability which might be useful for diagnosis (Figure 9). Small vessels outside the lesion are also better reconstructed by L+S. The gain in performance for this breast study was lower compared to the previous abdominal study, in part due to the absence of a marked background in dynamic contrast-enhanced breast MRI (since healthy breast tissue has very low intensity values).

Figure 9.

Representative slice corresponding to a tumor-enhancement phase for CS and L+S reconstruction of 4D dynamic contrast-enhanced breast data acquired with golden-angle radial sampling (21 spokes / frame, undersampling factor = 19.1, temporal resolution = 2.6 seconds per 3D volume). L+S improves the visualization of fine structures within the lesion (top arrow) and thin vessels (bottom arrow) compared to CS.

Discussion

Comparison to other methods that exploit low-rank and sparsity

The ideas introduced in the k−t SLR technique (14) and joint partial separability and sparsity method (15) also represent a combination of compressed sensing and low-rank matrix completion. However, these methods impose low-rank and sparsity constraints in the dynamic MRI data without trying to decompose the reconstruction. Moreover, k−t SLR uses Schatten p-norms with p<1, which are not convex and very challenging to optimize in general. Similarly, rank constrained problems are known to be NP hard. The L&S approach used in this work for comparison purposes is based on the nuclear-norm, which may empirically be outperformed by non-convex techniques. Our proposed convex L+S method has not been compared to the non-convex L&S techniques mentioned above and relative reconstruction performance to non-convex techniques is still an open question.

As was mentioned earlier, the work of Gao et al., established a precedent for use of the L+S model to reconstruct undersampled dynamic MRI data (20). However, this early work was limited to retrospective undersampling and considered one potential clinical application only. More recently, Gao et al. (21) and our own work (22,23) independently demonstrated L+S reconstruction using prospectively undersampled data. In this paper, we show improved reconstructions in a variety of clinical application areas using true prospective acceleration. We also introduce a range of novel and potentially clinically useful applications, including separation of contrast-enhanced information from non-enhanced background in DCE-MRI studies, and background suppression without the need of data subtraction in time-resolved angiography.

Separation of background and dynamic components

Full separation of background and dynamic components requires incoherence of low-rank and sparse representations. In certain dynamic MRI examples, such as cardiac cine and perfusion, this condition is not fully satisfied since (1) the L component has a sparse representation in the sparse domain or (2) the sparse component has a low-rank representation. The latter is due to the fact that dynamic information in MRI is usually structured and does not appear at random temporal locations. However, rank(L) is usually much lower than rank(S) and the singular values of L are much higher than the singular values of S, since most the signal power resides in the background. Under these conditions, the highest singular values representing the background will be absorbed by L, leaving the dynamic information for inclusion in S. This approach enables an approximate separation with a small contamination from dynamic features in the background component, but removes the risk of importing the high singular values that represent the background into the S component. Of course, it should be noted that in many applications, including the cardiac examples mentioned above, only the sum L+S is of interest and therefore incoherence between L and S is not strictly required. In these cases, the L+S approach outperforms standard compressed sensing techniques due to increased compressibility (Figure 2).

In other applications, such as time-resolved angiography, where background suppression is required to segregate the angiograms in the S component, there is ample incoherence between L and S, since no sparsifying transform is used and the L component does not have a sparse representation in x−t domain. Under these conditions separation is theoretically expected to perform robustly.

L+S reconstruction explicitly decomposes the reconstructed image series into L and S components, therefore reconstruction and decomposition cannot be performed in two separate steps. L+S decomposition can be used as an image processing tool to separate background and dynamic components in an image previously reconstructed with another method. However, this two-step approach does not improve the quality of the original reconstruction.

Selection of reconstruction parameters

The theory of L+S suggested using $\lambda =1/\sqrt{\rho \text{max}(n_1,n_2)}$ for matrices of size n₁×n₂ to solve the constrained optimization problem in Eq. (1), where ρ is the fraction of observed entries. The parameter λ represents the ratio of parameters λ_S and λ_L used in our proposed reconstruction algorithm. This approach works well for the case of matrix decomposition with true data consistency M=L+S. However, for reconstruction of undersampled data, true data consistency in the acquisition space results in noise amplification. Moreover, in addition to the parameter λ, we need to add another parameter to weight the data consistency portion of the reconstruction. Our reconstruction algorithm uses two regularization parameters λ_L and λ_S. We have adopted an empirical method to select the reconstruction parameters λ_L and λ_S, choosing those presenting the best reconstruction performance over a range of possible values. Even though this process might be lengthy and special care is required to select the right parameters to achieve a global minimum, it needs to be undertaken only once for each dynamic imaging technique, and the same parameters can be used for subsequent studies with similar dynamic information. Recent work on the automatic selection of parameters for matrix completion such as the SURE (Stein’s unbiased risk estimate) method (36) might also be applicable for L+S reconstruction.

The regularization parameters balance the contribution of the low-rank and sparse components. If the information of interest resides only in L or S, which requires an accurate separation of L and S, careful selection of regularization parameters is required in order to avoid propagation of dynamic information into L or background features into S. However, if we are only interested in the overall reconstruction L+S, strict separation between background and dynamic components is not required and the approach is less sensitive to the selection of regularization parameters.

Selection of step size in the general solution

The step size t in the general algorithm given in Eq. (7) must be selected to be less than 1/‖E‖² to ensure convergence. Assuming a normalization in which ‖E‖² ≤ 1, we have chosen to work with a constant step size t=1. An alternative would be to use adaptive search strategies, such as backtracking line search, to possibly achieve faster convergence.

Computational complexity

The computation of the SVD in each iteration constitutes the additional computational burden imposed by the L+S reconstruction, which has been reduced considerably by using a partial SVD approach. Moreover, the partial SVD is computed in the coil-combined image and not on a coil-by-coil basis since our reconstruction approach enforces low-rank in the image that results from the combination of all coils. The major computational burden in this type of iterative reconstruction is the Fourier transform, which must be applied for each coil separately to enforce data consistency. Particularly, the reconstruction of non-Cartesian data will suffer from longer reconstruction times due to the computational cost of the non-uniform FFT.

Conclusions

The L+S decomposition enables the reconstruction of highly-accelerated dynamic MRI data sets with separation of background and dynamic information in various problems of clinical interest without the need for explicit modeling. The higher compressibility offered by the L+S model results in higher reconstruction performance than when using a low-rank or sparse model alone, or even a model in which both constraints are enforced simultaneously. The reconstruction algorithm presented in this work enforces joint multicoil low-rank and sparsity to exploit inter-coil correlations and can be used in a general way for Cartesian and non-Cartesian imaging. The separation of the background component without the need of subtraction or modeling provided by the L+S method may be particularly useful for clinical studies that require background suppression, such as contrast-enhanced angiography and free-breathing abdominal studies, where conventional data subtraction is sensitive to motion.

Supplementary Material

Supp FigureS1

Figure S1: RMSE corresponding to L+S reconstruction of (a) cardiac perfusion data with retrospective undersampling factor of 10 and (b) cardiac cine data with retrospective undersampling factor of 8 for different combinations of regularization parameters λ_L and λ_S. The regularization parameters with lowest RMSE were employed in subsequent reconstructions.

Supp TableS1

Table S1: RMSE / SSIM values for reconstruction of cardiac perfusion and cine data sets with retrospective undersampling (R: undersampling factor). Lower RMSE and higher SSIM represent improved reconstruction results.

Supp VideoS1

Video 1: Video showing reconstructions of cardiac perfusion data with retrospective 10-fold undersampling using compressed sensing (CS) (second column), simultaneous low-rank and sparsity constraints (L&S) (third column) and L+S decomposition (L+S) (fourth column), as illustrated with static images in Figure 4. Conventional reconstruction of the fully sampled data is shown in the first column.

Supp VideoS2

Video 2: Video showing reconstructions of cardiac cine data with retrospective 8-fold undersampling using compressed sensing (CS) (second column), simultaneous low-rank and sparsity constraints (L&S) (third column) and L+S decomposition (L+S) (fourth column), as illustrated with static images in Figure 5. Conventional reconstruction of the fully sampled data is shown in the first column.

Supp VideoS3

Video 3: Video showing reconstructions of 8-fold prospectively accelerated cardiac perfusion data acquired on a patient, as illustrated with static images in Figure 6. From left-to-right: CS reconstruction, L+S reconstruction, L component and S component.

Supp VideoS4

Video 4: Video showing reconstructions of 7.5-fold prospectively accelerated time-resolved angiography data, as illustrated with static images in Figure 7. From left-to-right: CS reconstruction with data subtraction, L+S reconstruction, L component (background) and S component (angiogram).

Supp VideoS5

Video 5: Video showing reconstructions of 4D dynamic contrast-enhanced abdominal data acquired with golden-angle radial sampling (8 spokes / frame, undersampling factor = 48, temporal resolution = 0.94 seconds), as illustrated with static images in Figure 8. From left-to-right: CS reconstruction, L+S reconstruction, L component and S component.