Abstract
Over decades, the theoretical and applied mechanics community has developed sophisticated approaches for analysing the behaviour of complex engineering systems. Most of these approaches have targeted systems in the transportation, materials, defence and energy industries. Applying and further developing engineering approaches for understanding, predicting and modulating the response of complicated biomedical processes not only holds great promise in meeting societal needs, but also poses serious challenges. This report, prepared for the US National Committee on Theoretical and Applied Mechanics, aims to identify the most pressing challenges in biological sciences and medicine that can be tackled within the broad field of mechanics. This echoes and complements a number of national and international initiatives aiming at fostering interdisciplinary biomedical research. This report also comments on cultural/educational challenges. Specifically, this report focuses on three major thrusts in which we believe mechanics has and will continue to have a substantial impact. (i) Rationally engineering injectable nano/microdevices for imaging and therapy of disease. Within this context, we discuss nanoparticle carrier design, vascular transport and adhesion, endocytosis and tumour growth in response to therapy, as well as uncertainty quantification techniques to better connect models and experiments. (ii) Design of biomedical devices, including point-of-care diagnostic systems, model organ and multi-organ microdevices, and pulsatile ventricular assistant devices. (iii) Mechanics of cellular processes, including mechanosensing and mechanotransduction, improved characterization of cellular constitutive behaviour, and microfluidic systems for single-cell studies.
Keywords: nanoparticle-mediated drug delivery, biomedical device design, cell mechanics
1. Introduction
For many years, the theoretical and applied mechanics community has addressed complex engineering problems, primarily in the fields of energy, materials, transportation and defence. In addressing these problems, a broad array of tools, both experimental and theoretical, have been developed, tested and honed. These techniques allow for detailed characterization and behavioural prediction of the highly complex systems encountered in engineering applications. The traditional applications for which these tools were developed have large numbers of degrees of freedom and operate under unpredictable conditions. However, by using the framework of engineering and science, engineers and scientists can design these systems with a high degree of fidelity.
For most of its history, medical practice has been based on qualitative approaches often guided solely by external inspections and the analysis of the patients' vital signs, such as the body temperature, blood pressure, pulse, respiration rate and weight. The interconnection of medicine and technology has led to the development of a series of instruments and equipment that are used daily in clinical practice to assist medical intervention and planning of treatment. This includes the development of the imaging technologies, such as X-ray, ultrasound, magnetic resonance and nuclear imaging, and any combination thereof, for the non-invasive, internal inspection of a patient's body; external machines for assisting the natural function of the kidneys, heart and lungs; artificial implants for cardiovascular and orthopaedic applications. The recent strides in computational engineering and sciences and nano/microtechnologies present the field of medicine with new opportunities for developing personalized interventions and predictive tools and, possibly, for radically changing clinical practice. Mechanics, intended as the science concerned with the behaviour of bodies and their interaction with the environment, can contribute significantly to this development.
In this report, prepared for the US National Committee on Theoretical and Applied Mechanics (USNCTAM), we identify and discuss what we consider to be the most pressing challenges in biological sciences and medicine for which mechanics can have a substantial impact. These challenges are (i) the rational engineering of injectable nano/microdevices for imaging and therapy of disease, with discussions on nanoparticle (NP) carrier design, vascular transport and adhesion, endocytosis, tumour growth in response to therapy, and uncertainty quantification techniques to better guide models and experiments, (ii) design of biomedical devices, including point-of-care (POC) diagnostic systems, model organ and multi-organ microdevices and pulsatile ventricular assistant devices, and (iii) mechanics of cellular processes, including mechanosensing and mechanotransduction, improved characterization of cellular constitutive behaviour and microfluidic systems for single-cell studies. In addition to these specific, scientific problems, we highlight the educational/cultural challenges and opportunities stemming from the interdisciplinary nature of mechanics in medicine.
2. Nanoparticle-mediated drug delivery
2.1. Overview
The history of applications of mechanics to medicine and biology is extraordinarily rich and diverse; suffice it to recognize its fundamental role in orthopaedics, or the absolute reliance of pharmacokinetics and pharmacodynamics on the equations of mass transport, or the centrality of fluid dynamics in the understanding of cardiovascular physiology and pathology. Beyond these traditional, yet still very productive and important areas, it is now possible to envision novel connections between mechanics and medicine in ways that were unimaginable until recent times, because they are made possible by the emergence of novel disciplines.
A first paradigm for this convergence is embodied by the triangulation of biology and medicine with mechanics by means of nanotechnology; a second, corollary example is the framework of transport oncophysics; yet another is the new field of predictive anatomy. By way of illustration, one may consider the problem of transport of nanoscale objects (biological such as protein, or synthetic such as a chemotherapeutic molecule, a radiological contrast agent or an NP) inside the body. Although they obviously obey the general mechanical laws of transport, their distribution in the body is largely impossible to predict a priori, in view of the impossibility to establish general governing equations, which will take into account the various biological barriers of the body, which in turn ultimately determine the transport profiles. However, this is as central a problem as there can be in the field of biomechanics—life is predicated upon the ability of the body to succeed in transporting nanoscale objects in a very accurately controlled manner. Although there is no current hope for a master equation of transport of an arbitrary biological nanoscale object, great simplifications can be attained by considering the body transport of synthetic NPs with precise engineering properties, so that the number of independent variables may be reduced to reason. Thus, nanotechnology enables the understanding of some fundamental aspects of biomechanics of mass transport in a manner that was unattainable before the development of precise methods for the manufacturing of NPs and their characterization. The additional beauty of this is that the very NPs that are developed for the study of the mechanics of body transport can then be used as agents of therapy once the ability to distribute preferentially in target organs of the body is understood—this is the basis for new perspectives of cancer therapy and the personalization of treatment, based on mechanics and the rational design of vectors for the targeted delivery of drugs. A second example of nanotechnologies as models for otherwise intractable biomechanical transport problems is the use of synthetic nanochannels to replicate and study transport through nanoscale environments such as ionic and molecular channels on the surfaces of biological cells.
It is insightful to observe that the study of the body transport and selective accumulation of chemotherapeutic agents and nanomedicines has revealed that cancer is in reality a proliferative disease of mass transport disregulation, at multiple scales, from the local (tissue invasion by cells) to the systemic (distant metastases) and the molecular level (subcellular signalling pathologies). In this case, mechanics by way of nanotechnology yielded transport oncophysics, i.e. the recognition of entirely novel perspectives on the nature of a major class of diseases such as cancer. Based on this paradigm, it may well be expected that further advances in mechanics could offer transformational insights into many other domains of medicine and biology.
Predictive anatomy uses the mechanical tools of mathematical, multi-scale homogenization theory to predict the characteristics of body parts, as they are most likely to emerge in the course of evolutionary selection. The engineering counterpart of this novel discipline is the methodology of optimal design, which involves the statement of an objective function to be optimized, a space of design variables and a set of constraints. Exactly the same approach can be applied to yield ‘best designs’ of body parts that serve mechanical functions such as the ability to bear loads, or transport mass and heat. Thus, recent methodologies such as the emergence of nanotechnology and advances in the mathematical theory of multi-scale homogenization can serve to join mechanics with medicine and biology in very innovative manners that provide new horizons for scientific advances, and opportunities for medical breakthroughs.
The expansion of nanotechnology over the past two decades has led to a paradigm shift in drug delivery. For most of the history of chemical therapeutics, delivery was non-specific and the single controllable parameter was concentration. Although targeting of specific pathways through drug design was first introduced in the 1950s [1], the control over molecular properties afforded by advances in nanotechnology has ushered in a new era in drug delivery. Whereas early targeting strategies relied on chemical changes to individual molecules, it is now possible to synthesize NPs with precisely controlled size, shape, stiffness and surface chemistry to efficiently deliver drug molecules into diseased cells/tissues [2,3]. Although researchers now have a greatly expanded set of knobs to turn when designing NPs, it is generally not clear how a change to a specific vehicle feature will alter the effectiveness of a drug, and hence design of novel drug carriers requires extensive and costly parametric studies that are generally specific to the system upon which the experiments were performed. Theoretical and computational modelling of the delivery process can greatly reduce the need for physical experiments and provide general design principles to expedite the design process [4–9].
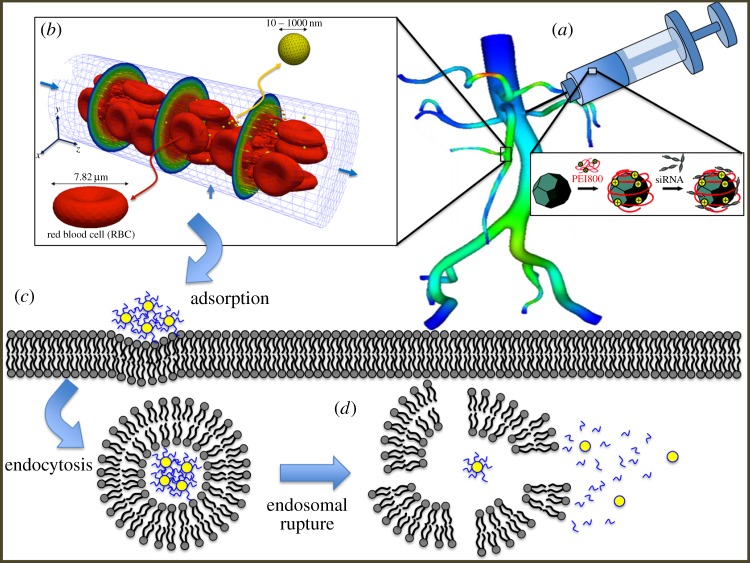
Any modelling strategy that aims to predict a drug's effectiveness based on the nanoscopic features of the delivery platform must account for processes across the disparate spatial and temporal scales travelled by an NP during delivery. Initially, a solution of drug carriers is introduced to the circulatory system, either through absorption or direct injection (figure 1a). The circulation of the particles in the vasculature network can greatly affect the concentration of drug delivered to the area of diseased cells and depends on the geometry and chemistry of the particles. Modelling transport through the vasculature has presented significant challenges owing to the vastly different length scales of the vascular network, which can range from centimetres for the diameter of the ascending aorta to micrometres in the case of capillaries [11–15]. In the macrovasculature, particle transport can be modelled as an advection–diffusion process through complex networks. State-of-the-art techniques involve simulations through patient-specific vascular networks [13]. However, near the endothelium and in the microvasculature, complex interactions between blood plasma, red blood cells (RBCs) and NPs require more detailed approaches that explicitly account for the interactions between RBCs and NPs (figure 1b). These complex interactions can be studied by the immersed finite-element technique [12,15–33], accounting for the microcirculation behaviour of NPs, under the influence of RBCs and fluid flow. These models are proved to be capable of capturing the segregation of NPs and RBCs as well as particle adhesion to the vascular walls [12,14].
Figure 1.
A schematic of the nanoparticle-mediated drug delivery process [10]. (a) A solution containing nanoparticle delivery platforms is injected into a patient's circulatory system [11]. (b) In the microvasculature, nanoparticles are segregated from red blood cells, increasing their interaction with the endothelium, eventually leading to their removal from circulation [12]. (c) Nanoparticles diffuse through the extracellular matrix, eventually adsorbing onto the surface of a target cell. The nanoparticles are then endocytosed from the lipid membrane. (d) The endosome containing the drug delivery complex ruptures, releasing the therapeutic agents into the cytoplasm. When released from the endosome, the nanoparticle cargo may be dissociated due to the local pH environment change.
Upon adhesion, particles diffuse through the extracellular matrix (ECM), eventually reaching a cell possessing the targeted marker (figure 1c). The adsorption of NPs onto the cell membrane is heavily influenced by the functionalization of the carrier surface, the local molecular composition of the membrane and extracellular environmental variables such as pH and salt concentration [34]. Adsorbed particles are then wrapped by the cell membrane and endocytosed. The endosomes containing the NP–drug complexes can then either fuse into lysosomes, which can degrade the drug molecules in the process, or they can rupture, releasing their contents into the cytoplasm (figure 1d). To understand the interactions between particles and cell membranes, it is necessary to model the systems at the molecular scale. Techniques such as molecular dynamics and molecular mean-field theory calculations are capable of illuminating the effect of particle size, shape and chemistry on cellular uptake rates [35,36]. Although molecular calculations provide far more detail for specific systems, continuum theories can also provide useful guiding principles for NP design, even at length scales of the order of a single NP [37–41].
2.2. Nanoparticle-based drug carrier design
Nanoscale technologies can improve the bioavailability and biodistribution of systemically injected therapeutic and imaging agents [42,43]. Nanoconstructs can navigate through the circulatory system and preferentially recognize the tumour neovasculature [5,44] and encapsulate large amounts of different agents, for both therapy and imaging [45]. It is known that the blood vessel network in primary and metastatic tumours is different from the healthy vasculature [46,47]. Endothelial cells form an imperfect lining with wide junctions (fenestrations), ranging in size from 100 to 1000 nm. This leads to vascular hyper-permeability, lower mean blood velocity (1–10 versus approx. 100 µm s−1 in normal microvessels) and higher interstitial fluid (IF) pressure (up to 5–7 kPa). Furthermore, the surface density of inflammatory vascular molecules, such as intercellular cell adhesion molecules (ICAM-1) and E-selectin, is one to two orders of magnitude higher on the tumour endothelium. In addition, tumour-specific vascular receptors, such as the αvβ3 integrins, are expressed at levels of 100–1000 molecules μm−2 [48]. Taking advantage of all of these differences between healthy and diseased vessels, a plethora of nanoconstructs with different sizes, surface properties and, more recently, shapes have been developed over the past 20 years for delivering imaging and therapeutic agents preferentially to the malignant tissue. Indeed, the encapsulation of different, and multiple, agents into nanoconstructs has provided significant improvements in pharmacokinetics, toxicity and biodistribution. Despite all of this, the effective detection and treatment of malignant masses via the systemic injection of nanoconstructs is still limited by insufficient accumulation at the biological target (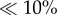
injected dose per gram tumour—%ID g−1) and non-specific sequestration by organs of the reticulo-endothelial system (RES; tumour-to-liver < 0.1). Even the notion of targeting nanoconstructs to specific receptors, expressed on the tumour neovasculature or cells, has often led to contradictory results. The development of novel, clinically relevant delivery systems with high tumouritropic accumulation is critical for further improvement of therapeutic outcomes and the early detection of solid tumours.
The size, surface properties, stiffness and shape of the nanoconstructs affect their in vivo behaviour and therapeutic efficacy. The importance of tuning the nanoconstruct size and surface properties has been recognized since the late 1990s. In a series of seminal papers, Jain and co-workers [49] showed that liposomes and latex beads smaller than 300–400 nm in diameter would accumulate more efficiently in tumours than larger beads, via passive extravasation at the tumour fenestrations. This is the ‘dogma’ that has guided the field of nanomedicine since then and is known as the enhanced permeability and retention (EPR) effect. In addition, further studies [50,51] showed that the surface charge of lipid-based nanoconstructs can control accumulation in tumours as well as in the liver and lungs. These were followed by many studies further elaborating on the role of nanoconstruct size and surface charge, for different material formulations and surface chemistry [52–54]. Molecular-specific nanoconstructs have also been developed, where the particle surface is coated with ligand molecules capable of recognizing and binding to counter molecules (receptors) expressed on the target cells [55]. Despite its high in vitro efficiency, this approach suffers in vivo owing to reduced binding affinity, lack of ligand immunogenicity and the limited number of ligand molecules available, especially for the smaller particles. Because of this, data in the literature on specific tumour targeting of nanoconstructs are still highly controversial [56,57]. Following the EPR dogma, a myriad of nanoconstructs have been developed with different surface properties and sizes, often presenting only minimal improvements in terms of tumour accumulation and liver escape. More recently, novel nanofabrication strategies have been presented for the synthesis of non-spherical nanoconstructs [58–61]. This fostered new theoretical [5,38,39,62–64], in vitro [65–69] and in vivo [44,70–74] studies demonstrating the importance of shape in controlling the vascular behaviour, cellular uptake and differential organ accumulation of the systemically injected nanoconstructs. Size, shape and surface properties can be envisioned as three independent variables in an optimization problem where the objectives are to maximize tumour accumulation and minimize the non-specific sequestration of nanoconstructs.
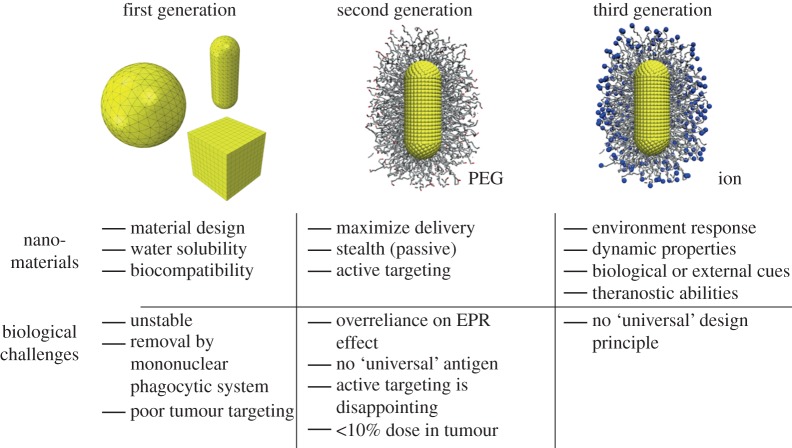
The physico-chemical properties of NPs, such as size, shape, surface charge and stiffness, can affect their biological clearance. Therefore, NPs can be modified in various ways to extend their circulation time. In recent decades, the design of NPs for biomedical applications has been advanced by studying their biological responses. The evolution of the NP carriers has followed advances in understanding of how size, shape, surface and stiffness affect efficacy. As shown in figure 2, there are three generations of NPs developed for biomedical applications [75]. In the first generation of NPs, the NPs are functionalized with basic surface chemistry (charges/ligands) and are evaluated through their biocompatibility and toxicity [76,77]. However, these NPs are unstable and usually internalized by the immune cells during circulation. To overcome these problems in the second generation, the surfaces of NPs are grafted with polymer chains, improving their water solubility and allowing them to avoid aggregation and opsonization. Compared with the first generation, the second-generation NPs demonstrate improved stability and targeting in biological systems. However, the active targeting of these NPs to the tumour cells (TCs) or other diseased cells is still disappointing. Thus, the third-generation NPs shift the design paradigm from stable materials to ‘intelligent’ and environmentally responsive materials with improved targeting capabilities. Local environmental (i.e. pH value) changes cause the properties of these NPs to change in a prescribed way. Here, we should emphasize that although the design of NPs shifts from the first generation to the third generation, the first- and second-generation NPs still have many applications in different areas, and their behaviours are still poorly understood. Moreover, a comprehensive understanding of the first- and second-generation NPs will help us to efficiently design the third-generation NPs.
Figure 2.
Evolution of NP design with their properties and biological challenges. The figure is taken and modified from [75].
2.3. Vascular dynamics and adhesion
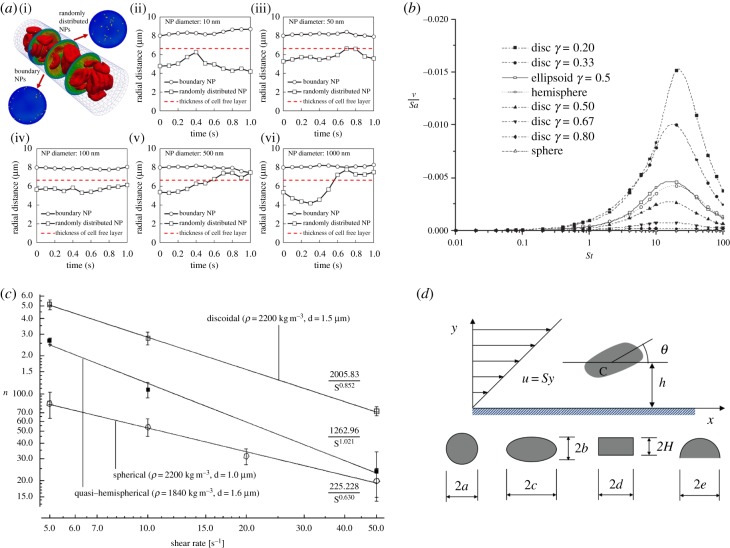
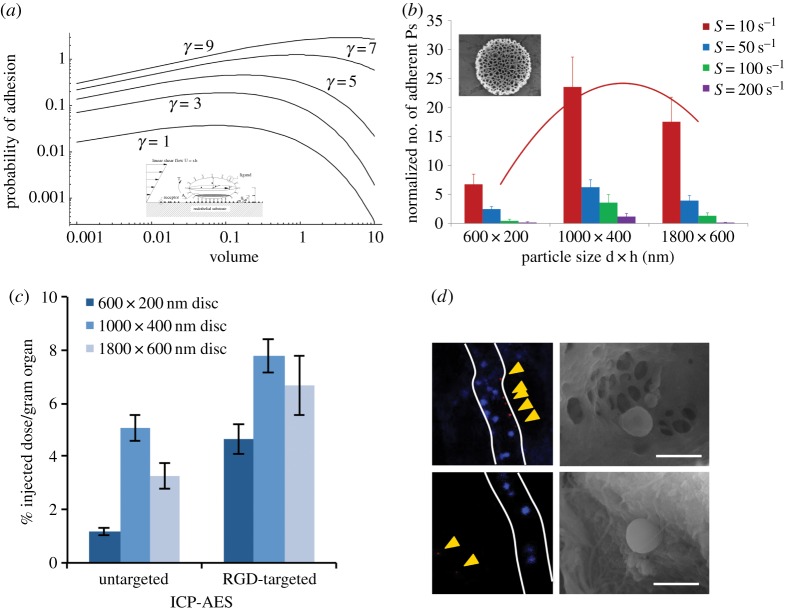
The solution of such a problem requires the understanding and mathematization of the fundamental events in the journey of systemically injected nanoconstructs. In the case of nanoconstructs designed to adhere to the tumour microvasculature, these events are (i) transport within the vascular network, (ii) firm adhesion at the diseased vessel walls, and (iii) recognition/uptake by macrophages in the RES organs (mostly the liver, spleen, lungs). As per the vascular transport, small nanoconstructs (less than 500 nm) tend to follow the streamlines moving parallel to the blood vessel walls with minimal interaction with the fast moving RBCs (figure 3a) [12]. However, submicrometre-sized (and larger) nanoconstructs are pushed laterally by the RBCs and forced to move within the so-called cell free layer in proximity of the vessel walls (figure 3a). Note that this is similar to the behaviour extensively documented for platelets and leucocytes [80]. Moreover, we have shown that thin discoidal submicrometre nanoconstructs are the most efficient to drift laterally across the streamlines (margination dynamics), which increases their likelihood of recognizing the diseased vasculature [5,64,65,81]. This is evident in figure 3, where the margination performance of nanoconstructs with different size and shape combinations is presented. As per the vascular adhesion, the firm arrest of nanoconstructs at the vessel walls under flow is achieved only if the hydrodynamic forces are balanced out by sufficiently strong interfacial adhesive interactions. The latter could be specific, i.e. mediated by the formation of stable ligand–receptor bonds, and non-specific, i.e. resulting from colloidal interactions (van der Waals, electrostatic, steric forces) and non-specific molecular interactions, as mediated by plasma proteins adsorbed on the nanoconstruct surface. Theoretical predictions, in vitro analysis, and in vivo experiments have demonstrated that thin discoidal submicrometre nanoconstructs more firmly adhere to the vessel walls under flow when compared with spherical and slender cylindrical particles [5,39,44]. Furthermore, figure 4a shows that for each particle shape there is an optimal size (or volume) that maximizes adhesion. In particular, thin discoidal nanoconstructs offer a larger surface of adhesion and oppose a smaller cross section to the flow thus reducing the dragging forces that would dislodge them away [39]. And for these reasons, thin discoidal particles are more efficient in adhering to the vessel walls. This has been confirmed also in vivo using two different orthotropic tumour models: melanoma and breast cancer (figure 4d) [44,73]. As per cell internalization, nanoconstruct geometry has been shown by several authors to dramatically affect the rates and mechanisms of uptake (see the following sections). For instance, it is known that the rate of internalization of large spherical particles (more than 500 nm) decreases as their diameter increases [5]. This can be predicted in terms of the geometrical and surface properties of the particles [38,63]. Indeed, internalization can be limited by increasing the density of polyethylene glycol (PEG) chains on the nanoconstruct surface, which leads to larger interfacial repulsive steric interactions. However, PEG chains tend to progressively detach and, consequently, nanoconstructs lose their shielding over time. On the other hand, it has been shown that elongated particles, laying with their major axes parallel to the cell membrane, can more efficiently resist cell internalization [83]. This has been demonstrated for elliptical particles and observed experimentally for micrometric and submicrometric particles exposed to macrophages and TCs [66,67]. This has suggested the use of non-spherical nanoconstructs, in particular discoidal nanoconstructs with a submicrometre size to maximize accumulation at the diseased vasculature.
Figure 3.
Vascular dynamics of non-spherical nanoconstructs. (a) Fast moving RBCs confine submicrometre-sized nanoconstructs in proximity of the vessel walls, which favours the recognition of the diseased endothelium [12]. (b) Thin discoidal nanoconstructs drift laterally, across the stream lines, with a higher velocity as compared to spherical, quasi-hemispherical or thick discoidal nanoconstructs [78]. (c) In vitro parallel plate flow chamber experiments confirm that thin discoidal nanoconstructs would deposit and adhere more efficiently than spherical and quasi-hemispherical nanoconstructs, over a wide range of wall shear rates S [79].
Figure 4.
Vascular adhesion of non-spherical nanoconstructs. (a) The probability of vascular adhesion grows as the shape deviates from spherical (γ = 1, sphere;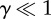 
, quasi-discoidal particles) [2]. (b) Parallel plate flow chamber experiments showing a maximum vascular adhesion occurring for 1000 × 400 nm discoidal nanoconstructs [82]. (c) Tumour accumulation of untargeted and RGD-4C targeted discoidal nanoconstructs, demonstrating again a maximum accumulation for the 1000 × 400 nm discoidal nanoconstructs [44]. (d) Fluorescent images and scanning electron micrographs showing discoidal nanoconstructs (see yellow arrows) laying on the tumour neovasculature. 10% of the RBCs were stained in blue [44].
The above description demonstrates that nanoconstructs can be engineered by rationally selecting their size, shape, surface properties with the objective of maximizing their accumulation within the diseased tissue while limiting the sequestration in healthy organs. The rational design of nanoconstructs should integrate sophisticated computational modelling, accounting for the complexity of the blood flow, vascular geometry and uncertainty in the quantification of the biological variables (receptor density, blood velocity and so on); devices and apparatus for accurate in vitro characterization of vascular adhesion under complex flow patterns, internalization by endothelial cells and professional phagocytes; and eventually in vivo experiments through which one can quantify the circulation half-life and organ-specific accumulation of the nanoconstructs over time. Such an endeavour requires the convergence of multiple disciplines and expertise pertaining to the field of computational mechanics, chemistry, physics as well as biology, immunology and biomedical sciences. This will eventually lead to the development of a new class of truly interdisciplinary scientists that would grasp the details of each individual field, facilitate constructive synergies, and be capable of synthesis towards the achievement of the common goal.
2.4. Endocytosis
2.4.1. Cell uptake of one-dimensional nanomaterials
Various types of NPs, nanowires, nanofibres, nanotubes and atomically thin plates and sheets have emerged as promising candidates for potential applications in next-generation biosensors, drug delivery and medical imaging. There is an urgent societal need for better understanding of both beneficial and hazardous effects of these nanotechnologies. Below is a summary of some recent work on the mechanics of cell uptake of one-dimensional nanomaterials such as nanotubes and nanowires. A combined study based on electron microscopy, theoretical modelling and molecular dynamics simulations shows that carbon nanotubes (CNTs) enter cells via a tip recognition pathway that involves receptor binding, tube rotation driven by elastic energy at the tube–bilayer interface and near-vertical entry.
Research on the mechanics of cell–nanomaterials interaction is of significance not only to the understanding of hazardous effects of viruses and nanomaterials in general, but also to biomedical applications such as gene/drug delivery and medical imaging [84–86]. A current problem of immediate concern to society is that nanomaterials, which include various types of NPs, nanowires, nanofibres, nanotubes and atomically thin plates and sheets, could penetrate the membrane of human and animal cells. It is known that geometrical properties of NPs such as size [37,40], shape [5,38,39,87–90], elastic modulus [41] and surface microstructure [91,92] can substantially influence endocytosis, phagocytosis, circulation [85] and targeting [86]. Below is a summary of some recent work at Brown University on the mechanics of cell uptake of one-dimensional nanomaterials [35]. Compared with other non-spherical NPs, the cellular interactions of one-dimensional nanomaterials such as CNTs are particularly important for biomedical diagnostics and therapies [93,94], and for managing health impacts of nanomaterials following occupational or environmental exposure [95–97].
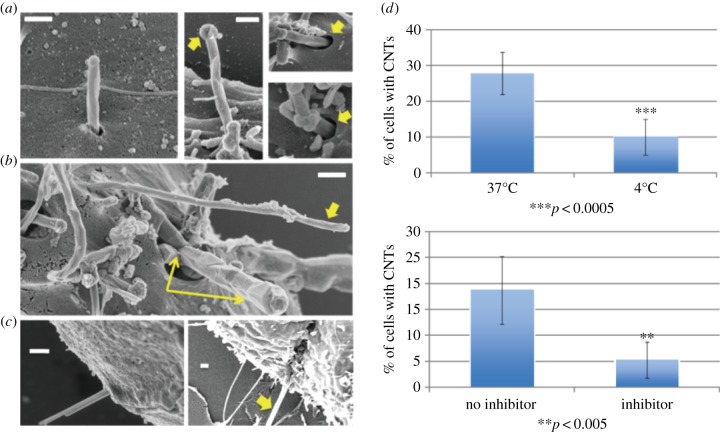
Recently, we carried out a combined study by electron microscopy, theoretical modelling and molecular dynamics to elucidate the fundamental interactions of cylindrical one-dimensional nanomaterials with eukaryotic cell membranes [35]. Figure 5 shows electron micrographs of common morphologies in the near-membrane region following in vitro exposure of murine liver cells or human mesothelial cells to different types of one-dimensional nanomaterials, including CNTs, crocidolite asbestos nanofibres and amine-terminated gold nanowires [35]. It can be seen that near-vertical tip entry is a common uptake pathway for geometrically similar, but chemically very different nanomaterials. To determine whether the uptake of CNTs is mediated by energy-dependent endocytosis, murine liver cells were incubated either at 4 or 37°C. Internalization of CNTs was significantly decreased at 4°C (figure 5d). In the presence of metabolic inhibitors, the uptake of CNTs was also significantly decreased (figure 5d) confirming that this uptake requires adenosine triphosphate.
Figure 5.
Experimental observations of energy-dependent tip entry of one-dimensional nanomaterials into cells. (a) Carbon nanotubes entering murine liver cells. Arrow in middle panel shows carbon shell at the tube tip that distinguishes the nanotubes from surface microvilli. Arrows in right panels show close views of membrane invaginations surrounding the tubes at the point of entry. (b) Examples of nanotube tip entry in human mesothelial cells. Both an isolated tube (single arrow) and a tube bundle (double arrow) are seen in the process of high-angle entry. (c) Examples of active tip entry for other one-dimensional materials: 30 nm gold nanowires (left) and a 500 nm crocidolite asbestos fibre (right). (d) Effects of temperature and metabolic inhibitors on multi-walled CNT uptake as tests for active endocytic uptake. All images are obtained by field emission scanning electron microscopy following fixation and contrast enhancement with osmium tetroxide. All scale bars are 300 nm. Figure from [35].
Why is tip entry the preferred mode of cellular uptake of one-dimensional nanomaterials? This fundamental question has been investigated using coarse-grained molecular dynamics simulations under the basic hypothesis that nanotubes with closed, rounded caps can mimic particles and initiate endocytosis, and that elastic energy in the plasma membrane provides a driving force to rotate one-dimensional nanostructures from their initial angle of contact to high angles. In the simulations, a capped multi-walled CNT is initially positioned in close proximity above the surface of a patch of bilayer. The initial angle between the axis of the nanotube and the bilayer is pre-selected and a range of receptor densities, ϕ, are considered. The receptors diffuse along the bilayer and aggregate around the nanotube owing to binding affinity. As receptors cluster and adhere to the nanotube surface, the tube is pulled into the bilayer and wrapped. In this process, the tube is observed to spontaneously rotate to achieve an entry angle close to 90°, driven by membrane elastic energy minimization during wrapping (figure 6). Figure 6b shows that, at a higher receptor density of ϕ = 0.33, the nanotube can become fully wrapped before it reaches the 90° entry angle. Generally, increasing receptor density tends to hinder the rotation towards 90° entry. In the extreme case of ϕ = 1, in which the adhesion loses specificity, the membrane on the right side of the nanotube adheres to the tube much faster than that on the left side (figure 6c), and the nanotube adopts a very small entry angle. This can be understood from the fact that, for non-specific adhesion, the right side membrane has the distinct advantage of being initially closer to the tube surface and dominates the early-stage receptor binding before rotation can occur. These simulations reveal two competing kinetic processes: rotation of the tube towards a 90° entry angle to relax elastic energy in the membrane and wrapping speeds on different sides of the tube governed by receptor diffusion. If the former prevails, as would be expected at relatively low receptor densities, then the final entry angle will be close to 90°. Note that the extreme case of non-specific interactions shown in figure 6c is an interesting theoretical limit which is not expected to be important for a real cellular system.
Figure 6.
Time sequence of coarse-grained molecular dynamics simulation results showing a multi-walled carbon nanotube penetrating a cell membrane at an initial entry angle of θ0 = 45° as a function of receptor density. The receptor (green) densities are (a) ϕ = 0.25, (b) ϕ = 0.33 and (c) ϕ = 1. Figure from [35].
Similar observations of tip entry and rotation towards 90° entry have been noted in simulations for different CNT diameters and lengths, receptor densities, receptor binding strengths and initial entry angles, and the results show that the tube still adopts a 90° entry pathway [35]. Further simulations show that the tip-entry mechanism is essentially unchanged if the hemispherical caps are replaced by enlarged shells typical of catalytically produced CNTs, or if the nanotubes exist in suspension as small bundles. Interestingly, it is found that open-ended nanotubes do not undergo tip entry because they lack carbon atom sites for receptor binding on the cap in the early stages of wrapping. This suggests that oxidative cutting or other intelligent tip modification may be used to control the membrane interaction and cell entry of a subclass of hollow one-dimensional nanomaterials. Moreover, simple analytical models and coarse-grained molecular dynamics simulations show that the time scale for tip rotation is one or two orders of magnitude smaller than that for the overall wrapping of the NPs, and tip entry is expected to be a favourable pathway for cellular uptake of capped nanotubes and other one-dimensional nanomaterials [35]. This tip-entry mechanism is proposed as a key initiator of frustrated uptake and toxicity, because a vertical alignment provides no opportunity for the cell membrane to sense or anticipate the ultimate length of the fibrous target material.
The latest theoretical studies in molecular dynamics simulations show that the cell uptake of one-dimensional nanomaterials via receptor-mediated endocytosis is governed by a single dimensionless parameter, the normalized membrane tension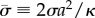 
, where a denotes the nanomaterial radius, σ is the membrane tension and κ is the bending stiffness of cell membrane. As cell membrane internalizes one-dimensional nanomaterials, the uptake follows a near-perpendicular entry mode at small membrane tension but it switches to a near-parallel interaction mode at large membrane tension. This 
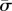-dependent uptake behaviour is also found to be ubiquitous in the interplay between cell membranes and one-dimensional nanostructures, and has broad implications for the different interaction modes exhibited by single nanotubes and nanotube bundles, tubulation of NPs and bacterial toxins on cell membranes, control of the size of filopodia and measurement of cell membrane tension [98].
In physiological situations such as endocytosis, adhesion bonds between biomolecules on NPs and cell surfaces usually operate cooperatively, and an initial phase of particle attachment or docking should, in fact, play a very important role in the overall process of endocytosis. The large surface area enables CNTs to achieve sidewall functionalization, to act as a template for cargo molecules such as proteins [99], small molecules [100] and nucleic acids [101]. It will be interesting to consider different functional groups on CNT walls, the kinetic process of receptor diffusion [102–105], interaction and docking of particles of different sizes, shapes and elastic modulus near a cell, extending a recent study by Shi et al. [89]. It can be imagined that CNTs with different sizes, tip shapes and patterns of functional groups can form a tunable platform for designing controlled cellular uptake. Substantial challenges exist when considering elastic nanofibres instead of stiff CNTs. This extension will require solving diffusion equations on curved deforming surfaces, and can therefore be extremely difficult especially in three-dimensional modelling. Simulation studies will also play critical roles in the interaction mechanism between cell membranes and nanomaterials, especially in the case where NPs can penetrate into or destructively extract phospholipids [90,106]. Overall, the cellular uptake of NPs is a multi-scale process both in spatial and temporal scales, which requires a coordinated study between experimental, theoretical or atomic/molecular simulation approaches.
2.4.2. Cell uptake of polymer-coated nanomaterials
In the first-generation NPs, only ligands are attached to their surfaces. To improve the water solubility and avoid aggregation of NPs, the surfaces of the second-generation NPs are usually grafted with polymer chains, i.e. PEG, which is a hydrophilic and biocompatible polymer. After PEGylation, the properties of the NPs are dramatically changed. For example, the surface charge of the NPs will be shielded by tethered chains, and NPs with grafted chains can be well dispersed in the solution. More importantly, a ‘stealth’ shell will be formed by the grafted chains which can prevent clearance by the immune system (opsonization) [52,107]. Therefore, PEGylated NPs display prolonged blood circulation time. To improve the endoctyosis of NPs, the free ends of grafted chains are conjugated with targeting moieties, e.g. cell-penetrating peptides [108–110], RGD peptides [111,112] and anti-HER2 antibodies [113]. With the help of these specific ligand–receptor interactions, the cellular uptake of PEGylated NPs is tremendously enhanced. However, the interplay between NP core diameter, grafting density and polymer chain length makes cellular uptake of the second-generation NPs distinct from the first-generation NPs [114]. To understand these effects, we study the receptor-mediated endocytosis of polymer-coated NPs through large-scale coarse-grained molecular dynamics simulations and self-consistent field theory [114]. A realistic coarse-grained model has also been developed to correctly reproduce the conformation of PEG polymers in water [114,115], based on the inverse Boltzmann method [116–118]. The following results are obtained through our simulations. First, the non-specific steric (repulsive) interaction between grafted chains and the cell membrane is found to have an effect which is comparable to, or even larger than, the bending energy of the membrane during endocytosis. By incorporating this non-specific steric interaction, the critical ligand–receptor binding strength for NPs to be internalized can be correctly predicted by a simple analytical equation. Second, an optimal grafting density of approximately 0.80 chain nm−2, which can enhance the specific ligand–receptor interactions and reduce both non-specific steric repulsions and opsonization during blood circulation, is also identified through our simulations. Third, a phase diagram has been constructed according to the polymer grafting density and ligand–receptor binding strength, as described in figure 7. Three different phases, including no wrapping, partial wrapping and complete wrapping, have been identified through our simulations. These findings pave the way for designing new-generation, NP-based therapeutic carriers with improved cellular targeting and uptake.
Figure 7.
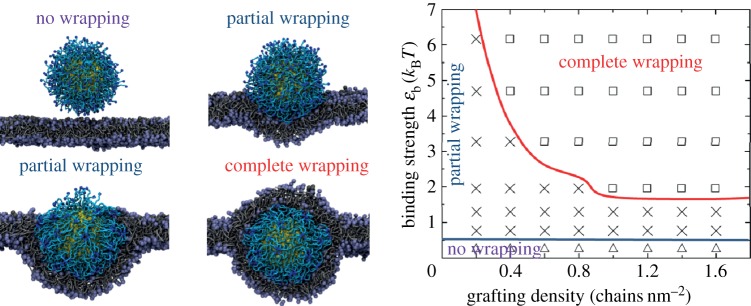
Phase diagram of receptor-mediated endocytosis of the second-generation NPs. The figure is taken and modified from [114].
2.5. Uncertainty quantification of drug delivery process
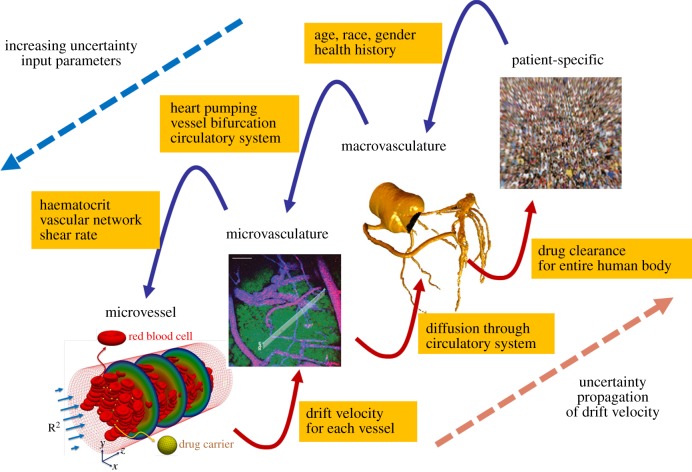
The NP-mediated drug delivery process involves many different spatial and temporal scales. These different scales interplay with each other with many uncertainties. To design efficient delivery platforms, these uncertainties cannot be ignored. For example, individual patients have different health histories, which may affect their immune systems. The heart pumping rate, vasculature network and circulatory network may also vary from one person to another. The circulation of NPs in the body can be greatly affected by these factors. The local-specific vessel characteristics, i.e. vessel diameter, flow rate and haematocrit, can change the near-wall concentration of NPs tremendously during microcirculation. As we have seen, the endocytosis of NPs depends on cell types, ligand–receptor interactions and particle sizes and shapes [5,38]. Uncertainties in a model at one scale can propagate to the others when the inputs to simulations are informed by results of another, as described in figure 8. The transport of NPs in the circulatory network can change their concentrations in microvasculature network. The near-wall concentration of NPs can influence the endocytosis process. Therefore, it is crucial to consider these uncertainties in the modelling and design of NP platforms, especially connecting models across scales [15].
Figure 8.
Uncertainty of NP transport in the multi-scale vascular system.
However, there is not a truly multi-scale computational method connecting these different models together to bridge different spatial and temporal scales [10]. In future, we expect that such a multi-scale model will be available, allowing for the prediction of a drug-delivery vehicle's efficiency and specificity, and hence design based on the optimal performance across all stages of the delivery process, as opposed to optimization for specific portions of the drug carrier's life. The flexibility of the method allows for rapid computational prototyping and testing of drug delivery complexes under realistic conditions within a short time, providing new insights into the interplay between molecular-scale interactions of intricate delivery vehicles and their transport within a specific patient. Enhanced targeting will also alleviate patient suffering by reducing required dosage of highly toxic cancer drugs. In addition, medical expenses can be reduced as a result of shorter treatment durations and fewer serious side-effects.
2.6. Application of patient-specific computational modelling to detect and/or treat cardiovascular disease
The foundations of science and engineering were rapidly, dramatically and irrevocably changed by the advent of the computer. Over the past decade in particular, the exponential growth of computing speed and capacity has transformed mankind's ability to assimilate immense amounts of data, analyse them and apply them to solve global problems of extraordinary complexity [119]. Perhaps nowhere is the scientific revolution sparked by computational mechanics more promising than in the field of medicine.
This approach to problem-solving using theoretical and applied mechanics allows us to simulate physical events and thus take much of the guesswork out of scientific research while simultaneously accelerating its pace. We can test our ideas in a virtual world and, with a high degree of accuracy, predict the outcomes. How will a medical treatment work on an individual patient? How will production of a particular energy resource affect the environment? Through the power of simulation and visualization, we can actually predict and see changes that are likely to occur. Thanks to these techniques, the holy grail of personalized medical treatments—those based on an individual's anatomy, genome, family history and environmental history—is now realistically in sight. One such example is presented below.
Cardiovascular disease is the leading cause of death in the USA and represents more than a half-trillion-dollar business in research and treatment in the USA alone. Most people do not know that 70% of all fatal heart attacks are caused by rupture of plaques with large cores of lipid and necrotic debris encased by a fibrous cap, so-called vulnerable plaques (VPs), which often do not create significant narrowing of the lumen and therefore are not detected with standard medical imaging modalities, such as computed tomography, magnetic resonance imaging, coronary angiography and external ultrasound (figure 9). Both detection and treatment of VPs present huge unmet clinical needs. It has been postulated that diseased arteries can be diagnosed and/or acutely treated with drugs delivered locally to rupture prone plaques using NPs in order to promote rapid plaque stabilization and/or passivation.
Figure 9.
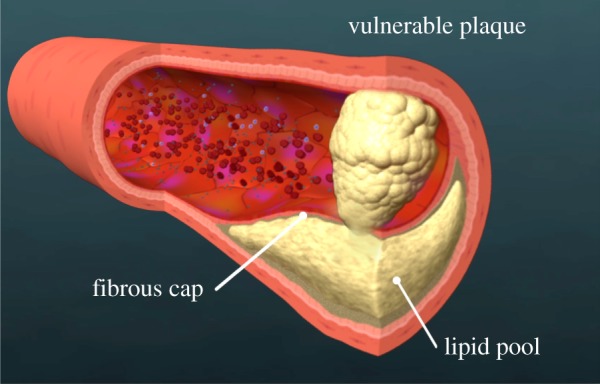
A schematic of a typical vulnerable plaque with a large lipid pool and a thin fibrous cap that separates the thrombogenic components of the plaque from the lumen.
In addition to the size of the necrotic lipid core, the extent and location of plaque inflammation appear to be key factors in determining plaque instability [120,121]. Along with immune cell activation, inflammation contributes to the loss of collagen in the fibrous cap, a prelude to fibrous cap rupture. Inflammation is also known to induce differential surface expression of specific vascular molecules such as ICAM-1, intravascular cell adhesion molecules and selectins. Blood-borne NPs, conjugated with targeting ligands and loaded with therapeutic and/or imaging agents, can potentially recognize and use these molecules as vascular docking sites, thereby helping to detect VPs and/or deliver site-specific acute therapy [121,122].
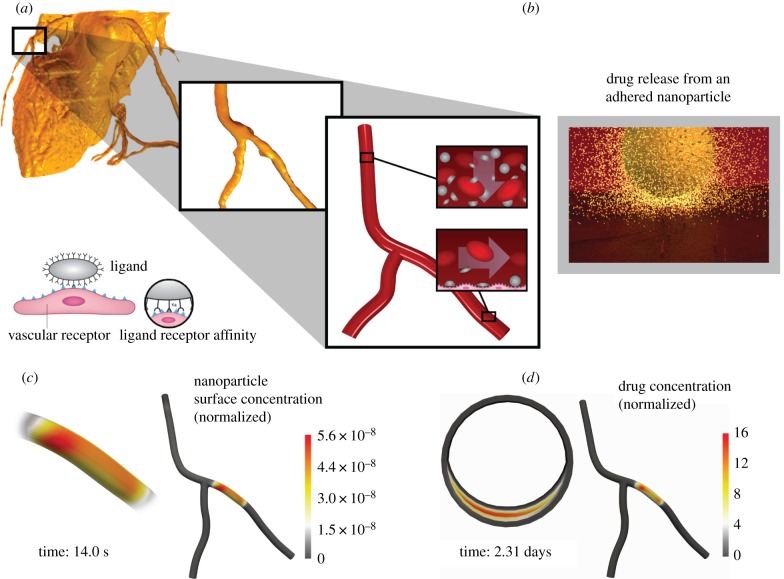
In a typical local drug delivery system, drug-encapsulated polymeric NPs are injected directly into the blood stream. These NPs are sufficiently small, 20–500 nm in diameter, to be administered at the systemic level. Carried by the blood stream, these NPs can reach any biological target. Some of the NPs marginate or drift towards the artery wall facilitating local interactions with the endothelium. To enhance the specific recognition of the biological target (NP docking sites), in this case receptors expressed in and around the VP at the diseased site, the NP surface is covered with ligand molecules and antibodies through nanoengineering. Through the formation of ligand–receptor bonds, the particles firmly adhere to the vessel wall, withstanding the hydrodynamic forces that tend to dislodge them (figure 10a). From this privileged position, the NPs can release the encapsulated drug (or even smaller drug-encapsulated particles) towards the extravascular space in the vessel wall (figure 10b). The released molecules can then propagate through the artery wall to exert a therapeutic effect on the target region, the VP.
Figure 10.
(a) Patient-specific modelling of vascular deposition of nanoparticles from [7]. (b) Drug release from adhered nanoparticles. (c) Simulated results of nanoparticle distribution in the targeted region (near the vulnerable plaque, VP) with a higher density of receptor expression. (d) The corresponding drug distribution pattern within an idealized VP.
It has been previously demonstrated how a patient's local blood flow features, such as wall shear stress, targeted receptor density and physico-chemical properties of the NPs, including size, shape and surface characteristics, can influence NP deposition pattern and consequently therapeutic efficacy [14,123]. There is therefore an overwhelming need for mathematical models that can account for patient-specific attributes, along with NP design parameters, to ensure maximum NP targeting efficiency, thereby helping to personalize, and thus optimize, nanoparticulate therapeutic intervention in an individual patient.
To that end, a three-dimensional computational toolset has been developed that uses patient-specific information (e.g. three-dimensional geometry, blood flow features, vessel wall characteristics) as input to analyse and predict the vascular deposition of surface functionalized NPs within an inflamed arterial tree [14,123]. The methodology allows the simulation of NP transport through the blood stream, their adhesion onto and penetration into the vessel wall and the subsequent release and propagation of the encapsulated drug (or imaging agent) through the tissue in a patient-specific vasculature within an isogeometric analysis (IGA) framework [13,14]. IGA is an improvement on the traditional finite-element method, which has been shown to be particularly suitable for such cardiovascular applications because of its precise and efficient geometric modelling, capability to appropriately capture both laminar and turbulent blood flow regimes and accurate representation of stresses and near-wall quantities. Figure 10c,d depicts simulation results for NP deposition pattern and the corresponding drug distribution, respectively, within an idealized VP when using a catheter-based nanoparticulate drug delivery system.
The next step is to apply the computational tool in a clinical setting at Texas Heart Institute. The main goal was to validate the model in vivo, then collect data from a population of patients and incorporate the information into the model to predict the nanoparticulate drug (or imaging agent) delivery system that would be most efficacious. Successful realization of this goal will lead to a robust computational framework that can potentially answer critical questions such as, given a desired drug-tissue/imaging agent-tissue concentration in the targeted region (e.g. inflammation in VPs), what would be the optimum NP delivery mechanism, NP shape, size and surface properties, and drug release rate, for maximum efficacy in a patient? This computational–clinical marriage will ultimately enable physicians to develop a personalized treatment for individual patients and potentially predict with a high degree of accuracy its effects on the patient before administering it.
2.7. Multi-phase computational modelling for predicting tumour growth and response to therapy
In transport oncophysics [124,125], cancer is defined as a proliferative disease of mass transport deregulation which manifests itself primarily in the disruption of the biological barriers that separate body compartments [126]. The most important consequences of this deregulation are invasion, the ability to ‘push’ its way into host tissue; metastasis, the ability to move to distant locations; and angiogenesis, upsetting the balance of nutrient distribution and elimination of metabolites [126]. Tumour growth and connected nutrient and drug transport is a field of choice for numerical modelling. Many models related to this subject can be found in the published literature, see for instance the review papers [127,128]. Most models are fluid–fluid mixture models such as [129,130], whereas fewer are solid–fluid models. The latter of which either consider the tumour as a solid, permeated by IF [131] or are composed of an ECM permeated by one or several fluids [132]. This last one seems to be the most versatile and will be considered in more detail. It can handle situations such as a melanoma growing on the skin or experiments such as the one in [133] where cells are grown in an acellular ECM. The model comprises the following phases: (i) the TCs, which partition into living cells and necrotic cells, (ii) the healthy cells (HCs), (iii) the ECM, and (iv) the IF (figure 11). The ECM and IF pervade the whole computational domain, whereas the TCs and HCs are limited only to the subdomains with the tumour mass and healthy tissue, respectively. The ECM is modelled as a solid, whereas all other phases are fluids. The TCs become necrotic upon exposure to low nutrient concentrations or excessive mechanical pressure. The IF, transporting nutrients, is a mixture of water and biomolecules as well as nutrients, oxygen and waste products.
Figure 11.
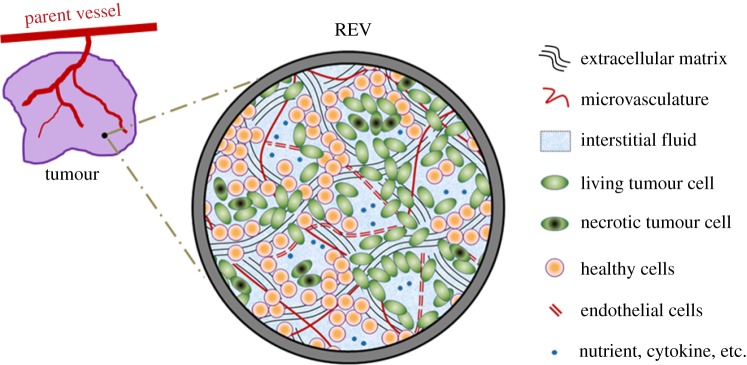
The multi-phase system within a representative elementary volume (REV) [128].
Existing blood vessels are modelled by line elements, and blood flow is taken into account. The governing equations are obtained via the thermodynamically constrained averaging theory (TCAT) [128]. The resulting set of equations involves second-order partial differential operators and is solved by the finite-element method to predict the growth rate of the tumour mass as a function of the initial tumour-to-HC density ratio, nutrient concentration, mechanical strain, cell adhesion and geometry. TCAT provides a rigorous yet flexible method for developing multiphase, continuum models at any scale of interest [134].
Contrary to mixture theories applied in legacy models, TCAT considers the interfaces between constituents with interfacial properties throughout the domain, and there is no need to trace sharp interfaces between constituents or to introduce computationally expensive phase field models which require higher-order partial differential operators, as in legacy models. Macroscopic interfaces arise naturally from the solution of an initial-boundary value problem that must be composed of the mass balance equations of all phases involved. The ECM is treated as a viscoelastic solid material in the finite strain regime or as an elastoviscoplastic material if ECM remodelling has to be considered [135]. This paves the way for a better understanding of the tissue's mechanical properties on the development and growth of tumour masses [136]. The model has a modular structure and further species and phases can be easily added.
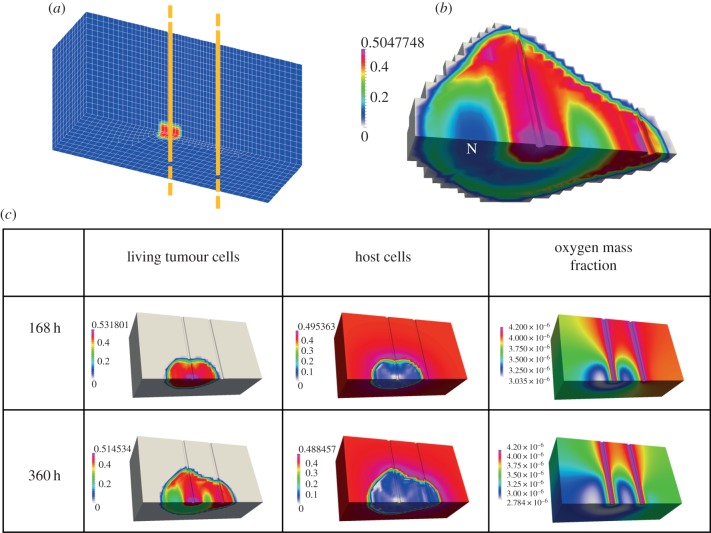
As an example of the TCAT model, we show the case where TCs grow in proximity of two otherwise healthy blood vessels that are the only source of oxygen. The TCs are initially located around one vessel only. The volume fractions at 7 and 15 days of the HC phase and of the living TC phase are shown in figure 12. The HCs are almost completely displaced by the TCs and necrosis occurs in locations within the tumour which are further from the left blood vessel.
Figure 12.
(a) Geometry; yellow lines show the axes of the two capillary vessels. (b) Volume fractions of the living tumour cells at 20 days; ‘N’ indicates the necrotic areas. (c) Volume fractions of the living tumour cells (first column) of the healthy cells (second column) and mass fraction of oxygen (third column) [132].
From a more complete understanding of the growth and response dynamics of cancer, one may indeed expect to identify promising clues for the development of more effective treatments.
3. Biomedical device design
3.1. Rapid and simple preparation of nucleic acids using micro- and nanostructures
Rapid and simple preparation of nucleic acids is important for disease diagnosis, DNA sequencing and forensic investigations. The challenge for rapid DNA preparation is to purify and concentrate DNA without compromising the performance of large laboratory equipment. The current methods are based on centrifugation, microfiltration, toxic buffers and skilled personnel. Microscale and nanoscale mechanics can offer ample opportunity to replace the complex functions of equipment.
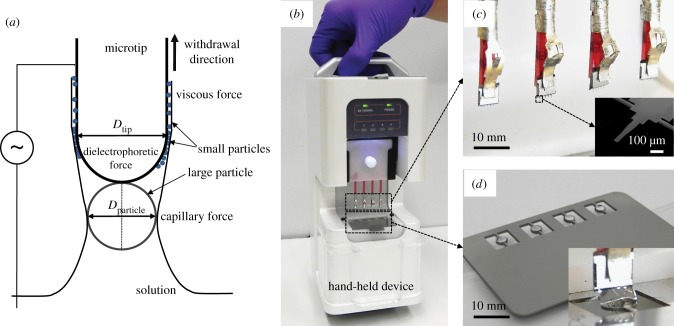
Electric fields can be combined with capillary action for preparation of microscale and nanoscale objects in liquid. When microscale or nanoscale tips are immersed in solution, the forces induced from capillary action and viscosity, in combination with an attractive electric-field-induced force, can capture or release the particles (figure 13a). The size-selective capture can purify DNA molecules in a sample matrix, replacing the function of centrifugation. Figure 13b shows a DNA extraction device designed for processing four DNA samples in one batch. Four chips are loaded onto a plastic coupon (figure 13c). Each individual chip has five microtips, which are made of a 1 µm thick silicon nitride layer supported on a 500 μm thick silicon layer. The top sides of the microtips are coated with a 20 nm thick gold layer for electrical connection and preservation of DNA. Metallic rings are used to suspend sample solutions by surface tension (figure 13d). The device can yield similar performance to a commercial kit, but it can simplify the operation and requires no toxic reagent. A nanotip also showed similar performance with a more straightforward operation, which demonstrates the application of microscale and nanoscale mechanics for novel biodevices.
Figure 13.
(a) Force mechanics on a nanotip and microtip surface in the capturing process [137]. (b) A portable prototype device [138]. (c) Magnified view showing four chips in the holders. The inset shows a scanning electron microscopy image of a single microtip. (d) An array of wells containing the solution. The inset shows the immersion of the chip into the solution.
Towards commercialization of similar microscale and nanoscale devices, the remaining challenges are (i) scalable production of microscale and nanoscale structures, (ii) integration of such small structures into a device, and (iii) quality control of the devices for uniform and reproducible performance. In the future, novel working principles in small-scale mechanics will lead to a revolution in the field of biomedical devices. The role of numerical simulation in commercial applications is to clarify the mechanics in the multi-scale regime, which will explain the behaviour of nanoscale objects and uncover underlying mechanisms which can be used for novel device design. In practice, numerical approaches have explained the sophisticated interaction of molecules in liquid [139], which will shorten the incubation time for device applications.
3.2. Point-of-care diagnostics using nanosensors
POC diagnostic systems are a rapidly growing segment of biosensors that will eventually lead to home-diagnostic sensors. To date, many methods have been developed for POC diagnosis: assays based on polymerase chain reaction, immunoassays, etc. These methods are more sensitive and rapid than the traditional detection methods; however, the performance is still not satisfactory. In addition, owing to the low analyte concentration in the actual samples, a pre-concentration step is critical. Currently available concentration methods use centrifugation, microfiltration or magnetic beads. However, the methods are limited by cumbersome preparation steps, low yield and low throughput. To address the challenge, electric-field-induced concentration has the potential for application in highly sensitive detection of molecular biomarkers for disease diagnosis and drug discovery. Using a nanostructured tip, a high-strength electric field can be generated to concentrate molecules larger than 2 nm in size with high efficiency. However, designing a tip that reliably concentrates a specific target molecule requires a detailed understanding of the physical interactions governing the separation process. Mechanics has already influenced the design process of mechanical and aerospace applications [140–144], as well as biosensors through the immersed finite-element technique [20–23,25,145,146], which is capable of accurately modelling the various forces experienced by a biomolecule during separation such as fluid–structure interaction (FSI) of arbitrarily shaped structures, large structural deformations, electrokinetics, temperature-dependent thermal fluctuations and molecular interactions [21]. The developed numerical tool accurately predicts the efficacy of pre-concentration of molecular targets, in agreement with experimental results [32]. Once pre-concentrated, the detection can be carried out by fluorescence and electrical measurement [147]. Such an amplification-free platform can show a high sensitivity equivalent to polymerase chain reaction but with a short assay time [148]. The nanostructured tip offers a simple configuration for POC diagnosis as well as a convenient home-diagnostic platform, and mechanical analysis plays an important role in rapid development of novel tip designs for specific problems. Furthermore, the numerical methods established in this context are ripe for further development and application to other important processes involving complex interactions with biomolecules, both in vitro and in vivo.
3.3. Developing model organ or multi-organ (in vitro) microdevices for the rapid and effective screening of pharmaceuticals
During the past decade, the capabilities of microfluidics, enabled by the development of soft lithography [149], have expanded dramatically and now encompass a broad range of medical and biological applications ranging from single-molecule measurements to single-cell or cell-population studies. Indeed, the recent development of techniques that enable the co-culture of multiple cell types in two- or three-dimensional co-culture has led to breakthroughs in our capability of recreating many aspects of organ function in a single microfluidic chip. This has numerous applications, among which are the abilities to replicate certain biological or pathological processes outside the body and to create model organ or tissue systems that can be used to screen for new therapeutics. Because these innovative microfluidic platforms are capable of capturing multi-cell-type interactions, they better mimic the real physiological situation. In addition, and importantly, they have the potential to take advantage of rapid advances in cellular reprogramming to produce human, induced pluripotent cells (iPSCs) [150]. By using the iPSCs from a particular patient, the prospect of patient-specific screening is brought one step closer to being a reality.
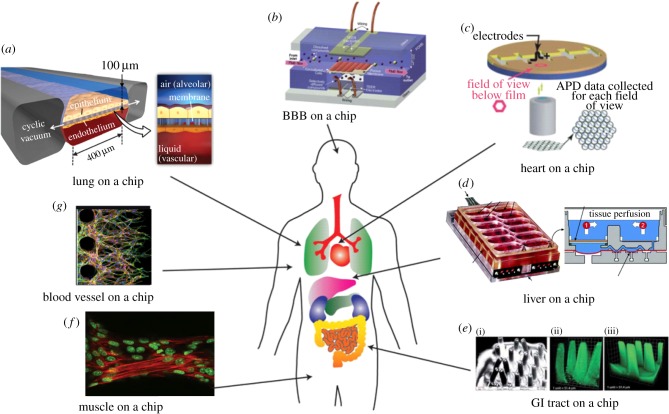
What are our current capabilities for producing these ‘organs-on-a-chip’ technologies? Over the past several years, research has emerged demonstrating the capability to reproduce some functions of a variety of organs (figure 14) [151]. While these vary in their ability to truly reproduce or mimic organ function, they clearly reach far beyond the ability of single-cell-type drug screening in well-plate systems, which is still the standard approach used by the pharmaceutical industry. One example is illustrated in figure 14a, the ‘lung-on-a-chip’ [153]. Designed to simulate conditions in the gas exchange or alveolar region of the lung, it incorporates multiple cell types (e.g. both endothelial and epithelial cell monolayers), allows chemical signalling between them and subjects the cells to cyclic stretch by varying the air pressure inside channels, thereby stretching the elastic substrate on which the monolayers are grown. It also includes an air–liquid interface, which is necessary for the epithelial cells to take on the right morphology, and also stimulates the synthesis and secretion of pulmonary surfactant, which is critical for many lung functions.
Figure 14.
The spectrum of model systems (‘organs on a chip’) is being developed for drug screening purposes. Systems have been developed for (a) lung, (b) the blood–brain barrier, (c) heart tissue, (d) liver, (e) the gastrointestinal tract, (f) muscle and (g) the microcirculation. Reproduced from [151], adapted from [152] with permission.
Other systems incorporate the capabilities to grow cells on a two-dimensional surface, appropriate for cellular monolayers, but in many cases also within three-dimensional gels that mimic the microenvironment essential for natural function of cells embedded in the interstitial space. Examples of three-dimensional gel microenvironments include the ‘liver bioreactors’ produced by several groups [154] and model gastrointestinal tracts [152], blood–brain barriers and muscles, both cardiac or skeletal. In these systems, simultaneous two- and three-dimensional cultures allow cells to interact in a natural way, exchanging signalling factors via the interstitial spaces of the gel, and allowing for a more realistic, cell-specific morphology. The enormous flexibility of these systems is only now being fully realized as the models become increasingly complex and more realistic. This poses new opportunities to the research community, especially in terms of creating computational models that capture the transport characteristics through channels, gels and within more complex tissues, while also incorporating the increased complexity of the biology.
Of particular note, efforts have recently been launched, under the support of substantial government programmes from the Defense Advanced Research Projects Agency and National Institutes of Health, to combine single-organ models of this type to produce ‘body-on-a-chip’ systems in which multiple ‘organs’ can interact in a realistic way. One of the major driving forces behind this effort is the need to understand and be able to anticipate off-target effects of drugs, deleterious effects on organs other than the one for which the drug is targeted.
An important feature of many tissue models is the capability to incorporate vascular perfusion and the exchange of various metabolites throughout the tissue space. Previous inability to do so has also been one of the major limitations in the development of engineered organs, with the exception of those tissues, such as cartilage or cornea, for which blood circulation is not essential. Recently, several groups have demonstrated methods in model systems to produce a vascular network that can be perfused. Two approaches have been developed. In one, the vessels are either etched onto the surface of the device, or cast into it [155] or created by other means [156], inside a three-dimensional gel that may or may not be biodegradable. The channels produced are then seeded with endothelial cells that adhere to and form a confluent monolayer over the walls of the gel channels. These systems tend to be limited at present to channels that are larger than natural capillaries, but new methods are constantly emerging that are sure to reduce vessel diameter further. An alternative method that has been used by several groups [112,157,158] is to induce the vascular cells to bore into the hydrogel from a monolayer and form new vessels by the process of angiogenesis [159,160]. Another approach is to draw upon the natural capabilities of the cells to form networks when dispersed uniformly within the three-dimensional matrix, termed vasculogenesis [112,157,158]. Either approach produces networks with morphologies that are both controllable and have dimensions closer to those of normal capillaries.
Numerous challenges exist in the design of systems that possess the same transport and mechanical properties of living tissue. Matrix materials are needed that replicate both the chemical and mechanical characteristics of normal human ECM. Abundant evidence exists supporting the critical role of matrix mechanics in behaviours ranging from cell migration [161], to cytoskeletal functions [162], to stem cell differentiation [163], and the biomechanics community has made considerable progress in understanding these effects.
However, much of the design currently is based on trial and error, and a need exists to meld a fundamental understanding of biology with a sound approach to the mechanical issues. Computational approaches rely now primarily on agent-based models [164], in which the cell behaviour is described by a collection of rules that are largely determined empirically. Few if any models can be found that are based on first principles, although the mechanical properties and transport characteristics of cell and ECM have been reasonably well characterized. Flows, both intravascular and interstitial, exert important influences on tissue function, and these can be modelled by conventional means. The greatest challenge is to meld these more traditional models with the intrinsic biology of the systems in order to create truly predictive simulations.
3.4. Fluid–structure interaction modelling, simulation and optimization of paediatric pulsatile ventricular assist devices
Heart failure is a common condition in the USA, with more than 600 000 cases diagnosed annually [165]. Cardiac transplantation remains the preferred treatment; however, a lack of suitable donors restricts this option for many patients, and the median survival with this condition is only 2–3 years after initial diagnosis. Ventricular assist devices (VADs) pump blood in parallel with the native heart function and provide full or partial mechanical circulatory support to one or both ventricles of the heart. They are used clinically in a range of adult and paediatric diseases, including congenital heart disease, cardiomyopathy and post-infarction heart failure. They were first developed as a bridge to transplant, in order to prolong life of critically ill patients awaiting organ availability. However, as designs have evolved to become smaller and even fully implantable, they can now be used as destination therapy, supporting one or both ventricles. More recently, there has also been success, most notably in paediatric patients, with use of VADs in bridge to recovery scenarios, allowing sufficient offloading for myocardial remodelling and recovery.
The need for reliable and safe mechanical circulatory support is also growing in the paediatric population [166]; however, the number of available donor hearts for this population has remained fixed at approximately 500 each year. VAD usage has thus increased in this population, although paediatric VADs have a notably poorer performance than available adult models. Development of VAD technology has taken place almost exclusively for the adult population. The Berlin EXCOR (figure 15), a pulsatile device, remains the only US Food and Drug Administration-approved device for children. However, adverse clinical effects occur in these devices at an alarming rate. Particularly troubling is the consistently high rate of thromboembolic events (22%).
Figure 15.
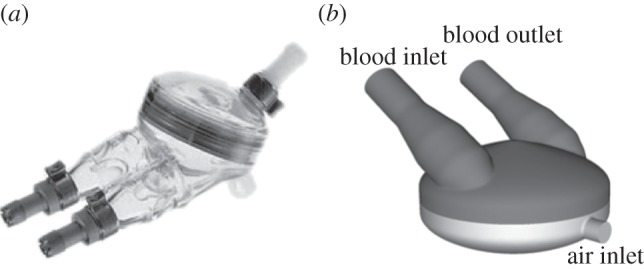
(a) The Berlin EXCOR PVAD. (b) Geometrical model of the PVAD containing the blood and air chamber with the corresponding inlets and outlets. The model is used in fluid–structure interaction simulations in [165].
With the increasing prevalence of VADs in clinical use, there is now focus on improving design performance to reduce comorbidities, reducing device size and allowing patients a more active lifestyle. Computational-mechanics simulations, coupled with optimization techniques, can be used to accelerate the design process and optimize current and future designs. Simulations offer a promising means to cheaply and efficiently test and optimize competing device prototypes, thereby reducing time to market and identifying potential performance enhancements. Computational-mechanics modelling and simulation is an integral part of the design process in many industries (e.g. aerospace, automotive). Almost every automobile manufacturer makes use of detailed, large-deformation structural-mechanics simulations to model car crashes in an effort to assess vehicle safety for the passengers. Aircraft manufacturers use computational fluid mechanics coupled to rigorous optimization algorithms as a crucial and cost saving part of the design chain for all major aircraft. However, despite its demonstrated success in these large-scale applications, adoption of simulation tools has lagged behind in the medical device industry. This is due in part to initial success with designs identified through trial and error and experimentation as well as challenges associated with complicating factors of blood biochemistry, mechanobiology and physiological response, which make simulations challenging. While simulations have been applied more recently, particularly in the design of the HeartMate II and HeartAssist 5 blood pumps, there remains a need for increased adoption of simulation technology and formal design optimization algorithms.
To model pulsatile VADs (PVADs), dynamic interaction of air, blood and a thin membrane separating the two fluids needs to be considered. Coupled FSI simulations at full scale are essential for realistic and accurate modelling of PVADs. This is because the motion and deformation of the thin membrane depend on the flow in the device blood and air chambers, and the flow patterns, in turn, depend on the motion and deformation of the membrane. As a result, the fluid and structural mechanics equations need to be solved simultaneously, with appropriate kinematic and traction coupling at their interface. The computational challenges for FSI of PVADs include large, buckling motions of a very thin membrane, the need for periodic remeshing of the fluid mechanics domain (owing to the large motions of the membrane, which induce very large changes in the blood and air flow domain geometry during the cycle), and the necessity to use tightly coupled FSI solution strategies owing to the very strong added structural-mass effect present in the problem.
The state of the art in FSI modelling and simulation is able to address these challenges (see a recent book on FSI [167] and references therein); however, there is currently no readily available, off-the-shelf commercial software where these techniques are implemented and that may be robustly deployed for this class of problems. The successful, one-of-a-kind, physiological FSI simulations of PVADs, as accomplished in the recent work (see [168] and figure 16), present an important first step towards computer-aided engineering design of these devices.
Figure 16.
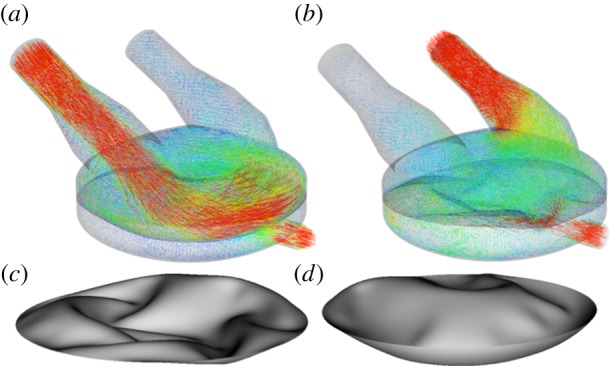
Top: snapshots of the blood flow velocity during the fill (a) and eject (b) stages of the PVAD operation. Bottom: snapshots of the deformed configuration of the thin structural membrane during the fill (c) and eject (d) stages of the PVAD operation. The FSI simulations shown are from [168].
Thrombus formation (i.e. blood clotting) is the major problem in VADs and, in particular, PVADs. However, determining thrombotic risk factors in these devices is challenging. Thrombus formation is the result of a complex sequence of chemical reactions in the bloodstream, resulting in platelet activation and aggregation and the formation of fibrin networks around these aggregations. Thus, it is desirable to not only model the FSI in PVADs, but also the process of blood coagulation in order to understand the source of the problem, and to propose device design modifications to mitigate it. Some research has been dedicated to this, although determining an appropriate blood coagulation model for our purposes is quite challenging. As a result, we explore other surrogates for thrombotic risk that may be directly computed from FSI simulation data. Long residence times and areas of blood recirculation or stagnation may lead to increased risk of thrombosis in PVADs [169]. A method for calculating particle residence time for flows in moving spatial domains was proposed in [170], and the developments for PVAD FSI and residence time computations were used to perform a shape-optimization study of a paediatric device, as in [171]. The optimization using a derivative-free surrogate management framework (SMF) [172] was carried out for a full-scale three-dimensional device, with time-dependent FSI simulations performed under physiologically realistic conditions (figure 17).
Figure 17.
Progression of the optimal design as determined by the FSI-based SMF optimization scheme. The optimization cost function value, which is derived from particle residence time in the blood chamber, is displayed under each model. The strong inclination toward vertically oriented arms is reasonable, as this configuration enables the incoming blood to move more quickly and uniformly toward the outlet than other designs. However, the idea to vertically mount the inlet/outlet arms is non-intuitive, a result that reinforces the value and importance of systematic design space optimization for PVADs. See [171] for more details.
Despite recent progress, challenges remain to increase the relevance and utility of VAD simulations in the device design process and in the clinic. First, complete modelling of blood biochemistry remains computationally intractable owing to high computational cost. There is therefore a need for continued development and validation of reduced-order models to measure the risks of thrombosis and haemolysis. Second, there is a need for integration of the advanced simulation and formal optimization methods outlined above to accelerate the design process in the presence of constraints and uncertainties. As the optimization process identifies new designs, the need will also arise for rapid prototyping of simulation-derived designs for experimental testing. Third, as simulation methods mature, there is an increased need for validation of simulated risk of thrombosis and haemolysis against clinical data in VAD patients and animal models. Finally, one cannot ignore the underlying physiology of the patient, and VAD models should be coupled to lumped parameter network models of circulatory physiology to elucidate the interplay between the device and physiological conditions. This is particularly compelling in paediatric cardiology owing to the complex physiology and unusual anatomy in congenital heart disease patients.
4. Cell mechanics
4.1. Mechanosensing and mechanotransduction
As the basic unit of life, living cells perform an enormous variety of functions through synthesis, sorting, storage and transport of biomolecules; expression of genetic information; recognition, transmission and transduction of signals; and conversion between different forms of energy. Many of these cellular processes can generate, or be regulated by, mechanical forces at the cellular, subcellular and molecular levels. For example, during cell migration, contractile forces are generated within the cell in order for the cell body to move forward. These contractile forces, in combination with the adhesion of cells to ECM through focal adhesion complexes, enable cells to sense the stiffness of the surrounding substrate and respond to it. Many normal and pathological conditions are dependent upon or regulated by their mechanical environment. Some cells, such as osteoblasts and vascular cells, are subjected to specific forces as part of their ‘native’ physiological environment. Others, such as muscle and cochlear outer hair cells, perform their mechanical function either by converting an electrical or chemical stimulus into mechanical motion or vice versa.
Of particular importance is the ability of cells to sense mechanical force or deformation and transduce these mechanical signals into a biological response. For example, endothelial cells can recognize the magnitude, mode (steady or pulsatile), type (laminar or turbulent) and duration of applied shear flow, and respond accordingly, maintaining healthy endothelium or leading to vascular diseases, including thrombosis and atherosclerosis. Vascular smooth muscle cells in the arterial wall remodel when subjected to pressure-induced wall stress. Fibroblast cells ‘crawl’ as an inchworm by pulling the cell body forward using contractile forces. Bone alters its structure to adapt to changes in its mechanical environment as occurs, for example, during long bed rest. Stem cells sense the elasticity of the surrounding substrate and differentiate into different phenotypes accordingly. These and other examples demonstrate the ability of cells to sense and respond to their local mechanical environment. However, little is currently known about the fundamental molecular mechanisms by which cells sense mechanical force or deformation, and transduce the mechanical signal into a biological response. Answering this fundamental question in biomechanics will provide a quantum leap in our understanding of the essential roles of mechanical forces in biology and medicine.
A possible unifying mechanism for mechanosensing and mechanotransduction in living cells is protein deformation, broadly defined as protein conformational change under force. It has been well established that the three-dimensional conformation of a protein largely determines its function. However, the conformation of a protein can be altered by applied mechanical force, resulting in changes of the functional states of the protein and inducing downstream biochemical and biological effects. Therefore, protein conformational change under mechanical force is an excellent candidate as the unifying molecular mechanism of mechanosensing and mechanotransduction in living cells. Shown in figure 18 are some examples of the possible effect of protein deformation in a living cell. Many proteins have specific ligand binding sites buried initially by a protein domain or a peptide (a ‘lid’). As illustrated in figure 18a, upon applying mechanical forces to such a protein, the ‘lid’ opens, exposing the ligand binding site. The reverse is also true: protein deformation can close the ‘lid’ that is initially open, thereby burying the ligand binding site. Alternatively, a protein globular domain can unfold under mechanical force, exposing the ligand binding site that is buried inside the globular domain (figure 18b). Mechanical forces can also unfold a globular domain and thus expose the non-polar residues (figure 18c), which may cause non-specific interaction between the protein domain and other biomolecules, and thus alter protein function. It is well known that proteins interact with each other based on conformational matches: good conformational match leads to high binding specificity and affinity between two proteins, whereas poor conformational match does the reverse. As shown schematically in figure 18d, when proteins 1 and 2 have good conformational match, they have strong interactions to realize their functions, for example, to activate a signalling cascade, or facilitate an enzymatic activity. However, when one of the proteins, say, protein 2, sustains a force-induced conformational change, the interaction between proteins 1 and 2 becomes weak owing to the poor conformational match, thus altering the function of protein 2. The reverse is also true: deformation of a protein can increase its affinity to another protein that otherwise would not interact owing to the poor conformational match in its native state. This concept is not limited to protein–protein interactions; protein–DNA, protein–RNA and protein–small molecule interactions can be also altered by force-induced protein conformational change.
Figure 18.
Examples of biological consequences of protein deformation. Mechanical forces can (a) switch a ‘lid’ in a protein from ‘closed’ to ‘open’ position, or (b) unfold a protein domain, thus exposing the ligand binding site. Protein deformation can also (c) expose the non-polar residues, causing non-specific interaction between the protein domain and other biomolecules; or (d) induce a change in binding affinity, altering protein–protein interactions.
4.2. Deformation and constitutive behaviour of cells
Over the past few decades, extensive experimental and modelling/simulation studies have been performed to determine the deformation of cells and tissues under applied force, and their constitutive behaviours. Typical experimental set-up for single-cell mechanical testing is shown in figure 19. However, in most of the modelling studies and constitutive equations developed for living cells, the active feature of living animal cells has been either ignored or poorly captured. It has been well established that most of the living animal cells are ‘active’ materials and structures, i.e. their structure, morphology and thus constitutive behaviours change with applied mechanical load. Cell structural changes, including structural alterations in cytoskeleton and changes in density and/or distribution of local adhesion complexes, may happen within a few minutes upon loading. Therefore, it is likely that as mechanical measurement of cells is being conducted, significant changes in cell structure and/or surface contact occur concurrently, leading to an altered force–deformation response of the cell. The degree of changes in cell deformation behaviour depends on both the magnitude and rate of applied force. Adding to the complexity is that certain cells also have force-generating functions, which should be considered in the constitutive behaviour of cells as well. Thus, there is a critical need to develop better constitutive models for single-cell mechanical behaviour, taking into account the active behaviour of cells. However, it remains very challenging to quantify accurately the distribution of forces among various subcellular structures inside a living cell. It is well known that a significant portion of the forces is supported as well as generated by the cell cytoskeleton, but cells are active and the cytoskeletal structures are dynamic; they can undergo remodelling or reorganization in response to mechanical perturbations. Further, the measurement of mechanical behaviour of individual cells may give rise to different results, which may depend on cell morphology, stage in the cell cycle, as well as how different subcellular structures respond to mechanical perturbation. This raises a fundamental paradox: how can we measure mechanical behaviour of living cells if they react to our measurement tools? These issues are fundamental to the study of the mechanics of living cells.
Figure 19.
Schematic of the three types of experimental techniques used to probe living cells. Atomic force microscopy (AFM) (a) and magnetic twisting cytometry (MTC) (b) are type A methods which can probe cell components at force resolution of 10−10 and 10−12 N, respectively, and displacement resolution of at least 1 nm. Micropipette aspiration (MA) (c) and optical trap (OT) (d) are type B techniques that can deform an entire cell at force resolution of 10−10 and 10−11 N, respectively. Shear flow (e) and substrate stretching (f) methods are capable of mechanical response evaluation of a population of cells.
4.3. Microfluidics systems for single-cell studies
Life-science researchers typically study cell behaviour by performing experiments on populations of cells because the standard bulk methods are simple, available and well established [173,174]. Millions of cells are normally used for a bulk experiment, especially when robust and readily available cell lines are used. However, it is well known that cells in a seemingly identical environment can show heterogeneous behaviour within a population [175,176]. For instance, cells can be at different stages of the cell cycle or exhibit variations in gene expression owing to the stochastic nature of biochemical processes. This biological variability is becoming increasingly recognized by the biological research community as an important factor [177,178]. Indeed, potentially significant cellular behaviour may not be captured by bulk techniques, because the experimental ensemble average across the population can obscure an important subset within the data or lead to incorrect conclusions [173,174]. In fact, cell heterogeneity has been posited as the cause of error in disease classification [179].
Unlike conventional bulk methods, single-cell studies can provide biochemical characterization of individual cells without the loss of specificity associated with ensemble averaging. This unique advantage is the key for capturing the effects of gene expression variations leading to different cell states, for enabling an understanding of the mechanisms inherent in biological noise, and for probing complex phenomena including cell differentiation and cancer proliferation. For example, cell signalling pathways—the link between inputs and outputs through interconnected molecular interactions—during stem cell differentiation display stochastic behaviour within the pathways owing to cross talk between multiple pathways, localization of reactions and the low concentration of molecules involved in signalling [180]. To understand the complex intercellular input–output relationship and to develop mathematical descriptions of cellular behaviour, it is essential to have tools for systematic single-cell analyses that can be performed with throughput that is statistically significant and practical with respect to research time per data point. Fundamental understanding of cellular variation will have a significant impact on biological studies and lead to advancements in our ability to predict input–output relationships in cells using mathematical models and predictive analyses. This ability is vital for understanding higher-level systems, such as tissues and organisms, and for developing therapeutic approaches [180].
Micro- and nano-fabricated devices are tools that possess great potential to address these needs. Microfluidic tools offer unique advantages for in vitro assays such as low-volume sampling and rapid analysis, owing to short diffusion distances and small areas of interest for optical analysis [173,174]. For example, microwell arrays [174,181] have been used to acquire data from large sets of individual cells, offering statistically significant conclusions. In general, the miniaturization of tools used for biological applications is attractive because it reduces the volume of (often) expensive reagents, requires less space for replicates, allows automation and integration for sequential analyses, enables portability and reduces waste [174]. Using these advantages, many methods from single-cell transfection, sampling, and analysis to on-chip cell manipulation and culture have been developed, which are critical towards the development of single-cell studies.
For direct delivery of molecules into single cells, microfluidics systems are often integrated with microelectrodes to achieve electroporation, which is the transient and reversible formation of nanometre pores, in the cell membrane, by application of an electric field. For example, the Espinosa group has recently developed a microfluidic tool for single-cell electroporation using nanofountain-probe (NFP) technology (figure 20). The NFP is a cantilever probe, with embedded microchannels, which allows the application of a local electric field when the probe and cell membrane are in contact. Unprecedented transfection efficiency and delivery of DNA, RNA, plasmids and small molecules were achieved with dosage control and very high viability [182]. In addition, other groups demonstrated successful single-cell transfection using polydimethylsiloxane (PDMS)-based microfluidic devices, e.g. droplet and nanochannel electroporation [183,184].
Figure 20.
Transfection of single cells using nanofountain probe electroporation developed by the Espinosa group. HeLa cells were transfected with fluorophore-tagged dextran with 95% efficiency and high viability (>90%) after electroporation [182].
In addition to single-cell transfection, reversed electroporation on a microfluidic chip has recently been shown to permit minimally invasive sampling of intracellular contents through transient and reversible nanopores on a cell membrane [185,186]. By tuning parameters of the applied electrical input, i.e. polarity, voltage, frequency and duration of input signal, during electroporation, precise and reproducible sampling of cells is possible while maintaining cell viability. These studies demonstrate the possibility of using electroporation for sampling. Such sampling must be followed by a robust bio-detection module. Indeed, biomolecular detection with up to attomolar resolution was achieved by combining a microfluidic device with electronic or optical signal detection [187]. Goluch developed a bio-barcode assay for single protein detection by using functionalized NPs [188]. Gong developed integrated nanoelectronic and electrokinetic devices for label-free attomolar detection of proteins [189]. Jung used a capillary electrophoresis assay by combining on-chip isotachophoresis with laser-induced confocal fluorescence detection [190]. The Heath group developed an integrated blood barcode chip, which can sample a large panel of plasma proteins from whole blood samples within 10 min of sample collection [191]. The Quake group has pioneered large-scale gene expression analysis from single cells that has been exploited in a wide range of applications such as whole-genome molecular haplotyping of a single human metaphase cell [192].
Microfluidics systems have become important tools for single-cell studies, yet many challenges remain. For example, microfluidic tools often operate separately for different applications, e.g. single-cell manipulation, isolation, culture, transfection, sampling or analysis. As a result, time-dependent high-throughput study of individual live cells is still unattainable. This calls for efforts to integrate modular tools, with different functions, into one multi-functional microfluidics system. Moreover, the sensitivity limit of the detection scheme needs further enhancement, as small quantities of target biomolecules are often available in single cells. An example is the study of the role of low-copy number proteins (approx. 1000 molecules per cell) in cell functions such as signalling and regulation of gene expression. Finally, a method offering high throughput is very desirable to obtain statistically significant biological data from which meaningful conclusions can be drawn.
In order to establish a transformative engineering tool for single-cell studies, the Espinosa group and co-workers are pursuing the development of an integrated microfluidic system (figure 21). This effort spans fields ranging from mechanics to multiphysics computational analyses to nanotechnology and to systems biology. Such an interdisciplinary approach will provide unique opportunities to the mechanics community to explore complex systems with application to biological variability and input–output relationships that govern cell function. Moreover, emergent fundamental insights, enabled by such engineered system, will lead to advances in the understanding of regulatory pathways and complex disease mechanisms, which are vital to explain higher-level biological systems, such as tissues and organs, and for developing early diagnostic and therapeutic approaches.
Figure 21.
Integrated microfluidics system for single-cell studies. The system would consist of several modules for multi-functions including single-cell manipulation, isolation, culture, transfection, sampling and analysis [181,183,184,189,191,192] in an automated and high-throughput manner. Such a system would enable time-dependent studies of cell response with single-cell resolution.
5. Educational prospectus and summary
The interdisciplinary nature of mechanics in medicine requires significant changes be made in the educational curriculum of mechanics students. The classical model for mechanics education, consisting of fluid and solid mechanics course series, falls short of preparing students for interactions with biologists and medical doctors, which greatly hinders collaboration. A strong basis in mechanics is still required, but it must be augmented by additional courses designed to teach the essentials of biology and chemistry. Clearly, it is not reasonable to expect mechanics students to develop the level of expertise in biology and medicine as biologists or medical doctors, but a basic understanding of biological processes will greatly facilitate discussion with experts in the field. In addition to courses aimed at the basic science behind medicine and biomedical research, core mechanics courses should draw upon biological problems for illustrative examples. There is a long history of using biological examples to motivate mechanics problems, especially in fluid mechanics, but including modern case studies of mechanics guiding medicine would be greatly beneficial. Specific examples such as drug delivery platforms or model in vitro organs would expose students to archetypal medical applications while providing fascinating engineering systems in which to learn mechanics. Progress in this direction is underway. For example, Northwestern University has recently revamped a course series entitled ‘multi-scale modelling and simulation of solids and fluids’, which now draws heavily on biomedical and biotechnological examples to illustrate modelling methods ranging from molecular dynamics to finite-element simulations. In future, we envision courses jointly taught by biologists or medical doctors and mechanicians, for students from both medicine and mechanics, with the aim of exposing each group to the capabilities and current research issues of the other. Courses intended to drive collaboration and the exchange of ideas between the two groups are essential for the full potential of mechanics in medicine to be reached. Training future researchers in mechanics in medicine requires a substantial effort to reimagine mechanics education. Fortunately, mechanics has proved itself capable of nimbly transitioning into new realms, keeping the field relevant in the face of rapidly changing research environments. With thoughtful changes and additions to the classical curriculum, mechanicians of the future will be capable of bringing quantitative engineering principles to poorly understood areas of medicine.
Acknowledgements
H.D.E. acknowledges support from the National Science Foundation under award IIP-1142562 and the National Institutes of Health under award 1R41GM101833-01. R.D.K. acknowledges support from the National Science Foundation Science and Technology Center (STC) Emergent Behaviours of Integrated Cellular Systems (EBICS) grant CBET-0939511. The authors graciously thank Ying Li and Wylie Stroberg for their helpful comments and suggestions in preparing the manuscript.
References
- 1.DeVita VT, Chu E. 2008. A history of cancer chemotherapy. Cancer Res. 68, 8643–8653. ( 10.1158/0008-5472.Can-07-6611) [DOI] [PubMed] [Google Scholar]
- 2.Tasciotti E, et al. 2008. Mesoporous silicon particles as a multistage delivery system for imaging and therapeutic applications. Nat. Nanotechnol. 3, 151–157. ( 10.1038/nnano.2008.34) [DOI] [PubMed] [Google Scholar]
- 3.Alivisatos P. 2004. The use of nanocrystals in biological detection. Nat. Biotechnol. 22, 47–52. ( 10.1038/nbt927) [DOI] [PubMed] [Google Scholar]
- 4.Decuzzi P, Ferrari M. 2008. Design maps for nanoparticles targeting the diseased microvasculature. Biomaterials 29, 377–384. ( 10.1016/j.biomaterials.2007.09.025) [DOI] [PubMed] [Google Scholar]
- 5.Decuzzi P, Pasqualini R, Arap W, Ferrari M. 2009. Intravascular delivery of particulate systems: does geometry really matter? Pharm. Res. 26, 235–243. ( 10.1007/s11095-008-9697-x) [DOI] [PubMed] [Google Scholar]
- 6.Adnan A, Lam R, Chen HN, Lee J, Schaffer DJ, Barnard AS, Schatz GC, Ho D, Liu WK. 2011. Atomistic simulation and measurement of pH dependent cancer therapeutic interactions with nanodiamond carrier. Mol. Pharmaceut. 8, 368–374. ( 10.1021/mp1002398) [DOI] [PubMed] [Google Scholar]
- 7.Man HB, Kim H, Kim HJ, Robinson E, Liu WK, Chow EK, Ho D. 2014. Synthesis of nanodiamond-daunorubicin conjugates to overcome multidrug chemoresistance in leukemia. Nanomedicine 10, 359–369. ( 10.1016/j.nano.2013.07.014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Greene MS, Li Y, Chen W, Liu WK. 2014. The archetype-genome exemplar in molecular dynamics and continuum mechanics. Comput. Mech. 53, 687–737. ( 10.1007/s00466-013-0925-9) [DOI] [Google Scholar]
- 9.Kim H, Bin Man H, Saha B, Kopacz AM, Lee OS, Schatz GC, Ho D, Liu WK. 2012. Multiscale simulation as a framework for the enhanced design of nanodiamond-polyethylenimine-based gene delivery. J. Phys. Chem. Lett. 3, 3791–3797. ( 10.1021/jz301756e) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li Y, Stroberg W, Lee TR, Kim HS, Man H, Ho D, Decuzzi P, Liu WK. 2014. Multiscale modeling and uncertainty quantification in nanoparticle-mediated drug/gene delivery. Comput. Mech. 53, 511–537. ( 10.1007/s00466-013-0953-5) [DOI] [Google Scholar]
- 11.Zhang YJ, Bazilevs Y, Goswami S, Bajaj CL, Hughes TJR. 2007. Patient-specific vascular NURBS modeling for isogeometric analysis of blood flow. Comput. Methods Appl. Mech. Eng. 196, 2943–2959. ( 10.1016/j.cma.2007.02.009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee TR, Choi M, Kopacz AM, Yun SH, Liu WK, Decuzzi P. 2013. On the near-wall accumulation of injectable particles in the microcirculation: smaller is not better. Sci. Rep. 3, 2079 ( 10.1038/srep02079) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hossain SS, Hossainy SFA, Bazilevs Y, Calo VM, Hughes TJR. 2012. Mathematical modeling of coupled drug and drug-encapsulated nanoparticle transport in patient-specific coronary artery walls. Comput. Mech. 49, 213–242. ( 10.1007/s00466-011-0633-2) [DOI] [Google Scholar]
- 14.Hossain SS, Zhang YJ, Liang XH, Hussain F, Ferrari M, Hughes TJR, Decuzzi P. 2013. In silico vascular modeling for personalized nanoparticle delivery. Nanomedicine 8, 343–357. ( 10.2217/Nnm.12.124) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lee T-R, Greene MS, Jiang Z, Kopacz AM, Decuzzi P, Chen W, Liu WK. 2013. Quantifying uncertainties in the microvascular transport of nanoparticles. Biomech. Model. Mechanobiol. 13, 515–526. ( 10.1007/s10237-013-0513-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang X, Liu WK. 2004. Extended immersed boundary method using FEM and RKPM. Comput. Methods Appl. Mech. Eng. 193, 1305–1321. ( 10.1016/j.cma.2003.12.024) [DOI] [Google Scholar]
- 17.Gay M, Zhang L, Liu WK. 2006. Stent modeling using immersed finite element method. Comput. Methods Appl. Mech. Eng. 195, 4358–4370. ( 10.1016/j.cma.2005.09.012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kopacz AM, Liu WK. 2013. Immersed molecular electrokinetic finite element method. Comput. Mech. 52, 193–199. ( 10.1007/s00466-012-0806-7) [DOI] [Google Scholar]
- 19.Kopacz AM, Liu WK, Chung JH. 2010. Design and optimization of a nanotip sensor via immersed molecular electrokinetic finite element method. In Proc. ASME First Global Congress on Nanoengineering for Medicine and Biology, Houston, TX, USA, 7–10 February 2010, pp. 59–60. ( 10.1115/NEMB2010-13299) [DOI] [Google Scholar]
- 20.Kopacz AM, Patankar NA, Liu WK. 2012. The immersed molecular finite element method. Comput. Methods Appl. Mech. Eng. 233–236, 28–39. ( 10.1016/j.cma.2012.04.005) [DOI] [Google Scholar]
- 21.Kopacz AM, Yeo WH, Chung JH, Liu WK. 2012. Nanoscale sensor analysis using the immersed molecular electrokinetic finite element method. Nanoscale 4, 5189–5194. ( 10.1039/c2nr31279d) [DOI] [PubMed] [Google Scholar]
- 22.Liu WK, et al. 2006. Immersed finite element method and its applications to biological systems. Comput. Methods Appl. Mech. Eng. 195, 1722–1749. ( 10.1016/j.cma.2005.05.049) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liu Y, Liu WK. 2006. Rheology of red blood cell aggregation by computer simulation. J. Comput. Phys. 220, 139–154. ( 10.1016/j.jcp.2006.05.010) [DOI] [Google Scholar]
- 24.Liu Y, Oh K, Bai JG, Chang C-L, Yeo W, Chung J-H, Lee K-H, Liu WK. 2008. Manipulation of nanoparticles and biomolecules by electric field and surface tension. Comput. Methods Appl. Mech. Eng. 197, 2156–2172. ( 10.1016/j.cma.2007.08.012) [DOI] [Google Scholar]
- 25.Zhang L, Gerstenberger A, Wang X, Liu WK. 2004. Immersed finite element method. Comput. Methods Appl. Mech. Eng. 193, 2051–2067. ( 10.1016/j.cma.2003.12.044) [DOI] [Google Scholar]
- 26.Liu Y, Liu WK, Belytschko T, Patankar N, To AC, Kopacz A, Chung JH. 2007. Immersed electrokinetic finite element method. Int. J. Numer. Methods Eng. 71, 379–405. ( 10.1002/nme.1941) [DOI] [Google Scholar]
- 27.Liu WK, Kim DW, Tang SQ. 2007. Mathematical foundations of the immersed finite element method. Comput. Mech. 39, 211–222. ( 10.1007/s00466-005-0018-5) [DOI] [Google Scholar]
- 28.Lee TR, Chang YS, Choi JB, Kim DW, Liu WK, Kim YJ. 2008. Immersed finite element method for rigid body motions in the incompressible Navier–Stokes flow. Comput. Methods Appl. Mech. Eng. 197, 2305–2316. ( 10.1016/j.cma.2007.12.013) [DOI] [Google Scholar]
- 29.Wang H, Chessa J, Liu WK, Belytschko T. 2008. The immersed/fictitious element method for fluid–structure interaction: volumetric consistency, compressibility and thin members. Int. J. Numer. Methods Eng. 74, 32–55. ( 10.1002/nme.2153) [DOI] [Google Scholar]
- 30.Wang XS, Zhang LT, Liu WK. 2009. On computational issues of immersed finite element methods. J. Comput. Phys. 228, 2535–2551. ( 10.1016/j.jcp.2008.12.012) [DOI] [Google Scholar]
- 31.Lee TR, Chang YS, Choi JB, Liu WK, Kim YJ. 2009. Numerical simulation of a nanoparticle focusing lens in a microfluidic channel by using immersed finite element method. J. Nanosci. Nanotechnol. 9, 7407–7411. ( 10.1166/jnn.2009.1787) [DOI] [PubMed] [Google Scholar]
- 32.Yeo WH, Kopacz AM, Kim JH, Chen XQ, Wu JS, Gao DY, Lee KH, Liu WK, Chung JH. 2012. Dielectrophoretic concentration of low-abundance nanoparticles using a nanostructured tip. Nanotechnology 23, 485707 ( 10.1088/0957-4484/23/48/485707) [DOI] [PubMed] [Google Scholar]
- 33.Kopacz AM, Liu WK, Liu SQ. 2008. Simulation and prediction of endothelial cell adhesion modulated by molecular engineering. Comput. Methods Appl. Mech. Eng. 197, 2340–2352. ( 10.1016/j.cma.2008.01.016) [DOI] [Google Scholar]
- 34.Nap RJ, Won YY, Szleifer I. 2012. Confinement induced lateral segregation of polymer coated nanospheres. Soft Matter 8, 1688–1700. ( 10.1039/C2sm06549e) [DOI] [Google Scholar]
- 35.Shi XH, von dem Bussche A, Hurt RH, Kane AB, Gao HJ. 2011. Cell entry of one-dimensional nanomaterials occurs by tip recognition and rotation. Nat. Nanotechnol. 6, 714–719. ( 10.1038/nnano.2011.151) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yang K, Ma YQ. 2010. Computer simulation of the translocation of nanoparticles with different shapes across a lipid bilayer. Nat. Nanotechnol. 5, 579–583. ( 10.1038/nnano.2010.141) [DOI] [PubMed] [Google Scholar]
- 37.Gao HJ, Shi WD, Freund LB. 2005. Mechanics of receptor-mediated endocytosis. Proc. Natl Acad. Sci. USA 102, 9469–9474. ( 10.1073/pnas.0503879102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Decuzzi P, Ferrari M. 2007. The role of specific and non-specific interactions in receptor-mediated endocytosis of nanoparticles. Biomaterials 28, 2915–2922. ( 10.1016/j.biomaterials.2007.02.013) [DOI] [PubMed] [Google Scholar]
- 39.Decuzzi P, Ferrari M. 2006. The adhesive strength of non-spherical particles mediated by specific interactions. Biomaterials 27, 5307–5314. ( 10.1016/j.biomaterials.2006.05.024) [DOI] [PubMed] [Google Scholar]
- 40.Zhang SL, Li J, Lykotrafitis G, Bao G, Suresh S. 2009. Size-dependent endocytosis of nanoparticles. Adv. Mater. 21, 419–424. ( 10.1002/adma.200801393) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yi X, Shi XH, Gao HJ. 2011. Cellular uptake of elastic nanoparticles. Phys. Rev. Lett. 107, 098101 ( 10.1103/Physrevlett.107.098101) [DOI] [PubMed] [Google Scholar]
- 42.Ferrari M. 2005. Cancer nanotechnology: opportunities and challenges. Nat. Rev. Cancer 5, 161–171. ( 10.1038/nrc1566) [DOI] [PubMed] [Google Scholar]
- 43.Schroeder A, Heller DA, Winslow MM, Dahlman JE, Pratt GW, Langer R, Jacks T, Anderson DG. 2012. Treating metastatic cancer with nanotechnology. Nat. Rev. Cancer 12, 39–50. ( 10.1038/nrc3180) [DOI] [PubMed] [Google Scholar]
- 44.van de Ven AL, et al. 2011. Rapid tumoritropic accumulation of systemically injected plateloid particles and their biodistribution. J. Control. Release 158, 148–155. ( 10.1016/jconrel.2011.10.021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Peer D, Karp JM, Hong S, FaroKHzad OC, Margalit R, Langer R. 2007. Nanocarriers as an emerging platform for cancer therapy. Nat. Nanotechnol. 2, 751–760. ( 10.1038/nnano.2007.387) [DOI] [PubMed] [Google Scholar]
- 46.Hobbs SK, Monsky WL, Yuan F, Roberts WG, Griffith L, Torchilin VP, Jain RK. 1998. Regulation of transport pathways in tumor vessels: role of tumor type and microenvironment. Proc. Natl Acad. Sci. USA 95, 4607–4612. ( 10.1073/pnas.95.8.4607) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jain RK, Stylianopoulos T. 2010. Delivering nanomedicine to solid tumors. Nat. Rev. Clin. Oncol. 7, 653–664. ( 10.1038/nrclinonc.2010.139) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Decuzzi P, Lee S, Bhushan B, Ferrari M. 2005. A theoretical model for the margination of particles within blood vessels. Ann. Biomed. Eng. 33, 179–190. ( 10.1007/s10439-005-8976-5) [DOI] [PubMed] [Google Scholar]
- 49.Schmitt-Sody M, Strieth S, Krasnici S, Sauer B, Schulze B, Teifel M, Michaelis U, Naujoks K, Dellian M. 2003. Neovascular targeting therapy: paclitaxel encapsulated in cationic liposomes improves antitumoral efficacy. Clin. Cancer Res. 9, 2335–2341. [PubMed] [Google Scholar]
- 50.Campbell RB, Fukumura D, Brown EB, Mazzola LM, Izumi Y, Jain RK, Torchilin VP, Munn LL. 2002. Cationic charge determines the distribution of liposomes between the vascular and extravascular compartments of tumors. Cancer Res. 62, 6831–6836. [PubMed] [Google Scholar]
- 51.Dellian M, Yuan F, Trubetskoy VS, Torchilin VP, Jain RK. 2000. Vascular permeability in a human tumour xenograft: molecular charge dependence. Brit. J. Cancer 82, 1513–1518. ( 10.1054/bjoc.1999.1171) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Perrault SD, Walkey C, Jennings T, Fischer HC, Chan WCW. 2009. Mediating tumor targeting efficiency of nanoparticles through design. Nano Lett. 9, 1909–1915. ( 10.1021/nl900031y) [DOI] [PubMed] [Google Scholar]
- 53.Stroh M, et al. 2005. Quantum dots spectrally distinguish multiple species within the tumor milieu in vivo. Nat. Med. 11, 678–682. ( 10.1038/nm1247) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Yuan F, Leunig M, Huang SK, Berk DA, Papahadjopoulos D, Jain RK. 1994. Microvascular permeability and interstitial penetration of sterically stabilized (stealth) liposomes in a human tumor xenograft. Cancer Res. 54, 3352–3356. [PubMed] [Google Scholar]
- 55.Wang MD, Shin DM, Simons JW, Nie S. 2007. Nanotechnology for targeted cancer therapy. Expert Rev. Anticancer Ther. 7, 833–837. ( 10.1586/14737140.7.6.833) [DOI] [PubMed] [Google Scholar]
- 56.Huang XH, Peng XH, Wang YQ, Wang YX, Shin DM, El-Sayed MA, Nie SM. 2010. A reexamination of active and passive tumor targeting by using rod-shaped gold nanocrystals and covalently conjugated peptide ligands. ACS Nano 4, 5887–5896. ( 10.1021/nn102055s) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Nie SM. 2010. Understanding and overcoming major barriers in cancer nanomedicine. Nanomedicine 5, 523–528. ( 10.2217/nnm.10.23) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Key J, Aryal S, Gentile F, Ananta JS, Zhong M, Landis MD, Decuzzi P. 2013. Engineering discoidal polymeric nanoconstructs with enhanced magneto-optical properties for tumor imaging. Biomaterials 34, 5402–5410. ( 10.1016/j.biomaterials.2013.03.078) [DOI] [PubMed] [Google Scholar]
- 59.Godin B, et al. 2010. Tailoring the degradation kinetics of mesoporous silicon structures through PEGylation. J. Biomed. Mater. Res. A 94, 1236–1243. ( 10.1002/jbm.a.32807) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Rolland JP, Maynor BW, Euliss LE, Exner AE, Denison GM, DeSimone JM. 2005. Direct fabrication and harvesting of monodisperse, shape-specific nanobiomaterials. J. Am. Chem. Soc. 127, 10 096–10 100. ( 10.1021/ja051977c) [DOI] [PubMed] [Google Scholar]
- 61.Champion JA, Katare YK, Mitragotri S. 2007. Making polymeric micro- and nanoparticles of complex shapes. Proc. Natl Acad. Sci. USA 104, 11 901–11 904. ( 10.1073/pnas.0705326104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lee SY, Ferrari M, Decuzzi P. 2009. Shaping nano-/micro-particles for enhanced vascular interaction in laminar flows. Nanotechnology 20, 495101 ( 10.1088/0957-4484/20/49/495101) [DOI] [PubMed] [Google Scholar]
- 63.Decuzzi P, Ferrari M. 2008. The receptor-mediated endocytosis of nonspherical particles. Biophys. J. 94, 3790–3797. ( 10.1529/biophysj.107.120238) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Shah S, Liu Y, Hu W, Gao J. 2011. Modeling particle shape-dependent dynamics in nanomedicine. J. Nanosci. Nanotechnol. 11, 919–928. ( 10.1166/jnn.2011.3536) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Gentile F, Chiappini C, Fine D, Bhavane RC, Peluccio MS, Cheng MM, Liu X, Ferrari M, Decuzzi P. 2008. The effect of shape on the margination dynamics of non-neutrally buoyant particles in two-dimensional shear flows. J. Biomech. 41, 2312–2318. ( 10.1016/j.jbiomech.2008.03.021) [DOI] [PubMed] [Google Scholar]
- 66.Champion JA, Mitragotri S. 2006. Role of target geometry in phagocytosis. Proc. Natl Acad. Sci. USA 103, 4930–4934. ( 10.1073/pnas.0600997103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Gratton SE, et al. 2008. The effect of particle design on cellular internalization pathways. Proc. Natl Acad. Sci. USA 105, 11 613–11 618. ( 10.1073/pnas.0801763105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sharma G, Valenta DT, Altman Y, Harvey S, Xie H, Mitragotri S, Smith JW. 2010. Polymer particle shape independently influences binding and internalization by macrophages. J. Control. Release 147, 408–412. ( 10.1016/j.jconrel.2010.07.116) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Hauck TS, Ghazani AA, Chan WCW. 2008. Assessing the effect of surface chemistry on gold nanorod uptake, toxicity, and gene expression in mammalian cells. Small 4, 153–159. ( 10.1002/smll.200700217) [DOI] [PubMed] [Google Scholar]
- 70.Gratton SE, Pohlhaus PD, Lee J, Guo J, Cho MJ, Desimone JM. 2007. Nanofabricated particles for engineered drug therapies: a preliminary biodistribution study of PRINT nanoparticles. J. Control. Release 121, 10–18. ( 10.1016/j.jconrel.2007.05.027) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Merkel TJ, et al. 2011. Using mechanobiological mimicry of red blood cells to extend circulation times of hydrogel microparticles. Proc. Natl Acad. Sci. USA 108, 586–591. ( 10.1073/pnas.1010013108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Muro S, Garnacho C, Champion JA, Leferovich J, Gajewski C, Schuchman EH, Mitragotri S, Muzykantov VR. 2008. Control of endothelial targeting and intracellular delivery of therapeutic enzymes by modulating the size and shape of ICAM-1-targeted carriers. Mol. Ther. 16, 1450–1458. ( 10.1038/mt.2008.127) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Decuzzi P, Godin B, Tanaka T, Lee SY, Chiappini C, Liu X, Ferrari M. 2010. Size and shape effects in the biodistribution of intravascularly injected particles. J. Control. Release 141, 320–327. ( 10.1016/j.jconrel.2009.10.014) [DOI] [PubMed] [Google Scholar]
- 74.Chauhan VP, Popovic Z, Chen O, Cui J, Fukumura D, Bawendi MG, Jain RK. 2011. Fluorescent nanorods and nanospheres for real-time in vivo probing of nanoparticle shape-dependent tumor penetration. Angew. Chem. Int. Ed. Engl. 50, 11 417–11 420. ( 10.1002/anie.201104449) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Albanese A, Tang PS, Chan WC. 2012. The effect of nanoparticle size, shape, and surface chemistry on biological systems. Annu. Rev. Biomed. Eng. 14, 1–16. ( 10.1146/annurev-bioeng-071811-150124) [DOI] [PubMed] [Google Scholar]
- 76.Chithrani BD, Ghazani AA, Chan WCW. 2006. Determining the size and shape dependence of gold nanoparticle uptake into mammalian cells. Nano Lett. 6, 662–668. ( 10.1021/nl052396o) [DOI] [PubMed] [Google Scholar]
- 77.Kirchner C, Liedl T, Kudera S, Pellegrino T, Javier AM, Gaub HE, Stolzle S, Fertig N, Parak WJ. 2005. Cytotoxicity of colloidal CdSe and CdSe/ZnS nanoparticles. Nano Lett. 5, 331–338. ( 10.1021/nl047996m) [DOI] [PubMed] [Google Scholar]
- 78.Rudin M, Weissleder R. 2003. Molecular imaging in drug discovery and development. Nat. Rev. Drug Discov. 2, 123–131. ( 10.1038/nrd1007) [DOI] [PubMed] [Google Scholar]
- 79.Pichler BJ, Kolb A, Nagele T, Schlemmer HP. 2010. PET/MRI: paving the way for the next generation of clinical multimodality imaging applications. J. Nucl. Med. 51, 333–336. ( 10.2967/jnumed.109.061853) [DOI] [PubMed] [Google Scholar]
- 80.Fung YC. 1981. Biomechanics: mechanical properties of living tissues, p. 433 New York, NY: Springer. [Google Scholar]
- 81.Lee SY, Ferrari M, Decuzzi P. 2009. Design of bio-mimetic particles with enhanced vascular interaction. J. Biomech. 42, 1885–1890. ( 10.1016/j.jbiomech.2009.05.012) [DOI] [PubMed] [Google Scholar]
- 82.Adriani G, de Tullio MD, Ferrari M, Hussain F, Pascazio G, Liu X, Decuzzi P. 2012. The preferential targeting of the diseased microvasculature by disk-like particles. Biomaterials 33, 5504–5513. ( 10.1016/j.biomaterials.2012.04.027) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Tanaka T, Decuzzi P, Cristofanilli M, Sakamoto JH, Tasciotti E, Robertson FM, Ferrari M. 2009. Nanotechnology for breast cancer therapy. Biomed. Microdevices 11, 49–63. ( 10.1007/s10544-008-9209-0) [DOI] [PubMed] [Google Scholar]
- 84.Peppas NA, Langer R. 1994. New challenges in biomaterials. Science 263, 1715–1720. ( 10.1126/science.8134835) [DOI] [PubMed] [Google Scholar]
- 85.Geng Y, Dalhaimer P, Cai SS, Tsai R, Tewari M, Minko T, Discher DE. 2007. Shape effects of filaments versus spherical particles in flow and drug delivery. Nat. Nanotechnol. 2, 249–255. ( 10.1038/nnano.2007.70) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Tao SL, Desai TA. 2005. Micromachined devices: the impact of controlled geometry from cell-targeting to bioavailability. J. Control. Release 109, 127–138. ( 10.1016/j.jconrel.2005.09.019) [DOI] [PubMed] [Google Scholar]
- 87.Champion JA, Katare YK, Mitragotri S. 2007. Particle shape: a new design parameter for micro- and nanoscale drug delivery carriers. J. Control. Release 121, 3–9. ( 10.1016/j.jconrel.2007.03.022) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Shi XH, Kong Y, Gao HJ. 2008. Coarse grained molecular dynamics and theoretical studies of carbon nanotubes entering cell membrane. Acta Mech. Sin. 24, 161–169. ( 10.1007/s10409-007-0131-0) [DOI] [Google Scholar]
- 89.Shi W, Wang J, Fan X, Gao H. 2008. Size and shape effects on diffusion and absorption of colloidal particles near a partially absorbing sphere: implications for uptake of nanoparticles in animal cells. Phys. Rev. E 78, 061914 ( 10.1103/PhysRevE.78.061914) [DOI] [PubMed] [Google Scholar]
- 90.Li YF, Yuan HY, von dem Bussche A, Creighton M, Hurt RH, Kane AB, Gao HJ. 2013. Graphene microsheets enter cells through spontaneous membrane penetration at edge asperities and corner sites. Proc. Natl Acad. Sci. USA 110, 12 295–12 300. ( 10.1073/pnas.1222276110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Verma A, Uzun O, Hu YH, Hu Y, Han HS, Watson N, Chen SL, Irvine DJ, Stellacci F. 2008. Surface-structure-regulated cell-membrane penetration by monolayer-protected nanoparticles. Nat. Mater. 7, 588–595. ( 10.1038/Nmat2202) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Li YF, Li XJ, Li ZH, Gao HJ. 2012. Surface-structure-regulated penetration of nanoparticles across a cell membrane. Nanoscale 4, 3768–3775. ( 10.1039/C2NR30379e) [DOI] [PubMed] [Google Scholar]
- 93.Bianco A, Hoebeke J, Godefroy S, Chaloin O, Pantarotto D, Briand JP, Muller S, Prato M, Partidos CD. 2005. Cationic carbon nanotubes bind to CpG oligodeoxynucleotides and enhance their immunostimulatory properties. J. Am. Chem. Soc. 127, 58–59. ( 10.1021/ja044293y) [DOI] [PubMed] [Google Scholar]
- 94.Cheung W, Pontoriero F, Taratula O, Chen AM, He HX. 2010. DNA and carbon nanotubes as medicine. Adv. Drug Deliver. Rev. 62, 633–649. ( 10.1016/j.addr.2010.03.007) [DOI] [PubMed] [Google Scholar]
- 95.Brown DM, Kinloch IA, Bangert U, Windle AH, Walter DM, Walker GS, Scotchford CA, Donaldson K, Stone V. 2007. An in vitro study of the potential of carbon nanotubes and nanofibres to induce inflammatory mediators and frustrated phagocytosis. Carbon 45, 1743–1756. ( 10.1016/j.carbon.2007.05.011) [DOI] [Google Scholar]
- 96.Sanchez VC, Pietruska JR, Miselis NR, Hurt RH, Kane AB. 2009. Biopersistence and potential adverse health impacts of fibrous nanomaterials: what have we learned from asbestos? Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 1, 511–529. ( 10.1002/wnan.41) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Donaldson K, Murphy FA, Duffin R, Poland CA. 2010. Asbestos, carbon nanotubes and the pleural mesothelium: a review of the hypothesis regarding the role of long fibre retention in the parietal pleura, inflammation and mesothelioma. Part. Fibre Toxicol. 7, 5 ( 10.1186/1743-8977-7-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Yi X, Shi X, Gao H. 2014. A universal law for cell uptake of one-dimensional nanomaterials. Nano Lett. 14, 1049–1055. ( 10.1021/nl404727m) [DOI] [PubMed] [Google Scholar]
- 99.Mu QX, et al. 2008. Protein binding by functionalized multiwalled carbon nanotubes is governed by the surface chemistry of both parties and the nanotube diameter. J. Phys. Chem. C 112, 3300–3307. ( 10.1021/jp710541j) [DOI] [Google Scholar]
- 100.Zhou HY, et al. 2008. A nano-combinatorial library strategy for the discovery of nanotubes with reduced protein-binding, cytotoxicity, and immune response. Nano Lett. 8, 859–865. ( 10.1021/nl0730155) [DOI] [PubMed] [Google Scholar]
- 101.Li X, Peng Y, Ren J, Qu X. 2006. Carboxyl-modified single-walled carbon nanotubes selectively induce human telomeric I-motif formation. Proc. Natl Acad. Sci. USA 103, 19 658–19 663. ( 10.1073/pnas.0607245103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Qian J, Gao HJ. 2010. Soft matrices suppress cooperative behaviors among receptor–ligand bonds in cell adhesion. PLoS ONE 5, e12342 ( 10.1371/journal.pone.0012342) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Qian J, Wang J, Gao H. 2008. Lifetime and strength of adhesive molecular bond clusters between elastic media. Langmuir 24, 1262–1270. ( 10.1021/La702401b) [DOI] [PubMed] [Google Scholar]
- 104.Qian J, Wang JZ, Lin Y, Gao HJ. 2009. Lifetime and strength of periodic bond clusters between elastic media under inclined loading. Biophys. J. 97, 2438–2445. ( 10.1016/j.bpj.2009.08.027) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Gao HJ, Qian J, Chen B. 2011. Probing mechanical principles of focal contacts in cell–matrix adhesion with a coupled stochastic-elastic modelling framework. J. R. Soc. Interface 8, 1217–1232. ( 10.1098/rsif.2011.0157) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Tu YS, et al. 2013. Destructive extraction of phospholipids from Escherichia coli membranes by graphene nanosheets. Nat. Nanotechnol. 8, 594–601. ( 10.1038/nnano.2013.125) [DOI] [PubMed] [Google Scholar]
- 107.Immordino ML, Dosio F, Cattel L. 2006. Stealth liposomes: review of the basic science, rationale, and clinical applications, existing and potential. Int. J. Nanomed. 1, 297–315. ( 10.2217/17435889.1.3.297) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Nativo P, Prior IA, Brust M. 2008. Uptake and intracellular fate of surface-modified gold nanoparticles. ACS Nano 2, 1639–1644. ( 10.1021/nn800330a) [DOI] [PubMed] [Google Scholar]
- 109.Tkachenko AG, Xie H, Coleman D, Glomm W, Ryan J, Anderson MF, Franzen S, Feldheim DL. 2003. Multifunctional gold nanoparticle-peptide complexes for nuclear targeting. J. Am. Chem. Soc. 125, 4700–4701. ( 10.1021/ja0296935) [DOI] [PubMed] [Google Scholar]
- 110.Oh E, et al. 2011. Cellular uptake and fate of PEGylated gold nanoparticles is dependent on both cell-penetration peptides and particle size. ACS Nano 5, 6434–6448. ( 10.1021/nn201624c) [DOI] [PubMed] [Google Scholar]
- 111.de la Zerda A, et al. 2012. Family of enhanced photoacoustic imaging agents for high-sensitivity and multiplexing studies in living mice. ACS Nano 6, 4694–4701. ( 10.1021/nn204352r) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Chen HW, Paholak H, Ito M, Sansanaphongpricha K, Qian W, Che Y, Sun DX. 2013. ‘Living’ PEGylation on gold nanoparticles to optimize cancer cell uptake by controlling targeting ligand and charge densities. Nanotechnology 24, 355101 ( 10.1088/0957-4484/24/35/355101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Cho EC, Au L, Zhang Q, Xia YN. 2010. The effects of size, shape, and surface functional group of gold nanostructures on their adsorption and internalization by cells. Small 6, 517–522. ( 10.1002/smll.200901622) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Li Y, Kroger M, Liu WK. Endocytosis of PEGylated nanoparticles: what is the role of grafted polyethylene glycol? doi: 10.1016/j.biomaterials.2014.06.032. Submitted. [DOI] [PubMed] [Google Scholar]
- 115.Lee H, de Vries AH, Marrink SJ, Pastor RW. 2009. A coarse-grained model for polyethylene oxide and polyethylene glycol: conformation and hydrodynamics. J. Phys. Chem. B 113, 13 186–13 194. ( 10.1021/jp9058966) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Li Y, Abberton BC, Kroger M, Liu WK. 2013. Challenges in multiscale modeling of polymer dynamics. Polymers-Basel 5, 751–832. ( 10.3390/polym5020751) [DOI] [Google Scholar]
- 117.Li Y, Tang S, Abberton BC, Kroger M, Burkhart C, Jiang B, Papakonstantopoulos GJ, Poldneff M, Liu WK. 2012. A predictive multiscale computational framework for viscoelastic properties of linear polymers. Polymer 53, 5935–5952. ( 10.1016/j.polymer.2012.09.055) [DOI] [Google Scholar]
- 118.Li Y, Kroger M, Liu WK. 2011. Primitive chain network study on uncrosslinked and crosslinked cis-polyisoprene polymers. Polymer 52, 5867–5878. ( 10.1016/j.polymer.2011.10.044) [DOI] [Google Scholar]
- 119.Oden JT, et al. 2006. Revolutionizing engineering science through simulation. Nat. Sci. Found. Blue Ribbon Panel Rep. 65, 1–57. [Google Scholar]
- 120.Ross R. 1999. Mechanisms of disease: atherosclerosis: an inflammatory disease. N. Engl. J. Med. 340, 115–126. ( 10.1056/NEJM199901143400207) [DOI] [PubMed] [Google Scholar]
- 121.Drakopoulou M, Toutouzas K, Michelongona A, Tousoulis D, Stefanadis C. 2011. Vulnerable plaque and inflammation: potential clinical strategies. Curr. Pharm. Design 17, 4190–4209. ( 10.2174/138161211798764816) [DOI] [PubMed] [Google Scholar]
- 122.Camici PG, Rimoldi OE, Gaemperli O, Libby P. 2012. Non-invasive anatomic and functional imaging of vascular inflammation and unstable plaque. Eur. Heart J. 33, U1309–U1329. ( 10.1093/eurheartj/ehs067) [DOI] [PubMed] [Google Scholar]
- 123.Hossain SS, Hughes TJR, Decuzzi P. 2013. Vascular deposition patterns for catheter-injected nanoparticles in an inflamed patient-specific arterial tree. Biomech. Model. Mechanobiol. 13, 585–597. ( 10.1007/s10237-013-0520-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Ferrari M. 2010. Frontiers in cancer nanomedicine: directing mass transport through biological barriers. Trends Biotechnol. 28, 181–188. ( 10.1016/j.tibtech.2009.12.007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Michor F, Liphardt J, Ferrari M, Widom J. 2011. What does physics have to do with cancer? Nat. Rev. Cancer 11, 657–670. ( 10.1038/nrc3092) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Ferrari M. 2013. Problems in (nano)medical mechanics. Int. J. Non-Linear Mech. 56, 3–19. ( 10.1016/j.ijnonlinmec.2013.03.008) [DOI] [Google Scholar]
- 127.Lowengrub JS, Frieboes HB, Jin F, Chuang YL, Li X, Macklin P, Wise SM, Cristini V. 2010. Nonlinear modelling of cancer: bridging the gap between cells and tumours. Nonlinearity 23, R1–R9. ( 10.1088/0951-7715/23/1/R01) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Sciumè G, Gray WG, Ferrari M, Decuzzi P, Schrefler BA. 2013. On computational modeling in tumor growth. Arch. Comput. Methods Eng. 20, 327–352. ( 10.1007/s11831-013-9090-8) [DOI] [Google Scholar]
- 129.Cristini V, Li X, Lowengrub JS, Wise SM. 2009. Nonlinear simulations of solid tumor growth using a mixture model: invasion and branching. J. Math. Biol. 58, 723–763. ( 10.1007/s00285-008-0215-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Hawkins-Daarud A, van der Zee KG, Tinsley Oden J. 2012. Numerical simulation of a thermodynamically consistent four-species tumor growth model. Int. J. Numer. Methods Biomed. Eng. 28, 3–24. ( 10.1002/cnm.1467) [DOI] [PubMed] [Google Scholar]
- 131.Sarntinoranont M, Rooney F, Ferrari M. 2003. Interstitial stress and fluid pressure within a growing tumor. Ann. Biomed. Eng. 31, 327–335. ( 10.1114/1.1554923) [DOI] [PubMed] [Google Scholar]
- 132.Sciume G, Shelton S, Gray W, Miller C, Hussain F, Ferrari M, Decuzzi P, Schrefler B. 2013. A multiphase model for three-dimensional tumor growth. New J. Phys. 15, 015005 ( 10.1088/1367-2630/15/1/015005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Mishra DK, Sakamoto JH, Thrall MJ, Baird BN, Blackmon SH, Ferrari M, Kurie JM, Kim MP. 2012. Human lung cancer cells grown in an ex vivo 3D lung model produce matrix metalloproteinases not produced in 2D culture. PLoS ONE 7, e45308 ( 10.1371/journal.pone.0045308) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Gray WG, Miller CT. 2005. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 1. Motivation and overview. Adv. Water Resour. 28, 161–180. ( 10.1016/j.advwatres.2004.09.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Preziosi L, Ambrosi D, Verdier C. 2010. An elasto-visco-plastic model of cell aggregates. J. Theor. Biol. 262, 35–47. ( 10.1016/j.jtbi.2009.08.023) [DOI] [PubMed] [Google Scholar]
- 136.Sciumè G, Gray WG, Hussain F, Ferrari M, Decuzzi P, Schrefler BA. 2014. Three phase flow dynamics in tumor growth. Comput. Mech. 53, 465–484. ( 10.1007/s00466-013-0956-2) [DOI] [Google Scholar]
- 137.Yeo W-H, et al. 2010. Size-selective immunofluorescence of Mycobacterium tuberculosis cells by capillary- and viscous forces. Lab Chip 10, 3178–3181. ( 10.1039/c0lc00077a) [DOI] [PubMed] [Google Scholar]
- 138.Kalyanasundaram D, et al. 2013. Rapid extraction and preservation of genomic DNA from human samples. Anal. Bioanal. Chem. 405, 1977–1983. ( 10.1007/s00216-012-6637-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Liu Y, Chung JH, Liu WK, Ruoff RS. 2006. Dielectrophoretic assembly of nanowires. J. Phys. Chem. B 110, 14 098–14 106. ( 10.1021/jp061367e) [DOI] [PubMed] [Google Scholar]
- 140.Liu WK, Chen YJ, Uras RA, Chang CT. 1996. Generalized multiple scale reproducing kernel particle methods. Comput. Methods Appl. Mech. Eng. 139, 91–157. ( 10.1016/S0045-7825(96)01081-X) [DOI] [Google Scholar]
- 141.Liu WK, Hao W, Chen Y, Jun S, Gosz J. 1997. Multiresolution reproducing kernel particle methods. Comput. Mech. 20, 295–309. ( 10.1007/s004660050252) [DOI] [Google Scholar]
- 142.Liu WK, Jun S. 1998. Multiple-scale reproducing kernel particle methods for large deformation problems. Int. J. Numer. Methods Eng. 41, 1339–1362. () [DOI] [Google Scholar]
- 143.Liu WK, Jun S, Li SF, Adee J, Belytschko T. 1995. Reproducing kernel particle methods for structural dynamics. Int. J. Numer. Methods Eng. 38, 1655–1679. ( 10.1002/nme.1620381005) [DOI] [Google Scholar]
- 144.Liu WK, Jun S, Zhang YF. 1995. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 20, 1081–1106. ( 10.1002/fld.1650200824) [DOI] [Google Scholar]
- 145.Liu YL, Zhang L, Wang XD, Liu WK. 2004. Coupling of Navier–Stokes equations with protein molecular dynamics and its application to hemodynamics. Int. J. Numer. Methods Fluids 46, 1237–1252. ( 10.1002/fld.798) [DOI] [Google Scholar]
- 146.Tefft BJ, Kopacz AM, Liu SQ, Liu WK. 2011. Enhancing endothelial cell retention on ePTFE constructs by siRNA-mediated SHP-1 gene silencing. J. Nanotechnol. Eng. Med. 2, 011007 ( 10.1115/1.4003273) [DOI] [Google Scholar]
- 147.Kim J-H, Hiraiwa M, Lee H-B, Lee K-H, Cangelosi GA, Chung J-H. 2013. Electrolyte-free amperometric immunosensor using a dendritic nanotip. RSC Adv. 3, 4281–4287. ( 10.1039/c3ra40262b) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Yeo WH, Lee HB, Kim JH, Lee KH, Chung JH. 2013. Nanotip analysis for dielectrophoretic concentration of nanosized viral particles. Nanotechnology 24, 185502 ( 10.1088/0957-4484/24/18/185502) [DOI] [PubMed] [Google Scholar]
- 149.Kane RS, Takayama S, Ostuni E, Ingber DE, Whitesides GM. 1999. Patterning proteins and cells using soft lithography. Biomaterials 20, 2363–2376. ( 10.1016/S0142-9612(99)00165-9) [DOI] [PubMed] [Google Scholar]
- 150.Armstrong L, Lako M, Buckley N, Lappin TRJ, Murphy MJ, Nolta JA, Pittenger M, Stojkovic M. 2012. Our top 10 developments in stem cell biology over the last 30 years. Stem Cells 30, 2–9. ( 10.1002/stem.1007) [DOI] [PubMed] [Google Scholar]
- 151.Kamm RD, Bashir R. 2013. Creating living cellular machines. Ann. Biomed. Eng. 42, 445–459. ( 10.1007/s10439-013-0902-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Sung JH, Esch MB, Prot JM, Long CJ, Smith A, Hickman JJ, Shuler ML. 2013. Microfabricated mammalian organ systems and their integration into models of whole animals and humans. Lab Chip 13, 1201–1212. ( 10.1039/C3Ic41017j) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Huh D, Matthews BD, Mammoto A, Montoya-Zavala M, Hsin HY, Ingber DE. 2010. Reconstituting organ-level lung functions on a chip. Science 328, 1662–1668. ( 10.1126/science.1188302) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Domansky K, Inman W, Serdy J, Dash A, Lim MHM, Griffith LG. 2010. Perfused multiwell plate for 3D liver tissue engineering. Lab Chip 10, 51–58. ( 10.1039/B913221J) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Fidkowski C, Kaazempur-Mofrad MR, Borenstein J, Vacanti JP, Langer R, Wang YD. 2005. Endothelialized microvasculature based on a biodegradable elastomer. Tissue Eng. 11, 302–309. ( 10.1089/ten.2005.11.302) [DOI] [PubMed] [Google Scholar]
- 156.Zheng Y, et al. 2012. In vitro microvessels for the study of angiogenesis and thrombosis. Proc. Natl Acad. Sci. USA 109, 9342–9347. ( 10.1073/pnas.1201240109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Moya ML, Hsu YH, Lee AP, Hughes CCW, George SC. 2013. In vitro perfused human capillary networks. Tissue Eng. C 19, 730–737. ( 10.1089/ten.tec.2012.0430) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Kim S, Lee H, Chung M, Jeon NL. 2013. Engineering of functional, perfusable 3D microvascular networks on a chip. Lab Chip 13, 1489–1500. ( 10.1039/C3lC41320a) [DOI] [PubMed] [Google Scholar]
- 159.Song JW, Munn LL. 2011. Fluid forces control endothelial sprouting. Proc. Natl Acad. Sci. USA 108, 15 342–15 347. ( 10.1073/pnas.1105316108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Chung S, Sudo R, Vickerman V, Zervantonakis IK, Kamm RD. 2010. Microfluidic platforms for studies of angiogenesis, cell migration, and cell–cell interactions. Ann. Biomed. Eng. 38, 1164–1177. ( 10.1007/s10439-010-9899-3) [DOI] [PubMed] [Google Scholar]
- 161.Lange JR, Fabry B. 2013. Cell and tissue mechanics in cell migration. Exp. Cell Res. 319, 2418–2423. ( 10.1016/j.yexcr.2013.04.023) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Fletcher DA, Mullins D. 2010. Cell mechanics and the cytoskeleton. Nature 463, 485–492. ( 10.1038/nature08908) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Engler AJ, Sen S, Sweeney HL, Discher DE. 2006. Matrix elasticity directs stem cell lineage specification. Cell 126, 677–689. ( 10.1016/j.cell.2006.06.044) [DOI] [PubMed] [Google Scholar]
- 164.Izaguirre JA, et al. 2004. CompuCell, a multi-model framework for simulation of morphogenesis. Bioinformatics 20, 1129–1137. ( 10.1093/bioinformatics/bth050) [DOI] [PubMed] [Google Scholar]
- 165.Lloyd-Jones D, et al. 2010. Heart disease and stroke statistics—2010 update: a report from the American Heart Association. Circulation 121, e46–e215. ( 10.1161/CIRCULATIONAHA.109.192667) [DOI] [PubMed] [Google Scholar]
- 166.Clark JB, Pauliks LB, Myers JL, Undar A. 2011. Mechanical circulatory support for end-stage heart failure in repaired and palliated congenital heart disease. Curr. Cardiol. Rev. 7, 102–109. ( 10.2174/157340311797484222) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Bazilevs Y, Takizawa K, Tezduyar TE. 2013. Computational fluid–structure interaction: methods and applications. Chichester, UK: Wiley. [Google Scholar]
- 168.Long CC, Marsden AL, Bazilevs Y. 2013. Fluid–structure interaction simulation of pulsatile ventricular assist devices. Comput. Mech. 52, 971–981. ( 10.1007/s00466-013-0858-3) [DOI] [Google Scholar]
- 169.Reininger AJ, Reininger CB, Heinzmann U, Wurzinger LJ. 1995. Residence time in niches of stagnant flow determines fibrin clot formation in an arterial branching model: detailed flow analysis and experimental results. Thromb. Haemost. 74, 916–922. [PubMed] [Google Scholar]
- 170.Long CC, Esmaily-Moghadam M, Marsden AL, Bazilevs Y. In press. Computation of residence time in the simulation of pulsatile ventricular assist devices. Comput. Mech. ( 10.1007/s00466-013-0931-y) [DOI] [Google Scholar]
- 171.Long CC, Marsden AL, Bazilevs Y. In press. Shape optimization of pulsatile ventricular assist devices using FSI to minimize thrombotic risk. Comput. Mech. ( 10.1007/s00466-013-0967-z) [DOI] [Google Scholar]
- 172.Booker AJ, Dennis JE, Frank PD, Serafini DB, Torczon V, Trosset MW. 1999. A rigorous framework for optimization of expensive functions by surrogates. Struct. Optimiz. 17, 1–13. ( 10.1007/BF01197708) [DOI] [Google Scholar]
- 173.Svahn HA, van den Berg A. 2007. Single cells or large populations? Lab Chip 7, 544–546. ( 10.1039/b704632b) [DOI] [PubMed] [Google Scholar]
- 174.Lindström S, Andersson-Svahn H. 2011. Miniaturization of biological assays: overview on microwell devices for single-cell analyses. Biochim. Biophys. Acta 1810, 308–316. ( 10.1016/j.bbagen.2010.04.009) [DOI] [PubMed] [Google Scholar]
- 175.Altschuler SJ, Wu LF. 2010. Cellular heterogeneity: do differences make a difference? Cell 141, 559–563. ( 10.1016/j.cell.2010.04.033) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Snijder B, Pelkmans L. 2011. Origins of regulated cell-to-cell variability. Nat. Rev. Mol. Cell Biol. 12, 119–125. ( 10.1038/nrm3044) [DOI] [PubMed] [Google Scholar]
- 177.Bakstad D, Adamson A, Spiller DG, White MRH. 2012. Quantitative measurement of single cell dynamics. Curr. Opin. Biotechnol. 23, 103–109. ( 10.1016/j.copbio.2011.11.007) [DOI] [PubMed] [Google Scholar]
- 178.Spiller DG, Wood CD, Rand DA, White MRH. 2010. Measurement of single-cell dynamics. Nature 465, 736–745. ( 10.1038/nature09232) [DOI] [PubMed] [Google Scholar]
- 179.Marko NF, Quackenbush J, Weil RJ. 2011. Why is there a lack of consensus on molecular subgroups of glioblastoma? Understanding the nature of biological and statistical variability in glioblastoma expression data. PLoS ONE 6, e20826 ( 10.1371/journal.pone.0020826) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180.Di Carlo D, Lee LP. 2006. Dynamic single-cell analysis for quantitative biology. Anal. Chem. 78, 7918–7925. ( 10.1021/ac069490p) [DOI] [PubMed] [Google Scholar]
- 181.Han Q, Bagheri N, Bradshaw EM, Hafler DA, Lauffenburger DA, Love JC. 2012. Polyfunctional responses by human T cells result from sequential release of cytokines. Proc. Natl Acad. Sci. USA 109, 1607–1612. ( 10.1073/pnas.1117194109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182.Kang W, Yavari F, Minary-Jolandan M, Giraldo-Vela JP, Safi A, McNaughton RL, Parpoil V, Espinosa HD. 2013. Nanofountain probe electroporation (NFP-E) of single cells. Nano Lett. 13, 2448–2457. ( 10.1021/nl400423c) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Qu B, Eu Y-J, Jeong W-J, Kim D-P. 2012. Droplet electroporation in microfluidics for efficient cell transformation with or without cell wall removal. Lab Chip 12, 4483–4488. ( 10.1039/C2lC40360a) [DOI] [PubMed] [Google Scholar]
- 184.Boukany PE, et al. 2011. Nanochannel electroporation delivers precise amounts of biomolecules into living cells. Nat. Nanotechnol. 6, 747–754. ( 10.1038/nnano.2011.164) [DOI] [PubMed] [Google Scholar]
- 185.Zhan Y, Martin VA, Geahlen RL, Lu C. 2010. One-step extraction of subcellular proteins from eukaryotic cells. Lab Chip 10, 2046–2048. ( 10.1039/c005152g) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Zhan Y, Sun C, Cao Z, Bao N, Xing J, Lu C. 2012. Release of intracellular proteins by electroporation with preserved cell viability. Anal. Chem. 84, 8102–8105. ( 10.1021/ac302462s) [DOI] [PubMed] [Google Scholar]
- 187.Huang B, Wu H, Bhaya D, Grossman A, Granier S, Kobilka BK, Zare RN. 2007. Counting low-copy number proteins in a single cell. Science 315, 81–84. ( 10.1126/science.1133992) [DOI] [PubMed] [Google Scholar]
- 188.Goluch ED, Nam JM, Georganopoulou DG, Chiesl TN, Shaikh KA, Ryu KS, Barron AE, Mirkin CA, Liu C. 2006. A bio-barcode assay for on-chip attomolar-sensitivity protein detection. Lab Chip 6, 1293–1299. ( 10.1039/B606294f) [DOI] [PubMed] [Google Scholar]
- 189.Gong J-R. 2010. Label-free attomolar detection of proteins using integrated nanoelectronic and electrokinetic devices. Small 6, 967–973. ( 10.1002/smll.200902132) [DOI] [PubMed] [Google Scholar]
- 190.Jung BG, Zhu YG, Santiago JG. 2007. Detection of 100 aM fluorophores using a high-sensitivity on-chip CE system and transient isotachophoresis. Anal. Chem. 79, 345–349. ( 10.1021/ac060949p) [DOI] [PubMed] [Google Scholar]
- 191.Fan R, et al. 2008. Integrated barcode chips for rapid, multiplexed analysis of proteins in microliter quantities of blood. Nat. Biotechnol. 26, 1373–1378. ( 10.1038/nbt.1507) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Fan HC, Wang JB, Potanina A, Quake SR. 2011. Whole-genome molecular haplotyping of single cells. Nat. Biotechnol. 29, 51–57. ( 10.1038/nbt.1739) [DOI] [PMC free article] [PubMed] [Google Scholar]