Quantitative analyses of the plant cytoskeleton reveal underlying organizational principles

Abstract

The actin and microtubule (MT) cytoskeletons are vital structures for cell growth and development across all species. While individual molecular mechanisms underpinning actin and MT dynamics have been intensively studied, principles that govern the cytoskeleton organization remain largely unexplored. Here, we captured biologically relevant characteristics of the plant cytoskeleton through a network-driven imaging-based approach allowing us to quantitatively assess dynamic features of the cytoskeleton. By introducing suitable null models, we demonstrate that the plant cytoskeletal networks exhibit properties required for efficient transport, namely, short average path lengths and high robustness. We further show that these advantageous features are maintained during temporal cytoskeletal rearrangements. Interestingly, man-made transportation networks exhibit similar properties, suggesting general laws of network organization supporting diverse transport processes. The proposed network-driven analysis can be readily used to identify organizational principles of cytoskeletons in other organisms.

1. Introduction

Complex systems can be represented by networks that capture the underlying components, as nodes, and their interactions, as links. Network representations have provided insights into the organizational principles of a variety of systems, ranging from man-made to systems shaped by evolution, such as: metabolic networks [1,2], neural networks [3,4], food webs [5,6] and transportation systems, including: vascular [7,8] and leaf venation networks [9,10].

The cytoskeleton represents yet another type of biological network. It is composed of actin filaments (AFs), microtubules (MTs) and intermediate filaments that form intricate interconnected arrays. Plant cells lack intermediate filaments, and their actin and MT cytoskeleton exhibits structural and functional differences from those of animal and yeast cells. These differences may be due to the presence of a rigid cell wall, a large central vacuole, the absence of discrete cytoskeleton organizing centres or the general need of plants, as sessile organisms, to cope with changing environmental conditions [11,12].

In plant interphase cells, AFs exhibit extraordinarily dynamic behaviours [13]. A major function of the actin cytoskeleton is to support cytoplasmic streaming, the directed flow of cytosol and organelles, which is mainly powered by adenosine triphosphate-driven myosin movement of compartments along the actin cytoskeleton [14,15]. Furthermore, recent studies have shown that transportation of organelles depends on the micro-environment of the actin structures, where organelles are rapidly transported along actin bundles and display reduced motility when surrounded by thin AFs [16,17].

The behaviour of single MTs, as well as MT arrays, has been described throughout the cell cycle and for different cell types [18–20]. Their dynamics has been well characterized [11,21,22] and can lead to the formation of self-organized patterns that largely explain the MTs’ orientation in growing cells [23–26]. While MTs sustain vesicle motility in certain plant cells [27], they are typically located at the cell cortex and support the synthesis of cellulose microfibrils in interphase cells [28]. Nevertheless, there is emerging evidence for transport along MTs also in these cell types, e.g. Golgi and small cellulose-containing compartments have been reported to track along cortical MTs [29].

Several studies have investigated the mechanical properties of the cytoskeleton in yeast and animal cells both experimentally [30,31] and theoretically [31–33]. Models of AFs as a system of stiff, spring-connected rods have demonstrated a percolation-related transition in the viscoelastic properties [34,35], similar to signal propagation in a cytoskeleton model of connected rods [36,37].

The above studies employed a bottom-up approach in which the behaviour of a system is explained based on the dynamics of its components. However, the interconnected structure and the rapid dynamics of the cytoskeleton lend themselves to a top-down approach, which is independent of detailed molecular knowledge and better suited for uncovering the principles underlying cytoskeletal organization. Two studies have used such an approach in animal systems: AF arrays have been described as a superposition of different tessellation models [38] and a theoretical investigation of cytoskeletal transport in a system with passive diffusion and active transport along a random network of segments has demonstrated different regimes of transport [39]. Therefore, there is need for a network-based representation of the cytoskeleton that: (i) captures its complex network structure, (ii) is based on biologically solid ground, (iii) can be used to describe dynamic network processes, and (iv) may uncover organizational principles of the cytoskeleton in plant and animal cells.

In this study, we propose a novel framework that captures the structure and dynamics of the actin and MT cytoskeleton as complex networks. We used this framework to quantify and compare the behaviour of AFs and MTs in plant interphase cells under different conditions. We tested the hypothesis that the cytoskeleton is well suited to support transport processes. By developing suitable null models as references, we show that the cytoskeleton indeed exhibits biologically desirable transport-related properties, such as short average path lengths (APLs) and high robustness against disruptions of the network. Finally, we demonstrate that man-made transportation networks display similar properties. The developed framework is readily applicable to study the cytoskeleton of other organisms or under different conditions.

2. Results

2.1. Reconstruction of complex networks from cytoskeletal images

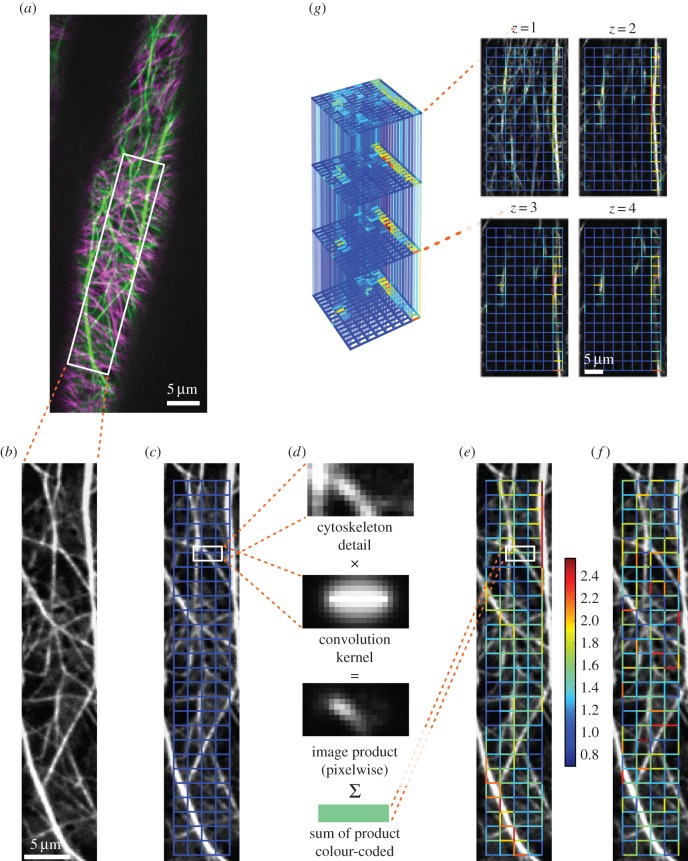
To investigate the networks of AFs and MTs, we grew Arabidopsis thaliana FABD : GFP and TUA5 : mCherry dual-labelled seedlings [40] in the dark and imaged elongating hypocotyl cells. To capture rapid changes and to minimize bleaching, we used a spinning-disc confocal microscope (figure 1a,b; see the electronic supplemental material, S1). To generate complex networks from the cytoskeleton image series, we followed a two-step procedure: we placed a grid over the cytoskeleton, which covers the cell's cytoskeleton (figure 1c). From the grid, we constructed an edge-weighted network in which nodes represent the grid's junctions, and edges represent the grid's links. We assigned a weight to each edge by creating convolution kernels with Gaussian profiles for each edge (figure 1d), thus projecting the cytoskeleton onto the overlaid grid. This results in a weighted, undirected network (figure 1e) where the weights reflect the intensity of the underlying filaments/bundles. Using confocal z-stack image series, these steps were also used to construct three-dimensional cytoskeletal networks (figure 1g). The procedure was repeated for all images of the recorded actin and MT time series, separately. As a result, each network captures information of the time-dependent cytoskeletal component whose properties may be readily investigated.

Figure 1.

From fluorescence image to reconstructed network, null model and three-dimensional extension. (a) Coloured overlay of unprocessed snapshots of the AFs (green) and MTs (magenta) of a dual-labelled, 3-day-old A. thaliana hypocotyl cell. (b) Single preprocessed image of one cytoskeletal component, here AFs. (c) Grid used for network reconstruction (a uniform rectangular grid with 10 pixel spacings is shown in blue). (d) Using convolution kernels, the links of the grid are assigned scalar values by pixelwise multiplication of the kernel with the cytoskeleton image and subsequent summation. (e) Weighted, undirected network with edges given by the links of the chosen grid type and weights obtained via the kernel method (weights are colour-coded from blue to red). (f) To assess the biological relevance of various properties of the cytoskeletal network, a null model is introduced through an ensemble of networks with shuffled edge weights (one exemplary realization is depicted). (g) From confocal z-stack recordings, a three-dimensional cytoskeletal network is reconstructed (grid spacings are 20 pixels; edges connecting different z-layers are set transparent for better visibility of the full network).

To determine whether the studied network properties carry a biological signal, we developed several null models that randomize parts of the cytoskeletal structures while preserving the total amount of cytoskeleton in the cell (cf. electronic supplementary material, S2). If a given network property is significantly higher or lower than expected by chance, we conclude that the underlying cytoskeletal organization is non-random and, therefore, biologically relevant. This may suggest that the cytoskeleton is tuned to guarantee such values of the structural or functional network property.

2.2. The reconstructed networks capture biologically relevant features of the actin and microtubule cytoskeletal components

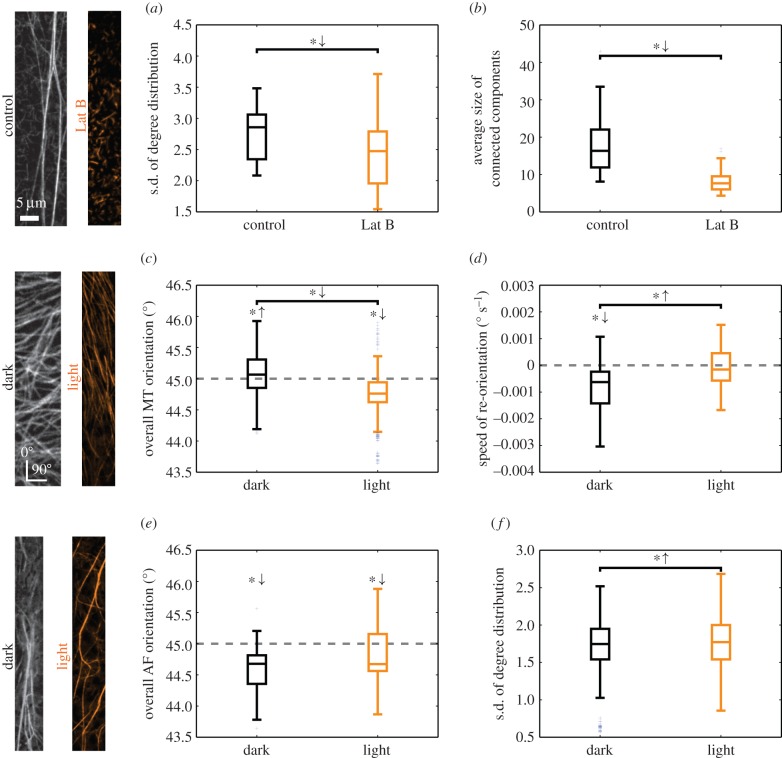
To test whether the proposed network-based approach captures biologically meaningful features, we used chemical treatments and environmental stimuli to alter the behaviour of the cytoskeleton. First, we quantified the effect of the actin-disrupting drug Latrunculin B on the actin cytoskeleton. This drug binds to monomeric actin and, thereby, inhibits AF formation [41]. We reconstructed the AF networks for both the control and the treated plants for each frame of the image series. The structure of the AFs and their drug-induced fragmentation were quantified by two network properties, which can be related to the biological phenomenon (see the electronic supplementary material, S3, for a mathematical description and detailed interpretation of these quantities): the standard deviation of the degree distribution [42] captures the spatial heterogeneity of the distribution of actin structures, i.e. images with regions of low and high cytoskeletal intensities yield both small and large edge weights and consequently a broader degree distribution (cf. figure 1e). As the edge weights integrate intensities of possibly multiple filaments, our approach does not resolve differences in thicknesses or numbers of individual filament but only a combination thereof. By comparing the standard deviations of the degree distributions of control and treated plants, we found a statistically significant reduction by Latrunculin B (figure 2a; independent two-sample t-test: p-value = 7.0 × 10⁻⁹; for treated and non-treated plants, respectively, we pooled the standard deviations of the degree distributions across the first 20 time points of the image series). We then determined the average number of nodes per connected, non-trivial network component after thresholding the edge weights, providing an estimate for the extent to which the cytoskeletal filaments form connected networks. By using the 50th percentile as a threshold, we found that Latrunculin B reduces the average size of the resulting connected components (figure 2b; independent two-sample t-test: p-value = 2.9 × 10⁻⁴²). These findings are in agreement with visual reports on the fragmented actin structure of Latrunculin B-treated cytoskeletons [41].

Figure 2.

Network properties capture biologically relevant aspects of cytoskeletal organization for different scenarios. The first 20 frames of the image series are used for the analysis. Symbols *↓ and *↑ above a bar denote a decrease or increase of the properties of the treated relative to those of the control plants (independent two-sample t-test: p-value < 0.05). Symbols *↓ and *↑ above a box plot denote network properties that fall below or exceed a reference value marked by a grey, dotted line (one-sample two-sided t-test: p-value < 0.05). (a) The AF network of Latrunculin B-treated plants displays a smaller standard deviation of the network's degree distribution. (b) The connected patches of AFs are smaller after Latrunculin B treatment. (c) The orientation of MTs is predominantly horizontal in dark-grown plants and vertical in light-exposed plants. (d) Computing the change in MT orientation per unit time shows a difference between control and light-treated plants. In dark-grown plants, a significant change towards a vertical orientation is observed, which is absent for light-treated plants. (e) The (horizontal) orientation of AFs is not altered in plants exposed to light. (f) Light induces a dispersion of AFs which yields a broader degree distribution.

By using the reconstructed MT network, we quantified the overall orientation of MTs in plants that had been exposed to light several hours before imaging. Light is one of the environmental factors that determine plant growth, and it is well established that the MT array rapidly changes from largely transverse to generally longitudinal when seedlings are exposed to light [43–45]. As our method does not detect individual filaments, we inferred the MT orientation indirectly (see the electronic supplementary material, S4, for a detailed derivation). By placing an imaginary rod of a specific length and orientation over the grid, we calculated its contributions to the weights of edges with different orientations by using our kernel method (cf. figure 1d). Here, we solved the inverse problem to obtain the overall MT orientation α from the weight distribution of edges with different orientations. Angles α ∈ [0°, 45°) and α ∈ [45°, 90°) indicate overall vertical and horizontal orientations of the MTs, respectively. We estimated the MT orientation for seedlings grown under dark and light conditions and found a significant difference (figure 2c; independent two-sample t-test: p-value = 5.8 × 10⁻⁵²) with a horizontal and longitudinal orientation, respectively (one-sample two-sided t-tests: dark p-value = 6.3 × 10⁻⁸, light p-value = 4.7 × 10⁻⁴⁵). These findings are in agreement with known results [40,43,44,46]. They further revealed that despite the strong correlation between light exposure and longitudinal MT orientation, there are also deviations (cf. figure 2c): under dark condition, a fraction of about 40% of the MT networks shows an, unexpected, overall vertical orientation, while under light conditions, about 20% of the analysed MT networks display an overall horizontal orientation, contrary to expectations. These deviations from the expected results may highlight the inherent variability of cytoskeletal responses to external stimuli and support the view that hypocotyl cells may be in different stages of growth [44,47,48].

We also studied the speed of MT reorientation under the microscope by computing the slope of the average orientation time series via a linear regression. There was a significant difference between the two treatments (figure 2d; independent two-sample t-test: p-value = 2.5 × 10⁻³), i.e. while the change in orientation is negative in dark, it does not significantly differ from zero in light (one-sample two-sided t-test: dark p-value = 2.5 × 10⁻⁵, light p-value = 0.6). Therefore, we conclude that over the range of 5 min of the experiment, the confocal laser light does induce a reorientation of the MTs towards the longitudinal cell axis in dark-grown plants; however, this is not the case in plants exposed to light before imaging as reorientation of MTs has already progressed further in these cells.

Next, we employed our network-based framework to investigate the behaviour of AFs in response to light in growing hypocotyls. Like for MTs, we inferred the overall orientation of the AFs for dark-grown and light-treated plants, respectively. We found no significant difference in actin orientation between the treatments (figure 2e; independent two-sample t-test: p-value = 6.6 × 10⁻²), with a consistent major longitudinal orientation (one-sample two-sided t-test: dark p-value = 3.8 × 10⁻⁷, light p-value = 4.4 × 10⁻²). To quantify the heterogeneity of the actin distribution, we computed the standard deviation of the degree distributions for both scenarios. In light-treated plants, the actin cytoskeleton displayed a more heterogeneous distribution across the cell than in dark-grown plants (figure 2f; independent two-sample t-test: p-value = 1.5 × 10⁻⁴), implying the prevalence of bundles. These findings agree with reports on the impact of light on the organization of AFs in maize coleoptiles [49]. However, they do not agree with the qualitative findings in a different species, i.e. rice, where light was shown to promote a change in AF orientation from transverse to longitudinal and to disperse actin bundles [50]. Interestingly, the rearrangement of AFs under light has been linked to that of MTs [40]. Therefore, our findings suggest that a change in environmental conditions would impose a need for rapid redistribution of cellular material in the cell, which is known to be facilitated by actin bundles [16].

2.3. Accessibility and robustness of cytoskeletal networks

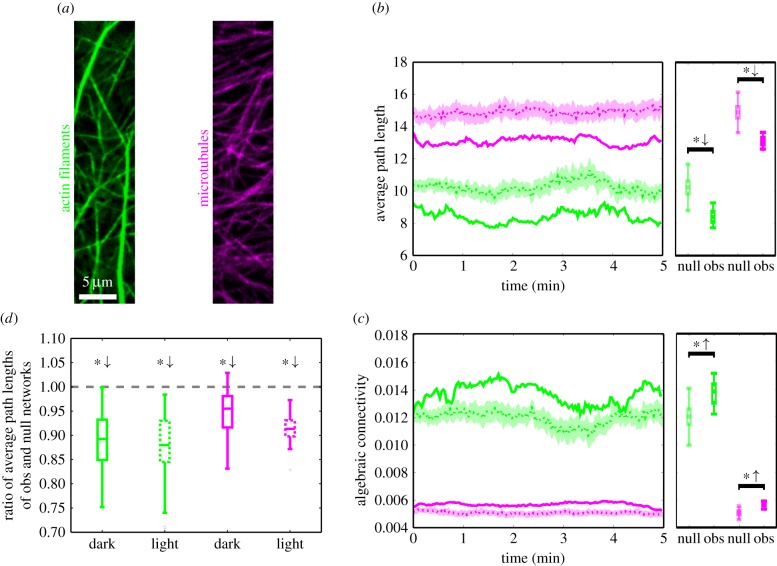
After demonstrating the inherent ability of our network approach to capture biologically relevant information on cytoskeletal organization, we focused on identifying network properties that reflect the functions of the cytoskeleton. To investigate the transport efficiency of the AF and MT networks (figure 3a), we computed APL (as a measure for the cellular accessibility of the cytoskeleton) and algebraic connectivity (AC) (as a measure for the cytoskeleton robustness against disruptions) (see the electronic supplementary material, S3, for the mathematical formulation and a detailed interpretation of the properties).

Figure 3.

Time-resolved APL and AC of cytoskeletal networks and null model networks. In (b,c), the results for the observed networks (solid lines) of AFs (green) and MTs (magenta) are compared to those of the null model (dashed lines: ensemble-mean; shaded regions: ensemble-mean ± s.d.). The box plots show the distribution of values of a network property used in the statistical test. (a) Green- and magenta-coloured images of AFs and MTs, respectively. (b) The APLs of AF and MT networks (solid lines) fluctuate over time and stay well below the APLs of the null model (dashed lines and shaded regions). (c) The AC is consistently larger for both AFs and MTs in the observed cytoskeletal networks (solid lines) than in the null model networks (dashed lines and shaded regions). (d) Comparing the ratios of APLs of the observed networks and their null model networks for AFs and MTs yields no statistically significant difference between dark and light conditions.

The APL (shortest) [42] is the average of the minimum distances between all pairs of nodes in a (edge-weighted) network. Here, the length of an edge is given by the inverse of its weight, i.e. thick actin bundles or tubulin filaments yield small edge lengths. This is reasonable since cytoskeletal bundles typically facilitate faster transport compared with thinner filaments [16], which may, in general, depend on the size of the cargo. The APL provides an estimate of how close any two nodes are expected to be and, hence, the accessibility in the cytoskeleton. By computing the APLs for the sequence of the AF and MT networks, we obtained two time series (figure 3b, green and magenta, solid lines). The corresponding values largely reflect the overall intensity distribution of the images and, by themselves, carry little information about the underlying network structure. As a reference, we calculated the APLs for ensembles of AF or MT null model networks, i.e. networks obtained by shuffling edge weights (figure 3b, green and magenta, dashed lines and shaded regions). We found that the observed networks exhibit significantly smaller APLs than their respective null models (independent two-sample t-test: AF p-value = 7.8 × 10⁻²⁷³, MT p-value = 2.2 × 10⁻³⁰⁸).

The AC [42] is the second smallest eigenvalue of the network's graph Laplacian, which is closely related to the weight matrix of the network, and reflects how well knit the network is. While a vanishing AC indicates the decomposition of the network into two or more disconnected components, larger values correspond to a higher robustness of the network against disruptions. By comparing the AC of the observed actin and MT networks (figure 3c, green and magenta, solid lines) to their null model counterparts (figure 3c, green and red, dashed lines and shaded regions), we found that the observed networks yield significantly larger ACs than their respective null model networks (independent two-sample t-test: AF p-value = 7.5 × 10⁻¹³⁹, MT p-value = 2.9 × 10⁻²⁷⁸).

These findings may be graphically explained as follows. Networks of MTs, and even more so AFs, possess filaments and bundles that stretch across large parts of the cell. These structures establish connected paths in the networks with large weights and therefore small lengths. In the computation of shortest path lengths, they act as ‘highways’ that efficiently connect spatially distant regions. Furthermore, the AF and MT networks exhibit larger regions that are particularly strongly linked and result in a higher robustness of the networks against disruption. To support this interpretation, we computed the degree assortativity [51] given by the correlation between degrees of nodes and those of their neighbours. It quantifies the extent to which nodes of (dis-)similar degree are connected to each other. Both the AF and MT networks exhibit significantly higher assortativity than their corresponding null model networks and are hence more spatially clustered (independent two-sample t-tests: AF p-value < 2.2 × 10⁻³⁰⁸, MT p-value < 2.2 × 10⁻³⁰⁸). We note that both APL and AC are summary statistics that do not capture differences in local connectivity patterns but reflect network properties that relate to the network's overall transport capacity.

Interestingly, despite the differences in the network architecture of AFs and MTs under dark and light conditions (cf. figure 2), there were no significant differences in the ratios of APLs of observed and null model networks (figure 3d). Moreover, these ratios stay consistently below one throughout the time series (one-sample two-sided t-tests: p-value < 0.05 for AF/MT dark/light), reflecting small effort for reaching any part of the cytoskeletal networks. Thus, the cytoskeleton preserves its advantageous transport properties over time and across conditions.

While the MT network can largely be captured at the cell cortex in interphase cells, the actin cytoskeleton constitutes a three-dimensional structure that spans the expanding cell. To ensure that we captured the volumetric behaviour of the AFs, we also recorded confocal z-stack image series of such cells and used our framework to reconstruct the AF network as a three-dimensional network (cf. figure 1g). To assess whether the additional information about AFs below the cortical plane changes the transport efficiency of the AF network, we compared the APL and AC of the three-dimensional network to that of the two-dimensional network obtained by averaging the intensities of edges at the same x–y-position across all z-layers. In both cases, the ratio of network properties of the observed network and the null model networks stays well below one (one-sample two-sided t-test: p-value < 0.05 for two-/three-dimensional APL/AC; see the electronic supplementary material, S2, for details). Analogously to the bundle structures in the two-dimensional networks, the actin structures that reach deeper into the cell provide strong connections in the three-dimensional reconstruction (figure 1g) that naturally equip the network with shorter paths and higher robustness.

Taken together, AF as well as MT networks display highly non-random features. In particular, short APL (good accessibility) and large AC (high robustness) are preserved over time and across different environmental conditions. These findings provide quantitative support for the idea that plants reliably establish and maintain cytoskeletal structures that are optimized for transport processes throughout the cell [14,17,28].

2.4. The cytoskeleton and the German autobahn exhibit similar network properties

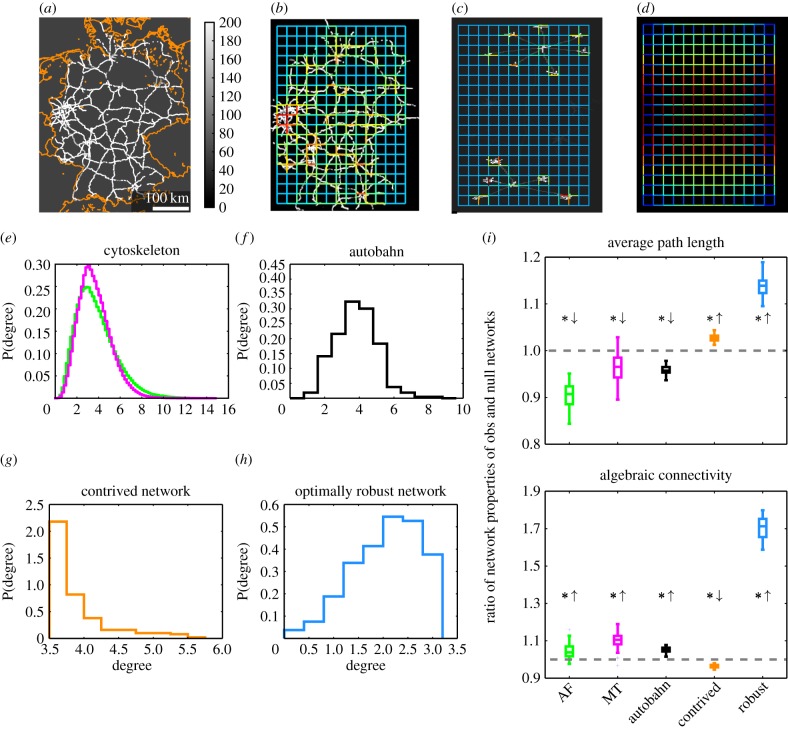
We next asked whether the observed efficiency in network properties is unique to the cytoskeleton or if it can also be observed in other transportation networks. As a prominent example, we generated images of the German autobahn with colour-coded speed limits (figure 4a; the maximum speed limit is set to 200 km h⁻¹, the speed limit outside of the autobahn is set to 50 km h⁻¹; however, our findings are largely independent of this choice, see the electronic supplementary material, S5). By using our established framework, we obtained a weighted network for the autobahn (figure 4b) and corresponding null model networks by shuffling edge weights. For the APL and the AC, we computed the ratios for the respective network properties of the autobahn and its null model networks and we found that the autobahn network exhibits shorter APLs and higher ACs than expected by chance (figure 4i, black). These results are similar to what we found for the cytoskeleton (figure 4i, green and magenta). Furthermore, we note that the degree distributions of the cytoskeletal networks and the autobahn are unimodal and peak around their means (figure 4e,f).

Figure 4.

Comparison of cytoskeleton, German autobahn and other types of networks. (a) The autobahn network of Germany with colour-coded speed limits and national borders (orange) for guidance. (b) Network reconstructed from the autobahn image. (c) Reconstructed network for a contrived underlying structure with different structural and transport-related properties. (d) Network with maximal AC for the given grid-topology and normalized sum of weights (here, the network is constructed via an optimization procedure and not inferred from an underlying image intensity distribution; the black background is for better visibility only). (e) The degree distributions of the AF (green) and MT (magenta) networks are unimodal and peak around their means (excess kurtosis > 0; the resolution of the histograms is higher as they include all networks of an image series, cf. figure 3). (f) The degree distribution of the autobahn network is unimodal and peaks around its mean (excess kurtosis > 0). (g) For the contrived network, the degree distribution is also peaked (excess kurtosis > 0) but shows a more heavy right tail compared with (e,f). (h) The degree distribution of the optimally robust network is broader around the peak and has thinner tails (kurtosis < 0). (i) The ratios of APLs of observed and null model networks are below one for the cytoskeletal and the autobahn networks and above one for the contrived and the optimally robust networks. The ACs are bigger than expected by chance for all studied networks, except for the contrived networks that show a smaller AC. All deviations from the unit ratio are statistically significant (one-sample two-sided t-tests: all p-values < 0.05).

To differentiate these networks from networks with different structural and transport-related properties, we further studied a contrived network with a stronger local structure and weaker long-ranged connections (figure 4c). The contrived network displays a heavy-tailed degree distribution (figure 4g) as well as properties associated with poor transport efficiency, namely, longer APL and smaller AC than expected from the null model (figure 4i, orange).

Another interesting comparison is that of the cytoskeleton and the autobahn to networks in which one or several transport-related properties are optimized. The weight distribution of a network with a fixed sum of edge weights and maximal AC may be computed efficiently by solving a semi-definite optimization problem whose solution is unique [52,53] (figure 4d). Such an optimally robust network outperforms the cytoskeletal and the autobahn networks by a factor of eight with respect to the ratio of AC of observed and null model networks (figure 4i, blue). However, it is less efficient in terms of its APL, which is higher than expected by chance, demonstrating a trade-off between different measures of network optimality.

While there are certainly differences in the structure as well as the function of the cytoskeleton and the autobahn, the network properties studied here are summary statistics and it is not possible to infer local structural differences from them. In particular, we do not study their absolute values but the relative efficiency of these networks with respect to their respective null model which may point to their organizational principles.

To conclude, both the actin and MT cytoskeleton display characteristics typical of transportation networks, such as the autobahn, and exhibit structures which may not be aimed at optimizing a single property indicative of efficient transport. Our data therefore provide quantitative measures to support a view of the plant interphase cytoskeleton as an efficient transportation network.

3. Discussion

Though many studies have analysed the cytoskeleton, most of them have relied on qualitative observations or manual tracking of up to some dozens of AFs and MTs. The rapid dynamics, as well as strong variability of cytoskeletal organization across different cell types, stages of cell life and environmental conditions, necessitate a framework that allows for a fast and objective quantification of the cytoskeletal components in living cells. This would then allow for biologically meaningful interpretations that go beyond strictly theoretical studies to investigate the structure of the system. Here, we described one such framework that captures biologically relevant variations.

Many studies have used a bottom-up approach to the cytoskeleton, in which the molecular principles are presupposed and used to infer the behaviour of the system. Instead, we pursued a top-down strategy to represent the cytoskeletal organization without the need for detailed molecular knowledge. Hence, our approach hints at the underlying organizational principles of the cytoskeleton. More specifically, by choosing a representation through complex networks, we could exploit the well-equipped toolkit from graph theory to investigate the structure of the cytoskeleton and its relation to, for example, efficient transport processes in the cell.

For a careful interpretation of these findings, we need to bear in mind several points. (i) Our network reconstruction method creates nodes at positions given by the chosen grid (cf. figure 1). Hence, not all nodes correspond to crossings of the filaments. Moreover, despite our focus on the largely planar cortical cytoskeleton even apparently crossing filaments may be separated by hundreds of nanometres in z-direction. Using our current imaging techniques, such distances may not be resolved in the three-dimensional reconstruction either (see outlook below). In particular, such distances prohibit the switching of motor proteins (e.g. [54] for MT). Yet, the edge weights in our method agglomerate local intensities that may originate from multiple filaments in different depths. More importantly, typical cargo such as mitochondria, Golgi bodies or chloroplasts range from several hundred nanometres to several micrometres in size and may thus easily bridge even larger distances between filaments, thereby justifying our assumption of transport along edges and via nodes. (ii) In our approach, all edges are undirected, i.e. they allow bi-directional transport. While bi-directional transport may occur along single actin or microtubular filaments, e.g. due to different motor proteins or fluctuations [55–57], bundles of filaments typically allow uni-directionality only. This uni-directionality is further amplified by the cytoplasmic bulk flow generated by the coordinated movement of motor proteins [14]. Yet again, our reconstruction methods assign edge weights by integrating local intensities of possibly multiple filaments with different orientations. Thus, fully bi-directional of transport is unlikely (but not excluded) and, as it cannot be inferred from the cytoskeletal images alone, we use it as an approximation of the potential transport capacity. (iii) This potential transport capacity is modelled to be higher in regions with many/thick cytoskeletal filaments, as described by the edge weights. However, the edge weights do not quantify the speed/amount of cargo that is really transported (and we do not measure it, see outlook below). (iv) Finally, we note that AF and MT networks generally transport different cargo (cf. [14,28]), although there is evidence for transport of, for example, small cellulose-containing vesicle along both structures [58,59]. In addition, different types of cells may require different modes of transportation [60]. Here, we focused on the potential transport capacity of the cytoskeleton in interphase hypocotyl cells, but our framework may readily be used to study other scenarios.

There is a rich literature on the comparison of structures of different networks. Many biological and man-made networks show scale-free degree distributions, i.e. there are a few nodes with many neighbours [61], e.g. airway networks [62]. However, nodes in other transportation networks are restricted regarding the number of potential neighbours due to the physical limitations. Road and railway networks display degree distributions that peak around their average values [63], which we also demonstrated for the cytoskeletal networks. Despite the apparently diverse principles underlying man-made transportation networks, studies have revealed strong agreement in a number of their properties, e.g. degree distribution. This agreement may be explained by costs associated with the establishment of new nodes and links [64–66]. Our findings suggest that comparable cost-related restrictions may play a role in the formation of the cytoskeleton, leading to similar structures and transport properties as in man-made networks.

In summary, our framework captures the complex network structure of filamentous cytoskeletal components. We used this framework to derive organizational principles of the cytoskeleton. We further showed that AF and MT networks display biologically desirable characteristics, such as short APLs and high robustness, similar to characteristics found in non-biological transportation networks. In particular, these features of efficient transportation networks are maintained over time and across conditions.

Possible directions of future efforts are manifold. (i) Our framework can be employed to quantify the complex structures of AF and MT networks, and thus enables an automated and objective comparison of the complex structures of cytoskeletal networks in other biological systems, e.g. focusing on the cytoskeleton connecting the nucleus to other parts of the cell. (ii) The resolution of the fine cytoskeletal structures may be improved by using more advanced imaging techniques like total internal reflection fluorescence microscopy, at least for the cortical cytoskeleton. (iii) Another promising direction is the comparison of reconstructed cytoskeletal networks to networks that optimize one or several seminal network properties. As different network structures favour specific properties, the cytoskeleton may represent an evolutionarily shaped compromise between them. While such a balance has been suggested, e.g. between the speed and the sensitivity in the polarization of the cytoskeleton [67], quantitative evidence for a trade-off in the cytoskeleton's transport properties is lacking. We note that besides its vital role in cellular transport processes, the plant cytoskeleton strikingly determines the mechanical properties of the cell. (iv) Finally, our work paves the way for direct studies of the cytoskeleton as a transportation network. Employing actin and organelle dual-labelled plants, it is appealing to correlate actual biological transport processes with flow-related network measures. While several studies have investigated the transport of organelles and vesicles along the cytoskeleton [14,54,58,68], none have quantitatively linked it to the complex structure of the cytoskeletal network. Answering these questions may contribute to a better understanding of the organizing and dynamic principles of the cytoskeleton.

4. Material and methods

The experimental set-up includes dual-labelled A. thaliana Columbia-0 seedlings to which different treatments were applied prior to imaging in a spinning-disc confocal microscope set-up. For further details, refer to the electronic supplementary material, S1. The computational network-based investigation of the image series, as illustrated in figure 1, includes: (i) the preprocessing of the images in Fiji [69], (ii) the creation and quantification of the weighted cytoskeletal and null model networks, and (iii) their statistical analyses in Python [70] (using SciPy [71], NumPy [72], NetworkX [73] and the Matplotlib [74] libraries). The construction of an optimally robust network was performed by solving a semi-definite optimization problem using the Cvxopt Python package [75]. Detailed descriptions of these steps are given in the electronic supplementary material, S2, and the studied network properties are described in detail in the electronic supplementary material, S3. The overall orientation of cytoskeletal components is inferred from the network's weight distribution as described in the electronic supplementary material, S4. The data of the German autobahn, as depicted in figure 4, are collected from OpenStreetMap and filtered as explained in the electronic supplementary material, S5.

Funding statement

D.B., A.I., S.P. and Z.N. were supported by the Max-Planck-Gesellschaft.