Computational modelling suggests good, bad and ugly roles of glycosaminoglycans in arterial wall mechanics and mechanobiology

Abstract

The medial layer of large arteries contains aggregates of the glycosaminoglycan hyaluronan and the proteoglycan versican. It is increasingly thought that these aggregates play important mechanical and mechanobiological roles despite constituting only a small fraction of the normal arterial wall. In this paper, we offer a new hypothesis that normal aggregates of hyaluronan and versican pressurize the intralamellar spaces, and thereby put into tension the radial elastic fibres that connect the smooth muscle cells to the elastic laminae, which would facilitate mechanosensing. This hypothesis is supported by novel computational simulations using two complementary models, a mechanistically based finite-element mixture model and a phenomenologically motivated continuum hyperelastic model. That is, the simulations suggest that normal aggregates of glycosaminoglycans/proteoglycans within the arterial media may play equally important roles in supporting (i.e. a structural role) and sensing (i.e. an instructional role) mechanical loads. Additional simulations suggest further, however, that abnormal increases in these aggregates, either distributed or localized, may over-pressurize the intralamellar units. We submit that these situations could lead to compromised mechanosensing, anoikis and/or reduced structural integrity, each of which represent fundamental aspects of arterial pathologies seen, for example, in hypertension, ageing and thoracic aortic aneurysms and dissections.

1. Introduction

Glycosaminoglycans (GAGs) compose only 2–5%, by dry weight, of the wall of normal elastic arteries [1], which may be one reason why their potential mechanical roles have not been well studied in arterial wall mechanics. Nevertheless, increasing evidence shows that GAGs are important contributors to normal arterial structure and function [2–4], and that GAG content tends to increase in hypertension, ageing, atherosclerosis and thoracic aortic aneurysms and dissection [5–8]. That is, GAGs now appear to be important contributors to arterial morphogenesis, homeostasis and pathogenesis. The three primary classes of GAGs within the arterial wall are hyaluronan, chondroitin/dermatan sulfate and heparan sulfate; hyaluronan and the chondroitin/dermatan sulfate GAGs are synthesized mainly by smooth muscle cells, whereas the heparan sulfate GAGs are synthesized mainly by endothelial cells [9]. Hyaluronan does not associate with a protein core, but chondroitin, dermatan and heparan sulfate GAGs bind to protein cores to form larger molecules called proteoglycans (PGs). The two primary classes of PGs of importance in arterial mechanics and biology are those that aggregate with hyaluronan and contribute to the compressive stiffness and viscoelasticity of the wall (e.g. the chondroitin sulfate-rich PG called versican) and those that participate in collagen fibrillogenesis and the sequestering of growth factors (e.g. the small leucine-rich PGs called biglycan and decorin). Herein, however, we are motivated by the potential mechanical roles of aggregates of hyaluronan and versican, which are found primarily within the extracellular space of the media of elastic arteries [10]. A recent study suggested, for example, that medial GAGs/PGs may contribute to the existence of residual stress in arteries [11], which of course play important roles in homeostasis as well as adaptations to altered haemodynamics [12].

Hyaluronan is a high-molecular-weight biomolecule that sequesters considerable water, and thereby contributes to the compressive stiffness and viscoelastic behaviour of many soft tissues [13]. Versican contains 15–20 chondroitin sulfate side chains, which are highly negatively charged [1]. Hence, versican tends to attract positive ions (e.g. Na⁺) to enforce local electroneutrality, which in turn imbibes water and generates an associated local swelling pressure. This so-called Donnan swelling pressure is well known in physical chemistry [14] and is well studied in cartilage mechanics wherein PGs play a fundamental structural role [15]. Of particular relevance herein, research on cartilage revealed that a local swelling pressure can cause collagen II fibres to be in tension despite the existence of an overall compressive stress [16]. Motivated by this finding, our focus is on potential effects of intralamellar aggregates of hyaluronan and versican on the elastic fibre-associated microfibrillar connections between smooth muscle cells and the delimiting elastic laminae in large arteries. In particular, we hypothesize that, in addition to contributing to the compressive load carrying capability of the extracellular matrix, normal intralamellar aggregates of hyaluronan and versican can place radially oriented microfibrillar connections in tension despite the overall compressive radial stress in the arterial wall. This tension, in turn, could provide a means for the smooth muscle cells to sense directly the mechanical loads in the elastic fibre network that is fundamental to normal large artery structure and function. Pathological accumulations of these GAG/PG aggregates could overload these connections, however, thus resulting in compromised or lost mechanosensing. Indeed, in the extreme cases of localized pooling of these aggregates, a complete loss of fibre–cell connections may result in smooth muscle anoikis [17] or cause high-stress concentrations that could adversely affect the structural integrity of the wall and lead to delaminations [18].

In this paper, we use two complementary biomechanical modelling approaches—a mechanistic mixture-based finite-element model, and a phenomenological continuum-based semi-analytic model—to illustrate these potentially good, bad and ugly roles of medial GAGs/PGs in large arteries. Although contributions to normal load bearing and mechanosensing are obviously good, abnormal increases in GAGs/PGs that compromise or sever elastic fibre–smooth muscle connections would be bad, for this would adversely affect mechanosensing or cell survival in ways that further diminish the structural integrity of the wall. Finally, following up on a recent hypothesis [8], we re-emphasize that a pathological local pooling of GAGs/PGs could lead to the ugly situation of local stress concentrations that may initiate potentially lethal intramural delaminations/dissections.

2. Illustrative artery of interest

Our hypothesis should hold for elastic arteries in general, but owing to the availability of copious data on the murine common carotid artery in our laboratory (cf. [19]), we illustrate our ideas based on simulations for this vessel. The normal mouse carotid artery consists of two structurally important layers, the media and adventitia, which occupy approximately 40% and 60% of the wall, respectively. The media consists of two to three medial lamellar units, which in turn consist of smooth muscle, collagen and GAGs/PGs bounded by paired elastic laminae; the adventitia consists of a single layer of fibrillar collagen, with small amounts of elastic fibres. Of particular importance herein, there also exist elastin-associated microfibrils that either connect the smooth muscle cells to the elastic laminae or connect the elastic laminae to each other; these microfibrils are so thin that they are best seen via electron microscopy [20,21]. Reports differ on the overall mass fractions of these primary constituents, perhaps depending on the amount of perivascular tissue/adventitia that is removed during dissection. We use the report that the murine common carotid artery consists of approximately 26% elastic fibres, 21% smooth muscle and 50% collagen, with the remaining 3% mainly medial GAGs/PGs [22]. When transected, these vessels tend to retract approximately 70%, which is thought to be due primarily to recoil of the elastic fibres [23], which are deposited and cross-linked during the perinatal period [4] and subsequently extended elastically during somatic growth [24]. When a traction-free ring is cut radially, a small opening angle Φ_o occurs owing to the relief of residual stresses (cf. [25]). We note that medial aggregates of hyaluronan–versican would cause an intralamellar swelling which, along with radial gradients in material properties [12] and the remaining recoil of elastic fibres [26], probably affects the measured opening angle (cf. [11]) and hence the overall distribution of wall stress.

3. Finite-element model

3.1. General framework

Ateshian et al. [27] developed a mixture-based finite-element approach to describe nonlinear responses of GAG-endowed continua; this formulation was implemented in the open source software FEBio (www.sci.utah.edu/software/40-mrl/39-febio). They demonstrated the utility of this approach, for example, by studying residual stresses in rodent aortic tissue having layer-specific differences in fixed charge density (FCD; i.e. GAG-associated negative charges), as described in [11]. Herein, we use their approach as implemented in FEBio. Figure 1 shows half of our baseline axisymmetric finite-element model of an intact artery to emphasize the need to model possible transmural differences in the FCD, that is, the distribution of GAGs. Also shown is an illustrative computational result for the radial cutting of an intact traction-free configuration. A series of such computations of the resulting opening angle served to validate our use of FEBio via a comparison of results with those in [11]. That is, although our focus herein is on the in vivo, not residual, stress field, calculation of residual stress-related quantities proved useful in comparing our two models. As shown below, we also used FEBio to model a small portion (intramural tangent plane) of the arterial wall that contained a focal, rather than diffuse, accumulation of GAGs. Convergence of solutions in both cases was ensured via standard mesh refinement and comparison of results.

Figure 1.

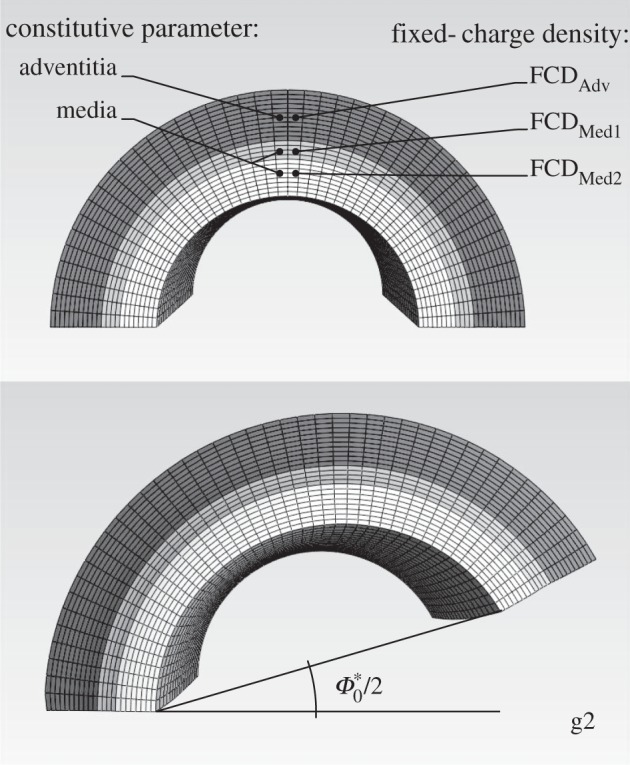
Finite-element model of a segment of a murine common carotid artery, where g2 represents a possible ‘good’ situation with FCD_Med2 =−70, FCD_Med1 = −40 and FCD_Adv = −20 mEq l⁻¹. Mechanical properties (i.e. strain energy parameters) were prescribed separately for the media and adventitia and similarly for the swelling related fixed charge density (FCD), with the exception of radial differences in FCD also within the media.

3.2. Constitutive behaviour

Consistent with the vast majority of the literature on arterial wall mechanics [12], we used a locally homogenized stored energy function W(C) to describe the material behaviour, albeit separately for the media and adventitia. Here, where C is the right Cauchy–Green tensor, and F is the deformation gradient tensor. To facilitate comparisons between the finite-element and continuum (described below) models, we used a strain energy function W in the finite-element simulations having both neo-Hookean and exponential (four fibre families) contributions. This so-called four fibre family constitutive relation has been shown to describe well the mean biaxial mechanical data of central arteries in mice [19,22]. Relative to the mass-averaged strain energy function that we used for the continuum model (see below), the finite-element model (FEM) accounted for an amorphous matrix consisting of elastin plus GAGs/PGs and modelled as a single material; it also combined the circumferential behaviours of the collagen fibres and smooth muscle. Hence, the overall relation is

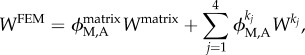where are mass fractions that can be prescribed separately in the media (M) and adventitia (A). As is usual (cf. [28]), we let

where is a material parameter and . Note, therefore, that effects of ‘swelling’ associated with the GAGs/PGs were accounted for in the finite-element model by an additional contribution to the tangent stiffness matrix that depends on and the FCD (cf. equation 9 in [11]).

Similarly, we described the behaviour of the four fibre families (dominated by collagen) using a Fung exponential strain energy function, namely

where and are material parameters (the former with dimension of stress and the latter non-dimensional) and represent squares of the stretch of the jth fibre family. The definition of fibre orientations was consistent with that for the continuum model: family one in the axial direction, family two in the circumferential direction and families three and four representing symmetric-diagonal orientations. It is important to note that we allowed the three primary families of fibres (i.e. axial, circumferential and symmetric-diagonal) to have different material behaviours, hence necessitating estimation of up to seven fibre-related material parameters (see table 1). This material characterization differed between the two models as noted below.

Table 1.

Best-fit values of model parameters for both the continuum and finite-element models. Note that the finite-element model accounts further for the effect of the GAGs via a swelling induced contribution to the tangent stiffness matrix (cf. [11,27]).

continuum model	cGAGs (kPa)	ce (kPa)		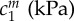				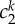βθ	βz
	172.18	118.10	1275.97	1.47	449.44	19.43	36.67	0.11	0.14
FEM model	cmatrix (kPa)		c11 (kPa)	c21	c12 (kPa)	c22	c13,4 (kPa)	c23,4	α0k (deg)
two layers	19.51		142.10	0.05	80.88	0.05	2.58 × 10−4	2.19	28.25
one layer	17.64		81.47	0.05	28.01	2.27 × 10−2	1.09 × 10−4	2.10	27.75

4. Continuum model

Although one should prefer a mixture-based finite-element model that directly includes effects of FCD on the local Donnan swelling pressure, information on spatial and temporal changes in the FCD in arteries remains wanting (cf. [18]). Hence, phenomenological continuum models can serve as useful tools for studying parametrically the consequences of changes in Donnan swelling pressures, that is, imposed local changes in volume . Although swelling causes a change in volume, the swollen artery appears to deform isochorically thereafter in response to transient loading; hence, one can use incompressible finite elasticity provided the swelling is included. Towards this end, we used but extended the method of Demirkoparan & Pence [29], who analysed effects of swelling on fibre-reinforced cylindrical tubes with a constant function of radius. We first studied the effect of a constant swelling on a bilayered arterial model, but then studied effects of more physiological situations wherein the media swelled more than the adventitia. This transmural difference was quantified using a sigmoidal function

where and represent values of swelling in inner (medial side) and outer (advential side) portions of the wall, respectively, and represents the location of the medial–adventitial interface. In this way, we were able to compare, for the first time, the predictions of a mechanistic finite-element model and a phenomenological continuum model.

4.1. Configurations of interest

Figure 2 is a schema of general configurations of interest computationally; others can be obtained easily from the ones shown. We again modelled the normal arterial wall as a bilayered structure, noting that the inner (i.e. medial) layer is normally swollen slightly relative to the outer (adventitial) layer owing to the presence of hyaluronan and versican in the former [10]. The homeostatic configuration κ_h (with coordinates r, θ, z) at mean arterial pressure (MAP) ∼ 93 mmHg and the in vivo axial stretch defined a computationally convenient and biologically relevant reference configuration; note that this choice was different from the classical use of a traction-free reference that was used in the finite-element model, but it proved useful in the continuum model and is more relevant to the physiology [26]. Towards this end, we defined a natural, stress-free configuration for each structurally significant constituent α (= e, k_j, m, PG for elastic fibres, j = 1, 2, 3, 4 families of collagen fibres, smooth muscle cells and GAGs/PGs, respectively). Mappings from these natural configurations to the in vivo homeostatic reference configuration were defined by G^α, the constituent-specific deposition stretch tensors. From the central reference configuration, one can obtain any non-homeostatic configuration κ_P at pressure P and (with coordinates r_P , θ_P , z_P), the intact, traction-free unloaded configuration κ_tf (with coordinates ), and the radially cut, traction-free configuration κ_c (with coordinates R, Θ, Z).

Figure 2.

Schematic diagram of key configurations that were used either in the nonlinear regression or to test the predictive ability of the constitutive formulations for the mouse carotid artery. , homeostatic (swollen homeostatic) configuration at a mean arterial pressure of 93 mmHg and in vivo axial stretch 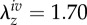(). κ_p (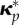), loaded (swollen loaded) configurations at  () and any pressure P, with representative values shown for P = 220 mmHg. κ_tf (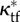), intact (swollen intact), traction-free configuration. κ_c (), radially cut (swollen radially cut), traction-free configuration. κ_n, natural (i.e. stress-free) configurations for individual constituents.

To examine consequences of medial swelling, we also let the intact configuration κ_tf be mapped into a swollen, intact, traction-free configuration (with coordinates ). From this swollen, traction-free configuration one can axially stretch and pressurize the carotid to MAP to obtain a new swollen and physiologically loaded configuration 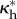(with coordinates r*, θ*, z*) or pressurize the vessel to any perturbed pressure P to obtain (with coordinates 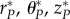). Of course, as in the finite-element model, one can also introduce a radial cut numerically to obtain a nearly stress-free swollen configuration (with coordinates 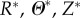), which as noted above was useful in comparing results across models. The mappings of material points among the different configurations shown in figure 2 are given by

Similarly, consider mappings of the swollen wall,

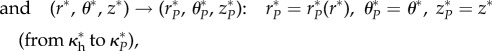where Φ₀ and are the opening angle in the cut, stress-free configuration and the opening angle in the swollen, cut, stress-free configuration, respectively. The deformation gradients F associated with these mappings, as shown in figure 2, are computed via

while assumes the same form as when r becomes , ϱ becomes and becomes . Similarly, assumes the same form as F_c when R becomes , ϱ becomes , Φ₀ becomes and Λ_z becomes , and assumes the same form of F_P when r becomes and r_P becomes . The associated deformation gradients of interest for stress analysis were obtained via multiplicative operations. For example, relative to κ_h, the deformation gradient associated with was 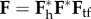. Of course, this general schema allowed different degrees of swelling (parametrized by ) as well as different levels of biaxial loading via pressurization and applied axial loads.

In general, the value of the relative volume change (equals to either 1 or ) allowed the radial stretch to be computed, in each deformation process, from the circumferential and axial stretches and the radial position occupied by each material particle that was mapped between different configurations, namely

where subscripts i denote inner radii.

4.2. Constitutive relation

Consistent with the kinematics, our constitutive approach borrowed ideas from the growth and remodelling literature, which allowed us to endow each constituent with not only a different stored energy function, but also a different strain in the homeostatic configuration. Briefly, the elastin-dominated behaviour was described by a neo-Hookean relation, whereas both the collagen-dominated and the passive smooth muscle behaviours were described by locally parallel fibre families described by Fung exponentials [26]. In addition, however, we added a new term (modified Blatz–Ko material) to account for the GAG/PG-dominated behaviour and related swelling. Although each constituent was constrained to deform with the wall (i.e. the mixture), its individual natural configuration allowed different levels of deformation within any overall configuration. Recalling that mappings between each natural configuration and the homeostatic reference configuration κ_h were described by the linear transformations G^α, the constituent-specific deformations needed in the stored energy functions were , where F represents any deformation of the arterial wall relative to the homeostatic reference configuration, as described previously. Hence, F = I in the homeostatic (loaded) configuration whereby F^α = G^α, by definition. Moreover, note that G^α account for both the cell-mediated deposition stretch (e.g. when collagen fibres are deposited at a preferred stress in extant matrix) and developmentally induced stretches (e.g. in the elastic fibres, which are deposited during the perinatal period and have a long half-life).

The mass-averaged strain energy function for the continuum model (CM) was thus assumed of the form

where superscripts PG, e, m and k_j refer to GAGs/PGs, elastin, smooth muscle and each of the four families of collagen fibres (j = 1, 2, 3, 4), and W^α and are the strain energy density functions and the mass fractions of the α constituents that compose the mixture, whereas a subscript M or A again refers separately to the medial or adventitial layer, respectively. Similar to that in the finite-element model, we modelled the elastin-dominated behaviour using a neo-Hookean model,

where c^e is a material parameter with the dimension of stress, but C^e is now the constituent-specific right Cauchy–Green tensor for elastin, where and 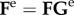. Also, similar to the finite-element model, we let the behaviour of the fibrillar collagen and passive smooth muscle in tension be described by Fung exponential strain energy functions, namely

and

where and are material parameters with dimension of stress, and 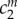are non-dimensional material parameters for the collagen-dominated (superscript k) and smooth muscle-dominated (superscript m) behaviours, respectively. Neither the smooth muscle nor the collagen fibres were endowed with a compressive stiffness. Rather, the compressive behaviour of the mixture was modelled by the mechanical properties of the amorphous matrix. The deformation of each family of fibres was evaluated as , for the jth collagen fibre family, and for the circumferentially oriented smooth muscle (i.e. ). The collagen fibre orientations were defined by the unit vectors , where angles are defined between directions of fibre reinforcement and the axial direction. Hence, axial and circumferential fibres are fixed at and , respectively, whereas symmetric-diagonal fibres are accounted for by , which was determined via parameter estimation using in vitro biaxial data.

Finally, we modelled the behaviour of the GAGs/PGs using a modified Blatz–Ko model for a material that can swell, namely

where is a function of the second and third invariant of , namely , where and , is a material parameter with the dimension of stress, is the right Cauchy–Green tensor for the GAGs/PGs, evaluated as , where describes the deformation gradient experienced by this amorphous matrix, and ν* describes the relative change in volume with respect to the intact traction-free configuration κ_tf.

4.3. Parameter estimation

Biaxial data from three different cyclic pressure–diameter protocols at multiple fixed axial stretches [19] were used to find best-fit material parameters for the bilayered constitutive relations used in both the finite-element and continuum models. Specifically, best-fit values were determined by minimizing the error between theoretically predicted (th) and experimentally measured (exp) pressures and axial forces via a nonlinear least-squares regression, namely by minimizing the objective function

where N is the total number of data points and the overbars denote mean values. Goodness of fit, evaluated in terms of the root mean sum-of-the-squares of the error, was always between 0.02 and 0.15. The resulting best-fit parameters as well as values of the mass fractions and distributions of constituents in each layer determined from histology (cf. [26]) are in tables 1 and 2. Note that the parameters β_θ and β_z, which describe in the continuum model the fraction of collagen fibres-oriented circumferentially and axially, respectively, were considered free parameters in the nonlinear regression.

Table 2.

Distributions of primary load bearing constituents motivated by microstructural information for the mouse common carotid artery [22,26]. Area fractions were obtained by analysing histological samples using a custom code in Matlab; the percentage of the constituents in each layer was inferred from considerations of the macroscopic behaviour of the vessel in vitro.

continuum model	GAGs	elastin	SMCs	collagen
				circumferential	axial	diagonal
area fraction	0.050	0.199	0.279	0.051	0.065	0.342
media (%)	80	97	100	0	15	15
adventitia (%)	20	3	0	100	85	85

FEM	amorphous matrix	fibre families
		circumferential	axial	diagonal
area fraction	0.250	0.280	0.230	0.230
media (%)	80	5	15	15
adventitia (%)	20	95	85	85

In addition, based on prior work [26], we prescribed the deposition stretches for each constituent in the continuum model. For the elastic network, the deposition stretch tensor for the radial, circumferential and axial directions, respectively. For the collagen fibres, for axial fibres, for circumferential fibres (located only in the adventitial layer) and for diagonal fibres. For the smooth muscle, which was directed circumferentially within the media, we assigned a deposition stretch of G^m = 1.03. Finally, the PGs were assumed to be in traction in the radial direction in the homeostatic configuration to mimic the small swelling observed in vivo and, via incompressibility, compressed in the other two directions, thus yielding a deposition stretch tensor of relative to radial, circumferential and axial directions, respectively.

Finally, values of FCD in the finite-element model were studied parametrically based on expected mean basal values of FCD = −50 mEq l⁻¹ in the media and −20 mEq l⁻¹ in the adventitia under normal conditions [11,18,30]. Consequences of differences in FCD in the media were considered over the range −50 to −160 mEq l⁻¹, which yielded macroscopic changes in opening angle over a range from 12.8 to 114.8 deg (table 3).

Table 3.

Values of the inner and outer radii, medial–adventitial border and opening angle for four cases of swelling for both the continuum (CM) and finite-element (FEM) models. Shown, also, is the percentage difference between the model predictions, which represents the first such inter-model comparison of the effects of intramural swelling.

		g1	g2	b1	b2
inner radius (µm)	CM	123	129	145	156
	FEM	120	126	142	157
	% diff	2.43	2.60	2.07	0.93
medial–adventitial border (µm)	CM	166	173	191	202
	FEM	162	168	186	199
	% diff	2.77	2.99	2.72	1.34
outer radius (µm)	CM	216	220	231	239
	FEM	216	221	237	248
	% diff	0.15	0.62	2.61	3.76
opening angle (deg)	CM	12.21	31.13	78.33	114.35
	FEM	12.78	31.62	76.79	114.76
	% diff	4.46	1.55	2.01	0.36

5. Results

Figure 3 shows data (mean ± s.d.) from a pressure–diameter protocol performed on wild-type murine common carotid arteries at the in vivo axial stretch, consistent with that found in [19]. Shown, also, are best-fit results for the aforementioned constitutive relations for the uni- and bilayered finite-element models as well as the continuum model. Results were similar for data from the other protocols, but are not shown for clarity. Table 1 lists the associated best-fit values of the parameters for all three models and table 2 lists layer-specific (medial versus adventitial) ‘mass’ fractions for the different structurally significant constituents for the bilayered finite-element and continuum models; fractions for the unilayer finite-element model of the wall (see below) necessarily account for the global mass fractions.

Figure 3.

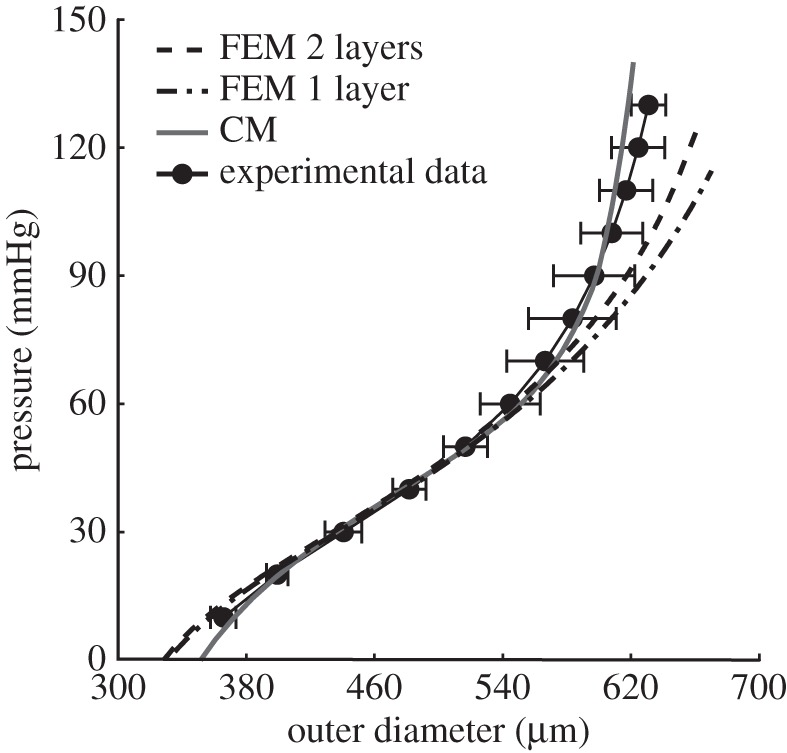
Representative luminal pressure–outer diameter responses for a simulated (lines) and experimental (closed circles) biaxial pressurization and axial extension protocol, consistent with that in Ferruzzi et al. [19]. Shown, specifically, are the biaxial responses for the CM (solid line) and for both a unilayered (FEM 1 layer; dotted-dashed line) and bilayered (FEM 2 layers; dashed line) finite-element model.

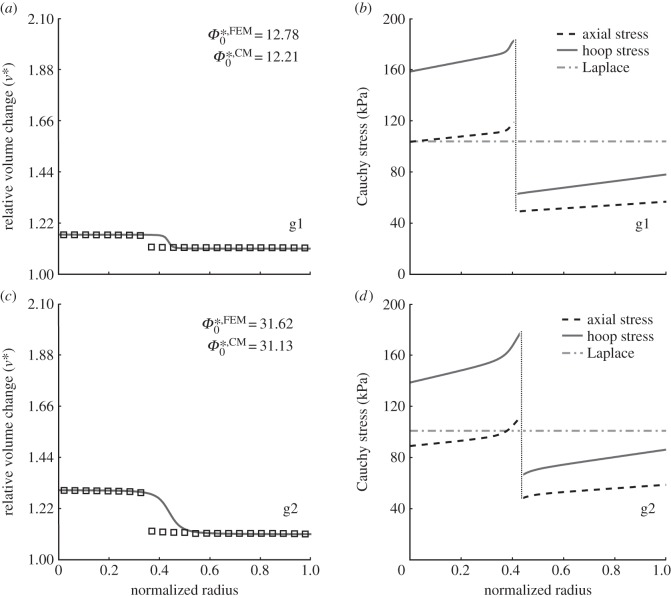
Figure 4 (left column) shows the relative volume change ( during swelling, not transient loading) for both the bilayered finite-element (open squares) and continuum (solid line) models for two cases of swelling that generated two different residual stress-related opening angles . In particular, the distribution of swelling in the continuum model was chosen to mirror phenomenologically the macroscopic consequences of prescribed mechanistic variations in FCD in the finite-element model (−50 and −70 mEq l⁻¹, respectively). Clearly, the two models yielded similar (i.e. within typical experimental uncertainty) results as desired, in this case. In addition, there was good agreement in other measurable metrics: inner and outer radii as well as location of the medial–adventitial border in the swollen configuration differed by less than 4% between the finite-element and continuum computations (table 3). These findings represent, to the best of our knowledge, the first demonstration of model equivalency for these two very different but complementary approaches, and thereby provide confidence in interpreting additional results from the continuum model.

Figure 4.

Volume change (a,c), relative to κ_tf (cf. figure 2), for the finite-element (open squares) and continuum (solid line) models for two cases of swelling (g1 and g2, that represent ‘good’ situations associated with FCD_Med2 = −50 and −70 mEq l⁻¹, respectively), which generated two different residual stress-related opening angles . Note the good agreement between the two different modelling approaches. (b,d) Associated transmural distributions of circumferential (solid line) and axial (dashed line) Cauchy wall stress calculated using the continuum model for an axial stretch of (top) and (bottom) and an internal pressure of 93.3 mmHg. Also shown is the mean circumferential stress obtained via the classical Laplace relation (dotted-dashed line).

Figure 4b,d also shows predicted transmural distributions of circumferential and axial Cauchy stress obtained with the continuum model. Albeit not shown, the radial stress varied continuously through the wall (as required by traction continuity at the medial–adventitial interface) and was compressive, from negative the luminal pressure (P = 93 mmHg) at the inner wall to zero at the outer wall, which satisfied radial traction boundary conditions. Note, also, the predicted jumps in circumferential and axial stress at the medial–adventitial interface as expected (cf. [12]), and that the mean circumferential stress (obtained via the Laplace relation, Pa/h) agreed well with the computed distributions. Consistent with findings by Bellini et al. [26], which did not include effects of swelling, both the circumferential and axial stresses were nearly uniform within each layer, with mean values of both stresses being higher in the media than in the adventitia at mean arterial pressure and the in vivo axial stretch. This result is consistent with the thought that the media bears most of the load under normal conditions, with the adventitia serving primarily as a protective sheath that is progressively engaged as the blood pressure increases acutely above normal levels. Of particular note, however, the increased medial swelling (good case g2 relative to g1) tended to give rise to a larger opening angle consistent with findings in [11] as well as slightly lower values of the stress in the media and slightly higher values in the adventitia. This latter finding suggests a ‘good’ consequence of normal swelling, which could help homogenize the transmural distribution of stress with the adventitia protecting the media to some extent.

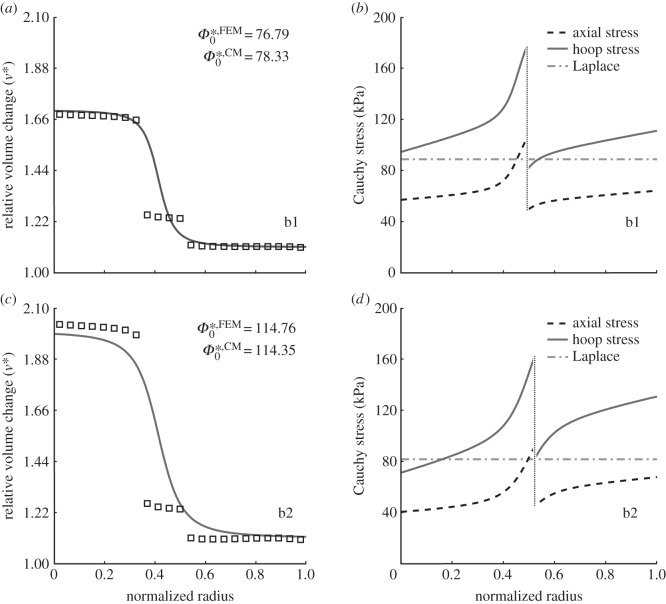
Figures 5 and 6 show two cases (b1 and b2) that we submit could be potentially bad consequences of intralamellar swelling. In particular, figure 5 shows that increased medial swelling could increase the opening angle further, but also increase the transmural gradient in stress in both the media and adventitia while decreasing the mean stress in the former and increasing it in the latter. This potentially remarkable change in the stress field could alter the mechanobiological responses by both the medial smooth muscle cells and adventitial fibroblasts. Indeed, this effect is even clearer in figure 6, which compares transmural circumferential stresses in the unswollen homeostatic condition with all four swelling cases (g1, g2, b1, b2), for two values of pressure: P = 120 mmHg (figure 6a) and P = 220 mmHg (figure 6b). The higher acute pressure mimics exercise conditions independent of any remodelling that would occur if the increased pressure were sustained. The effect of swelling was exacerbated by the higher pressure, suggesting that in the extreme cases it could increase stress in the adventitial layer by approximately 100 kPa.

Figure 5.

Volume change (a,c), relative to κ_tf (cf. figure 1), for the finite-element (open squares) and continuum (solid line) models for two cases of swelling (b1 and b2, that represent ‘bad’ situations associated with FCD_Med2 = −120 and −160 mEq l⁻¹, respectively), which generated two different residual stress-related opening angles . (b,d) Associated transmural distributions of circumferential (solid line) and axial (dashed line) Cauchy wall stress calculated using the continuum model for an axial stretch of (top) and (bottom) and an internal pressure of 93.3 mmHg. Also shown is the mean circumferential stress obtained via the classical Laplace relation (dotted-dashed line).

Figure 6.

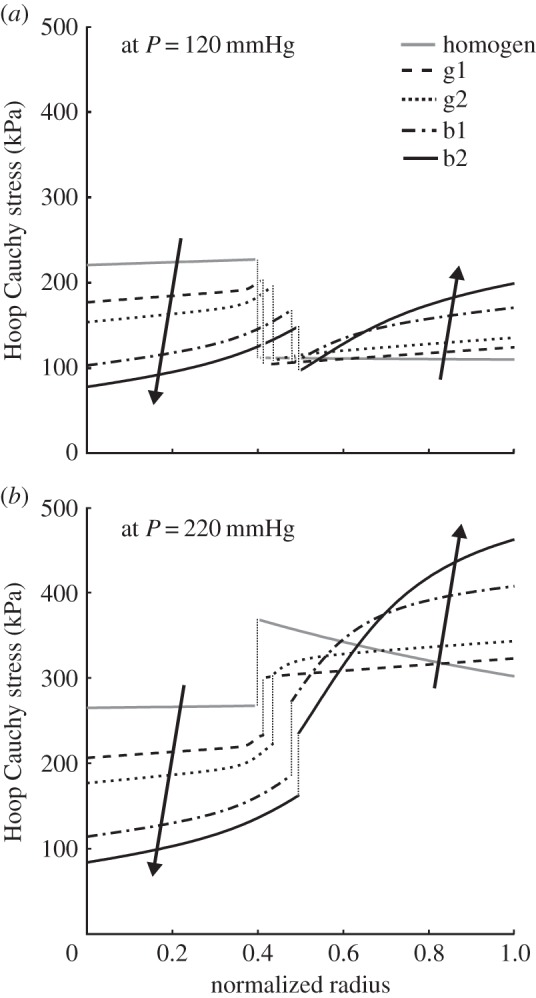
Representative transmural distributions of circumferential Cauchy stress for (a) systolic and (b) acutely elevated blood pressure, each evaluated for five different degrees of swelling: good g1 (dashed line) and g2 (dotted line) distributions (see figure 4), bad b1 (dotted-dashed line) and b2 (solid black line) distributions (figure 5), and a non-swollen homogeneous (grey solid line) distribution, i.e. J = 1 at every point of the wall. The effect of the intramural swelling was similar in some ways to an increase in luminal pressure: it increased the tensile stress in the adventitia while decreasing it in the medial layer. The same trend can be seen for the mean arterial pressure (MAP) by comparing circumferential values of the Cauchy stress in figures 4 and 5.

Figure 7 collects together results associated with those of figures 4 and 5, but shows the transmural distribution of radial stretch (λ_r = detF/λ_θλ_z) evaluated for the whole mixture for the different cases of swelling as well as for the case of no swelling (solid grey line) in the homeostatic condition (MAP and ). Recall that, with the unswollen ‘homeostatic’ configuration serving as the reference, F^h = I and the radial stretch is equal to 1 in this case. Hence, increased values of radial stretch owing to swelling can be considered as fold-changes. Given these results, one sees that the intralamellar units would necessarily experience radial expansion (i.e. λ_r > 1, relative to the unswollen in vivo state), not compression, owing to swelling of the media. Under normal conditions, such intralamellar separation could put radially oriented elastic fibres/microfibrils in tension, which would be advantageous for mechanosensing and thus good (cf. results in figure 4). Extreme swelling, however, could possibly overextend such fibres/fibrils and result in damage, which would be bad from the perspective of mechanosensing despite the possible existence of favourable macroscopic circumferential and axial stresses within the media (cf. results in figure 5). This is, to the best of our knowledge, the first recognition of these potentially competing effects between the mechanosensing and mechanics within the arterial wall. Indeed, overextending all such radial connections could result in a loss of contact with a medial smooth muscle cell and thereby anoikis (i.e. a form of apoptosis owing to lost connections within the matrix; [17]). Although we do not know the extension at which microfibrils would sever, large elastic fibres appear to fail at extensions on the order of 1.8–2.2 [31], which is well within the range predicted here.

Figure 7.

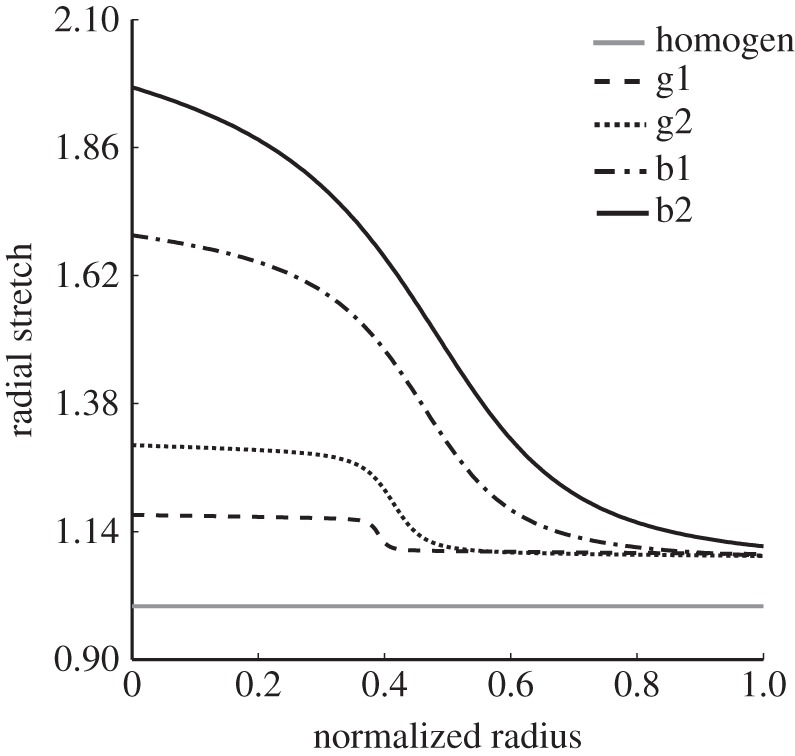
Transmural distribution of radial stretch for the different cases of swelling considered in figures 4 and 5: g1, dashed line; g2, dotted line; b1, dotted-dashed line; b2, solid black line and the case of no swelling (solid grey line). Because the homeostatic configuration is taken as a reference, the radial stretches represented here are ‘real’ not ‘relative’ and the numerical values can be interpreted as fold-changes owing to swelling.

Finally, figure 8 shows a finite-element solution for a highly localized pooling of GAGs/PGs that caused a localized swelling within a simple planar model (intramural tangent plane) of the arterial wall (cf. [18]). As it can be seen, a local rather than diffuse accumulation of GAGs/PGs could result in a significant stress concentration near the leading edge of the pool. Indeed, the predicted local tensile radial stresses (approx. 140 kPa tensile, with associated relative radial stretches > 1) are of sufficient magnitude to cause a local tearing of tissue and thus delamination (cf. [32]). This potentially ugly consequence of the GAGs/PGs re-emphasized that which was presented in [18] based on material properties for the human aorta. The predicted stress concentration was higher for the baseline murine model, however, which reminds us that the wall properties and aspect ratio of the pool can also play significant roles. Moreover, noting that the far-field baseline wall stresses (approx. 100 kPa circumferentially and axially) at mean arterial pressure and the in vivo axial stretch were obtained by applying appropriate displacement boundary conditions at the outer edges of the rectangular domain, the more compliant murine artery required greater prescribed displacements than did the stiffer human artery (i.e. the prescribed displacements were 45% and 30% greater herein in the circumferential and axial directions, respectively). This difference proved to be a challenge for the meshing, with nearly twice as many elements (150 000 in this model versus 75 000 in [18]) needed to achieve convergence.

Figure 8.

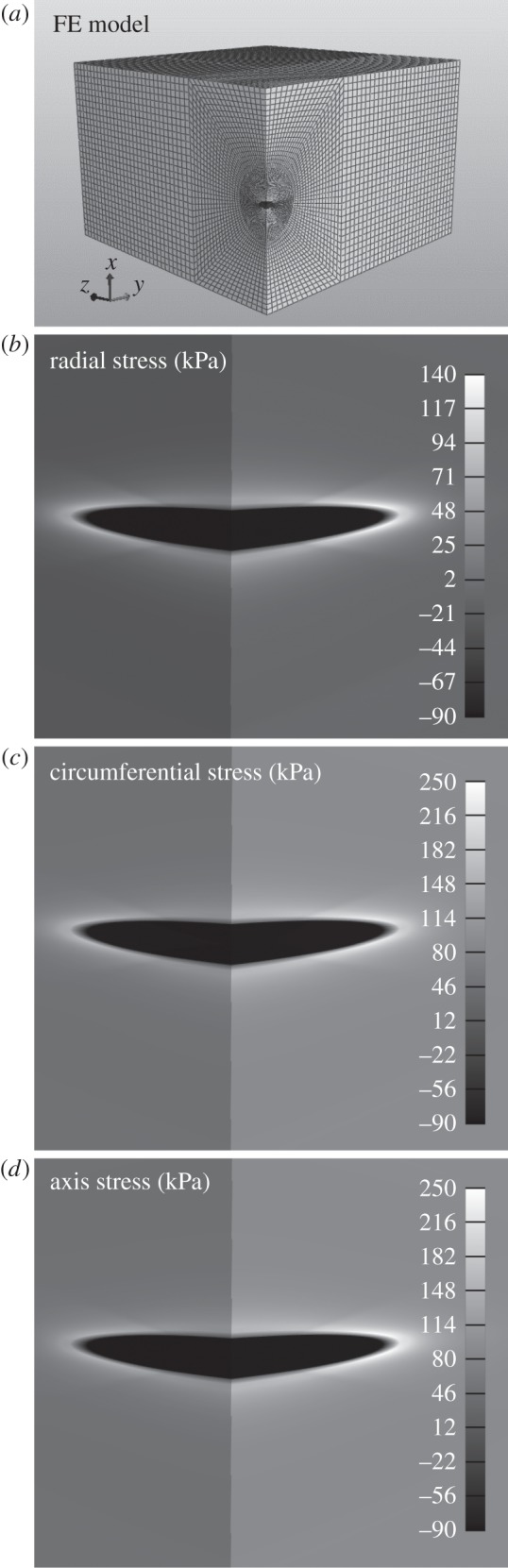
(a) Final quarter-symmetric finite-element model (approx. 150 000 hexahedral elements) of the overall 250 × 250 × 84 μm rectangular portion of the murine carotid wall, including a single centrally located GAG/PG inclusion (volume of 574.7 μm³). The value of the fixed charge density equals −160 mEq l⁻¹ for the GAG inclusion and −50 mEq l⁻¹ for the non-affected aortic wall. The far-field stresses correspond to those developed in the wall owing to the homeostatic blood pressure evaluated in a unilayer cylindrical simulation (radial = −6 kPa, circumferential and axial = 100 kPa) and induced here via appropriate displacement boundary conditions. (b­–d) Shown is a greyscale representation of multi-axial stresses in and near the GAG/PG inclusion. Note, in particular, the transition of radial stress from compressive to highly tensile near the leading edge of the inclusion.

6. Discussion

It has long been known that vascular smooth muscle cells are highly mechanosensitive; they change their gene expression in response to changes in mechanical loading [33–35]. Indeed, smooth muscle cells express multiple integrins (e.g. α₁β₁, α₅β₁ and α_vβ₃; [36]), which are known to be important mechanosensors [37,38]. Yet, similar to most studies on other vascular cells [39,40], data on smooth muscle mechanobiology have come primarily from studies of cells plated on two-dimensional substrates, not those seeded within three-dimensional matrices, and, consequently, there has yet to be a careful study of potential mechanosensing via the radial elastic fibres/microfibrils that connect smooth muscle cells to the delimiting elastic laminae in central arteries (cf. [2,21,41]). Indeed, even the precise molecular connection between smooth muscle cells and elastic fibres has yet to be agreed upon. Some have postulated the existence of unique elastin–laminin receptors [42,43], whereas others have focused on both direct and indirect connections via elastin-associated glycoproteins such as the fibulins or fibrillins (e.g. via α₅β₁ and α_vβ₃; [44,45]). Regardless, it is intuitive that mechanical connections between smooth muscle cells and the elastic laminae may affect both passive and active mechanics of the wall [46] and it is now clear that the presence of functional elastic fibres exerts a strong direct influence on smooth muscle phenotype [46]. Hence, loss of such connections should be expected to result in phenotypic modulation [47] or, in the extreme cases, apoptosis via anoikis [17]. It is these expectations that motivated the present work.

We used both a mixture-based finite-element model [27] to examine gross mechanical consequences of transmural differences in GAG-associated FCD in the arterial wall and a semi-analytical continuum model [29] to examine phenomenologically the biomechanical consequences of the resulting transmural differences in intralamellar swelling. Consistent with general findings on the equivalence of short-term soft tissue responses modelled using a biphasic mixture theory and an incompressible finite elasticity theory [48], we also found that predicted gross mechanical metrics were very similar using these two approaches (table 3 and figure 4). The importance of this cross-validation is that one can exploit a mixture theory to examine physico-chemical mechanisms by which GAGs influence arterial mechanics, but because of the continuing lack of detailed information on regional and longitudinal changes in the FCD in normalcy, ageing and disease, one can also use a mechanically equivalent continuum model to quantify structural and biological implications of histologically observed differences in regional swelling. This comparison also validated, for the first time, use of the in vivo configuration as a reference given constituent-specific deposition stretches and material properties. We submit that both are important findings.

We also compared parametrically two possible classes of transmural distributions of FCD and arterial swelling (uniform versus sigmoidal). Consistent with prior findings, however, we focused on the preferential presence of GAGs within the arterial media [9,11]. As revealed by figure 4, modelling the effects of higher concentrations of GAGs in the media was essential to capture empirically observed increases in the residual stress-related opening angle (cf. [11]). Of course, although carotid arteries dissect [49], it is the thoracic aorta that is most vulnerable [50]. Hence, although the present results should hold qualitatively for any elastic artery, our use of data from the mouse carotid was dictated primarily by the availability of relevant data. There is a pressing need, therefore, to perform similar studies based directly on data for the thoracic aorta, which has, for example, a higher basal FCD than the abdominal aorta [30] and a higher propensity to dissect spontaneously [8].

It has long been known from the cartilage literature that local GAG-induced swelling pressures can cause nearby connective tissue fibres to be in tension despite an overall compressive state of stress [16], but we are the first to suggest the potential role of this mixture phenomenon in smooth muscle mechanosensing within the arterial wall (cf. figure 6). As revealed by the exquisite transmission electron micrographs reported by Davis [21], the elastic laminae of large arteries connect to the resident smooth muscle cells via elastic fibre/microfibrillar extensions that consist primarily of elastin-associated fibrillin-1. Although mechanobiological roles of these connections have not been elucidated, we submit that they could serve an important role in mechanosensing, particularly because they tend to colocalize with dense plaques (i.e. focal adhesions) and co-align with associated intracellular contractile proteins [21]. Indeed, Bunton et al. [47] hypothesized that ‘loss of cell attachments signals a nonproductive program to synthesize and remodel an elastic matrix’ in Marfan syndrome, which results from mutations in the gene encoding fibrillin-1. This concept of adverse effects of compromised elastic fibre–smooth muscle connections is also consistent with the demonstrated role of elastin in influencing smooth muscle phenotype. Karnik et al. [46] showed using an elastin haploinsufficient mouse that ‘elastin stabilizes the arterial structure by inducing a quiescent contractile state in vascular smooth muscles’. That is, interactions between elastic fibres and smooth muscle cells are essential determinants of smooth muscle phenotype, thus it follows that altered interactions can result in phenotypic modulation and thus altered intracellular signalling and resulting gene products. Noting that O'Connell et al. [41] reported that 29% of all medial elastin is found within the intralamellar spaces, either connecting laminae to the cells or connecting laminae to laminae, suggests that we must understand better both the structural and the instructional roles of non-laminar elastic fibres. The present simulations suggest, for the first time, that these future studies should include the related effects of the GAGs/PGs in stretching these fibres. That is, as should be the case, theory/computation should guide experiments.

We are not the first to suggest, however, that GAGs/PGs might affect the mechanobiology of arterial smooth muscle cells. Evanko et al. [51] noted that aggregates of hyaluronan and versican tend to localize near cells but away from focal adhesions, and suggested that ‘by altering the tension of the cell-matrix interaction, this ‘replusive’ but relatively malleable quality of the HA–PG (hyaluronan–proteoglycan) matrix could potentially perturb matrix-induced signalling that occurs via integrin–fibronectin or integrin–collagen interactions’. Our computational results are the first to support such speculations, however. Although we agree with these prior suggestions, we submit further that these aggregates could similarly perturb signalling that is mediated directly via the smooth muscle cell–elastic fibre connections, not just integrins targeting fibronectin or collagen. Although each of these effects could be mediated solely via the mechanical effects of aggregated hyaluronan and versican (i.e. Donnan swelling), it should also be noted that excessive GAGs/PGs may also interfere sterically with normal cellular interactions with matrix via focal adhesions [1]. Hence, there is a need to investigate broadly how GAG/PG aggregates affect diverse aspects of mechanosensing. Indeed, notwithstanding our current focus, other mechano- and chemo-mediated mechanisms certainly contribute further to the integrity of elastic fibre–smooth muscle interactions. As noted by Sherratt [52], ‘mechanical fatigue has also been postulated as a mechanism of age-related elastic fibre failure, with indirect evidence suggesting that the microfibril/elastin interface may be the main weak point in the composite elastic fibre’. Increased proteolysis via elastases (cf. [53]) would also be expected to affect first the thinner elastic fibres and thus the microfibrillar connections (cf. [47]). Indeed, blocking lysyl oxidase in rats revealed that the radial elastic fibres were lost prior to any notable damage to the thicker elastic fibres that constitute the elastic laminae [20]. There are, therefore, multiple means by which smooth muscle cells might lose their mechanosensing capability via compromised microfibrillar connections. Clearly, there is a need to consider roles of radial stresses/strains, not just the traditionally considered correlations between altered circumferential and axial stresses and arterial growth and remodelling (cf. [54]).

Finally, we would be remiss not to mention the potential importance of the present findings to Marfan syndrome and related diseases of the thoracic aorta. This connective tissue disorder results from mutations in the gene encoding fibrillin-1, the primary glycoprotein constituting the elastin-associated microfibrils [55]. Like most extracellular matrix constituents, fibrillin-1 plays multiple roles. It appears to confer long-term stability to elastic fibres, that is, to decrease elastic fibre susceptibility to both mechanical damage (fatigue) and chemical insult (proteolysis); it participates in sequestering latent TGF-β, which thereby affects many cell behaviours, including control of matrix turnover; and it appears to be the main intralamellar connection between smooth muscle cells and the elastic laminae [21], which implies a role in mechanosensing. Although loss of all three functions of microfibrils probably contributes to aortic dilatation and dissection in Marfan syndrome, we recently suggested that associated increases in TGF-β activity may promote the characteristic increased accumulation of GAGs/PGs within the ascending aorta (cf. [56]), because TGF-β is a known promoter of the synthesis of GAGs/PGs by smooth muscle cells [3,57]. We suggested further that localized pooling of GAGs/PGs could result in stress concentrations that initiate delaminations of the media, which in turn could initiate dissections. This hypothesis was supported by simulations reported in [18]. In this paper, we extended our prior findings by suggesting that diffuse accumulations of GAGs/PGs may also perturb or eliminate smooth muscle mechanosensing via microfibrils, whether they are compromised by genetic mutations, fatigue, proteolysis or other factors, and in the extreme cases lead to anoikis. This latter possibility is consistent with the suggestion of Allaire et al. [58] that ‘enhanced TGF-β signalling in MFS (Marfan syndrome) is thought to increase VSMC (vascular smooth muscle cell) apoptosis and impair aortic healing because of hyaluronan up-regulation’.

Regarding the control of GAG/PG production within the arterial wall, cyclic mechanical stress, angiotensin-II and TGF-β all promote the synthesis of GAGs/PGs by arterial smooth muscle cells [1,3,59]. Blocking effects of Ang-II via the angiotensin-II type 1 receptor (e.g. via losartan) or blocking TGF-β via neutralizing antibodies could thus decrease the synthesis of GAGs/PGs and, notably, attenuate the incidence of GAG-related dissection. Caution must be exercised in drug treatments, however, because TGF-β is also involved in the maintenance of adventitial collagen, which serves as a protective sheath for the arterial wall [60]. Nevertheless, whereas normal mechanical loading of radial elastic fibres could promote matrix homeostasis within the media, loss of such loading and thus loss of mechanosensing could result in marked changes in matrix, including the early upregulation of hyaluronan and versican as is typical in wound healing [61]. That is, without proper mechanosensing, the resident cells will not be able to maintain, remodel or repair the extracellular matrix that is fundamental to the overall structural integrity of the wall [62]. The complexity of such interactions among cell membrane bound receptors and their signalling pathways is mirrored by the complexity of extracellular matrix interactions [63]. For example, versican not only interacts with hyaluronan, but it also interacts with the fibulins and fibrillins that associate with elastin [55], and it has been suggested that increased versican could compromise effective elastic fibre assembly [3]. Clearly, the potential consequences of altered GAGs/PGs can go well beyond just the mechanics, although ultimately it is the mechanics that determines the fate of an artery (e.g. dissection or rupture).

In conclusion, as with so many things in life, too much of a good thing can be a bad thing. For example, Galis & Khatri [64] noted that, at normal concentrations, active matrix metalloproteinases are essential for tissue homeostasis, yet when these concentrations deviate from normal the consequences can be dire. We similarly submit that normal distributions and concentrations of GAGs/PGs within the arterial wall are essential for proper mechanical and biological functions, including homeostasis, yet, when increased above normal levels, these same GAGs/PGs may compromise or eliminate particular aspects of normal mechanosensing, or, if pooled, they may initiate potentially lethal dissections. There is, therefore, a pressing need to increase our understanding of GAGs/PGs and their potentially good, bad and ugly roles in arterial health and disease, which will require increased experimental information and advances in computational modelling.

Funding statement

This work was supported, in part, by grants from the NIH (R01 HL086418, R01 HL105297 and U01 HL116323) and the National Marfan Foundation.