Extinction risk and eco-evolutionary dynamics in a variable environment with increasing frequency of extreme events

Abstract

One of the most dramatic consequences of climate change will be the intensification and increased frequency of extreme events. I used numerical simulations to understand and predict the consequences of directional trend (i.e. mean state) and increased variability of a climate variable (e.g. temperature), increased probability of occurrence of point extreme events (e.g. floods), selection pressure and effect size of mutations on a quantitative trait determining individual fitness, as well as the their effects on the population and genetic dynamics of a population of moderate size. The interaction among climate trend, variability and probability of point extremes had a minor effect on risk of extinction, time to extinction and distribution of the trait after accounting for their independent effects. The survival chances of a population strongly and linearly decreased with increasing strength of selection, as well as with increasing climate trend and variability. Mutation amplitude had no effects on extinction risk, time to extinction or genetic adaptation to the new climate. Climate trend and strength of selection largely determined the shift of the mean phenotype in the population. The extinction or persistence of the populations in an ‘extinction window’ of 10 years was well predicted by a simple model including mean population size and mean genetic variance over a 10-year time frame preceding the ‘extinction window’, although genetic variance had a smaller role than population size in predicting contemporary risk of extinction.

1. Introduction

Evidence of changes of climate, including ocean warming, altered wind and precipitation patterns, and increase of global average air temperature is now rapidly building up [1,2]. Most of the empirical and theoretical research on the ecological effects of a changing climate has focused on directional climate changes (trends of the mean of climate variables), which are often the most pertinent characteristics of the environment [3,4]. However, assuming a given probability distribution of occurrence for any climate variable, changes in the mean and variance of the distribution will inevitably lead to even more frequent and more intense extreme events, such as high temperatures, storms, droughts, floods, cold spells and heat waves [5] (figure 1). This pattern of increased mean and variance of climate variables is consistent with recent observations of intensification and increased frequency of extreme events [1,6–8].

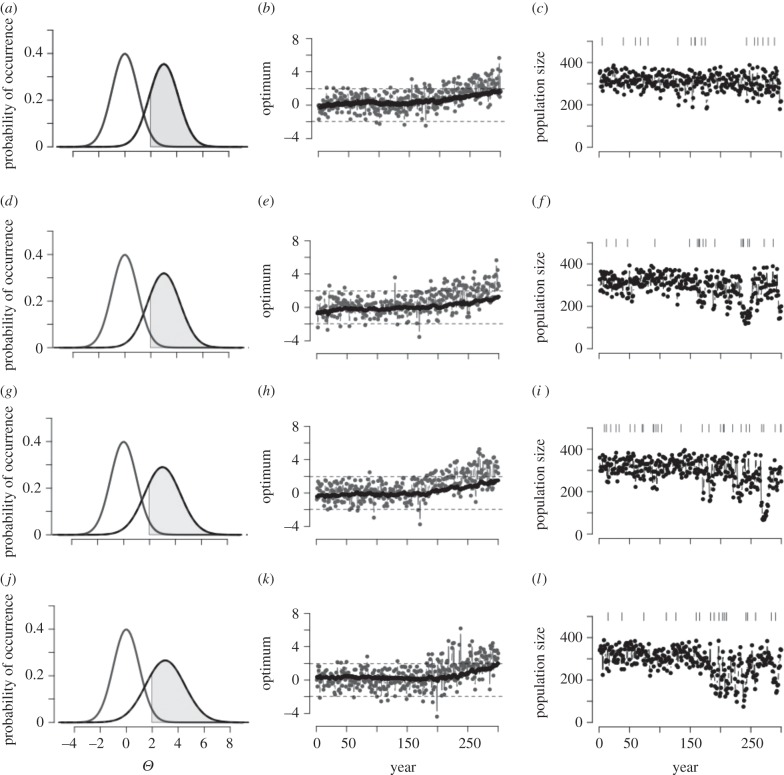
Figure 1.

Increase of the probability of extremes and consequences for evolution of a quantitative trait and population size over time. Increase in variability for 25 years after climate change β_σ,Θ = 0.5 (a–c), 1.0 (d–f), 1.5 (g–i), 2.0 (j–l) × 10⁻². For all rows, β_μ,Θ = 2 × 10⁻². (a,d,g,j) Shift of the normal distribution of a climate variable (e.g. mean or maximum summer temperature) from year 1 (start of simulation time, grey line) to year 300 (end of simulation time, black line), with a directional increase of the mean of the distribution β_μ,Θ and increase in the variability of the optimum from year 150 to year 175 (β_σ,Θ). The grey region defines the events in the distribution of the climate variable at the end of simulation time that would be considered extreme events at t = 1 (e.g. in the right 2.5% of the distribution). (b,h,h,k) Example of change of the optimum phenotype Θ(t) through simulation time (grey) and change of the mean phenotype (black). The dashed lines define the 95% central portion of the normal distribution of the climate variable at t = 1. (c,f,i,l) Population size though time with variation of the optimum phenotype as in (b,h,h,k). Vertical segments indicate point extreme events with p(E_a) = 7.5 × 10⁻².

The distinction between extreme weather events and extreme climate events—although often not clear nor consistent in the literature [1,6]—may be defined by the timescale of the event, with extreme weather events typically associated with changing weather patterns (from less than a day to a few weeks, e.g. heavy rains, unusually high or low temperatures) and extreme climate events occurring on longer timescales (from weeks to months, e.g. the number or fraction of cold/warm days/nights above or below a certain percentile with respect to a reference period). Extreme climate events may also be driven by the accumulation of several weather events (e.g. below-average rainy days over a season leading to a drought [9]).

From another point of view, extreme events may be defined in terms of extreme values of a continuous variable on the basis of the available climate record [9] (e.g. temperature, precipitation levels) or in the form of a discrete (point) perturbation, such as a hurricane or a heavy storm. This latter category also includes environmental extremes such as unusually big fires, aseasonal floods or rain-on-snow events [10]. I will use the terms climate extremes (i.e. extreme values of a continuous environmental variable, such as temperature) and point extremes to indicate the different types of extremes throughout this work.

Climate and point extremes may have substantial ecological and genetic effects, such as dramatic crashes or extinction of populations or species [11], genetic bottlenecks [12], substantial changes in age- and size-structure [13], changes in community structure and ecosystem functions [5,14], shifts in the phenology of plant and animal species [15] and species invasion [16]. However, there are often clear differences in the potential evolutionary consequences of climate and point extremes. For instance, while the occurrence of climate extremes may lead to the evolution of adaptive responses, at the level of single population point extremes generally have dramatic, but largely non-selective effects (i.e. all individuals share the same mortality risk). Thus, point extremes reduce genetic diversity by causing unselective population bottlenecks, while climate extremes reduce genetic diversity (often) through natural selection. Although both events have similar ecological consequences, their evolutionary consequences are radically different, since in the former case the collapse in population size reduces the evolutionary potential of the population, while in the latter case the reduction in population size may be a component of the evolutionary rescue process [17].

A motivating example is provided by freshwater fish populations, which may experience higher water temperatures during summers and an increased risk of severe flood events, including flash floods and debris flows, in other seasons [1]. Variability exists within fish populations in terms of optimal and critical temperatures for life histories such as growth, survival and reproduction [18], and thus traits related to thermal means and extremes can be selected for [19]. On the contrary, severe floods—especially when swift, aseasonal and with longer recurrence interval than species' generation time [20]—are likely to cause high and largely non-selective mortalities, for example by scouring eggs or killing fish by impact with rocks and boulders [21]. These non-selective population and (potential) genetic bottlenecks [22] caused by a point extreme are likely to contribute to the erosion of adaptive potential of populations (i.e. decrease additive genetic variance [23]). The affected population may poorly respond to the future water temperature extremes, drop in size or recover slower from the effects of the climate extreme, and be more vulnerable to the next point extreme event (e.g. extinction vortex [24]).

The consequences of changes of the mean state of climate and environmental variable on risk of extinction, adaptation and demographic dynamics of populations and species are reasonably well understood over various timescales [25–27]. Theoretical work that considered a single quantitative trait affecting fitness has shown that when the rate of directional change surpasses a critical threshold, mean fitness of individuals in the population is reduced below a level at which population size starts to decline. In the absence of immigration, population extinction is the most likely outcome [23,28–31]. Bürger & Lynch [29] and Huey & Kingsolver [32] found that for slow rates of environmental change, an intermediate strength of selection (i.e. width of the Gaussian fitness function) on a single quantitative trait determining fitness increased mean time to extinction, due to a trade-off between substitution load (the ‘cost of selection’ [33]), which increases with strength of selection, and lag load (or evolutionary load, i.e. the fitness cost of a population whose mean phenotype is at a given distance from the optimum [34]), which decreases with strength of selection.

On the contrary, Björklund et al. [35] found that in a variable environment extinction risk increased with the strength of selection, while Bürger & Lynch [29] found that mean extinction time alone did not provide sufficient information to describe the risk of population extinction, because the coefficient of variation of extinction time was strongly dependent on genetic and ecological parameters. However, it is unclear whether the theoretical and empirical insights described above would remain valid when a climate trend is accompanied by an increased frequency of climate and point extremes [36].

The general scope of this paper is to provide a picture of the eco-evolutionary dynamics involved in the extinction or persistence of populations when a climate trend is accompanied by an increased frequency of climate and point extremes, and how the results differ with respect to what has been found in the case of a climate trend with moderate environmental or climate variability. In particular, I investigated how (i) climate trend (e.g. increased mean of the probability distribution of occurrence of a continuous climate variable, such as mean of summer temperatures over a 10-year period), (ii) climate variability, (iii) increased probability of occurrence of point extremes (e.g. spring floods) and (iv) selective pressure, genetic variability and amplitude of mutation interact to determine: (a) risk of population extinction; (b) time to extinction; (c) the distribution of a single quantitative trait that determines relative fitness; and (d) changes in additive genetic variance for the quantitative trait.

Specific objectives were to test whether: (1) after accounting for their independent effects, the interaction between climate trend, variability and probability of occurrence of point extremes contributed to determine the ecological and genetic fate of the population; (2) intermediate selection strength maximized time to extinction and/or minimized risk of extinction with a slow rate of climate change; (3) mean time to extinction was related to risk of extinction; (4) greater mutation amplitude reduced the risk of population extinction by increasing genetic variability; and (5) a model including additive population size, selection strength, probability of point extremes and genetic variance for the quantitative trait under selection was able to predict contemporary risk of extinction.

Results show that in highly stochastic environments—after accounting for their independent effects—the interaction among climate trend, variability and probability of occurrence of point extremes has a minor effect on risk of extinction, time to extinction and distribution of the trait. Risk of extinction linearly decreases with selection strength, while the climate trend mostly drives the shift of the phenotype in response to the changing environment. Risk of extinction is negatively related to mean time to extinction. Mutation amplitude has no effect on the risk of population extinction. I found that in addition to small population size, lower additive genetic variance for the quantitative trait under selection moderately contributes to increase extinction risk at any point during simulation time, although in the simulations the role of additive genetic variance was partially confounded by its positive correlation with population size.

2. Material and methods

2.1. Overview of the model

I consider a population of monoecious diploid individuals living in a habitat whose population ceiling is K, here intended as the maximum number of individuals that can be supported. I chose K = 500 in order to represent a scenario of a population at risk of extinction with an increased probability of occurrence of extreme events. The population is assumed to be geographically isolated, thus immigration from other populations is not possible.

The population has discrete overlapping generations (i.e. reproduction is discrete in time) and is composed of N(t) individuals, where t is time in years. Each individual is characterized by a single quantitative trait a corresponding to its breeding value for a phenotypic trait z. The habitat is characterized by an optimum phenotype Θ(t) that changes over time as a result of variation in a climate driver, such as rainfall or temperature (i.e. a continuous climate variable), selecting for the phenotypic trait z. The distance between the optimum phenotype Θ(t) and the trait z_i of the individual i defines the maladaptation of the individual i with respect to the optimum phenotype. Point extreme events (e.g. floods and fires) cause non-selective (i.e. all individuals share the same risk) high mortality in the population. As this work is a first exploration of population and genetic dynamics in a highly stochastic environment, I did not include phenotypic plasticity. Model parameters are reported in table 1.

Table 1.

Values of parameters of the model of population dynamics.

parameters	values	description
K	500	population ceiling
λο	2	intensity of the Poisson distribution of offspring per mating pair
tch	150	years since the start of the simulation before climate change
tinc	25	time of increase of variability (variance of the normal distribution of the climate variable) after climate change
nl	20	number of diploid loci
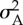	6.25 × 10−3	additive genetic variance per locus at the start of simulation
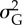	0.2	additive genetic variance of the quantitative trait at the start of simulation
μ	2 × 10−4	mutation rate per locus
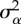	1, 2, 3, 4 × 10−1	variance of the normal distribution of mutation effect (mutation amplitude)
Smax	0.7	maximum survival probability
μE	0	mean environmental effect
	1	variance of the environmental effect
mE	0.3	mortality caused by the point extreme event
s	5, 8, 11, 13 × 10−2	strength of selection
p(Eb)	5 × 10−2	probability of occurrence of point extreme events before climate change
p(Ea)	5, 7.5, 10, 12.5 × 10−2	probability of occurrence of point extreme events after climate change
μΘ,0	0	mean of the normal distribution of the phenotypic optimum from year 1 to tch
σΘ,0	1	standard deviation of the normal distribution of the phenotypic optimum from year 1 to tch
βμ,Θ	1, 2 × 10−2	annual increase (directional trend) of the mean of the normal distribution of the climate variable from year tch to the end of simulation
βσ,Θ	0.5, 1.0, 1.5, 2.0 × 10−2	annual increase of the standard deviation of the normal distribution of the climate variable from year tch to tch + tinc

2.2. Temporal change of the optimum phenotype

A fluctuating environment with a directional component is the most biologically relevant way of how we can expect the climate to change [37]. A fluctuating environment with a directional component can be modelled via an optimum phenotype Θ(t) determined by some measures of a continuous climate variable (e.g. mean summer temperature) that moves at a constant rate β_μΘ over time, fluctuating randomly about its expected value μ_Θ(t) (figure 1). We can consider Θ(t) as either the optimum phenotype or a stochastic realization of climate, and I will use the two terms (optimum phenotype and climate) interchangeably throughout this work. Θ(t) is randomly drawn at each time-step t from a normal distribution Θ(t) ∼ N(μ_Θ(t),σ_Θ(t))

2.1

where t_ch is the time at which there is a change (ch) in the climate, is an indicator function equal to 1 when • is true and 0 otherwise (figure 1). Therefore, I assume that (i) while the directional climate trend (or the value of the optimum phenotype) increases through time after t_ch years, (ii) the increase in variability starts after t_ch years, but stops after t_ch + t_inc years. This avoids variability building up to unrealistic values through time (figure 1).

Point extreme events E leading to trait-independent high mortalities (i.e. increased mortality caused by the point extreme affects every individual the same way) occur with annual probability p(E_b) when t < t_ch (i.e. b—before climate change) and p(E_a) when t > t_ch (i.e. a—after climate change) (figure 1).

2.3. Quantitative trait and survival

I model the phenotype z of an individual i, z_i, as the sum of its genotypic value a_i and a statistically independent random environmental effect e_i drawn from N(μ_E, )

2.2

where the narrow sense heritability 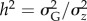indicates how much of the phenotypic variance 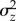present in the population is explained by the additive genetic variance 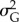, that is the variance of a in the population.

For an individual, the genetic value a_i is determined by n_l freely recombining diploid loci, with additive allelic effects within- and among-loci, that is 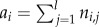, where n_i,j is the sum of the allelic values at locus j. As large n_l (i.e. up to 50 loci) did not substantially change model results, for computational reasons I chose n_l = 20. For simplicity, I did not model either dominance or epistatic variation. Although gene interactions within- and between-loci may be common [38], quantitative genetic variance has been found to be mostly additive [38,39]. In addition, for simplicity and easier interpretation of results, I did not include many other complicating factors such as genotype–environment interaction and linkage among loci. Thus, at the start of each simulation, alleles for each locus are drawn from 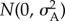, where 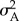is given by 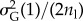(this simulates the continuum-of-alleles model of [40]). The mutation rate per haplotype is n_l μ, where μ is the mutation rate per locus [29]. During the reproduction phase of the simulation, each haplotype is given either one mutation (with a probability of n_l μ) or no mutation. Given a mutation, the locus at which it occurs is chosen randomly. The effect size (or amplitude) of the mutation is a random deviate from 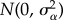and this value is added to the previous value of the allele at that locus. I chose the Gaussian distribution as it is consistent with the analysis of mutational effects [41].

Stabilizing selection is modelled with a Gaussian function [29], with fitness W [42] for an individual with phenotypic trait z_i equal to

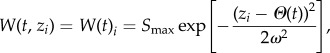2.3

where W(t)_i is equivalent in this model to the annual survival probability of individual i, and S_max is maximum annual survival. This corresponds to a situation where an environmental variable affects survival in a straightforward way. Given the temporal change of Θ described in equation (2.1), when t > t_ch the population experiences a combination of directional and stabilizing selection [29]. The curvature of the fitness function near its optimum increases with decreasing ω², where ω is the width of the fitness function [43]. Therefore, the smaller is ω², the stronger is selection. Stabilizing selection is usually measured by the standardized quadratic selection gradient γ, which is defined as the regression of fitness W on the squared deviation of trait value from the mean [44]. The median γ = −0.1 for stabilizing selection found by Kingsolver et al. [45] corresponds to a value of 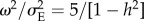, where 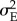is the variance of the environmental component of the phenotype defined in equation (2.2), when stabilizing selection is modelled using a Gaussian fitness function.

As values of the optimum phenotype in the tails of the distribution are far from the population mean value of the trait under selection, an optimum phenotype in the tails of the distribution is likely to cause a large drop in population size and can be considered an extreme climate event (figure 1).

Equation (2.3) can be written as

2.4

where s = 1/2ω². With γ = −0.1, 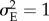, σ_max = 1 and h² = 0.2, the strength of selection s is about 0.08. In order to allow for a faster turnover of the population, I set  S_max = 0.7.

In my model, only the optimum phenotype Θ(t) is assumed to change over time, while strength of selection s is constant. When a trait-independent extreme event occurs, the annual fitness of individual i is , where 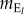is mortality caused by the point extreme event.

2.4. Simulations

As this study focuses on the more immediate effects of climate change, the simulations last 150 years after populations have achieved mutation-selection-balance (see §2.4.1). Offspring at time t become adults and are able to reproduce at time t + 1 (i.e. at age 1). At the start of each simulation, for each individual a value of a and e (equation (2.2)) is randomly drawn from their initial distribution. At each time step, the sequence of operations is mortality of adults, mating and reproduction, mutation, mortality of offspring. A population is considered extinct if at any time during the simulation there are less than two individuals in the population. Mating pairs are randomly drawn from the pool of adults without replacement and all adults reproduce. Each pair produces a number of offspring randomly drawn from a Poisson distribution with intensity λ_ο equal to 2. I chose 2 as the expected number of offspring produced by a pair following a pattern-oriented procedure [46] to allow for a fairly quick rebound of population size after a population crash. I allow for full genetic recombination, which decreases linkage disequilibrium and tends to increase additive genetic variance (i.e. reduces the Bulmer effect [47]). Offspring receive for the same locus one allele from each parent. Given a mutation with probability n_l μ, the locus of the offspring at which it occurs is chosen randomly. Offspring are randomly introduced in the population from the pool produced by all the mating pairs until K is reached, and the remaining offspring die. I also carried out simulations with λ_ο equal to 3 and I report some of the associated results in the electronic supplementary material.

2.4.1. Characterization of simulations

I reduced parameter space by fixing K = 500, μ_Θ,1 = 0, σ_Θ,1 = 1, μ_E = 0, 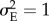, , 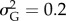p(E_I,b) = 0.05, m_E = 0.3 and t_inc = 25 years. For the other parameters, I chose a range of values that are both realistic for natural populations and instrumental for the main object of the study, e.g. investigate the consequences of extreme events on population dynamics, risk of extinction and evolution of a quantitative trait (table 1 and the electronic supplementary material, box S1).

To initialize the system and achieve mutation-selection-drift balance, I first let the population evolve for t_ch years in an environment in which mean and variance of the distribution of the optimal phenotype Θ are constant. In order to choose t_ch, I assessed with preliminary simulations at which point during the simulation both phenotypic mean and variance remained constant, and the results suggested the use of t_ch = 150 (results not shown).

I started every simulation replicate with 500 individuals. Over simulation time, 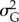and h² evolved depending on selection, mutation, drift and stochastic population dynamics. At the level of single replicate, to characterize the behaviour of the simulated populations I: (a) recorded whether the population was extinct or still persisting at the end of the simulation time (0 for persistence and 1 for extinction), and if extinct I recorded the year of extinction; (b) tracked z(t) and, in particular, the mean value of the phenotype 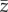at the end of simulation time when the population did not go extinct; (c) recorded population size after mortality of adults N(t); (d) mean fitness of adults 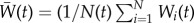; (e) additive genetic variance 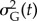(computed as the variance of breeding values a in the population at time t).

For an ensemble of realizations (50 replicates for a fixed set of parameters) I: (a) computed the frequency of population extinction as the number of replicates in which the population went below two individuals during simulation time (i.e. risk of extinction); (b) the time to extinction for the populations that went extinct; the average over the replicates for a fixed set of parameters of (c) 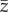and (d) 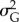at the end of simulation time for the populations that persisted. To avoid transient effects caused by the stochastic variation of optimal phenotypes over very short temporal scales, I average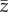d and 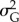in the last 10 years of the simulation.

2.5. Statistical analysis

I used simulation results as pseudo-empirical data and proceeded to analyse them with standard statistical techniques. For all models, I standardized the predictors in order to compare their importance [48], and I treated strength of selection and probability of occurrence of point extremes as continuous predictors. As I used realistic parameter values representing the variability that may be observed in nature, the estimated parameters can be compared in terms of effects on a standardized scale.

One of the hypotheses is that there might be intermediate values of selection strength and/or mutation amplitude that can maximize or minimize probability of extinction, time to extinction or shift of the mean phenotype in the population [29,32]. In the statistical analyses, I considered the 25 600 replicates as independent realizations. I estimated parameters of generalized additive models (GAMs [49]) with smooth (i.e. nonlinear) terms in strength of selection and mutation amplitude using as response variable either (i) extinction (1)/persistence (0), (ii) time to extinction for the populations that went extinct (excluding the few extinctions that occurred before climate change), (iii) mean phenotype 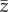and (iv) additive genetic variance 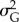at the end of simulation time for the populations that survived. For (i), I used a logit link function with binomial error distribution, while (ii–iv) were analysed on their natural scale. I also estimated parameters of a generalized linear model with a logit link function with binomial error distribution for (i) and of ordinary least-square regression models for (ii–iv). I included in the GLM and OLS models interactions between predictors in order to test whether after accounting for their individual effects, the interaction between climate trend, variability and point extremes was able to explain part of the variation in the response variable. Although I report p-values, I did not rely on statistical significance to determine the relative importance or presence/absence of effects of the various predictors, but rather on effect sizes and sign of the estimated regression parameters [50]. As predictors were standardized, their effects (i.e. regression coefficients) were measured in units of standard deviations of the predictors. In order to provide additional support for the estimates of the relative importance of predictors as provided by the regression coefficients, I also estimated partial R² (for OLSs) and Wald χ² (for GLM) for model predictors (electronic supplementary material, figure S13).

Then, I investigated whether a combination of genetic, demographic and environmental factors measured or estimated over a limited time window (‘sampling window’) can predict whether the population will go extinct in the following years (‘extinction window’). In particular, I fitted a GLM with a logit link function with population extinction (1) or persistence (0) between (t_ext − u) as response variable, where t_ext is either (a) the time at extinction for the replicate that went extinct or (b) a random deviate from a uniform distribution bounded between 175 and 290 (i.e. where more than 95% of the extinctions occurred) for the replicates that persisted up to the end of simulation time. u is a random deviate from a uniform distribution bounded between 10 and 1 years. This way, I am trying to model extinction or persistence not at a specific time, but in an ‘extinction window’ of 10 years.

I used candidate predictors as measured in the 10 years before the ‘extinction window’ mean population size, mean additive genetic variance, strength of selection and probability of occurrence of point extremes. In other words, I wanted to test whether ecological, demographic and genetic variables or quantities measured over a limited time frame (10 years) can predict the extinction or persistence of the population in the years following the end of the ‘sampling window’.

I divided the complete simulation dataset (25 600 replicates) in a calibration dataset (80% of the data) and validation dataset (20%), keeping the same proportion of replicates that went extinct and that persisted observed in the full dataset both in the calibration and validation datasets. I estimated the optimal cut-off given equal weight to sensitivity (probability that the model predicts extinction when the replicate went extinct) and specificity (probability that the model predicts persistence when the replicate persisted up to the end of simulation time). Then, I tested the model by predicting population extinction and persistence on the validation dataset using the computed optimal cut-off.

Further details about model, parameter values, code and simulations—along with additional results—are provided in the electronic supplementary material. Computer code for the analyses and simulation results can be accessed at http://dx.doi.org/10.6084/m9.figshare.706347.

3. Results

At t = 150, i.e. just before the change in climate, the standard deviation of the phenotypic trait z was on average approximately 10% smaller than at t = 1. After climate change, the directional trend and the increase in variability of climate increased the probability of climate extremes. Along with the occurrence of point extremes, this caused recurrent drops in mean fitness in the population and thus in population size (figure 1 and the electronic supplementary material, figure S1).

3.1. Risk of extinction

Risk of extinction increased with strength of selection, climate trend and climate variability (table 2, and figures 2 and 3; electronic supplementary material, figure S2). Strength of selection s was the most important predictor of population extinction, followed by climate variability and climate trend (table 2 and the electronic supplementary material, figure S13). Interaction between strength of selection and climate variability increased risk of population extinction, while interaction between climate (trend and variability) and probability of occurrence of point extremes did not substantially increase the risk of population extinction. A GAM with smooth terms in strength of selection and mutation amplitude did not reveal nonlinear contributions of the two predictors to the risk of extinction (table 2 and the electronic supplementary material, figure S4).

Table 2.

Results of statistical analyses on simulation results used as pseudo-empirical data when response variable is either extinction/persistence (binomial GAM and binomial GLM), time to extinction (Gaussian GAM and ordinary least-square regression, OLS) or mean phenotype 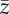or additive genetic variance at the end of simulation time for the populations that persisted (average of last 10 years) (Gaussian GAM and OLS). edf are the estimated degrees of freedom. Symbol (:) denotes interaction between terms. All terms with * are statistically significant at the 0.05 level. I report mean estimate and standard error of the regression coefficients.

	extinction			time to extinction
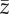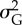	GLM R2 = 0.73	GAM R2 = 0.62	edf	OLS R2 = 0.27	GAM R2 = 0.27	edf	OLS R2 = 0.75	GAM R2 = 0.76	edf	OLS R2 = 0.14	GAM R2 = 0.14	edf
intercept	−1.83(0.04)*	2.16(0.05)*		261.33(1.02)*	245.40(0.37)*		1.416(0.002)*	1.341(0.002)*		1.370(0.001)*	0.151(0.001)*
s	3.09(0.04)*		1.97*	−21.00(0.92)*		1.00*	0.139(0.002)*		1.99*	−0.010(0.001)*		1.00*
p(Ea)	0.41(0.02)*	0.40(0.02)*		−3.21(0.39)*	−3.43(0.31)*		−0.001(0.002)	−0.004(0.002)*		−0.001(0.001)	−0.000(0.001)*
βσ,Θ	1.63(0.03)*	1.78(0.03)*		−10.68(0.84)*	−15.90(0.36)*		−0.005(0.002)*	−0.008(0.002)*		−0.001(0.001)*	−0.001(0.001)*
βμ,Θ	1.10(0.02)*	1.03(0.02)*		3.68(0.81)*	−1.43(0.32)*		0.504(0.002)*	0.471(0.002)*		0.010(0.001)*	0.006(0.001)*
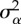	−0.11(0.02)*		1.00*	−0.63(0.30)*		1.90*	0.047(0.002)*		1.76*	0.010(0.002)*		1.00*
s: βσ,Θ	0.31(0.05)*			−4.82(0.76)*			0.012(0.002)*			−0.001(0.001)
s: βμ,Θ	−0.08(0.04)			−4.66(0.71)*			0.060(0.002)*			0.003(0.001)*
βμ,Θ: βσ,Θ	−0.12(0.03)*			−1.61(0.41)*			0.006(0.002)*			0.001(0.001)
βσ,Θ: p(Ea)	−0.03(0.02)			−0.38(0.38)			0.001(0.002)			0.001(0.001)
βμ,Θ: p(Ea)	−0.06(0.02)*			0.03(0.39)			0.004(0.002)*			0.001(0.001)
βμ,Θ: βσ,Θ:p(Ea)	0.11(0.02)			−0.19(0.38)			−0.001(0.002)			−0.001(0.001)

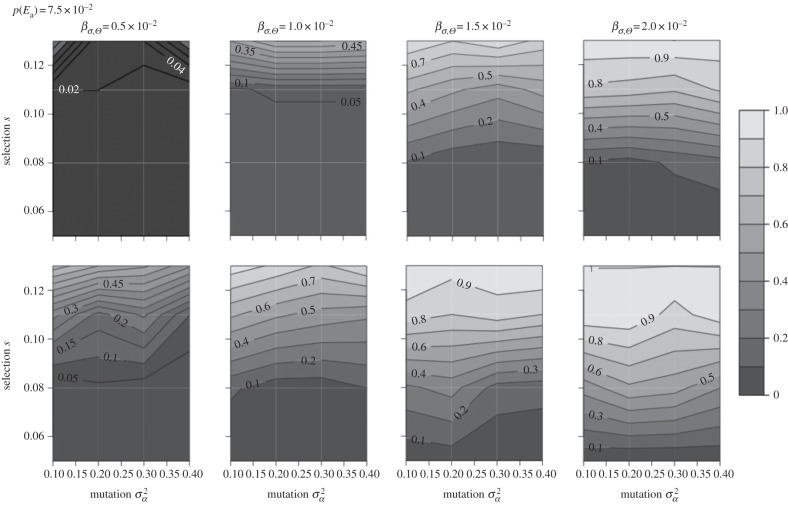
Figure 2.

Lines of equal probability of extinction (number of populations going extinct divided by the number of replicates for a given set of parameter values) in the mutation-selection plane for probability of occurrence of point extremes p(E_a) = 7.5 × 10⁻² and the four scenarios of increasing variability over simulation time of the optimum phenotype Θ (β_σ,Θ = 0.5, 1.0, 1.5, 2.0 × 10⁻²) and two scenarios of increase in trend (top row: β_μ,Θ = 1 × 10⁻²; bottom row: β_μ,Θ = 2 × 10⁻²). Results for the other probabilities of occurrence of point extremes are reported in the electronic supplementary material, figure S2.

Figure 3.

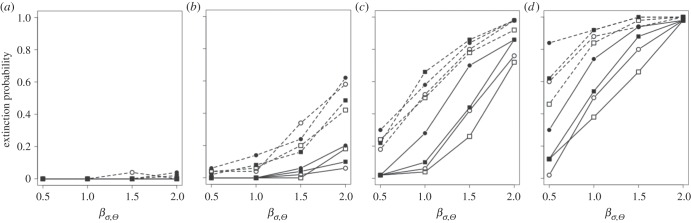
(a–d) Extinction probability (number of populations going extinct divided by the number of replicates for a given set of parameter values) for scenarios of increase variability of the optimum phenotype Θ (β_σ,Θ = 0.5, 1.0, 1.5, 2.0 × 10⁻²) with strength of selection from (a–d) s = 5, 8, 11, 13 × 10⁻². Symbols identify probability of occurrence of point extreme events after climate change p(E_a): open rectangle, p(E_a) = 5 × 10⁻²; open circle, 7.5 × 10⁻²; solid rectangle, 10 × 10⁻²; solid circle, 12.5 × 10⁻². Line type identifies rate of the directional change of the continuous climate variable. Solid line, β_μ,Θ = 1 × 10⁻²; dashed line, β_μ,Θ = 2 × 10⁻².

Across scenarios of climate trend and climate variability, for strength of selection s > 0.05 the proportion of populations going extinct increased with increasing probability of occurrence of point extremes (figure 3). Mutation had very little effect on the risk of population extinction (table 2 and figure 2; electronic supplementary material, figures S2 and S13). Between 0 and 20 mutants alleles were found at the end of simulation time (electronic supplementary material, figure S3), and only rarely mutant alleles were found in more than 10% of the individuals.

Thirty-four per cent of the 25 600 replicates went extinct. Among the replicates that went extinct, 50% of them were not affected by a point extreme in the 5 years before extinction, 35% were affected by one point extreme, and the remaining 15% by two or more point extremes. A χ²-test found significant differences in the frequency of replicates going extinct with 0, 1, or 2 or more point extremes in the 5 years before extinction among replicates with different strength of selection (χ² = 19, d.f. = 6, p = 0.005) (electronic supplementary material, figure S14).

3.2. Time to extinction

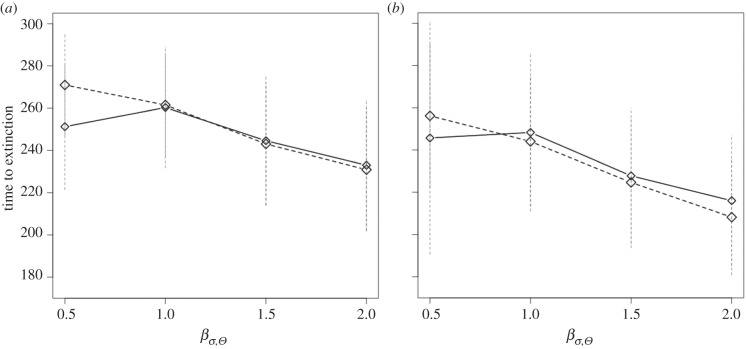
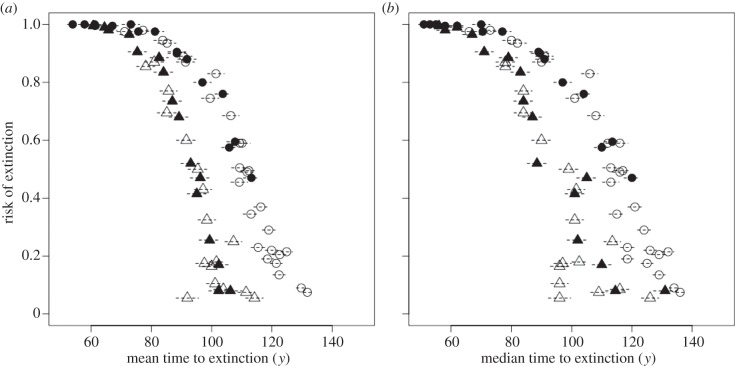
Time to extinction (mean ± s.d. = 237 ± 34 years) decreased with increasing strength of selection, climate variability and climate trend (table 2 and electronic supplementary material, figure S13). Interaction between strength of selection and climate trend, and strength of selection and variability decreased time to extinction, while interaction between climate trend and variability and probability of occurrence of point extremes had very little effect on time to extinction. Probability of occurrence of point extremes had very little effect on time to extinction (table 2 and figure 4; electronic supplementary material, figure S13). Time to extinction was maximized by intermediate mutation amplitude, but the effect size was negligible (table 2 and the electronic supplementary material, figure S5). Given a combination of parameters, there was a clear negative relationship between risk of extinction and mean (or median) time to extinction (figure 5). With equal risk of extinction, stronger climate trend tended to increase time to extinction (figure 5). Standard deviation of the time to extinction was generally high, but with no clear relationship with either risk of extinction or mean time to extinction (figure 5).

Figure 4.

(a,b) Mean time to extinction for populations that went extinct for scenarios of increase in the variability of the optimum phenotype Θ (β_σ,Θ = 0.5, 1.0, 1.5, 2.0 × 10⁻²) with selection strength from (a,b) s = 11 and 13 × 10⁻². I only report results for two selection strengths (with low selection a very small number of extinction was recorded) and a single probability of occurrence of point extreme events after climate change p(E_a) = 12.5 × 10⁻² (time to extinction was only slightly affected by p(E_a)). Line type identifies rate of the directional change of the continuous climate variable. Solid line, β_μ,Θ = 1 × 10⁻²; dashed line, β_μ,Θ = 2 × 10⁻². Vertical dashed segments represent standard deviations.

Figure 5.

Relationship between risk of extinction given a combination of parameter values and (a) mean and (b) median time to extinction (after climate change). Simulations with different mutation amplitudes were pooled together. Only combinations of parameters that caused a risk of extinction more than or equal to 0.05 were included in the figure. Triangles and circles are for climate trend β_μ,Θ = 1 × 10⁻² and 2 × 10⁻², respectively. Open and solid symbols are for s ≤ 0.11 and s = 0.13, respectively. Horizontal dashed segments represent standard deviation of time to extinction divided by 10 for graphical purposes.

3.3. Shift of the mean phenotype

Mean value of phenotype 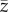at the end of simulation time increased with increasing climate trend and strength of selection (table 2 and figure 6; electronic supplementary material, figure S13). Interactions between predictors did not have any substantial effect on mean value of the phenotype. The smooth term for strength of selection suggested no differences in 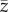for different values of selection strength when s was greater than 0.08 (electronic supplementary material, figure S6). At the end of simulation time, with 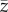had shifted on average 50% (s = 0.05) and 60% (s > 0.05) of the shift of the mean of the distribution of the optimum, although a large variability across replicates was observed. The shift corresponds to approximately 0.75 and 1.5 phenotypic standard deviations of z at t = t_ch for β_μ,Θ = 1 × 10⁻² and 2 × 10⁻², respectively (figure 6).

Figure 6.

(a–d) Average across replicates with the same set of parameter values of the mean value of the phenotype in the population 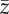for scenarios of increase in the variability of the optimum phenotype Θ (β_σ,Θ = 0.5, 1.0, 1.5, 2.0 × 10⁻²) with strength of selection from (a–d) s = 5, 8, 11, 13 × 10⁻². Replicates with different probability of point extreme events after climate change are pooled together. Line type identifies magnitude of the directional trend of the optimum phenotype. Solid line, β_μ,Θ = 1 × 10⁻²; dashed line, β_μ,Θ = 2 × 10⁻². Vertical dashed segments represent standard deviations. In the electronic supplementary material, figure S7, I report the results for 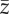at the end of simulation time stratified for probability of occurrence of point extreme events.

3.4. Change in additive genetic variance

Additive genetic variance 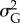at the end of simulation time tended to decrease with increasing strength of selection, probability of occurrence of point extremes and variability of the optimum, while it tended to increase with stronger climate trend and larger mutation amplitude (table 2 and electronic supplementary material, figure S13). Both strength of selection and mutation amplitude only linearly affected 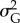(table 2). Interactions between predictions did not have any notable effect on 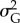. Model predictors were able to describe only a small part of the variation in 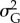(table 2).

3.5. Prediction of population extinction

Population size in the ‘sampling window’ was the most important predictor of extinction in the ‘extinction window’ (table 3). Higher values of additive genetic variance 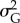had a positive effect on population probability of persistence, although the importance of population size was substantially greater than that of 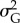. Both stronger selection and higher probability of occurrence of point extremes increased the risk of population extinction, although probability of occurrence of point extremes had a minor role (table 3). Across replicates, mean 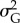and population size in the ‘sampling window’ were positively correlated (Pearson's r = 0.38, p < 0.01).

Table 3.

GLM with logit link function for prediction of extinction (1)/persistence (0) of a population over a 10-year period (‘extinction window’) with predictors mean population size 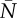and mean additive genetic variance 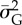measured in the 10 years before the start of the ‘extinction’ window (i.e. in the ‘sampling window’), along with selection strength and probability of point extreme events (full model). All predictors were standardized and I report mean estimate and standard error of the regression coefficients. Reduced model is without mean population size as predictor.

	full, R2 = 0.82	reduced, R2 = 0.56
intercept	−2.58 (0.06)	−1.38 (0.03)
s	1.19 (0.04)	1.84 (0.03)
p(Ea)	0.14 (0.03)	0.24 (0.02)
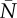	−3.09 (0.05)	—
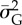	−0.25 (0.03)	−0.97 (0.03)

The model predicted an 8.0% false positive rate (model predicted extinction, but the populations persisted up to the end of simulation time) and a 7.3% false negative rate (model predicted persistence, but the populations went extinct) on the calibration dataset. Predictions on the validation dataset were slightly better than on the calibration dataset, with 7.7% of false positive and 6.1% of false negatives (figure 7 and the electronic supplementary material, figure S10).

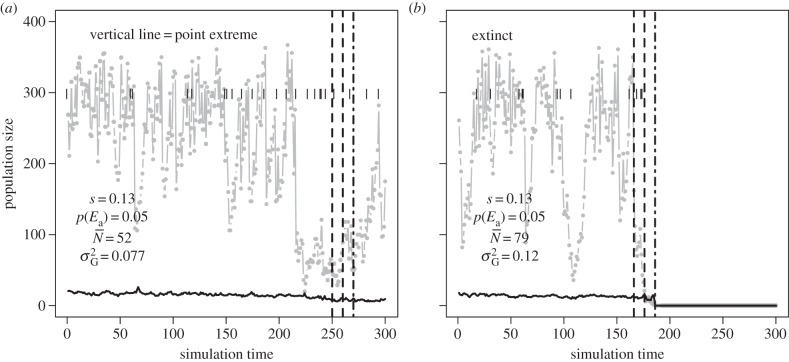
Figure 7.

Examples of wrong (a) and right (b) predictions of the GLM full model that predicts extinction in an ‘extinction window’ based on mean population size and additive genetic variance in a ‘sampling window’, along with strength of selection s and probability of point extreme p(E_a). For (a), risk of extinction as predicted by the GLM model is 0.92 (cut-off for binary assignment = 0.43, see the electronic supplementary material, figures S8 and S9), for (b) is 0.82. Black segments are point extremes, the black line is additive genetic variance multiplied by 100 for graphical purposes, the grey line and points represent population size. Between the two vertical dotted lines is the ‘sampling window’ and between the dotted line and the dotted-dashed line lays the ‘extinction window’. In each panel are reported strength of selection s, probability of occurrence of point extremes (p(E_a)), mean population size (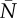) and mean additive genetic variance (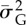) in the ‘sampling window’.

When considering the complete dataset, for 67% of the false negatives a point extreme occurred between the end of the ‘sampling window’ and the extinction of the population. For false positives, the proportion of replicates in which a point extreme occurred between the end of the ‘sampling window’ and the end of the ‘extinction window’ was 57%. Excluding mean population size from the predictors, the model with the remaining predictors had a substantially worse prediction accuracy, with 21% (21%) of false positives and 15% (15%) of false negatives on the calibration (validation) dataset (table 3).

4. Discussion

My results indicate that the conditions facilitating or hindering population extinction and evolution of a quantitative trait in a highly stochastic environment are substantially different from those operating when a climate (or environmental) trend is accompanied by a moderate increase in climate variability.

The interaction among climate trend, variability and probability of point extremes had a minor effect on risk of extinction, time to extinction and distribution of the quantitative trait under selection after accounting for their independent effects. The probability of occurrence of point extremes only slightly increased risk of extinction and decreased time to extinction. Stronger selection and greater variability of the optimum reduced the time to extinction and increased extinction risk. Contrary to what was previously found by Bürger & Lynch [29] and Huey & Kingsolver [32] in case of moderate increase in climate variability, intermediate strength of selection did not increase either time to extinction or risk of extinction. Populations that persisted up to the end of simulation time were able to track the directional component of the optimum, although with a temporal lag. Additive genetic variance for the trait under selection tended to decrease with increasing selection and increased with mutations of larger effect, but its value at the end of simulation time was largely unpredictable. A simple model including four ecological, genetic and demographic measures provided excellent prediction of the immediate risk of population extinction. Across simulations with all combinations of parameters, the effect size of mutations had essentially no role in either the persistence of the populations or the ‘tracking’ of the moving optimum.

4.1. Climate and point extremes

A higher probability of occurrence of point extremes (i) led to greater extinction risk by directly causing a collapse in population size, and (ii) contributed to erode the adaptive potential of populations by causing population and genetic bottlenecks. However, when the climate trend was sufficiently strong and climate extremes were numerous, an increased frequency of occurrence of point extremes only slightly increased the risk of population extinction, and point extremes were more likely to suddenly cause population extinction when selection for the quantitative trait was weaker. Results of the statistical analyses on simulation results do not support the hypothesis of a substantial contribution of the interaction between climate trend and variability and occurrence of point extremes on demographic and genetic dynamics after accounting for their individual effects.

Previous work found that populations that would be able to evolve and cope with a steadily changing environment might go rapidly extinct if random fluctuations of substantial size occur [29]. I found that in a highly stochastic environment, the importance of climate variability for population extinction strongly depended on the strength of selection. Only with strong selection, I observed a strong increase in extinction risk as well as a decrease in mean time to extinction with increasing climate variability.

My results showed that in a highly stochastic environment, the lag of the mean phenotype behind the environmental optimum does not depend on climate variability, although there was substantial variability among-replicates with the same combination of parameters. In other simulations reported in the electronic supplementary material, figure S11, I found that with a climate trend of approximately 0.02 phenotypic standard deviations per generation, and with no increase in the variability of the optimum after climate change and with moderate selection strength, populations were able to persist for thousands of years. This is consistent with the results coming from long-term selection experiments in small populations, where shifts of 10 or more phenotypic standard deviations have been observed [51].

Previous work estimated that genetic and demographic stochasticity alone can reduce the critical rate of environmental change to only 0.1 of phenotypic standard deviations per generation (less than 10% of what predicted by deterministic models, e.g. [28]) [29,30]. According to my simulations, given a certain fecundity and maximum annual survival, in a highly stochastic environment, the critical rate of directional climate change largely depends on selection strength and climate variability. With sufficiently strong selection, a large variability of the optimum reduced the critical rate of environmental change to less than 0.01 phenotypic standard deviations per generation. However, with low selection strength, a rate of environmental change of 0.02 phenotypic standard deviations per generation was not challenging enough to cause population extinction even when the climate was highly variable.

4.2. Strength of selection

Strong selection increased extinction risk and reduced mean time to extinction. As expected, additive genetic variance tended to decrease with increasing strength of selection [23].

Previous work found that both broad generalists and narrow specialists will be particularly vulnerable to extinction in a changing environment [29,32]. In particular, by applying the model presented in [28] to the evolution of thermal sensitivity, Huey & Kingsolver [32] found that an intermediate strength of selection (defined ‘intermediate performance breadth’) maximizes the critical rate of climate change above which extinction will occur. However, when performance breadth was linked to genetic variance, Huey & Kingsolver [32] found that there was no performance breadth maximizing the critical rate of climate change. On the other hand, Bürger & Lynch [29] found that in the case of a climate trend smaller than 0.1 phenotypic standard deviations per generation, mean time to extinction (given a combination of parameters) was maximized when the width ω of the fitness function was around 2 (corresponding to s = 0.125), and decreased for both stronger and weaker selection. In the case of very fast changes of the environment, Bürger & Lynch [29] found that weaker selection strength maximized the time to extinction. However, since in [29] maximum annual survival S_max was set to 1 (i.e. survival of an individual was entirely determined by a single quantitative trait), the width ω of their fitness function cannot be directly compared to the width of the fitness function used in this work.

In contrast to what found in studies with an environmental or climate trend and moderate variability, I conclude that in a highly stochastic environment and on contemporary timescales (i.e. 150 years of climate change), the cost of selection is higher than the fitness cost of lagging behind the environmental optimum. This is likely to be ascribed to the greater number of events potentially reducing population size via maladaption in a highly stochastic environment than in a less variable environment. It follows that in a highly stochastic environment, organisms with narrow tolerance (i.e. for which selection is stronger) may have a greater risk of extinction than generalist organisms, for which selection is weaker.

4.3. Mean time to extinction and extinction risk

There was a clear negative relationship between risk of extinction and mean time to extinction, with extinctions occurring on average faster when the climate trend was weaker. This happened because when extinction was almost inevitable (e.g. strong selection and high climate variability), it occurred within the first 75 years after the change in climate. Otherwise, the higher substitutional load caused by a stronger climate trend (i) maintained populations' mean phenotype closer to the moving optimum (although at smaller population sizes) and (ii) slightly increased additive genetic variance for the quantitative trait. Both (i) and (ii) tended to increase mean time to extinction.

4.4. Mutation

Studies with approaches similar to my simulation analysis rarely accounted for mutation amplitude, since the infinitesimal model—which implicitly includes mutation [44]—has often been used. On the other hand, when genetically explicit individual-based models accounted for mutation amplitude, a single value was commonly used in all simulations [29,31] or simulations were carried out for thousands of generations [52]. In those contexts, it has been found that the replenishment of genetic variation by recurrent polygenic mutation helps populations adapt to a changing environment, in particular after a steady-state lag of the mean phenotype has been attained.

As expected, in my simulations larger mutation amplitudes tended to slightly increase additive genetic variance [52], but with no associated reduction of extinction risk or closer tracking of the optimum. As populations that persisted up to end of simulation time were able to track the directional component of the optimum, my results thus support the hypothesis that adaptation to a novel environment would be fuelled mostly by standing variation (pre-existing segregating genetic variant) than from de novo mutation, as (i) potentially beneficial alleles are readily available, (ii) the frequency of those alleles in the population should be higher [53] and (iii) when a high number of loci control trait variation, the selective coefficients of alleles are small [54].

4.5. Additive genetic variance and prediction of contemporary risk of extinction

Population size and additive genetic variance in the ‘sampling window’, along with selection strength and probability of occurrence of point extremes, predicted very well the immediate risk of population extinction.

Genetic variance can drift substantially from generation to generation in small population [23] and may substantially decrease when strong demographic fluctuations occur (electronic supplementary material, figure S1) as well as when selection is stronger, with clear implications for the risk of population extinction [51,55]. From a modelling perspective, maintaining a fixed additive genetic variance throughout simulation time as in [35] may underestimate the risk of population extinction, as well the effects of selection and demographic fluctuations on extinction dynamics.

Although additive genetic variance is predicted to decrease after population bottlenecks, increases in additive genetic variance after drastic reductions in population size have often been observed in nature. This phenomenon has been ascribed to non-additive genetic effects, such as interactions between alleles at different loci (i.e. epistasis) and disruption of dominance (e.g. a population bottleneck can increase the frequency of recessive alleles) [56]. In my simulations, additive genetic variance often increased, albeit only temporarily, after a strong decline in population size (e.g. electronic supplementary material, figure S10), even in absence of non-additive genetic effects. However, this result does not imply that the adaptive potential of the population increased after a population bottleneck, since the observed spike of additive genetic variance was simply caused by the random survival of individuals that before the extreme event had breeding values at the opposite sides of the spectrum.

The importance of additive genetic variance for predicting population extinction was fairly low and partially confounded by the observed positive correlation with population size. This seems to confirm that demographic dynamics and stochastic factors are largely responsible for contemporary extinctions in highly stochastic environments [57]. However, other genetic challenges not accounted for in my model are likely to be encountered by populations that decline to very low numbers, such as a reduction of viability and/or fecundity due to either inbreeding or the expression of deleterious alleles [23]. Although in my model a very small population size substantially increased the risk of immediate extinction, it was not uncommon for populations to swiftly recover after a collapse (electronic supplementary material, figures S1 and S10). By increasing the intensity of the Poisson distribution of offspring per reproducing couple from 2 to 3, populations almost never went extinct (electronic supplementary material, figure S12). This result shows how a moderate increase in fecundity may have substantial effects on the survival of populations in highly stochastic environments, as also suggested by theoretical [29] and experimental [58] studies, although trade-offs with survival and other life histories should be considered [59]. This might explain why fecundity is strongly selected under environmental change in long running experimental populations [60,61], although whether this is caused by environmental variation or environmental trend is unclear.

4.6. Caveats

The model I use considered a single trait responding to selection in a straightforward way. However, it is well known that effects of climate may act on multiple traits. For example, the effects of climate change on temperature may select for thermal tolerance traits, but also for dispersal traits, since newly suitable areas may emerge outside the present distribution of the population. However, those traits under potential selection may not be independent and act differentially, synergistically or antagonistically, thus affecting the chances of population persistence. In addition, life-histories strategies may evolve very rapidly. For instance, although in my simulation individuals started reproducing at age 1 and thus evolution of younger age at reproduction in discrete time was not possible, according to life-history theory a highly variable and unpredictable environment should select for younger age at first reproduction and higher investment in current reproduction at the expense of probability of surviving and future reproduction [62]. Future and more context-specific investigations of extinction risk and eco-evolutionary dynamics of populations living in highly stochastic environments will benefit for more fine-grained representation of genetic architecture of traits, genetic covariance of traits and plasticity of life histories.

Data accessibility

Data and code: http://dx.doi.org/10.6084/m9.figshare.706347

Funding statement

Simone Vincenzi is supported by a Marie Curie International Outgoing Fellowship for the project ‘RAPIDEVO’ on the rapid evolution of life-history traits in response to climate and environmental change and by the Center for Stock Assessment Research (CSTAR).