Bayesian Generalized Low Rank Regression Models for Neuroimaging Phenotypes and Genetic Markers

Abstract

We propose a Bayesian generalized low rank regression model (GLRR) for the analysis of both high-dimensional responses and covariates. This development is motivated by performing searches for associations between genetic variants and brain imaging phenotypes. GLRR integrates a low rank matrix to approximate the high-dimensional regression coefficient matrix of GLRR and a dynamic factor model to model the high-dimensional covariance matrix of brain imaging phenotypes. Local hypothesis testing is developed to identify significant covariates on high-dimensional responses. Posterior computation proceeds via an efficient Markov chain Monte Carlo algorithm. A simulation study is performed to evaluate the finite sample performance of GLRR and its comparison with several competing approaches. We apply GLRR to investigate the impact of 1,071 SNPs on top 40 genes reported by AlzGene database on the volumes of 93 regions of interest (ROI) obtained from Alzheimer's Disease Neuroimaging Initiative (ADNI).

1 Introduction

The emergence of high-dimensional data in genomics and neuroimaging, among other areas, has presented us with a large number of predictors as well as many response variables, which may have strong correlations. For instance, in imaging genetics as an emerging field, such problems frequently arise when multivariate imaging measures, such as volumes of cortical and subcortical regions of interest (ROIs), are predicted by high-dimensional covariate vectors, such as gene expressions or single nucleotide polymorphisms (SNPs). The joint analysis of imaging and genetic data may ultimately lead to discoveries of genes for some complex mental and neurological disorders, such as autism and schizophrenia (Cannon and Keller, 2006; Turner et al., 2006; Scharinger et al., 2010; Paus, 2010; Peper et al., 2007; Chiang et al., 2011a,b). This motivates us to develop low rank regression models (GLRR) for the analysis of high-dimensional responses and covariates under the high-dimension-low-sample-size setting.

Developing models for high-dimensional responses and covariates poses at least four major challenges including (i) a large number of regression parameters, (ii) a large covariance matrix, (iii) correlations among responses, and (iv) multicollinearity among predictors. When the number of responses and the number of covariates, which are denoted by d and p, respectively, are even moderately high, fitting conventional multivariate response regression models (MRRM) usually requires estimating a d × p matrix of regression coefficients, whose number pd can be much larger than the sample size. Although accounting for complicated correlation among multiple responses is important for improving the overall prediction accuracy of multivariate analysis (Breiman and Friedman, 1997), it requires estimating d(d + 1)/2 unknown parameters in a d × d unstructured covariance matrix. Another notorious difficulty is that the collinearity among a large number of predictors can cause issues of over-fitting and model misidentification (Fan and Lv, 2010).

There is a great interest in developing new statistical methods to handle these challenges for MRRMs. The early developments involve a separation approach–variable selection to reduce dimension and then parameter estimation, when both p and d are moderate compared to the sample size (Breiman and Friedman, 1997). For instance, Brown et al. (2002) introduced Bayesian model averaging incorporating variable selection for prediction, which allows for fast computation for dimensions up to several hundred. Recently, much attention has been given to shrinkage methods for achieving better stability and improving performance (Tibshirani, 1996). Notably, the most popular ones are the L₁ and L₂ penalties. The L₂ penalty forces the coefficients of highly correlated covariates towards each other, whereas the L₁ penalty usually selects only one predictor from a highly correlated group while ignoring the others. L₁ priors can be seen as sparse priors since they create a singularity at the origin whose gravity pulls the smaller coefficients to zero under maximum a posteriori (MAP) estimation. There are fully Bayesian approaches with sparse priors for univariate responses like the Bayesian LASSO (Park and Casella, 2008), a generalization of the LASSO (Kyung et al., 2010), and the double Pareto (Armagan et al., 2011), among many others. These methods, however, are primarily developed under the univariate-response-high-dimensional-covariate setting.

There have been several attempts in developing new methods under the high-dimensional-response-and-covariate setting. When both p and d are moderate compared to the sample size, Breiman and Friedman (1997) introduced a Curds and Whey (C&W) method to improve prediction error by accounting for correlations among the response variables. Peng et al. (2010) proposed a variant of the elastic net to enforce sparsity in the high-dimensional regression coefficient matrix, but they did not account for correlations among responses. Rothman et al. (2010) proposed a simultaneous estimation of a sparse coefficient matrix and sparse covariance matrix to improve on estimation error under the L₁ penalty. Similarly, Yin and Li (2011) presented a sparse conditional Gaussian graphical model in order to study the conditional independent relationships among a set of gene expressions adjusting for possible genetic effects. Furthermore, several authors have explored the low rank decomposition of the regression coefficient matrix and then use sparsity-inducing regularization techniques to reduce the number of parameters (Izenman, 1975; Reinsel and Velu, 1998; Tibshirani, 1996; Turlach et al., 2005; Chen et al., 2012; Vounou et al., 2010). For instance, Chen et al. (2012) and Vounou et al. (2010) considered the singular value decomposition of the coefficient matrix and used the LASSO-type penalty on both the left and right singular vectors to ensure its sparse structure. Since all variable selection methods require a selection of a proper amount of regularization for consistent variable selection, some methods, such as stability selection and cross validation, are needed for such selection (Meinshausen and Buhlmann, 2010). They, however, do not provide a standard inference tool (e.g., standard deviation) on the nonzero components of the left and right singular vectors or the coefficient matrix. Moreover, frequentist inference is the primary approach for making statistical inferences in the high-dimensional-response-and-covariate setting.

In this paper, we propose a new Bayesian GLRR to model the association between genetic variants and brain imaging phenotypes. A low rank regression model is introduced to characterize associations between genetic variants and brain imaging phenotypes, while accounting for the impact of other covariates. We assume shrinkage priors on the singular values of the regression coefficient matrix, while not explicitly requiring orthonormality of left and right singular vectors. This facilitates fast computation of the regression coefficient matrix. We consider a sparse latent factor model to more flexibly capture the within-subject correlation structure and assume a multiplicative gamma process shrinkage priors on the factor loadings, which allow for the introduction of infinitely many factors (Bhattacharya and Dunson, 2011). We propose Bayesian local hypothesis testing to identify significant effects of genetic markers on imaging phenotypes, while controlling for multiple comparisons. Posterior computation proceeds via an efficient Markov chain Monte Carlo (MCMC) algorithm.

In Section 2, we introduce the NIH Alzheimer's Disease Neuroimaging Initiative (ADNI) dataset. In Section 3, we introduce GLRR and its associated Bayesian estimation procedure. In Section 4, we conduct simulation studies with a known ground truth to examine the finite sample performance of GLRR and compare it with the conventional LASSO method. Section 5 illustrates an application of GLRR in the joint analysis of imaging, genetic, and clinical data from ADNI. Section 6 presents concluding remarks.

2 Generalized Low Rank Regression Models

2.1 Model Setup

Consider imaging genetic data from n independent subjects in ADNI. For each subject, we observe a d × 1 vector of imaging measures, denoted by Y_i = (y_i1, …, y_id)^T, and a p × 1 vector of clinical and genetic predictors, denoted by X_i = (x_i1, …, x_ip)^T, for i = 1, …, n. Let Y = (y_ik) be an n × d matrix of mean centered responses, X = (x_ij) be an n × p matrix of standardized predictors, B = (β_jk) be a p × d matrix of regression coefficients, and E = (∊_ik) be an n × d matrix of residuals. We consider a multivariate response regression model given by

$$Y_i=B^{\mathrm{T}}{X}_i+{∊}_i,\mathrm{or}\mathit{Y}=\mathit{X}B+E,$$ (1)

where ∊_i ~ N_d(0, Σ = Θ⁻¹), in which Θ = Σ⁻¹ is the d × d precision matrix. There are several statistical challenges in fitting model (1) to real data. When both p and d are relatively large compared to n, the number of parameters in B equals p × d and can be much larger than n. Furthermore, the number of unknown parameters in Σ equals d(d+1)/2. In addition to the number of unknown parameters, there are some additional complexities arising from practical applications, including different scales for different response variables and collinearity among the predictors.

In model (1), multiple responses are measured from the same subject and share a set of common predictors. Therefore, the regression coefficient matrix B can have two-way linear dependence coming from both the correlated responses and covariates. This shared mean structure can lead to a low rank mean parameter matrix B. We exploit this shared structure of B by decomposing it as

$$B=U\Delta V^{\mathrm{T}}=\sum _{l=1}^r{B}_l=\sum _{l=1}^r{\delta }_l{\mathit{u}}_l{{\mathit{v}}_l}^{\mathrm{T}},$$ (2)

where r is the rank of B, B_l = δ_lu_lv_l^T is the l−th layer for l = 1, …, r, Δ = diag(δ₁, …, δ_r), U = [u₁, …, u_r] is a p × r matrix, and V = [v₁, …, v_r] is a d × r matrix. In (2), it is assumed that genetic variates that are associated with phenotypes may be relatively sparse and each column of U may group informative SNPs with similar association into clusters. Thus, under such assumption, a small rank of B may capture the major dependence structure between Y_i and X_i.

Given the large number of parameters in Σ, we consider a Bayesian factor model to relate the random effects ∊_i to the latent factors η_i as

$${∊}_i=\Lambda {\eta }_i+{\xi }_i,$$ (3)

where Λ is a d × ∞ factor loading matrix, η_i ~ N_∞(0, I_∞), and ξ_i ~ N(0, Σ_ξ) with ${\Sigma }_{\xi }=\text{diag}({\sigma }_1^2,\dots ,{\sigma }_d^2)$. As shown in Hyun et al. (2014), the factor model (3) is useful for delineating the medium-to-long-range (or global) spatial dependence of neuroimaging data. Another advantage of (3) is that it bypasses the challenging issue of selecting the number of factors through a delicate prior setting. To achieve dimensionality reduction, one would typically restrict the dimension of the latent factor vector η_i to be orders of magnitude less than that of ∊_i. By following Bhattacharya and Dunson (2011), we choose a prior that shrinks the elements of to zero as the column index increases. Thus, it bypasses the challenging issue of selecting the number of factors. Finally, our GLRR integrates the low rank model (2) and the Bayesian factor model (3). Specifically, our GLRR can be written as

$$Y_i=\sum _{l=1}^r{X_i}^{\mathrm{T}}{\delta }_l{\mathit{v}}_l{{\mathit{u}}_l}^{\mathrm{T}}+\Lambda {\eta }_i+{\xi }_i.$$ (4)

Other than genetic markers, such as SNP's, it is common that X_i has a subvector, denoted by X_Pi, consisting of several prognostic variables, such as age, gender, and disease status in real applications. There are two different methods to deal with prognostic factors in the presence of genetic markers. The first method is a two-step approach. The first step is to fit the MRRM solely with these prognostics factors as covariates and then calculate the fitted residuals as adjusted responses. The final step is to fit model (4) to the adjusted responses with genetic markers as X. The second method is to fit model (4) with both prognostic factors and genetic markers as covariates. Let B_P be the p_P × d matrix of coefficients associated with the prognostic factors and X_Si and B_S be, respectively, the subvector of X_i and the submatrix of B associated with genetic markers. It may be reasonable to assume that B_P may be unstructured and B_S admits the decomposition given by $B_S=U_S{\Delta }_S{V_S}^{\mathrm{T}}={\sum }_{l=1}^r{B}_{S,l}$. In this case, the model can be written as

$$Y_i=B_P^{\mathrm{T}}{X}_{Pi}+\sum _{l=1}^r{B}_{S,l}^{\mathrm{T}}{X}_{Si}+{∊}_i.$$ (5)

We take the second approach and fit model (5) in real data analysis.

2.2 Low Rank Approximation

The decomposition (2) is similar to the standard singular value decomposition (SVD), but it differs from SVD. Specifically, it is unnecessary that the columns of U and V in (2) are orthonormal and this allows that u_jl and v_jl can take any value in (−∞, ∞), since identifiability is not critical for making inference on B. Thus, the decomposition (2) can be regarded as a generalization of SVD in Chen et al. (2012). Moreover, compared to SVD, this decomposition leads to better computational efficiency, since sampling a unit vector in a high-dimensional sphere is computationally difficult. Nevertheless, each layer B_l is a factorization with unit rank, which amounts to estimating a common p × 1 vector of distinct regression coefficients and making the rest of the coefficients some linear combinations of this vector with d additional parameters. Within the l-th layer, each column of B_l shares the same u_l and δ_l, which facilitates the exploitation of a common dependence structure among the covariates collected from the same set of subjects. Similarly, each row of B_l shares the same v_l and δ_l facilitating the exploitation of a common dependence structure among the responses from the same set of subjects. The number of parameters at each layer is p + d and the total number of parameters equals r × (p + d). Since r << min(p, d), the use of the decomposition (2) leads to a huge dimension reduction.

The decomposition (2) differs from two other popular methods including multivariate response models and stepwise unit rank regression models. Multivariate response models estimate a separate p×1 vector of coefficients for each response totaling p×d parameters. In frequentist analysis (Chen et al., 2012), it is common to sequentially explore each layer of B based on the ordering of Δ, which leads to stepwise unit rank regressions (SURR). Specifically, one first fits the unit rank (r = 1) regression with the observed Y as the response to estimate the first layer ${\widehat{B}}_1$ and $\widehat{Y}=\mathit{X}{\widehat{B}}_1$. Subsequently, one fits another unit rank regression with $\mathit{Y}-\widehat{Y}$ as the response to estimate the second layer ${\widehat{B}}_2$. One can continue this process until the r-th rank. Thus, SURR can be viewed as a special case of GLRR.

2.3 Covariance Structure

The covariance structure for Y_i is given by

$$\Sigma ={ϴ}^{-1}=\Lambda {\Lambda }^{\mathrm{T}}+{\Sigma }_{\xi }.$$ (6)

It is common to impose a constraint on Λ to define a unique model free from identification problems, since Σ is invariant under the transformation Λ* = ΛP for any semi-orthogonal matrix P with P P^T = I. For instance, for identifiability purposes, one may impose a full rank lower triangular constraint, which implicitly specifies an order dependence among the responses (Geweke and Zhou, 1996). However, it is unnecessary to impose such a constraint on Λ if our primary interest is on covariance matrix estimation. Specifically, we will specify a multiplicative gamma process shrinkage prior in (7) on a parameter expanded loading matrix with redundant parameters. The induced prior on Σ is invariant to the ordering of the responses. This shrinkage prior adaptively selects a truncation of the infinite loadings to one having finite columns. Thus, it facilitates the posterior computation and provides an accurate approximation to the infinite factor model.

2.4 Priors

We first consider the priors on the elements of all layers B_l. When dealing with two highly correlated covariates, the L₁ prior tends to pick one and drop the other since it is typically a least angle selection approach to force some coefficients to zero, whereas the L₂ prior tends to force the coefficients towards each other to produce two highly correlated coefficients. In GLRR, since our primary interest is to exploit the potential two-way correlations among the estimated coefficients, we choose the L₂ prior. Let Ga(a, b) be a gamma distribution with scale a and shape b. Specifically, we choose

$${\delta }_l~N(0,{\tau }_{\delta }^{-1})\text{with}{\tau }_{\delta }~\mathrm{Ga}(a_0,b_0),$$

$${\mathit{u}}_l~N_p(0,{\tau }_u^{-1}{I}_p)\text{with}{\tau }_u~p+\mathrm{Ga}(c_0,d_0),$$

$${\mathit{v}}_l~N_d(0,\text{diag}({\tau }_{v,1}^{-1},\dots ,{\tau }_{v,d}^{-1}\left)\right)\text{with}{\tau }_{v,1},\dots ,{\tau }_{v,d}~d+\mathrm{Ga}(e_0,f_0),$$

where a₀, b₀, c₀, d₀, e₀, and f₀ are prefixed hyper-parameters. The number of predictors p is included in the hyperprior of τ_u to have a positive-definite covariance matrix of high dimensional u_l and fix the scale of u_l. Similarly, we add the dimension d to all hyper-priors for τ_v,l. Moreover, we standardize all predictors to have zero mean and unit variance, and thus a single prior is sensible for all elements of u_l. The varying dispersions τ_v,1, …, τ_v,d are chosen to account for different scales of different responses. For example, the volumes of different ROIs vary dramatically across ROIs, so it is more sensible to use separate dispersions for different ROIs.

We place the multiplicative gamma process shrinkage prior (Bhattacharya and Dunson, 2011) on Λ in order to increasingly shrink the factor loadings towards zero with the column index. Such shrinkage priors avoid the drawback of order dependence from the lower triangular constraint on Λ for identifiability. We use inverse gamma priors on the diagonal elements of Σ_ξ. Specifically, these priors are given as follows:

$$\begin{array}{cc}\hfill \Lambda & =\left\{{\lambda }_{kh}\right\},k=1,\dots ,d;h=1,\dots ,\infty ,\hfill \\ \hfill {\lambda }_{kh}\mid {\varphi }_{kh},{\tau }_{\lambda h}& ~N(0,{\varphi }_{kh}^{-1}{\tau }_{\lambda h}^{-1}),{\varphi }_{kh}~\mathrm{Ga}(v∕2,v∕2),{\sigma }_k^{-2}~\mathrm{Ga}(a_{\sigma k},b_{\sigma k}),\hfill \\ \hfill {\psi }_1& ~\mathrm{Ga}(a_1,1),{\psi }_g~\mathrm{Ga}(a_2,1),g\ge 2,{\tau }_{\lambda h}=\prod _{l=1}^h{\psi }_l,\hfill \end{array}$$ (7)

where ψ_g for g = 1, …, ∞ are independent random variables, τ_λh is a global shrinkage parameter for the h-th column, and the ϕ_khs are local shrinkage parameters for the elements in the h-th column. Moreover, v, a₁,, a₂, a_σk and b_σk are prefixed hyper-parameters. When a₂ > 1, the τ_λh's increase stochastically with the column index h, which indicates more shrinkage favored over the columns of higher indices. The loading component specific prior precision ${\varphi }_{kh}^{-1}{\tau }_{\lambda h}^{-1}$ allows shrinking the components of Λ. Straightforward Gibbs sampler can be applied for posterior computation

2.5 Posterior Computation

We propose a straightforward Gibbs sampler for posterior computation after truncating the loadings matrix to have k_* << d columns. An adaptive strategy for inference on the truncation level k_* has been described in (Bhattacharya and Dunson, 2011). The Gibbs sampler is computationally efficient and mixes rapidly. Starting from the initiation step, the Gibbs sampler at the truncated level k_* proceeds as follows:

1. Update (u_l, τ_u) according to their conditional distributions

   $$p({\mathit{u}}_l\mid -)~{\mathit{N}}_p({\delta }_l{\Sigma }_{{\mathit{u}}_l}{\mathit{X}}^{\mathrm{T}}{Y}_lϴ{\mathit{v}}_l,{\Sigma }_{{\mathit{u}}_l}),p({\tau }_u\mid -)~p+\mathrm{Ga}\left(c_0,d_0+0.5\sum _{l=1}^r{{\mathit{u}}_l}^{\mathrm{T}}{\mathit{u}}_l\right),$$

   where ${\Sigma }_{{\mathit{u}}_l}={\{{\tau }_u{I}_p+{\delta }_l^2({{\mathit{v}}_l}^{\mathrm{T}}ϴv_l\left){\mathit{X}}^{\mathrm{T}}\mathit{X}\right\}}^{-1}$.
2. Update (v_l, τ_v,k) according to their conditional distributions

   $$p({\mathit{v}}_l\mid -)~{\mathit{N}}_d({\delta }_l{\Sigma }_{{\mathit{v}}_l}ϴ{Y_l}^{\mathrm{T}}\mathit{X}{\mathit{u}}_l,{\Sigma }_{{\mathit{v}}_l}),p({\tau }_{v,k}\mid -)~d+\mathrm{Ga}\left(e_0,f_0+0.5\sum _{l=1}^r{\mathit{v}}_l^2\right)$$

   for k = 1, …, d, where ${\Sigma }_{{\mathit{v}}_l}={\left\{\text{diag}\right({\tau }_{v,1},\dots ,{\tau }_{v,d})+{\delta }_l^2({{\mathit{u}}_l}^{\mathrm{T}}{\mathit{X}}^{\mathrm{T}}\mathit{X}{\mathit{u}}_l\left)ϴ\right\}}^{-1}$.
3. Update (δ_l, τ_δ) according to their conditional distributions

   $$p({\delta }_l\mid -)~N({\sigma }_{{\delta }_l}^2{{\mathit{u}}_l}^{\mathrm{T}}{\mathit{X}}^{\mathrm{T}}{E}_lϴ{\mathit{v}}_l,{\sigma }_{{\delta }_l}^2),p({\tau }_{\delta }\mid -)~\mathrm{Ga}\left(a_0,b_0+0.5\sum _{l=1}^r{\delta }_l^2\right),$$

   where ${\sigma }_{{\delta }_l}^2={\{{\tau }_{\delta }+({\mathit{v}}_l{ϴ}^{\mathrm{T}}{\mathit{v}}_l\left)\right({{\mathit{u}}_l}^{\mathrm{T}}{\mathit{X}}^{\mathrm{T}}\mathit{X}{\mathit{u}}_l\left\}\right)}^{-1}$.
4. Update the kth row of Λ_k*, denoted by τ_k, from its conditional distribution

   $$p({\lambda }_k\mid -)~\mathit{N}({({\sigma }_k^{-2}{\eta }^{\mathrm{T}}\eta +D_k^{-1})}^{-1}{\eta }^{\mathrm{T}}{\sigma }_k^{-2}{E}_k,{({\sigma }_k^{-2}{\eta }^{\mathrm{T}}\eta +D_k^{-1})}^{-1}),$$

   where η = (η₁, …, η_n)^T, E_k = (∊_1k, …, ∊_nk)^T is the kth column of E = Y − XB, and $D_k=\text{diag}({\varphi }_{k1}^{-1}{\tau }_{\lambda 1}^{-1},\dots ,{\varphi }_{k{k}_{\ast }}^{-1}{\tau }_{\lambda k_{\ast }}^{-1})$ for k = 1, …, d.
5. Update ϕ_kh from its conditional distribution

   $$p({\varphi }_{kh}\mid -)~\mathrm{Ga}\left(\frac{v+1}{2},\frac{v+{\lambda }_{kh}^2{\tau }_{\lambda h}}{2}\right).$$
6. Update ψ₁ from its conditional distribution

   $$p({\psi }_1\mid -)~\mathrm{Ga}\left(a_1+\frac{1}{2}d{k}_{\ast },1+\frac{1}{2}\sum _{g=1}^{k_{\ast }}{\tau }_{\lambda g}^{\left(h\right)}\sum _{k=1}^d{\varphi }_{kg}{\lambda }_{kg}^2\right),$$

   and update ψ_h, h ≥ 2 from its conditional distribution

   $$p({\psi }_h\mid -)~\mathrm{Ga}\left(a_2+\frac{1}{2}d(k_{\ast }-h+1),1+\frac{1}{2}\sum _{g=h}^{k_{\ast }}{\tau }_{\lambda g}^{\left(h\right)}\sum _{k=1}^d{\varphi }_{kg}{\lambda }_{kg}^2\right),$$

   where ${\tau }_{\lambda g}^{\left(h\right)}={\prod }_{t=1,t\ne h}^g{\psi }_t$ for h = 1, …, k_*.
7. Update ${\sigma }_k^{-2}$, k = 1, …, d, from its conditional distribution

   $$p({\sigma }_k^{-2}\mid -)~\mathrm{Ga}(a_{\sigma k}+\frac{n}{2},b_{\sigma k}+\frac{1}{2}\sum _{i=1}^n{(y_{ik}-{{\lambda }_k}^{\mathrm{T}}{\eta }_i)}^2).$$
8. Update η_i, i = 1, …, n, from conditionally independent posteriors

   $$p({\eta }_i\mid -)~N({(I_{k_{\ast }}+{\Lambda }^{\mathrm{T}}ϴ\Lambda )}^{-1}{{\Lambda }_{k_{\ast }}}^Tϴ{∊}_i,{(I_{k_{\ast }}+{\Lambda }^{\mathrm{T}}ϴ\Lambda )}^{-1}),$$

   where ∊_i is the ith row of E.

2.6 Determining the Rank of B

We consider different methods for determining the rank of B. For frequentist inference, many regularization methods have been developed to recover the low rank structure of a matrix, such as B, by shrinking δℓ's to zero in (2) (Chen et al., 2012). For Bayesian inference, it may be tempting to use Bayesian model averaging and allow varying number of layers in order to improve prediction performance, but it limits us on making statistical inference on each layer of B, U, and V . We take a fixed-rank approach and use some selection criteria to choose an optimal value of r. Specifically, we consider five different selection criteria including the Akaike information criterion (AIC), the Bayesian information criterion (BIC), the normalized prediction error (PEN), the multivariate R², and the normalized model error (MEN) for GLRR. Let $\widehat{Y}=\mathit{X}\widehat{B}$, where $\widehat{B}$ is the posterior estimate of B based on the MCMC samples. Let $\text{SSE}=\mathrm{tr}\left({(\widehat{Y}-\mathit{Y})}^{\mathrm{T}}\right(\widehat{Y}-\mathit{Y}\left)\right)$ be the error sum of squares and p_* = r(p + d) be the number of parameters in B. The five evaluation criteria are, respectively, given by

$$\begin{array}{cc}\hfill & \text{AIC}=\log \left(\text{SSE}\right)+2\frac{p_{\ast }}{nd},\text{BIC}=\log \left(\text{SSE}\right)+\frac{\log \left(nd\right)}{nd}{p}_{\ast },\hfill \\ \hfill & \text{PEN}(\widehat{Y},\mathit{Y})=\frac{\text{SSE}}{\mathrm{tr}\left({\mathit{Y}}^{\mathrm{T}}\mathit{Y}\right)}\times 100,R^2(\widehat{Y},\mathit{Y})=\frac{\mathrm{tr}\left({\widehat{Y}}^{\mathrm{T}}\widehat{Y}\right)}{\mathrm{tr}{\mathit{Y}}^{\mathrm{T}}\mathit{Y})}\times 100,\hfill \\ \hfill & \text{MEN}(\widehat{B},B)=\frac{\mathrm{tr}\left({(\widehat{B}-B)}^{\mathrm{T}}{\Sigma }_X\right(\widehat{B}-B\left)\right)}{\mathrm{tr}\left(B^{\mathrm{T}}{\Sigma }_{X}B\right)}\times 100.\hfill \end{array}$$ (8)

The numerator and denominator of the MEN are, respectively, the model error and measurement error of model (4) (Yuan et al., 2007). Thus, the MEN is the ratio of the model error over the measurement error as a percentage of the total magnitude of all parameters. Similarly, the PEN and R² are defined as percentages, which makes comparisons more meaningful and readily comparable across studies.

To illustrate the effectiveness of all five criteria, we independently simulated 100 data sets from model (4) with (n, p, d) = (100, 200, 100) and a rank 5 matrix B. For each simulated data set, we used the Gibbs sampler to draw posterior samples to estimate B and then calculated the five selection criteria in (8) as the rank varied from 1 to 10. Finally, based on all 100 simulated data sets, we calculated the mean and standard deviation of each selection criterion as the rank varied from 1 to 10. As shown in Figure 1, PEN, MEN, R², and AIC stabilize around the true rank, whereas BIC reaches the minimum at the true rank. This may indicate that BIC outperforms other selection criteria for determining the true rank of B. This result also agrees with the findings in Bozdogan (1987) such that in parametric settings, AIC tended to select a larger model than the true model even for large sample sizes, whereas BIC is asymptotically consistent in estimating the true model.

Figure 1.

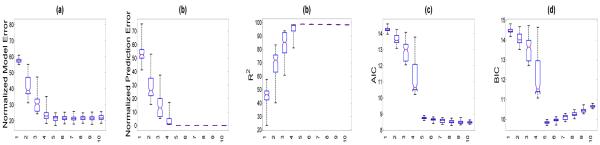
Simulation results: the box plots of five selection criteria including $\text{MEN}(\widehat{B},B)$, $\text{PEN}(\widehat{Y},\mathit{Y})$, $R^2(\widehat{Y},\mathit{Y})$, AIC, and BIC against rank r from the left to the right based on 100 simulated data sets simulated from model (4) with (n, p, d) = (100, 200, 100) and the true rank r₀ = 5.

2.7 Thresholding

Based on the MCMC samples obtained from the Gibbs sampler, we are able to identify three different sets of information including (i) SNPs that significantly contribute to a large portion of imaging phenotypes, (ii) imaging phenotypes that are associated with those SNPs in (i), and (iii) important individual SNP effects on individual imaging phenotypes. Statistically, (i), (ii), and (iii) can be formulated as testing significant elements in U, V , and B, respectively. For the sake of space, we focus on (i). Suppose that we draw a set of MCMC samples $U^{\left(m\right)}=\left(u_{jl}^{\left(m\right)}\right)$ for m = 1, …, M. Due to the magnitude ambiguity of U, we normalize each column of U = (u_jl) to calculate $U^{\ast }=\left(u_{jl}^{\ast }\right)$. Moreover, we develop a specific strategy to deal with the sign ambiguity of U*. For the l–th column of U*, we use the normalized MCMC samples $U^{\left(m\right)\ast }=\left(u_{jl}^{\left(m\right)\ast }\right)$ to empirically determine the j₀–th row such that $P(\mid u_{j_{0}l}^{\ast }\mid ={\max }_j\mid {\tilde{u}}_{jl}^{\ast }\mid )\ge P(\mid {\tilde{u}}_{j^{\prime }l}^{\ast }\mid ={\max }_j\mid {\tilde{u}}_{jl}^{\ast }\mid )$ for all j′ ≠ j₀. Then, we fix $u_{j_{0}l}^{\left(m\right)\ast }$ to be positive for l = 1, …, r and m = 1, …, M.

To detect SNPs in (i), we suggest to calculate the median and median absolute deviation (MAD) of $u_{jl}^{\left(m\right)\ast }$, denoted by ${\widehat{u}}_{jl}^{\ast }$ and s_u,jl, respectively, since the MCMC samples $\left\{u_{jl}^{\left(m\right)}\right\}$ may oscillate dramatically between the positive solution and the negative solution due to the sign ambiguity for all j, l. Then, one may formulate it as testing the local null and alternative hypotheses for $\mid u_{jl}^{\ast }\mid$ relative to s_u,jl given by

$$H_{0,jl}:\mid u_{jl}^{\ast }\mid \le T\ast \text{versus}{H}_{1,jl}:\mid u_{jl}^{\ast }\mid >T\ast ,$$

where T* is a specific threshold for each $u_{jl}^{\ast }$. One may calculate the probability of $\mid u_{jl}^{\ast }\mid T\ast =\mid {\widehat{u}}_{jl}^{\ast }\mid ∕\left(1.4826s_{u,jl}\right)$ given the observed data and then adjust for multiple comparisons (Müller et al., 2004; Wang and Dunson, 2010). Another approach is to directly calculate t_u,jl and apply standard multiple comparison methods, such as the false discovery rate, to determine T* (Benjamini and Hochberg, 1995). We have found that these two methods lead to similar results, and thus we take the second approach. Moreover, this Bayesian thresholding method works well even when different responses are not on the same scale. Compared to the `hard' thresholding methods used in shrinkage methods (Chen et al., 2012; Peng et al., 2010; Rothman et al., 2010; Yin and Li, 2011), this Bayesian thresholding method accounts for the variation of each $u_{jl}^{\ast }$ and has a probabilistic interpretation.

3 Simulation Study

3.1 Simulation Setup

We carried out some simulation studies to examine the finite-sample performance of the GLRR and its posterior computation. We generated all simulated data according to model (4). The simulation studies were designed to establish the association between a relatively high-dimensional phenotype vector with a set of continuous covariates or a set of commonly used genetic markers (e.g., SNP). For each case, 100 simulated data sets were generated.

We simulated ∊_i ~ N_d(0, Σ) and used two types of covariates including (i) continuous covariates generated from X_i ~ N_p(0, Σ_X) and (ii) actual SNPs from ADNI data set. We determined Σ and Σ_X as follows. Let p₀ be the binomial probability, which controls the sparsity of the precision matrix. We first generated a p×p matrix A = (a_jj′) with a_jj = 1 and a_jj′ = uniform(0, 1) × binomial(1, p₀) for j ≠ j′, set Σ_X = AA^T, and standardized Σ_X into a correlation matrix such that Σ_X,jj = 1 for j = 1, …, d. Similarly, we used the same method to generate Σ, the covariance matrix of ∊_i. For both Σ and Σ_X, we set about 20% of the elements of Σ⁻¹ and ${\Sigma }_X^{-1}$ to be zero, yielding that the means of the absolute correlations of Σ and Σ_X are close to 0.40, respectively. We chose actual SNPs from the ADNI data set. Specifically, we only considered the 10,479 SNPs collected on chromosome 19, screened out all SNPs with more than 5% missing data and minor allele frequency (MAF)< 0.05, and randomly selected 400 SNPs from the remaining SNPs. For n = 1, 000 case, 500 subjects were randomly chosen and then replicated twice, whereas for the n=100 case, 100 subjects were randomly chosen from ADNI data set.

We considered five structures of B in order to examine the finite-sample performance of GLRR under different scenarios.

• Case 1: X_i ~ N_p(0, Σ_X) and a “+” structure was preset for B with (p, d) = (100, 100) with the elements of B being set as either 0 or 1.

• Case 2: X_i × N_p(0, Σ_X) and B was set as a 200 × 100 matrix with the true rank r₀ = 5. Specifically, we set B = UΔV with U = (u_jl), Δ = diag(δ_ll) = diag(100, 80, 60, 40, 20), and V = (v_lk) being 200 × 5, 5 × 5, and 5 × 100 matrices, respectively. Moreover, we generated all elements u_jl and v_lk independently from a N(0, 1) generator and then orthonormalized U and V.

• Case 3: Covariates are actual SNPs and B has the same structure as that in Case 2 but with (p, d) = (400, 100).

• Case 4: X_i ~ N_p(0, Σ_X) and B was set as a 200 × 100 matrix with high degrees of correlation among elements with an average absolute correlation of 0.8, and then 20% of the elements of B were randomly forced to 0. After enforcing zeros, the true rank is 100 and the average absolute correlation is close to 0.7.

• Case 5: Covariates are actual SNPs and B is the same as that in Case 4 with (p, d) = (400, 100).

We chose noninformative priors for the hyperparameters of B and set α₀ = β₀ = a₀ = b₀ = c₀ = d₀ = e₀ = f₀ = 10⁻⁶. Since shrinkage is achieved through dimension reduction by choosing r << min(d, p), these noninformative choices of the hyperparameters suit well. For the hyperparameters of Σ, we chose somewhat informative priors in order to impose the positive-definiteness constraint and set ν = a₁ = b₂ = a_σk = b_σk = 1 for k = 1, …, d. The induced prior of Σ ensure that Σ is positive definite, while the prior variances are large enough to allow Σ to be primarily learned from the data. For each simulated dataset, we ran the Gibbs sampler for 10,000 iterations with 5, 000 burn-in iterations.

As a comparison, we considered a multivariate version of LASSO (Peng et al., 2010), Bayesian LASSO (BLASSO) (Park and Casella, 2008), and group-sparse multitask regression and feature selection (G-SMuRFS) (Wang et al., 2012) for all simulated data. For LASSO, we fitted d separate LASSO regressions to each response with a single tuning parameter across all responses by using a 5-fold cross validation. Since variances of all columns X and E are relatively equal, the variances of all columns of Y should be close to each other. In this case, a single tuning parameter is sensible. For BLASSO, we chose single priors for each column of the response matrix by setting all hyperparameters to unity. For G-SMuRFS, we used single group and selected the optimal values of the penalty parameters by using a 5-fold cross validation.

To compare different methods, we calculated their sensitivity and specificity scores under each scenario. For all regularization methods, since we choose all possible values of the tuning parameters for calculating their sensitivity and specificity scores, it is unnecessary to use the cross validation method to select the tuning parameters. Let I(·) be an indicator function of an event and $t_{jk}={\widehat{\beta }}_{jk}∕s_{\beta ,jk}$, where ${\widehat{\beta }}_{jk}$ and s_β,jk denote the posterior mean and standard deviation of β_jk, respectively. Specifically, for a given threshold T₀, sensitivity and specificity scores are, respectively, given by

$$\text{Se}\left(T_0\right)=\frac{\text{TP}\left(T_0\right)}{\text{TP}\left(T_0\right)+\text{FN}\left(T_0\right)},\text{and}\text{Sp}\left(T_0\right)=\frac{\text{TN}\left(T_0\right)}{\text{TN}\left(T_0\right)+\text{FP}\left(T_0\right)},$$

where TP(T₀), TP(T₀), TP(T₀), and TP(T₀) are, respectively, the numbers of true positives, false positives, true negatives, and false negatives, given by

$$\text{TP}\left(T_0\right)=\sum _{j,k}I(\mid t_{jk}\mid >T_0)I({\beta }_{jk}\ne 0),\text{FP}\left(T_0\right)=\sum _{j,k}I(\mid t_{jk}\mid >T_0)I({\beta }_{jk}=0),$$

$$\text{TN}\left(T_0\right)=\sum _{j,k}I(\mid t_{jk}\mid \le T_0)I({\beta }_{jk}=0),\text{FN}\left(T_0\right)=\sum _{j,k}I(\mid t_{jk}\mid \le T_0)I({\beta }_{jk}\ne 0),$$

Varying T₀ gives different sensitivity and specificity scores, which allow us to create receiver operating characteristic (ROC) curves. In each ROC curve, sensitivity is plotted against 1-specificity. The larger the area under the ROC curve, the better a method in identifying the true positives while controlling for the false positives.

3.2 Results

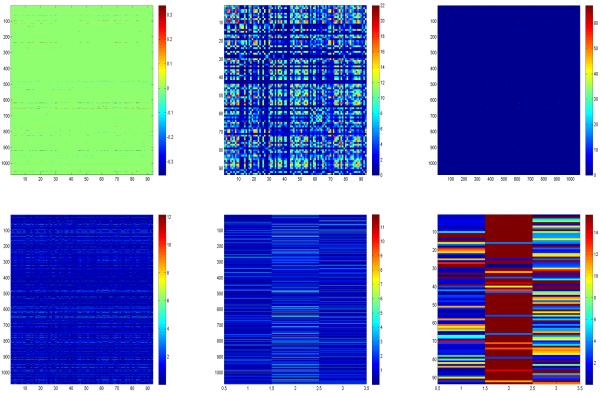
We first performed a preliminary analysis by using five data sets simulated according to the five structures of B and n = 1, 000. See Figure 2 for the true B and estimated $\widehat{\beta }$ by using GLRR3 (GLRR with r = 3), GLRR5 (GLRR with r = 5), BLASSO, G-SMuRFS, and LASSO under Case 1-Case 5. Inspecting Figure 2 reveals that for relatively large sample sizes, the fitted GLRR with r close to the true rank does a better job in recovering the underlying structure of B, while BLASSO and G-SMuRFS perform reasonably well for all cases. For the ”+” structure of B with the true rank r₀ = 2 in Case 1, GLRR3 performs the best, whereas LASSO does a poor job. For B with the true rank r₀ = 5 in Cases 2 and 3, GLRR5 performs the best. The LASSO method performs reasonably well in recovering B for continuous X, when B is a 200 × 100 matrix, whereas it performs poorly when X is the SNP matrix. For the high-rank B in Cases 4 and 5, LASSO performs the best in recovering B, while GLRR3 and GLRR5 perform reasonably well.

Figure 2.

Simulation results: comparisons of true B image and estimated true B images by using LASSO, BLASSO, G-SMuRFS, GLRR3, and GLRR5 under five different scenarios. $\text{MEN}(B,\widehat{B})$) and BIC were calculated for each estimated $\widehat{B}$. The sample size is n = 1000. Columns 1-5 correspond to Cases 1-5, respectively. The true ranks of B under Cases 1-5 are, respectively, 2, 5, 5, 100 and 100. The top row contains true B maps under Cases 1-5 and rows 2–6 correspond to the estimated $\widehat{B}$ under LASSO, Bayesian LASSO, G-SMuRFS, GLRR3, and GLRR5, respectively. For simplicity, only the first 100 rows and 100 columns of B were presented. Moreover, all plots in the same column are on the same scale.

Secondly, we examined the finite sample performance of LASSO, BLASSO, G-SMuRFS, GLRR3, and GLRR5 under Cases 1-5 for n = 100. In each case, 100 simulated data sets were used and the mean and standard deviation of each of the five selection criteria were calculated. The results are presented in Table 1. Inspecting Table 1 reveals that GLRRs outperform LASSO in most cases. As p increases, GLRRs outperform LASSO in terms of MEN, PEN, and R². Under Cases 3 and 5, GLRRs outperform LASSO with much smaller errors as well as lower standard deviations for MEN and PEN. LASSO performs much better for continuous covariates than for discrete SNPs, but such patterns do not appear for GLRRs. The results of GLRRs and BLASSO are comparable in terms of both AIC and BIC, but the number of parameters under GLRRs is much smaller than that under BLASSO. BLASSO and G-SMuRFS perform well in terms of both model error and prediction. The high R² and low prediction error of BLASSO and G-SMuRFS in the high dimension cases may be caused by over-fitting and model misidentification (Fan and Lv, 2010).

Table 1.

Empirical comparison of GLRR3, GLRR5, LASSO, BLASSO and G-SMuRFS under Cases 1-5 based on the five selection criteria. The means and standard deviations of these criteria are also calculated and their standard deviations are presented in parentheses. Moreover, UN denotes the unstructured B.

Case/(p, d, n)/X	B/r 0	Method	MEN	PEN	R 2	AIC	BIC
1 (100,100,100) Continuous	“+” 2	LASSO	6.21 (0.83)	3.98 (0.73)	89.50 (2.03)	9.54 (0.08)	12.45 (0.24)
		BLASSO	4.63 (0.48)	4.19 (0.57)	92.09 (1.13)	10.82 (0.08)	18.02 (0.07)
		G-SMuRFS	5.74 (0.65)	1.88 (0.30)	94.62 (0.71)	10.01 (0.10)	17.22 (0.10)
		GLRR3	11.81 (10.96)	3.17 (7.35)	94.71 (7.34)	8.27 (0.47)	8.70 (0.47)
		GLRR5	6.81 (6.87)	2.14 (3.69)	94.73 (3.72)	8.16 (0.31)	8.88 (0.31)
2 (200,100,100) Continuous	UΔV 5	LASSO	26.64 (2.15)	1.26 (1.49)	97.37 (6.01)	11.94 (0.77)	18.25 (0.93)
		BLASSO	22.38 (1.63)	1.24 (0.21)	98.55 (0.33)	13.39 (0.41)	27.78 (0.41)
		G-SMuRFS	21.87 (1.69)	1.11 (0.11)	98.20 (0.07)	9.95 (0.10)	24.38 (0.24)
		GLRR3	31.56 (6.56)	14.60 (9.24)	83.77 (9.75)	12.88 (0.61)	13.53 (0.61)
		GLRR5	21.69 (1.87)	0.36 (1.93)	98.54 (2.22)	8.90 (0.47)	8.88 (0.47)
3 (400,100,100) SNPs	UΔV 5	LASSO	50.41 (12.00)	50.87 (11.94)	19.59 (7.78)	12.81 (0.15)	13.66 (0.23)
		BLASSO	25.57 (0.02)	10.08 (2.04)	93.24 (3.29)	15.69 (0.39)	43.53 (0.39)
		G-SMuRFS	24.28 (0.02)	10.27 (2.01)	91.69 (4.01)	16.96 (0.01)	42.80 (0.01)
		GLRR3	20.23 (4.25)	21.39 (13.96)	76.74 (14.20)	11.86 (0.60)	12.93 (0.60)
		GLRR5	13.64 (7.88)	4.07 (7.77)	93.60 (7.97)	10.19 (0.60)	11.99 (0.60)
4 (200,100,100) Continuous	UN 100	LASSO	22.16 (1.93)	1.27 (1.49)	94.40 (6.16)	12.45 (0.88)	19.11 (1.12)
		BLASSO	19.44 (1.16)	1.22 (0.21)	98.32 (0.74)	13.21 (0.79)	27.63 (0.79)
		G-SMuRFS	15.00 (1.44)	1.10 (0.01)	98.40 (0.08)	9.74 (0.11)	24.16 (0.11)
		GLRR3	18.32 (1.53)	5.16 (0.64)	93.93 (0.73)	12.20 (0.04)	12.85 (0.04)
		GLRR5	16.02 (1.59)	4.30 (0.56)	94.26 (0.71)	12.14 (0.03)	13.22 (0.03)
5 (400,100,100) SNPs	UN 100	LASSO	39.14 (12.93)	39.11 (12.95)	24.53 (9.53)	14.60 (0.12)	17.22 (0.62)
		BLASSO	22.43 (1.13)	12.07 (0.03)	89.31 (0.24)	15.60 (0.35)	41.44 (0.35)
		G-SMuRFS	18.58 (0.02)	12.27 (0.01)	88.69 (0.01)	16.96 (0.01)	42.21 (0.01)
		GLRR3	19.88 (0.01)	20.01 (0.03)	77.15 (0.04)	13.56 (0.00)	14.64 (0.00)
		GLRR5	17.87 (0.01)	17.98 (0.03)	77.81 (0.04)	13.65 (0.00)	14.45 (0.00)

Thirdly, we used the ROC curve to compare LASSO, BLASSO, G-SMuRFS, GLRR3, and GLRR5 under Cases 1-5. See Figure 3 for details. For Case 1, BLASSO demonstrates consistently the best power for almost every level of specificity, while G-SMuRFS is the second best. GLRR3 and GLRR5 fall in the middle. For Case 4, all the methods appear to be comparable with GLRR3 and GLRR5. For Cases 2, 3, and 5, GLRRs consistently outperform all other methods.

Figure 3.

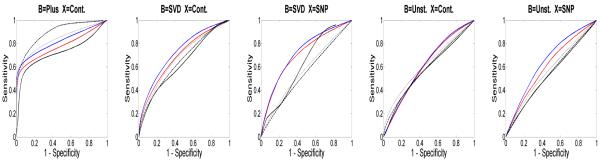
Comparisons of GLRR3, GLRR5, and LASSO under Cases 1-5: mean ROC curves based on GLRR3 (red line), GLRR5 (blue line), LASSO (black line), G-SMuRFS (dottedd line) and BLASSO (dashed line). For each case, 100 simulated data sets of size n = 100 each were used.

We also compared the timing of each method in a personal laptop with Intel Core i5 1.7 GHz processor and 4 GB memory. It takes LASSO and G-SMuRFS roughly 5 minutes to choose the optimal penalty and calculate estimates for a single sample of Case 5. All Bayesian methods take much longer since one has to sample many MCMC samples. Specifically, BLASSO takes about 2.75 hours to generate 10,000 samples plus 10,000 thousand burn-ins. For the same number of samples, GLRR3 takes about 30 minutes and GLRR5 takes about 40 minutes.

4 The Alzheimer's Disease Neuroimaging Initiative

4.1 Imaging Genetic Data

Imaging genetics is an emergent trans-disciplinary research field to primarily evaluate the association between genetic variation and imaging measures as continuous phenotypes. Compared to traditional case control status, since imaging phenotypes may be closer to the underlying biological etiology of many neurodegenerative and neuropsychiatric diseases (e.g., Alzheimer), it may be easier to identify underlying genes of those diseases (Cannon and Keller, 2006; Turner et al., 2006; Scharinger et al., 2010; Paus, 2010; Peper et al., 2007; Chiang et al., 2011b,a). A challenging analytical issue of imaging genetics is that the numbers of imaging phenotypes and genetic markers can be relatively high. The aim of this data analysis is to use GLRR to specifically identify strong associations between imaging phenotypes and SNP genotypes in imaging genetic studies.

The development of GLRR is motivated by the analysis of imaging, genetic, and clinical data collected by ADNI. “Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.ucla.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year publicprivate partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California, San Francisco. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org. ”

Our problem of interest is to establish the association between SNPs on the top 40 AD candidate genes as listed on the AlzGene database (www.alzgene.org) as of June 10, 2010 and the brain volumes of 93 regions of interest, whose names and abbreviation are given in the supplementary document, while accounting for other covariates, such as age and gender. By using the Bayesian GLRR, we can easily carry out formal statistical inferences, such as the identification of significant SNPs on the differences among all 93 ROI volumes.

The MRI data, collected across a variety of 1.5 Tesla MRI scanners with protocols individualized for each scanner, included standard T1-weighted images obtained using volumetric 3-dimensional sagittal MPRAGE or equivalent protocols with varying resolutions. The typical protocol included: repetition time (TR) = 2400 ms, inversion time (TI) = 1000 ms, flip angle = 8°, and field of view (FOV) = 24 cm with a 256×256×170 acquisition matrix in the x–, y–, and z–dimensions yielding a voxel size of 1.25×1.26×1.2 mm³. The MRI data were preprocessed by standard steps including anterior commissure and posterior commissure correction, skull-stripping, cerebellum removing, intensity inhomogeneity correction, segmentation, and registration (Shen and Davatzikos, 2004). Subsequently, we carried out automatic regional labeling by labeling the template and by transferring the labels following the deformable registration of subject images. After labeling 93 ROIs, we were able to compute volumes for each of these ROIs for each subject.

The Human 610-Quad BeadChip (Illumina, Inc., San Diego, CA) was used to geno-type 818 subjects with 228 Normal Controls (NC), 397 MCI, and 193 AD in the ADNI 1 database, which resulted in a set of 620,901 SNP and copy number variation (CNV) markers. Since the Apolipoprotein E (APOE) SNPs, rs429358 and rs7412, are not on the Human 610-Quad Bead-Chip, they were genotyped separately. These two SNPs together define a 3 allele haplotype, namely the ∊2, ∊3, and ∊4 variants and the presence of each of these variants was available in the ADNI database for all the individuals. The software EIGENSRAIT in the package of EIGENSOFT 3.0 was used to calculate the population stratification coefficients of all subjects. To reduce population stratification effects, we only used 761 Caucasians from all 818 subjects. We used the baseline T1 MRI scans and genetic data from all 742 Caucasians.

By following Wang et al. (2012), we selected SNPs belonging to the top 40 AD candidate genes by using quality control methods. The first line quality control steps include (i) call rate check per subject and per SNP marker, (ii) gender check, (iii) sibling pair identification, (iv) the Hardy-Weinberg equilibrium test, (v) marker removal by the minor allele frequency, and (vi) population stratification. The second line preprocessing steps include removal of SNPs with (i) more than 5% missing values, (ii) minor allele frequency smaller than 10%, and (iii) Hardy-Weinberg equilibrium p−value < 10⁻⁶. This left us with 1,071 SNPs on 37 genes. We used the 1071 SNP and APOE-∊4 to form X, that gives p = 1, 072.

4.2 Results

We fitted GLRR (5) with all the baseline volumes of 93 ROIs in 749 subjects as a multivariate response vector, the 1,072 selected SNPs as X matrix, and age, intracerebroventricular volume (ICV), gender, education and handedness as prognostic related covariates. To determine the rank of B, GLRR was fitted for up to r = 10 layers. By comparing the five different selection criteria, we chose r = 3 layers for the final data analysis. We ran the Gibbs sampler for 20, 000 iterations after 20, 000 burn-in iterations. Based on the MCMC samples, we calculated the posterior median and maximum absolute deviation (MAD) of the normalized U and V, and B, and then we used the standard normal approximation to calculate the p−values of each component of U, V, and B. The upper left panel of Figure 4 presents the estimated posterior median map of B, in which the elements with their p−values greater than 0.01 were set to zero, which reveals sparsely distributed points along the horizontal and vertical directions in the estimated B, indicating that the low-rank model would fit the ADNI data reasonably well.

Figure 4.

Results of ADNI data: the posterior estimate of $\widehat{B}$ matrix after thresholding out elements whose p− values are greater than 0.001 (left panel), $B_{bin}^T{B}_{bin}$ (middle panel) and $B_{bin}{B}_{bin}^T$ (right panel) in the first row; and the − log₁₀ p– value matrices corresponding to B (left panel), U (middle panel), and V (right panel) in the second row.

We used 1.426 × MAD to compute robust standard errors from the posterior median based MAD for each element of B and used a normal approximation to compute its −log₁₀(p). Specifically, we created two new matrices based on the estimated B in order to detect important ROIs and SNPs. We first applied this thresholding method to B in order to compute a new matrix B_bin, in which β_jk was set at zero if its −log₁₀(p) is less than 10, and set to 1 otherwise. Then, we calculated a 93 × 93 matrix $B_{bin}^T{B}_{bin}$ and a 1072 × 1072 matrix $B_{bin}{B}_{bin}^T$. See the upper middle and right panels of Figure 4. The second row of Figure 4 presents the −log₁₀(p) maps of B, U, and V, respectively.

We selected the top ROIs corresponding to the largest diagonal elementsof $B_{bin}^T{B}_{bin}$ which are listed in the first column of Table 2. We also picked the top ROIs based on the −log₁₀(p)−values in each column of V, which are shown in the second, third, and fourth columns in Table 2. The locations of these ROIs are shown in Figure 5. Among these ROIs, the left and right sides rank close to each other, which may indicate structural brain symmetry.

Table 2.

Ranked top ROIs based on the diagonal of $B_{bin}^T{B}_{bin}$ and columns of V.

$B_{bin}^T{B}_{bin}$	V 1	V 2	V 3
hiopp.R	caud.neuc.L	sup.t.gy.L	sup.p.lb.L
hiopp.L	caud.neuc.R	sup.t.gy.R	pstc.gy.L
amyg.R	post.limb.L	mid.t.gy.R	sup.o.gy.L
unc.L	post.limb.R	hiopp.R	prec.L
subtha.nuc.R	glob.pal.R	mid.t.gy.L	sup.p.lb.R
sup.t.gy.R	ant.caps.R	hiopp.L	pec.R
amyg.L	glob.pal.L	amyg.R	sup.o.gy.R
sup.t.gy.L	putamen. L	lat.ve.R	prec.gy.L
lat.ve.R	putamen. R	inf.t.gy.R	pstc.gy.R
nuc.acc.L	ant.caps.L	subtha.nuc.R	prec.gy.R
lat.ve.L	thal.R	amyg.L	me.f.gy.L
mid.t.gy.L	thal.L	unc.L	mid.f.gy.R
insula.L	tmp.pl.R	lat.ve.L	ang.gyr.L
sup.f.gy.L	subtha.nuc.L	inf.f.gy.R	sup.f.gy.L
insula.R	per.cort.L	lat.f-o.gy.L	fornix.L
mid.t.gy.R	tmp.pl.L	parah.gy.L	occ.pol.L
mid.f.gy.L	subtha.nuc.R	inf.t.gy.L	ang.gyr.R
unc.R	per.cort.R	parah.gy.R	cun.L
inf.t.gy.R	nuc.acc.L	nuc.acc.L	occ.pol.R
inf.f.gy.R	inf.t.gy.R	insula.L	mid.f.gy.L

Figure 5.

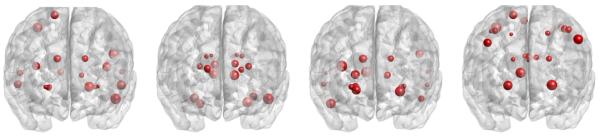
Results of ADNI data: the top 20 ROIs based on $B_{bin}^T{B}_{bin}$ and the first 3 columns of V. The sizes of the dots represent the rank of the ROIs.

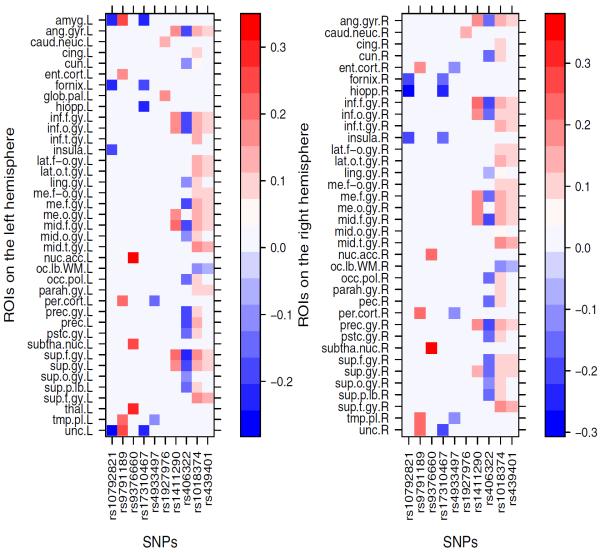
We ranked the SNPs in the B_binB_bin^T according to the sum of the columns, and in the first three columns of the U matrix by their −log₁₀(p)−values. The top 20 most significant SNPs and their corresponding genes are listed in Table 3 under columns B_binB_bin^T, U₁, U₂, and U₃, respectively. To investigate the top SNPs and their relationship with ROI volumes in the coefficient matrix. we retained SNPs, which are correlated with at least one ROI at a significant level smaller than 10^−6.3. For each SNP, we highlighted the locations of ROIs with correlation at a significant level smaller than 10^−6.3, which are shown in Figure 6. There are different patterns of SNPs' effects on ROIs: i) rs10792821 (PICALM), rs9791189 (NEDD9), rs9376660 (LOC651924), and rs17310467 (PRNP) are significantly correlated with a small number of ROIs with relative large coefficients; ii) rs4933497 (CH25H) and rs1927976 (DAPK1) are significantly correlated with a small number of ROIs with relative small coefficients; iii) rs1411290 (SORCS1), rs406322 (IL33), and rs1018374 (NEDD9) are significantly correlated with a large number of ROIs with medium coefficients; iv) rs1411290 (SORCS1), rs406322 (IL33) is significantly correlated with a large number of ROIs with small coefficients. Figure 7 shows the heatmap of coefficients among these 10 SNPs and the ROIs on the left and right hemispheres, respectively. The ROIs are chosen such that each ROI is significantly correlated to at least one of the 10 SNPs at a significance level small than 10^−6.3. We were able to detect some SNPs, such as rs439401 (gene APOE), among others. The use of imaging measures as endophenotype may dramatically increase statistical power in detecting much more informative SNPs and genes, which deserve further investigation in Alzheimer's research. In contrast, most GWA studies often use case-control status as the response variable, which leads to substantially power loss.

Table 3.

Ranked top SNPs based on the diagonal of $B_{bin}{B}_{bin}^T$ and columns of U.

$B_{bin}{B}_{bin}^T$		U 1		U 2		U 3
SNP	gene	SNP	gene	SNP	gene	SNP	gene
rs9376660	LOC651924	rs9389952	LOC651924	rs439401	APOE	rs1057490	ENTPD7
rs878183	SORCS1	rs1927976	DAPK1	rs1018374	NEDD9	rs406322	IL33
rs717751	SORCS1	rs659023	PICALM	rs4713379	NEDD9	rs6441961	CCR2
rs4713379	NEDD9	rs729211	CALHM1	rs9376660	LOC651924	rs913778	DAPK1
rs1411290	SORCS1	rs6037908	PRNP	rs878183	SORCS1	rs6457200	NEDD9
rs1930057	DAPK1	rs3014554	LDLR	rs1411290	SORCS1	rs1O18374	NEDD9
rs1O792821	PICALM	rs11757904	NEDD9	rs717751	ORCS1	rs10422797	EXOC3L2
rs406322	IL33	rs1336269	LOC651924	rs2327389	NEDD9	rs17310467	PRNP
rs9791189	NEDD9	rs1316801	CLU	rs10884402	SORCS1	rs11193593	SORCS1
rs1018374	NEDD9	rs744970	NEDD9	rs1251753	SORCS1	rs1O792821	PICALM
rs386880	IL33	rs1799898	LDLR	rs4796412	TNK1	rs9395285	CD2AP
rs17310467	PRNP	rs6133145	PRNP	rs2125071	SORCS1	rs2418960	SORCS1
rs4846048	MTHFR	rs7910584	SORCS1	rs6609709	OTC	rs10787011	SORCS1
rs10884402	SORCS1	rs1441279	SORCS1	rs4846048	MTHFR	rs7749883	LOC651924
rs3014554	LDLR	rs7067538	SORCS1	rs1360246	SORCS1	rs7025417	IL33
rs439401	APOE	rs10512188	DAPK1	rs9791189	NEDD9	rs10429166	TFAM
rs4878112	DAPK1	rs10491052	SORCS1	rs12625444	PRNP	rs1958938	DAPK1
rs10429166	TFAM	rs7929057	MS4A4E	rs10792821	PICALM	rs16871166	NEDD9
rs10787011	SORCS1	rs17475756	DAPK1	rs7918637	SORCS1	rs10948367	CD2AP
rs7095427	SORCS1	rs9496146	LOC651924	rs6088662	PRNP	rs13031703	BIN1

Figure 6.

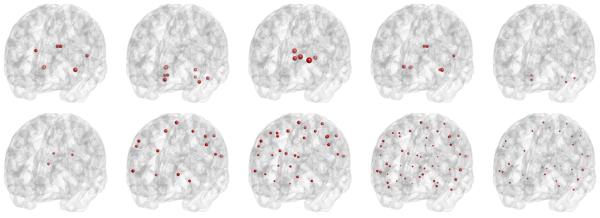
Results of ADNI data: at a −log₁₀(p) significance level greater than 6.3, the top row depicts the locations of ROIs that are correlated with SNPs rs10792821 (PICALM), rs9791189 (NEDD9), rs9376660 (LOC651924), rs17310467 (PRNP), rs4933497 (CH25H), respectively; the bottom row shows the ROIs correlated with SNPs rs1927976 (DAPK1), rs1411290 (SORCS1), rs406322 (IL33), rs1018374 (NEDD9), and rs439401 (APOE). The sizes of the dots represent the absolute magnitudes of the regression coefficients.

Figure 7.

Heatmaps of coefficients between SNPs and ROIs on the left (left panel) and right (right panel) hemispheres. Coefficients with −log₁₀(p)–value smaller than 6.3 are set to 0.

The correlation structure among imaging phenotypes and that among SNPs are characterized by the columns in U and V, respectively. Each column of U represents a group of SNPs that are similarly associated with a group of ROIs determined by the corresponding column of V. The identified correlated phenotypes and genotypes largely agree with the spatial and LD structure, which are shown in Table 3 and Figure 5. Multiple SNPs from the same gene appear in the same columns of U. However, due to different objectives, the structure captured by U and V may not be exactly identical to the correlation structure of imaging phenotypes only based on the phenotypes, and the LD structure of genotypes, respectively.

5 Discussion

We have developed a Bayesian analysis GLRR to model the association between high-dimensional responses and high-dimensional covariates with an novel application in imaging genetic data. We have introduced a low rank regression model to approximate the large association matrix through the standard SVD. We have used a sparse latent factor model to more flexibly capture the complex spatial correlation structure among high-dimensional responses. We have proposed Bayesian local hypothesis testing to identify significant effects of genetic markers on imaging phenotypes, while controlling for multiple comparisons. GLRR dramatically reduces the number of parameters to be sampled and tested leading to a remarkably faster sampling scheme and effcient inference. We have shown good finite-sample performance of GLRR in both the simulation studies and ADNI data analysis. Our data analysis results have confirmed the important role of well-known genes such as APOE-∊4 in the pathology of ADNI, while highlighting other potential candidates that warrant further investigation.

Many issues still merit further research. First, it is interesting to incorporate common variant and rare variant genetic markers in GLRR (Bansal et al., 2010). Second, external biological knowledge, e.g., gene pathways, may be the incorporated in the model through the use of more delicate priors to further regularize the solution (Silver et al., 2012). Third, it is important to consider the joint of genetic markers and environmental factors on high-dimensional imaging phenotypes (Thomas, 2010). Fourthly, the key features of GLRR can be adapted to more complex data structures (e.g., longitudinal, twin and family) and other parametric and semiparametric models. For instance, for longitudinal neuroimaging data, we may develop a GLRR to explicitly model the temporal association between high-dimensional responses and high-dimensional covariates, while accounting for complex temporal and spatial correction structures. Finally, it is important to combine different imaging phenotypes calculated from other imaging modalities, such as diffusion tensor imaging, functional magnetic resonance imaging (fMRI), and electroencephalography (EEG), in imaging genetic studies.