Accounting for Random Regressors: A Unified Approach to Multi-modality Imaging

Abstract

Massively univariate regression and inference in the form of statistical parametric mapping have transformed the way in which multi-dimensional imaging data are studied. In functional and structural neuroimaging, the de facto standard “design matrix”-based general linear regression model and its multi-level cousins have enabled investigation of the biological basis of the human brain. With modern study designs, it is possible to acquire multiple three-dimensional assessments of the same individuals — e.g., structural, functional and quantitative magnetic resonance imaging alongside functional and ligand binding maps with positron emission tomography. Current statistical methods assume that the regressors are non-random. For more realistic multi-parametric assessment (e.g., voxel-wise modeling), distributional consideration of all observations is appropriate (e.g., Model II regression). Herein, we describe a unified regression and inference approach using the design matrix paradigm which accounts for both random and non-random imaging regressors.

1 Introduction

The strong relationship between structure and biological function holds true from the macroscopic scale of multi-cellular organisms to the nano scale of biomacromolecules. Experience informs the clinical researcher that such structure-function relationships must also exist in the brain and, when discovered and quantified, will be powerful informers for early disease detection, prevention, and our overall understanding of the brain. Brain imaging modalities, such as positron emission tomography (PET) and magnetic resonance imaging (MRI), are primary methods for investigating brain structure and function. Quantification of the structure function relationship using imaging data, however, has been challenging owing to the high-dimensional nature of the data and issues of multiple comparisons.

Statistical Parametric Mapping (SPM) enables exploration of relational hypotheses without a priori assumptions of regions of interest (ROIs) where the correlations would occur [1, 2]. SPM was limited to single modality regression with imaging data represented only in the regressand until extensions (e.g., Biological Parametric Mapping, BPM) were developed to enable multi-modality regression, allowing for imaging data to use considered for both regressors and regressand [3, 4]. These multi-modal methods rely on the traditional ordinary least squares approach in which regressors are exactly known (i.e., conditional inference). Although this assumption may be reasonable in SPM, where scalar regressors are likely to have significantly less variance than the regressand imaging data, such an assumption is clearly violated when both regressors and regressand are observations from imaging data. With BPM inference is not inverse consistent; interchanging the regressors and regressand images would yield different estimates of relationships. The inconsistent inverse behavior of BPM is a result of violated mathematical assumptions, not underlying biological truths. A researcher is seeking to uncover the two way structure-function relationship and a mathematical technique that optimizes an inverse consistent mapping rather than a unidirectional mapping would bring estimates closer to modeling these underlying physical truths.

Regression analysis accounting for errors in regressors would greatly improve the credibility of the truth model whilst reasonably considering the randomness of the imaging modality. Statistical methods accounting for random regressors have been developed and are collectively known as Model II regression [5, 6]. Surprisingly, Model II regression has not been generalized for the massively univariate case. To more accurately reflect clinical imaging data, herein we develop a general model that accounts for both random regressors and non-random regressors for use in the context of BPM and multi-modality image regression.

2 Theory

Our aim is to explain the observed intensity from one imaging modality, y, with a set of regressors, x, of which at least one member is observed intensity from another imaging modality. We begin with a typical general linear model (GLM) and reformulate it to explicitly reflect the clinical imaging case of both random and non-random regressors. To begin, GLM is formulated as,

$$\mathit{y}={\sum }_{\mathit{l}=\mathbf{1}}^{\mathit{d}}{\mathit{x}}^{(\mathit{l})}{\mathit{\beta }}^{(\mathit{l})}+\mathit{\epsilon }$$ (1)

where d is the total number of regressors, ε is a parameterization of observational error in y, and β is a vector of the fitted coefficients. Let σ_x^(l) and σ_y represent the common variance of each element about its truth in x^(l) and y respectively. Then the x^(l) can be divided into two disjoint sets, fixed regressors whose values are considered to be exactly known, x_f, s.t. (σ_xf ≪ σ_y), and random regressors, x_r, s.t. (σ_xr not ≪ σ_y). In BPM, all regressors are treated as fixed regressors. By inclusion of random regressors, that Model-II diverges from BPM. Owing to their larger σ values, the observed x_r are only therefore noisy estimates of the truth, x_rT. Eq. 1 then becomes,

$$\mathbf{y}={\sum }_{j=1}^q{\mathbf{x}}_{\mathbf{rT}}^{(\mathit{j})}{\beta }_r^{(j)}+{\sum }_{k=1}^m{\mathbf{x}}_{\mathbf{f}}^{(\mathit{k})}{\beta }_f^{(k)}+\mathbf{\epsilon }$$ (2)

where q and m represent the total number of random and fixed regressors respectively. The challenge here, that is not present in Model-I, is to estimate β_r and β_f given that x_rT in Eq. 2 is not observed, but rather the noisy x_r. There are many possible methods for solving for β, here we choose an approach that follows the ordinary least squares example. We seek a solution for the parameters, β, that maximize the log-likelihood of the model given the observed data (maximize ln P(y, x_r|β, Σ, y_T, x_rT)).

Let i = 1,2, … n index the observations in y and in each of the ${\mathbf{x}}_{\mathbf{r}}^{(\mathit{j})}$ (e.g. n = the number of subjects and i indexes the subject number). Let z_i be a vector representing the i’th set of observational errors in y and in each ${\mathbf{x}}_{\mathbf{r}}^{(\mathit{j})}$. We can assume the errors follow a multivariate normal distribution with mean 0 and covariance matrix, Σ [7].

$${\mathbf{z}}_{\mathit{i}}=\left[\begin{array}{cccc}\text{y}-{\text{y}}_{\text{T}}& {\text{x}}_{\text{r}}^{(1)}-{\text{x}}_{\text{rT}}^{(1)}& \dots & {\text{x}}_{\text{r}}^{(q)}-{\text{x}}_{\text{rT}}^{(q)}\end{array}\right]\sim \mathrm{\Phi }(\mathbf{0},\mathrm{\sum })$$ (3)

Note that the observational errors, z, are errors across subjects and do not condition errors across an image. Given that each ${\mathbf{x}}_{\mathbf{r}}^{(\mathit{j})}$ vector is observed from a unique experimental technique, it is reasonable to assume that the columns of z_i are independent. We further assume that z_i is independent as each subject is independent. Under these assumptions (normal and i.i.d.), the log-likelihood of the observed data, given the model in Eq. 2 is,

$$ln\text{P}(\mathbf{y},{\mathbf{x}}_{\mathbf{r}}\mid \mathbf{\beta },\mathrm{\sum },{\mathbf{y}}_{\mathbf{T}},{\mathbf{x}}_{\mathbf{rT}})=\sum _{i=1}^{n}ln\left(2{\pi }^{-n/2}\left(det{(\mathrm{\sum })}^{-1/2}\right)\right)-\frac{1}{2}\sum _{i=1}^n({\mathbf{z}}_{\mathit{i}}{\mathrm{\sum }}^{-1}{\mathbf{z}}_{\mathit{i}}^{\prime })$$ (4)

Maximizing the log likelihood, Eq. 4, is equivalent to minimizing $s={\sum }_{i=1}^n({\mathbf{z}}_{\mathit{i}}{\mathrm{\sum }}^{-1}{\mathbf{z}}_{\mathit{i}}^{\prime })$. With the assumption of independent observations (independent subjects, i, and independent experiments, x_r^(j)), the covariance matrix, Σ, is diagonal with entries $\begin{array}{ccc}{\sigma }_y^2& {\sigma }_{x_r^{(1)}}^2& \dots {\sigma }_{x_r^{(q)}}^2\end{array}$. Hence, s can be re-expressed as,

$$s=\sum _{i=1}^n\left({\sigma }_y^{-2}{(y_i-y_{T_i})}^2+\sum _{j=1}^q{\sigma }_{x_r^{(j)}}^{-2}{\left(x_{r_i}^{(j)}-x_{{rT}_i}^{(j)}\right)}^2\right)$$ (5)

where $x_{r_i}^{(j)}$ represents the i^th element of ${\mathbf{x}}_{\mathbf{r}}^{(\mathit{j})}$. Eq. 5 is minimized when its partial derivatives w.r.t to each dependent variable is zero. We first solve for x_rT at the minimum of Eq.5 by differentiating s with respect to ${\mathbf{x}}_{\mathbf{rT}}^{(\mathit{j})}$ and setting the result to 0 gives q total equations, one for each ${\mathbf{x}}_{\mathbf{rT}}^{(\mathit{j})}$. With q equations and q unknowns, ${\mathbf{x}}_{\mathbf{rT}}^{(\mathit{j})}$ can be solved in terms of the other parameters. For a given term indexed by h,

$${\mathbf{x}}_{\mathbf{rT}}^{(\mathit{h})}=\frac{{\beta }_r^{(h)}{\sigma }_{x_r^{(h)}}^2\left(\mathbf{y}+{\mathbf{x}}_{\mathbf{r}}^{(\mathit{h})}{\beta }_r^h-{\sum }_{j=1}^q{\mathbf{x}}_{\mathbf{r}}^{(\mathit{j})}{\beta }_r^{(j)}-{\sum }_{k=1}^m{\mathbf{x}}_{\mathit{k}}^{(\mathit{j})}{\beta }_r^{(j)}\right)+{\mathbf{x}}_{\mathbf{r}}^{(\mathit{h})}\left({\sum }_{j=1}^q\left({\beta }_r^{(j)}{\sigma }_{x_r^{(j)}}^2\right)-{\beta }_r^{(h)}{\sigma }_{x_r^{(h)}}^2+{\sigma }_y^2\right)}{{\sigma }_y^2+{\sum }_{j=1}^q{\beta }_r^{(j)2}{\sigma }_{x_r^{(j)}}^2}$$ (6)

Substituting Eq. 6 for ${\mathbf{x}}_{\mathbf{rT}}^{(\mathit{j})}$ in Eq. 5, s becomes,

$$s=\frac{1}{{\sigma }_y^2}\sum _{i=1}^n\frac{{\left(y_i-\left({\sum }_{j=1}^q{x}_{r_i}^{(j)}{\beta }_r^{(j)}+{\sum }_{k=1}^m{x}_{f_i}^{(k)}{\beta }_f^{(k)}\right)\right)}^2}{{\sigma }_y^2+{\sum }_{j=1}^q{\beta }_r^{(j)2}{\sigma }_{x_r^{(j)}}^2}$$ (7)

Eq. 7 is now independent of the unknown x_rT and provides an intuitive form as the model error in the numerator is balanced by the individual variances in the denominator and mirrors the more readily available multivariate case with non-random x and the univariate case that accounts for a single random x [8]. Eq. 7 is a function of two unknowns, β and σ. Note that the true σ does not factor into s, only the ratio of variance matters. If these ratios are known, then β is the only unknown; and the β that maximizes Eq. 4 can be solved by taking the partial derivative of s with respect to β and setting the result to 0. The partial derivative equations are nonlinear w.r.t. β, and solving for the closed form solution of β is involved, so we employ numeric optimization methods.

In the Model II approach, the variance ratio needs to be known in order to minimize s by solving β. The restriction arises because the number of unknown parameters is larger than the number of equations [9]. If we add the further assumption that the ratio of the overall variance across subjects is proportional to the ratio of the image noise variance, then we can estimate the model variance ratio by estimating the ratio of image noise for each modality.

Inference on β

The maximum likelihood estimate of β, β_est, with a true value β_T, is asymptotically normally distributed as β_est − β_T)~Φ(0, nI⁻¹) where I is the Fisher information matrix (I_w,g = E[−∇_β^(w)β^(g) ln P_i(y_i, x_ri|β, Σ, y_T, x_rTi)]), with w = 1,2,…q+m, g = 1,2,…q+m, P_i is the probability function for data i. Noting the distribution ${\text{y}}_{\text{i}}-\left({\sum }_{j=1}^q{x}_{r_i}^{(j)}{\beta }_{\mathit{est},r}^{(j)}+{\sum }_{k=1}^m{x}_{r_i}^{(k)}{\beta }_{\mathit{est},f}^{(k)}\right)\sim N\left(0,{\sigma }_y^2+{\sum }_{j=1}^q{\beta }_{\mathit{est},r}^{(j)2}{\sigma }_{x_r^{(j)}}^2\right)$, the Fisher information can be estimated from prior ratio and dataset. Allowing c to represent the contrast vector and β_T = β_null to be the null hypothesis, then it follows that the test-statistic, ${{\mathbf{c}}^{\prime }}^{({\mathbf{\beta }}_{\mathbf{est}}-{\mathbf{\beta }}_{\mathbf{null}})}/\sqrt{{\mathbf{c}}^{\prime }{(\mathit{n}\widehat{\mathbf{I}})}^{-\mathbf{1}}\mathbf{c}}$ is t-distributed with n-(q+m) degrees of freedom. This is an asymptotic t-test as all estimated parameters and Fisher information are asymptotically valid.

3 Methods and Results

3.1 Single voxel simulations with known true variance ratios

Model II regression is implemented using the Nelder–Mead method to find the optimized solution of β. For each of the following 3 scenarios, a simulated voxel with 50 observations (i.e., subjects) was studied using a model with one random regressor, one fixed regressor, and a single constant: y_T = x_rTβ_r + x_fβ_f + β₁. In each of 500 Monte Carlo trials: β_T were chosen randomly from the uniform distribution (0–2); errors were added to y_Ti and x_rTi from a normal distribution with fixed standard deviations, and the true variance ratio was assumed known. Model II and OLS performance were evaluated with the relative root mean squared error in β (rβ_RMS).

1. Model II vs OLS response to σ_x: σ_y ratios (Figure 1A). Simulations were performed varying σ_x:σ_y. Model II regression performs equally well as OLS with small σ_x:σ_y, but becomes advantageous as more relative error is introduced into x_r observations. The improvement is observed specifically on β_r, whereas the constants not associated with random regressors, β₁ and β_f, remain with equal accuracy in estimation between the two models.

2. Model II vs OLS response to number of random x regressors (Figure 1B). The above model was altered by including up to 4 additional random regressors with randomized coefficients. Model II has smaller errors in the β_r estimates than OLS, however Model II becomes less advantageous with increases in the number of random x regressors. Note, the number of observations was not increased to compensate for the increased model complexity so less data per regressor is available with more regressors.

3. Model II sensitivity to the estimated ratio (Figure 1C). To assess the response of Model II to estimated ratios that deviate from the truth, the assumed true ratio of variance was altered between 1/10^th and 10 times its true value. Under the cases simulated here, Model II is insensitive to the ratio estimate for the range (0.5–2) and relatively insensitive over the range (.1–3).

Fig. 1.

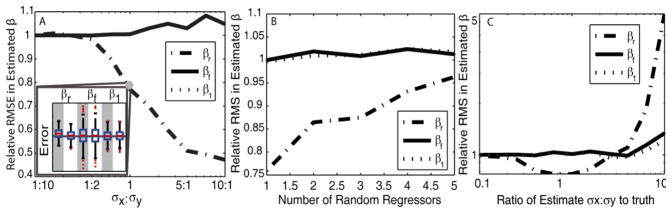
The relative RMSEs of Model II to OLS for each estimated coefficient (β_r, β_f, β₁) are plotted as a function of the ratio of the true standard deviations, σ_x:σ_y (A), the number of random regressors, $x_r^{(s)}$ (B) and the accuracy of the ratio estimate (C). With increasing σ_x:σ_y ratios, model II regression has increased relative accuracy in β_r estimates compared to OLS with increasing σ_x:σ_y ratios. Comparison of the β_f, β_r, and β₁ error distributions formed is shown explicitly in the inlay for the point σ_x/σ_y =1 in (A). The gray column shows the OLS error and the white column shows the Model II error, the horizontal line is where the error is zero. In (C), for one unit σ_y, the estimated ratio μ_x was allowed to deviate from the ideal case, μ_x/σ_x = 1. The common point shared in (A, B, C) is located in (B) at ‘Number of Random Regressors’ = 1, and (C) at ‘Ratio of Estimate to Truth’ = 1.

At extremely incorrect ratio values, the β_r estimate rapidly looses accuracy. Based on this analysis we can apply Model II regression using estimated error ratio, with reasonable confidence in the methods’ tolerance to mis-estimation of variance ratios.

3.2 Volumetric Imaging Simulation

Model II regression is incorporated as a regression method choice in the BPM toolbox for the SPM software using Matlab (Mathworks, Natick, MA). We simulated images of two modalities and regressed one modality on the other modality. The true regressor images are simulated from smoothed gray matter density images of 20 participants in the normal aging study of the BLSA neuroimaging project consisting of 79*95*69 voxels with 0.94*0.94*1.5 mm resolution [10]. The observed regressor images are simulated by adding zero mean Gaussian noise. The true regressand image intensity is “1.5*true regressor images – constant” inside the caudate region and equals a different constant everywhere else inside the brain mask. The observed regressand images were generated by adding zero mean Gaussian noise to the true regressand images. The standard deviation of the noise is selected to make SNR=15. (SNR is defined as the mean signal divided by the standard deviation of noise). The observed regressor images and observed regressand images are used for simulation and the ratio of noise standard deviation is used as the ratio of observation error in Model II regression.

Fig. 2 presents the results for 20 simulated subject brains, each represented by a pairs of images. The statistical significance map is shown according to uncorrected p-value with p<0.001 and 5 voxels extent threshold to exclude noise. Type I error and type II error are calculated at uncorrected p-value<0.001 inside (for true-positive, TP, and false-negative, FN) and outside a caudate mask (for false-positive, FP, and true-negative, TN). In this simple model, both OLS and Model II regression control type I error as expected. Meanwhile, Model II regression improves true positive rate as compared to OLS regression.

Figure 2.

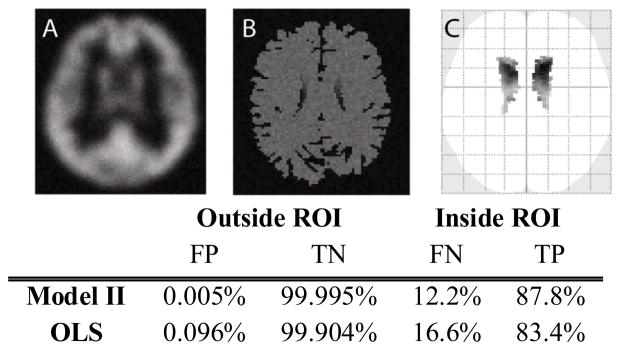
(A) is one regressor image, (B) is one regressand image in Model II BPM simulation. (C) is one dimension of the glass brain which is the projected statistical significance. The glass brain is shown according to uncorrected p-value p<0.001 and 5 voxels extent threshold to exclude noise. The table is calculated with p<0.001.

3.3 Empirical demonstration of Model II regression

Image-on-image regression offers a direct opportunity to study associations between differing spatially located factors. As an illustrative example, consider potential correlations between GM tissue density (a structural measure) and PET signal (a measure of functional activity). A first model would associate tissue presence with greater functional signal. An analysis of modulating factors for this relationship (such as disease condition, intervention, or task) could reveal anatomical correlates of functional reorganization and shed light on the applicability of the structural-functional hypothesis.

Following this approach, we perform regression analysis of the relationship between anatomical MRI gray matter images (GM, as classified by SPM5) and functional PET images. PET and GM data were collected on a total of n = 46 observations (23 subjects imaged twice). Regression was performed in both directions in order to quantify both structure→function and function→structure relationships. The regression model used 1 random regressor and a single constant. For the Model II ratio, noise ratio is estimated following the method in [11]. The raw data and the resulting regression lines for a single voxel comparison are displayed. Fi.e 3 shows that Model II is symmetric, i.e., the mapping PET→GM is the inverse of the mapping GM → PET. The corresponding estimated variances for Model II are also smaller than the corresponding estimated variances in OLS forward regression and OLS inverse regression.

4 Discussion

Properly accounting for error is essential for valid parameter estimation and statistical inference. Herein, we have demonstrated that a full consideration of observation variability is feasible within the confines of a design matrix paradigm. Furthermore, we can readily consider simultaneous treatment of parameters with measurement error (x_r) alongside traditionally defined fixed parameters (x_f). Our formulation of “random observations” remains within the context of a “fixed effects” model as the β_r are deterministic parameters, as opposed to the classic “random effects” model where parameters are stochastic. These two approaches are complementary and could be combined for an appropriate experimental framework. Extension of the Model II concepts to time series, hierarchical and complex model designs would be a fascinating area for continuing research.

We have observed substantial improvements in model fit and increased statistical power using Model II regression as opposed to OLS (Fig. 1A). While robust to model complexity (Fig. 1B) and prior estimation of observation variability (Fig. 1C), the improvements were not universal. When the OLS is appropriate (i.e., σ_x ≪ σ_y), there was a slight increase in observed error (Fig. 1A); however, as the relative variance in x increased, the OLS assumption of fixed regressors becomes increasingly violated and notable bias and increased variance could be observed in the OLS estimates. Examination of the inlays in Fig. 1 reveals a slight increase in error for the fixed parameters, β_f and β₁, but a lack of appreciable bias.

The generalized Model II regression model can be used to analyze any complicated relationship by applying Taylor series and expand design matrix. Our presentation of Model II regression is inverse consistent, provides a logical framework for exploring relationships in multi-modal image analysis, and can help model relative uncertainty in imaging methods. Other error models may be more appropriate for specific imaging modalities and warrant further consideration.

Our presentation of the empirical analysis is preliminary and ongoing as is highlighted by the single voxel presentation. Interpreting the ratio of model variances is subject of active consideration as must consider the potential impact of both the imaging variability and model fit error in multiple dimensions. As discussed, we currently approximate this combined quantity as proportional to the imaging variability alone. Relaxing this assumption would greatly aid in generalization of this approached. These methods are available in open source as plug-ins for the SPM package.

Figure 3.

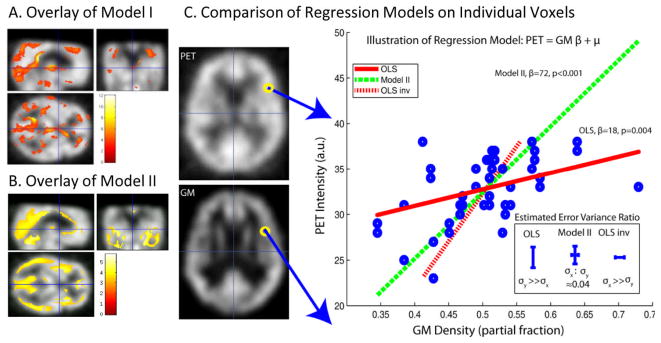
Model II and Model I (OLS) multi-modality regression analysis. Model I (A) and Model II (B) lead to distinct patterns of significant differences (p<0.001, uncorrected) when applied to identical empirical datasets and association models. Inspection of single voxel: PET vs Grey Matter MRI (GM) illustrates the reasons for the different findings (C). The GLM model used for the forward mapping is y = x_rβ_r + β₁, where y represents PET image intensity and x_r represents GM normalized image intensity. On the left-hand side of (C), example images of PET and GM are shown, along with the location of the single example voxel whose regression analysis is displayed in the right-hand plot. The individual data points (blue circles) were fit using OLS (red lines) and Model II regression (green dashed line). The inverse mapping for OLS (red dash) is unique from the forward mapping (red full). The Model II mapping was found to be reversible and can be represented by the same line. Resulting error bars and corresponding σ_x:σ_y value estimates are compared between OLS and Model II in the lower right-hand insert.