Abstract
Purpose:
Magnetic resonance imaging (MRI) is a prime candidate for image-guided radiotherapy. This study was designed to assess the feasibility of real-time MRI-guided proton therapy by quantifying the dosimetric effects induced by the magnetic field in patients’ plans and identifying the associated clinical consequences.
Methods:
Monte Carlo dose calculation was performed for nine patients of various treatment sites (lung, liver, prostate, brain, skull-base, and spine) and tissue homogeneities, in the presence of 0.5 and 1.5 T magnetic fields. Dose volume histogram (DVH) parameters such as D95, D5, and V20 as well as equivalent uniform dose were compared for the target and organs at risk, before and after applying the magnetic field. The authors further assessed whether the plans affected by clinically relevant dose distortions could be corrected independent of the planning system.
Results:
By comparing the resulting dose distributions and analyzing the respective DVHs, it was determined that despite the observed lateral beam deflection, for magnetic fields of up to 0.5 T, neither was the target coverage jeopardized nor was the dose to the nearby organs increased in all cases except for prostate. However, for a 1.5 T magnetic field, the dose distortions were more pronounced and of clinical concern in all cases except for spine. In such circumstances, the target was severely underdosed, as indicated by a decrease in D95 of up to 41% of the prescribed dose compared to the nominal situation (no magnetic field). Sites such as liver and spine were less affected due to higher tissue homogeneity, typically smaller beam range, and the choice of beam directions. Simulations revealed that small modifications to certain plan parameters such as beam isocenter (up to 19 mm) and gantry angle (up to 10°) are sufficient to compensate for the magnetic field-induced dose disturbances. The authors’ observations indicate that the degree of required corrections strongly depends on the beam range and direction relative to the magnetic field. This method was also applicable to more heterogeneous scenarios such as skull-base tumors.
Conclusions:
This study confirmed the dosimetric feasibility of real-time MRI-guided proton therapy and delivering a clinically acceptable dose to patients with various tumor locations within magnetic fields of up to 1.5 T. This work could serve as a guide and encouragement for further efforts toward clinical implementation of hybrid MRI–proton gantry systems.
Keywords: MRI-guided, proton therapy
1. INTRODUCTION
Proton therapy is one of the most advanced forms of cancer treatment. The main advantage of proton therapy compared to conventional photon therapy is the ability to reduce the integral dose to patients and thus reduce the side effects.1–3 This advantage is mainly due to the finite range, which also makes proton therapy more susceptible to uncertainties caused by the geometrical variations of the patient, i.e., setup misalignments, interfractional anatomy changes, and intrafractional motion.
Image-guided radiation therapy (IGRT) can reduce these uncertainties, and hence, reduce the associated safety margins used in the treatment planning protocols to compensate for any unexpected target changes, thus sparing more of the healthy tissue.4,5 An example of IGRT is cone beam computed tomography (CBCT) guided radiotherapy in which daily interfractional anatomy variations are captured by on-board CBCT detectors providing volumetric images. Time-resolved images can also be acquired before treatments to extract motion trajectories for intrafractional motion compensation.6,7 However, the excess radiation dose delivered to the patient by this method is undesirable, especially in treatments of pediatric patients who are more susceptible to developing secondary malignancies. Furthermore, the trade-off between the acquisition time and the accuracy of the motion patterns for 4D applications has imposed limitations.8 The use of ultrasound image guidance has also been investigated for almost a decade for pretreatment tumor localization and real-time tumor tracking. The drawbacks of this technique are realized to be the operator dependency of the image quality and difficulties of remote imaging operation during therapy.8,9 Due to its enhanced soft tissue contrast, ultrafast sequences, and the absence of ionizing radiation, magnetic resonance imaging (MRI) is an excellent candidate for real-time image guidance in radiotherapy. In addition, it could allow more precise soft tissue-based tumor delineation (e.g., liver). Several institutions have studied the clinical feasibility of combining MRI and Linac-based radiotherapy units and are currently developing prototype systems.9–14 Furthermore, a cobalt-60 based MRI-guided radiotherapy system has already been manufactured and is clinically available.15
Because of inherently higher geometrical sensitivity, proton and heavier particle therapy can benefit from IGRT even more than photon therapy. However, there is a lack of routine volumetric image guidance in proton therapy. Currently, only two orthogonal x-ray projection images are used to register the patient position at delivery to that of the treatment planning system in most proton centers. Systems allowing CBCT are being investigated and slowly introduced to the clinic for pretreatment setup and anatomy verification (Cho et al. 2009). For real-time soft tissue monitoring and motion mitigation, a MRI scanner could potentially be integrated with a proton therapy gantry to create a state-of-the-art hybrid system to provide real-time structural, functional, and physiological information during treatment, e.g., deformable organ motion and tumor hypoxia levels.16–19
Respiratory motion compensation (i.e., gating and tumor tracking) is the ultimate goal of IGRT. In proton and carbon ion therapy, tumor tracking can be achieved by updating the pencil beam spot positions during active scanning delivery, according to the live feedback from motion detection devices.20–22 For tumors in the thorax, abdomen, and pelvis, motion detection is currently performed using surrogate signals such as implanted markers, optical scanning of external surfaces, fluoroscopy, and ultrasound. However, these methods are either invasive and/or not sufficiently accurate.23,24 The real-time acquisition of MRI could be a perfect fit for providing instantaneous and accurate motion information to the delivery system.
Although the clinical feasibility of combining MRI and photon therapy Linac has been clearly demonstrated, additional challenges exist for the application in proton therapy. The key challenge involves the interferences between the therapy and imaging systems, i.e., geometrical restrictions in coupling the gantry and MRI systems, as well as the distortion of the primary beam trajectory by the MRI magnetic field. The effect of the magnetic field is larger for proton beams than for photon beams because for protons, both the primary as well as secondary electrons are effected. While an optimal design for the geometrical coupling of proton gantry and MRI scanner has not yet been investigated, a previous study has reported on initial findings of the functional aspect by examining the effect of magnetic fields on the proton dose in phantoms.25 They simulated a homogeneous water phantom without and with an air gap irradiated by pencil and broad monoenergetic proton beams in the presence of 0.5 and 3 T magnetic fields. However, the more clinically relevant aspect such as the impact on actual patient treatment (i.e., effects of tissue heterogeneity and clinical beam combinations) has not been investigated.
The goal of this study was to characterize the magnetic field-induced dose distortions in patient anatomies within realistic magnetic fields (in terms of amplitude and direction) and using therapeutic proton beams. The clinical significance of the dosimetric effects was examined for various treatment sites and field settings through Monte Carlo (MC) simulations. Strategies to further correct clinically unacceptable dose changes were explored. We aimed to determine the necessary plan corrections using patient-specific pretreatment MC calculations. This would decouple the magnetic field kernel from the treatment planning algorithm, allowing its application with any planning system. This strategy could be considered as an initial solution for correcting the dose effect within relatively large magnetic fields and the final clinical implementation might look different. The findings of this work could be applied to better understand the treatment site, tumor characteristic, beam setup and magnetic field dependency of the dose distortions, and to assess the potential feasibility of recovering the dosimetric quality of the patient plans for real-time MRI-guided proton treatments.
2. METHODS
2.A. Subject cohort
Nine patients treated with passively scattered protons were retrospectively selected from the institution database. The plans had been generated by clinical dosimetrists using the XiO (Elekta, Stockholm, Sweden) planning system. The aperture margins were site-dependent and ranged between 5 and 15 mm. All beams included 3.5% of the prescribed range plus 1 mm range uncertainty margins and 3–10 mm range compensator smearing. The tumor sites included prostate, lung, liver, spine, brain, and skull-base. Two patients were chosen from each of the former three sites, more likely to be affected by respiratory motion. They were deliberately selected to have tumors of different sizes and locations. One patient from each of the latter three sites, where targets are relatively stationary and immobilized, was included for comparison. The skull-base patient was a representative case of very heterogeneous tumor location (Fig. 1). The prescribed dose, tumor volume, number of beams, and average range for each case are summarized in Table I. Targets and organs at risk (OAR) were taken as originally delineated by the treating physician. Targets are defined as volumes used to construct the beam and beam shaping devices within the plan (CTV or PTV). All targets included safety margins typically used to account for setup errors, anatomy changes, and motion.
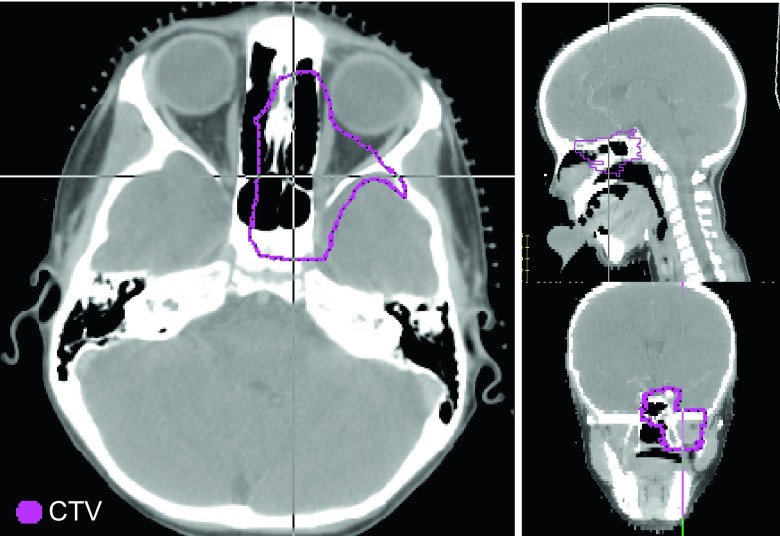
FIG. 1.
The skull-base case (patient 8) is a representative patient with CTV located within highly heterogeneous tissue.
TABLE I.
Patient cohort specifications and applied plan corrections (at 1.5 T magnetic field). Patient 1 plan includes no boost fields.
| Patients | Prescribed dose (Gy) | Target volume (cm3) | Average range (mm) | Number of beams | Feasible margin reduction (mm) | Isocenter shift (mm) | Gantry rotation (degrees) |
|---|---|---|---|---|---|---|---|
| 1-Prostate | 50.0 | 129.0 | 269.0 | 2 | 5.0 | 5.0–19.0 | — |
| 2-Prostate | 78.0 | 89.1 | 254.5 | 4 | 5.0 | 5.0–19.0 | — |
| 3-Liver | 52.5 | 306.6 | 140.5 | 2 | 4.0 | 0.0–4.0 | — |
| 4-Liver | 58.05 | 138.6 | 172.0 | 2 | 4.0 | 0.0–15.0 | — |
| 5-Lung | 66.0 | 318.0 | 178.5 | 2 | 10.0 | 15.0 | 10 (all) |
| 6-Lung | 48.0 | 2.3 | 80.0 | 2 | 10.0 | 6.0 | — |
| 7-Brain | 52.2 | 11.2 | 122.3 | 4 | 2.0 | 10.0 | 10 (SA) |
| 8-Skull base | 50.4 | 61.2 | 128.7 | 6 | 4.0 | 0.0–13.0 | — |
| 9-Spine | 50.4 | 46.9 | 103.0 | 1 | 5.0 | — | — |
2.B. Dose calculation
The impact of the magnetic field on the proton dose for each patient was calculated using topas (Tool for PArticle Simulation), an extensively validated MC framework based on geant4.26,27 topas tracks the primary protons through a detailed treatment head geometry and a patient CT.28,29 A magnetic field component was activated in the patient dose calculation phase of topas. The MRI system was represented by a box of air containing a uniform magnetic field. Magnetic fields of 0.5 and 1.5 T in caudal–cranial (longitudinal) and anterior–posterior (AP, transverse) directions with respect to the patient orientation were investigated. The nominal situation with no magnetic field was calculated as a reference. As an initial validation study, the deflection of 90 and 200 MeV pencil proton beams incident on uniform water phantoms in a magnetic field region of 0.5 and 1.5 T was calculated with topas and compared with theoretical calculations and previous MC studies.
2.C. Data analysis
The key goal of IGRT is to reduce the target margins that are normally applied to make the plan more robust to uncertainties from patient setup, motion, and anatomy changes. In this analysis, we investigated if this goal is realistic in the presence of the MRI magnetic field and estimated how much the margins could be reduced without compromising the target coverage. However, instead of replanning with smaller margins (thus smaller field size), we chose to keep the plan the same but analyze the dose on an expanded target volume. This procedure is equivalent to having a new plan made for a slightly larger target that has relatively smaller margins. With this new target definition, the coverage was made more vulnerable and sensitive to possible dose deviations due to the beam deflection induced by the magnetic field. This offers a better indication of the susceptibility to loss of coverage when the margins are potentially reduced owing to IGRT. For each case, the magnitude of this expansion was defined as the maximum amount that the target could be isotropically extended without compromising the prescribed target coverage. This was done by varying the target size post MC, and assessing the coverage of the new target. The feasible margin reduction for each case is equal to the magnitude of this expansion and is given in Table I.
The dose volume histograms (DVHs) for the target and OARs were extracted from the calculated dose distributions for each patient and magnetic field case. This was done using Computational Environment for Radiation Research (CERR).30 The OARs for each treatment site included organs that received mean dose of larger than 1 Gy. In each case, the DVH was compared with the nominal situation (no magnetic field). The equivalent uniform dose (EUD)31 as well as D95, D5, and V20 (doses at 95% and 5% volume, and volume at 20% of the prescribed dose) were calculated for each OAR. The organ-specific EUD model parameters are listed in Table II. The DVH parameters for the targets were evaluated on the expanded volumes, as described above, to examine the feasibility of potential margin reduction. If the DVH parameters, especially EUD and D95 were within 2% of the nominal case (less than 2% decrease for target and 2% increase for OAR), the dose distribution was considered clinically acceptable. This was assessed by calculating the percentage difference between the DVH parameters: ΔD = (D(0T) − D)/Dp∗100, where D is a given dose parameter and Dp is the prescribed dose, and ΔV = (V(0T) − V)∗100, where V is a given volume parameter.
TABLE II.
| Organ | a value | Organ | a value | Organ | a value |
|---|---|---|---|---|---|
| Tumor | −10.0 | Large bowel | 5.8 | Spinal cord | 20.0 |
| Bladder | 8.0 | Kidney | 1.4 | Ribs | 10.0 |
| Rectum | 8.0 | Protohepatis | 0.8 | Optic nerves | 10.0 |
| Femur | 12.0 | Lung | 1.2 | Brain | 10.0 |
| Liver | 3.1 | Heart | 2.9 | Brainstem | 12.0 |
| Chestwall | 8.0 | Esophagus | 16.6 | Lenses | 3.3 |
In situations where the deviation from the nominal dose distribution was larger than the accepted threshold (±2%), we explored methods to correct the plans using MC calculations. The aim here was to examine whether or not treatment delivery in the presence of large magnetic fields is feasible by using patient-specific plan corrections following the standard treatment planning procedures. This part of the study was mainly designed as a feasibility study, although the clinical realization of this aspect might eventually be different. We studied a method that involved modifying the plan parameters, by introducing small translations of the beam isocenter and/or extra rotations of the gantry. The translations were determined by identifying the lateral shift between the isocenter and a point within the deflected dose distribution corresponding to the original isocenter. The magnitude of translations estimated based on reviewing the dose profiles and visual inspection of the beam deflection was found to be generally consistent with the values determined using the magnetic field strength, beam direction, and the individual beam energy/range by applying analytical methods.32 This correction was necessary for all beams not parallel to the magnetic field direction. The gantry rotations (relative to the isocenter axis) were only needed if the applied isocenter translations could negatively impact the target coverage (due to large tissue heterogeneity) and/or the dose to OARs located lateral to the beam path. Rotations were used to restore the trajectory of the translated beam to approximately its original orientation. The magnitude of the rotations was estimated from the known beam range and isocenter shift. In most cases studied here, rotations were not necessary.
3. RESULTS
3.A. MRI-induced dose distortions
As the initial validation, lateral deflection of monoenergetic proton pencil beams of 90 and 200 MeV energy in a water phantom placed inside a uniform magnetic field of 0.5 and 1.5 T is shown in Fig. 2. The 90 MeV beam with a water equivalent range of 54 mm showed lateral deflection of 1.2 and 3.0 mm at the isocenter in the presence of 0.5 and 1.5 T magnetic field, respectively. These values increased to 10.0 and 28.0 mm in case of a 200 MeV beam with a range of 250 mm. These initial findings agreed well with the analytic calculations, which, for example, predict a 10-mm deflection of a 200 MeV proton beam at the end of range in a 0.5 T magnetic field,32 as well as previous phantom studies.25
FIG. 2.
(a) Dose distribution and (b) pristine peak profile in the presence of 0.5 T (solid line) and 1.5 T (dashed line) magnetic fields for (left) 90 MeV and (right) 200 MeV proton pencil beams.
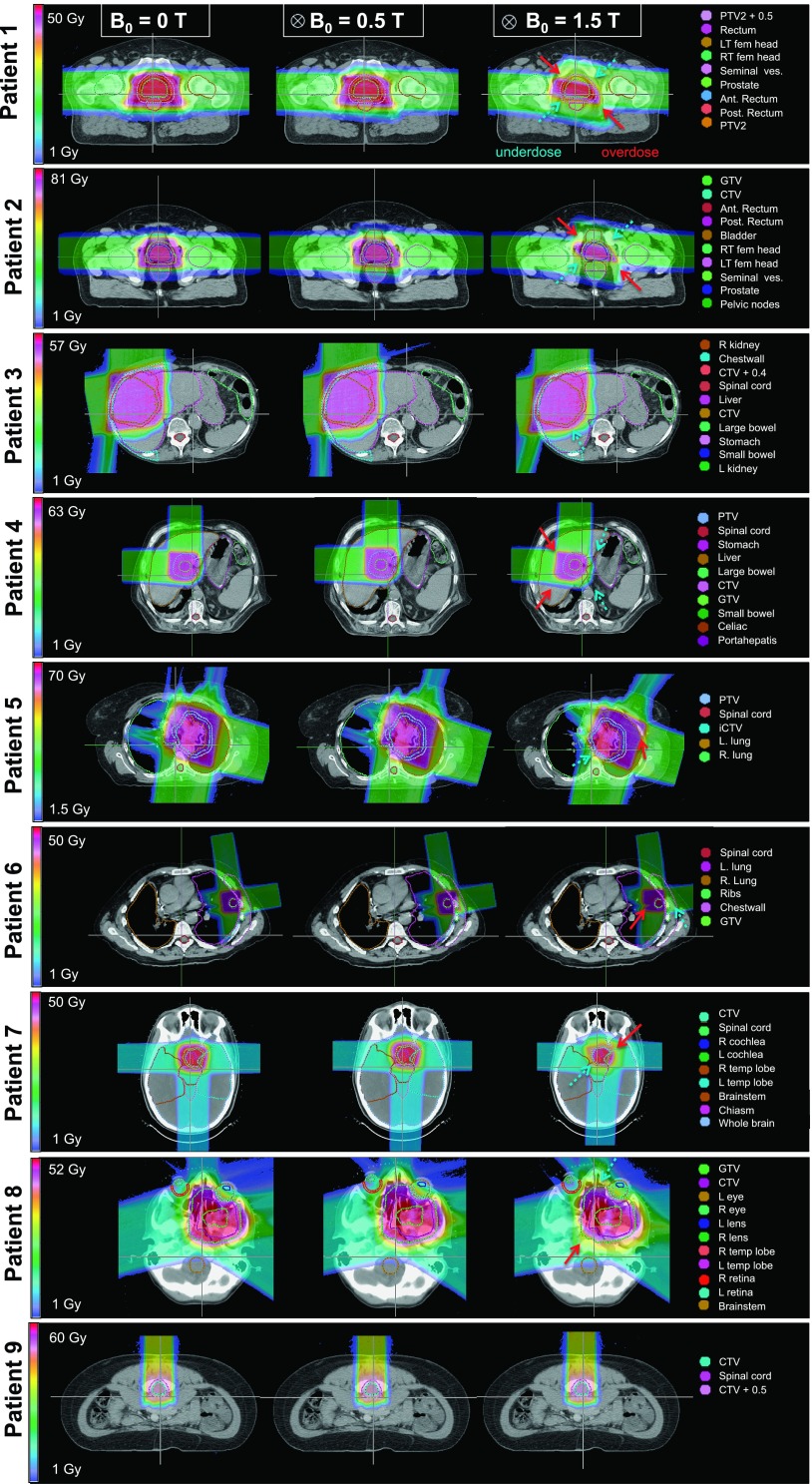
Figure 3 illustrates the MC dose distributions for all nine patients in the nominal setting (0 T), and in the presence of 0.5 and 1.5 T longitudinal magnetic fields. For all cases studied except prostate, the 0.5 T magnetic field did not imply clinically relevant deviations to the dose distributions (>2% decrease in D95/EUD for targets and increase in EUD for all OARs). For prostate, due to the large range and deflection of lateral opposed beams in opposite direction, target D95 decreased by up to 7% in both cases at 0.5 T, and the target coverage was extremely compromised at 1.5 T (EUD decrease up to 35% and D95 decrease up to 41%). For liver and lung, due to the combination of beam directions (lateral and AP), the high-dose region of the distribution remained intact and was shifted by 1–2 cm in the diagonal direction, which resulted in slightly smaller tumor underdose than prostate at 1.5 T (D95 decrease of up to 26%). For the head and neck cases, the prescription isodose volume also reduced in size due to the decreased overlap between the beams. Therefore, the tumors were subject to large underdose (EUD decrease of 10% and D95 decrease of 15%). The OAR doses were mainly decreased or almost unchanged, except, for example, the EUD for the right femur of patient 1 and the posterior rectum of patient 2, and the EUD, D95, and D5 for the left lens of patient 8 at 1.5 T. For the spine patient treated with a single posterior beam, no clinically relevant changes in the target or OAR doses were observed even at 1.5 T, as shown in Fig. 4. Detailed analysis of the DVHs indicated that the effect of 1.5 T magnetic field on most OAR doses, especially D95, was minimal. Larger effects were found on D5 in some OARs such as the dose decrease in the chestwall for patient 6, where the tumor was attached to this structure. Because many existing open MRI systems feature magnetic fields strengths of up to 1.5 T, addressing the residual dose distortions in these higher magnetic field levels is crucial.
FIG. 3.
Dose distribution for all patients, for nominal (B = 0), 0.5 T and 1.5 T magnetic field settings. Dashed and solid arrows indicate the regions of target underdose and nearby tissue overdose, respectively.
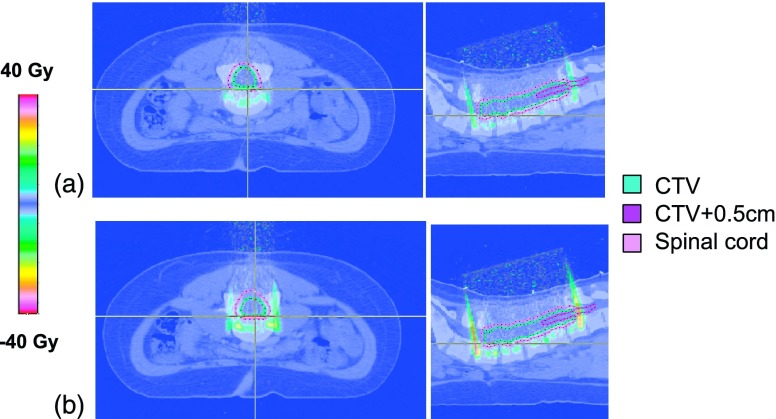
FIG. 4.
Dose difference maps for the spine case (patient 9), show no differences inside CTV and CTV + 0.5 cm structures for (a) 0.5 T and (b) 1.5 T magnetic fields compared to the nominal case (0 T).
3.B. Plan corrections
Our results indicate that a dosimetrically equivalent treatment might be feasible using simple MC-based plan corrections. Since proton beam deflection increased with the range, the most prominent dosimetric effects of the magnetic field was at end of range, leading to a lack of target coverage. We investigated whether the target coverage could be restored by modifying the plan parameters, independent of the plan optimization algorithm. This hypothesis was tested for all patients at 1.5 T magnetic field where the dose distortions could potentially be of clinical concern, and at 0.5 T only for the prostate patients. Figure 5 shows examples of prostate and lung (patients 2 and 5), magnifying the beam deflections at the end of range. It was found that in the prostate case, for example, shifting the beam by 19 mm (i.e., the amount of lateral beam deflection) in AP direction, opposite to the direction of the deflection, could fully compensate for the target underdose. The beam–patient relative shift can be achieved by adjusting the individual beam isocenters. Table I summarizes the treatment plan modifications necessary to correct for the presence of the magnetic field for all patients. Rotations were not necessary for most cases. An example where rotations helped preserve the target coverage was patient 5, with relatively large beam range and heterogeneous tissue on the beam path. Figure 6 illustrates the DVHs for the target and the OARs for all patients, for the nominal (0 T), 0.5 T, and 1.5 T without and with the applied corrections. Patient 9 (spine) did not require any corrections even at 1.5 T, mainly due to the small beam range leading to smaller beam deflection and ultimately negligible changes in dose (see Fig. 4). The largest dosimetric improvement as a result of plan correction was seen for prostate, lung, and head and neck patients. The isocenter shift improved the target coverage and restored the OAR dose to the nominal value in all cases. Table III presents the percent differences between D95, D5, and V20 of the nominal setting and each of the magnetic field settings, i.e., 0.5 and 1.5 T without and with corrections. A minus sign indicates smaller values compared to the nominal setting, which is a disadvantage for targets and an advantage for the OARs.
FIG. 5.

Dose distributions for (a) patient 2 and (b) patient 5 at 1.5 T field (top left). The directions of beam isocenter shifts are shown by arrows. The dose distributions after beam repositioning are compared (top right). The dose differences (nominal vs 1.5 T) without (bottom left) and with corrections (bottom right) show improved target conformity after implementing the plan corrections.
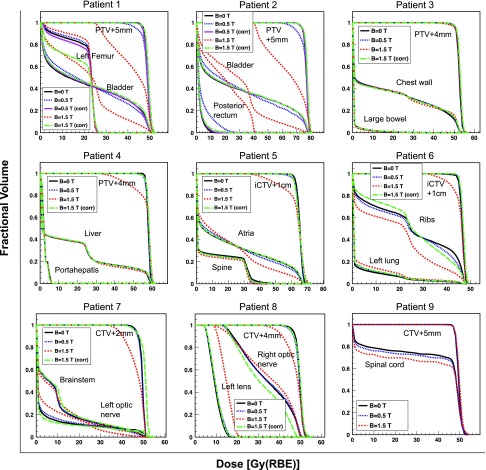
FIG. 6.
Dose volume histograms showing the tumors and the representative OARs for nominal, 0.5 T, 0.5 T (corrected) (for prostate only), 1.5 T, and 1.5 T (corrected) for all patients.
TABLE III.
DVH analysis: Differences between nominal D95, D5, and V20 and ones with 0.5 and 1.5 T (uncorrected: − , corrected: ✓) fields for all organs of all patients. Doses are presented in percent of the prescribed dose and volume in percent of total volume. Dashes indicate inapplicable fields.
| ΔD95 (%) | ΔD5 (%) | ΔV20 (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 T | 1.5 T | 0.5 T | 1.5 T | 0.5 T | 1.5 T | ||||||||
| Patient/Organ | − | ✓ | − | ✓ | − | ✓ | − | ✓ | − | ✓ | − | ✓ | |
| 1 | Target | −6.7 | −0.9 | −40.1 | 0.5 | — | — | — | — | — | — | — | — |
| Bladder | 0.1 | 0.0 | 0.7 | 0.1 | −0.3 | 0.0 | −4.4 | 0.9 | 4.3 | 0.8 | 18.9 | 1.8 | |
| Rectum | 0.2 | 0.0 | 4.1 | 0.0 | −2.1 | −0.2 | −24.5 | 0.9 | 7.3 | 0.5 | 24.0 | 1.2 | |
| Right femur | −3.9 | 6.2 | −8.2 | 27.2 | 0.7 | 0.5 | 1.6 | 5.4 | −1.9 | 1.8 | −7.3 | 5.8 | |
| Left femur | 1.1 | −0.8 | 4.1 | −2.6 | −0.6 | 0.1 | −0.8 | 0.5 | 1.7 | −2.5 | 4.5 | −14.7 | |
| 2 | Target | −7.1 | 0.1 | −41.2 | 0.5 | — | — | — | — | — | — | — | — |
| Bladder | 0.1 | 0.0 | 0.5 | 0.0 | 0.0 | 0.1 | −11.6 | 0.8 | 4.3 | 0.5 | 16.9 | 0.9 | |
| Ant. rectum | 0.1 | 0.0 | 0.8 | 0.0 | −2.8 | 0.3 | −38.7 | 0.8 | 5.3 | 0.5 | 13.6 | −0.3 | |
| Post. rectum | 0.0 | 0.0 | 0.3 | 0.0 | 14.3 | 0.9 | 42.3 | 2.5 | 7.5 | 0.1 | 55.0 | 1.3 | |
| Right femur | 0.9 | −0.9 | 4.6 | −25.1 | 0.1 | 0.0 | 0.6 | −0.3 | 0.0 | −0.6 | 0.0 | −11.8 | |
| Left femur | −0.6 | 1.5 | −1.5 | 5.0 | 0.0 | 0.4 | 0.2 | 1.6 | 0.1 | −0.3 | −0.1 | −1.5 | |
| 3 | Target | 0.2 | — | −0.3 | 1.1 | — | — | — | — | — | — | — | — |
| Liver | 0.0 | — | 0.0 | 0.0 | −0.1 | — | 0.0 | 0.8 | −0.7 | — | 1.8 | −2.3 | |
| Chestwall | 0.0 | — | 0.0 | 0.0 | 0.1 | — | 0.6 | 0.6 | 0.4 | — | 0.1 | −0.5 | |
| Large bowel | 0.0 | — | 0.0 | 0.0 | −0.9 | — | −2.2 | −0.2 | 0.2 | — | −0.4 | 0.1 | |
| Right kidney | 0.0 | — | 0.0 | 0.0 | −0.2 | — | 0.2 | −1.0 | 0.2 | — | 0.6 | −0.2 | |
| 4 | Target | −0.6 | — | −24.9 | −0.2 | — | — | — | — | — | — | — | — |
| Liver | 0.0 | — | 0.0 | 0.0 | −0.1 | — | 0.8 | 0.9 | 0.0 | — | 0.1 | 0.5 | |
| Portahepatis | 0.0 | — | −0.2 | −0.1 | −0.2 | — | −0.2 | −0.7 | 0.0 | — | 0.0 | 0.0 | |
| 5 | Target | −1.6 | — | −25.8 | −1.3 | — | — | — | — | — | — | — | — |
| Lung-iGTV | 0.0 | — | −0.1 | 0.0 | −0.3 | — | 0.1 | −1.1 | −2.4 | — | −5.1 | −0.8 | |
| Atria | 0.0 | — | 0.0 | 0.0 | −0.4 | — | −3.4 | 0.3 | 1.9 | — | 3.6 | 0.4 | |
| Ventricles | 0.0 | — | 0.0 | 0.0 | 0.4 | — | 2.0 | −0.4 | −1.4 | — | −1.0 | 0.2 | |
| Esophagus | 0.0 | — | 0.0 | 0.0 | 0.7 | — | −2.0 | 2.7 | −0.3 | — | −3.1 | 0.2 | |
| Spinal cord | 0.0 | — | 0.0 | 0.0 | −1.6 | — | −2.5 | −1.3 | −0.8 | — | −2.4 | −1.0 | |
| 6 | Target | 0.9 | — | −13.3 | 1.1 | — | — | — | — | — | — | — | — |
| Left lung | 0.0 | — | 0.0 | 0.0 | 1.4 | — | 5.0 | 1.2 | 1.2 | — | 4.1 | 1.5 | |
| Chestwall | 0.0 | — | 0.0 | 0.0 | −3.7 | — | −22.1 | −7.6 | −0.3 | — | −2.0 | 1.8 | |
| Ribs | −0.1 | — | −0.2 | 0.1 | −0.5 | — | −2.1 | −0.1 | −2.4 | — | −9.2 | 4.8 | |
| 7 | Target | −0.7 | — | −15.8 | −0.7 | — | — | — | — | — | — | — | — |
| R opt nerve | 0.0 | — | 0.1 | 0.0 | −0.2 | — | −13.3 | 0.8 | 1.0 | — | 11.5 | 5.1 | |
| L opt nerve | 0.0 | — | 0.0 | 0.0 | 0.6 | — | −7.7 | 2.7 | 2.0 | — | 7.9 | −1.6 | |
| R temp lobe | 0.0 | — | 0.0 | 0.0 | −3.2 | — | −6.5 | −4.8 | 0.1 | — | 0.7 | −4.3 | |
| L temp lobe | 0.0 | — | 0.0 | 0.0 | 5.4 | — | 3.7 | 8.5 | 0.6 | — | 4.7 | 6.2 | |
| Brainstem | 0.0 | — | 0.0 | 0.0 | −5.0 | — | −25.4 | 1.7 | 0.1 | — | 2.2 | 8.9 | |
| 8 | Target | −2.1 | — | −14.9 | −1.5 | — | — | — | — | — | — | — | — |
| R opt nerve | −1.2 | — | −4.2 | −1.0 | 0.6 | — | 0.1 | −4.4 | 0.0 | — | −0.8 | 0.0 | |
| Brainstem | 0.1 | — | 0.3 | 0.0 | 1.8 | — | 4.9 | −2.2 | 4.7 | — | 18.5 | −4.1 | |
| L lens | 0.0 | — | 9.5 | 0.2 | 1.3 | — | 9.7 | 0.8 | 4.0 | — | 55.5 | 4.0 | |
| 9 | Target | 0.1 | — | 0.3 | — | — | — | — | — | — | — | — | — |
| Spinal cord | −0.1 | — | −0.2 | — | −0.5 | — | 0.3 | — | −2.7 | — | −6.1 | — | |
A comparison of EUD values is illustrated in Fig. 7, which summarizes the findings of the patient and organ specific dose effects. It clearly demonstrates that for all patients the proposed corrections are sufficient to reinstate the target coverage and OAR nominal dose values. Although applying a magnetic field provides a dosimetric advantage for some OARs, the lack of sufficient target coverage necessitates the use of plan corrections despite canceling out this positive effect. Certain OARs, however, benefited from the corrections, e.g., the posterior rectum for patient 2 was spared after applying the beam translations in 1.5 T setting as evident from Fig. 7, and Table III.
FIG. 7.
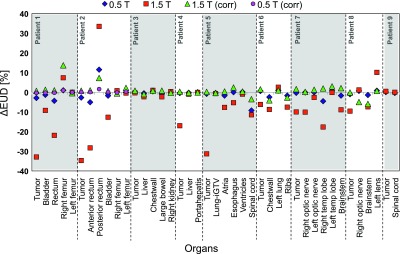
Difference between nominal EUD (in percent of the prescribed dose) and ones with magnetic fields, illustrating the impact of the magnetic fields on the organ doses and the effectiveness of the plan corrections. Negative values indicate decrease and positive values indicate increase of EUD compared to nominal.
In addition to longitudinal magnetic fields, transverse fields (in the AP direction) were also studied. The setup corrections mainly involved longitudinal isocenter shifts, similar to the AP/LAT shifts described in case of longitudinal magnetic fields.
4. DISCUSSION
MRI-guided proton therapy using 0.5 T magnetic field is dosimetrically viable without the need for any plan modifications for all sites studied except for prostate. Relatively large magnetic fields (up to 1.5 T) could potentially cause considerable tumor underdosage given the smaller relative target margins to be used during image guidance. However, careful analysis of the dose distortions for nine patients with various tumor sites suggests that even at 1.5 T, clinically acceptable dose distributions could be achieved after applying appropriate plan corrections. Through the proposed correction process, the magnetic field component could be implemented independent of the planning system, allowing for more flexibility and versatility of usage.
In addition to the magnetic field strength, the magnitude of dose effects and hence the required plan adjustments depends on several factors. One of the main factors is range, which determines the degree of beam deflection. This is evident by comparing the prostate patients presented here to patients in other site categories. The next factor is the beam direction relative to the magnetic field. For both longitudinal and transverse fields studied here, the dose effects were larger when the plan involves two lateral opposed beams compared to lateral–AP beam combinations. The level of surrounding tissue homogeneity and tumor size did not cause the plan correction process to fail or be particularly challenging, for the magnetic field strengths of this study. Patient 8 showcased an example of a highly heterogeneous tumor site whose plan could be sufficiently corrected to preserve the dose distribution, just like the more homogenous case of patient 7. Although the tumor size is very different in these two cases, the magnitude of isocenter shifts was quite similar.
We found that reducing the planning margins (simulated by analyzing the dose on enlarged targets while keeping the field size constant, see Sec. 2.C for details) for treatment delivery with the MRI magnetic field on, does not limit the ability to maintain the target coverage. By examining the case-specific planning margins and feasible margin reductions (Table I), we estimate that the margins (related to patient setup, motion, and anatomy changes) could on average be reduced by approximately half for real-time MRI guided proton delivery. It should be noted that these results were obtained for MC based dose calculations and more margins might be needed using analytical dose calculations.35 Although performing patient-specific MC simulations may not be efficient at the moment, the process is foreseen to be greatly accelerated and automated through the use of graphic processing units (GPUs) in the near future.36 GPU-based MC proton treatment planning is also under investigation.37 Although applying a simple formula to find the isocenter shifts and rotations was adequate for all nine patients studied, MC-based optimization of the correction parameters may also be feasible and is subject to future investigations. As an alternative to MC, corrections could be quantified using analytical algorithms (e.g., as developed by Wolf and Bortfeld32) after planning the nominal scenario.
The magnitude of the proton beam deflection in our initial phantom validation agreed well with the only previous study,25 who found 1 and 5 mm lateral proton beam shift in a water phantom at 90 MeV beam energy and 0.5 and 3 T magnetic field, respectively. Furthermore, the electron-return effect (secondary electron dose accumulation at the air–water interface) was negligible in patient tissue (due to the very low energy of the secondary electrons from proton interactions), similar to phantoms,25 but unlike the photon studies.10
In this study, we only used passive scattering plans due to the limited number of patients currently treated with pencil beam scanning (PBS). Since MRI-guided proton therapy and real-time treatment adaptation are more likely to be incorporated in PBS delivery rather than passive scattering, we further investigated the validity of the findings using PBS for the most heterogeneous case (patient 8) representing the worst case scenario. The in-house PBS planning system, astroid (v1.3), was used.38 An average spot size of 6 mm sigma was used and plans with both single field uniform dose (SFUD) and intensity modulated proton therapy (IMPT) were created. It was found that SFUD leads to similar conclusions as when using passively scattered fields, as expected. However, in IMPT, the situation was more complex due to highly modulated spot intensities and the same plan corrections were not sufficient to fully recover the target coverage. This was mainly true for beams with high intensity spots close to the target boundaries. In such cases, real-time optimization techniques may be required. Figure 8 presents the details of this finding.
FIG. 8.
Comparison of percent differences of target ΔD95 and Dmean for 0.5 T, 1.5 T, and 1.5 T (corrected) with respect to nominal (0 T), for passive scattering, SFUD, and IMPT plans.
Hybrid proton–MRI systems are currently not available. Integrating a MRI scanner in a proton therapy system is inherently more challenging than in photon therapy due to the nature of protons as highly interacting charged particles and the geometrical configuration of the proton gantry. Potential hybrid systems based on currently manufactured open bore or split-coil MRI systems could be explored.39 Custom system designs similar to MRI–Linac systems could also be considered.40,41
In addition to the design challenges, other important aspects should be carefully investigated, most of which are similar to photon therapy and are being explored by several groups. Some of these are the magnetic field inhomogeneity-induced image distortions,42 online treatment plan adaptation and dose recalculation using the MRI data,43–45 online reoptimization,46–49 target autosegmentation,50 motion prediction,51 and the latency between imaging and treatment of the moving anatomy,52 which could be reduced by applying motion prediction methods.51,53
Characterizing the effects of the magnetic field on the clinical dose distribution and patient treatment as addressed in this work is an important initial step toward future progress. Knowing that the magnetic field does not limit the treatment quality, at least for fields up to 1.5 T (sufficient for nondiagnostic applications), is encouraging and allows focusing on the potential design aspects of such hybrid system.
5. CONCLUSIONS
Considering recent interest and extensive research on MRI-guided radiotherapy, this modality might become a standard part of clinical practice in the future. Proton therapy could greatly benefit from MRI guidance by monitoring patient anatomy variations during or before treatments to reduce geometrical uncertainties and shrink the tumor margins.
This study demonstrated the dosimetric feasibility of real-time MRI guidance in proton therapy. It was shown that the effect of the MRI magnetic field on the proton dose distribution at field levels up to 0.5 T is negligible except for prostate. For 1.5 T field, the most prominent effect was target underdose of up to 41%, which could be effectively compensated by performing plan corrections. Considering various tumor sites to cover different scenarios in terms of tissue and plan characteristics, it was shown that the degree of corrections is mainly dependent on the magnetic field strength, range, and relative beam directions, and plan qualities similar to the nominal plan (no field) could always be achieved. These results are promising and will clear the path for future advances in MRI-guided proton therapy.
ACKNOWLEDGMENTS
This work was supported by the Federal Share of Project Income Program at Massachusetts General Hospital on C06 CA059267. The authors would like to give special thanks to Dr. Joseph Perl and Dr. Jungwook Shin from the topas collaboration for their help and support with incorporating the magnetic field module in topas.
REFERENCES
- 1.Suit H. D., “Protons to replace photons in external beam radiation therapy?,” Clin. Oncol. 15, S29–S31 (2003). 10.1053/clon.2002.0171 [DOI] [PubMed] [Google Scholar]
- 2.Yock T. I. and Tarbell N. J., “Technology insight: Proton beam radiotherapy for treatment in pediatric brain tumors,” Nat. Clin. Pract. Oncol. 1, 97–103 (2004). [DOI] [PubMed] [Google Scholar]
- 3.Levin W. P., Kooy H., Loeffler J. S., and DeLaney T. F., “Proton beam therapy,” Br. J. Cancer 93, 849–854 (2005). 10.1038/sj.bjc.6602754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lomax A. J.et al. , “A treatment planning inter-comparison of proton and intensity modulated photon radiotherapy,” Radiother. Oncol. 51, 257–271 (1999). 10.1016/S0167-8140(99)00036-5 [DOI] [PubMed] [Google Scholar]
- 5.Goitein M., “Magical protons?,” Int. J. Radiat. Oncol., Biol., Phys. 70, 654–656 (2008). 10.1016/j.ijrobp.2007.10.057 [DOI] [PubMed] [Google Scholar]
- 6.Qi Z. and Chen G. H., “Extraction of tumor motion trajectories using PICC-4DCBCT: A validation study,” Med. Phys. 38, 5530–5538 (2011). 10.1118/1.3637501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Park J. C., Park S. H., Kim J. H., Yoon S. M., Kim S. S., Kim J. S., Liu Z., Watkins T., and Song W. Y., “Four-dimensional cone-beam computed tomography and digital tomosynthesis reconstructions using respiratory signals extracted from transcutaneously inserted metal markers for liver SBRT,” Med. Phys. 38, 1028–1036 (2011). 10.1118/1.3544369 [DOI] [PubMed] [Google Scholar]
- 8.Riboldi M., Orecchia M., and Baroni G., “Real-time tumour tracking in particle therapy: Technological developments and future perspectives,” Lancet Oncol. 13, e383–e391 (2012). 10.1016/S1470-2045(12)70243-7 [DOI] [PubMed] [Google Scholar]
- 9.Dawson L. A. and Jaffray D. A., “Advances in image-guided radiation therapy,” J. Clin. Oncol. 25, 938–946 (2007). 10.1200/JCO.2006.09.9515 [DOI] [PubMed] [Google Scholar]
- 10.Raaijmakers A. J. E., Raaymakers B. W., and Lagendijk J. J. W., “Integrating a MRI scanner with a 6 MV radiotherapy accelerator: Dose increase at tissue–air interfaces in a lateral magnetic field due to returning electrons,” Phys. Med. Biol. 50, 1363–1376 (2005). 10.1088/0031-9155/50/7/002 [DOI] [PubMed] [Google Scholar]
- 11.Lagendijk J. J. W.et al. , “MRI/linac integration,” Radiother. Oncol. 86, 25–29 (2008). 10.1016/j.radonc.2007.10.034 [DOI] [PubMed] [Google Scholar]
- 12.Kirkby C., Stanescu T., Rathee S., Carlone M., Murray B., and Fallone B. G., “Patient dosimetry for hybrid MRI-radiotherapy systems,” Med. Phys. 35, 1019–1027 (2008). 10.1118/1.2839104 [DOI] [PubMed] [Google Scholar]
- 13.Cho M. K.et al. , “CBCT/CBDT with the equipped x-ray projection system for image-guided proton therapy,” Proc. SPIE 7258, 72582V (2009). 10.1117/12.811525 [DOI] [Google Scholar]
- 14.Li R., Keall P., and Xing L., Linac-based Image Guided Intensity Modulated Radiation Therapy , in Technical Basis of Radiation Therapy, Medical Radiology, Radiation Oncology edited by Levitt S. H., et al. (Springer; , Berlin Heidelberg, 2012), pp. 275–312 [Google Scholar]
- 15.View Ray, Inc., http://www.viewray.com (2012).
- 16.Cooper R. A.et al. , “Tumour oxygenation levels correlate with dynamic contrast-enhanced magnetic resonance imaging parameters in carcinoma of the cervix,” Radiother. Oncol. 57, 53–59 (2000). 10.1016/S0167-8140(00)00259-0 [DOI] [PubMed] [Google Scholar]
- 17.Lesniak J., Tokuda J., Kikinis R., Burghart C., and Hata N., “A device guidance method for organ motion compensation in MRI-guided therapy,” Phys. Med. Biol. 52, 6427–6438 (2007). 10.1088/0031-9155/52/21/006 [DOI] [PubMed] [Google Scholar]
- 18.Zahra M. A.et al. , “Dynamic contrast-enhanced MRI as a predictor of tumour response to radiotherapy,” Lancet Oncol. 8, 63–74 (2007). 10.1016/S1470-2045(06)71012-9 [DOI] [PubMed] [Google Scholar]
- 19.Søvik A., Malinen E., and Olsen D. R., “Strategies for biologic image-guided dose escalation: A review,” Int. J. Radiat. Oncol., Biol., Phys. 73, 650–658 (2009). 10.1016/j.ijrobp.2008.11.001 [DOI] [PubMed] [Google Scholar]
- 20.van de Water S., Kreuger R., Zenklusen S., Hug E., and Lomax A. J., “Tumour tracking with scanned proton beams: Assessing the accuracy and practicalities,” Phys. Med. Biol. 54, 6549–6563 (2009). 10.1088/0031-9155/54/21/007 [DOI] [PubMed] [Google Scholar]
- 21.Bert C., Saito N., Schmidt A., Chaudhri N., Schardt D., and Rietzel E., “Target motion tracking with a scanned particle beam,” Med. Phys. 34, 4768–4771 (2007). 10.1118/1.2815934 [DOI] [PubMed] [Google Scholar]
- 22.Saito N., Bert C., Chaudhri N., Gemmel A., Schardt D., and Rietzel E., “Speed and accuracy of a beam tracking system for treatment of moving targets with scanned ion beams,” Phys. Med. Biol. 54, 4849–4862 (2009). 10.1088/0031-9155/54/16/001 [DOI] [PubMed] [Google Scholar]
- 23.Jiang S. B., “Technical aspects of image-guided respiration-gated radiation therapy,” Med. Dosim. 31, 141–151 (2006). 10.1016/j.meddos.2005.12.005 [DOI] [PubMed] [Google Scholar]
- 24.Crijns S. P. M., Kok J. G. M., Lagendijk J. J. W., and Raaymakers B. W., “Towards MRI-guided linear accelerator control: Gating on an MRI accelerator,” Phys. Med. Biol. 56, 4815–4825 (2011). 10.1088/0031-9155/56/15/012 [DOI] [PubMed] [Google Scholar]
- 25.Raaymakers B. W., Raaijmakers A. J. E., and Lagendijk J. J. W., “Feasibility of MRI guided proton therapy: Magnetic field dose effects,” Phys. Med. Biol. 53, 5615–5622 (2008). 10.1088/0031-9155/53/20/003 [DOI] [PubMed] [Google Scholar]
- 26.Perl J., Shin J., Schümann J., Faddegon B., and Paganetti H., “ topas: An innovative proton Monte Carlo platform for research and clinical applications,” Med. Phys. 39, 6818–6837 (2012). 10.1118/1.4758060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Testa M., Schümann J., Lu H.-M., Shin J., Faddegon B., Perl J., and Paganetti H., “Experimental validation of the topas Monte Carlo system for passive scattering proton therapy,” Med. Phys. 40, 121719 (16pp.) (2013). 10.1118/1.4828781 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Paganetti H., Jiang H., Parodi K., Slopsema R., and Engelsman M., “Clinical implementation of full Monte Carlo dose calculation in proton beam therapy,” Phys. Med. Biol. 53, 4825–4853 (2008). 10.1088/0031-9155/53/17/023 [DOI] [PubMed] [Google Scholar]
- 29.Schümann J. and Paganetti H., “Streamlining Monte Carlo dose calculations for routine clinical use in proton therapy,” Med. Phys. 38, 3767 (2011). 10.1118/1.3613181 [DOI] [Google Scholar]
- 30.Deasy J. O., Blanco A. I., and Clark V. H., “CERR: A computational environment for radiotherapy research,” Med. Phys. 30, 979–985 (2003). 10.1118/1.1568978 [DOI] [PubMed] [Google Scholar]
- 31.Niemierko A., “A generalized concept of equivalent uniform dose (EUD),” Med. Phys. 26, 1100 (1999). [DOI] [PubMed] [Google Scholar]
- 32.Wolf R. and Bortfeld T., “An analytical solution to proton Bragg peak deflection in a magnetic field,” Phys. Med. Biol. 57, N329–N337 (2012). 10.1088/0031-9155/57/17/N329 [DOI] [PubMed] [Google Scholar]
- 33.Burman C., Kutcher G. J., Emami B., and Goitein M., “Fitting of normal tissue tolerance data to an analytic function,” Int. J. Radiat. Oncol., Biol., Phys. 21, 123–135 (1991). 10.1016/0360-3016(91)90172-Z [DOI] [PubMed] [Google Scholar]
- 34.Arvold N. D., Niemierko A., Broussard G. P, Adams J., Fullerton B., Loeffler J. S., and Shih H. A., “Projected second tumor risk and dose to neurocognitive structures after proton versus photon radiotherapy for benign meningioma,” Int. J. Radiat. Oncol., Biol., Phys. 83, e495–e500 (2012). 10.1016/j.ijrobp.2011.10.056 [DOI] [PubMed] [Google Scholar]
- 35.Schuemann J., Dowdell S., Grassberger C., Min C. H., and Paganetti H., “Site-specific range uncertainties caused by dose calculation algorithms for proton therapy,” Phys. Med. Biol. 59, 4007–4031 (2014). 10.1088/0031-9155/59/15/4007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jia X., Schuemann J., Paganetti H., and Jiang S. B., “GPU-based fast Monte Carlo dose calculation for proton therapy,” Phys. Med. Biol. 57, 7783–7797 (2012). 10.1088/0031-9155/57/23/7783 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kohno R., Hotta K., Nishioka S., Matsubara K., Tansho R., and Suzuki T., “Clinical implementation of a GPU-based simplified Monte Carlo method for a treatment planning system of proton beam therapy,” Phys. Med. Biol. 56, N287–N294 (2011). 10.1088/0031-9155/56/22/N03 [DOI] [PubMed] [Google Scholar]
- 38.Kooy H.et al. , “A case study in proton pencil-beam scanning delivery,” Int. J. Radiat. Oncol., Biol., Phys. 76, 624–630 (2010). 10.1016/j.ijrobp.2009.06.065 [DOI] [PubMed] [Google Scholar]
- 39.Mislow J. M., Golby A. J., and Black P. M., “Origins of intraoperative MRI,” Neurosurg. Clin. N Am. 20, 137–146 (2009). 10.1016/j.nec.2009.04.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.St Aubin J., Steciw S., and Fallone B. G., “Effect of transverse magnetic fields on a simulated in-line 6 MV linac,” Phys. Med. Biol. 55, 4861–4869 (2010). 10.1088/0031-9155/55/16/015 [DOI] [PubMed] [Google Scholar]
- 41.Santos D. M., St Aubin J., Fallone B. G., and Steciw S., “Magnetic shielding investigation for a 6 MV in-line linac within the parallel configuration of a linac-MR system,” Med. Phys. 39, 788–797 (2012). 10.1118/1.3676692 [DOI] [PubMed] [Google Scholar]
- 42.Crijns S. P. M., Raaymakers B. W., and Lagendijk J. J. W., “Real-time correction of magnetic field inhomogeneity-induced image distortions for MRI-guided conventional and proton radiotherapy,” Phys. Med. Biol. 56, 289–297 (2011). 10.1088/0031-9155/56/1/017 [DOI] [PubMed] [Google Scholar]
- 43.Kerkhof E. M., Balter J. M., Vineberg K., and Raaymakers B. W., “Treatment plan adaptation for MRI- guided radiotherapy using solely MRI data: A CT-based simulation study,” Phys. Med. Biol. 55, N433–N440 (2010). 10.1088/0031-9155/55/16/N01 [DOI] [PubMed] [Google Scholar]
- 44.Lee Y . K.et al. , “Radiotherapy treatment planning of prostate cancer using magnetic resonance imaging alone,” Radiother. Oncol. 66, 203–216 (2003). 10.1016/S0167-8140(02)00440-1 [DOI] [PubMed] [Google Scholar]
- 45.Khoo V. S. and Joon D. L., “New developments in MRI for target volume delineation in radiotherapy,” Br. J. Radiol. 79, S2–S15 (2006). 10.1259/bjr/41321492 [DOI] [PubMed] [Google Scholar]
- 46.Xing L., Siebers J., and Keall P., “Computational challenges for image-guided radiation therapy: Framework and current research,” Semin. Radiat. Oncol. 17, 245–257 (2007). 10.1016/j.semradonc.2007.07.004 [DOI] [PubMed] [Google Scholar]
- 47.de la Zerda A., Armbruster B., and Xing L., “Formulating adaptive radiation therapy planning into closed-loop control framework,” Phys. Med. Biol. 52, 4137–4153 (2007). 10.1088/0031-9155/52/14/008 [DOI] [PubMed] [Google Scholar]
- 48.Jiang S. B., Gu X., Men C., Jia X., Fluck O., Choi D., and Majumdar A., “Real-Time re-planning for online adaptive radiotherapy,” Med. Phys. 37, 3452 (2010). 10.1118/1.3469484 [DOI] [Google Scholar]
- 49.Men C., Jia X., and Jiang S. B., “GPU-based ultra-fast direct aperture optimization for online adaptive radiation therapy,” Phys. Med. Biol. 55, 4309–4319 (2010). 10.1088/0031-9155/55/15/008 [DOI] [PubMed] [Google Scholar]
- 50.Yun J.et al. , “Evaluation of a lung tumor autocontouring algorithm for intrafractional tumor tracking using low-field MRI: A phantom study,” Med. Phys. 39, 1481–1494 (2012). 10.1118/1.3685578 [DOI] [PubMed] [Google Scholar]
- 51.Yun J., Mackenzie M., Rathee S., Robinson D., and Fallone B. G., “An artificial neural network (ANN)-based lung-tumor motion predictor for intrafractional MR tumor tracking,” Med. Phys. 39, 4423–4433 (2012). 10.1118/1.4730294 [DOI] [PubMed] [Google Scholar]
- 52.Crijns S. P. M., Raaymakers B. W., and Lagendijk J. J. W., “Proof of concept of MRI-guided tracked radiation delivery: Tracking one-dimensional motion,” Phys. Med. Biol. 57, 7863–7872 (2012). 10.1088/0031-9155/57/23/7863 [DOI] [PubMed] [Google Scholar]
- 53.Sharp G. C., Jiang S. B., Shimizu S., and Shirato H., “Prediction of respiratory tumour motion for real-time image-guided radiotherapy,” Phys. Med. Biol. 49, 425–440 (2004). 10.1088/0031-9155/49/3/006 [DOI] [PubMed] [Google Scholar]