Comparing Cost-Effectiveness Results for a Vaccine Across Different Countries Worldwide: What Can We Learn?

Abstract

Introduction

Cost-effectiveness analysis (CEA) using country-specific thresholds tied to gross domestic product (GDP) might not be appropriate in countries with low healthcare investment and a high disease burden as a consequence.

Methods

Using data from previously published CEA of rotavirus vaccination across nine countries worldwide, we calculated the cost neutral price (Pn) for the new intervention that reflects the price resulting in no net increase in health care costs compared with the current situation, and the maximum price (Pm) obtained with an incremental cost-effectiveness ratio (ICER) at the threshold value of 1 × GDP/capita.

Results

In countries with low GDP/capita, the paradoxical finding for rotavirus vaccination is that the Pm is much higher than in countries with a high GDP/capita. On the other hand, the Pn for the low GDP/capita countries is much lower than for high GDP/capita countries because of the low investment in health care.

Conclusion

In countries with low healthcare investment and a high disease burden, the difference between the Pn and Pm for rotavirus vaccine which is the price range within which the ICER is below the World Health Organization (WHO) threshold value, is large. One reason could be that the WHO threshold value may not properly account for the local opportunity cost of health care expenditures. Therefore, either alternative threshold values should be selected or alternative economic assessment tools should be considered, such as budget optimisation or return on investment, if we want to communicate about real economic value of new vaccines in those countries.

Electronic supplementary material

The online version of this article (doi:10.1007/s12325-014-0160-6) contains supplementary material, which is available to authorized users.

Introduction

Current economic assessment of a new medical intervention such as a drug, device, or vaccine aims to provide local decision makers with information on the additional benefit generated for the additional cost incurred, compared with the existing situation [1, 2]. This is most commonly conducted using cost-effectiveness analysis (CEA), with results expressed with incremental cost-effectiveness ratios (ICERs). The ICER can be used to help define an acceptable “value-based” price range for the new intervention, with the maximum acceptable price being the price at which the ICER crosses a defined threshold [2]. The gross domestic product (GDP) per capita is a well-accepted threshold measure, as proposed and recommended by the World Health Organization (WHO) [3, 4]. If the price of the new technology leads to an ICER below the threshold, that price is qualified as being highly cost-effective following the interpretation of the WHO guidelines [5].

CEA is a well-established economic assessment technique in healthcare [6–8]. It was initially developed in industrialized countries with mature healthcare systems which had already made considerable investments in healthcare infrastructure. More recently, the use of CEA has been extended to economic evaluations of health interventions in developing countries. For example, CEA results for rotavirus vaccination have been reviewed in developed countries [9] and developing countries [10]. These two reviews reported that the vaccine was very cost-effective in low-income countries, but the picture was mixed in high-income countries. A similar result was reported by Rheingans et al. [11] comparing the cost-effectiveness and price setting of rotavirus vaccination for different country groups in Latin America from low income (L), via low middle (LM), to upper middle income (UM). They reported that the price per vaccine dose that is cost-effective was higher in L countries than in LM and UM countries. This is counter-intuitive, as it would be expected that the maximum price for favorable cost-effectiveness would be lower in L countries, reflecting the lower income and lower resources available for healthcare, compared with higher-income countries. The authors of these papers did not attempt to explain this paradoxical finding. The analysis provided here builds on these previous reports by seeking to explore how these apparently paradoxical results could arise.

This paper focuses on rotavirus vaccination as an example. It is an interesting example, as the rotavirus vaccine has been the subject of CEA in a range of countries worldwide, and the benefits obtained from the vaccine appear quite different in high- versus low-income countries [12]. In low-income countries, the benefit of vaccination is primarily a reduction in the high mortality rate. In high-income countries, in addition to a reduced need for hospital care the benefits are more subtle, such as better time management for working parents [11, 13].

In this paper, first a theoretical framework and interpretation of the “value-based” price range is presented for a new vaccine program. In the next step, an application in practice for rotavirus vaccination using published country-specific data for rotavirus to estimate the “value-based” price range in nine countries was conducted. This allowed an analysis of the relationship of the “value-based” price range for each country and the GDP/capita. Finally, the findings are interpreted and recommendations made for alternative/additional economic evaluations.

Methods

Compliance with Ethics Guidelines

This article does not contain any new studies with human or animal subjects performed by any of the authors.

Theoretical Framework

The first step demonstrates, using mathematical equations, the relationship between the price of a new intervention, the ICER, the threshold value for cost-effectiveness, and the cost neutral price (Pn) and the maximum price (Pm) linked to that threshold.

The relationship between the ICER and the price of a new intervention is expressed as a linear function (y = ax + b), where y (=ICER) is the dependent variable and x (=price or cost of the new intervention) is the independent variable, here the cost of the vaccine (CostV). This relationship is now considered within the context of a static cohort model for modeling the cost-effectiveness of the intervention of the rotavirus vaccine [14]. Additional equations and variables help to specify which exact parameters define the slope of the line (a) and which the intercept (b) that is the remaining disease cost after the impact of the new intervention divided by the difference in disease outcomes attributable to the new intervention. Calculating the association between the price of the new intervention and the ICER allows testing the price range over which it is still cost-effective. This is defined here as the price range for which the ICER lies below the threshold value, defined as 1 × GDP per capita [3]. The linear function also indicates at what price the ICER equals zero (because of no difference in total cost with the intervention compared with the total cost without the intervention). This is referred to as the cost neutral price (Pn). The maximum price (Pm) above which a new product is no longer cost-effective is defined by the point where the threshold value intersects with the increasing linear function for new interventions that are more effective but result in higher total costs than with the current health care program (see Fig. 1).

Fig. 1.

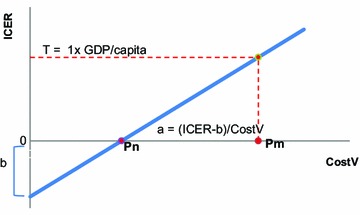
Cost neutral (Pn) and maximum price (Pm) of the vaccine per dose at a threshold T (e.g., $40,000/life-year gained). a Slope, b intercept, CostV vaccine cost, GDP gross domestic product, ICER incremental cost-effectiveness ratio, Pm maximum price, Pn cost neutral price, T threshold

Now, we further elaborate on the mathematical properties of the relationship described above. In its simplest form, the relationship between the ICER and the cost (price) of a new intervention (vaccine) is defined by the following equations:

$$\frac{\left({\text{CostD}}_{\text{V}}+\text{CostV}\right)-{\text{CostD}}_{\text{NV}}}{E_{\text{NV}}-E_{\text{V}}}=\text{ICER}\le T$$

$$\frac{\text{CostV}}{E_{\text{NV}}-E_{\text{V}}}+\frac{\left({\text{CostD}}_{\text{V}}-{\text{CostD}}_{\text{NV}}\right)}{E_{\text{NV}}-E_{\text{V}}}=\text{ICER}$$

$$a=\frac{1}{E_{\text{NV}}-E_{\text{V}}}$$

$$b=\frac{\left({\text{CostD}}_{\text{V}}-{\text{CostD}}_{\text{NV}}\right)}{E_{\text{NV}}-E_{\text{V}}}$$

where:

CostD_v

Remaining disease-related cost with vaccination

CostV

Acquisition cost of the new intervention (vaccine)

CostD_NV

Initial disease-related cost in the absence of vaccination (no vaccine)

E_NV

Health losses without vaccination (no vaccine)

E_V

Remaining health losses (effects) with vaccination

ICER

Incremental cost-effectiveness ratio

T

Threshold (here defined as the GDP/capita)

a

Slope of the line

b

Intercept

From the equations above, the slope (a) is defined by the inverse of the effect difference, while the intercept (b) is defined by the cost difference without including CostV divided by the effect difference.

There is one additional variable to be defined in the equations, the vaccine impact on disease-related costs and negative health outcomes:

$${\text{CostD}}_{\text{V}}={\text{CostD}}_{\text{NV}}\times \left(1-{\text{VaccineEffect}}_{\text{C}}\right)$$

$$E_{\text{V}}=E_{\text{NV}}\times \left(1-{\text{VaccineEffect}}_{\text{E}}\right)$$

where:

• VaccineEffect_C and VaccineEffect_E: the vaccine effects on costs and negative outcomes (range of values between 0 and 1) obtained from randomized clinical trials entered into the model. For simplicity only two factors are assessed here, disease-specific mortality (negative outcomes) and hospitalization (costs). The output of E _V and E _NV is expressed in survival loss expressed in life-years, in which the difference between the two is presented as a gain in survival time.

The vaccine may have different effects on costs and health outcomes in different elements of the disease burden. For example, the effect of the vaccine in reducing hospitalizations, medical visits or total numbers of cases may vary, and the effect on the total cost will depend on the frequency of each of these elements in the total cost burden. To simplify the model, in the present paper only one cost component is considered, hospitalization. In rotavirus disease, it is normally assumed that deaths occur in hospitalized cases. Thus, in this simplified case that reflects an environment with a well-established health care system, the effects of the vaccine on costs (hospitalizations) and health outcomes (deaths) are likely to be equi-proportionate. It may be different in those situations where the health care system is less well developed.

Hypothetical Baseline Model

To illustrate this theoretical framework a model was constructed for a hypothetically developed country with a threshold value of $40,000/life-year gained, equivalent to the GDP per capita of the hypothetical country. The currency was selected as $ because international data are commonly expressed in $. The model development is based on experience obtained from rotavirus disease and the impact of pediatric rotavirus vaccination in Europe. The model assumes vaccine coverage of 100%, but the coverage rate has no impact on the ICER as long as a static epidemic model is used, because the coverage rate affects both sides of the ratio (higher coverage results in both higher costs and higher effect). Table 1 summarizes the input values selected.

Table 1.

Variables, formulae, input values, and output results to calculate the ICER, the cost neutral price (Pn), and the maximum price of a new intervention (Pm) using a hypothetical model

Variable	Formula	Input	Output
CostDNV		$60
CostDv	CostDNV × (1 − VaccineEffect)		$6
CostV at Pn	CostDNV − CostDv		$54
E NV		0.00031
E V	E NV × (1 − VaccineEffect)		0.000031
ICER (=y) at Pn	((CostDv + CostV) − CostDNV)/(E NV − E V)		$0
VaccineEffect		0.9
a	1/(E NV − E V)		3,584.23
b	(CostDv − CostDNV)/(E NV − E V)		–193,548.39
y	a × Pn + b		$0
Threshold value		$40,000/E
Maximum price/course (Pm)	(40,000 − b)/(a)		$65.16

a slope of the linear regression, b intercept, CostD _NV initial disease-related cost in the absence of vaccination (no vaccine), CostD _v remaining disease-related cost with vaccination, CostV vaccine cost; E effect unit (life-year gained), E _NV health losses without vaccination (no vaccine), E _V remaining health losses (effects) with vaccination, ICER incremental cost-effectiveness ratio, Pm maximum price, Pn cost neutral price

The baseline value for CostD_NV was $60/subject, calculated from data in studies in a recent literature review [9]. It represents the average cost for rotavirus hospitalization in Europe per child in the birth cohort (i.e., the total cost of rotavirus hospitalizations averaged across all children in the cohort). As only a small percentage of children in the birth cohort will be hospitalized for rotavirus, the cost per subject is much smaller than the cost per hospitalized case or per hospitalization event. The baseline value for E _NV (0.00031/subject) is based on the following reasoning. The maximum individual loss in health outcome is the loss of full life expectancy at birth (78 years, discounted at 3% per year = 31 years). That value is multiplied by the disease-specific mortality rate (0.00001 per year) for infants in the region to estimate the individual loss in health outcomes per unvaccinated subject in the infant population. The perspective is that of the healthcare system.

Figure 2 shows how the vaccine price range (Pm–Pn) can shift and change for countries with different cost-effectiveness thresholds but also different potential gains in health outcomes resulting in a change of the slope. As the threshold value increases, Pm becomes larger. In addition, as the absolute effect difference becomes smaller because of a smaller disease burden in the absence of vaccination (E _NV) the slope of the line steepens. As the amount of current spend on the disease increases, Pn becomes larger. Such a situation would be expected in a high-income country (indicated by the high GDP per capita threshold value), with a low disease burden (indicated by the steeper slope) and a higher current expenditure on the disease (Pn and Pm both shifted to the right). Thus, the slope of the line is likely to be steeper and the absolute difference between Pn and Pm is lower for countries with a higher GDP/capita associated with a lower disease burden and higher disease expenditures in the absence of vaccination (see Fig. 2).

Fig. 2.

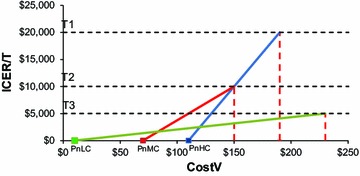
Cost neutral (Pn) and maximum price (Pm) at different thresholds and slope lines. The green line indicates a country with a low threshold (T3), the red line a country with an intermediate threshold (T2), and the blue line a country with a high threshold (T1). As the threshold increases the cost neutral point (where the line intercepts the x-axis) shifts to the right and the slope steepens, reflecting higher healthcare expenditure and lower remaining disease burden. CostV vaccine cost, ICER incremental cost-effectiveness ratio, P _nHC cost neutral price in high-income country, P _nLC cost neutral price in low-income country, P _nMC cost neutral price in middle-income country, T threshold

Country-Specific Data

The next step is to apply this theoretical approach to real-life published data from nine countries across the world for which the cost-effectiveness of rotavirus vaccine has been evaluated using a similar model [15], taking the country-specific GDP per capita as the threshold value. The model adjusts for different current disease-related costs and different vaccine impacts in high-income and low-income countries, and for other factors related to country-specific conditions such as life expectancy, unit cost (expressed in $), disease management, and GDP, among others. Effects are consistently discounted at 3% per year. The same current intervention CostD_NV (hospitalization) and E _NV (disease-specific mortality) variables are used as in the base case model. Cost variables were not discounted because of the short period (the first 2–3 years) when health care expenditure on vaccination and disease-related cost occurs.

Results

Hypothetical Baseline Model

Table 1 shows the results of the base case model.

The two critical points of the vaccine price, Pn and Pm, related to the ICER and the threshold value are shown in Fig. 1. The cost neutral point (Pn = $54) and the maximum price point (Pm = $65.16) define the price range over which the vaccine could still be cost-effective with the threshold set at $40,000 per life-year gained.

Country-Specific Data

For each country, country-specific values for the variables of current cost (CostD_NV) and loss in health outcomes (E _NV) were used to calculate the Pn and Pm of the vaccine at the country-specific threshold (GDP per capita). This exercise provides a better understanding of the meaning of a cost-effectiveness result for countries with different income levels, expressed through their GDP values. Table 2 presents the input data for each country, obtained from published sources as follows: Vietnam [16], Egypt [17], Philippines [18], Algeria [19], Turkey [20], Portugal [21], France [15], The Netherlands [22], and Norway [23]. Life expectancy data for all countries were obtained from WHO Health Statistics 2013 [24], and GDP per capita from World Bank data [5]. Table 2 also shows the CostD_NV and E_NV per subject with the calculated Pn and Pm at the GDP threshold for each country.

Table 2.

Input and output values for each country selected

Country	Vietnam [16]	Egypt [17]	Philippines [18]	Algeria [19]	Turkey [20]	Portugal [21]	France [15]	The Netherlands [22]	Norway [23]
Birth cohort	1,639,000	1,909,000	2,266,887	621,790	1,257,583	109,457	750,000	187,910	60,000
Life expectancy (years) [24]	71.6	68.0	66.6	74.3	73.3	76.6	77.5	78.5	80
Hospitalizations up to age 5 years	32,331	53,342	17,448	11,000	36,797	1,200	17,932	2,940	905
Hospital rate for the birth cohort	1.97%	2.79%	0.77%	1.77%	2.93%	1.10%	2.39%	1.56%	1.51%
Hospital cost per event	$20	$19	$45	$650	$400	$2,172	$1,400	$2,172	$2,382
Deaths up to age 5 years	6,050	3,200	4,438	300	13	1	9	2	1
Death rate	0.37%	0.17%	0.20%	0.048%	0.0010%	0.0009%	0.0012%	0.0011%	0.0017%
GDP [5]	$3,359	$6,455	$4,080	$7,325	$14,393	$23,363	$35,068	$42,023	$53,396
VE in the model	64%	64%	64%	64%	87%	90%	90%	90%	90%
Pn (per dose)	$0.12	$0.15	$0.16	$3.76	$5.58	$11.30	$15.80	$16.09	$17.81
Pm (per dose)	$111.26	$145.61	$101.29	$52.61	$7.61	$14.04	$20.53	$20.13	$28.56
Price range (Pm–Pn)	$111.14	$145.46	$101.13	$48.85	$2.03	$2.74	$4.73	$4.04	$10.75
CostDNV	$0.39	$0.54	$0.35	$12.69	$11.70	$23.81	$33.47	$33.98	$35.97
CostDV	$0.14	$0.23	$0.03	$5.18	$0.54	$1.22	$1.87	$1.80	$0.38
CostDNV − CostDv	−$0.25	−$0.31	−$0.32	−$7.51	−$11.16	−$22.59	−$31.60	−$32.18	−$35.59
E NV	−0.105	−0.0471	−0.0560	−0.014	−0.000297	−0.00025	−0.000297	−0.00022	−0.00041
E V	−0.039	−0.0021	−0.0064	−0.0006	−0.000014	−0.00002	−0.000027	−0.000023	−0.000004
E NV − E V	0.066	0.045	0.0496	0.0134	0.000283	0.00023	0.000270	0.000197	0.000406
a	15	22	20	75	3,534	4,348	3,704	5,076	2,463
b	−4	−7	−6	−560	−39,431	−98,217	−117,037	−163,350	−87,660

a slope of the linear regression, b intercept, CostD _NV initial disease-related cost in the absence of vaccination (no vaccine), CostD _v remaining disease-related cost with vaccination, E _NV health losses without vaccination (no vaccine), E _V health losses after vaccination, GDP gross domestic product, Pm maximum price, Pn cost neutral price, VE vaccine efficacy

Figure 3 presents the relationship between Pm and GDP per capita across the nine countries, plotted from the data in Table 2. It shows that the countries fall into two groups for the relationship between Pm and the country-specific GDP threshold values. For the cluster of countries with a GDP per capita >$10,000, the lower the GDP threshold, the lower the Pm. In this group of countries, the slope is steep, with a fairly narrow range between Pn and Pm (see Table 2).

Fig. 3.

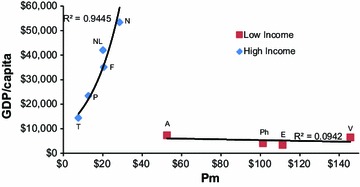
Relationships between baseline values of Pm and GDP by country. Countries with low GDP per capita (squares): A Algeria, E Egypt, Ph Philippines, V Vietnam. Countries with high GDP per capita (diamonds): F France, N Norway, NL Netherlands, P Portugal, T Turkey. GDP Gross domestic product, Pm maximum price

Figure 4 shows an example that illustrates how the Pm will vary according to the cost-effectiveness threshold value with a similar disease burden in the absence of vaccination. The difference between Norway (GDP per capita $53,396) and Portugal (GDP per capita $23,363) illustrates that effect on Pm with a higher threshold. The Pm with one rotavirus death per year is $28.56 in Norway, considerably higher than the maximum price of $14.04 in Portugal (left hand of the three lines for Portugal in the figure [dash-dotted line]). The three lines for Portugal illustrate the effect of increasing the disease burden in the absence of vaccination from one rotavirus death per year (left-hand [dash-dotted] line) to two rotavirus deaths per year (middle [dashed] line) and then to three rotavirus deaths per year (right-hand [dashed] line), while assuming expenditure for the disease treatment remains constant. It can be seen that as the disease burden (number of rotavirus deaths per year) increases, as expected Pm also increases even without a change in the threshold. This is because as the disease burden at baseline increases with the increasing number of deaths, the benefit of the vaccine in reducing the disease burden will also be higher in absolute value, the slope of the line in Fig. 4 will be lower and therefore the price range over which the vaccine is cost-effective will be larger. The vaccine price range for cost-effectiveness (Pm–Pn) is, however, much larger in Norway than in Portugal, despite a disease burden that is 1.3 times lower in Norway than Portugal.

Fig. 4.

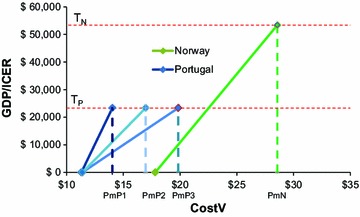
Effect on the maximum price (Pm) of increasing the threshold (GDP in Norway compared with Portugal) and increasing the disease burden (number of rotavirus deaths per year in Portugal increased from P1 to P2 to P3). CostV Vaccine cost, GDP gross domestic product, ICER incremental cost-effectiveness ratio, Pm maximum price, T _N threshold for Norway, T _P threshold for Portugal

In the second cluster of countries, those with a low GDP per capita, the pattern of systematic decline of the Pm with lower GDP per capita no longer fits the data. The baseline disease-related healthcare costs are so low (CostD_NV), and the remaining health burden (E _NV) so high that the slope factor ‘a’ is also very low (see Table 2). The slope factor is given by the equation:

$$a=\frac{1}{E_{\text{NV}}-E_{\text{V}}}$$

The slope angle is very shallow because of the high reduction in losses in health outcomes, and the Pn value is close to zero because of the low current expenditure per case for the disease and thus the potential for only minimal cost offsets.

Discussion

An important outcome from the analyses presented in this paper is that the results for rotavirus vaccination split the countries into two clusters with different characteristics using the GDP per capita as a measure of distinction.

Countries with a High GDP/Capita

CEA has been applied mainly in higher-income countries for many years now as a technique currently used to compare the value of alternative treatments and/or in combination with threshold values representing willingness to pay for an incremental unit of health as the basis for “value-based” pricing. It is an established method in health economic assessment to help to define the price at which a new intervention is considered good value for money compared with the current standard of care at the individual, most often, patient level [25, 26].

Typically, a new intervention has an impact on both the cost and the effect side in the ICER. CEA makes most sense in capturing the value of a new intervention when there is investment in healthcare for the disease of interest but with disease burden still remaining. Under such circumstances a new intervention can achieve both an important cost offset and a reasonable effect gain. It is then meaningful to estimate a cost per life-year or quality-adjusted life-year gained in relation to a pre-specified threshold within a price range. Such situations are likely to occur within mature healthcare markets. ICER values calculated from CEA can be useful in defining the acceptable price range in such countries. The steeper the line in Fig. 1, the narrower the price band over which the ICER moves from Pn to Pm. When Pn equals Pm, the focus of price setting may shift from cost-effectiveness to cost savings.

The maximum price in this group of countries is strongly influenced by the threshold value (GDP per capita) and the remaining disease burden in the absence of vaccination. As the threshold value increases, the maximum price also increases. In addition, as the disease burden in the absence of vaccination increases, the slope of the line decreases and the maximum price increases even without a change in the threshold, as illustrated in the present analysis using Norway and Portugal as examples.

Countries with Low GDP/Capita

The situation is quite different when conducting CEA outside mature healthcare markets. This reflects an environment with low existing healthcare investment (CostD_NV) and high disease burden (E _NV) as a consequence. The low existing healthcare expenditure on the disease allows minimal scope for cost offsets, so the Pn is close to zero. The high disease burden has the potential for large reductions in health outcome losses, so an effective intervention can be cost-effective (as defined by the GDP per capita threshold) over a wide price range, because of the low slope.

This wide price range within which rotavirus vaccination is cost-effective offers a possible explanation for the paradoxical results for rotavirus vaccination CEA reported in the literature. Reviews of rotavirus vaccination reported high cost-effectiveness in low-income countries and a mixed picture in high-income countries [10]. A study in Latin America found that the vaccine price that was apparently cost-effective was higher in low-income countries than in middle-income countries [11]. Yet, it is clear that high prices are not affordable or acceptable for low-income countries. The present analysis suggests that the apparently better cost-effectiveness results at a relatively high intervention price in countries with low GDP per capita reflects the large increases in health outcomes possible in such environments.

In situations with high potential increases in health outcomes accompanied by low current health care expenditures, ICER values calculated by conventional CEA have limited value in defining a reasonable price band for a new intervention. Even if the estimated ICER value indicates that a high price would be cost-effective based on a 1 × GDP threshold, the price may be rejected on the basis of the affordability of the acquisition cost [27]. A price close to the Pn is likely to be preferred by the low-income country, but as the Pn is likely to be very low (because low existing healthcare expenditure offers minimal scope for cost offsets), such a price might not be seen as reasonable by the seller of the new intervention. Thus, if Pn and Pm define price bands in low-income countries that are questionable at the extremes for both payers and producers, CEA performed under these conditions might not be able to serve the same function in low-income countries as in high-income countries, where CEA is used to help define a reasonable price band.

Although the value of $10,000 GDP per capita that differentiates the two groups of countries in this analysis is an arbitrary threshold, it acts as a proxy for the degree of healthcare development in a country. Countries in the group with a high GDP per capita typically have well-established healthcare systems with infrastructure already in place. In these countries, the fixed cost of healthcare infrastructure is already accounted for and variable costs for treatment are well accepted. In these cases, decisions about new interventions can be made at the margin using incremental costs and benefits for individuals, as described in the ICER calculated by conventional CEA that assumes that prices are a fair representation of opportunity costs. Conversely, in the countries with a low GDP per capita, healthcare infrastructure may be limited and the healthcare system not yet fully developed. Because of this, prices defined as acquisition costs may not reflect the true opportunity cost of the intervention. In these situations, affordability and practical considerations such as the alternative possible uses for the additional healthcare investment (including other health investments or non-health investments) are important considerations.

Potential Future Directions

Our results suggest that CEA is not necessarily the optimum economic analysis method for defining a feasible price band for a new intervention in low-income countries [28]. Measuring shadow prices could be an alternative if cost-benefit analysis or CEA is used for economic assessment of new interventions in those situations [29]. In low-income environments with low health investment and a high disease burden, almost any improvement in health will require extra spending. The question therefore should be phrased not as a comparison of the new intervention with the existing situation which could be considered as a substitution economy, but as a consideration of which alternative interventions would provide the greatest additional health benefit for a given amount of extra money spent—an add-on economy instead of substitution [30].

Health problems that affect a whole population (as is often the case in low-income countries) should be assessed using economic approaches, tools or techniques that describe the problem well at the population level. In addition, the impact of increased spending on health care on other sectors of the economy should be included in the analyses.

Budget optimization modeling (BOM) [31] and return on investment (ROI) [17] are possible alternative economic techniques for estimating the true value of a new intervention in low-income countries. The choice of technique should be driven by the economic question asked, a good understanding of the economic problem to be solved, data availability, and the requirements of the decision makers who need to understand and use the economic analysis.

BOM is attractive when the problem is one of integrating different management options into a specific health goal within certain constraints, such as budgets and/or logistics [32]. Its application is not especially complicated. Furthermore, the BOM is well suited to the type of problem that needs to be addressed in low healthcare investment areas. Instead of comparing a new intervention with the existing situation, which as described here has weaknesses when applied to countries with a low GDP/capita, it considers the question of how best to optimize the use of the health investment budget available today. It is essentially a more flexible and dynamic version of budget impact assessment. However, a limitation of budget optimisation is that it is more difficult to evaluate the effects of uncertainty than in conventional CEA, because the effects of varying the proportions of different interventions in the mix have to be taken into account, as well as uncertainty in the parameters describing each intervention.

ROI analysis is also attractive. It is based on the premise that the health problem must be substantial at population level and compares different investment policies in terms of benefit within that population projected over time as a function of tax payment/income for the government. It can compare investment in prevention through vaccination with either doing nothing or increasing healthcare infrastructure to reach the same health benefit level. However, a limitation is that it considers health benefits only in terms of the effects on future tax revenues, and does not take into account intangible benefits such as the improvement in human welfare arising from reductions in the disease burden.

A further area of uncertainty is whether the average GDP per capita reflects the right threshold value [33]. First, the distribution of GDP per capita in low-income countries is often skewed, and much of the population may receive little benefit from any healthcare services offered because they do not have access to them. This issue is not reflected in the average per-capita GDP value, but is reflected in the remaining health problem (E _NV). For example, Egypt has a relatively high GDP per capita, close to the value reported for Algeria, while the disease burden (E _NV) is high and comparable with populations such as the Philippines (see Table 2). Second, GDP per capita does not necessarily relate to the investment a country is willing to make in healthcare, which may be affected by other competing priorities.

The present analysis has limitations. Not all the different costs and benefits related to rotavirus vaccination have been included in the analysis, as the focus was only on the parameters that drive the main results, hospitalization and mortality. However, a more detailed assessment is not likely to change the main discrepancy between the clusters of countries with high versus low income. Furthermore, the analysis has only investigated a single intervention and disease, rotavirus vaccination. The next step would be to explore whether other disease areas show similar patterns, which would indicate whether the findings are likely to be generalizable.

Conclusion

The paradoxical results of CEA in countries with low GDP per capita described in this paper suggest that conventional CEA may have limited applicability for defining an acceptable price range in such situations. This may be because current methods for cost-effectiveness analyses do not properly account for the opportunity costs of the new intervention in low-income countries. Alternative economic methods may be better suited to the economic assessment of healthcare interventions in low-income countries, and this should be explored in greater detail.

Electronic supplementary material

Below is the link to the electronic supplementary material.