Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Oct 27;4:6771. doi: 10.1038/srep06771

Polarization selective phase-change nanomodulator

Kannatassen Appavoo 1,2,a, Richard F Haglund Jr 1,3,b
PMCID: PMC4209465  PMID: 25346427

Abstract

Manipulating optical signals below the diffraction limit is crucial for next-generation data-storage and telecommunication technologies. Although controlling the flow of light around nanoscale waveguides was achieved over a decade ago, modulating optical signals at terahertz frequencies within nanoscale volumes remains a challenge. Since the physics underlying any modulator relies on changes in dielectric properties, the incorporation of strongly electron-correlated materials (SECMs) has been proposed because they can exhibit orders of magnitude changes in electrical and optical properties with modest thermal, electrical or optical trigger signals. Here we demonstrate a hybrid nanomodulator of deep sub-wavelength dimensions with an active volume of only 0.002 µm3 by spatially confining light on the nanometre length scale using a plasmonic nanostructure while simultaneously controlling the reactive near-field environment at its optical focus with a single, precisely positioned SECM nanostructure. Since the nanomodulator functionality hinges on this near-field electromagnetic interaction, the modulation is also selectively responsive to polarization. This architecture suggests one path for designing reconfigurable optoelectronic building blocks with responses that can be tailored with exquisite precision by varying size, geometry, and the intrinsic materials properties of the hybrid elements.

As the transistor reaches its fundamental size and speed limits, new elementary switching structures based on optoelectronics are being developed for next-generation computers1,2. Plasmonics has the potential to create the requisite optoelectronic building blocks by integrating electronics and photonics on a single chip, enabling the exchange of data at larger bandwidth and at ultrafast speeds3. Although light can be squeezed and manipulated at sub-wavelength scale, recently reaching confinement dimensions of λ/165 in quantum metallic nanostructures4 and λ/200 for point defects in graphene5, dynamically modulating the intensity or phase of optical signals at these dimensions at THz frequencies and at a maximal energy cost per bit of 100 fJ remains a challenge6.

Active modulation of plasmon optical response has been demonstrated by optical excitation of a thin layer of quantum dots7, the electro-optic effect in barium titanate thin films8, optically induced refractive index changes in silicon9 and recently, using transparent conductive oxides10. In optical modulation of the surface plasmon polariton by quantum dots, for example, energy costs of less than 1 fJ per bit were derived from a thin-film geometry, but the speed would be limited to sub-GHz range because of the spontaneous lifetime of the optical transition. The refractive-index change in silicon is ultrafast, but the modulation depth is small because of the small index change (Δn = 0.005) available from the electro-optic effect in silicon. And in all these operational schemes, it appears that plausible thin-film devices would have areas of several square micrometres.

Here we demonstrate active modulation of optical-frequency plasmonic resonance peaks by about 12 nm in a device whose footprint is less than 0.1 μm2 by using a reversible phase transition (PT) in a prototypical strongly electron-correlated material (SECM), vanadium dioxide (VO2). Vanadium dioxide undergoes a metal-to-insulator (MIT) phase transition near 68°C with a concomitant atomic rearrangement from tetragonal to rutile that leads to dramatic changes in optical and electrical properties. The phase transformation can be driven optically on time scales less than 100 fs11,12,13 and as recently demonstrated by Wall et al.14,15, the ultrafast PT can be modulated optically at low fluences by femtosecond excitation of specific VO2 vibrational modes. Moreover, VO2 nanostructures exhibit size-dependent switching as well as a dipolar plasmon response in the near-IR when the nanostructures metallize16,17.

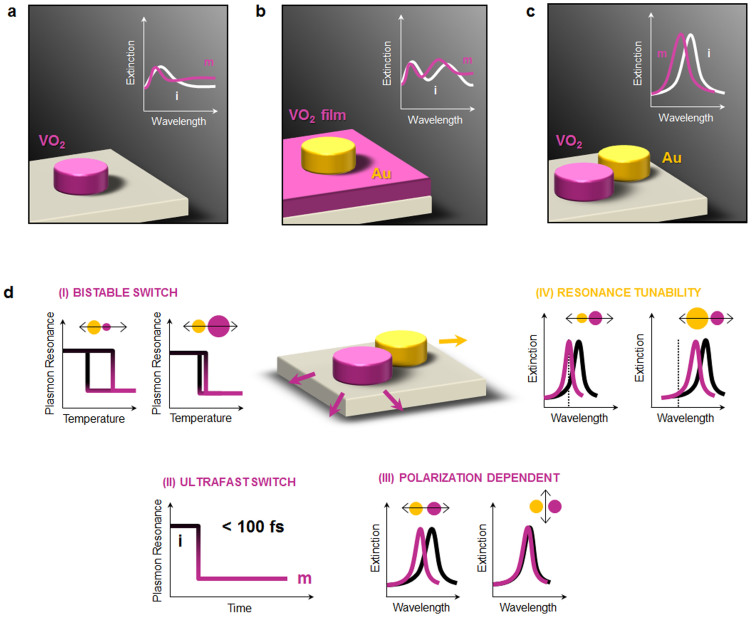
As schematically represented in Fig. 1a, the intrinsic plasmonic response of VO2 nanostructures is strongly damped17, limiting their utility when deployed as the sole switchable component in a nanostructure. However, the large change in dielectric function – of order unity18 – between the “on” and “off” states in a single VO2 nanodisk placed in the optical near field of a metal nanodisk enables effective modulation of the plasmon resonance (Fig. 1b vs. 1c). This modular nanoarchitecture – relying solely on the near-field electromagnetic interaction between the metallic and SECM nanostructure – enables various functions, as illustrated in Fig. 1d. For example, spectral response from the visible to the mid-IR is obtained by varying the size and shape of the metallic nanostructure. The intrinsic phase-changing properties of the VO2 can also be harnessed to create bistable nanoswitches or colour nanorouters19 by exploiting thermally, optically or electrically driven, size-dependent VO2 switching16,17.

Figure 1. Illustrations highlighting advantages of phase-change nanomodulator.

Figure 1

Open in a new tab

(a), Sketch based on experimental results of references 16 and 17 with modulation of the optical properties of an isolated vanadium dioxide (VO2) nanostructure by thermally triggering its phase transition from insulating (white) to metallic (magenta) state. When the VO2 nanostructure becomes metallic, an intrinsic localized surface plasmon is formed in the near-IR region, albeit strongly damped. (b), Metallic nanostructure on PC-VO2 film with a strongly damped plasmon resonance of Au due strong interaction with the active substrate and a strong absorption in the visible due to the film geometry, based on Suh et al. work41. (c), Modulation of the gold plasmonic resonance with a VO2 nanostructure that modifies only the near-field nanoenvironment of the metallic nanostructure (present work). (d), Combining these two nanostructures as shown in (c) provides reconfigurability: (I) using the size-dependent properties of VO2 for bistable switches (II) ultrafast plasmonic switch underlined by the ultrafast switching of the intrinsic PC-VO2, (III) polarization selectively activating the modulation, (IV) Tuning the operating wavelength of the hybrid nanomodulator by varying the plasmonic nanostructure size and shape.

This design flexibility is achieved by controlling the size of the VO2 nanodisks, dictating the density of defects that nucleate the phase transition and thus hysteresis width (or operational range) of the nanomodulator (Fig. 1d–I). Nanomodulators operating at THz frequencies can be envisioned in the non-equilibrium limit (Fig. 1d-II)20,21. Furthermore, since the hybrid nanomodulator functions via the electromagnetic near-field interaction, selectivity is achieved by polarization as well (Fig. 1d-III), as will be experimentally and computationally demonstrated below.

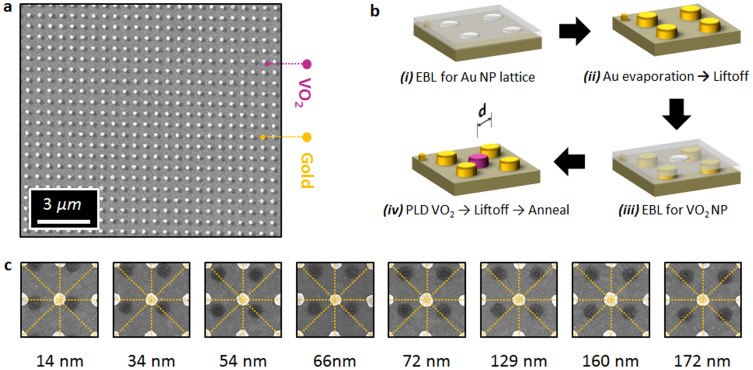
The prototype hybrid nanomodulator was fabricated using a three-stage electron-beam lithographic method (EBL) illustrated in Fig. 2 (see Methods). Such a fabrication protocol, to the best of our knowledge, has been successfully achieved only by Liu et al. for gas sensing using a gold/palladium nanoarchitecture22. Here, lithographically fabricated gold nanomarkers were used to position a gold nanodisk on an indium-tin-oxide (ITO)-covered glass substrate in a lattice configuration. Using the same nanomarkers, a single VO2 nanodisk was subsequently positioned adjacent to its neighbouring gold nanodisk. The sample was then annealed to render the VO2 nanostructure crystalline (insulating-M1) and phase transforming23. As shown in the scanning electron micrograph (SEM, Fig. 2a), the differential contrast of the two nanostructures clearly shows the efficacy of the design. To demonstrate that the nanomodulator operates solely by near-field electromagnetic interactions, we fabricated ten similar patterns on that same substrate with varying separations between the gold and VO2 nanodisks (Fig. 2c). Using this protocol, we achieved a minimum edge-to-edge nanostructure separation of about 14 nm as confirmed by SEM in Figs. 2a, c.

Figure 2. Fabrication process of the nanomodulator arrays.

Figure 2

Open in a new tab

(a), Scanning electron micrograph (SEM) for the 14 nm separation hybrid nanostructured array. (b), Fabrication protocol of a planar plasmonic/phase-changing materials using a three-step electron-beam lithography process including gold evaporation, pulsed laser deposition with subsequent lift-off procedures after each deposition method. A final annealing step renders the vanadium dioxide nanodisks crystalline and phase-switching. (c), SEMs of the eight nanomodulators under study with varying edge-to-edge separation (d nm) between the Au and VO2 nanostructures.

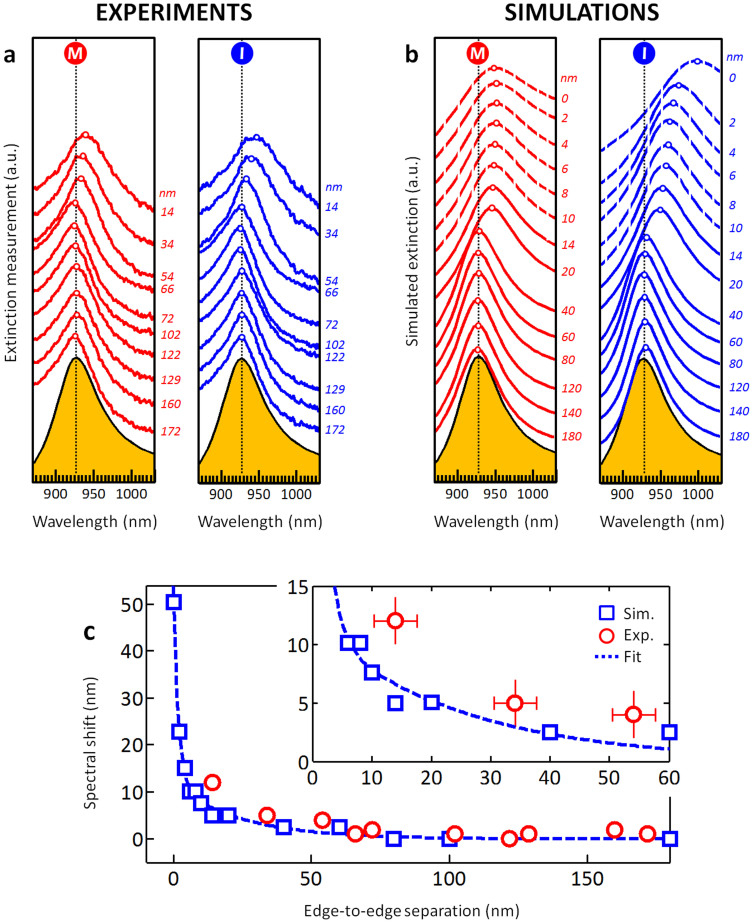
Following fabrication, white-light broadband extinction was measured on each nanomodulator array both when the VO2 nanostructure was in the insulating (blue, room temperature) and metallic (red, 95°C) states (Fig. 3a, see Methods), with the light polarized parallel to the long axis of the nanomodulator. When the VO2 nanodisk is located at a distance of 180 nm from the gold nanodisk, no modulation of the plasmonic extinction spectrum is observed. However, at an edge-to-edge separation of about 34 nm, the nanomodulator shows the first signs of spectral tuning. As the VO2 nanostructure approaches the near-field of the gold nanodisk, the wavelength shift increase. At the minimum separation that could be achieved with the available EBL tool, a blue shift in the modulation of about 12 nm between the spectral peaks of the hot-metallic and cold-insulating states is obtained. This is better than or comparable to previous studies using thin films as active switching media.

Figure 3. Experimental and simulated optical spectra of nanomodulators.

Figure 3

Open in a new tab

(a), Experimental extinction spectra for the 172, 160, 129, 122, 102, 72, 66, 54, 34, 14 nm interparticle separation arrays when the vanadium dioxide nanostructures are in the metallic (red) or insulating (blue) state. (b), Simulated extinction spectra of the hybrid nanomodulator for interparticle separation of 180, 140, 120, 80, 60, 40, 20, 14, 10, 8, 6, 4, 2, 0 nm in metallic (red) and insulating (blue) state. The orange-shaded plots in each figure represent the simulated optical response of the gold lattices that match closely both with the experimental results and with the cases where the VO2 nanostructures are not in the near-field region of the plasmonic nanostructure. Spectral modulation is visible when edge-to-edge separation is less than 35 nm (c), Summary of spectral shifts for both experimental and simulated results. The error bar for the interparticle separation was estimated to be ± 4 nm while the peak determination is ± 2 nm. We note that all measurements (experimental and simulated) shown here are for light polarized along the long axis (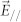Inline graphic).

Consequently, this proof-of-concept experiment demonstrates that a single nanostructure of strongly electron-correlated material carefully positioned with respect to the plasmonic nanostructure can effectively modulate optical signals in a nanoscale volume. The high contrast in dielectric function between the metallic and insulating states of the VO2 makes it possible to achieve effective modulation in substantially smaller volumes than other material systems; in the present case, the active volume is less than 0.002 µm3 compared to 5–100 µm3 for conventional electro-optic modulators. If triggered optically, such a hybrid phase-change/plasmonic nanomodulator has been shown to require at most 250 μJ/cm2 12,20, comparable to but less than the optical fluence needed to initiate refractive index changes in silicon (~1000 μJ/cm2)9 or control surface plasmon-polariton propagation at an aluminium/silica interface (~10000 μJ/cm2)24. Given that the area of the modulator is of order 0.1 μm2, a switching threshold12 of 250 µJ/cm2 corresponds to an energy cost of order 20 fJ per bit for a wavelength shift of 1 nm, assuming that the wavelength shift is to zeroth order linearly proportional to the absorbed energy. This is well within the canonical energy cost per bit for a photonic switching system25. We note that when light is polarized along the short axis (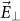Inline graphic), no modulation is observed experimentally.

To estimate the maximum possible modulation in this geometry, three-dimensional full-field finite-difference, time-domain simulations with light polarized either parallel (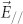Inline graphic) or perpendicular (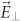Inline graphic) to the axis of the nanomodulator were carried out, with nanostructure edge-to-edge separation as small as 0 nm (“kissing” nanostructures). As shown in Fig. 3b, there is no modulation for edge-to-edge distances from 180 nm to 40 nm. However, when the VO2 nanostructure reaches the electromagnetic near-field of the Au nanodisk, a progressively stronger modulation of the plasmon resonance wavelength between the hot and cold VO2 states is achieved. As seen in Fig. 3c, the simulated and the experimental extinction spectra agree over the range of fabricated nanostructures. Modulation begins only when the two nanostructures are less than approximately 35 nm apart; inspection of Fig. 3b shows that this is in the weak-coupling regime where minimal plasmon hybridization occurs and the VO2 nanodisk can be effectively treated as a dielectric perturbation. While a systematic redshift occurs as the insulating VO2 approaches the Au-nanostructure, we observe a slight blueshift when the nanostructure is in its metallic state, consistent with an intrinsic plasmonic response in the near-IR for a plasmonic density of states smaller than that of the gold nanostructure26,27. More importantly, the simulations show that a wavelength modulation approaching 50 nm is achievable for the “kissing” nanostructures; however, this must be taken as only an indication of an extreme value, since at this spacing other mechanisms come into play, such as quantum tunnelling and electronic spill-out effects28.

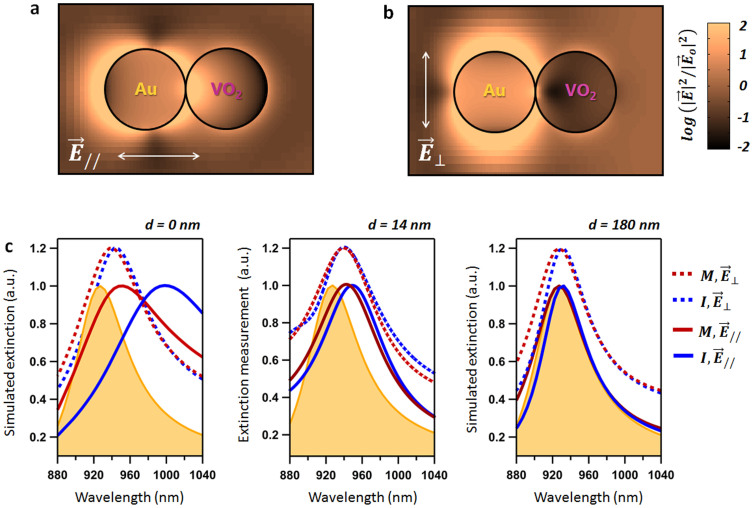
Experimental tests of the polarization dependence of the hybrid nanomodulator showed no sign of spectral tuning when light was polarized perpendicular to its axis. Since a separation of 14 nm was the smallest achieved experimentally, we used simulations to understand how polarization affects the behavior of the nanomodulator for smaller separations. Comparing the near-field electromagnetic profiles for parallel (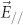Inline graphic) and perpendicular (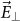Inline graphic) polarization (Fig. 3b), it is clear that the EM fields interact strongly with the VO2 nanostructure only for parallel polarization. The field distortion created by the VO2 nanostructure within the lobe of the Au dipolar resonance therefore dictates the overall modulation effect of the device. This implies that nano-focusing using more complex architectures like nanopyramids22 is not necessary as even with a relatively broader “spillout” of the plasmon near-field from the gold nanostructure, selective modulation can be achieved by polarization. This can be visualized in Fig. 4b (right) where the symmetric distortion of the dipole field with respect to the entire nanomodulator results in no spectral tuning, albeit with a slight broadening in linewidth, requiring a near-perfect positioning of a phase-changing nanostructure to maximize modulation (Fig. 3b).

Figure 4. Polarization selectivity of hybrid nanomodulator.

Figure 4

Open in a new tab

(a), (b), Electromagnetic field enhancement profiles for a single hybrid nanomodulator (gap distance = 0 nm and VO2 state is metallic) for the two extreme polarization cases. (c), Collection of simulated (left and right) and experimental (middle) spectra comparing the effect of polarization and edge-to-edge separation, with blue and red curves for insulating and metallic cases, respectively. For clarity, all spectra have been normalized and the results for the perpendicular polarized light (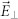Inline graphic) have a vertical offset of 0.2.

Although the hybrid Au-VO2 nanomodulator cannot be compared directly to conventional electro-optic modulators, its critical parameters – modulation speed, extinction ratio, bandwidth, power consumption, and device footprint – still measure up well. With a single nanostructure having an active volume of only 0.002 µm3, the modulation depth for this hybrid nanomodulator is ~1.3 dB, calculated by comparing the transmission intensity change at the peak plasmon resonance when the VO2 nanostructure is metallic. However, increasing the modulation depth is straightforward by implementing strategies such as optimization of the size and shape of the VO2 nanostructure (for example a split-ring circular structure) or implementing this near-field design in well-established photonic devices such as ring resonators29 or interferometers30. We note that our nanomodulator was not optimized at telecommunication wavelengths but operation bandwidths greater than 100 nm can be realized with modulation speed of 1 GHz, while shifting the operational bandwidth can be achieved by varying the size of the plasmonic nanostructure. Although our polarization-selective hybrid nanomodulator has been demonstrated with two nanodisks of similar size, other geometries such as nanorods31 to decrease the plasmonic linewidth or plasmonic oligomers32,33,34 making use of Fano resonances (in order to increase modulation depth) can be readily designed and fabricated. Additionally, even though this demonstration experimentally focused on modulation of a single localized surface-plasmon resonance, the application to modulating information-carrying chains of nanoparticles would appear to be straightforward as well35,36.

Technologically, this simple nanoarchitecture provides substantial design flexibility, enabling other potential applications requiring minimal footprints, such as trapping37, beam steering and focusing, where dictating the optical phase of light is critical38. Moreover, the unique nonlinear optical properties of VO2 allow for non-centrosymmetric nanomodulator designs to access second- and third-order nonlinearities39. This simple architecture also makes it possible to study the interactions of ensemble nanostructures in which one or more components has an intrinsically variable plasmonic density of states40.

Methods

Fabrication

Gold markers were lithographically fabricated on ITO-coated glass substrate by means of (1) electron-beam lithography (EBL) on PMMA, spun at 2500 rpm and baked at 180°C for 90 sec; (2) e-beam evaporation of 20 nm of gold on the patterned substrate, measured by a quartz-crystal microbalance; (3) subsequent lift-off procedure using a Remover PG bath at 70°C for 20 min. The gold nanodisk lattices were fabricated using the same protocol, resulting in nanodisks of height 20 nm and unit cell of 600 nm, each plasmonic lattice having a footprint of 100 × 100 µm2. Using the gold alignment markers, a third step lithography was performed by coating once more PMMA resist on the sample and writing the phase-changing lattice pattern at sub-20-nm level. Subsequently, the vanadium dioxide nanodisks were generated by (i) pulse laser ablation of a vanadium metal target (PLD: λ = 248 nm, 25 ns pulse duration, 3.86 J/cm2 fluence, 10 Hz repetition rate and 10 mTorr of O2 gas) to yield, after subsequent lift-off, nanodisks of amorphous, sub-stoichiometric vanadium dioxide (40 nm VOX = 1.7 nominal thickness); (iii) thermal anneal of the sample (450°C, O2 gas at 250 mTorr for 20 min) to render the NPs crystalline and stoichiometric.

Optical measurements

Extinction measurements were acquired as follows: (i) the 100 × 100 μm2 plasmonic lattice of interest was positioned using micrometre drives under white light illumination from a tungsten lamp (90 μm spot size and polarized at 45° (perpendicular) or 135° (parallel) to the interacting dimer) while concurrently being imaged onto a CCD camera in the x-y plane; (ii) the focus (z-plane) was then visually adjusted by displacing the 5X microscope objective with a numerical aperture of 0.12; (iii) extinction at room temperature was then measured (integration time of 8 ms and average of 200) (iv) the sample was then heated to 95°C, well above the transition temperature of the VO2 nanodisks, and extinction measurements for the various lattices were repeated. As flat-field, transmission spectra of the ITO-coated glass at room temperature and at 95°C were used when the VO2 nanodisks were insulating and metallic respectively. We note that this is in contrast to using the insulating or metallic VO2 film as the flat-field41,42,43, emphasizing the hybrid nanomodulator concept as a distinct entity.

FDTD simulations

3D full-field electromagnetic wave calculations were performed using Lumerical FDTD Solutions®, a commercially available software package. A unit cell of the plasmonic lattice structure (Au nanodisks of height 20 nm and radial dimension of 96 nm; VO2 nanodisks of height 32 nm as averaged by atomic force microscopy on another sample and radial dimensions of about 96 nm), including the ITO-coated glass substrate, was simulated using periodic boundary conditions along the x and y axes and perfectly matched layers along the propagation of the electromagnetic waves. Broadband planes waves (700–1200 nm) were launched incident to the unit cell. While one monitor was placed in the glass substrate to record transmission (z = - 400 nm), another monitor (z = 10 nm) was used to record the spatial near-field enhancements. In all the simulations, we employed an auto-meshing accuracy of 3 units, combined with an overriding cubic mesh size of 1 nm3 around the nanostructures and the gap. The dielectric functions for the Au was obtained from Johnson and Christy's data44 while those of the VO2 (insulating and metallic) were obtained from Verleur's work20.

Author Contributions

K.A. conceived and performed the experiments and the full-field electromagnetic simulations. K.A. and R.F.H. developed the interpretation of the data and wrote the paper.

Acknowledgments

The authors thank B.K. Choi for help with Au deposition. K.A. was supported by research assistantships provided by the National Science Foundation (ECE-0801980) and the Defence Threat-Reduction Agency (HDTRA1-10-1-0047). Portions of this work were performed at the Vanderbilt Institute of Nanoscale Science and Engineering, using facilities renovated under NSF ARI-R2 DMR-0963361.

References

  1. Dionne J. A., Diest K., Sweatlock L. A. & Atwater H. A. PlasMOStor: A Metal-Oxide-Si Field Effect Plasmonic Modulator. Nano Lett. 9, 897–902 (2009). [DOI] [PubMed] [Google Scholar]
  2. Dionne J. A., Sweatlock L. A., Sheldon M. T., Alivisatos A. P. & Atwater H. A. Silicon-Based Plasmonics for On-Chip Photonics. IEEE Journal of Selected Topics in Quantum Electronics 16, 295–306 (2010). [Google Scholar]
  3. Zia R., Schuller J. A., Chandran A. & Brongersma M. L. Plasmonics: the next chip-scale technology. Mater. Today 9, 20–27 (2006). [Google Scholar]
  4. Scholl J. A., Koh A. L. & Dionne J. A. Quantum plasmon resonances of individual metallic nanoparticles. Nature 483, 421–U468 (2012). [DOI] [PubMed] [Google Scholar]
  5. Zhou W. et al. Atomically localized plasmon enhancement in monolayer graphene. Nature Nanotechnology 7, 161–165 (2012). [DOI] [PubMed] [Google Scholar]
  6. Liu N. et al. Individual Nanoantennas Loaded with Three-Dimensional Optical Nanocircuits. Nano Lett. 13, 142–147 (2012). [DOI] [PubMed] [Google Scholar]
  7. Pacifici D., Lezec H. J. & Atwater H. A. All-optical modulation by plasmonic excitation of CdSe quantum dots. Nature Photonics 1, 402–406 (2007). [Google Scholar]
  8. Dicken M. J. et al. Electrooptic Modulation in Thin Film Barium Titanate Plasmonic Interferometers. Nano Lett. 8, 4048–4052 (2008). [DOI] [PubMed] [Google Scholar]
  9. Caspers J. N., Rotenberg N. & van Driel H. M. Ultrafast silicon-based active plasmonics at telecom wavelengths. Opt. Express 18, 19761–19769 (2010). [DOI] [PubMed] [Google Scholar]
  10. Shi K., Haque R. R., Zhao B., Zhao R. & Lu Z. Broadband electro-optical modulator based on transparent conducting oxide. Opt. Lett. 39, 4978–4981 (2014). [DOI] [PubMed] [Google Scholar]
  11. Cavalleri A. et al. Femtosecond structural dynamics in VO2 during an ultrafast solid-solid phase transition. Phys. Rev. Lett. 87 (2001). [DOI] [PubMed] [Google Scholar]
  12. Rini M. et al. Optical switching in VO2 films by below-gap excitation. Appl. Phys. Lett. 92, 181904 (2008). [Google Scholar]
  13. Pashkin A. et al. Ultrafast insulator-metal phase transition in VO2 studied by multiterahertz spectroscopy. Physical Review B 83, 195120 (2011). [Google Scholar]
  14. Wall S. et al. Ultrafast changes in lattice symmetry probed by coherent phonons. Nature Communications 3, 721 (2012). [DOI] [PubMed] [Google Scholar]
  15. Wall S. et al. Tracking the evolution of electronic and structural properties of VO2 during the ultrafast photoinduced insulator-metal transition. Physical Review B 87, 115126 (2013). [Google Scholar]
  16. Lopez R., Feldman L. C. & Haglund R. F. Size-Dependent Optical Properties of VO2 Nanoparticle Arrays. Phys. Rev. Lett. 93, 177403 (2004). [DOI] [PubMed] [Google Scholar]
  17. Appavoo K. et al. Role of Defects in the Phase Transition of VO2 Nanoparticles Probed by Plasmon Resonance Spectroscopy. Nano Lett. 12, 780–786 (2012). [DOI] [PubMed] [Google Scholar]
  18. Verleur H. W., Barker A. S. & Berglund C. N. Optical Properties of VO2 between 0.25 and 5 eV. Physical Review 172, 788 (1968). [Google Scholar]
  19. Shegai T. et al. A bimetallic nanoantenna for directional colour routing. Nature Communications 2 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Appavoo K. et al. Ultrafast Phase Transition via Catastrophic Phonon Collapse Driven by Plasmonic Hot-Electron Injection. Nano Letters 10.1021/nl4044828 (2014). [DOI] [PubMed] [Google Scholar]
  21. Liu M. et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 487, 345–348 (2012). [DOI] [PubMed] [Google Scholar]
  22. Liu N., Tang M. L., Hentschel M., Giessen H. & Alivisatos A. P. Nanoantenna-enhanced gas sensing in a single tailored nanofocus. Nature Materials 10, 631–636 (2011). [DOI] [PubMed] [Google Scholar]
  23. Suh J. Y., Lopez R., Feldman L. C. & Haglund R. F. Semiconductor to metal phase transition in the nucleation and growth of VO2 nanoparticles and thin films. J. Appl. Phys. 96, 1209–1213 (2004). [Google Scholar]
  24. MacDonald K. F., Samson Z. L., Stockman M. I. & Zheludev N. I. Ultrafast active plasmonics. Nature Photonics 3, 55–58 (2009). [Google Scholar]
  25. Reed G. T., Mashanovich G., Gardes F. Y. & Thomson D. J. Silicon optical modulators. Nat Photon 4, 518–526 (2010). [Google Scholar]
  26. Le F. et al. Plasmons in the Metallic Nanoparticle−Film System as a Tunable Impurity Problem. Nano Lett. 5, 2009–2013 (2005). [DOI] [PubMed] [Google Scholar]
  27. Halas N. J., Lal S., Chang W.-S., Link S. & Nordlander P. Plasmons in Strongly Coupled Metallic Nanostructures. Chem. Rev. 111, 3913–3961 (2011). [DOI] [PubMed] [Google Scholar]
  28. Esteban R., Borisov A. G., Nordlander P. & Aizpurua J. Bridging quantum and classical plasmonics with a quantum-corrected model. Nat Commun 3, 825 (2012). [DOI] [PubMed] [Google Scholar]
  29. Ryckman J. D., Hallman K. A., Marvel R. E., Haglund R. F. & Weiss S. M. Ultra-compact silicon photonic devices reconfigured by an optically induced semiconductor-to-metal transition. Opt. Express 21, 10753–10763 (2013). [DOI] [PubMed] [Google Scholar]
  30. Joushaghani A. et al. Sub-volt broadband hybrid plasmonic-vanadium dioxide switches. Appl. Phys. Lett. 102, - (2013). [Google Scholar]
  31. Sonnichsen C. et al. Drastic reduction of plasmon damping in gold nanorods. Phys. Rev. Lett. 88 (2002). [DOI] [PubMed] [Google Scholar]
  32. Hentschel M., Dregely D., Vogelgesang R., Giessen H. & Liu N. Plasmonic Oligomers: The Role of Individual Particles in Collective Behavior. ACS Nano 5, 2042–2050 (2011). [DOI] [PubMed] [Google Scholar]
  33. Hentschel M. et al. Transition from Isolated to Collective Modes in Plasmonic Oligomers. Nano Lett. 10, 2721–2726 (2010). [DOI] [PubMed] [Google Scholar]
  34. McGahan C., Appavoo K., Haglund R. F. & Shapera E. P. Switchable plasmon-induced transparency in gold nanoarrays on vanadium dioxide film. Journal of Vacuum Science & Technology B 31, - (2013). [Google Scholar]
  35. Maier S. A., Brongersma M. L., Kik P. G. & Atwater H. A. Observation of near-field coupling in metal nanoparticle chains using far-field polarization spectroscopy. Physical Review B 65 (2002). [Google Scholar]
  36. Maier S. A. et al. Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides. Nature Materials 2, 229–232 (2003). [DOI] [PubMed] [Google Scholar]
  37. Chen K.-Y., Lee A.-T., Hung C.-C., Huang J.-S. & Yang Y.-T. Transport and Trapping in Two-Dimensional Nanoscale Plasmonic Optical Lattice. Nano Lett. 13, 4118–4122 (2013). [DOI] [PubMed] [Google Scholar]
  38. Yu N. et al. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334, 333–337 (2011). [DOI] [PubMed] [Google Scholar]
  39. Lopez R., Haglund R. F., Feldman L. C., Boatner L. A. & Haynes T. E. Optical nonlinearities in VO2 nanoparticles and thin films. Appl. Phys. Lett. 85, 5191–5193 (2004). [Google Scholar]
  40. Boltasseva A. & Atwater H. A. Low-Loss Plasmonic Metamaterials. Science 331, 290–291 (2011). [DOI] [PubMed] [Google Scholar]
  41. Suh J. Y. et al. Modulation of the gold particle-plasmon resonance by the metal-semiconductor transition of vanadium dioxide. Journal of Optics a-Pure and Applied Optics 10, 055202 (2008). [Google Scholar]
  42. Appavoo K. & Haglund R. F. Detecting Nanoscale Size Dependence in VO2 Phase Transition Using a Split-Ring Resonator Metamaterial. Nano Lett. 11, 1025–1031 (2011). [DOI] [PubMed] [Google Scholar]
  43. Ferrara D. W., Nag J., MacQuarrie E. R., Kaye A. B. & Haglund R. F. Plasmonic Probe of the Semiconductor to Metal Phase Transition in Vanadium Dioxide. Nano Lett. 13, 4169–4175 (2013). [DOI] [PubMed] [Google Scholar]
  44. Johnson P. B. & Christy R. W. Optical constants of noble metals. Physical Review B 6, 4370–4379 (1972). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES