4D ACTIVE CUT: AN INTERACTIVE TOOL FOR PATHOLOGICAL ANATOMY MODELING

Abstract

4D pathological anatomy modeling is key to understanding complex pathological brain images. It is a challenging problem due to the difficulties in detecting multiple appearing and disappearing lesions across time points and estimating dynamic changes and deformations between them. We propose a novel semi-supervised method, called 4D active cut, for lesion recognition and deformation estimation. Existing interactive segmentation methods passively wait for user to refine the segmentations which is a difficult task in 3D images that change over time. 4D active cut instead actively selects candidate regions for querying the user, and obtains the most informative user feedback. A user simply answers ‘yes’ or ‘no’ to a candidate object without having to refine the segmentation slice by slice. Compared to single-object detection of the existing methods, our method also detects multiple lesions with spatial coherence using Markov random fields constraints. Results show improvement on the lesion detection, which subsequently improves deformation estimation.

1. INTRODUCTION

Quantitative studies in longitudinal pathology such as traumatic brain injury (TBI), autism, and Huntington‘s disease are important for measuring treatment efficacy or making predictions. The modeling of 4D pathological anatomy is essential to understand the complex dynamics of pathologies and enables other analysis such as structural pathology and brain connectivity [1]. This is a challenging task because of the difficulties in localizing multiple lesions at specific time points and estimating deformations between time points. In effect, this involves solving interdependent segmentation and registration problems. In the analysis of magnetic resonance (MR) images of severe TBI patients, more difficulties arise such as multiple lesions with complex shapes, multi-modal information, and lack of prior knowledge of lesion location.

Graph cuts based user-interactive image segmentation methods have been applied to 2D and 3D imaging data [2, 3]. In particular, the GrabCut method [3] integrates human experts’ knowledge and the algorithm’s computation power. In GrabCut, one typically gives an initial guess of the region of interest (foreground), for example a bounding box. The algorithm estimates globally optimal boundaries between the foreground and background regions. The user then inspects the segmentation results, and adjusts the boundary by drawing a region as a hard constraint. This user interaction process works well on 2D images, as users can quickly find incorrectly classified regions. However, such interaction is a huge burden to users once applied to 3D volume data, since one has to visually inspect each slice and correct it. The algorithm is in a passive learning state, and its performance entirely depends on user’s active inspection and correction. This passive learning process is the bottleneck of the GrabCut algorithm when applied to 3D data.

We propose 4D active cut, a method that uses active learning for guiding interactive segmentation of 4D pathological images, specifically longitudinal TBI data. We adopt a minimalist approach such that our algorithm needs the least amount of user involvement. Using active learning, the algorithm queries the user only on the most important regions. Accordingly, the user’s response to such query will be the most informative, and the number of user interaction is minimized. Our algorithm learns the model from a simple user initialization, finds the candidate objects and submits them to a user for inspection. The user is now in a passive state, and are only required to answer a ‘yes’ or ‘no’ question for the queried candidates. The algorithm does the remaining work including refining the candidate objects, learning model parameters and running graph cut algorithm to find a globally optimal map. In addition, with sufficient confidence, the algorithm automatically identifies additional lesion objects without user interaction by self-training. Self-training further decreases user involvement, without losing segmentation accuracy. Our algorithm can detect multiple lesions, while standard graph cut algorithm [3] only detects single objects. Moreover, we introduce spatial context constraints using Markov random fields (MRF) so that the estimated label maps will become piecewise constant. We also define the MRF prior on the candidate objects submitted to the user, so the candidates are spatially coherent objects instead of individual voxels.

Several researchers have applied active learning to 3D image segmentation. Top et al. [4] proposed to query users the most uncertain 2D slices. Iglesias et al. [5] used active learning for constructing manually labeled dataset for training supervised classifiers. Veeraraghavan et al. [6] used grow cut for segmentation and estimated the uncertainty using a support vector machine classifier. Our method is different from them in that 1) it solves both segmentation and registration in a unified 4D framework, and 2) instead of learning 2D slices or individual voxels, it learns new 3D objects that better fit human visual perception due to their spatial coherence.

In the remaining part of the paper, we discuss the model and interaction framework in section 2, give the 4D modeling results in section 3 and conclude in section 4.

2. METHOD

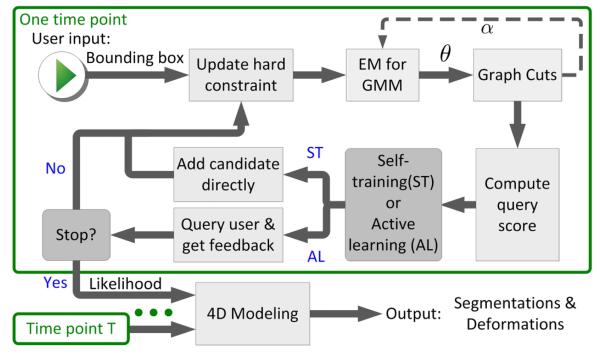
An overview of our algorithm is shown in Fig. 1. At each time point, the algorithm takes a bounding box as the initial user input, learns the model parameters, estimates graph cuts for detecting the lesions, and queries a user by submitting one or more candidate objects. The 3D label information from all time points are then integrated by fitting a 4D model that describes the changes across time as deformations.

Fig. 1.

Flowchart of the proposed algorithm.

2.1. Extension to GrabCut

We extend GrabCut [2, 3] to include hierarchical smoothness constraints. We build two GMM models for the normal brain regions and the lesions, and use the expectation maximization (EM) method to estimate both the class labels and the model parameters θ. In the graph cut step, the algorithm takes model parameters of both GMMs as input, and estimates a hard label α ∈ {0, 1} representing if each voxel n is normal (α_n = 0) or lesions (α_n = 1). In addition to smoothness constraint on the lesion boundary, we also apply MRF constraints on the label maps within normal and lesion regions. These soft constraints guarantee that the estimated labels are spatially coherent.

Within-Class MRF and Variational Inference

Define the class label map z = {z₁, …, z_N}, where z_n is a K dimensional binary random variable for voxel n such that Σ_kz_nk = 1. An element z_nk = 1 indicates voxel n is in Gaussian component k. The prior distribution of z takes the MRF constraints into account as well as the atlas, and is defined as

$$p\left(\mathbf{z}\right)=\frac{1}{C}\exp (\underset{n=1}{\overset{N}{\Sigma }}\underset{k=1}{\overset{K}{\Sigma }}{z}_{nk}\log {\pi }_{nk}+\beta \underset{(n,m)}{\Sigma }\langle z_n,z_m\rangle ),$$

where π_nk is the affine-registered atlas prior probability of n being in component k, (n, m) is a pair of neighboring voxels, and 〈, 〉 is the inner product of two vectors, representing our preference of a piecewise constant label map, with the constraint strength given by β. Given z_n, the likelihood function is defined as a multivariate Gaussian $p(x_n\mid z_n)=\mathcal{N}(x_n;\theta (z_n\left)\right)$, with x_n being the observed data vector of the multi-modality images at n. In EM, one needs to evaluate ${𝔼}_{P(\mathbf{z}\mid \mathbf{x})}\left[\log p\right(\mathbf{x},\mathbf{z}\left)\right]$, which is intractable due to the MRF prior on z. Here we use the variational inference method that iteratively updates $p(z_n\mid z_{\mathcal{N}\left(n\right)},x_n)$ given the expected value of z_n’s neighbors $\mathcal{N}\left(n\right)$. The update equation takes the form

$$\log p\left(z_{nk}\right)=z_{nk}{\pi }_{nk}+\underset{m\in \mathcal{N}\left(n\right)}{\Sigma }\langle {\overline{z}}_m,z_n\rangle +\log \mathcal{N}(x_n;\theta (z_n\left)\right),$$

where ${\stackrel{‒}{z}}_m$ is the expected value at neighbor m. We compute log p(z_nk) for all k and compute p(z_n) by taking the exponential and normalize. ${\stackrel{‒}{z}}_n$ is just p(z_n) for binary variables and is used for updating z_n’s neighbors. In the M step, we use z to estimate θ = {μ, Σ} for all components. The variational procedure stops when there are no changes of z_n. Given α, EM runs on both GMMs separately, with a uniform atlas map on lesion’s GMM.

2.2. Guided User Interaction Using Active Learning

The algorithm conducts active learning by taking α and θ as input, and computing the probability of each voxel belonging to the lesions. It then builds a connected component map, since a high-level object-based representation is convenient for user interaction. We sort the multiple objects in a descending order of the probability of being lesions, and submit the top ranked objects for queries to the user. When the algorithm detects that the top ranked object should be lesion with a confidence above a user-given threshold, it adds the object to lesion in a self-training process without querying users, further reducing user involvement.

Query Score

The log-odds of α_n is defined as

$$a_n=\log p({\alpha }_n=1)+{𝔼}_{p(z_n\mid x_n)}\left[\log p\right(x_n,z_n;\theta ({\alpha }_n=1)\left)\right]-\log p({\alpha }_n=0)+{𝔼}_{p(z_n\mid x_n)}\left[\log p\right(x_n,z_n;\theta ({\alpha }_n=0)\left)\right],$$

where 𝔼 is the expectation, α is a MRF in the form of p(α) = (1/C_α) exp(η Σ_(αm,αn) ψ(α_m, α_n)) to model its spatial coherence, with ψ = 1 if α_m = α_n, and ψ = 0 otherwise. The predictive probability of a voxel being in lesion is computed by the standard logistic function p(α_n = 1|x_n) = 1/(1+exp(−a_n)) once a is estimated by the variational inference. We obtain a binary map w by thresholding the predictive map at 0.5, and identify a series of objects R_i by running a connected component detection on w. To further select the most salient objects, we sort the objects in decending order of the following score:

$$q\left(R_i\right)=\left(\underset{n\in R_i}{\Sigma }p(\alpha =1\mid x_n)\right)/\mid \{n:n\in \mathcal{B}(R_i\left)\right\}\mid .$$ (1)

$\mathcal{B}\left(R_i\right)$ is the set of voxels on R_i’s boundary, and the denominator denotes the number of voxels on the boundary of R_i. The above query score prefers objects with larger volumes of posterior probability. The score also prefers blob-like objects since such an object has large volume-surface ratio. Such criteria reflects our prior knowledge on the lesion object’s shape.

4D Pathological Anatomy Modeling

We integrate the 3D information across time by taking z and θ for both normal and lesion classes as input, and estimate the atlas prior π by computing the deformation from the healthy template to the images at each time point. We follow the 4D pathological anatomy modeling framework of Wang et al. [7], and define π_k,t = A_k o φ_t + Q_k,t, where A is the tissue class probability that is initially associated with the healthy template, φ_t is the diffeomorphic deformation from time t to the atlas, and Q_t is the non-diffeomorphic probabilistic change. We use alternating gradient descent to estimate A, φ_t and Q_t by optimizing $\mathcal{F}(A,{\varphi }_t,Q_t)=-{\sum }_{t=1}^T{𝔼}_{p(\mathbf{z}\mid \mathbf{x})}\left[\log p\right(\mathbf{z},\mathbf{x}\mid \theta ,{\pi }_t\left)\right]$

Interaction Framework

With the above framework, the learning process is described in Fig. 1. Given the user defined bounding box, the hard-constraint map is set to ‘normal’ outside the box, and ‘uncertain’ inside. Then, we initialize the map such that α = 1 (lesion) in the ‘uncertain’ region of the hard-constraint, and α = 0 elsewhere. The EM learns θ of both GMMs given α, then a graph-cut step [3] updates only the α for voxels within the ‘uncertain’ region. This update strategy of graph-cuts prevents false-positive detections. Upon EM & graph cuts convergence, there may be some false-negative voxels in ‘normal’ regions. We group these voxels into spatially coherent objects and find the one with highest score computed from (1). The algorithm either automatically adds the candidate to lesions or queries user for answer, depending on its confidence on the candidate. We then update the hard-constraint map to reflect the knowledge learned from the new object, and a new EM & graph cuts iteration starts. Objects already accepted or rejected in previous steps are recorded so they will be excluded from future queries. This learning process repeats until user stops the algorithm. Finally, we integrate information in all time points of the datasets by fitting a 4D pathological anatomy model.

3. RESULTS

We applied our method to a dataset of longitudinal multi-modal MR images of four severe TBI patients. Each patient was scanned twice: an acute scan at about 5 days and a chronic scan at about 6 months post injury. Each subject’s data includes T1, T2, FLAIR, and GRE. In lesions’ GMM model, we chose K = 2 for bleeding and edema component, and in normal regions we chose K = 3 for gray matter, white matter and CSF. We took a 6 neighborhood system and set the smoothness parameters γ = β = η = 1. The image intensity of each modality was normalized to the range [0, 255] before the learning process. We used the K-Means clustering together with the atlas prior to initialize the GMM. The threshold used to decide self-training or active-learning was set to 3.0.

Fig. 2 shows the dynamic learning process of subject I. In iteration 1, given the user initialized bounding box, 4D active cut successfully detected the lesion object, as shown in the bottom map. In iteration 2, the candidate object has a large query score, so the algorithm decided to do self training and added the candidate to the lesion class. This object is indeed part of the lesion in the previous bounding box. That shows when the user leaves a portion of the lesion outside the box, the algorithm still detects the missing portion. This result shows the robustness of the algorithm given inaccurate user initialization. In iteration 3 and 4, the user rejected some candidate objects and accepted some others. The accepted objects are not connected to the major lesion but our algorithm still captured them. This result shows that our method is able to detect multiple objects. We also note that by using object volume, predictive probability and shape information, most of the top-ranked candidates are indeed true positive ones; showing the effectiveness of the proposed query score.

Fig. 2.

Illustration of the iterative process of 4D active cut on subject I. Iteration 1: User-initialized bounding box. Iteration 2: Self training. Iteration 3 and 4: Active learning. The user stopped the process at 5th iteration. Arrows point to the changes between iterations. The white matter surface is visualized in all figures as reference.

In order to show the efficacy of the proposed method, we used GrabCut without user interaction as a baseline method and also allowed outside of the bounding box to switch labels in order to detect multiple lesion objects. Fig. 3 shows the qualitative comparison of the baseline method and 4D active cut. Without user interaction, the baseline algorithm detected a large number of false-positive voxels due to the ambiguity between lesion and CSF. Table 1 shows the quantitative comparison of both methods. The proposed method is able to significantly improve the segmentation.

Fig. 3.

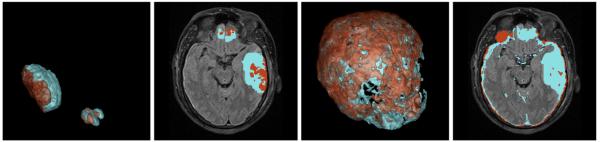
Comparison between GrabCut and the proposed method. Left: our method in 3D space and axial view. Right: GrabCut. Light blue: edema. Brown: bleeding. Note the large false-positive detection of GrabCut in the CSF region.

Table 1.

Dice values comparing 4D active cut and GrabCut to ground truth. HL and NHL are acute hemorrhagic and non-hemorrhagic lesions. UI denotes the number of interactions a user performed using 4D active cut. Subject II has no ground truth for HL due to the lack of GRE modality.

	Baseline		4D active cut
Subject	NHL	HL	NHL	HL	UI
I	0.2503	0.0613	0.6349	0.5698	5
II	0.3269	-	0.6910	-	4
III	0.1311	0.2288	0.4512	0.4840	6
IV	0.0918	0.0998	0.3503	0.1153	5

As part of 4D active cut, we updated the atlas prior using a 4D modeling method [7]. Fig. 4 shows the parcellation labels mapped to the space of each time point by using the estimated deformation field. The result shows the obtained parcellation maps match the data well, even in the presence of large deformations at different time points. Therefore, our integrated framework has the potential of becoming an important processing step for connectivity analysis of pathological brain with longitudinal data [1], where the mapping of parcellation labels to individual time points in the presence of large pathologies presents the biggest obstacle and currently requires tedious manual corrections and masking.

Fig. 4.

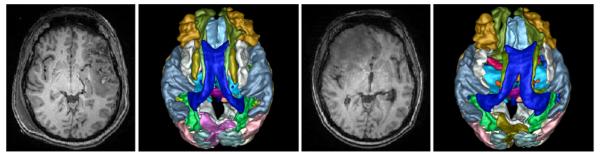
Result of mapping parcellation labels associated with the healthy template to each time point. The left two images are the T1 reference TBI image at acute stage and mapped parcellations, and the right two images are the same at chronic stage.

4. CONCLUSIONS

We presented 4D active cut for quantitative modeling of pathological anatomy. The new algorithm can detect multiple lesion objects with minimal user input. The MRF prior ensures the spatially coherent label maps within class and within candidates. In the future, we will explore integration of active learning and 4D modeling, as well as the validation and verification on other image data presenting pathologies.