Spatial Aggregation and the Ecological Fallacy

30.1 Introduction

In general, ecological studies are characterized by being based on grouped data, with the groups often corresponding to geographical areas, so that spatial aggregation has been carried out. Such studies have a long history in many disciplines including political science [33], geography [40], sociology [49] and epidemiology and public health [39]. Our terminology will reflect the latter application, though the ideas generalize across disciplines. Ecological studies are prone to unique drawbacks, in particular the potential for ecological bias, which describes the difference between estimated associations based on ecological- and individual-level data. Ecological data are a special case of spatially misaligned data, a discussion of which is the subject of Chapter 29.

Ecological data may be used for a variety of purposes including mapping (the geographical summarization of an outcome, see Chapter 14), and cluster detection (in which anomalous areas are flagged); here we focus on spatial regression in which the aim is to investigate associations between an outcome and covariates, which we will refer to as exposures. In mapping ecological bias is not a problem as prediction of area-level outcome summaries is the objective, rather than the estimation of associations. Although ecological covariates may be used within a regression model to improve predictions, the coefficients are not of direct interest. Interesting within-area features may be masked by the process of aggregation, however ([68] provides more discussion). Cluster detection is also not concerned with regression analysis and again, though small area anomalies may be “washed away” when data are aggregated, ecological bias as defined above is not an issue.

There are a number of reasons for the popularity of ecological studies, the obvious one being the wide and increasing availability of aggregated data. Improved ease of analysis also contributes to the widespread use of ecological data. For example, a geographical information system (GIS) allows the effective storage and combination of data sets from different sources and with differing geographies, and recent advances in statistical methodology allow a more refined analysis of ecological data, references [15] and [70] contain reviews in a spatial epidemiological setting.

The fundamental problem of ecological analyses is the loss of information due to aggregation — the mean function, upon which regression is often based, is usually not identifiable from ecological data alone. This lack of identifiability can lead to the ecological fallacy in which individual and ecological associations between the outcome and an explanatory variable differ, and may even reverse direction. There are two key issues that we wish to emphasize throughout this chapter. First, hierarchical models cannot account for the loss of information, and the use of spatial models in particular will not resolve the ecological fallacy. Second, the only solution to the ecological fallacy, and thereby to provide reliable inference, is to supplement the ecological-level data with individual-level data.

30.2 Motivating Example

To motivate the discussion that follows we introduce an example. Of interest is an investigation of the association between asthma hospitalization and air pollution, specifically PM_2.5 (particulate matter less than 2.5 microns in diameter) in California — this example is typical of many studies performed in environmental epidemiology. Ideally we would have access to individual-level outcomes, along with individual-level predictors and some measure of exposure. Such data are costly and logistically difficult to collect, however, and often unavailable for reasons of patient confidentiality. Instead, we consider the analysis of county-level asthma hospitalization data collected in 58 counties in California over the period 1998–2000. We wish to combine these data with point level pollution monitor data, so strictly speaking the exposure data are not aggregate in nature; we have data from 86 monitor sites.

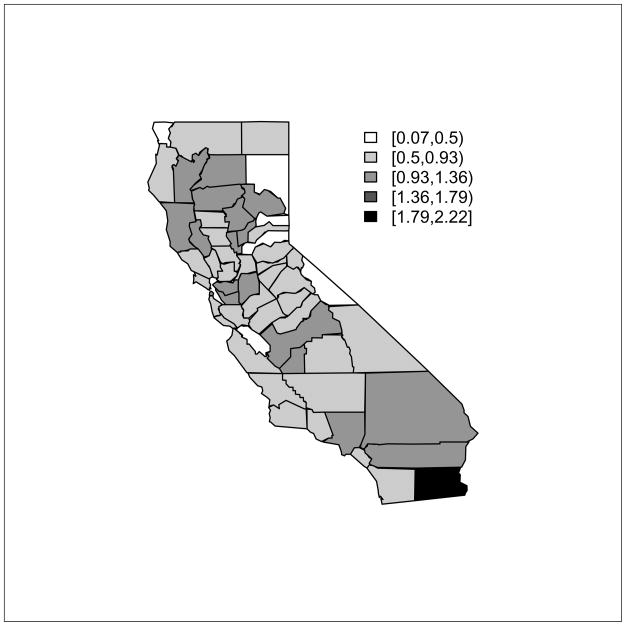
We let Y_i represent the total disease counts in county i over the 3-year period, and x_ik the average log exposure in the last year of that period (PM_2.5 measured at monitor k in county i, i = 1, …, m, k = 1, …, m_i). The m_i’s range between 0 and 9, with ${\sum }_{i=1}^{58}{m}_i=86$. We also have population counts N_ic in area i and for confounder stratum c, c = 1, …, C. In our case we have two age categories (≤ 14/> 15) and four race categories (non-Hispanic white/black/Asian or Pacific Islander/Hispanic), so that C = 8. We also have the elevation of the centroid of block groups (elevation has been shown to have an association with asthma incidence) within the area which may be population-averaged to create a single number per county, z_i. There are 22,133 block groups in California. A common descriptive measure for data of this type is the standardized morbidity ratio (SMR) which is given by Y_i/E_i where the expected numbers $E_i={\sum }_{c=1}^C{N}_{ic}{\widehat{q}}_c$ control for differences in outcome by stratum. The SMR is a summary (across confounder stratum) of the area level relative risk. Here q̂_j are reference risks; one must be wary in the manner by which these are calculated in a regression setting, so as to not bias the regression estimates, [68]. Here we use reference rates calculated from data for California from a previous period. Figure 30.1 maps the county-level SMRs and we see a relatively large range of variability across California with minimum of 0.07 and maximum of 2.22. The variability associated with the SMR in area i is proportional to $E_i^{-1}$, however, so it is unclear as to the extent the map is displaying true differences, as compared to sampling variability.

Figure 30.1.

SMRs for asthma hospitalization in Californian counties.

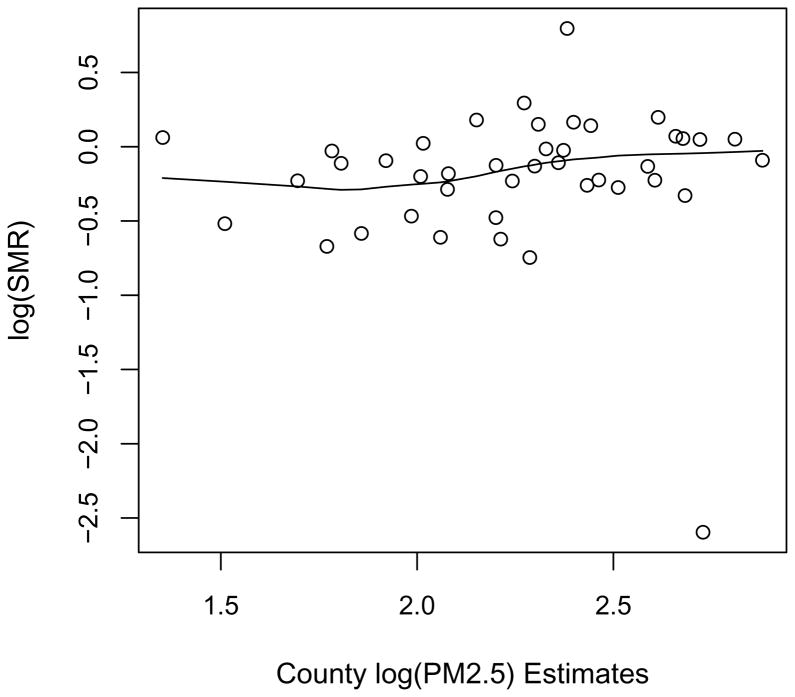
Figure 30.2 plots the SMRs versus the mean of the monitors in the 42 counties containing monitors. There is no clear pattern though a slight suggestion of increased county-level relative risks in those counties with higher average log PM_2.5.

Figure 30.2.

log SMR versus mean log PM_2.5 for counties with monitors, with a local smoother imposed.

A simple model is provided by the county-level regression:

$$E[Y_i\mid {\overline{x}}_i,z_i]={\mu }_i=E_{i}exp({\beta }_0+{\beta }_1{\overline{x}}_i+{\beta }_2{z}_i)$$ (30.1)

where x̄_i is the (log) exposure within county i, i = 1, …, m. These exposures were obtained as kriged values at the county centroid, Section 30.7 contains details on this procedure. In this model exp(β₁) is the ecological county-level relative risk associated with a unit increase in log PM_2.5; similarly exp(β₂) is the ecological county-level relative risk associated with a unit increase in elevation, in each case with the other variable held constant. Model (30.1) may be fitted via likelihood-based methods under the assumption that Y_i ~ Poisson(μ_i). However, for data such as these there is usually excess-Poisson variability due to unmeasured variables, measurement error in the exposures, problems with the population/confounder data, or other sources of model misspecification ([61]). A simple fix is to utilize quasi-likelihood ([38]) to allow for overdispersion in a semi-parametric way via the second moment assumption var(Y_i) = κ × E[Y_i]. Alternatively we may assume a negative binomial model so that overdispersion is incorporated via a parametric specification.

The first three rows of Table 30.1 gives the maximum likelihood estimates (MLEs) along with their asymptotic standard errors for the Poisson, quasi-likelihood and negative binomial models. Under a Wald test the Poisson model gives significant (at the 5% level) associations for both exposure and elevation, with PM_2.5 harmful). When moving from the Poisson to the quasi-likelihood model we see a very large increase in the standard error, reflecting the huge excess-Poisson variability in these data. The standard errors are multiplied by κ̂^1/2 = 9.8. We see a further increase in the standard error with the negative binomial model, and a substantial decrease in the point estimate. On examination of residuals versus fitted values (not shown) we are lead to prefer the negative binomial model (under this model we have a quadratic mean variance model, as compared to a linear relationship under the quasi-Poisson model). Neither the quasi-Poisson or negative binomial models suggest a significant association.

Table 30.1.

Association between asthma hospitalization and log PM_2.5 (β̂₁) and elevation (β̂₂). The four models above the line are fitted using maximum and quasi-maximum likelihood estimation, the two below are Bayesian hierarchical models (and assume a Poisson likelihood). The “Log-Linear Model” refers to model (30.1) while the “Aggregate Exposure Model” refers to model (30.15) using modeled exposures. “Convolution” refers to the model with non-spatial and spatial random effects modeled via an ICAR model.

Mean Model	Estimation Model	β̂1	Std. Err.	β̂2	Std. Err.
Log-linear Model	Poisson	0.306	0.013	−0.017	0.007
Log-linear Model	Quasi-Likelihood	0.306	0.128	−0.017	0.064
Log-linear Model	Negaive Binomial	0.227	0.171	−0.143	0.045
Aggregate Exposure Model	Quasi-Likelihood	0.261	0.092	0.011	0.058
Log-linear Model	Hierarchical Non-Spatial	0.240	0.177	−0.146	0.047
Log-linear Model	Hierarchical Convolution	0.230	0.217	−0.146	0.048

These results are all subject to ecological bias, since we have used aggregate risk and exposure measures averaged over monitors within counties. We now discuss sources of ecological bias.

30.3 Ecological Bias

There is a vast literature describing sources of ecological bias [48, 41, 21, 19, 22, 42, 57, 34, 39, 47, 64, 66, 68, 60]. The fundamental problem with ecological inference is that the process of aggregation reduces information, and this information loss usually prevents identification of parameters of interest in the underlying individual-level model. When trying to understand ecological bias it is often beneficial to specify an individual-level model, and aggregate to determine the consequences [67, 54, 66]. The majority of the literature on ecological bias is less specific about the model, however. For example, in Robinson’s famous 1950 paper [49], the correlation between literacy and race was calculated at various levels of geographic aggregation, and compared with the individual-level correlation, without reference to an explicit model.

If there is no within-area variability in exposures and confounders, then there will be no ecological bias; hence ecological bias occurs due to within-area variability in exposures and confounders. There are a number of distinct consequences of this variability. Throughout, unless stated otherwise, we assume that at the individual level the outcome, y, is a 0/1 disease indicator, though ecological bias can occur for any type of outcome.

30.4 Ecological Bias: Pure Specification Bias

So-called pure specification bias, [20] (also referred to as model specification bias, [54]) arises because a nonlinear risk model changes its form under aggregation. We initially assume a single exposure x and the linear individual-level model

$$E[Y_{ij}\mid x_{ij}]={\beta }_0+{\beta }_1{x}_{ij}$$ (30.2)

where Y_ij and x_ij are the outcome and exposure for individual j within area i, i = 1, …, m, j = 1, …, n_i. The aggregate data are assumed to correspond to the average risk ${\overline{y}}_i=\frac{1}{m_i}{\sum }_{j=1}^{m_i}{y}_{ij}$ and average exposure ${\overline{x}}_i=\frac{1}{m_i}{\sum }_{j=1}^{m_i}{x}_{ij}$. On aggregation of (30.2) we obtain

$$E[{\overline{Y}}_i\mid {\overline{x}}_i]={\beta }_0+{\beta }_1{\overline{x}}_i$$ (30.3)

so that in this very specific scenario of a linear model we have not lost anything by aggregation (and this is clearly true regardless of whether Y is discrete or continuous).

Unfortunately a linear model is often inappropriate for the modeling of risk and for rare diseases the individual-level model:

$$E[Y_{ij}\mid x_{ij}]={\text{e}}^{{\beta }_0+{\beta }_1{x}_{ij}}$$ (30.4)

is often more appropriate. In this model e^β₀ is the risk associated with x = 0 (baseline risk) and e^β₁ is the relative risk corresponding to an increase in x of one unit. The logistic model, which is often used for non-rare outcomes, is unfortunately not amenable to analytical study and so the effects of aggregation are difficult to discern [53]. Aggregation of (30.4) yields:

$$E[{\overline{Y}}_i\mid x_{ij},j=1,\dots ,n_i]=\frac{1}{n_i}\sum _{j=1}^{n_i}{\text{e}}^{{\beta }_0+{\beta }_1{x}_{ij}}$$ (30.5)

so that the ecological risk is the average of the risks of the constituent individuals. A naive ecological model would assume

$$E[{\overline{Y}}_i\mid {\overline{x}}_i]={\text{e}}^{{\beta }_0^e+{\beta }_1^e{\overline{x}}_i}$$ (30.6)

where the ecological parameters, ${\beta }_0^e,{\beta }_1^e$ have been super-scripted with “e” to distinguish them from the individual-level parameters in (30.4). Model (30.6) is actually a so-called contextual effects model since risk depends on the proportion of exposed individuals in the area (contextual variables are summaries of a shared environment). Interpreting e^βe as an individual association would correspond to a belief that it is average exposure that is causative, and that individual exposure is irrelevant. As an aside we mention the atomistic fallacy which occurs when inference is required at the level of the group but is incorrectly estimated using individual-level data ([11]).

The difference between (30.5) and (30.6) is clear, while the former averages the risks across all exposures, the latter is the risk corresponding to the average exposure. Without further assumptions on the moments of the within-area exposure distributions, we can guarantee no ecological bias, i.e. ${\text{e}}^{{\beta }_1}={\text{e}}^{{\beta }_1^e}$, only when there is no within-area variability in exposure so that x_ij = x̄_i for all j = 1, …, n_i individuals in area i and for all areas, i = 1, …, m. Hence pure specification bias is reduced in size as homogeneity of exposures within areas increases — small areas are advantageous in this respect. Unfortunately data aggregation is usually carried out according to administration groupings and not in order to obtain areas with constant exposure. As we shortly describe there are other specific circumstances when pure specification is likely to be small and these depend on the moments of the exposure distributions.

Binary exposures are the simplest to study analytically. Such exposures may correspond to, for example, an individual being below or above a pollutant threshold. For a binary exposure (30.4) can be written

$${\text{e}}^{{\beta }_0+{\beta }_1{x}_{ij}}=(1-x_{ij}){\text{e}}^{{\beta }_0}+x_{ij}{\text{e}}^{{\beta }_0+{\beta }_1}$$

which is linear in e^β₀ and e^β₀+β₁. This form yields the aggregate form:

$$E[{\overline{Y}}_i\mid {\overline{x}}_i]=(1-{\overline{x}}_i){\text{e}}^{{\beta }_0}+{\overline{x}}_i{\text{e}}^{{\beta }_0+{\beta }_1}$$ (30.7)

where x̄_i is the proportion exposed in area i. Hence with a linear risk model there is no pure specification bias so long as model (30.7) is fitted using the binary proportion, x̄_i, and not model (30.6). If model (30.6) is fitted, there will be no correspondence between e^β₁ and ${\text{e}}^{{\beta }_1^e}$ since they are associated with completely different comparisons.

The extension to general categorical exposures is straightforward, and the parameters of the disease model are identifiable so long as we have observed the aggregate proportions in each category. We now demonstrate that for a continuous exposure pure specification bias is dominated by the within-area mean-variance relationship. In an ecological regression context a normal within-area exposure distribution $N(x\mid {\overline{x}}_i,s_i^2)$, and the log-linear model (30.4), has been considered by a number of authors [48, 42, 67]. We assume that n_i is large so that the summation in (30.5) can be approximated by an integral. For a normally distributed exposure this integral is available as

$$E[{\overline{Y}}_i\mid {\overline{x}}_i]=exp({\beta }_0+{\beta }_1{\overline{x}}_i+{\beta }_1^2{s}_i^2/2)$$ (30.8)

which may be compared with the naive ecological model ${\text{e}}^{{\beta }_0^e+{\beta }_1^e{\overline{x}}_i}$. To gain intuition as to the extent of the bias we observe that in (30.8) the within-area variance $s_i^2$ is acting like a confounder, and consequently there is no pure specification bias if the exposure is constant within each area or if the variance is independent of the mean exposure in the area. The expression (30.8) also allows us to characterize the direction of bias. For example, suppose that $s_i^2=a+{b\overline{x}}_i$ with b > 0 so that the variance increases with the mean (as is often observed with environmental exposures). In this case the parameter we are estimating from the ecological data is

$${\beta }_1^e={\beta }_1+{\beta }_1^{2}b/2.$$

If β₁ > 0 then overestimation will occur using the ecological model, and if β₁ < 0 the ecological association, ${\beta }_1^e$, may reverse sign when compared to β₁.

In general, there is no pure specification bias if the disease model is linear in x, or if all the moments of the within-area distribution of exposure are independent of the mean. If β₁ is close to zero pure specification bias is also likely to be small (since then the exponential model will be approximately linear for which there is no bias), though in this case confounding is likely to be a serious worry (Section 30.5). Unfortunately the mean-variance relationship is impossible to assess without individual-level data on the exposure. If the exposure is heterogeneous within areas we need information on the variability within-each area in order to control the bias. Such information may come from a sample of individuals within each area; how to use this individual-level data (beyond assessing the within-area exposure mean-variance relationship) is the subject of Section 30.6.

30.5 Ecological Bias: Confounding

We assume a single exposure x_ij, a single confounder z_ij, and the individual-level model

$$E[Y_{ij}\mid x_{ij},z_{ij}]={\text{e}}^{{\beta }_0+{\beta }_1{x}_{ij}+{\beta }_2{z}_{ij}}$$ (30.9)

As with pure specification bias, the key to understanding sources of, and correction for, ecological bias is to aggregate the individual-level model to give

$$E[{\overline{Y}}_i\mid x_{ij},z_{ij},j=1,\dots ,n_i]=\frac{1}{n_i}\sum _{j=1}^{n_i}{\text{e}}^{{\beta }_0+{\beta }_1{x}_{ij}+{\beta }_2{z}_{ij}}.$$ (30.10)

To understand why controlling for confounding is in general impossible with ecological data we consider the simplest case of a binary exposure (unexposed/exposed) and a binary confounder, which for ease of explanation we assume is gender. Table 30.2 shows the distribution of the exposure and confounder within area i. The complete within-area distribution of exposure and confounder can be described by three frequencies, but the ecologic data usually consist of two quantities only, the proportion exposed, x̄_i, and the proportion male, z̄_i. From (30.10) the aggregate form is

Table 30.2.

Exposure and gender distribution in area i, x̄_i is the proportion exposed and z̄_i is the proportion male; p_i00, p_i01, p_i10, p_i11 are the within-area cross-classification frequencies.

	Female	Male
Unexposed	pi00	pi01	1 − x̄i
Exposed	pi10	pi11	x̄i
	1− z̄i	z̄i	1.0

$$E[{\overline{Y}}_i\mid p_{i00},p_{i01},p_{i10},p_{i11}]=(1-{\overline{x}}_i-{\overline{z}}_i+p_{i11}){\text{e}}^{{\beta }_0}+({\overline{x}}_i-p_{i11}){\text{e}}^{{\beta }_0+{\beta }_1}+({\overline{z}}_i-p_{i11}){\text{e}}^{{\beta }_0+{\beta }_2}+p_{i11}{\text{e}}^{{\beta }_0+{\beta }_1+{\beta }_2}$$

showing that the marginal prevalences, x̄_i, z̄_i, alone, are not sufficient to characterize the joint distribution unless x and z are independent, in which case z is not a within-area confounder. This scenario has been considered in detail elsewhere [35], where it was argued that if the proportion of exposed males (p_i11) is missing it should be estimated by the marginal prevalences (x̄_i × z̄_i). It is not possible to determine the accuracy of this approximation without individual-level data, however. This is a recurring theme in the analysis of ecological data, bias can be reduced under model assumptions, but estimation is crucially dependent on the appropriateness of these assumptions, which are uncheckable without individual-level data.

We now examine the situation in which we have a binary exposure and a continuous confounder. Let the confounders in the unexposed be denoted, z_ij, j = 1, …, n_i0, and the confounders in the exposed, z_ij, j = n_i0 + 1, …, n_i0 + n_i1, with n_i0 + n_i1 = n_i. In this case the ecological form corresponding to (30.9) is

$$E[{\overline{Y}}_i\mid q_{i0},q_{i1}]=q_{i0}\times r_{i0}+q_{i1}\times r_{i1}$$

where q_i0 = n_i0/n_i and q_i1 = n_i1/n_i are the probabilities of being unexposed and exposed, and

$$r_{i0}=\frac{{\text{e}}^{{\beta }_0}}{n_{i0}}\sum _{j=1}^{n_{i0}}{\text{e}}^{{\beta }_2{z}_{ij}},r_{i1}=\frac{{\text{e}}^{{\beta }_0+{\beta }_1}}{n_{i1}}\sum _{j=n_{i0}+1}^{n_{i0}+n_{i1}}{\text{e}}^{{\beta }_2{z}_{ij}}$$

are the (aggregated) risks in the unexposed and exposed. The important message here is that we need the confounder distribution within each exposure category, unless z is not a within-area confounder. Again it is clear that if we fit the model:

$$E[{\overline{Y}}_i\mid {\overline{x}}_i,{\overline{z}}_i]={\text{e}}^{{\beta }_0^e+{\beta }_1^e{\overline{x}}_i+{\beta }_2^e{\overline{z}}_i}$$

where ${\overline{z}}_i=\frac{1}{n_i}{\sum }_{j=1}^{n_i}{z}_{ij}$, then it is not possible to equate the ecological coefficient ${\beta }_1^e$ with the individual-level parameter of interest β₁.

We now extend our discussion to multiple strata and show the link with the use of expected numbers (as defined in Section 30.2). Consider the continuous exposure x_icj for the j-th individual in stratum c and area i, and suppose the individual level model is given by

$$E[Y_{\mathit{icj}}\mid x_{\mathit{icj}},\text{strata}c]={\text{e}}^{{\beta }_0+{\beta }_1{x}_{\mathit{icj}}+{\beta }_{2c}},$$

for c = 1, …, C stratum levels with relative risks e^β_2c (with e^β₂₁ = 1 for identifiability), and with j = 1, …, n_ic. For ease of exposition suppose c indexes age categories. Let ${\overline{Y}}_{ic}=\frac{1}{n_{ic}}{\sum }_{j=1}^{n_c}{Y}_{\mathit{icj}}$ be the proportion with the disease in area i, stratum c. Then

$$E[{\overline{Y}}_{ic}\mid x_{\mathit{icj}},j=1,\dots ,n_{ic}]=\frac{{\text{e}}^{{\beta }_0+{\beta }_{2c}}}{n_{ic}}\sum _{j=1}^{n_{ic}}{\text{e}}^{{\beta }_1{x}_{\mathit{icj}}}.$$

Summing over stratum and letting Ȳ_i be the proportion with disease in area i:

$$E[{\overline{Y}}_i\mid x_{\mathit{icj}},j=1,\dots ,n_{ic},c=1,\dots ,C]=\frac{1}{n_i}\sum _{c=1}^C{n}_{ic}\left\{{\text{e}}^{{\beta }_0+{\beta }_{2c}}\sum _{j=1}^{n_{ic}}{\text{e}}^{{\beta }_1{x}_{\mathit{icj}}}\right\}.$$ (30.11)

If we assume a common exposure distribution across stratum and let x_ij, j = 1, …, m_i be a representative exposure sample then we could fit the model

$$\begin{array}{l}E[Y_i\mid x_{ij},j=1,\dots ,m_i]=\sum _{c=1}^C{n}_{ic}{\text{e}}^{{\beta }_{2c}}\times {\text{e}}^{{\beta }_0}\sum _{j=1}^{m_i}{\text{e}}^{{\beta }_1{x}_{ij}}\\ =E_i\times {\text{e}}^{{\beta }_0}\sum _{j=1}^{m_i}{\text{e}}^{{\beta }_1{x}_{ij}}\end{array}$$ (30.12)

where $E_i={\sum }_{c=1}^C{n}_{ic}{\text{e}}^{{\beta }_{2c}}$ are the expected numbers. Model (30.12) attempts to correct for pure specification bias, but assumes common exposure variability across areas. Hence we see that in this model (which has been previously used, [24]) we have standardized for age (via indirect standardization) but for this to be valid we need to assume that the exposure is constant across age groups (so that age is not a within-area confounder). This can be compared with the model that is frequently fitted:

$$E[Y_i\mid {\overline{x}}_i]=E_i\times {\text{e}}^{{\beta }_0+{\beta }_1{\overline{x}}_i}$$

Validity of this model goes beyond a constant exposure distribution across stratum within each area, we also require no within-area variability in exposure (or, recalling our earlier discussion, the exposure variance being independent of the mean, in addition to constant distributions across stratum).

This discussion is closely related to the idea of mutual standardization in which if the response is standardized by age (say) the exposure variable must also be standardized for this variable ([50]). The correct model is given by (30.11), and requires the exposure distribution by age group, or at least a representative sample of exposures from each age group. The above discussion makes it clear that we need individual-level data to characterize the within-area distribution of confounders and exposures.

The extension to general exposure and confounder scenarios is obvious from the above. If we have true confounders that are constant within areas (for example, access to health care) then they are analogous to conventional confounders, since the area is the unit of analysis, and so the implications are relatively easy to understand and adjustment is straightforward.

Without an interaction between exposure and confounder the parameters of a linear model are estimable from marginal information only, though if an interaction is present within-area information is required [64].

30.6 Combining Ecological and Individual Data

As we saw in Section 30.3 the only solution to the ecologic inference problem that does not require uncheckable assumptions is to add individual-level data to the ecological data. Here we briefly review some of the proposals for such an endeavor. Another perspective is that ecological data can supplement already available individual data, in order to improve power.

Table 30.3 summarizes four distinct scenarios in terms of data availability, [34, 54]. All entries but the individual-individual cell concern change of support situations (Chapter 29). The obvious approach to adding individual-level data is to collect a random sample of individuals within areas. For a continuous outcome, Raghunathan et al. [44] show that moment and maximum likelihood estimates of a common within group correlation coefficient will improve when aggregate data are combined with individual data within groups, and Glynn et al. [18] derive optimal design strategies for the collection of individual-level data when the model is linear. With a binary non-rare outcome the benefits have also been illustrated [66, 58].

Table 30.3.

Study designs by level of outcome and exposure data.

		Exposure
		Individual	Ecological
Outcome	Individual	Individual	Semi-Ecological
	Ecological	Aggregate	Ecological

For a rare disease few cases will be present in the individuals within the sample, and so only information on the distribution of exposures and confounders will be obtained via a random sampling strategy (which is therefore equivalent to using a survey sample of covariates only). This prompted the derivation of the so-called aggregate data method of Prentice and Sheppard [43, 55, 56], which is the bottom left entry in Table 30.3. Inference proceeds by constructing an estimating function based on the sample of m_i ≤ n_i individuals in each area. For example, with samples for two variables, {x_ij, z_ij, j = 1, …, m_i} we have the mean function:

$$E\left[{\overline{Y}}_i\mid x_{ij},z_{ij},j=1,\dots ,m_i\right]=\frac{1}{n_i}\frac{n_i}{m_i}\sum _{j=1}^{m_i}{\text{e}}^{{\beta }_0+{\beta }_1{x}_{ij}+{\beta }_2{z}_{ij}}.$$

There is bias involved in the resultant estimator since the complete set of exposures are not available, but Prentice and Sheppard give a finite sample correction to the estimating function based on survey sampling methods. This is an extremely powerful design since estimation is not based on any assumptions with respect to the within-area distribution of exposures and confounders (though this distribution may not be well characterized for small samples, [52]). An alternative approach is to assume a particular distribution for the within-area variability in exposure, and fit the implied model ([48, 67, 3, 31, 30]). The normal model is usually assumed, in which case (for a single model) the mean model is (30.8). This method implicitly assumes that a sample of within-area exposures is available since the within-area moments need to be available. More recently an approach has been suggested that takes the mean as a combination of the Prentice and Sheppard and the parametric approaches, with the latter dominating for small samples (when the aggregate data method can provide unstable inference), [52].

In the same spirit as Prentice and Sheppard, Wakefield and Shaddick, [63], described a likelihood-based method for alleviating ecological bias. If data on all individual exposures were available then we would fit the model

$$E[{\overline{Y}}_i\mid x_{ij},j=1,\dots ,n_i]=\frac{{\text{e}}^{{\beta }_0}}{n_i}\sum _{j=1}^{n_i}{\text{e}}^{{\beta }_1{x}_{ij}}$$ (30.13)

which will remove ecological bias, but will result in a loss of power relative to an individual-level study since we have not used the linked individual disease-exposure data. Usually we will not have access to all of the individual exposures, but instead we may have access to data in sub-areas at a lower level of aggregation, e.g. block groups within counties. Suppose that we have m_i sub-areas within area i and providing an exposure measure x_ij, and N_ij is the number of individuals in this sub-area, j = 1, …, m_i, so that $n_i={\sum }_{j=1}^{m_i}{N}_{ij}$. For example, x_ij may represent a measure of exposure at the centroids of sub-area j within area i. We then alter model (30.13), and act as if there were N_ij individuals each with exposure x_ij (so that we are effectively ignoring within sub-area variability in exposure):

$$E[{\overline{Y}}_i\mid x_{ij},j=1,\dots ,m_i]=\frac{{\text{e}}^{{\beta }_0+{\beta }_2{z}_i}}{n_i}\sum _{j=1}^{m_i}{N}_{ij}{\text{e}}^{{\beta }_1{x}_{ij}}$$ (30.14)

where j indexes the number of sub-areas within area i. If we have population information at the sub-area level, for example age and gender, then we may calculate expected numbers, E_ij, and these will then replace the N_ij within (30.14). We can also dd in an area-level covariate z_i to give

$$E[Y_i\mid x_{ij},j=1,\dots ,m_i,z_i]={\text{e}}^{{\beta }_0}\sum _{j=1}^{m_i}{E}_{ij}{\text{e}}^{{\beta }_1{x}_{ij}}$$ (30.15)

We call this latter form the aggregate exposure model. Valid estimates from this model require that population sub-gourps have the same exposure within each sub-area (and these are constant across the stratum over which the expected numbers were calculated), but if the heterogeneity in exposure is small within these sub-areas, little bias will result. Often the collection x_i1, …, x_imi will be obtained via exposure modeling and the validity of estimation requires that these exposure measures are accurate, which may be difficult to achieve unless the monitoring network is dense (relative to the variability of the exposure).

A different approach to adding individual data in the context of a rare response is outcome dependent sampling, which avoids the problems of zero cases encountered in random sampling. For the situation in which ecologic data are supplemented with individual case-control information gathered within the constituent areas, inferential approaches have been developed, [26, 25, 27]. The case-control data remove ecological bias while the ecological data provide increased power and constraints on the sampling distribution of the case-control data, which improves the precision of estimates.

Two-phase methods have a long history in statistics and epidemiology [71, 69, 6, 7] and are based on an initial cross-classification by outcome and confounders and exposures; this classification providing a sampling frame within which additional covariates may be gathered via the sampling of individuals. Such a design may be used in an ecological setting, where the initial classification is based on one or more of area, confounder stratum, and possibly error-prone measures of exposure, [62].

In all of these approaches it is clearly vital to avoid response bias in the survey samples, or selection bias in outcome-dependent sampling, and establishing a relevant sampling frame is essential.

30.7 Example Revisited

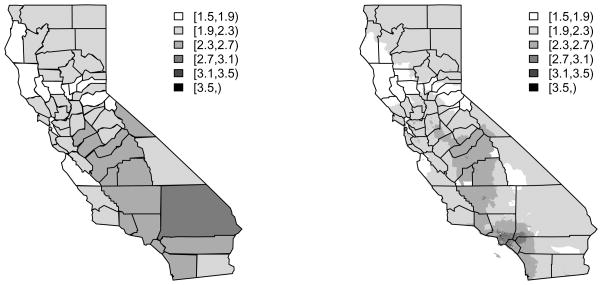
For the California data we have information on census block groups within counties. Recall there are 58 counties and 22,133 census block groups. We assume that the logged PM_2.5 monitor data are a realization from a Gaussian random field, and we fit this model to the monitor data using restricted maximum likelihood (REML) and a mean linear in population density. Given the fitted model we impute exposures at each block group centroid. Figure 30.3 displays exposure maps at both the county and the block group level. We now treat these exposures as known and examine the association between asthma hospitalization and exposure to PM_2.5. This approach may be criticized at a number of levels. Since we have not jointly modeled the health and exposure variables the uncertainty in the exposure predictions are not propagated through the estimation, and there is no feedback in the model. This can be advantageous, however, since misspecification of either the health or the expsoure component can can cause problems for the other component. Probably the biggest problem with this approach, however, is that we need sufficient monitor data to impute accurate exposures for unmonitored locations.

Figure 30.3.

Predicted exposures for (a) and (b) census block groups, in California.

To utilize the census block group information we used a quasi-likelihood model with E[Y_i] = μ_i, var(Y_i) = κ × E[Y_i] and where μ_i is given by (30.15), and obtained the estimates, via quasi-likelihood, in Table 30.1, line 4. We see that the association is attenuated when compared with the previous quasi-likelihood estimate, as we might expect if the within-area variability in exposure increases with the mean, all other things being equal (Section 30.4). The standard error is increased also.

The biggest advantage of the above approach is that ecological bias can be overcome. An alternative approach that was followed by Zhu et al. ([72]) is to obtain county average exposures via kriging (Chapter 3) and then use model (30.6). However, this will produce ecologically biased estimates since within-area variability in exposure has not been acknowledged. We re-iterate that it is the average of the risk functions that is required for individual-level inference, and not the risk function evaluated at the average exposure.

30.8 Spatial Dependence and Hierarchical Modeling

When data are available as counts from a set of contiguous areas we might expect residual dependence in the counts, particularly for small-area studies, due to the presence of unmeasured variables with spatial structure. The use of the word “residual” here acknowledges that variables known to influence the outcome have already been adjusted for in the mean model. Analysis methods that ignore the dependence are strictly not applicable, with inappropriate standard errors being the most obvious manifestation. A great deal of work has focused on models for spatial dependence [10, 2, 9, 12, 36, 4, 32, 8]; Richardson [46] provides an excellent review of this literature, see also Chapter 14. With respect to ecological bias, however, the most important message is that unless the mean model is correct, adjustment for spatial dependence is a pointless exercise [68].

Spatial smoothing models have also been proposed to control for “confounding by location” [9]. A subtle but extremely important point is that such an endeavor is fraught with pitfalls since the exposure of interest usually has spatial structure and so one must choose an appropriate spatial scale for smoothing. If the scale is chosen to be too small the exposure effect may be attenuated, while if too large a scale is chosen the signal that is due to confounding may be absorbed into the exposure association estimate. Practically one can obtain estimates from models with and without spatial smoothing, and with a variety of spatial models, to address the sensitivity of inference concerning parameters of interest. See [45] for further discussion. Similar issues arise in time series analysis when one must control trends by selecting an appropriate level of temporal smoothing [14]. Such analyses are more straightforward since time is one-dimensional, the data are generally collected at regular intervals (often daily), and the data are also abundant, perhaps containing many years of data.

In a much-cited book [33] a hierarchical model was proposed for the analysis of ecologic data in a political science context, as “a solution to the ecological inference problem”. Identifiability in this model is imposed through the random effects prior, however, and it is not possible to check the appropriateness of this prior from the ecological data alone [17, 66].

We have concentrated on Bayesian hierarchical spatial models, but a number of frequentist approaches are possible, though currently they have not been investigated in detail. Thurston et al. ([59]) describe a negative binomial additive model, that could provide a useful alternative to the models described here. The negative binomial aspect allows for overdispersion, while a generalised additive model would allow flexible modelling of latitude and longitude to model non-small scale spatial variability. More generally, recent work on generalised linear models with splines may be applicable in the setting described here, see for example [37] and [23]. Allowing for small-scale residual spatial dependence in these models would be desirable, however. It would be desirable to perform sandwich estimation in a spatial regression setting, but unfortunately the non-lattice nature of the data does not easily allow any concept of replication across space (as has been used for lattice data, [29]).

30.9 Example Revisited

The first hierarchical model we fit adds a single non-spatial random effect, $V_i\sim N(0,{\sigma }_v^2)$ to the linear predictor; this gives the same (quadratic) marginal mean-variance structure as the negative binomial model, and we would expect to see similar inference under the two models. This is confirmed in Table 30.1 for the naive models.

To acknowledge spatial dependence we now fit the log-linear model Y_i|x_i ~ Poisson(E_ie^{β₁x_i+U_i+V_i}) where $V_i{\sim }_{\mathit{iid}}N(0,{\sigma }_v^2)$ are independent random effects and the U_i have spatial structure, in particular we choose an intrinsic conditional autoregressive model (ICAR), as suggested elsewhere [2]. For inference we utilized, in addition to MCMC, the integrated nested Laplace approximation scheme described in [51]. MCMC displayed very poor convergence for the spatial log-linear model for these data. We attempted to fit the aggregate data model using MCMC but the chain was extremely poorly behaved.

We place a prior on the total residual variance and upon the proportion of the variance that is spatial, approximately scaling the conditional variance in the ICAR model so that it is comparable with ${\sigma }_v^2$, [68]. From Table 30.1 we see that when the ICAR component is included in the model we see a very similar estimate of the association with PM_2.5 as with the non-spatial hierarchical model, but with an increased standard error.

For these ecological data we would conclude that there is no evidence of an association. The reliability of the aggregate exposure model here is questionable, however, since validation of the exposure model has not been carried out. Unmeasured confounding is a serious worry here, and in particular ecological bias due to within-area confounding.

30.10 Semi-Ecological Studies

In a semi-ecological study, sometimes more optimistically referred to as a “semi-individual study”, [34], individual-level data are collected on outcome and confounders, with exposure information arising from another source. The Harvard six-cities study, [13], provides an example in which the exposure was city-specific and was an average exposure from pollution monitors over the follow-up of the study.

We consider the risk for individual j in confounder stratum c and area i, c = 1, …, C, j = 1, …, n_c, i = 1, …, m. Let x_icj be the exposures of the individuals within stratum c, j = 1, …, n_c and area i, and β_2c the baseline risk in stratum c. Under exposure aggregation we have

$$\begin{array}{l}E[Y_{\mathit{icj}}\mid x_{ic1},\dots ,x_{{\mathit{icn}}_c}]=E_{x\mid x_{ic1},\dots ,x_{{\mathit{icn}}_c}}\{E[Y_{\mathit{icj}}\mid x]\}\\ ={\text{e}}^{{\beta }_0+{\beta }_{2c}}\sum _{j=1}^{n_c}{\text{e}}^{{\beta }_1{x}_{\mathit{icj}}}\end{array}$$

since the distribution of x|x_ic1, …, x _icnc is discrete over the n_c exposures, x_ic1, …, x _icnc. A naive semi-ecologic model is:

$$E[Y_{\mathit{icj}}\mid {\overline{x}}_i]={\text{e}}^{{\beta }_0^e+{\beta }_{2c}^e+{\beta }_1^e{\overline{x}}_i}$$ (30.16)

where x̄_i is an exposure summary in area i. Kunzli and Tager [34] argue that semi-ecological studies are free of ecological bias, but this is incorrect since there are two possible sources of bias in model (30.16); the first is that we have pure specification bias because we have not acknowledged within-area variability in exposure, and the second is that we have not allowed the exposure to vary by confounder stratum so we have not controlled for within-area confounding. In an air pollution study in multiple cities x may correspond to a monitor average or an average over several monitors. In this case (30.16) will provide an approximately unbiased estimate of β₁ if there is small exposure variability in cities and if this variability is similar across confounder stratum.

Semi-ecological studies frequently have survival as an endpoint but there has been less focus on the implications of aggregation in the context of survival models, with few exceptions [1, 28]

30.11 Concluding Remarks

The use of ecological data is ubiquitous, and so is the potential for ecological bias. A skeptic might conclude from the litany of potential biases described in Section 30.3 that ecological inference should never be attempted, but this would be too pessimistic a view. A useful starting point for all ecological analyses is to write down an individual-level model for the outcome-exposure association of interest, including known confounders. Ecological bias will be small when within-area variability in exposures and confounders is small, and for small-area studies in particular this may be approximately true. A serious source of bias is that due to confounding, since ecological data on exposure are rarely stratified by confounder strata within areas. If a small area study has been carried out with a correctly aggregated individual-level model then parameter estimates can be cautiously interpreted at the individual-level and compared with other studies at the individual level, and hence add to the totality of evidence for a hypothesis. When comparing ecological and semi-ecological estimates with individual-level estimates it is clearly crucial to have a common effect measure (e.g. a relative risk or a hazard ratio). So, for example, it will be difficult to compare an ecological correlation coefficient, which is a measure that is often reported, with an effect estimate from an individual-level study.

Less well-designed ecological studies can be suggestive of hypotheses to investigate if strong ecological associations are observed. An alternative to the pessimistic outlook expressed above is that when a strong ecological association is observed an attempt should be made to explain how such a relationship could have arisen, if it is not due to the ecological predictor.

There are a number of issues that we have not discussed. Care should be taken in determining the effects of measurement error in an ecological study since the directions of bias may not be predictable. For example, in the absence of pure specification and confounder bias for linear and log-linear models, if there is non-differential measurement error in a binary exposure there will be overestimation of the effect parameter, in contrast to individual-level studies, [5]. We refer interested readers to alternative sources, [61, 16], for other issues such as consideration of migration, latency periods, and the likely impacts of inaccuracies in population and health data.

Studies that investigate the acute effects of air pollution are another common situation in which ecological exposures are used. For example, daily disease counts in a city are often regressed against daily and/or lagged concentration measurements taken from a monitor, or the average of a collection of monitors to estimate the acute effects of air pollution. If day-to-day exposure variability is greater than within-city variability then we would expect ecological bias to be relatively small. We have not considered ecological bias in a space-time context, little work has been done in this area, see [65] for a brief development.

With respect to data availability, exposure information is generally not aggregate in nature (unless the “exposure” is a demographic or socio-economic variable), and in an environmental epidemiological setting the modeling of pollutant concentration surfaces will undoubtedly grow in popularity. However, an important insight is that in a health-exposure modeling context it may be better to use measurements from the nearest monitor, rather than model the concentration surface, since the latter approach may be susceptible to large biases, particularly when, as is usually the case, the monitoring network is sparse [63]. A remaining challenge is to diagnose when the available data are of sufficient abundance and quality to support the use of complex models.

In Section 30.6 we described a number of proposals for the combination of ecological and individual data. Such endeavors will no doubt increase and will hopefully allow the reliable exploitation of ecological information.