Emergence of long-range order in sheets of magnetic dimers

Significance

Magnetic materials are composed of individual spins that interact with each other and under suitable conditions can arrange themselves in an ordered array. When spins are confined to two-dimensional sheets, small perturbations can disrupt their order and destroy the magnetic state. We show how a set of interacting, quantum-mechanical spins placed on the corners of a square array evolves from a set of locally bonded entities to a globally ordered structure. The system stabilizes itself against fluctuations through subtle local contractions, elongations, and tilts. The combination of neutron and X-ray scattering at pressures up to 60,000 atmospheres reveals the complex interplay of structural distortions and spin alignments that permit long-range order to emerge in this model quantum magnet.

Abstract

Quantum spins placed on the corners of a square lattice can dimerize and form singlets, which then can be transformed into a magnetic state as the interactions between dimers increase beyond threshold. This is a strictly 2D transition in theory, but real-world materials often need the third dimension to stabilize long-range order. We use high pressures to convert sheets of Cu²⁺ spin 1/2 dimers from local singlets to global antiferromagnet in the model system SrCu₂(BO₃)₂. Single-crystal neutron diffraction measurements at pressures above 5 GPa provide a direct signature of the antiferromagnetic ordered state, whereas high-resolution neutron powder and X-ray diffraction at commensurate pressures reveal a tilting of the Cu spins out of the plane with a critical exponent characteristic of 3D transitions. The addition of anisotropic, interplane, spin–orbit terms in the venerable Shastry–Sutherland Hamiltonian accounts for the influence of the third dimension.

Two-dimensional systems lie at the boundary between the order-destroying effects of fluctuations in lower dimension and the emergence of true long-range order in higher dimension. How ordered states form and remain stable at finite temperature is a fundamental question that cuts across the sciences. In physics, surfaces, quantum wells, and layered compounds all have provided insights into the peculiar nature of 2D phases, phase transitions, and dimensional cross-over effects. Of particular interest for quantum phase transitions is the theoretically tractable case of interacting magnetic spins placed on a 2D square lattice, the Shastry–Sutherland model (1). The geometry prevents simultaneous satisfaction of all spin–spin coupling terms, leading to a frustrated state that in turn enhances the effects of quantum fluctuations. As the coupling terms are tuned, magnetic order can emerge, but its nature and the potential influence of other sheets of spins in a real physical system have not been probed directly.

The Shastry–Sutherland model can be described by the Hamiltonian:

$$\mathrm{\mathscr{H}}=J{\displaystyle \sum _{nn}{S}_i\cdot S_j}+J\prime {\displaystyle \sum _{nnn}{S}_i\cdot S_j},$$ [1]

where a set of S = 1/2 spins sits on a square lattice and interacts via a regular array of diagonal bonds. This creates a network of dimers with antiferromagnetic intradimer coupling $J$ and interdimer coupling $J^{\prime }$. The ground state depends on the ratio of $J^{\prime }/J=x$. For x < 0.7, the ground state consists of S = 0 singlets, whereas for x > 0.9 a global antiferromagnetic phase is expected. For intermediate values of x, a variety of locally ordered states has been predicted (2).

The first known experimental realization of the Shastry–Sutherland lattice is SrCu₂(BO₃)₂ (SCBO) (3). The magnetism in SCBO consists of S = 1/2 Cu²⁺ ions in well-separated planes whose nearest-neighbor interactions are mediated by in-plane oxygen bonds; layered Cu–O compounds of this kind are of broad interest due to their role in driving phenomena such as high-temperature superconductivity. At ambient conditions, SCBO forms a crystal in the tetragonal space group I-42m with a = b = 8.995 Å and c = 6.659 Å. The Cu²⁺ ions form orthogonal structural and magnetic dimers in the a–b plane (4). As each dimer sits on a mirror plane that passes through the center of its orthogonal neighbor, the unit cell contains four dimers on two layers with alternating orientations (3) (Fig. 1). SCBO has a nonmagnetic, singlet ground state (5), with 0.6 < x < 0.69 (6). Hydrostatic pressure can be used to tune x, with a transition into an intermediate phase observed at P ∼2 GPa (7, 8). The magnetic characteristics of the singlet–triplet transition emerge even in X-ray scattering experiments due to a remarkably robust spin–lattice coupling (7, 9, 10). At P ∼4.5 GPa a second phase transition has been observed, marked by a structural transition from tetragonal to monoclinic ordering (7, 11). In this article, we use both X-ray and neutron scattering measurements to illuminate the structural and magnetic configurations that permit long-range order to emerge for P > 5 GPa, directly identifying for the first time, to our knowledge, the predicted antiferromagnetic state.

Fig. 1.

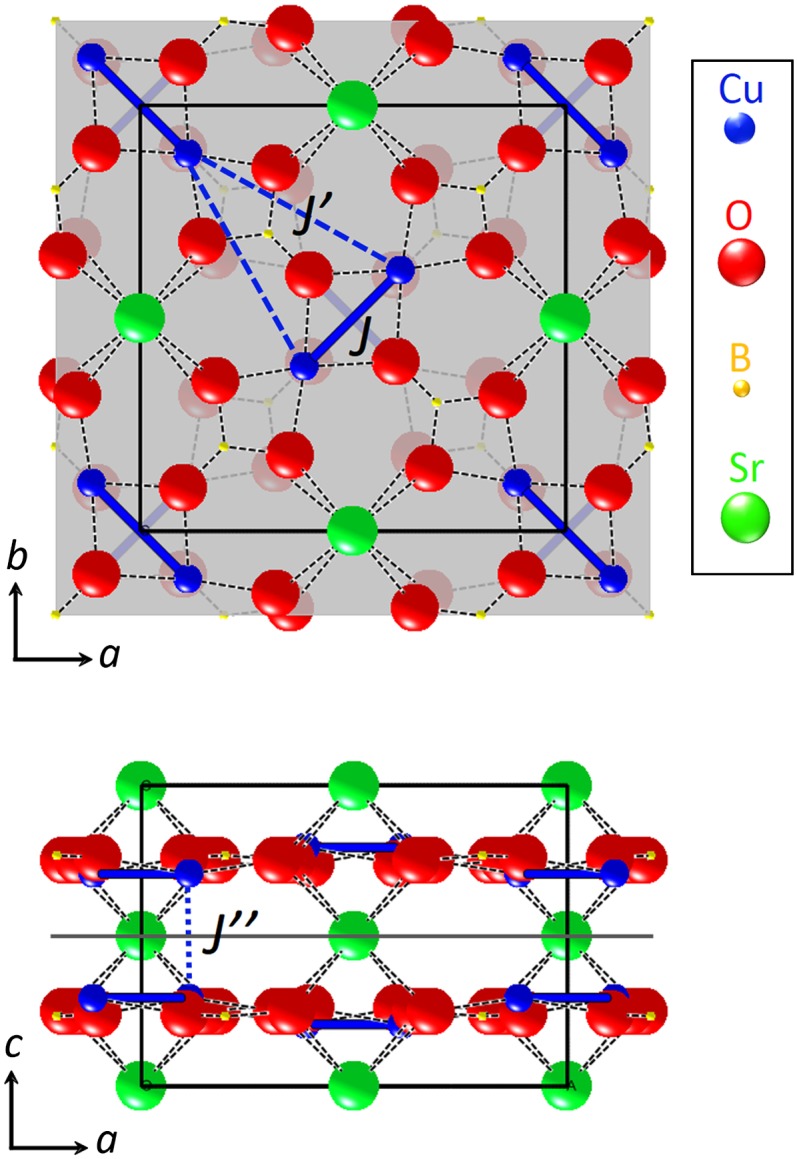
Crystallographic structure of SrCu₂(BO₃)₂ (SCBO). (Upper) Low-temperature structure of SCBO projected into the a–b plane. (Lower) a–c plane. Solid, dashed, and dotted blue lines show the interactions between the dimerized Cu²⁺ ions, representing the intradimer (J = 84 K), in-plane interdimer (J' = 54 K), and out-of-plane interdimer (J′′ = 8 K) (6) interactions, respectively. This hierarchy of direct exchange interactions underlies the effectively 2D nature of the system in the absence of global magnetic order.

Results and Discussion

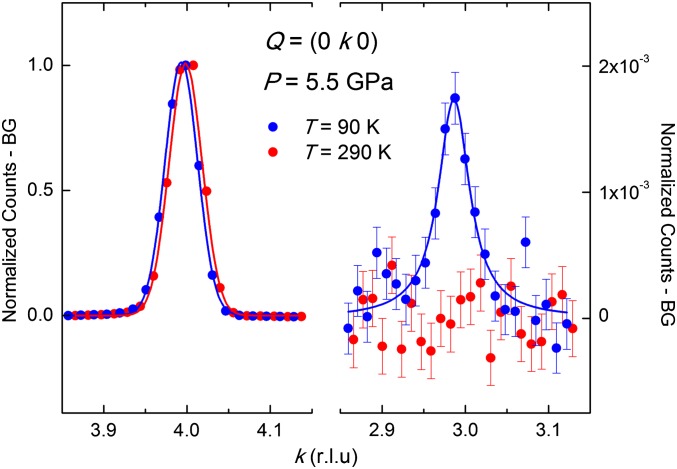
We begin with fundamental symmetry considerations. In SCBO’s low-pressure tetragonal phase, structural Bragg reflections satisfying h + k + l = 2n+1 are forbidden due to the symmetry of the I-42m space group. Above the monoclinic transition at P ∼ 4.5 GPa, the presence or absence of diffraction intensity at these locations serves to indicate which symmetries associated with the tetragonal I-42m parent structure are preserved in the reconfigured lattice. We performed high-resolution single-crystal neutron diffraction at P = 5.5 ± 0.2 GPa, well above the 4.5-GPa pressure for which SCBO has been predicted to eventually enter an antiferromagnetic ordered phase (7, 8). We plot in Fig. 2 data at P = 5.5 GPa and T = 90 and 290 K, where we observe the low-temperature emergence of a peak at Q = (0 3 0) which is structurally forbidden due to the symmetry of the I-42m lattice space group. This peak can be understood as a signature of long-range Néel order creating a magnetic supercell, within which orthogonal Cu–Cu dimers have opposite spin orientations. These two inequivalent types of Cu dimers reduce the symmetry compared with the bare lattice and allow scattering intensity at the previously forbidden position. The Néel ordering arises from pressure tuning of the ratio of the coupling constants: for sufficiently large intradimer coupling J′ compared with the antiferromagnet interdimer coupling J, the individual spins in each dimer align ferromagnetically and the set of dimers in one sheet forms a square Néel-ordered lattice. This ordering corresponds to the expected antiferromagnetic long-range order on the Shastry–Sutherland lattice.

Fig. 2.

Signature of the antiferromagnetic ordered phase in SCBO. Single-crystal neutron diffraction intensities of SCBO at T = 90 K (blue) and T = 290 K (red) at P ∼ 5.5 GPa vs. reciprocal lattice units (r.l.u). A high-temperature (T = 290 K) background has been subtracted from these data sets. Solid lines are Voigt fits to the data. (Left) Structural Bragg peak at Q = (0 4 0). The intensity stays constant with changing temperature. The height of the peak is normalized to unity. (Right) Emergence of the magnetic Bragg peak at the structurally forbidden reflection (0 3 0) at lower temperature. The intensity of the (0 3 0) peak is normalized to the intensity of the (0 4 0) structural Bragg peak.

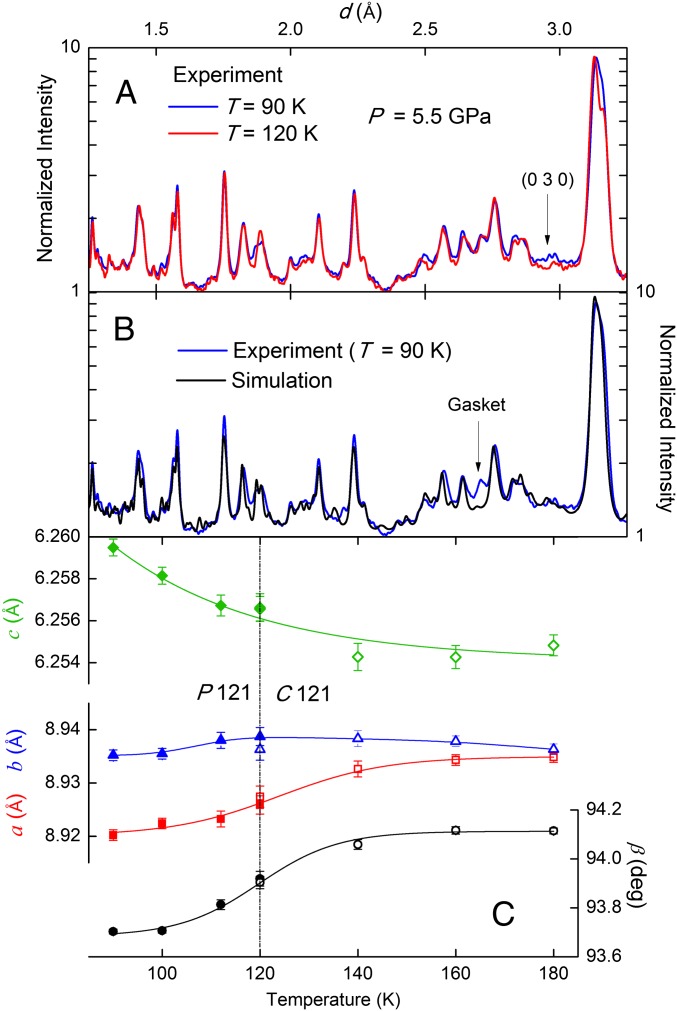
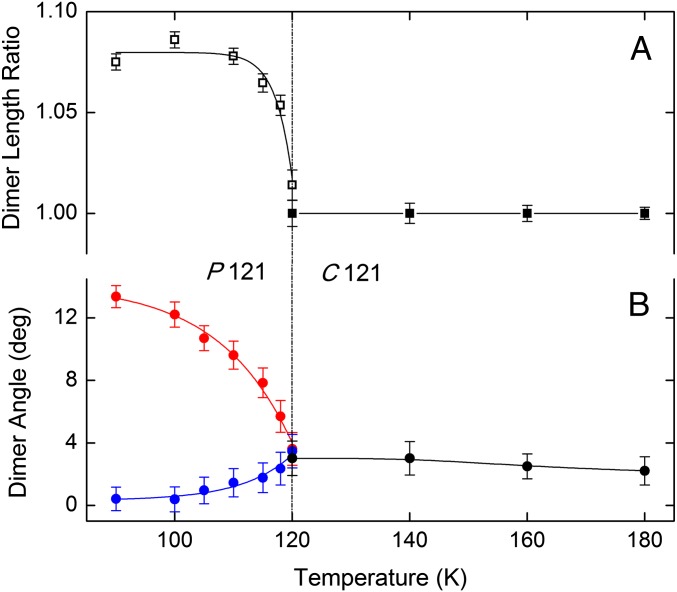
To elucidate the microscopic underpinnings of the magnetic and structural configuration in the high-pressure phase, we performed high-resolution powder neutron diffraction, refined using the Rietveld method (12–14), at P = 5.5 GPa for a range of temperatures. We plot in Fig. 3A data at T = 90 and 120 K, where we observe a change in the scattered neutron intensity at the forbidden peak (0 3 0). Above T ∼ 120 K, the observed diffraction peaks obey the selection rule h + k + l = 2n; i.e., the same set of peaks that were forbidden in the low-pressure tetragonal phase are similarly forbidden in the monoclinic high-pressure, high-temperature phase. C121 (#5) is the only monoclinic space group that arises from the tetragonal parent structure and hews to this selection rule. Below T ∼ 120 K, the selection criterion is violated, with finite intensity at previously forbidden peaks, and a structural refinement indicates a space group of P121 (#3). We test this identification using a simulation of the expected neutron diffraction intensity at T = 90 K, including the cross-sections for both SCBO’s structural and antiferromagnetic components, and compare experiment and computer simulation in Fig. 3B. The space group identifications also permit us to track the lattice parameters as a function of temperature. We see in Fig. 3C that the evolution can be described as an increase in c associated with a simultaneous decrease in a, and a slight decrease in b as temperature is cooled below T ∼ 120 K. The change in lattice constants is accompanied by a decrease in the monoclinic angle β; the overall volume of the unit cell changes by less than 1%.

Fig. 3.

Symmetry reduction with decreasing temperature at high pressure in SCBO. (A) Powder neutron diffraction intensity vs. lattice spacing for SCBO at T = 90 K (blue) and 120 K (red) at P = 5.5 GPa. A forbidden peak emerges at the lower T. Data at T = 120, 160, and 180 K all behave similarly. (B) Simulation of neutron powder diffraction cross-section for antiferromagnetic SCBO (black) in its high-pressure, low-temperature phase compared with actual data collected at T = 90 K and P = 5.5 GPa (blue). Scattering from the pressure cell gasket occurs at d ∼ 2.7 Å. (C) SCBO lattice parameters as a function of temperature extracted from powder neutron diffraction data collected at P = 5.5 GPa. Data at temperatures below T = 120 K are refined using a P121 symmetry; data collected for T > 120 K are refined using a C121 model.

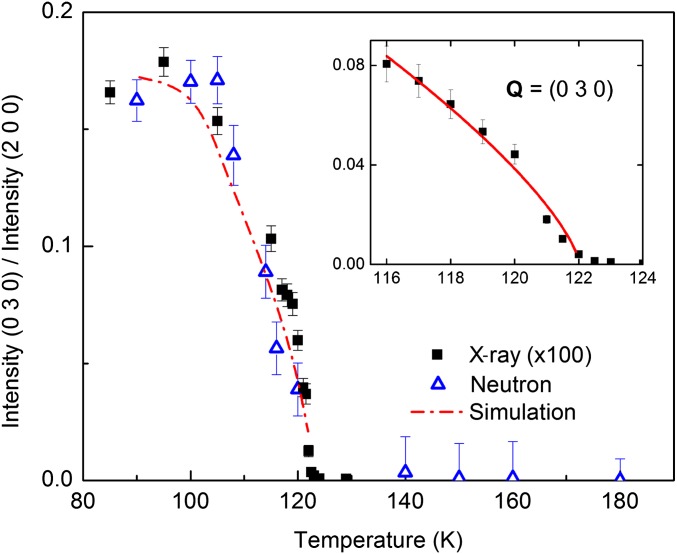
We plot in Fig. 4 a comparison between single-crystal X-ray diffraction in a diamond anvil cell and powder neutron diffraction in a Paris–Edinburgh cell for P = 5.5 GPa at the position and temperature where a forbidden (0 3 0) peak develops. The intensity scaling by 100 is consistent with the relative cross-sections for X-ray and neutron scattering. The simulation of the neutron intensity (dashed line) incorporates the antiferromagnetic structure described below; different spin configurations contribute from 0 to 30% of the total neutron signal at (0 3 0) (Fig. S1) and provide a quantitative test of the enhancement measured at that Q in Fig. 3A. The high-resolution single-crystal synchrotron X-ray data permit us to focus in on the critical behavior of the symmetry change from C121 to P121 with decreasing T (Fig. 4, Inset). A power-law fit to the data gives T_c = 122 ± 0.2 K and a critical exponent β = 0.36 ± 0.04, consistent with the value of β = 0.37 expected for a 3D Heisenberg transition (15) rather than the nominally expected 2D behavior. That this transition is associated with magnetic order is further corroborated by the rapid decrease in the neutron diffraction intensity at the forbidden odd-index peaks as expected for the Q dependence of Cu’s magnetic form factor.

Fig. 4.

Onset of antiferromagnetic order. Temperature dependence of the integrated intensity of X-ray single-crystal diffraction data (black solid squares) times 100 and of neutron powder diffraction data (open blue triangles) for (0 3 0) reflection at P = 5.5 GPa. The integrated intensity of the (0 3 0) peak in antiferromagnetic SCBO was calculated from a simulation of structural and magnetic neutron cross-sections (red dashed line). All integrated intensities at (0 3 0) are normalized to the integrated intensities of their corresponding (2 0 0) reflection. (Inset) Single-crystal X-ray diffraction data collected at the emergence of the forbidden (0 3 0) reflection. The solid line is a power-law fit to I = I_o [(T_c − T)/T_c]^2β, with T_c = 122 ± 0.2 K and a critical exponent, β = 0.36 ± 0.04, associated with a 3D universality class.

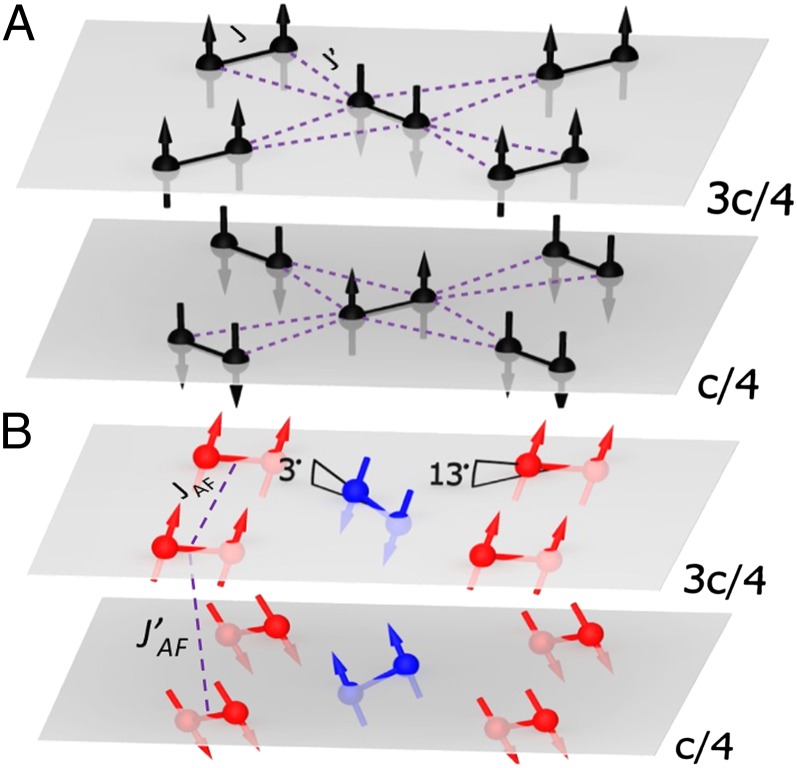
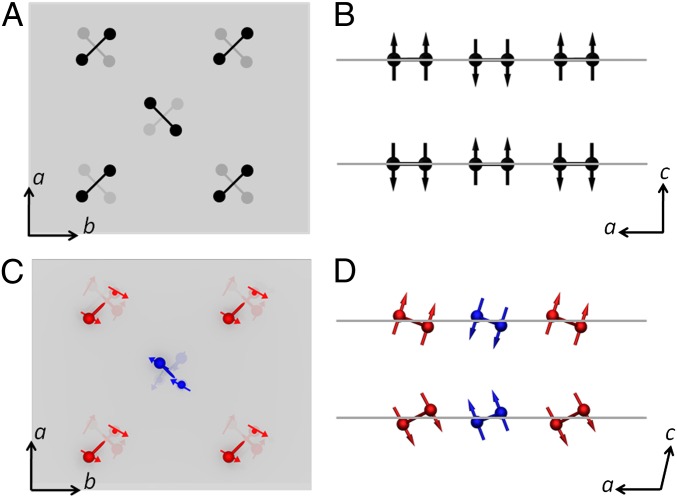
The full structural refinement derived from the powder neutron measurements allows for the determination of the copper atomic positions within the unit cell and permits us to interrogate the influence of the third dimension on the emergence of long-range magnetic order. We sketch in Fig. 5 an overall schematic of the Cu dimer structure in the antiferromagnet phase, including the spin configuration. The conventional Shastry–Sutherland model is shown in Fig. 5A. It consists of triplet dimers that are antiferromagnetically coupled along the diagonal directions in the a–b plane, with a 90° rotation between planes. The symmetry reduction which we have uncovered at T_c has two effects on the structure of the dimers, sketched in Fig. 5B (see Fig. 6 for in-plane projections) and shown quantitatively as a function of temperature in Fig. 7. First, the previously equivalent dimers separate into two interleaved sets of different lengths. One set, shown in red in Fig. 5B, elongates starting at T_c. The other set, shown in blue, contracts. Second, both sets of dimers begin to tilt out of the plane, with the elongated dimers showing a larger slant (13°) than the subtle tilt (3°) evidenced by the contracted dimers.

Fig. 5.

Schematic of local dimer rearrangements at the onset of global order. (A) Magnetic structure of SCBO based on the Shastry–Sutherland model’s prediction of an antiferromagnetic ground state. The solid lines show the intradimer Cu²⁺ (S = 1/2) interactions (J) and the dashed lines represent the interdimer Cu²⁺ (S = 1/2) interactions (J'). (B) Proposed magnetic structure of SCBO extracted from neutron powder diffraction data collected at P = 5.5 GPa and temperatures below T ∼ 120 K. The dashed lines show the in-plane dimer–dimer (S = 1) interactions (J_AF) and the interplane dimer–dimer (S = 1) interactions (J'_AF). The no longer equivalent red and blue Cu–Cu dimers are elongated and compressed, respectively, and tilt out of the a–b plane.

Fig. 6.

Schematic view of magnetic planes of SCBO in the unit cell. A and B show the schematic views of the projections of the spin orientations of Cu²⁺ ions of SCBO along the (A) a–b and (B) a–c crystallographic planes according to the 2D antiferromagnetically ordered Shastry–Sutherland model. (C and D) Schematic views of the projections of the spin orientations of Cu²⁺ ions of SCBO along the (C) a–b and (D) a–c crystallographic planes according to the modified model described in the text. The effects of the anisotropic DM interaction in the 3D long-range ordered phase results in the slight divergence of the projections of the spin orientations from exactly parallel–perpendicular to the dimer axes alignments. B and D show that in the proposed 3D compared with the pure Shastry–Sutherland 2D ordering, the dimers are tilted with respect to the a–b plane and their bonds are expanded (red) and contracted (blue).

Fig. 7.

Dimensional cross-over reflected in changed angle and length of dimers. The temperature dependence of Cu–Cu bond lengths and tilt angles with respect to the a–b plane derived from neutron powder diffraction at high pressure. A symmetry change from C121 to P121 occurs at T_c = 122 K. (A) The relative ratio of the bond lengths of the red to the blue Cu–Cu dimers of Fig. 5B (solid squares) diverges from 1 for T < T_c, where all Cu–Cu dimers are no longer equivalent. (B) Tilting of the red and blue dimers out of the a–b plane below T_c.

The starting point for understanding the magnetic structure in SCBO and the connection it might have to the structural distortions is Eq. 1, which has been eminently successful in describing the magnetic behavior of SCBO at low pressure and low temperature (7). If the magnetic structure of SCBO were completely described as a topological realization of the pure 2D Shastry–Sutherland model with x > 0.7 and no interplanar coupling, then the unit cell of SCBO would include four equivalent Cu–Cu dimers on two different layers (Fig. 5A). The spin structure at each plane would be expected to consist of spin triplets located on each Cu–Cu dimer with moments ferromagnetically aligned and antiferromagnetically coupled to neighboring dimers. Although the Shastry–Sutherland model does not specify the absolute orientation of spins, considering the symmetry of the lattice and the fact that neutrons can only probe the component of the magnetic moment perpendicular to Q, a plausible high-symmetry orientation is to have the spins perpendicular to the dimer axis and pointing out of the magnetic plane. Under this simplifying assumption, the dimer arrangements retain their mirror symmetry and the onset of magnetic ordering would at most result in an overall expansion or contraction of the lattice with no change in symmetry.

Given that a change in symmetry is experimentally observed with the emergence of peaks at h + k + l = 2n + 1, we extend the planar Shastry–Sutherland model of Eq. 1 to incorporate both direct antiferromagnetic coupling between dimers on adjacent layers as well as anisotropic Dzyaloshinskii–Moriya (DM) interactions (16–19). This gives a full spin Hamiltonian of

$$\mathrm{\mathscr{H}}={\displaystyle \sum _{\langle i,j\rangle }{\displaystyle \sum _l{J}_{\mathit{AF}}{\overrightarrow{S}}_i^l\cdot {\overrightarrow{S}}_j^l+{J\prime }_{\mathit{AF}}{\overrightarrow{S}}_i^l\cdot {\overrightarrow{S}}_i^{l+1}+J_{\mathit{DM}}{\overrightarrow{D}}_{\mathit{ij}}\cdot \left({\overrightarrow{S}}_i^l\times {\overrightarrow{S}}_j^l\right)+{J\prime }_{\mathit{DM}}{\overrightarrow{D}\prime }_l\cdot \left({\overrightarrow{S}}_i^l\times {\overrightarrow{S}}_i^{l+1}\right)}},$$ [2]

where sums over nearest-neighbor Cu–Cu dimers in each (0 0 n) plane are given by <ij> whereas l sums over adjacent planes (with two planes per unit cell), the spins here are the effective spins (S = 1) of the triplet state of a dimer as opposed to the true spins (S = 1/2) of Eq. 1, and D and D′ are unit vectors indicating the directions of the in-plane and interplane DM interactions, respectively. J_AF and J′_AF are the in-plane and interplane antiferromagnetic exchange interactions between the effective S = 1 spins of the triplet state of the dimers (Fig. 5B). Previous work on the magnetic structure of SCBO in the low-pressure phase suggests that the in-plane antiferromagnetic exchange interaction J_AF dominates the in-plane DM term J_DM, and that to leading order the latter term can be neglected (18, 19). For the interplane case, however, the direct antiferromagnetic exchange coupling J′_AF is significantly smaller as the system is constructed of well-isolated dimer sheets, allowing the interplane component of the DM interaction J′_DM to play a large role in the determination of the low-temperature, high-pressure spin structure. In the low-pressure tetragonal phase of SCBO, the presence of an inversion center at the midpoint of each Cu–Cu dimer gives an alternating structure to the DM interaction, with the direction vector D′(l) proportional to (−1)^l (18, 20). The small monoclinic distortion of the high-pressure phase is unlikely to qualitatively change this sign structure. If we then start with the spin configuration illustrated in Fig. 5A and add the weak DM interactions as a first-order perturbation, the magnetic energy of the system can be reduced by slightly tilting the dimer magnetizations away from the (0 0 n) planes while constraining the in-plane projections in consecutive planes to order at right angles with respect to each other. Due to the alternating sign of D′(l), these projections do not order helically, but instead alternate between clockwise and counterclockwise rotations, resulting in the spin structure illustrated in Fig. 5B. In-plane projections are shown in Fig. 6 C and D.

The effects of this tilting magnetization on the dimer lengths depend on whether the dimer has magnetization projections parallel or perpendicular to its axis. Note that a small but nonzero J_DM will rotate the in-plane spin components slightly away from these directions (Fig. 6C); however, due to the large in-plane direct couplings this effect does not significantly change the overall magnetic structure. In the case of the blue dimers, the in-plane spin components are aligned axially, resulting in a dipole–dipole-based magnetostrictive force that compresses the dimers. In the case of the red dimers, the in-plane components of the spins making up the triplet state are aligned side by side, the sign of the dipole interaction is reversed, and the magnetostrictive force tends to expand the dimer bond length. The expanded red dimers then have a tendency to tilt out of plane to minimize the strain on the surrounding oxygen atoms. By contrast, the contracted blue dimers see a reduction in their tilt angles (Fig. 6D). This difference in behavior is again consistent with the analysis of the neutron powder diffraction data shown in Fig. 7, in which the red dimers are seen to tilt over a much larger angle than the blue ones. As the overall staggered magnetization increases below T_c, these tendencies become stronger, and the 3D antiferromagnetic order stabilizes. The small nonzero tilt angle remaining in the contracted dimers can be attributed to the overall contraction of the lattice as a function of decreasing temperature.

The dimensionality of a system has long been known to have a strong effect on the existence and nature of any ordered state. In the case of sheets of magnetic dimers placed on a square lattice, we report the signature of the long-anticipated antiferromagnetic ordered phase in a Shastry–Sutherland model system, induced by high pressure at low temperatures, and find that this antiferromagnetic phase arises from an inherently 3D magnetic and structural distortion. The ordered, tilted dimers in SCBO deduced from powder neutron diffraction can be described by the Shastry–Sutherland model, as modified by the inclusion of a subdominant DM term that couples consecutive layers in the crystal structure. This is in agreement with our finding that the thermal evolution of the single-crystal X-ray diffraction intensity of corresponding (0 2n+1 0) peaks is best fit with a critical exponent belonging to the 3D universality class. Although well-described by 2D theory in its low-pressure singlet phase, antiferromagnetic SCBO at high pressure supports the well-known Mermin–Wagner theorem (21, 22) that long-range order can only survive fluctuations in three dimensions (23, 24), and joins geometrically frustrated chiral magnets (25–29) in underscoring the importance of the DM interaction to the formation of exotic magnetic ground states.

Methods

The SrCu₂(¹¹BO₃)₂ single-crystal sample was cut from the same high-quality single crystal used in previous magnetic neutron scattering experiments (9, 19, 30). It was grown using a floating-zone image furnace at a rate of 0.2 mm/h in an O₂ atmosphere. ¹¹B was used to avoid the high neutron absorption cross-section of natural boron. The sample was cut and polished in a shape of a disk with diameter of 3.4 mm and height of 1.3 mm in the center and 0.7 mm on the edges. X-ray Laue measurements established that the sample was a single crystal with no grain boundaries, with the (0 0 n) crystallographic direction perpendicular to its surface. The crystal was mounted between two pressed pellets of lead and placed at the center of a Paris–Edinburgh cell, fitted with null-scattering TiZr alloy gaskets with self-collimating c-BN anvils (31). Time-of-flight neutron diffraction measurements were performed at the Spallation Neutrons and Pressure (SNAP) beamline of the Spallation Neutron Source at Oak Ridge National Laboratory to pressures as high as 6 GPa, using lead as a monometer, and temperatures down to 90 K. The cell was mounted in the equatorial configuration with the sample’s (h k 0) plane coincident with the horizontal scattering plane, such that the wavevectors near the (0 3 0) magnetic Bragg peak could be accessed. Detectors were placed 50 cm from the sample at 48° and 90° relative to the incident beam. Incident neutron wavelengths ranged from 0.6 to 4.0 Å.

Neutron scattering measurements were performed using a separate powder sample grown with high-purity ¹¹B to reduce the absorption cross-section. A pressed pellet was loaded into a Paris–Edinburgh cell with toroidal boron nitride anvils (31), using 4:1 methanol:ethanol as a hydrostatic pressure medium. Time-of-flight neutron diffraction measurements were performed at the SNAP beamline of the Spallation Neutron Source at Oak Ridge National Laboratory to pressures as high as 6 GPa and temperatures down to 90 K. The cell was used in the equatorial configuration allowing a wide angular aperture for the scattered beam; detectors were placed 50 cm from the sample at 50° and 90° relative to the incident beam. Incident neutron wavelengths ranged from 0.3 to 3.7 Å. The pressure was determined by comparing the lattice parameters of the sample with previously measured X-ray diffraction results (7, 11).

A high-quality single crystal of SrCu₂(BO₃)₂ was grown using a floating-zone image furnace and cleaved to a 50 μm × 50 μm × 30-μm sample for high-pressure X-ray measurements (30). The sample was placed in a diamond anvil cell using 4:1 methanol:ethanol as a hydrostatic pressure medium and a piece of polycrystalline silver as a manometer; a helium gas membrane provided in situ pressure tuning at cryogenic temperatures (32). X-ray diffraction measurements were performed at experimental station 4-ID-D of the Advanced Photon Source at Argonne National Laboratory using a six-circle diffraction stage.

Fig. S1 shows computer simulations of the neutron powder diffraction cross-section for the high-pressure, low-temperature antiferromagnetic phase using the FULLPROF refinement program (14) which were performed based on the proposed model for the crystal and magnetic structure of SrCu₂(BO₃)₂ as shown in Fig. 5B and Fig. 6 C and D. In these calculations, the atomic positions are in the P121 space group, and the spins align in the a–c plane such that they are perpendicular to the dimer axes, with (1 0 0) and (0 1 0) propagation vectors. The comparison between the pure structural and the structural plus magnetic neutron cross-section simulations for T = 90 K in the high-pressure phase shows an increased intensity of ∼30% for (0 3 0) reflection at d = 2.9 Å, in agreement with the data. Additionally, we simulated powder neutron diffraction cross-sections for temperatures up to T_c = 120 K. The crystal structures used in these simulations are the same as those extracted from experimental powder neutron diffraction data at each temperature. When the spin orientations are aligned in the a–c plane such that they stay perpendicular to the dimer axes, the results are in agreement with the experimental data showing the evolution of the normalized intensity of the (0 3 0) magnetic peak as a function of T.