Vivid, full-color aluminum plasmonic pixels

Significance

Full-color displays are typically fabricated using a combination of chromatic materials of various types, introduced into an addressable pixel-based electronic device. Here we show that brightly colored, highly vivid pixels, directly suitable for RGB displays, can be fabricated using periodic areas of Al nanorods in each pixel. Both nanorod length and spacing are critically important in achieving strong and spectrally distinct scattering signatures across the visible spectrum. This use of a low-cost, abundant metal for achieving full-spectrum coloration is compatible with complementary metal-oxide semiconductor manufacturing methods and directly applicable to current liquid crystal display technology.

Abstract

Aluminum is abundant, low in cost, compatible with complementary metal-oxide semiconductor manufacturing methods, and capable of supporting tunable plasmon resonance structures that span the entire visible spectrum. However, the use of Al for color displays has been limited by its intrinsically broad spectral features. Here we show that vivid, highly polarized, and broadly tunable color pixels can be produced from periodic patterns of oriented Al nanorods. Whereas the nanorod longitudinal plasmon resonance is largely responsible for pixel color, far-field diffractive coupling is used to narrow the plasmon linewidth, enabling monochromatic coloration and significantly enhancing the far-field scattering intensity of the individual nanorod elements. The bright coloration can be observed with p-polarized white light excitation, consistent with the use of this approach in display devices. The resulting color pixels are constructed with a simple design, are compatible with scalable fabrication methods, and provide contrast ratios exceeding 100:1.

Display technologies have been evolving toward vivid, full-color, flat-panel displays with high resolution and/or small pixel sizes, higher energy efficiency, and improved benefit/cost ratios. Some of the most popular current technologies are liquid crystal displays (LCD), laser phosphor displays, also known as electroluminescent displays, and light-emitting diode (LED)-based displays. A common characteristic of all color display technologies is the incorporation of various color-producing media, which can be inorganic, organic, or polymeric materials, into the device. These chromatic materials are chosen to produce the fundamental components of the color spectrum in additive color schemes such as the standard red–green–blue (sRGB) when illuminated by an internal light source or when an electrical voltage is applied.

Inorganic chromatic materials have the potential to greatly extend the durability and lifetime of color displays. Inorganic nanoparticles have recently begun to be used in color displays in the form of quantum dot LEDs, which have excellent display lifetimes and industry-scalable, size-based, and material-based color tunability (1–3). However, obtaining blue colors from quantum dots has been challenging (4) owing to the requirement of synthesizing nanoparticles in the small size range required to achieve optical transitions in this wavelength range. Au nanoparticles can produce green and red colors based on their surface plasmon resonances (5), but shorter-wavelength hues are quenched because of interband transitions for wavelengths below 520 nm (6). Ag has also been investigated for display applications (7, 8), but although spectral features can be achieved across the visible region the material readily oxidizes (9, 10), requiring additional passivation layers.

Al is potentially a highly attractive material for plasmon-based full-spectrum displays. Al is the third most abundant element in the earth’s crust, behind silicon, another suitable nanophotonic display material (11). Al is low in cost and compatible with mainstream manufacturing processes in the electronics industry (complementary metal-oxide semiconductor processing, known as CMOS) (12, 13). Al has recently been identified as a highly promising chromatic material for color filters, for instance using structures such as hole arrays (14–16) or arrays of Al crosses (17). Although the plasmon resonances of Al nanostructures typically have been studied in the UV region of the spectrum (18), they can also be tuned into the visible region (19, 20), exhibiting a sensitivity to size and shape similar to Au and Ag nanostructures (21, 22). The structural tuning of the Al plasmon resonance into the visible yields excellent blue colors, but as the resonance is red-shifted across the visible spectrum its linewidth broadens, primarily owing to the interband transition of Al that occurs at nominally 1.5 eV. The increased spectral broadening and damping in Al results in complex and pastel chromaticities (23, 24), not the vivid monochromatic colors required by full-color display technologies.

In this paper, we show that Al pixels composed of sparse arrays of Al nanorods can be fabricated and provide strong, spectrally narrow, and vivid colors ideal for full-color LCD displays. By combining the tunable plasmon resonances of individual nanorods with diffractive coupling effects we achieve strong and sufficiently narrow optical resonances to produce vibrant RGB colors suitable for additive color displays. The colors appear in p-polarized white light excitation, consistent with illumination geometries used in display technologies. We demonstrate this effect with pixel sizes of 5 × 5 μm—two orders of magnitude smaller than the pixel area in most display technologies. The polarization-selective plasmon resonant nanorod structures (25, 26) fabricated here represent a first step toward the fabrication of active liquid crystal-based pixels. The enhanced intensities, tunable peak positions, and strong polarization characteristics of these pixels make them immediately compatible with LCD-based displays, without the need for color filters or multiple polarizers.

Results and Discussion

The Al nanorod array-based pixels were prepared using standard electron beam lithography and metal evaporation techniques on a glass substrate with a coating of indium tin oxide (ITO), as schematically illustrated in Fig. 1A. The size of each pixel was 5 × 5 μm and consisted of a finite array of nanorods each having the same length, width, height, and edge-to-edge spacing. Nanorods were chosen as the repeat unit because their plasmon resonance is strongly sensitive to changes in the nanorod length, and because their spectral response is highly polarized. The use of more symmetric nanostructures such as disks or spheres is predicted to yield a much weaker in-plane polarization response, even when D_y and D_x are dissimilar (SI Appendix, Fig. S1). The nanorods were patterned in an approximately hexagonal arrangement, as shown in the SEM image in Fig. 1B, with well-defined periods along the D_x and D_y directions (Fig. 1B, Inset). All nanorods had widths w = 40 nm and heights h = 35 nm but lengths l varying from 85 nm to 155 nm depending on the color of the pixel. The values of D_x and D_y were varied from 180 nm to 360 nm and from 220 nm to 470 nm, respectively. An approximately hexagonal array was chosen because this geometry enhances the diffractive far-field coupling (27). The use of different values for D_x and D_y provides an additional enhancement of the coupling (28, 29). Although the Al nanorods in a pixel form their own self-terminating oxide layer very quickly after fabrication (20, 30, 31), the sample was coated with a 50- to 60-nm-thick layer of polyimide (PI) for additional protection against further oxidation in ambient air (SI Appendix, Fig. S2).

Fig. 1.

Design of an Al pixel. (A) Schematic showing the unit cell of a pixel. The physical parameters (length l, width w, height h, and edge-to-edge spacing Γ) of the nanorods in an Al pixel are shown. All nanorods in this study have the same width of 40 nm and height of 35 nm. (B) SEM image of a 5- × 5-μm plasmonic pixel with the inset illustrating a high magnification image of the lower right corner. The unit cell of this design is marked with a white dotted line, defining the periods in the D_x and D_y directions. Pixel dimensions are l = 80 nm, w = 40 nm, h = 35 nm, D_x = 270 nm, and D_y = 300 nm. (C) Schematic of the excitation geometry. P-polarized white light is coupled into the sample using an equilateral triangular prism. The nanorods are excited by p-polarized light, with the light propagating along the yz plane. The PI–air interface has a critical angle of θ_c ∼40°.

Plasmonic pixels were imaged and spectrally resolved using an inverted microscope under p-polarized excitation conditions (Fig. 1C). P-polarized light was incident on the glass substrate side of the sample, where an equilateral prism was used for coupling incident light into the pixel plane. Prism coupling creates an evanescent wave owing to total internal reflection at the PI–air interface, strongly reducing interfacial background scattering, but does not occur at the substrate–PI interface. Although diffractive coupling in nanostructure arrays typically is studied using normal incidence (18, 31–33), it can also be achieved using the off-normal angles of incidence used here (28, 34–37). Images were obtained by mounting a digital single-lens reflex (DSLR) camera into the eyepiece of the microscope; spectra were obtained by directing the signal toward a CCD camera attached to a spectrograph.

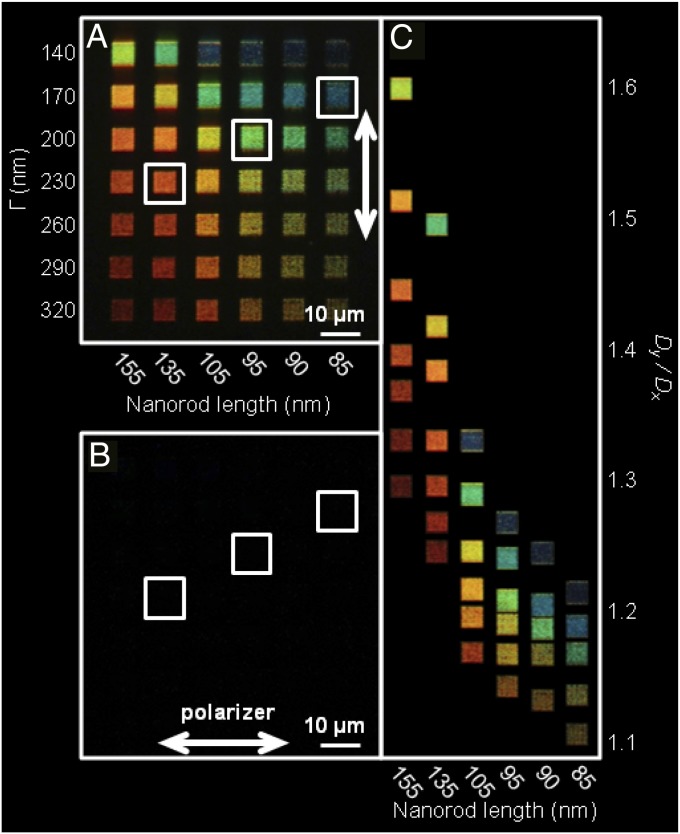
In each pixel, the individual longitudinal nanorod plasmon resonance, determined by l, is shifted and enhanced through far-field diffractive coupling, which is controlled by D_x and D_y. As the length of the nanorods decreases (left to right in Fig. 2A) the color of the pixels blue-shifts, showing a dependence on both nanorod length and aspect ratio (25, 38, 39). As the edge-to-edge spacing, roughly Γ = D_x − w = D_y − l, is increased (top to bottom in Fig. 2A), the pixel color red-shifts. The dependence on edge-to-edge spacing Γ reflects the dependence on D_y and D_x, which are the parameters controlling diffractive coupling. In the diffractive coupling regime, the individual nanorod plasmon modes interact with the diffractive grating orders defined by D_x and D_y, resulting in a shifting and narrowing of the resonance and an increase of its intensity (27, 34, 40–44). The PI coating, in addition to protection against sample degradation, surrounds the pixels with a relatively uniform refractive index, further enhancing the effects of diffractive coupling (34). Furthermore, the PI coating makes the substrate smoother (SI Appendix, Fig. S2), which reduces background scattering. It is clear from the images in Fig. 2 that vivid RGB colors can be achieved with this pixel design and illumination geometry.

Fig. 2.

Scattering DSLR camera images of Al pixels. (A) Polarized image of an array of six by seven pixels with different nanorod lengths in each column (varying from 85 nm at the right to 155 nm at the left) and different values of Γ in each row (varying from 140 nm at the top to 320 nm at the bottom). A polarizer in the y direction is present in the detection path, showing the on state of the pixels. The highlighted pixels display red, green, and blue colorations with corresponding spectra shown in Fig. 3. (B) Image of the same region as in A, with the polarizer parallel to the x axis, showing the off state of the pixels. (C) An unpolarized, composite DSLR camera image of individual pixels plotted as a function of D_y/D_x ratio and nanorod length l. Six Al pixels are omitted owing to chromatic redundancy. All three images were obtained using a 50× objective with N.A. = 0.8, ISO = 100 (lowest gain setting) and exposure times of 10 s (A and B) and 5 s (C).

Because nanorods, with their highly polarized optical response, are the fundamental color element of these pixels, the color scattered by the pixels is highly polarized along the longitudinal axis of the nanorods, yielding contrast ratios on the order of 100:1. Fig. 2A shows the “on state” of an array of different pixels, which was obtained by placing a polarizer oriented in the y direction in the detection path of the microscope. Fig. 2B shows the “off state” of the same array, with the polarizer oriented in the x direction. Contrast ratios have been calculated for each pixel by selecting the region of one Al pixel and adding together the measured intensity values of the RGB channels. This RGB-based integrated intensity for the on state was then divided by the integrated intensity for the off state to obtain a contrast ratio. The average contrast ratio for the pixels shown in Fig. 2 is 81:1, although the highest contrast ratio obtained for a single pixel in this sample is 139:1. Calculations for similar arrays of Al nanospheres confirm that sphere-based pixels do not display the same sensitivity to different incident polarizations as the present nanorod pixels (SI Appendix, Fig. S1).

The ratio D_y/D_x of the hexagonal lattice also affects pixel color and intensity. In Fig. 2C, an unpolarized, composite image of the pixels imaged in Fig. 2A is shown, with the pixels ordered according to nanorod length (horizontal axis) and D_y/D_x (vertical axis). Higher values of D_y/D_x correspond to increased pixel brightness. Because diffractive coupling also affects pixel color, different combinations of nanorod length and D_y/D_x can yield similar colors. For example, the pixels with l = 105 nm, D_y/D_x = 1.25, and l = 135 nm, D_y/D_x = 1.42 are both yellow, whereas the pixels with l = 105 nm, D_y/D_x = 1.29, and l = 135, D_y/D_x = 1.50 are both cyan. A recent study on the plasmonic response of 2D rectangular arrays of Au nanorods reported that the strongest enhancement of the scattered field with diffractive coupling occurred for 0.5 < D_y/D_x < 1 (28). Here we find that for Al larger D_y/D_x values of ∼1.5 correspond to the strongest diffractive enhancements.

To confirm the overall importance of diffractive coupling, Al pixel patterns were alternatively created with oriented nanorods having random, aperiodic spacings with the same total number of nanorods as the periodic pixel design (SI Appendix, Fig. S3). Some limited color tuning as a function of nanorod density is observed, but these pixels lack the strong enhancement observed when pixels are composed of ordered nanorod arrays. In addition, we imaged the periodic arrays in Figs. 1 and 2 under direct reflectance where diffractive coupling is suppressed (SI Appendix, Fig. S4). In this geometry the pixels appear dim and with similar colors which now are determined by the aspect ratio of the individual nanorods and are independent of D_y/D_x.

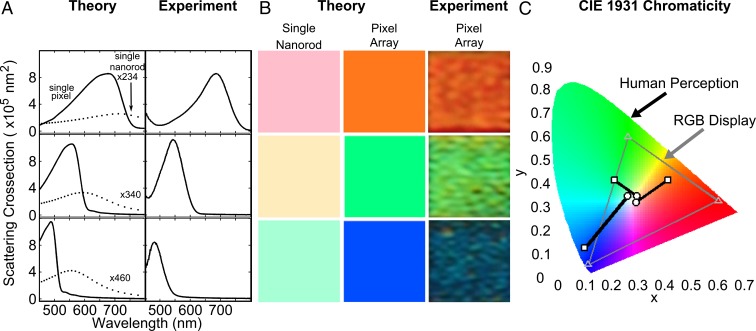
The patterning of Al nanorods into oriented periodic arrays has three main effects on the surface plasmon resonance: (i) a substantial narrowing of the lineshape, overcoming the intrinsic broadening characteristic of the Al dielectric function, (ii) an increase in the intensity of scattered light relative to the additive scattering of an equal number of oriented but randomly spaced nanorods, and (iii) a shifting of the peak wavelength of the scattered light relative to that of the individual nanorods. To examine these effects in greater detail, we compare experimental and theoretical spectra obtained for the three RGB pixels highlighted in Fig. 2. These pixels are selected because their spectral peak positions correspond to the wavelengths of standard RGB colors (red = 635 nm, green = 535 nm, and blue = 435 nm).

The top left panel of Fig. 3A shows the theoretical spectrum of a pixel with identical physical parameters as the experimental system (solid line), calculated using a coupled dipole method where the nanorods are described as point dipoles with a polarizability obtained from finite element method modeling (COMSOL) (45, 46). For a more complete description of the theory, see SI Appendix, Fig. S5. The unpolarized spectrum of the red pixel (l = 135 nm, D_x = 270 nm, D_y = 360 nm, containing 234 nanorods), obtained in a p-polarized excitation geometry, are shown in the top right panel of Fig. 3A. The experimental spectrum of the red pixel is scaled to about the same peak scattering cross-section as the theoretical spectrum, and subsequent experimental spectra are plotted relative to the experimental red pixel. The middle panels of Fig. 3A correspond to the green pixel (l = 95 nm, D_x = 240 nm, D_y = 290 nm, containing 340 nanorods), and the bottom panels of Fig. 3A to the blue pixel (l = 85 nm, D_x = 210 nm, D_y = 250 nm, containing 460 nanorods). Experimental spectra for every pixel in Fig. 2 are plotted in SI Appendix, Fig. S6. Both the lineshape and relative intensities of the theoretical spectra agree well with the experimental data. For comparison, the individual nanorod spectra were also calculated for these geometries, clearly showing that the spectral peaks and lineshapes obtained are largely controlled by diffractive coupling effects. Whereas the pixel spectra show far narrower lineshapes than the individual nanorods, they are not as narrow as those observed for infinite square arrays of nanospheres or nanodisks (47, 48). All simulations were performed using experimental (nonadjustable) structural parameters. The incident angle in the calculation was adjusted to 53° to account for the light passing through the prism, silicon dioxide, ITO, and PI interfaces. The slight deviation from the nominal 60° incident angle is consistent with the angular uncertainty of the incident beam in the experimental setup.

Fig. 3.

Unpolarized theoretical and experimental spectra of the red, green, and blue Al pixels highlighted in Fig. 2 and corresponding chromaticity calculations. (A) Unpolarized theoretical (Left) and experimental (Right) spectra. (Top Left) A theoretical spectrum of an Al pixel (solid line) with parameters l = 135 nm, D_x = 270 nm, and D_y = 360 nm. For comparison, a single nanorod spectrum (dotted line) with l = 135 nm is shown. (Top Right) The experimental spectrum of a nanorod pixel with the same physical parameters (l = 135 nm, D_x = 270 nm, and D_y = 360 nm). (Middle) The same as the top two panels for the green pixel with l = 95 nm, D_x = 240 nm, and D_y = 290 nm. (Bottom) The same for the blue pixel with l = 85 nm, D_x = 210 nm, and D_y = 250 nm. (B) Apparent colors of the theoretical individual nanorods (Left) and pixel array (Center) spectra when analyzed with the CIE 1931 color matching functions compared with observed colors from experimental pixels (Right). (C) CIE 1931 chromaticity diagram overlaid with the sRGB gamut outlined in gray, single-nanorod colors (circles) and pixel array colors (squares). The square for the blue pixel array lies outside of the sRGB gamut. Although it can be perceived by the human eye, it is beyond the display range of standard display technologies.

The simulations shown in Fig. 3A convincingly illustrate the effects of diffractive coupling by comparing theoretical spectra for individual Al pixels (solid lines) with individual Al nanorods (dotted lines). For the green pixel (Fig. 3A, middle panels), diffractive coupling blue-shifts the peak wavelength of the pixel by ∼35 nm relative to the single nanorod scattering spectrum, and narrows the linewidth by over 100 nm. The scattering cross-section of the Al pixel consisting of 340 nanorods exceeds that of the sum of 340 isolated, noninteracting nanorods, making the observed enhancement of the scattering cross-section due to diffractive coupling a synergistic effect, as further demonstrated in SI Appendix, Fig. S7.

By convolving the theoretical individual nanorod and pixel array spectra with the Commission Internationale de l’Elcairage (CIE) 1931 color matching functions the apparent color of the two systems can be compared (Fig. 3B). In the case of an individual nanorod, the relatively large linewidth of the longitudinal resonance results in a weak pastel color. The color determined by the peak wavelength for each nanorod is muted by the contributions from the broad range of wavelengths within the envelope of the resonance, making the perceived color more pastel. The narrow spectral peak created by the pixel configuration minimizes the contributions from these additional wavelengths, producing a much purer color. These pixel colors are verified by imaging the corresponding experimental arrays with a DSLR camera. In Fig. 3C, the color of each single nanorod and array pixel is plotted on the CIE 1931 chromaticity diagram labeled with the limits of the sRGB color gamut. The colors of the single red, green, and blue nanorods (circles) are weak pastels and bunch around the white point because of their broad linewidths. The pure color of the pixel arrays (squares) lies far away from the white point toward the limits of the sRGB gamut. The color of the blue pixel actually lies outside the sRGB gamut, meaning it has such a saturated color that it cannot be duplicated by standard display technologies. The same analysis based on the experimental scattering spectra is presented in SI Appendix, Fig. S8.

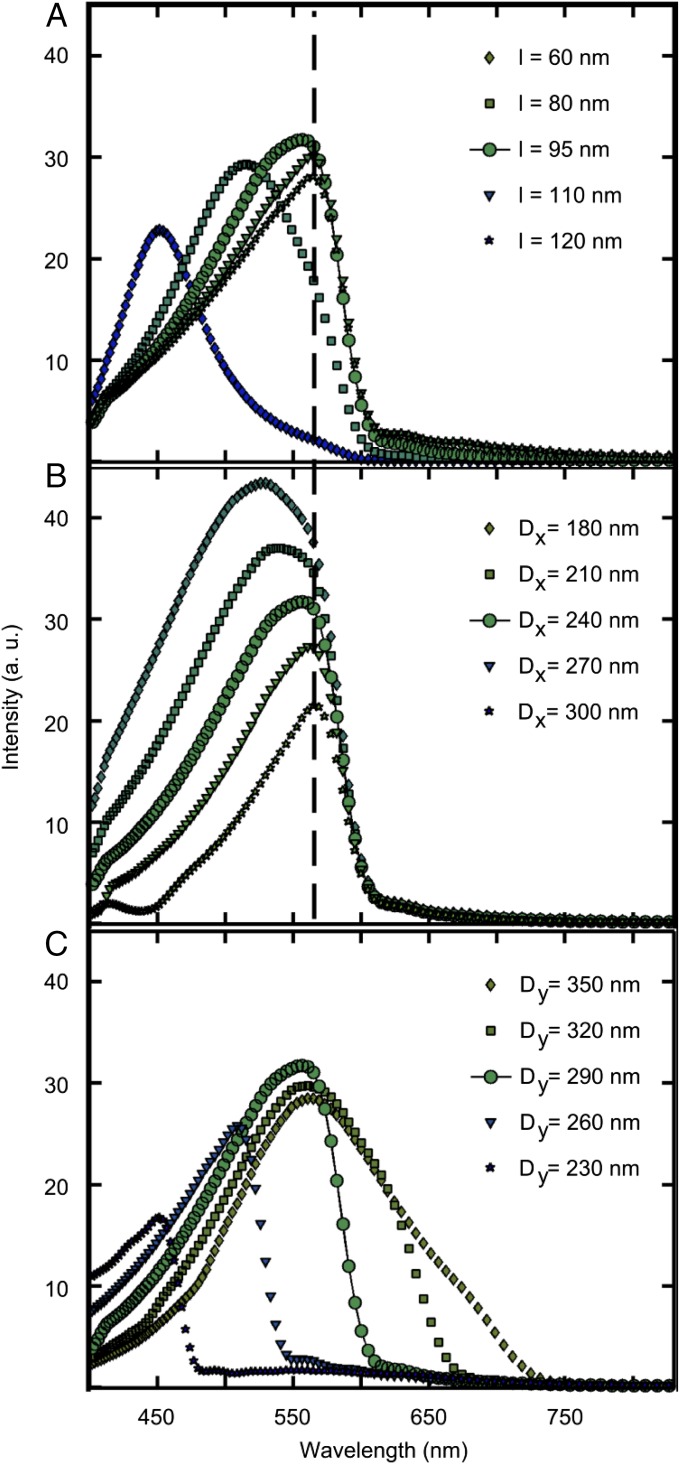
Both the experimental and theoretical spectra for the pixels shown in Fig. 3 have asymmetric lineshapes, which are controlled by specific combinations of the nanorod length l, D_y, and D_x. Here we focus on the green pixel (Fig. 3A, middle panels) and examine the origin of this unusual lineshape by varying l, D_y, and D_x independently (Fig. 4). Changing only the nanorod length from 60 nm (diamonds) to 120 nm (stars) while maintaining a constant array spacing (Fig. 4A), we find that the plasmon resonance maxima initially red-shift as the nanorod length increases. However, once a resonance wavelength of nominally 560 nm is reached, no further shifts occur and the intensity decreases, with no observable plasmon response beyond a cutoff wavelength of 600 nm. If instead D_x is varied from 180 nm (diamonds) to 300 nm (stars) with constant values for l and D_y (Fig. 4B) the same general trend is seen with a similar cutoff wavelength as in Fig. 4A, but the intensity drop is significantly more pronounced. This larger intensity decrease is in part due to the decrease in the number of nanorods when the periodicity is increased for a constant pixel area (357 for D_x = 180 nm to 294 for D_x = 300 nm).

Fig. 4.

Simulations of pixel spectra with l, D_x, and D_y varied individually, using the spectrum of the green pixel as a starting point (l = 95 nm, D_x = 240 nm, and D_y = 290 nm; circles and solid line). (A) Pixel spectra with D_x = 240 nm and D_y = 290 nm held constant while varying the nanorod length, l = 60 nm (diamonds), 80 nm (squares), 95 nm (circles), 110 nm (triangles), and 120 nm (stars). (B) Pixel spectra with l = 95 nm and D_y = 290 nm held constant with D_x varying from 180 nm (diamonds), 210 nm (squares), 240 nm (circles), 270 nm (triangles), to 300 nm (stars). (C) Pixel spectra with l = 95 nm and D_x = 240 nm held constant with D_y varying from 350 nm (diamonds), 320 nm (squares), 290 nm (circles), 260 nm (triangles), to 230 nm (stars).

A much stronger effect is apparent when varying D_y (Fig. 4C). This is because for p-polarized light the cutoff wavelength is controlled by D_y. Only wavelengths on the blue side of the cutoff are diffracted at collection angles over which constructive interference of the nanorod-scattered light occurs. As D_y is increased (Fig. 4C) the cutoff wavelength red-shifts by ∼60 nm for every 30-nm increment of D_y. This behavior arises because the nanorods are excited at an incident angle θ_i, and the scattered light is collected with a maximum collection angle θ_o, defined by the N.A. of the collection objective. This geometry introduces a phase difference in the light scattered from nanorods at different y positions and defines a maximum wavelength λ_max above which no constructive interference can occur:

$${\lambda }_{max}=D_{y}n(sin{\theta }_i+sin{\theta }_o).$$ [1]

Here, n is the refractive index, for which we assume an average value of n = 1.55, because the nanorods are on an ITO-coated glass substrate (n = 1.50) and surrounded by PI (n = 1.65). Therefore, for pixels with D_y = 350 nm, 320 nm, 290 nm, 260 nm, and 230 nm, the λ_max should occur at 704, 644, 583, 523, and 462 nm, respectively. These values are in good agreement with the spectra in Fig. 4C, despite the fact that this simple equation assumes an infinite array of nanorods, whereas the calculations are performed on a finite area. Larger arrays approaching the infinite limit will produce a sharper intensity drop-off at the cutoff wavelength, whereas smaller arrays will reduce the intensity more gradually.

The wavelength cutoff (through its dependence on D_y) provides an excellent tuning knob for controlling and fine tuning RGB colors and their intensities. However, also the incident angle θ_i and maximum collection angle θ_o play a role. These angles are related to the refractive index n, which determines the critical angle for total internal reflection θ_c at the PI–air interface using prism excitation. The critical angle θ_c is ∼40° for our system and determines the maximum collection angle (i.e., θ_o ≤ θ_c), as well as the minimum incident angle (i.e., θ_i ≥ θ_c). The maximum collection angle in this study, limited by the objective, is close to the critical angle, because N.A. = 0.8 corresponds to a 30° angle. Spectra collected using an objective with a higher collection angle therefore do not differ significantly from our results. However, using objectives with smaller N.A.s yields blue-shifted spectra (SI Appendix, Fig. S9). Nevertheless, as a step toward display technology we show in SI Appendix, Fig. S10 that a diffuser placed in front of the pixel array sufficiently mixes all diffracted angles and makes these pixels capable of providing a more spatially uniform viewing experience. Furthermore, in consideration of display power consumption, the power scattered by the pixels can be easily calculated by taking the product of their scattering cross-section (Fig. 3A) and the incident intensity.

Conclusions

Our results demonstrate that highly polarized, vivid colors in the visible spectrum can be designed by arranging Al nanorods into well-ordered finite arrays termed plasmonic pixels. The colors of these pixels are determined by diffractive coupling and are tunable through a combination of nanorod length l, D_x, and D_y, resulting in bright, vivid RGB pixels compatible with additive color schemes. Because of the use of nanorods as the basic component, the signal is strongly polarized, making these Al plasmonic pixels compatible with liquid crystal switching technology (49–51). For display purposes, a viewing angle-dependent signal would be problematic but could be remedied by placing a diffusing layer on top of the pixel layer. Although the standard electron beam lithography methods used in this work are not currently scalable to industrial requirements, nanorods of similar sizes have been produced by extreme UV lithography (21), which uses an interference mask, a coherent light source, and otherwise standard lithography techniques. This combination of highly tunable, vibrant RGB colors, a highly polarized response, and potential industrial scalability suggests that the Al plasmonic pixel is a promising platform for future display technologies in the not-so-distant future.

Materials and Methods

A clean glass slide coated with ITO (120 nm thick, 8–12 ohm sheet resistance; Delta Technologies Ltd) was spin-coated with a positive electron beam resist (a 50/50 mixture of PMMA 495 A4 and A2; MicroChem) and baked at 180 °C for 90 s. After patterning (JEOL 6500F SEM equipped with beam blanker and associated with Nabity NPGS software) and development, 35 nm of Al was evaporated onto the substrate at a base pressure of ∼2 × 10⁻⁷ torr to promote low oxide content in the bulk Al (30). Lift-off consisted of soaking the sample in acetone for 15 h, followed by gentle rinsing with fresh acetone. Shorter soaking times resulted in nanorods with rough edges or pixels with missing regions. The substrate with Al structures was then spin-coated with a polyimide solution (SE-3510; Nissan Chemical) and baked at 180 °C for 45 min.

Individual pixels were designed to fit within a footprint of 5 × 5 μm, so that the number of nanorods in the x direction is 5,000 nm/D_x and the number of rows in the y direction is 5,000 nm/D_y. These numbers were rounded to the lowest whole number and used to prepare the design. Exact physical parameters for all pixels presented in this paper are available in SI Appendix, Table S1.

The Al pixels were characterized using SEM (JEOL 6500F or FEI Quanta) and scattering microscopy. For scattering images and spectra, the sample was placed on an inverted microscope (Axiovert 200; Zeiss) with the glass substrate side facing up and the pixel side facing down toward the objective (50×, N.A. = 0.8, Epiplan-Neofluar; Zeiss). An equilateral prism (Thorlabs) was used to couple white light from a tungsten lamp (Newport) into the sample. The lamp was mounted in a cage system (Thorlabs) that included a polarizer set to select only p-polarized excitation light. Images were collected using a Canon EOS Rebel T3 DSLR camera with ISO set to 100 and various exposure times on the order of 1 s. Spectra were collected by passing the light scattered from an individual pixel through a 50-μm pinhole at the first image plane of the microscope to a spectrometer (Acton SP2150i; Princeton Instruments) and CCD camera (PIXIS 400BR; Princeton Instruments). The CCD camera exposure time was 40 s with the grating set to a center wavelength of 600 nm. For each spectrum three repetitions were averaged. All spectra were corrected by subtracting a background spectrum recorded with the same exposure time from the pixel spectrum and dividing by a transmission spectrum of the lamp through the same substrate at a location with no structures presents.