Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Oct 7;54(10):2744–2750. doi: 10.1021/ci500325b

BFMP: A Method for Discretizing and Visualizing Pyranose Conformations

Spandana Makeneni †, B Lachele Foley †,*, Robert J Woods †,‡,*
PMCID: PMC4210171  PMID: 25289680

Abstract

graphic file with name ci-2014-00325b_0011.jpg

We report a new classification method for pyranose ring conformations called Best-fit, Four-Membered Plane (BFMP), which describes pyranose ring conformations based on reference planes defined by four atoms. The method is able to characterize all asymmetrical and symmetrical shapes of a pyran ring, is readily automated, easy to interpret, and maps trivially to IUPAC definitions. It also provides a qualitative measurement of the distortion of the ring. Example applications include the analysis of data from crystal structures and molecular dynamics simulations.

Introduction

The vast majority of all mammalian glycans exist as branched polymers, in which the monosaccharides are present in their six-membered ring (pyran) form. Pyran ring conformations depend on the nature of the substituents around the ring and may be highly dynamic in solution.1 In addition, the monosaccharide rings may alter conformation upon binding to enzymes such as glycosyl hydrolases.2 In some cases, biological function depends on the ability of a protein to bind to a glycan displaying a particular conformation, selected from an ensemble of solution conformations, of the pyran ring. For example, the anticoagulant activity of Antithrombin III depends on the specific interaction of the protein with a bioactive conformation of the polysaccharide heparin.3,4 Pyran ring conformational propensity has been linked to the chemical reactivity of monosaccharides5,6 as well as the physiochemical properties, such as elasticity, of the resultant polymers.7

The nomenclature adopted by the International Union of Pure and Applied Chemistry (IUPAC) for describing pyran-ring conformation8 divides six-membered ring shapes into 38 distinct conformations: 2 chairs, 6 boats, 6 skew-boats, 12 half-chairs, and 12 envelopes.9 These descriptors correspond to pyran rings in idealized, symmetrical conformations and do not provide any quantification of the extent to which any given conformation deviates from ideality. However, experimental data from NMR spectroscopy10 as well as from crystallography11 show that pyran rings adopt nonidealized, asymmetrical conformations. It is important to precisely quantify the geometry of these structures to understand the process of ring puckering, and methods exist for doing so, but there exist no simple methods for qualitative classification of all ring shapes. Two popular methods are available for the quantification of pyran ring shapes: Whitfield classification12 and Cremer-Pople parameters.13 The Whitfield method employs a linear combination of idealized IUPAC shapes to describe ring conformations. For example, a chair form might be characterized as being 89% chair (1C4) + 8.5% boat (1,4B) −1.9% skew (OS2).12 While quantitative, this approach precludes intuitive understanding: it is difficult to construct a mental image from such a linear combination. Cremer-Pople parameters13 employ a set of abstracted spherical-polar coordinates, Q, ϕ, and θ, where the polar angle, θ, provides a description of the symmetry of puckering around the ring, the phase angle, φ, describes the position around the ring where the puckering occurs, and the amplitude, Q, describes the magnitude of the puckering. For example, an idealized symmetrical chair might have an amplitude (Q) of 0.61, phase angle φ = 0.5°, and polar angle θ = 176°; an asymmetrical chair might have Q = 0.51, φ = 131°, and θ = 157°. In practice, Q is often ignored, and the values of φ and θ are plotted on a sphere of constant Q (the “Q-sphere”). These parameters provide a quantitative description of every possible ring shape, and while mapping the parameters to idealized conformations is straightforward,14 describing nonstandard ring shapes again requires a linear combination of canonical conformations. More recently Hill and Reilly15 proposed a quantification method based on a triangular reference plane and a set of three angles. This method is useful to quantify ring puckering and is more intuitive in comparison to the other two methods. However, while basic visualization of the conformation is straightforward, translation to an IUPAC descriptor, where one exists, is not.

Here, we propose a new naming convention, Best-fit Four-Member Plane (BFMP), which can describe all the canonical and asymmetrical conformations adopted by six-membered rings using descriptors comprised of a single letter and one or two numerals. The letters used in the descriptors are derived from the number of consecutive atoms in a reference plane, where the reference planes are consistent with those used by IUPAC. For example, a pyranose in a 4C1 conformation has at most two consecutive atoms in the IUPAC reference plane (C2 and C3 or C5 and O, Figure 1) and would be described by BFMP as a 4d1 conformation, where d, for “di”, indicates the two consecutive atoms. Additionally, this method provides quantification of degree of deviation from ideality in two ways. One, the average torsion angle associated with the reference plane represents the coplanarity of the four atoms defining the reference plane. That is, it provides quantification of the degree of distortion of the atoms from their reference plane. Two additional numbers report the distances of the other one or two atoms above or below the reference plane. Any, or none, of these quantifications might be included along with the descriptor. Thus, an idealized (IUPAC) chair conformation would be represented in the BFMP convention as 4d1, whereas a typical, slightly distorted chair might be represented as 4d1, 4d1(6°), or as 4(0.70)d1(0.42)(6°), depending on the information required. This method offers several advantages, including the ability to more precisely describe nonideal conformations without introducing a linear combination of states (Table S1 and Figure S1) as well as retaining a straightforward way to map the new nomenclature back to established IUPAC conformations. In addition, the approach is readily amenable to the automatic detection and characterization of conformational states from experimental or theoretical data. The method and its automation are described below, with applications to an analysis of crystallographic data, as well as data from molecular dynamics (MD) simulations.

Figure 1.

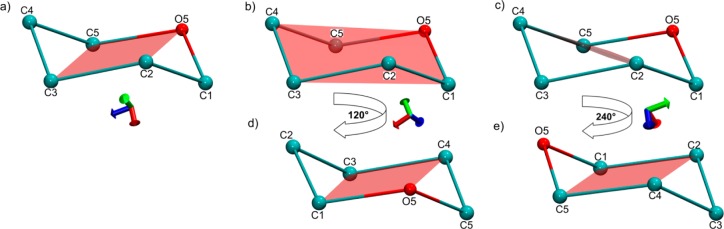
Figure 1

Open in a new tab

a) A pyranose ring in an idealized, symmetrical 4C1 conformation. Atoms C4 and C1 are above and below the reference plane formed by atoms C2, C3, C5, and O5. Two additional planes can also define this conformation: b) with reference atoms C1, C3, C4, and O5 and c) with reference atoms C1, C2, C4, and C5. d) and e) show the planes illustrated in b) and c) from a different view. The reference planes for all other IUPAC shapes are given in Figure S2 and Table S2 in the Supporting Information.

Methods

Theory

Each of the 38 canonical IUPAC shapes contains one, two, or three sets of four coplanar atoms.16 While 15 unique four-atom sequences exist in a six-membered ring, in only 3 or fewer are the atoms coplanar in any given canonical conformation. For example, a 4C1 conformation contains three such planes. Its standard, reference plane contains atoms C2, C3, C5, and O5, with atoms C4 and C1 above and below the plane, respectively. However, 2 other four-membered planes are also present in, and could be used to define, this canonical, idealized, symmetrical chair conformation (Figure 1).

In the BFMP method, a best-fit plane13 is calculated for each of the 15 possible four-atom sequences. The plane in which the 4 atoms are closest to being coplanar is chosen as the reference plane. Planarity is defined by the average dihedral angles associated with the 4 atoms around the perimeter of each quadrilateral: a value of zero indicates that the 4 atoms are coplanar. The particular conformational assignment also depends on the positions of the remaining 2 atoms above or below the reference plane (Figure 2).

Figure 2.

Figure 2

Open in a new tab

a) Distorted 1C4 conformation in PDB ID 1AXM, in which reference atoms C2, C3, C5, and O5 (dihedral = 19.3°) fit poorly to a plane. b) The best-fit plane in this case is formed by reference atoms C1, C3, C4, and O5 (dihedral = 5.6°). c) The average dihedral (9.1°) for the atoms defining the third 1C4 reference plane falls below the cutoff used in this work, but the fit is still poor when compared to the reference plane in b). Distances from the remaining atoms to the planes are shown in all three cases. The BFMP method may be used to classify this generally as a 5d2 conformation, or with increasing quantitation, as a 5d2(5.6°), or 5(0.71)d2(0.44)(5.6°) conformation.

The coplanarity of the four atoms defining the reference plane indicates the maximum extent to which the overall conformation could be symmetrical. That is, a reference plane with a torsion angle close to 0° does not necessarily imply that the remaining two atoms are in symmetrical positions or that the overall conformation approximates one of the 38 idealized IUPAC structures. Therefore, the distances of the remaining two atoms to the reference plane are used to provide additional quantification of the structure’s ideality. If they occupy differing distances from the reference plane, or if they are unusually close to, or far from, it, then the overall shape cannot be symmetrical. While this combination of dihedral angle and distances cannot be used to perfectly reconstruct the shape, and while it also does not provide strict quantification of ideality, it does provide an intuitive estimate of the minimum deviation from ideality.

While the BFMP descriptors can be used to describe all the ring conformations, an equivalent, dihedral-based method cannot be used to assign descriptors for conformations which employ five (envelope) or six-membered planes. It is not possible to calculate a dihedral for five atoms, and the varying distances between the atoms precludes a simple comparison, for example, of root mean distances of the atoms to reference planes defined by four, five, and six atoms. In such cases, it is useful to employ cutoffs. The procedures used in this work for assigning p-type (envelope) and h-type (planar) conformations are detailed in Section S1. The cutoffs can also be employed to classify highly distorted structures in which none of the atoms in the 15 four-atom sequences are nearly coplanar. For example, in this work, an average dihedral angle greater than 10° is considered too poor an approximation to planarity (Figure S3 and Section S1). Thus, in the case that the best reference plane is described by an average dihedral greater than 10°, the conformation m would be assigned. These cutoffs can be altered to suit the requirements of the particular study in which they are employed.

This method not only can readily identify all of the 38 IUPAC conformations but also can be employed to assign asymmetrical shapes to one of an additional 48 conformations. The automation of this method is detailed in the Supporting Information (Section S1and Figures S3, S4, and S5), and the program is available at http://glycam.org/publication-materials/bfmp/. This and future versions of the program and documentation should also be accessible from http://glycam.org/downloads.

BFMP Nomenclature

The letters used in the nomenclature are derived from the number of consecutive atoms in the reference plane. For example, as stated in the Introduction, a pyranose in a 4C1 conformation has 2 consecutive atoms in the reference plane (C2 and C3 or C5 and O, Figure 1) and hence would be described as a 4d1 conformation, where “d”, for “di”, indicates the two consecutive atoms. This designation also corresponds to a boat conformation, which has 2 consecutive atoms in its IUPAC reference plane, and hence a 1,4B boat conformation would be described as 1,4d. A skew boat conformation has 3 consecutive atoms, and a half-chair conformation has 4 consecutive atoms; thus, a 1S3 can be referred to as 1t3 (“t” for tri) and a 2H1 as 2q1 (“q” for quatro) using the BFMP descriptors. The letters used in the BFMP naming scheme as well as example standard conformations are given in Table 1.

Table 1. BFMP Nomenclature, Including Corresponding IUPAC Nomenclature Where Relevant.

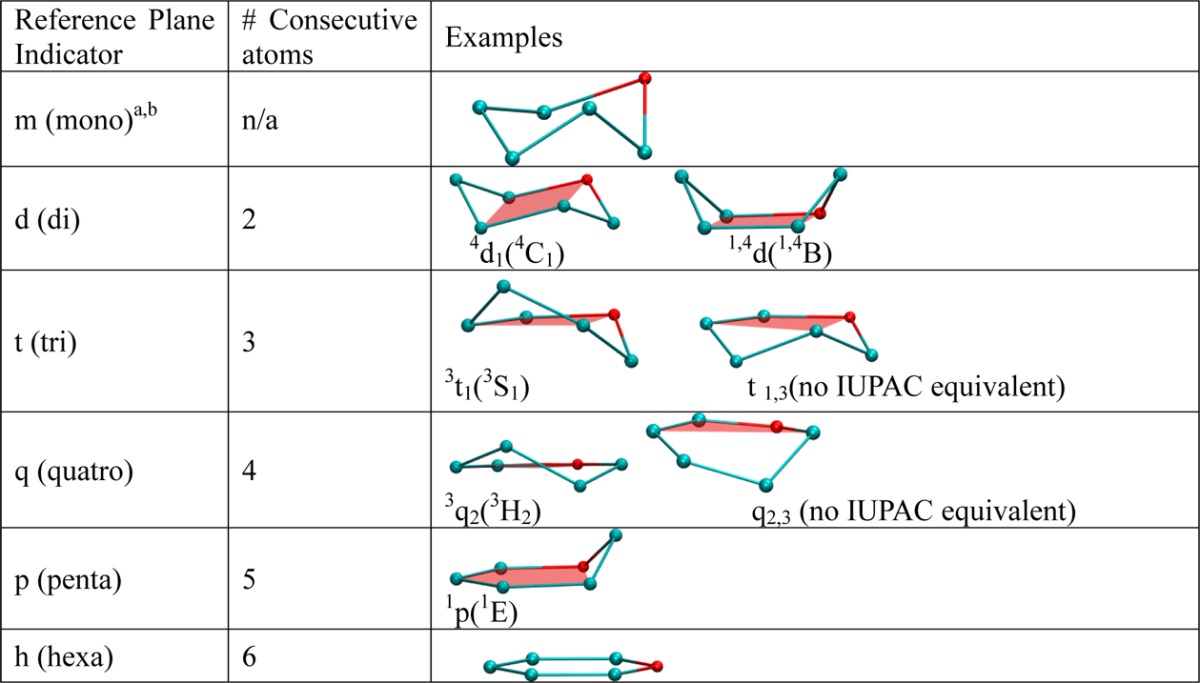
graphic file with name ci-2014-00325b_0010.jpg

Open in a new tab
a

Descriptor “m” describes highly distorted structures, for which no set of four atoms is well represented by a plane.

b

Lower case letters are used to avoid confusion with the existing IUPAC nomenclature.

An advantage of the BFMP nomenclature is that it can describe many more conformations than encompassed by the IUPAC descriptions. For example, the iduronic acid (IdoA) residue in the CTX A3–heparin hexasaccharide complex (PDB ID 1XT3)17 can be described as 1,Oq (4.2°) using a BFMP descriptor. The closest IUPAC conformation is 1HO and shares a reference plane (C2, C3, C4, and C5) with the 1,Oq descriptor. However, the 1HO description incorrectly defines the positions of the out-of-plane atoms (C1 and O5) (Figure 3).

Figure 3.

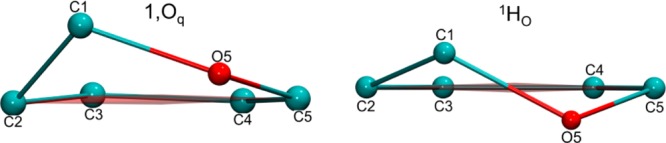
Figure 3

Open in a new tab

Ring conformation of IdoA in PDB ID 1XT3 (left) and nearest IUPAC structure (right).

Example Applications

Conformational Analysis of Iduronate Residues in the PDB

IdoA, predominately in its iduronate form, is a major component of glycosaminoglycans (GAGs), such as heparin and heparan sulfate. Unlike most monosaccharides, which exist primarily in a single ring conformation, IdoA adopts multiple ring conformations.5,18,19

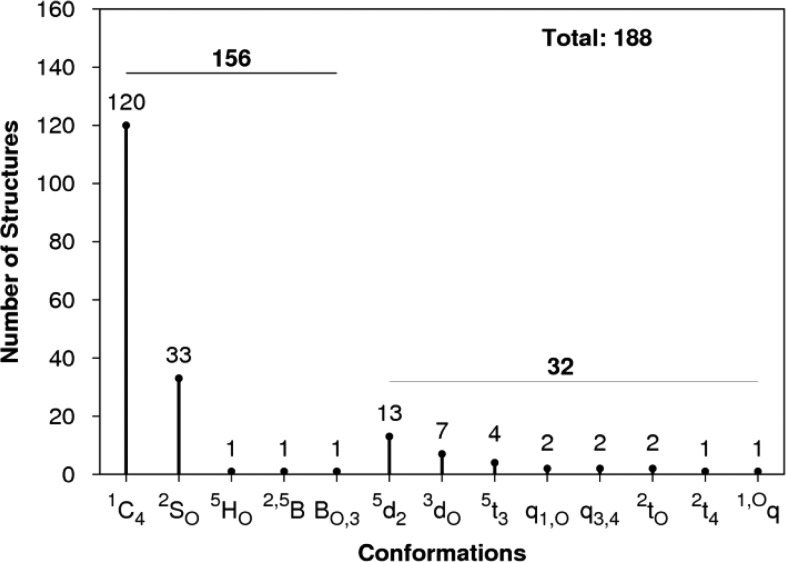
A survey of the PDB20 identified 188 IdoA residues, of which 83% could be assigned, using the cutoffs described in the SI, to standard IUPAC conformations (1C4, 2SO, 3S1). Thus, 17% of the conformations of IdoA appeared to be nonstandard (Figure 4).

Figure 4.

Figure 4

Open in a new tab

BFMP classification of 188 IdoA residues present in crystal complexes, of which 32 are in nonstandard conformations.

Of the 32 nonstandard conformations, using BFMP, 24 could be classified as 5d2, 3do (chair), or 5t3 (skew) conformers, which are distorted forms of the 1C4 and 2SO forms, respectively. For example, the IdoA ring in the crystal structure NK1–heparin complex21 has Cremer-Pople parameters of φ = 131.4, θ = 157.6, which when mapped onto a constant-Q sphere places the ring between a 1C4 chair and a 5HO half-chair. Only by visually examining an image of the shape is it possible to deduce that it is a chairlike conformation. In contrast, the BFMP classification directly identifies the structure as a 5d2 chair (Figure 5).

Figure 5.

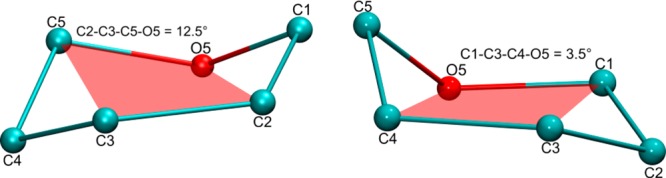
Figure 5

Open in a new tab

Ring conformation of IdoA in PDB ID 1GMO. The residue is in a conformation partway between 1C4 and 5HO (left). The BFMP method provides a less ambiguous classification as the 5d2 conformer (right) since atoms C1, C3, C4, and O5 best approximate a plane.

Application in Inhibitor Design

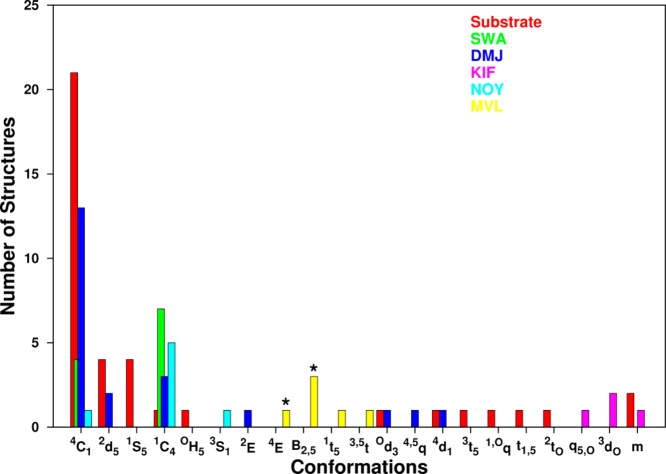
Aberrant cell-surface glycosylation is an indicator of malignant transformations and is often used to diagnose and monitor the stage of tumor progression.22−24 Alterations in glycosylation are caused by changes in enzyme activity; for example altered activity of glycosyltransferases and glycosidases in cancer cells leads to modified glycoprofiles.25 Human breast and colon cancers often overexpress N-acetylglucosaminyltransferase V (GlcNAcT-V), which leads to an increase in branched N-glycans,26 and inhibition of earlier stage α-mannosidase activity has shown clinical potential in treating malignancies.27,28 Inhibitors may be designed to mimic the ground-state or transition-state conformations of the substrate; in the crystal structure of a Golgi α-mannosidase II in complex with the inhibitor mannoimidazole,29 the six-membered ring of the inhibitor adopts a conformation similar to that of the presumed (B2,5) transition state30 (see Figure 6). Here we employed the BFMP method to classify the conformations of the terminal mannose ring in exomannosidases present in the PDB (22 complexes) and compared them to the conformations of known inhibitors swainsonine, deoxymannojirimycin, noeuromycine, kifunensine, and mannoimidazole extracted from enzyme cocomplexes (49 total complexes) (Table S3). The results showed that 51% of the substrates and 36% of the inhibitors adopted a 4C1 conformation. Of the remainder, 35% of the substrates and 22% of the inhibitors were present in asymmetrical conformations. Kifunensine in particular appeared to exist only in asymmetrical conformations. Very often, these asymmetrical shapes cannot be classified qualitatively and are described as distorted chair or skew-boat conformations. The BFMP method can be used not only to qualitatively describe these conformations but also to quantify the orientation of the atoms relative to the best-fit plane of the ring. This information may be helpful in identifying inhibitors that optimally mimic the orientation of atoms of the substrate in the enzyme substrate complex.30

Figure 6.

Figure 6

Open in a new tab

Comparison of ring conformations of mannopyranose substrates (red) extracted from cocrystal structures with mannosidases (n = 41), and the inhibitors (n = 50) swainsonine (SWA, green), deoxymannojirimycin (DMJ, blue), kifunensine (KIF, pink), noeuromycine (NOY, cyan), and mannoimidazole (MVL, yellow). Presumed transition states for mannosidases indicated by (*).

Using BFMP To Define Conformational Interconversions of Pyranose Rings

The pseudorotation pathways associated with the interconversion of ring forms can provide insight into enzyme mechanisms31−34 and chemical reactions.35 Molecular dynamics (MD) simulations can be particularly useful to study the dynamic properties of flexible molecules such as carbohydrates. Here we demonstrate the strengths of the BFMP method monitoring the conformational changes that occur during a 10 ns MD simulation (details in Section S2 of the SI) of α-l-idopyranose (Ido). The pyranose ring in Ido is known to interchange between at least three conformations in solution: 4C1, 1C4, and 2SO,36,37 and stable nonstandard conformations between the 2SO and 1S3 regions have been identified.10 Although 10 ns is far too short a time scale to observe conformational convergence,1 it is long enough to capture many of the conformational states of the Ido ring.

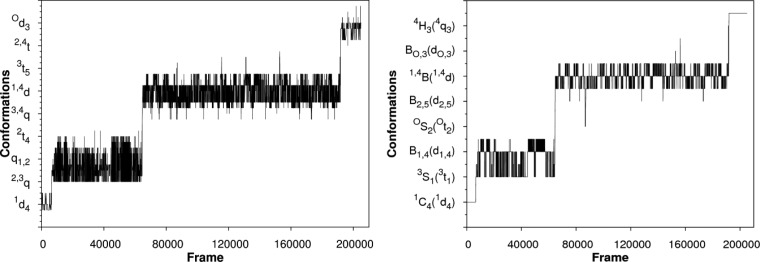
Analysis of the MD data showed that the ring converted from a 1C4 to a 4C1 conformation, populating over 50 intermediate conformations characterizable by BFMP. Only 15 of these conformers could be described using IUPAC nomenclature (Figure 7). The IUPAC conformers account for only 39% of the total number of conformations.

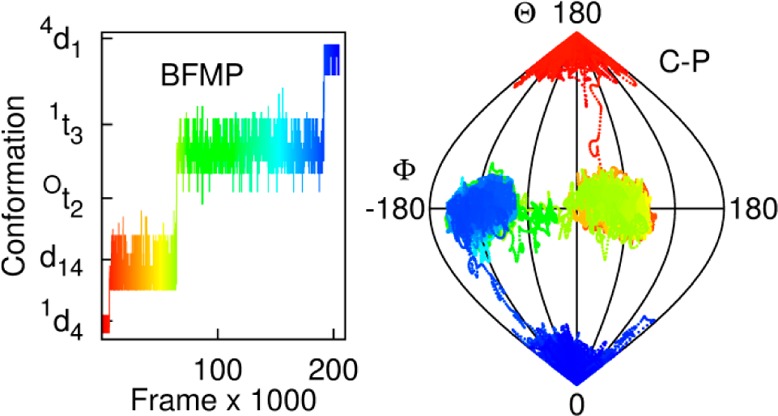
Figure 7.

Figure 7

Open in a new tab

Ring conformations, (left) identified by the BFMP method and (right) identified here as being well-described by IUPAC, over the course of a 10 ns MD simulation of Ido plotted as a function of simulation frame. For visual clarity, only subsets of the BFMP and IUPAC descriptors are noted on the y-axes. The complete list of BFMP conformations is provided in Table S4.

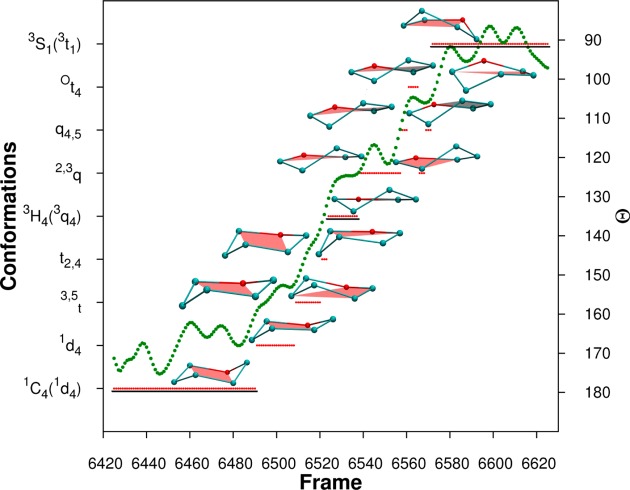
The BFMP descriptors provide a uniquely detailed insight into the interconversion pathway. In contrast, the use of IUPAC descriptors fails to capture the continuity of the changes in ring shape associated with this process (Figure 8) and implies a rapid flip from the 1C4 to 3H4 to 3S1 states, that is not supported by the MD data.

Figure 8.

Figure 8

Open in a new tab

Frames, corresponding to 200 fs, extracted from the MD simulation shown in Figure 7. The BFMP descriptors are shown by red lines. The lines are underlined for shapes that can be identified as standard IUPAC conformations 1C4, 3H4, and 3S1. Cremer-Pople θ values are plotted as green dots. Schematic representations of the BFMP-defined conformations, in order of occurrence, during the transition from 1C4 to 3H4 to 3S1 conformations are also shown. The structures shown to the left of the green dots are oriented with respect to the IUPAC reference planes, and the structures shown on the right are oriented to reference planes used by BFMP.

While CP parameters can be calculated for each of these states, it is difficult to deconvolute these into discrete states. The θ values for these states range from 90° to 180° (Figure 8). However, it is difficult to map each of these values to one of the standard IUPAC conformations. The intermediate values between 90°–105°, 120°–135°, and 165°–180° can be classified as skew-boat (3S1) half-chair (3H4), or chair (1C4), respectively (Figures S6 and S7). The remaining values cannot be mapped back to a standard IUPAC conformation and hence the conformations for these states cannot be identified without visualization of the shape. Even when there is an obvious IUPAC state as determined by BFMP, it will sometimes map to a different state using the typical IUPAC–CP mappings (Figures S7 and S8). This mapping issue arises because the two classification methods are not equivalent: the Cremer-Pople method quantifies rings based on an average six-membered reference plane, whereas the IUPAC descriptors are based on idealized four-membered planes.

An analysis of the MD data in terms of BFMP descriptors provides a straightforward, objective classification of more conformational states associated with the conformational interconversion of the Ido ring than possible within the IUPAC constraints.

Conclusions

IUPAC nomenclature and Cremer-Pople parameters are the most commonly used methods to describe and quantify the conformations adopted by pyran rings. We have shown that the IUPAC conformations cannot describe the nonstandard conformations adopted by these rings. Because of this, while Cremer-Pople parameters can be calculated for any given ring shape, mapping them to one of the IUPAC conformations can be cumbersome if not impossible. The BFMP conformations are described in terms of reference planes, making it trivial to translate to IUPAC nomenclature when relevant, but giving sufficient diversity to classify nonstandard conformations. In addition, the BFMP descriptors provide an objective method for identifying and comparing six-membered ring shapes, facilitating discussions of mechanistic details and transition state structures.

Acknowledgments

The authors would like to thank Dr. Matthew Tessier for useful discussions and for providing preliminary MD data.

Glossary

Abbreviations:

IUPAC

International Union of Pure and Applied Chemistry

MD

Molecular Dynamics

CP

Cremer-Pople

PDB

Protein Data Bank

Supporting Information Available

Execution protocol for this classification method. Additional tables and figures that aid in understanding the method are also listed here. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

S.M.: Designed and performed the applications; identified application targets; analyzed the data; wrote the source code for and codesigned the automation of the method; authored the paper and prepared figures. B.L.F.: Conceived, designed, and directed the project; authored the paper. R.J.W.: Specified application targets and methods for data presentation; authored the paper.

This work was supported by National Institutes of Health (GM094919 (EUREKA) and GM100058 (R01)) as well as the Science Foundation of Ireland (08/IN.1/B2070).

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

ci500325b_si_001.pdf (1.2MB, pdf)

References

  1. Sattelle B. M.; Bose-Basu B.; Tessier M.; Woods R. J.; Serianni A. S.; Almond A. Dependence of Pyranose Ring Puckering on Anomeric Configuration: Methyl Idopyranosides. J. Phys. Chem. B 2012, 116, 6380–6386. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Karaveg K.; Siriwardena A.; Tempel W.; Liu Z.-J.; Glushka J.; Wang B.-C.; Moremen K. W. Mechanism of Class 1 (Glycosylhydrolase Family 47) α-Mannosidases Involved in N-Glycan Processing and Endoplasmic Reticulum Quality Control. J. Biol. Chem. 2005, 280, 16197–16207. [DOI] [PubMed] [Google Scholar]
  3. Guerrini M.; Guglieri S.; Beccati D.; Torri G.; Viskov C.; Mourier P. Conformational transitions induced in heparin octasaccharides by binding with antithrombin III. Biochem. J. 2006, 399, 191–198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Hricovíni M.; Guerrini M.; Bisio A.; Torri G.; Petitou M.; Casu B. Conformation of heparin pentasaccharide bound to antithrombin III. Biochem. J. 2001, 359, 265–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Casu B.; Petitou M.; Provasoli M.; Sinaÿ P. Conformational flexibility: a new concept for explaining binding and biological properties of iduronic acid-containing glycosaminoglycans. Trends Biochem. Sci. 1988, 13, 221–225. [DOI] [PubMed] [Google Scholar]
  6. Venkataraman G.; Sasisekharan V.; Cooney C. L.; Langer R.; Sasisekharan R. A stereochemical approach to pyranose ring flexibility: its implications for the conformation of dermatan sulfate. Proc. Natl. Acad. Sci. U. S. A. 1994, 91, 6171–6175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Marszalek P. E.; Oberhauser A. F.; Pang Y.-P.; Fernandez J. M. Polysaccharide elasticity governed by chair-boat transitions of the glucopyranose ring. Nature 1998, 396, 661–664. [DOI] [PubMed] [Google Scholar]
  8. Schwarz J. C. P. Rules for conformation nomenclature for five- and six-membered rings in monosaccharides and their derivatives. J. Chem. Soc., Chem. Commun. 1973, 505–508. [Google Scholar]
  9. Stoddart J. F.Stereochemistry of carbohydrates; Wiley Interscience: New York, 1971. [Google Scholar]
  10. Ernst S.; Venkataraman G.; Sasisekharan V.; Langer R.; Cooney C. L.; Sasisekharan R. Pyranose Ring Flexibility. Mapping of Physical Data for Iduronate in Continuous Conformational Space. J. Am. Chem. Soc. 1998, 120, 2099–2107. [Google Scholar]
  11. Mulloy B.; Forster M. J. Conformation and dynamics of heparin and heparan sulfate. Glycobiology 2000, 10, 1147–1156. [DOI] [PubMed] [Google Scholar]
  12. Bérces A.; Whitfield D. M.; Nukada T. Quantitative description of six-membered ring conformations following the IUPAC conformational nomenclature. Tetrahedron 2001, 57, 477–491. [Google Scholar]
  13. Cremer D.; Pople J. A. General definition of ring puckering coordinates. J. Am. Chem. Soc. 1975, 97, 1354–1358. [Google Scholar]
  14. Jeffrey G. A.; Yates J. H. Stereographic representation of the Cremer-Pople ring-puckering parameters for pyranoid rings. Carbohydr. Res. 1979, 74, 319–322. [Google Scholar]
  15. Hill A. D.; Reilly P. J. Puckering Coordinates of Monocyclic Rings by Triangular Decomposition. J. Chem. Inf. Model. 2007, 47, 1031–1035. [DOI] [PubMed] [Google Scholar]
  16. Rao V. S. R.Conformation of Carbohydrates; CRC Press: 1998. [Google Scholar]
  17. Lee S.-C.; Guan H.-H.; Wang C.-H.; Huang W.-N.; Tjong S.-C.; Chen C.-J.; Wu W.-g. Structural Basis of Citrate-dependent and Heparan Sulfate-mediated Cell Surface Retention of Cobra Cardiotoxin A3. J. Biol. Chem. 2005, 280, 9567–9577. [DOI] [PubMed] [Google Scholar]
  18. Ochsenbein P.; Bonin M.; Schenk-Joß K.; El-Hajji M. The 2SO Skew-Boat Conformation in L-Iduronic Acid. Angew. Chem., Int. Ed. 2011, 50, 11637–11639. [DOI] [PubMed] [Google Scholar]
  19. Ferro D. R.; Provasoli A.; Ragazzi M.; Casu B.; Torri G.; Bossennec V.; Perly B.; Sinaÿ P.; Petitou M.; Choay J. Conformer populations of l-iduronic acid residues in glycosaminoglycan sequences. Carbohydr. Res. 1990, 195, 157–167. [DOI] [PubMed] [Google Scholar]
  20. Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lietha D.; Chirgadze D. Y.; Mulloy B.; Blundell T. L.; Gherardi E. Crystal structures of NK1–heparin complexes reveal the basis for NK1 activity and enable engineering of potent agonists of the MET receptor. EMBO J. 2001, 20, 5543–5555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Dennis J. W.; Granovsky M.; Warren C. E. Glycoprotein glycosylation and cancer progression. Biochim. Biophys. Acta, Gen. Subj. 1999, 1473, 21–34. [DOI] [PubMed] [Google Scholar]
  23. Fuster M. M.; Esko J. D. The sweet and sour of cancer: glycans as novel therapeutic targets. Nat. Rev. Cancer 2005, 5, 526–542. [DOI] [PubMed] [Google Scholar]
  24. Dube D. H.; Bertozzi C. R. Glycans in cancer and inflammation [mdash] potential for therapeutics and diagnostics. Nat. Rev. Drug Discovery 2005, 4, 477–488. [DOI] [PubMed] [Google Scholar]
  25. Drake P. M.; Cho W.; Li B.; Prakobphol A.; Johansen E.; Anderson N. L.; Regnier F. E.; Gibson B. W.; Fisher S. J. Sweetening the Pot: Adding Glycosylation to the Biomarker Discovery Equation. Clin. Chem. 2010, 56, 223–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Handerson T.; Camp R.; Harigopal M.; Rimm D.; Pawelek J. β1,6-Branched Oligosaccharides Are Increased in Lymph Node Metastases and Predict Poor Outcome in Breast Carcinoma. Clin. Cancer Res. 2005, 11, 2969–2973. [DOI] [PubMed] [Google Scholar]
  27. Goss P. E.; Baker M. A.; Carver J. P.; Dennis J. W. Inhibitors of carbohydrate processing: A new class of anticancer agents. Clin. Cancer Res. 1995, 1, 935–944. [PubMed] [Google Scholar]
  28. Goss P. E.; Reid C. L.; Bailey D.; Dennis J. W. Phase IB clinical trial of the oligosaccharide processing inhibitor swainsonine in patients with advanced malignancies. Clin. Cancer Res. 1997, 3, 1077–1086. [PubMed] [Google Scholar]
  29. Tailford L. E.; Offen W. A.; Smith N. L.; Dumon C.; Morland C.; Gratien J.; Heck M.-P.; Stick R. V.; Bleriot Y.; Vasella A.; Gilbert H. J.; Davies G. J. Structural and biochemical evidence for a boat-like transition state in [beta]-mannosidases. Nat. Chem. Biol. 2008, 4, 306–312. [DOI] [PubMed] [Google Scholar]
  30. Williams R. J.; Iglesias-Fernández J.; Stepper J.; Jackson A.; Thompson A. J.; Lowe E. C.; White J. M.; Gilbert H. J.; Rovira C.; Davies G. J.; Williams S. J. Combined Inhibitor Free-Energy Landscape and Structural Analysis Reports on the Mannosidase Conformational Coordinate. Angew. Chem., Int. Ed. 2014, 53, 1087–1091. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sinnott M. L. Catalytic mechanism of enzymic glycosyl transfer. Chem. Rev. 1990, 90, 1171–1202. [Google Scholar]
  32. Horenstein B. A.; Bruner M. The N-Acetyl Neuraminyl Oxecarbenium Ion Is an Intermediate in the Presence of Anionic Nucleophiles. J. Am. Chem. Soc. 1998, 120, 1357–1362. [Google Scholar]
  33. Nukada T.; Berces A.; Whitfield D. M. Acyl Transfer as a Problematic Side Reaction in Polymer-Supported Oligosaccharide Synthesis. J. Org. Chem. 1999, 64, 9030–9045. [Google Scholar]
  34. Nukada T.; Berces A.; Zgierski M. Z.; Whitfield D. M. Exploring the Mechanism of Neighboring Group Assisted Glycosylation Reactions. J. Am. Chem. Soc. 1998, 120, 13291–13295. [Google Scholar]
  35. Brameld K. A.; Goddard W. A. Substrate Distortion to a Boat Conformation at Subsite −1 Is Critical in the Mechanism of Family 18 Chitinases. J. Am. Chem. Soc. 1998, 120, 3571–3580. [Google Scholar]
  36. Snyder J. R.; Serianni A. S. D-Idose: a one- and two-dimensional NMR investigation of solution composition and conformation. J. Org. Chem. 1986, 51, 2694–2702. [Google Scholar]
  37. Kurihara Y.; Ueda K. An investigation of the pyranose ring interconversion path of α-l-idose calculated using density functional theory. Carbohydr. Res. 2006, 341, 2565–2574. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ci500325b_si_001.pdf (1.2MB, pdf)

Articles from Journal of Chemical Information and Modeling are provided here courtesy of American Chemical Society

RESOURCES