AWE-WQ: Fast-Forwarding Molecular Dynamics Using the Accelerated Weighted Ensemble

Abstract

A limitation of traditional molecular dynamics (MD) is that reaction rates are difficult to compute. This is due to the rarity of observing transitions between metastable states since high energy barriers trap the system in these states. Recently the weighted ensemble (WE) family of methods have emerged which can flexibly and efficiently sample conformational space without being trapped and allow calculation of unbiased rates. However, while WE can sample correctly and efficiently, a scalable implementation applicable to interesting biomolecular systems is not available. We provide here a GPLv2 implementation called AWE-WQ of a WE algorithm using the master/worker distributed computing WorkQueue (WQ) framework. AWE-WQ is scalable to thousands of nodes and supports dynamic allocation of computer resources, heterogeneous resource usage (such as central processing units (CPU) and graphical processing units (GPUs) concurrently), seamless heterogeneous cluster usage (i.e., campus grids and cloud providers), and support for arbitrary MD codes such as GROMACS, while ensuring that all statistics are unbiased. We applied AWE-WQ to a 34 residue protein which simulated 1.5 ms over 8 months with peak aggregate performance of 1000 ns/h. Comparison was done with a 200 μs simulation collected on a GPU over a similar timespan. The folding and unfolded rates were of comparable accuracy.

Introduction

Proteins are complex molecules of fundamental importance in biological processes. Numerical simulation using molecular dynamics (MD) has proven to be a powerful tool to predict many important properties such as the native state of the protein or its free energy.^1,2 In this paper, we will focus on methods, based on MD, to calculate reaction rates, which are defined as transition rate between metastable states or conformations of the protein. As a byproduct of our analysis, we will also calculate the main mechanisms of the reaction, i.e., the transition pathways. For example, a cartoon model of the free energy for a biomolecule is shown in Figure 1. It illustrates schematically how MD trajectories explore the conformational space. The left region represents the reactant states (R), and the right the product states (P). Trajectories spend most of their time in R or P with infrequent transitions due to the energy barrier that separates the two states.

Figure 1.

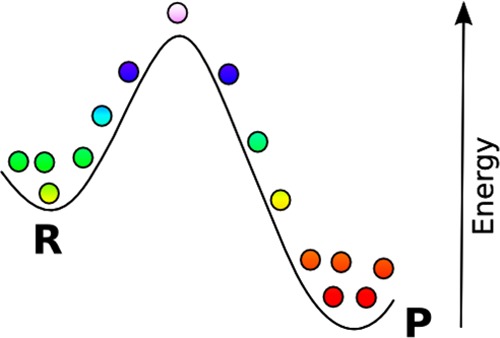
Molecular dynamics sampling of a one-dimensional free-energy surface between reactant (R) and product (P) states. By periodically recording the molecular conformation, energy, and other observables, various relevant properties of the protein can be computed.

In 1977 McCammon et al. applied MD to the bovine pancreatic trypsin inhibitor (BPTI).³ While the system was simple (vacuum with a crude force field), the simulation nonetheless contributed to shifting the view of proteins as rigid “brass models.” Since this initial simulation, MD has been used to study a wide variety of topics, such as identification of integral motions such as hinge bending modes,⁴ tRNA flexibility,⁵ and the study of E. coli chaperone GroEL.⁶ The application of MD to larger and more complicated molecules impacts development of force-field parameters such as the CHARMM^7,8 and AMBER families,⁹ and solvent models (generaly categorized as implicit¹⁰ or explicitly defined¹¹⁻¹³). Recently, MD has been used to study an HIV capsid¹⁴ and a complete satellite tobacco mosaic virus,¹⁵ as well as screening designed proteins.¹⁶

MD simulation of protein is a notoriously difficult computational task. In fact, a large portion of the major supercomputers’ time is currently dedicated to this type of simulation. The main difficulty is that the time scales of interest are typically in the millisecond (10^–3 s) while a typical time step in MD is on the order of the femtosecond (10^–15 s). Therefore, a brute force simulation would require on the order of 1000 billion time steps, which is impractical given the current hardware.

High-performance computing infrastructures allow development of efficient parallel algorithms to speed up simulations.¹⁷⁻¹⁹ Specialized hardware, such as MDGRAPE^20,21 and Anton,^22,23 provide orders-of-magnitude speedup over traditional high-power computing (HPC) simulations. Similarly, work with graphical processing units (GPUs) have shown the that GPUs achieved greater performance over a single cntral processing unit (CPU),²⁴⁻²⁷ allowing a single GPU to simulate biological systems with comparable performance to a cluster.^27,28

Most approaches to date attempted to accelerate a single (or a few) very long simulations. Due to the sequential nature of MD simulations, this is clearly a challenging task, which limited scalability. Force-calculations are a major bottleneck for MD. As such, much work has gone into the development of fast and efficient algorithms to dedicate large resources to long simulations of molecules. For instance, NAMD and AMBER were among the first to achieve scaling to hundreds of nodes and microsecond-time scales using parallel implementations.^29,30 Improvements to constraint algorithms,^31,32 particle interactions,³³⁻³⁵ and memory access patterns^17,36 have resulted in significant performance improvements over the decades.

At the other end, a recent class of methods is attempting to predict equilibrium properties, such as free energy, reaction rate and reaction pathways, from a large number of short trajectories. Since the trajectories are largely independent, this approach is naturally scalable. In fact, in this paper, we will demonstrate large-scale simulations using parallel computer grids, showing that scalability and performance can be achieved even on slow networks or when using geographically remote compute nodes.

This class of approaches have been applied with great success by several groups, using a method called the Markov state model (MSM).³⁷⁻⁴⁰ This method partitions the conformational space into cells or states. Then a stochastic transition matrix is computed. The entry (i ,j) in the matrix stores the probability of a trajectory to go from cell i to cell j after some lag time τ. From the eigenvalues, eigenvectors, and other properties of the matrix, we can extract all relevant time scales and kinetics of interest.

This type of approach requires running a large number of trajectories of length τ and as such is easily parallelizable. The accuracy of this method is independent of the presence of energy barriers or of the metastability of regions in conformational space. Instead it relies on efficient local sampling to predict time scales that can be orders of magnitude longer than the aggregate simulation time.

One limitation of MSM is that its accuracy depends on the choice of τ. In fact, getting converged rates is very difficult. At short lag times τ, a significant bias is present in the prediction, that is even in the presence of infinite sampling the predicted rate is incorrect. This can be addressed by increasing the lag time but this has two limitations. First, this leads to an increase in required simulation time. Second, this typically leads to a larger variance. In practice, it is difficult to obtain converged results with respect to the lag time and sampling size.

Once a MSM has been computed, one can obtain the implicit time scales from the diagonalization of the stochastic transition matrix. These implicit time scales are highly sensitive to the time lag, or the time between samples used to construct the transition matrix: at short time lags implicit time scales have a bias that makes them appear much faster than they really are. At large time lags the statistical error dominates, and it is hard to find a compromise that balances these two errors.

In this paper, we considered a variant method, called the weighted ensemble (WE) approach which has a higher computational cost but convergence is more robust and easier to monitor.⁴¹⁻⁴³ WE also avoids the systematic biases found in MSM.⁴⁴ The WE method was introduced by Huber and Kim⁴¹ to address the problem of capturing infrequent reaction events under Brownian dyanamics. Further studies have applied it to simulated annealing (SI) obtaining higher success rate (order of magnitude) for finding the global optimum as compared to traditional SI,⁴⁵ as well as in the investigation of super oxide dismutase and monoclonal antibody NC6.8. Zuckerman et al. have extended WE and describe several key properties:⁴⁶ (i) WE produces unbiased results for both Markovian and non-Markovian dynamics, indicating that the method is much more general than previously understood and (ii) the method depends on the number of cells, which may be updated dynamically, allowing the system to discover unknown cells without loss of accuracy in the calculation of reaction rates. Applications of WE to toy models and alanine dipeptid1e,⁴² coarse-grained models of adenylate cyclase,⁴³ and the sodium symport Mhp2 transporter protein⁴⁷ have yielded promising results.

In WE a large number of parallel walkers (MD trajectories) are used. Later, we will explain in more details the algorithm, but the basic process is to start a large number of trajectories from regions in a partitioning of the free-energy surface. After a small number of MD integration steps we consider the population of walkers in each cell. Then, using a statistically unbiased procedure, we are able to either remove walkers from overpopulated cells or, on the contrary, repopulate cells that are becoming depleted. This is done through an appropriate subselection (killing walkers) or duplication process. This ensures that when the simulation restarts the number of walkers in each cell is the same, and is equal to some target number. Then, we resume the simulation and integrate forward in time each walker using MD. This process is repeated until the quantities of interest, such as the reaction rates, which are computed through an appropriate postprocessing procedure, are converged.

This method avoids the slow time scales found in MD by ensuring that all cells are equally populated. This means for example that regions near the transition barrier between two metastable regions are sampled as often as minimum free energy basins. This method can be interpreted as a way of enhancing the sampling of conformational space. We note that its efficiency still depends on an appropriate choice of macro-states or cells, although the fact that these cells form a simple partition and can be constructed in a variety of ways (e.g., they can be simple Voronoi cells) gives a lot of flexibility to the method. Some of the advantages of WE is that it is easy to setup, is inherently massively parallel and scalable, and is unbiased. For example, unlike MSM, WE is guaranteed to converge to the exact result with enough samples.

Notwithstanding these properties, AWE, like MSM and other related methods, remains computationally expensive due to the large number of walkers that need to be run. This paper will present a software infrastructure we developed to facilitate running such calculations with accelerated convergence. This is achieved by an appropriate selection of the initial conditions as described in^43,44 hence the method is known as accelerated weighted ensemble (AWE), an extension of WE where the initial weights have been approximated to the steady state weights to accelerate the convergence. We compute them from a transition matrix obtained from the simulation, based on cells as they come from clustering, perhaps using MSMBuilder. AWE also uses a simpler and more accurate method for resampling and generating new walker populations through splitting and merging of walkers.⁴⁴

AWE allows one to eliminate the bias introduced in MSM by generating the statistically exact distribution of walkers inside each cell. MSM uses the equilibrium distribution for the walkers in each cell, which causes a bias. Instead, AWE uses an out-of-equilibrium distribution corresponding to walkers flowing from reactants to product states (e.g., folding/unfolding) and vice versa, thereby producing exact statistics.⁴⁴

We focused on the following main goals when designing the software:

• 1.Allow using any MD code in a black-box manner, without having to make intrusive changes inside the code. This is important since many MD codes are available and people are often required to use a particular MD code because of some special required capability. For instance, the following MD codes are usable with our framework: AMBER,⁴⁸ CHARMM,⁴⁹ GROMACS,^17,50 LAMMPS,⁵¹ NAMD,¹⁸ MDynaMix,⁵² Orac,^53,54 GROMOS,⁵⁵ Tinker,⁵⁶ Desmond,⁵⁷ DL_POLY.⁵⁸
• 2.Dynamically scale to available resources as they are added and removed as availability or funding allows and robustly handle resource failure. Details are discussed later, but the main idea is to support, for example, starting AWE using a dedicated cluster locally then adding cloud infrustructure such as Amazon EC2.
• 3.Use a scripting language for quick prototyping, interactive simulations, and user-friendly codes. We based our software on Python for this purpose. The use of this simple scripting interface also means that it is not difficult to reuse our framework for other methods that require running a large number of short trajectories with some appropriate postprocessing, e.g., MSM and other related methods.

In this paper, we present a distributed computing implementation of AWE, based on WorkQueue (WQ), that is capable of using computing resources with different architectural properties (e.g., GPU, CPU), as well as different job execution semantics such as dedicated (HPC grid) or cycle-scavenging (Condor) resources. At peak performance, for our validation, AWE-WQ simulated an aggregate 1.5 ms, with a peak performance of 1000 ns/h, showing that a large amount of resources can be efficiently managed by the system.

Similar software packages include the Copernicus framework developed by Pronk et al.,⁵⁹ Adaptive Markov State Models (adaptive MSMs) by Bowman et al.,⁶⁰ and the Weighted Ensemble Simulation Toolkit with Parallelization and Analysis (WESTPA) developed by Zwier et al.⁶¹ Copernicus is a framework for running ensemble molecular dynamics that allows multiple resources to be used, supports multiple project types, and adaptive sampling. Adaptive MSMs iteratively build MSM models to determine the contribution of each state to the slowest kinetic process. Based on this information further simulations are run from states based proportionally to their contribution to the uncertainty. WESTPA is a software framework for running WE simulations. Currently under development by Lillian Chong and Dan Zuckermann, WESTPA has been used to study several systems, such as molecular association⁶² and the sodium symporter Mhp1.⁴⁷

The fault-tolerance model, intelligent task scheduling, and caching distinguish AWE-WQ. These features allow the program to dynamically handle resource addition and removal, automatically handle worker failures, recover from machine failures, support clusters of heterogeneous computers, and minimize data transfer.

We first describe the algorithm, design challenges, and implementation in the Design and Implementation section and provide a brief overview of usage. Second, in the Results section, we demonstrate that AWE-WQ meets the criteria described in the Design and Implementation section as well as provide a validation of the implementation on a nontrivial protein. Finally, we provide public access to the software and the data sets used for the results as well as describe the current limitations and future directions in Availability and Future Directions section.

Design and Implementation

Accelerated Weighted Ensemble Algorithm

The WE approach proceeds as follows and illustrated in Figure 2.

• 1.Partition state-space into C cells.
• 2.Determine W number of simulations (walkers) to maintain in each cell.
• 3.Parallel step (walk): run the N = W × C short simulations, assign each of the N final conformations to a cell.
• 4.Synchronization barrier (resample): once all the N simulations are assigned, merge and split the walkers to maintain W walkers in each cell and update the associated weights.
• 5.Go to step 3 unless weights converged.

Figure 2.

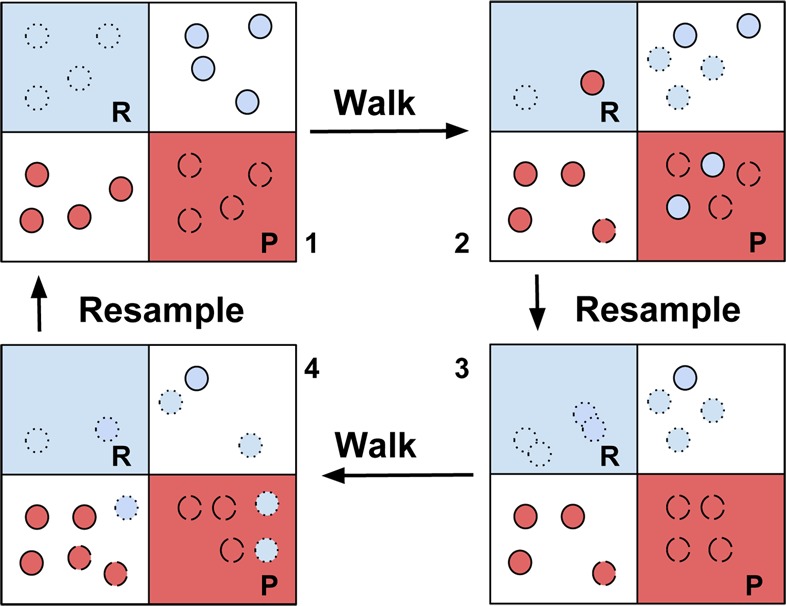
Illustration of WE algorithm. Each region represents a cell on the energy surface, the circles the walking simulations, the colors the association with the reactant (R) or product (P) regions.

The splitting and merging technique¹⁷ used in AWE generally works as follows. Given a population of walkers with weights w_i, we first calculate a mean weight W_m = Σ_i(w_i/ntarget_walkers), where ntarget_walkers is the desired number of walkers that we are trying to achieve. Then, if a walker has a weight greater than W_m, it is split into an integer number of walkers of weight W_m, with a remainder that is reinserted into the list of walkers to process. Walkers that have a weight less than W_m are merged in a statistically exact way to create walkers with a weight greater or equal to W_m. By repeating this process of splitting and merging walkers, we are able to generate a population of walkers with weights exactly equal to W_m, in a statistically exact manner. This is different from the procedure in the work of Huber and Kim⁴¹ that generates walkers with weights between W_m/2 and 2W_m but not exactly equal to the target weight W_m.

The choice of method for defining cells is orthogonal to WE. As long as a cell definition exists, in cells.dat currently, AWE-WQ is able to use it. This allows one to define cells arbitrarily to examine the effect of a cell definition method. We based the cells on the MSM construction in order to accelerate the convergence of cell weights. As explained previously, the main reason to use WE is to remove the bias present in MSM models due to the lag time and the (incorrect) distribution of walkers inside each cell.

Upon reaching steady-state the weight of each cell converges to its probability, allowing this procedure to calculate free energy. The resampling procedure allows even low-probability cells to be accurately sampled.

Calculation of transition rates requires a further modification: Define two sets of states, R and P, associated with the reactant and product regions (Figure 2). Each walker is assigned a color, such as blue for R and red for P, corresponding to the previously visited region. At each step in the simulation whenever a blue walker enters P, its color changes to red, and vice versa. The rate from R to P is then directly obtained by computing the flux of blue particles that change color, and similarly for the P to R rate. If extended to multiple colors and sets multiple kinetic rates can be determined. In practical terms, the R and P regions may correspond to the unfolded and folding regions and the fluxes to the folding and unfolding rates. By providing an initial approximation of the free energy the convergence to steady state can be accelerated.

From an implementation standpoint, the method requires the following three steps (as illustrated in Figure 3): (1) Most of the work is done in parallel as a large number of independent short MD trajectories. (2) The parallel barrier: wait for all MD steps to complete then collect walker assignments and final positions, split and merge walkers, and update weights. (3) Go to step 1 if needed.

Figure 3.

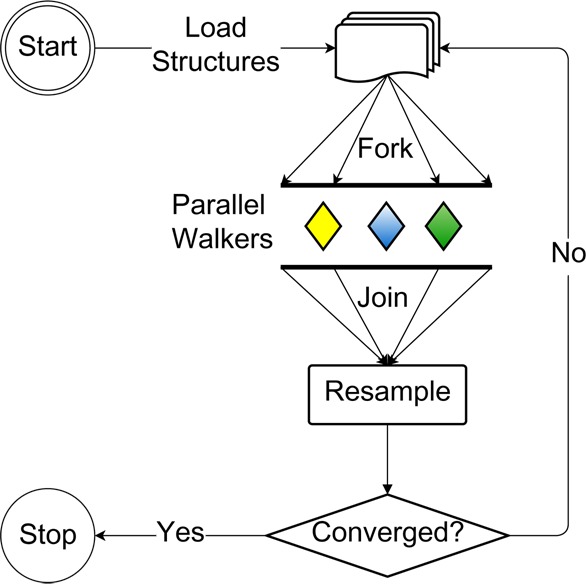
AWE-WQ flowchart of the major steps. On startup molecule conformations are loaded into the walker datastructures. Each walker is then, in parallel, executed and assigned to a cell. The join waits for all walkers to finish, before the resample procedure is applied. If the system has converged then the program halts, others walkers are rerun.

Usage

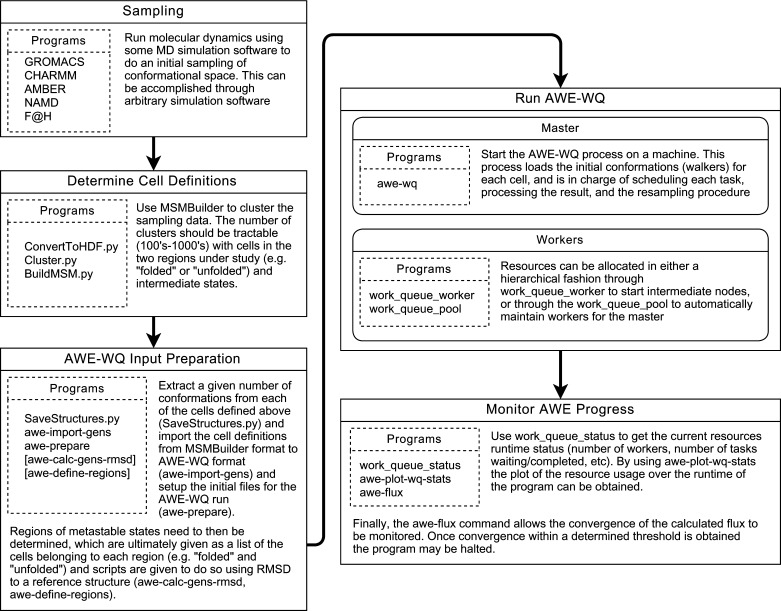
In order to use AWE-WQ one must define the cells from which to run the walkers. The general protocol, illustrated in Figure 4, is as follows: (1) sample the search space, (2) determine cell definitions, (3) prepare input files, (4) run AWE-WQ, (5) monitor progress.

Figure 4.

Diagram of the workflow to run AWE-WQ with associated programs and descriptions. First a sampling must be run with some MD software such as GROMACS, CHARMM, AMBER, etc. Next, define the cells using some clustering procedure. In this case, the MSMBuilder package provides some infrastructure. Prepare the input to AWE-WQ by converting the files and defining metastable states. Run AWE-WQ by starting the master process and allocating workers with various resources. Finally, continuously monitor the status and progress of AWE-WQ.

Sampling

First some sampling must be done to explore state space. This can be accomplished with programs such as GROMACS, CHARMM, AMBER, NAMD, or using infrastructure such as Folding@home. For this instance, sampling of alanine dipeptide has been run previously, which can be extracted:

Determine Cell Definitions

To start, we have collected MD data and stored them in the XTC directory. The directory structure is XTC/RUN#/frame0.xtc, where # is the trajectory number. The sampling data is imported into MSMBuilder using the ConvertDataToHDF.py command, paramterized with a PDB file containing the system coordinates and the path to the MD data:

The next step defines the cells. Conformations are clustered with a hybrid k-centers/k-medoids algorithm using the RMSD between atoms as the distance metric. The AtomIndices.dat defines the atoms to consider when computing the distance between conformations. Using a subset (such as all non-hydrogens) prevents too fine a granularity from overfitting the data. Finally, we will cluster the data into 100 groups.

By inspecting the implied time scales (not shown) we build a Markov state model at lagtime 10.

AWE-WQ Input Preparation

Extract a given number of conformations from each of the cells defined above (SaveStructures.py) and import the cell definitions from MSMBuilder format to AWE-WQ format (awe-import-gens) and setup the initial files for the AWE-WQ run (awe-prepare). Regions of metastable states need to then be determined, which are ultimately given as a list of the cells belonging to each region (e.g., “folded” and “unfolded”) and scripts are given to do so using RMSD to a reference structure (awe-calc-gens-rmsd, awe-define-regions). We plan to maintain 10 simulations in the cells, so we need to extract conformations from the states using MSMBuilder.

In order to run AWE-WQ we must then import the cell definitions which were written by MSMBuilder to Gens.lh5.

In order to compute the fluxes we need specify regions of metastable states. AWE-WQ provides some commands to assist with this process: awe-calc-gens-rmsd and awe-define-regions. We use awe-calc-gens-rmsd to compute the RMSD of each cell to some reference conformation such as the native state.

By plotting the distribution of values we can classify conformations with RMSD ≤ 2.3 Å as folded and those with RMSD ≥ 2.5 Å as unfolded. The two output files folded.dat and unfolded.dat now contain the integer indices of the states belonging to these regions.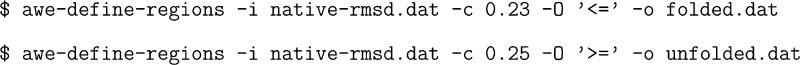

We can now prepare for AWE-WQ by checking dependencies and populating the directory with other necessary files by running awe-prepare.

Running AWE-WQ

There are two components to consider when running AWE-WQ: the master process and the resources. The master is the driver of the algorithm, managing task definitions, scheduling, processing, and the resampling procedure. In order to run the walkers, resources must be allocated.

Master

Start the AWE-WQ process on a machine. This process loads the initial conformations (walkers) for each cell, and is in charge of scheduling each task, processing the result, and the resampling procedure. This runs AWE-WQ maintaining 10 walkers in 100 cells, whose definition is provided in cells.dat with initial weights in Data/Populations.dat. The coordinates for the walkers are found in the Walkers directory. The metastable regions are provided in folded.dat and unfolded.dat as a list of cell id numbers belonging to each region. Finally, we give a name to the master (“awe-wq”) to that workers can easily locate the host and port.

Workers

Resources can be allocated either directly using work_queue_worker or managed automatically using work_queue_pool. Using work_queue_worker also allows the worker to operate as a “Foreman”, enabling the hierarchical distribution of tasks. The work_queue_pool program maintains workers for the master based on need and is in charge of submission to various backends such as the local machine, Condor, SGE, PBS, etc. Since the master has started we can start some workers locally.

Monitoring AWE Progress

Use work_queue_status to get the current resources runtime status (number of workers, number of tasks waiting/completed, etc.). By using awe-plot-wq-stats the plot of the resource usage over the runtime of the program can be obtained.

Additionally, the current status of the master, such as workers busy and tasks complete can be viewed using the work_queue_status command.

The awe-flux command allows the convergence of the calculated flux to be monitored. Once convergence within a determined threshold is obtained the program may be halted.

Additionally, other analyses are appropriate. For instance, the energy surface for alanine dipeptide can be visualized as a function of its dihedral angles. As such, we can plot, as shown in Figure 5, the cell coordinates and the initial estimation of the weights as well as computed weights after several iterations of AWE-WQ.

Figure 5.

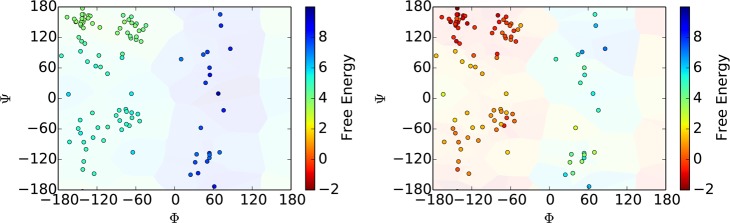
Cell weights before and after running AWE-WQ.

Design and Implementation

Since the AWE method follows a pattern of fan-out followed by fan-in we implement using a master/worker paradigm. AWE-WQ is designed to (1) support off-the-shelf MD backend software, (2) dynamically scale according to resource availability, (3) support heterogeneous runtime environments, and (4) be robust in the face of system failure. Application of AWE to a nontrivial biological system may have on the order of 10 000 simulations per iteration. On one CPU, if each walker requires 30 min to simulate, 7 months would be required to run a single iteration of AWE. Since walkers are short, assuming 30 min per walker, 7 months would be required to run 10 000 walkers for each AWE iteration using a single processor. With 1000 CPUs, the expected time drops to 5 h, assuming uniform performance. Additionally, the synchronization barrier allows straggling workers to slow down the entire application. Since we expect to need hundreds of iterations to converge, the challenge is to implement AWE such that it scales to 1000+ processors and can be sustained for months with no major slowdown due to stragglers.

Support of à la Carte MD Software

Rather than reimplement the core MD algorithms which are present in multiple software packages (i.e., GROMACS, AMBER, CHARMM, etc.) we decided to provide flexibility of MD backend. This flexibility presented several challenges by imposing a requirement of specifying the steps needed to run the backend, the transfer of files, the execution environment, and the interaction with the other steps of the procedure. The approach taken in the following: a walker is described as a task which consists of a program to run and the input and output files. Once specified, this task is scheduled to run on an available worker, which is a process that accepts any input files, executes the task’s command, and returns the results upon request.

We used GROMACS 4.5 for the MD backend. The awe-prepare script sets up files and scripts in the local directory necessary to run awe-wq. One of these scripts, execute-task.sh, executes the commands on the worker. In order to use a different MD backend execute-task.sh needs to define how to run the MD, and awe-wq needs to specify the files to send to the worker.

Dynamically Using Available Resources

Our solution to the worker fault-tolerance problem implies the elasticity—the ability to dynamically scale to available resources—of the program. If a task fails during execution, it is rescheduled to run on the next available worker. As resources are added or removed, tasks are started or reschedule, respectively. This allows a project to be started with the campus cluster, then EC2 machines run until budget exhaustion, then continued with only the cluster. Managing the resource pools are the interactions between the master, the Catalog Server (CS), and WorkQueue Pool (WQP) processes. The CS allows workers to dynamically determine the location of the master by mapping a project name (e.g., awe-wq) to a hostname and port (e.g., fah.crc.nd.edu:1024). The master registers this information when started, which allows it to be restarted in the event of machine failure without requiring the resources to be reallocated. In addition, the CS store information about the current resource requirements of a master, such as the number of tasks waiting to be scheduled. A WQP can thus use this information to automatically start workers based on the runtime needs. This is further enabled by the asynchronous model, which treats tasks as independent, arbitrarily executable entities. This would not have been possible using an MPI-based implementation.

Heterogeneous Runtime Environments

Additionally, AWE-WQ can use heterogeneous resources, allowing systems with different properties and (potentially) operational semantics to be used. For instance, this supports using GPU-based as well as CPU-based MD backend codes. This is accomplished by extending the task abstraction to dynamically resolve file location upon worker connection rather than statically. For example, an input file can be specified for a task as binaries/$OS/$ARCH/mdrun. When a worker connects to the master it reports the operating system and architecture of the remote node in the $OS and $ARCH variables, which may then be expanded to send binaries/Linux/i686/mdrun and binaries/Darwin/x86_64/mdrun to to workers running on a 32-bit Linux and 64-bit Mac OS machine, respectively. Finally, these variables can be overridden by the user to provide additional granularity.

Fault-tolerance

AWE-WQ is implemented with the assumption that machine failures are not only possible but in fact common, which is the opposite of the paradigm underlying MPI infrastructures. As such two broad categories of failures need to be accounted for: failure of the worker or master processes. In the first case, worker failure are handled transparently and tasks rescheduled to the next available worker.

Failure of the master node would normally result in the termination with an inability to resume. This is overcome by using a transactional logging mechanism: a combination of persistent and volatile logs. Each result from a walker is added to a log and after each AWE iteration the state of the system is checkpointed to disk and the log cleared. If the process fails, then the state is initialized from the checkpoint and the log used to replay and missed results from that iteration. This way only uncompleted walkers need to be restarted.

Intelligent Scheduling

Several components of task scheduling affect the scalability. The first is knowledge of a worker’s past task execution times. This allows tasks to be scheduled preferentially to the most performant machines. The second involves task replication to remove the effect of straggling workers. By monitoring the state of the workers—either busy or idle (w_i)—and the number of tasks waiting to be assigned a worker, task replication can be engaged when w_i > 0. Once a task returns, all its replicates are canceled, results are accepted in a first-come-first-serve fashion. By combining replication with preferential scheduling, workers are continuously used and slow workers allowed to contribute results until the fast machines are available, which then run the replicated tasks.

Event Model

The inner loop of AWE-WQ is an event-loop with asynchronous task execution. Each iteration begins by translating the internal data model of the walkers into task, which are submitted to the WQ scheduler. While tasks are executing, the program is idle until a result is returned. Each result creates an event that must be handled, either by translation or resubmission. Handlers are lightweight: read the final coordinates and cell assignment into the data models. Since task executions are asynchronous and results are processed serially, the event model enforces load balancing by spreading out the calls to the event handlers.

Caching Allows Scaling

Increasing scalability is further accomplished by minimizing the communication overhead and maximizing the parallel work. Ideally, the master process will spend most of its time waiting. By categorizing files as those common to all tasks (common) or specific to the current one (unique), the common files can be cached on the workers. Since we expect the number of walkers to be larger than resource availability the caching mechanism shifts overhead to depend on resources rather than problem size. For instance, using a GROMACS backend each task requires 34 MB in input files, binaries, and miscellaneous files.

In the case of the WW domain simulation, each task required 34 MB of GROMACS-related files as overhead and 100 KB of task specific data. Assuming 10 000 tasks/iteration and 500 iterations, the total amount of data transferred is 34 (MB/task) × 10 000 (tasks/iteration) × 500 iterations × 2^–20 (TB/MB) = 162 TB. By caching input files, data transferred depends only on the number of new workers seen, rather than total number of tasks, which may be orders of magnitude greater. In this case, assuming 1000 workers are connected the total data transferred becomes 34 MB × 1000 × 2^–10 (GB/MB) = 33 GB.

Results

We have run AWE-WQ for several months where 3.5 million tasks have executed over 600 compute years in a heterogeneous environment simulating over 1.5 ms of time. In this section we describe the application the AWE algorithm to a nontrivial biological system.

Heterogeneous Resource Usage

Available resources consisted of the following: Notre Dame HPC grid with 6000 cores shared among campus users; Notre Dame Condor pool with variable (usually around 1200) cores and flocking capabilities with Purdue University and the University of Wisconsin–Madison; Stanford University’s Institute for Computational and Mathematical Engineering (ICME) cluster with 200 CPUs and 100 NVIDIA GPUs, and cloud virtual machines via Amazon EC2 and Microsoft Azure.

Figure 6 displays the distribution of task execution times. The multimodal distribution reflects the differences of performance within each pool. The GPU cluster executes tasks within minutes, while the ND HPC grid and EC2 machines are the best performant CPU-based pools. The range of performance of Condor machines is unsurprising and illustrative of the cycle-scavenging nature of the platform. The Azure machines were the least performant resources, partly due to the necessity of running the tasks via Cygwin.

Figure 6.

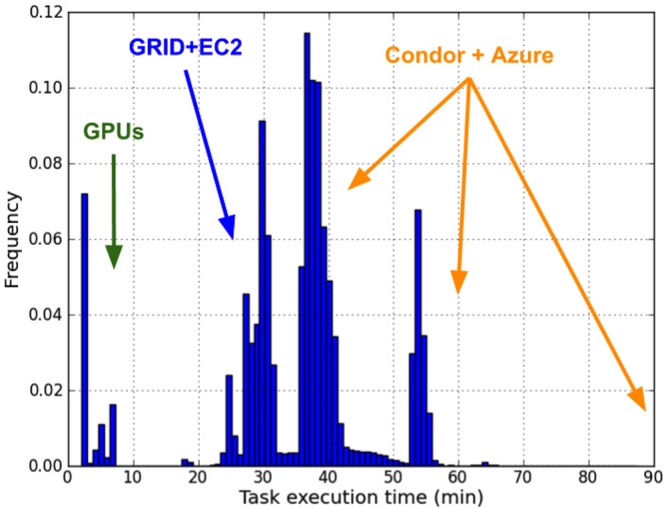
Distribution of task execution times indicate several peaks associated with the different underlying resources being used.

Elasticity and Scalability

Figure 7 demonstrates the fault-tolerance elasticity and scalability of the application as an expanded view of the number of busy resources over the runtime—the inset shows the entire run. Unexpected failures of the master (months 4, 6) initiated development and integration of features, bug fixes, and monitoring capabilities. Due to power outages and infrastructure upgrades the master process restarted multiple times. In spite of these failures over 250 iterations were completed without data loss due to the transactional logging mechanism. The periodically persisting state additionally allowed us to integrate new features, such as task replication, and bug fixes over the course of the project’s execution.

Figure 7.

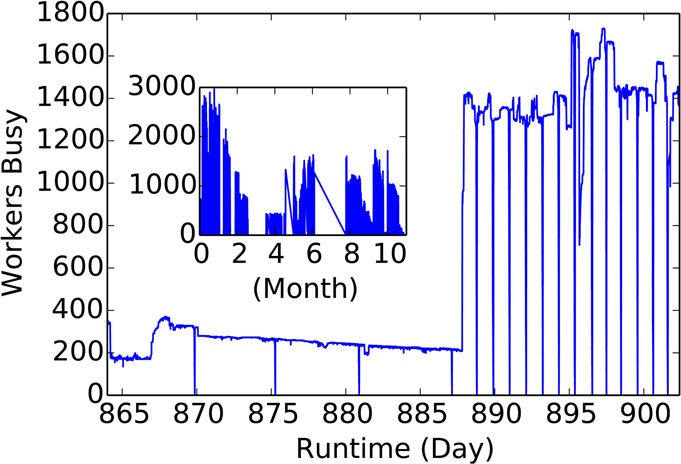
Expanded view of the entire run (inset) demonstrating elasticity, scalability, and fault-tolerance. In the inset, long gaps (such as the sudden failures at month 4 and 6) in activity indicate times when major development was done on the code (features added, bugs fixed). Despite the troubles experienced by the master node, calcuation of the results resumed once the code was deployed. Plotting the number of busy workers over many days shows the ability of the software to adapt to a changing environment. The periodic dips indicate the global synchronization barrier, each requiring 12 000 tasks to complete. A large increase after day 885 occurred when many nodes were suddenly available and were automatically incorporated.

Focusing on the region between days 865 and 900 shows a steady decrease in the number of busy resources until a new pool of workers became available and AWE-WQ automatically started using them. It must be emphasized as well that minimal human input was needed to take advantage of the additional resources: due to the use of the Catalog Server all that was required was to start a WQ Pool process for the additional resources.

The periodic dips, every 5 days in the first half and every ≈20 h for the second, correspond to the global synchronization barrier, each period requiring 12 000 tasks to complete. By scheduling the tasks based on resource availability and progression through the AWE algorithm, resources are fully utilized and the long tail effect from straggling workers is eliminated. Due to the use of the caching mechanism communication overhead is reduced: while the entire task payload (common and unique files) is 34 MB it is only for the first task a worker executes that his is transferred. Each subsequent task only requires 100 KB of data to be transferred (both in- and outbound traffic).

WW Domain Protein

The WW Domain is a 34 residue protein domain with two conserved tryptophan (W) residues and comprised of two antiparallel β-sheets as shown in Figure 8. We studied a mutant which is known to fold in 13 μs.⁶³ Simulation parameters were the Amber96 force field with generalized Born implicit solvent, a viscosity parameter (γ) of 1 ps^–1, temperature of 395 K (close to the optimal folding temperature⁶⁴), saving conformations every 1 ns. The simulation was run for 200 μs during which multiple folding and unfolding events were observed. The conformations sampled by the simulation were then clustered using the α and β carbons using a cutoff of 3 Å. In order to reduce the time spent sampling the unfolded space we established that conformations with an RMSD to the folded structure less than 3 and 6 Å, and greater as folded, intermediate, and unfolded, respectively. Using these definitions the number of unfolded states was reduced, for a total of 601 cells. The AWE-WQ parameters were thus 601 cells, 20 walkers per cell, and walker length of 500 ps using the same MD parameters as the source data. GROMACS 4.5 was used for the MD backend.

Figure 8.

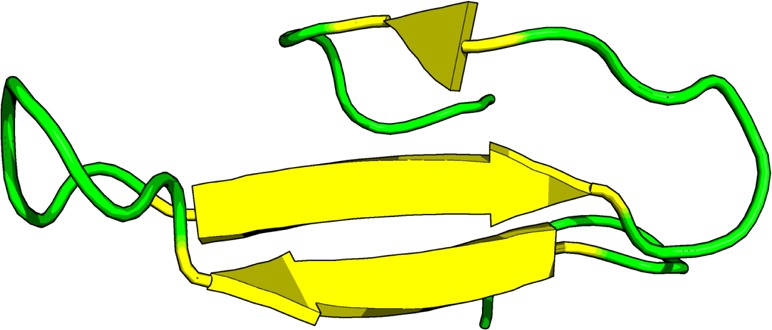
WW domain forming three antiparallel β-sheets separated by two flexible loop regions.

WW Results

Over the course of many months AWE-WQ completed 345 iterations, with an aggregate 2.3 ms of time simulated using 3.6 million tasks, and a peak performance of 1000 ns/h. Analysis indicates that the AWE-WQ results converge within acceptable error tolerance. Table 1 displays the forward and backward rate estimations computed using AWE-WQ and the 200 μs simulation. The AWE estimation lies within the confidence interval—with smaller statistical error—than the brute force simulation.

Table 1. Forward and Backward Reaction Rates As Computed from AWE-WQ and the Brute-Force Simulation.

method	forward (μs–1)	backward (μs–1)
AWE-WQ	1.5 ± 0.3	2.5 ± 0.5
brute-force	1.8 ± 1.0	2.0 ± 0.9

Figure 9 illustrates that forward and backward fluxes took 30 iterations to converge to the confidence interval built from brute force simulation and are stabilized within the interval afterward. The resampling procedure of AWE introduces no bias in the estimation of transition rates while exhibiting smaller statistical error, showing an improvement over the brute force method.

Figure 9.

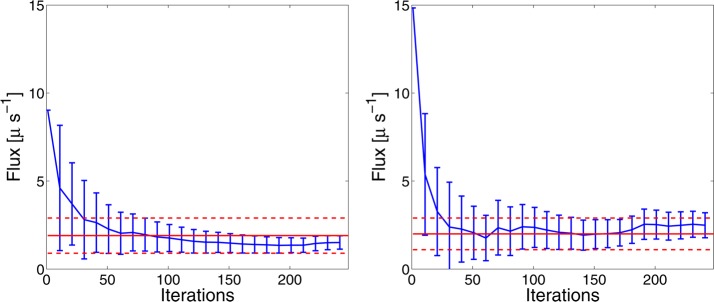
Average forward (top) and backward (bottom) flux from AWE (blue curve) with error bar of one standard deviation estimated by the block averaging method, compared with confidence interval built from the brute-force simulation. The red solid line represents the mean flux from the brute-force simulation, and the dashed lines are mean flux plus/minus one standard deviation.

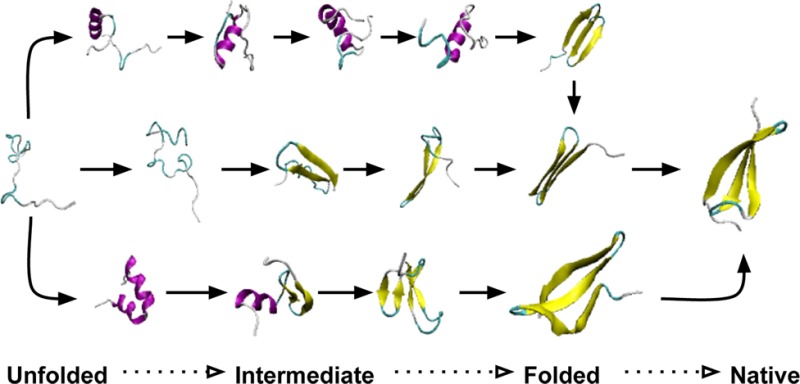
Transitions among the states are examined with a time lag of τ = Δt = 0.5 ns. Three significant pathways from extended to folded state are extracted from the network and shown in Figure 10. Starting from an unfolded conformation, two pathways involve multiple helical intermediate structures before β-sheet formation occurs via rearrangement. The third pathway occurs as a rapid collapse before the formation of Loop 2. Loop 1 is then able to form, after which the molecule undergoes further refinement to arrive at the native state.

Figure 10.

First three significant pathways from extended to folded conformations. Two pathways (top, middle) involve helix formation as an intermediary while the third pathway (bottom) consists of a collapse then refinement.

Conclusions

AWE-WQ meets our criteria: allowing the use of off-the-shelf components for MD backends, pooling of heterogeneous resources, scalability to over 1000 workers, and ability to cope with failures of both worker and master processes. The WW domain was used to validate AWE-WQ by applying the method to a long MD simulation in which multiple folding events are observed. The forward and backward reaction rates computed by AWE-WQ are within the range and have smaller error, of the rates calculated from the reference simulation.

Availability and Future Directions

Availability

AWE-WQ is available under the GPLv2 license. Documentation and data sets are available online.⁶⁵ The source repository for AWE-WQ can be found online on Github.⁶⁶ Build dependencies for AWE-WQ include a Python interpreter, the GROMACS xtc library,⁶⁷ and the GNU Scientific Library.⁶⁸

Future Directions

We are working on improvements to the AWE and WorkQueue components of AWE-WQ.

The current version requires initial sampling for cell definition. These cell are static for the AWE-WQ run. Thus, AWE-WQ is limited by the sampling techniques applied and is unable to discover new regions of state-space. Furthermore, a uniform partitioning scheme is used, which potentially leads to overrepresentation of uninteresting regions (such as unfolded protein). Reducing the number states for computational efficiency risks reduction in granularity in the regions that benefit the most (e.g., transition regions) and reduces accuracy. Goals for future versions of AWE-WQ are planned to allow for cell discovery and improved cell partitioning methods.

With regards to infrastructure, the next challenges to overcome are the continuous usage of 5000 and 10 000 workers. Recent development to the WorkQueue infrustructure have demonstrated that using a hierarchical topology can reduce communication overhead on the master by 96%.⁶⁹ Additionally, support for other MD backend software, as well as explicit solvent models, is under development.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States