Intrinsic disorder as a generalizable strategy for the rational design of highly responsive, allosterically cooperative receptors

Significance

Control over the sensitivity with which biomolecular receptors respond to small changes in the concentration of their target ligand is crucial to many cellular processes and likely could be of value in many biotechnologies. In nature, this control is often achieved using “Hill-type” allosteric cooperativity, an elegant mechanism that has, unfortunately, hitherto proven difficult to achieve via generalizable design strategies. In response, we demonstrate here a quantitative and apparently versatile means of rationally introducing this useful mechanism into a range of normally noncooperative receptors. We achieve in the best of our examples cooperativity, and thus sensitivity, experimentally indistinguishable from the theoretically expected maximum.

Abstract

Control over the sensitivity with which biomolecular receptors respond to small changes in the concentration of their target ligand is critical for the proper function of many cellular processes. Such control could likewise be of utility in artificial biotechnologies, such as biosensors, genetic logic gates, and “smart” materials, in which highly responsive behavior is of value. In nature, the control of molecular responsiveness is often achieved using “Hill-type” cooperativity, a mechanism in which sequential binding events on a multivalent receptor are coupled such that the first enhances the affinity of the next, producing a steep, higher-order dependence on target concentration. Here, we use an intrinsic-disorder–based mechanism that can be implemented without requiring detailed structural knowledge to rationally introduce this potentially useful property into several normally noncooperative biomolecules. To do so, we fabricate a tandem repeat of the receptor that is destabilized (unfolded) via the introduction of a long, unstructured loop. The first binding event requires the energetically unfavorable closing of this loop, reducing its affinity relative to that of the second binding event, which, in contrast occurs at a preformed site. Using this approach, we have rationally introduced cooperativity into three unrelated DNA aptamers, achieving in the best of these a Hill coefficient experimentally indistinguishable from the theoretically expected maximum. The extent of cooperativity and thus the steepness of the binding transition are, moreover, well modeled as simple functions of the energetic cost of binding-induced folding, speaking to the quantitative nature of this design strategy.

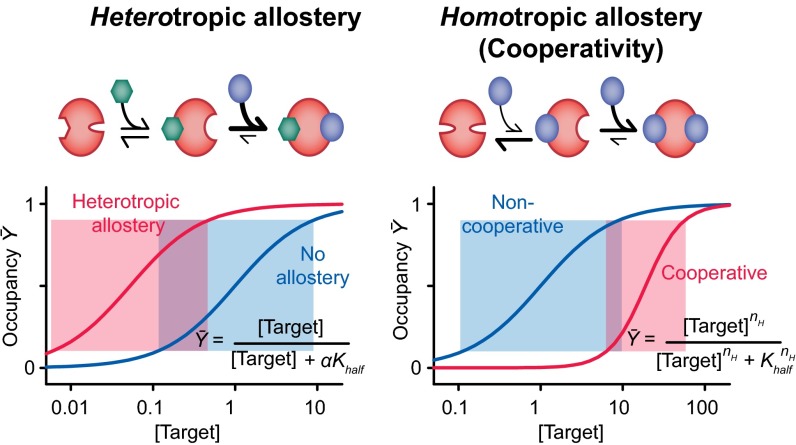
The ability to control the shape and midpoint of binding curves is critical to nature’s ability to optimize many cellular processes (1). One of the most widely used mechanisms by which nature so tunes the behavior of her receptors is allostery, in which the binding of one ligand alters the affinity with which subsequent ligands bind. Allostery comes in two “flavors.” Heterotropic allostery, in which the two ligands differ, provides a means of shifting the midpoint of a binding curve to higher or lower target concentrations without changing the curve’s intrinsically hyperbolic shape and thus without altering its sensitivity to small changes in the relative concentration of its molecular target (Fig. 1, Left). An example is the binding of bisphosphoglycerate to mammalian hemoglobin, which decreases the protein’s affinity for oxygen, thus pushing its binding curve to higher concentrations and enhancing oxygen transport efficiency, while leaving the intrinsic shape of its binding curve unaltered. Homotropic allostery, in contrast, occurs when the ligands are the same; that is, when the binding of one copy of a ligand changes the affinity with which subsequent copies of the same molecule bind. This mechanism, commonly referred to as “cooperativity,” changes not only the placement but also the shape of the binding curve, producing either a more responsive, higher-order dependence on ligand concentration (positive cooperativity) (Fig. 1, Right) or a less responsive, lower-order dependence (negative cooperativity). Like heterotropic allostery, cooperativity is also seen in the function of hemoglobin; the protein uses this mechanism to bind four oxygen molecules in a positively cooperative, approximately “all-or-nothing” fashion, steepening its binding curve and enhancing its ability to deliver oxygen over the rather modest concentration gradient present between the lungs and the peripheral tissues.

Fig. 1.

Nature often controls the shape and position of ligand–response curves via allostery. (Left) In heterotropic allostery, the binding of one ligand to a receptor increases or decreases the affinity with which a second, different ligand binds, shifting the placement of the binding curve without altering its shape and thus without altering the width of its useful dynamic range (shaded boxes) or, in turn, its sensitivity to small changes in target concentration. (Right) In homotropic allostery, in contrast, the binding of one copy of target ligand changes the affinity with which additional copies of the same ligand bind, altering both the placement and the shape of the binding curve. The latter effect allows the system to respond more (positive cooperativity) or less (negative cooperativity) sensitively to changes in target ligand concentration. For positive cooperativity, receptor occupancy is a higher (than unity) order function of target concentration, with the exponent, n_H, being known as the Hill coefficient.

The ubiquity with which nature exploits homotropic and heterotropic allostery has motivated efforts to rationally engineer these mechanisms into biomolecular receptors normally lacking them, both to test our understanding of the principles underlying these effects and to harness them to improve the utility of artificial biotechnologies. The rational introduction of heterotropic allostery into otherwise nonallosteric receptors, for example, has seen significant prior exploration (e.g., refs. 2–8), with both mechanical coupling (e.g., refs. 2 and 5–8) and mutually exclusive folding (e.g., refs. 3 and 4) approaches all having been used to successfully introduce this useful mechanism into a range of protein- and nucleic acid-based receptors. The design of allosterically cooperative receptors, in contrast, has seen far less success. That is, although a handful of examples of rationally designed cooperativity have been reported to date (9–12), no general approach has previously been reported by which such behavior can be rationally introduced into any arbitrarily complex biomolecule. This failure has limited the extent to which cooperativity, which could provide a powerful means of improving the ability of artificial biotechnologies to respond to small changes in molecular concentration (9, 13), can be applied in applications, such as biosensing (14, 15), “smart” drug delivery materials (16, 17), and molecular (18) and genetic (19) logic gates, in which such enhanced responsiveness would be of value.

Two reasons account for why, despite its underlying simplicity and elegance, achieving the rational design of positive cooperativity has proven far from straightforward. First, to achieve the effect requires the creation of systems in which a higher affinity site is occupied only after a lower affinity site (which would normally be filled only at higher ligand concentrations) that binds the same ligand is already filled. This contrasts sharply with heterotropic allostery, in which the two binding sites typically exhibit little if any cross-reactivity. Second, all of the binding sites of a cooperative receptor recognize copies of the same ligand, rendering it more difficult to alter the affinity of one independently of that of the others. This is again in contrast to heterotropic allostery, in which each binding site is chemically distinct, allowing each to be independently optimized. Given these difficulties, and given the relative infancy of biomolecular design efforts (20–22), the ability to perform the structure-based design of cooperativity appears beyond current capabilities except for the simplest, most well-understood receptors (9–12). Here, however, we use an approach to the rational engineering of allosterically cooperative receptors that does not require detailed, structure-based design. Indeed, our approach is so simple that it can be performed, as demonstrated here, even in the absence of detailed knowledge of the parent receptor’s structure.

Our design approach is inspired by intrinsically disordered proteins, proteins that are normally unfolded and only fold upon binding their target ligand. Specifically, both theoretical (23) and experimental (24, 25) studies have demonstrated that the global conformation change these proteins undergo upon an initial ligand binding event provides a convenient means of preorganizing a second, distal ligand binding site. This improves the affinity of the second binding event (because binding need no longer pay the unfavorable cost associated with folding), leading to positive allosteric behavior. Ferreon et al. (24), for example, have shown that the intrinsically disordered oncoprotein adenovirus early region 1A (E1A) folds upon binding either of its two (different) target ligands (CREB binding protein or retinoblastoma protein), thus increasing the affinity with which the second ligand binds and rendering the system heterotropically allosteric. In addition, Furukawa et al. (25) have shown that the partially intrinsically disordered protein STIM 1 exhibits strongly homotropic allosteric binding to calcium. Here, we use this same mechanism to rationally introduce cooperativity into a number of normally noncooperative aptamers (DNA-based receptors often adopting complex tertiary folds), thus producing steeper, more responsive binding curves than those seen for the unmodified parent molecule.

Results

Positive cooperativity arises when the first binding event on a multisite receptor improves the binding affinity of additional copies of the same ligand. Thus, once one copy of the ligand is bound the probability of the second binding event becomes high, generating effectively “all-or-none” behavior. The resulting binding curve (26) is given by the Hill equation:

$$\text{Receptor}\hspace{0.17em}\text{site}\hspace{0.17em}\text{occupancy}\overline{Y}=\frac{{\left[\text{target}\right]}^{n_{\text{H}}}}{{\left[\text{target}\right]}^{n_{\text{H}}}+{\left(K_{1/2}\right)}^{n_{\text{H}}}},$$ [1]

in which K_1/2 is the ligand concentration at which one-half of the receptor sites are bound, and n_H, the Hill coefficient, describes the order of the dependence on ligand concentration (Fig. 1, Bottom Right). For a noncooperative receptor, in which each copy of the ligand binds independently of all others, n_H = 1. For an ideally cooperative receptor, in which all of the binding sites on any one receptor molecule are simultaneously either fully occupied or fully unoccupied, the Hill equation equals the number of binding sites. The Hill coefficient is, in turn, related to the useful dynamic range of a receptor (a convenient measure of responsiveness that is typically defined as the ratio between the target concentration at which occupancy is 90% to that at which it is 10%; C_90% and C_10%, respectively) by the following (27):

$$\text{Dynamic}\hspace{0.17em}\text{range}=\frac{C_{90\%}}{C_{10\%}}={81}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n_{\text{H}}$}\right.}.$$ [2]

From this, we see that the useful dynamic range of a noncooperative receptor (n_H = 1) is quite broad; such a receptor requires an 81-fold change in target concentration to transition from 10% occupancy to 90% occupancy, rendering it relatively insensitive to small changes in this input. The dynamic range falls to just ninefold, however, for an ideally cooperative, two-site receptor (n_H = 2), rendering such a receptor many times more sensitive to small changes in target concentration.

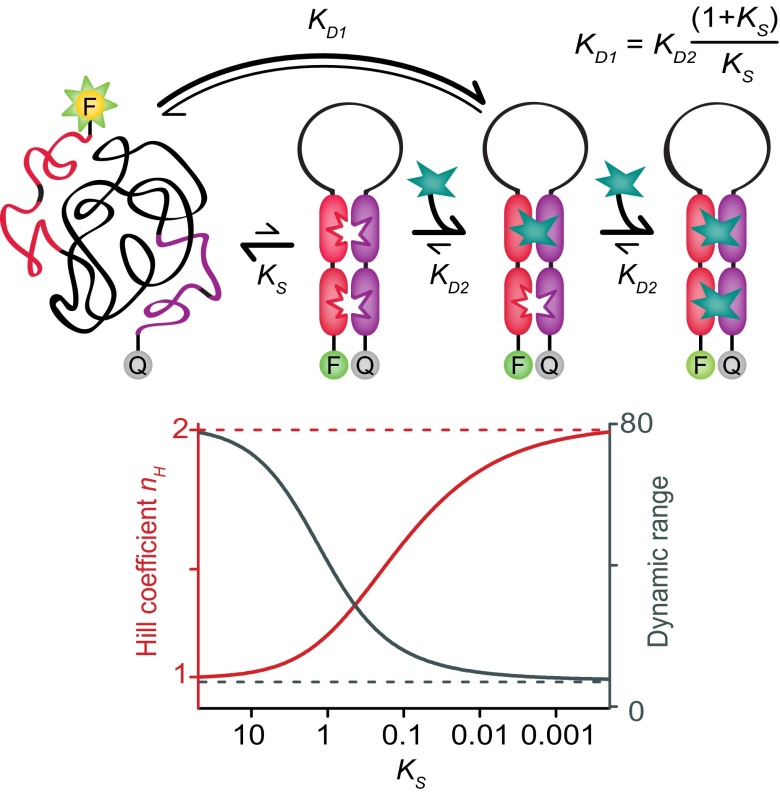
In naturally occurring receptors, the energetic difference between the first and subsequent binding events required to generate allosteric cooperativity usually arises due to mechanical coupling between the relevant binding sites. That is, structural changes that occur upon the first binding event are transduced throughout the receptor in a manner that improves affinity at other, distal, sites. In hemoglobin, for example, this occurs when the protein undergoes a global conformational switch from a low-affinity state that dominates when no ligand is bound, to a higher affinity conformation upon the binding of the first oxygen molecule. Here, we hypothesize that the requisite global conformational switch can also be driven by a mechanism analogous to the binding-induced folding seen for intrinsically disordered proteins. That is, via a binding-induced switch from a largely or entirely disordered state lacking preconfigured binding sites to a well-defined folded conformation exposing multiple, well-structured binding sites (Fig. 2, Top). In this scenario, the affinity of a binding site is reduced when its neighboring site is empty because the receptor is unfolded, and thus binding must pay the cost associated with folding it. Equivalently, the affinity of a binding site is enhanced when its neighboring site is already occupied. The relative (microscopic; see refs. 27 and 28) dissociation constants of the two binding scenarios (neighboring site open, K_D1, and neighboring site occupied, K_D2) are then related to K_S, the equilibrium constant for forming the folded conformation in the absence of the target ligand, by the following (12):

$$\frac{K_{\text{D}2}}{K_{\text{D}1}}=\frac{K_{\text{S}}}{1+K_{\text{S}}}.$$ [3]

The Hill coefficient, in turn, is related to this ratio by the following (12, 27):

$$n_{\mathrm{H}}=\frac{2}{1+\sqrt{\frac{K_{\mathrm{D}2}}{K_{\mathrm{D}1}}}}=\frac{2}{1+\sqrt{\frac{K_{\mathrm{S}}}{1+K_{\mathrm{S}}}}}.$$ [4]

From this, we see that a folding equilibrium constant of just 0.1, which corresponds to a folded state that is unstable in the absence of the target ligand by just 6 kJ/mol (at room temperature), is sufficient to achieve n_H = 1.5. This, in turn, narrows the receptor’s dynamic range by more than a factor of 4 (Eq. 2), significantly enhancing sensitivity to small changes in the concentration of the target ligand (Fig. 2, Bottom).

Fig. 2.

Our approach to the rational design of cooperativity employs receptor architectures that fold upon binding the first target molecule. (Top) Specifically, our receptor architectures consist of two copies of one half of a receptor (red), a variable length, unstructured linker (black), and two copies of the second half of the receptor (purple). In the absence of target ligand, the construct exists primarily in a disordered state lacking preformed binding sites. This disordered state, however, is in equilibrium (equilibrium constant, K_S) with the fully folded receptor. The first target molecule to bind must overcome the unfavorable free energy associated with forming this structure, reducing its affinity compared with that of the preformed aptamer by the factor (1 + K_S)/K_S. The second target molecule binds to a preformed binding site, thus improving its affinity relative to that of the first binding event. (Bottom) The degree of cooperativity, i.e., the Hill coefficient (n_H) and the useful dynamic range (typically defined as the ratio between the target concentration at which occupancy is 90% to that at which it is 10%), depend strongly on K_S. So much so that an equilibrium constant as great as ∼0.1 (i.e., receptors that populate their high-affinity state to the level of ∼10% even in the absence of ligand) still produces near-maximum sensitivity to small changes in the concentration of the target ligand.

To physically realize such folding-based cooperativity, we have reengineered several normally noncooperative receptors into constructs comprised of a tandem repeat of one half of the receptor connected to a tandem repeat of the second half of the same receptor via an unstructured linker (Fig. 2, Top). In the absence of target, the unfavorable entropic cost of closing this linker, i.e., of ordering this disordered region, destabilizes the folded, binding-competent conformation, producing a largely unfolded state lacking structured binding sites. The binding of the first copy of the target ligand brings the two halves of the construct into association, forming both binding sites. The second binding event thus need not pay the unfavorable free energy cost associated with folding, improving its affinity and, in turn, producing a cooperative response.

For the preliminary exploration of our design approach, we used as our recognition sites a simple, mercury(II)-binding thymine–thymine mismatch (29). Specifically, we inserted two thymine–thymine mismatches into an otherwise complementary DNA stem, the two strands of which are linked via an unstructured poly-AC loop, and the two termini of which are modified with a fluorophore–quencher pair that reports on folding (Fig. 3, Left). Using a loop length of 50 bases, this construct is reasonably cooperative, achieving a Hill coefficient of 1.51 ± 0.03 and a useful dynamic range of just 18 (±1)-fold (Fig. 3, Middle). This represents a substantial increase in responsiveness relative to that of the equivalent, 50-base linker receptor in which one of the two thymine–thymine mismatch sites has been replaced with a nonbinding cytosine–cytosine mismatch; as expected, this single-site construct exhibits a Hill coefficient within experimental uncertainty of unity and a dynamic range within uncertainty of 81-fold (Fig. S1).

Fig. 3.

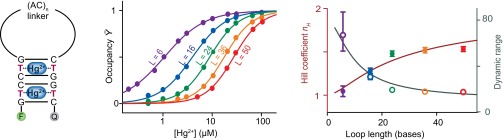
Our first test bed system is a cooperative mercury(II)-binding receptor (Left), which consists of a short, double-stranded stem containing two mercury(II)-binding thymine–thymine mismatches linked via a variable length, unstructured, poly-AC sequence. (Middle) The cooperativity and binding affinity of these constructs scales monotonically with the loop length, ranging from a Hill coefficient of 1.51 ± 0.03 (dynamic range, 18-fold) for the construct with a 50-base loop to a Hill coefficient of 1.05 ± 0.05 (dynamic range, 66-fold) for the construct with a 6-base loop, with the latter being quite close to the behavior observed for single-site binding (Fig. S1). (Right) Speaking to the quantitative nature of this design, the observed Hill coefficients and dynamic ranges fit Eqs. 7 and 2 with R² values of 0.920 and 0.956, respectively, using only a single fitted parameter (K_close), the best-fit value of which is within experimental uncertainty of independent estimates (see Results). Of note, all of these constructs equilibrate within the 30- to 60-s mixing dead time of our experiments (Fig. S2).

The degree of cooperativity depends on the equilibrium constant for switching the receptor from its low-affinity state to its high-affinity state (Eq. 4). In our design, this equilibrium constant is the product of the equilibrium constant for forming the intact binding sites in the absence of the linker, K_close, and the unfavorable equilibrium constant associated with closing the linker, K_link:

$$K_{\mathrm{S}}=K_{\text{link}}{K}_{\text{close}}.$$ [5]

Consistent with this, the cooperativity of our two-site mercury receptor falls monotonically as we shorten its loop (thus decreasing K_link) from 50 bases (n_H = 1.51 ± 0.03) to 6 bases (n_H = 1.05 ± 0.05) (Fig. 3, Middle). To put these observations on a still more quantitative footing, we note that, for linkers longer than the ∼3-base persistence length of single-stranded DNA (30), K_link is dominated by the entropic cost of loop closure and thus should go as follows:

$$K_{\text{link}}=L^{\mathrm{-}1.75},$$ [6]

where L is linker length (31). Combining Eqs. 4–6, we can thus relate the degree of cooperativity of our constructs to the length of their unstructured loops as follows:

$$n_{\mathrm{H}}=\frac{2}{1+\sqrt{\frac{K_{\mathrm{close}}{L}^{-1.75}}{1+K_{\mathrm{close}}{L}^{-1.75}}}}.$$ [7]

Despite using only a single floating parameter, K_close, this equation fits the observed Hill coefficients of our family of cooperative mercury receptors quite well (R² = 0.92), speaking to the validity of our design model (Fig. 3, Right). Moreover, the fitted value of K_close, 59 ± 30, corresponds to a free energy of −10.6 (±1.4) kJ/mol for the formation of the two-mismatch–containing stem. This, in turn, agrees to within experimental uncertainty with the −12.2 (±1.6) kJ/mol predicted by adding the −4.6 kJ/mol stability of the stem as predicted by the “DINAMelt Mfold” secondary structure prediction algorithm (32, 33) to the −7.6 (±1.6) kJ/mol prior literature estimates of the stabilization produced by the fluorophore–quencher pair we have used (34, 35).

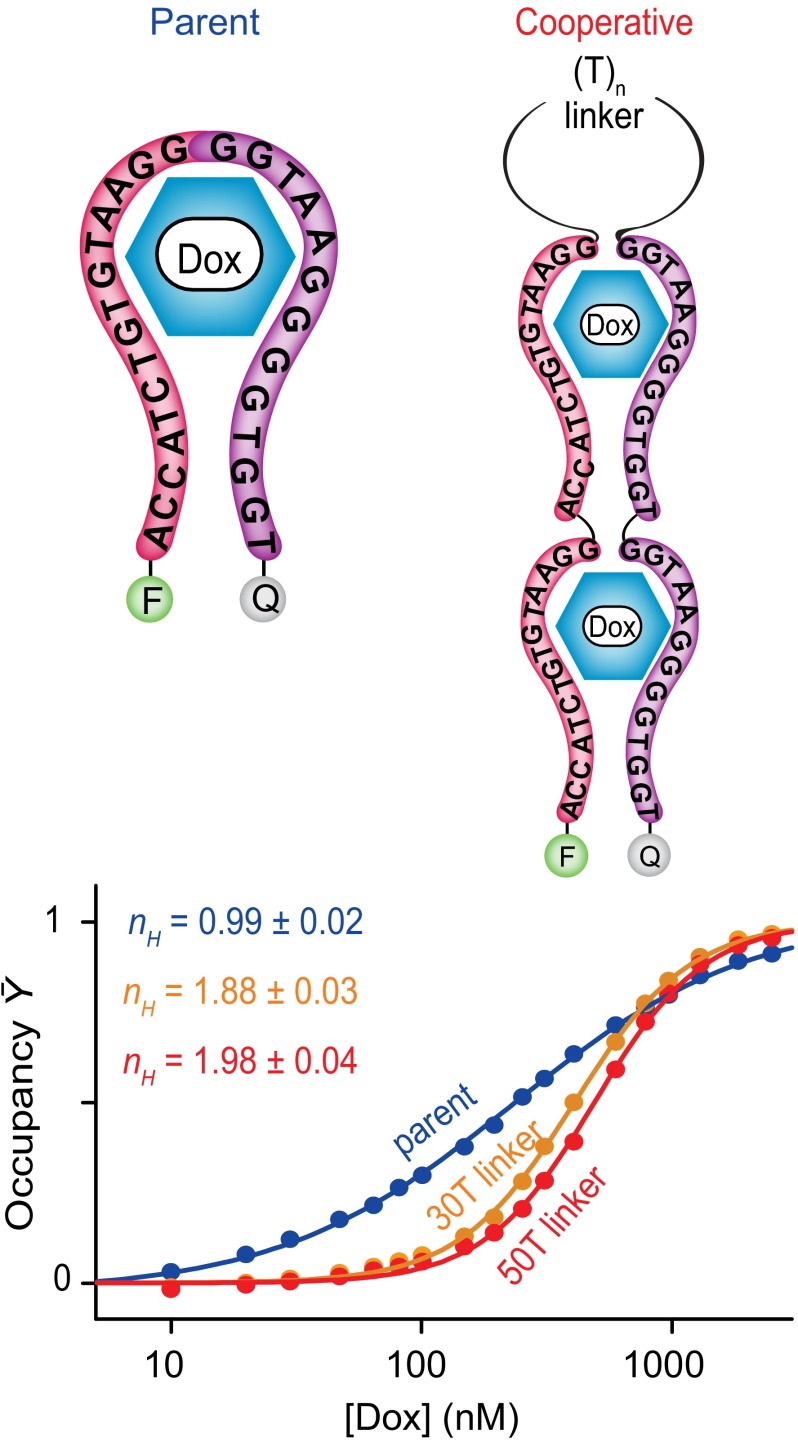
Encouraged by these successful test case design efforts, we next adapted our simple strategy to engineering cooperativity into two structurally more complex receptors. For the first, we employed a sequence based on the doxorubicin-binding aptamer of Wochner et al. (36), which binds this important cancer chemotherapeutic with a dissociation constant of ∼200 nM. Of note, the 3D structure of this aptamer is not known, rendering this a significantly more challenging test of our design approach. To introduce cooperativity into the doxorubicin-binding aptamer, we first used DINAMelt Mfold as a guide to predict its likely secondary structure (Fig. 4, Top). We then “cut” the parent aptamer sequence at a position within the single putative loop identified by Mfold and linked tandem repeats of the two resulting half-aptamers via unstructured polythymine sequences of either 30 or 50 bases. As expected, the construct using a 50-base linker is quite cooperative, exhibiting a Hill coefficient of 1.98 ± 0.04 and a dynamic range of just 9.2 (±0.4)-fold (Fig. 4, Bottom), values within experimental uncertainty of ideal behavior for a fully cooperative, two-site receptor. The construct using the shorter, 30-base linker is, as likewise expected, slightly less cooperative, achieving a Hill coefficient of 1.88 ± 0.03 and a useful dynamic range of 10.4 (±0.8)-fold. The parent, single-site doxorubicin aptamer, in contrast, exhibits a Hill coefficient of 0.99 ± 0.02 and a useful dynamic range of 85 (±10)-fold.

Fig. 4.

(Top) We have also applied our approach to engineer cooperativity into a doxorubicin-binding aptamer, which, although predicted to form a stem loop, is ultimately of unknown structure. (Bottom) Constructs using either 30- or 50-base linkers achieve Hill coefficients of 1.88 ± 0.03 and 1.98 ± 0.04, respectively, corresponding to useful dynamic ranges of 10.4-fold and 9.2-fold. The Hill coefficient of the parent aptamer, in contrast, is within experimental uncertainty of unity.

The quantitative model for folding-based cooperativity outlined above (Eq. 7) for our mercury receptors likewise describes the behavior of our doxorubicin-binding constructs. Specifically, Mfold (32, 33) predicts that the parent aptamer forms a stem loop structure with folding free energy that is unstable by 0.75 kJ/mol (per monomeric aptamer) in the absence of doxorubicin. When added to the favorable association energy of the fluorophore–quencher pair (34, 35), this yields a closing free energy of −6.1 kJ/mol and a K_close of 11.2 for the tandem repeat. Inserting the latter value into Eq. 7 predicts Hill coefficients of 1.71 and 1.80 for our 30-thymine and 50-thymine constructs, respectively, estimates that are reasonably close to the experimental values.

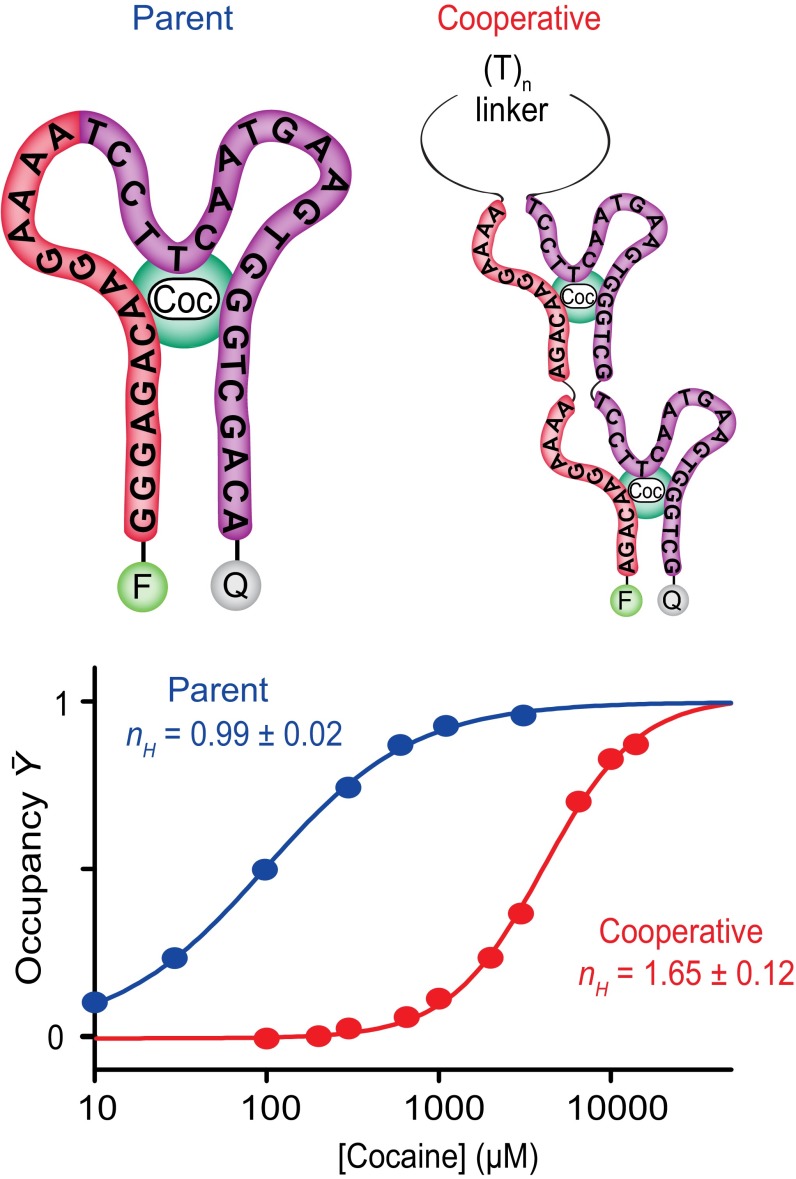
As a final test of the generality of our approach, we applied it to the cocaine-binding aptamer of Stojanovic et al. (37), the conformation of which is likewise not known in detail. Using a previously identified cut site (38), we engineered a cooperative receptor in which tandem repeats of the two halves of the aptamer are linked via an unstructured, 50-base polythymine sequence (Fig. 5, Top). The resultant construct exhibits a Hill coefficient of 1.65 ± 0.12 and dynamic range of binding of 14 (±3)-fold (Fig. 5, Bottom). As with the cooperative mercury(II)- and doxorubicin-binding aptamers, the behavior of the cooperative cocaine-binding aptamer likewise appears consistent with Eq. 7. Complicating this analysis, however, is the fact that the aptamer is thought to contain a large number of non-Watson–Crick base pairs (38), and thus DINAMelt Mfold likely fails to accurately model its folding free energy. To overcome this, we instead used the experimentally determined folding free energy of the parent aptamer (39) to determine K_close. Specifically, the folding free energy of the fluorophore-and-quencher–modified parent aptamer is −7.5 kJ/mol. Given the known stabilizing effects of the fluorophore–quencher pair (34, 35), we thus estimate that the folding free energy of the dye-free parent aptamer is +0.1 kJ/mol. The folding free energy of a dimer of aptamers, one of which is dye-labeled, should thus be −7.4 kJ/mol, which in turn corresponds to a K_close of 19. Inserting this value into Eq. 7 predicts a Hill coefficient of 1.75, which is again within experimental uncertainty of the observed value.

Fig. 5.

As a final test of the generality of our approach, we have applied it to the cocaine-binding aptamer of Stojanovic et al. (37). (Top) This aptamer is thought to form a three-way junction. (Bottom) The modified aptamer achieves substantial cooperativity, exhibiting a Hill coefficient of 1.65 ± 0.12. The parent aptamer, in contrast, exhibits a Hill coefficient within experimental uncertainty of unity.

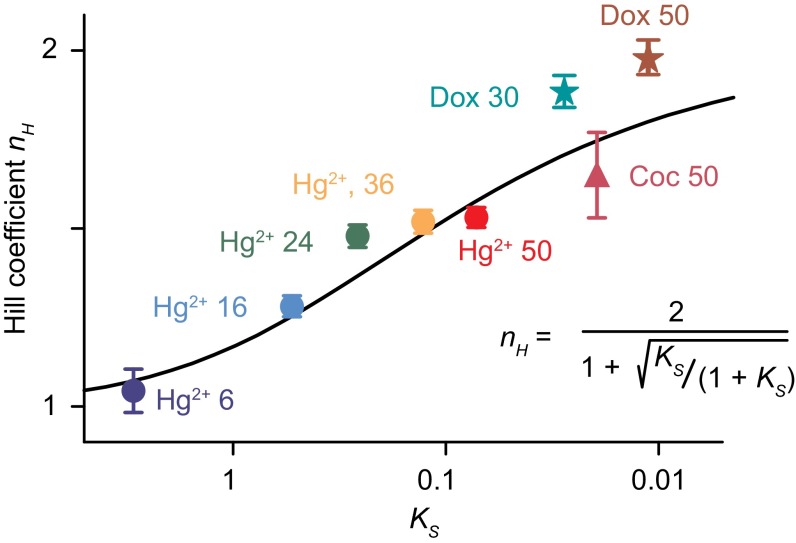
Here, we have demonstrated the utility of using binding-induced folding as an effective, quantitative, and potentially versatile means of engineering allosteric cooperativity into normally noncooperative biomolecular receptors. Specifically, we have used this approach to generate cooperative receptors starting from three distinct, unrelated aptamers that bind three distinct and unrelated molecular targets. The most cooperative of these redesigned receptors exhibits a Hill coefficient within experimental uncertainty of the theoretically expected maximum, thus converting the 81-fold dynamic range associated with single-site binding to a ninefold dynamic range and rendering the resultant receptor far more sensitive than its parent to small changes in the concentration of its target ligand. Finally, the approach is quantitative, with the degree of cooperativity attained for each of eight different receptors (again, binding three quite different molecular targets) closely matching the values expected given the switching equilibrium constant, K_S, of each of the modified aptamers (Fig. 6).

Fig. 6.

We have achieved the rational, quantitative introduction of cooperativity into a range of aptamer-based receptors. As shown here, for example, Eq. 4 (solid line), which defines the expected relationship between K_s, the equilibrium constant for receptor “folding,” and n_H, the Hill coefficient, describes the behavior of all eight of the receptors reported in this paper with reasonable accuracy despite its lacking any fitted parameters. The biomolecules shown include receptors designed to cooperatively bind mercury ions [Hg(II)], doxorubicin (Dox), and cocaine (Coc), and featuring, as denoted in the figure, unstructured loops of between 6 and 50 bases.

The ability to rationally engineer biomolecular receptors such that they overcome the “tyranny of the Langmuir isotherm” (40) and respond robustly to relatively small changes in the concentration of their target ligand has proven an important goal in molecular engineering and synthetic biology (14–19). Unfortunately, however, although nature frequently uses the simple, elegant mechanism of allosteric cooperativity to overcome this limitation, the generalizable ability to recapitulate this behavior in normally noncooperative biomolecular receptors has hitherto remained elusive, with successful examples of artificially engineered, allosteric cooperativity having been restricted to a small number of more-or-less nongeneralizable examples (9–12). In part, this is because our ability to rationally design biomolecules that switch reversibly between two well-defined conformations likewise remains limited (22). In response, we have demonstrated here a means of engineering cooperativity that circumvents this challenge by using the (easily achievable) unfolded state as one of the two required conformations. Given the ease with which single domain proteins can similarly be reengineered to undergo binding-induced folding (see, e.g., refs. 41 and 42), and the recent report of a naturally occurring protein that employs intrinsic disorder to generate cooperative binding (25), we suspect that intrinsic disorder may also prove a useful means of rationally optimizing the responsiveness of protein-based receptors.

Materials and Methods

Detailed methods are available in SI Materials and Methods. Briefly, DNA probes modified with a carboxyfluorescein (FAM) and a black-hole-quencher-1 (BHQ-1) were used as purchased (BioSearch Tech and IBA). We obtained all fluorescence measurements with excitation at 485 (±5) nm and acquisition at 515 (±10) nm. We used GraphPad Prism plotting software to fit titrations curves to the Hill equation. Confidence intervals represent 95% confidence based on SEs derived from the fitting software.