Role of pendant proton relays and proton-coupled electron transfer on the hydrogen evolution reaction by nickel hangman porphyrins

Significance

The conversion of solar energy into fuels involves coupled multiproton–multielectron reactions. Because of different length scales for electron transfer and proton transfer, efficient catalysts must couple proton hops to redox events. We have developed a hangman motif where placing a pendant acid–base group over the face of a redox macrocycle ensures coupling of the electron to the proton. We now show that the presence of the pendant acid relay of a Ni hangman porphyrin facilitates proton-coupled electron transfer (PCET) during turnover of the hydrogen evolution reaction (HER). By comparing HER activity of the Ni hangman catalyst to its Co analog, a unified HER mechanism begins to emerge for complexes that use a secondary coordination sphere to manage PCET.

Abstract

The hangman motif provides mechanistic insights into the role of pendant proton relays in governing proton-coupled electron transfer (PCET) involved in the hydrogen evolution reaction (HER). We now show improved HER activity of Ni compared with Co hangman porphyrins. Cyclic voltammogram data and simulations, together with computational studies using density functional theory, implicate a shift in electrokinetic zone between Co and Ni hangman porphyrins due to a change in the PCET mechanism. Unlike the Co hangman porphyrin, the Ni hangman porphyrin does not require reduction to the formally metal(0) species before protonation by weak acids in acetonitrile. We conclude that protonation likely occurs at the Ni(I) state followed by reduction, in a stepwise proton transfer–electron transfer pathway. Spectroelectrochemical and computational studies reveal that upon reduction of the Ni(II) compound, the first electron is transferred to a metal-based orbital, whereas the second electron is transferred to a molecular orbital on the porphyrin ring.

Solar-to-fuels conversions provide a path to harnessing the ubiquitous albeit intermittent renewable energy resource offered by the sun (1–6). Efficient catalysis of transformations of energy consequence (7–13) mandates the coupling of electron transfer (ET) to proton transfer (PT) in proton-coupled electron transfer (PCET) reactions (14–20). In the absence of PCET, intermediates possessing equilibrium potentials that are prohibitively large depreciate the storage capacity offered by the solar-to-fuels conversion process. The coupling of protons to changes in electron equivalency offers the possibility of restricting the equilibrium potentials of the redox steps to a more narrow potential range, thereby minimizing the overpotential required to sustain catalysis at a desired turnover rate. Thus, the exploitation of PCET pathways to permit potential-leveling effects is a crucial prerequisite for the efficient catalytic conversion reactions of energy relevant molecules.

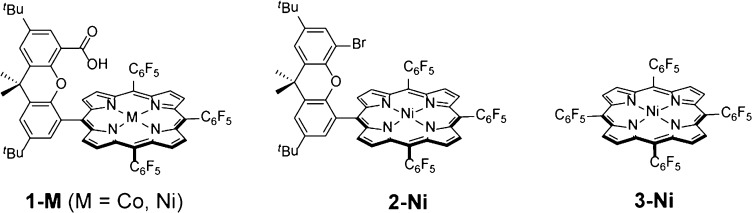
PCET reactions may be classified into stepwise and concerted pathways (14, 16, 20, 21). Stepwise PCET may involve ET first followed by PT (ETPT), or PT followed by ET (PTET). In concerted proton–electron transfers (CPET), the proton and electron traverse a common transition state. Whereas concerted pathways avoid the formation of thermodynamically costly intermediates, CPET reactions may incur kinetic penalties associated with the requirements for proton tunneling (19, 20, 22). The competition between these dynamics during catalysis determines the most efficient route of reaction. Studies that explore the interplay between these factors are crucial to designing catalytic reactions of high efficiency. Along these lines, the incorporation of proton relays in the second coordination sphere of molecular catalysts has emerged as a useful tool in optimizing PCET transformations (23–29). We have focused on the synthesis and mechanistic investigation of a class of metalloporphyrin molecules attached to a xanthene backbone bearing a carboxylic acid functional group—“hangman” porphyrins (1-M, Scheme 1) (23, 30, 31). These hangman porphyrins have been especially useful for examining the PCET reactions of O₂ (25, 32, 33), H₂O (34), and H₂ (35). Recently, we established quantitatively the value of the hangman effect for hydrogen evolution reaction (HER) by cobalt hangman porphyrin 1-Co (Scheme 1) (35). Mechanistic studies (36) unveiled a stepwise ETPT generation of a formal Co^II hydride intermediate from the Co^I resting state. Comparison of the catalysis of 1-Co with its nonhangman cobalt porphyrin congener showed that a significant catalytic enhancement of the HER was manifested in a rapid intramolecular rate-limiting PT (k_PT = 8.5 × 10⁶ s^–1) from the pendant acid. In contrast, the corresponding second-order rate constant for proton transfer of the nonhangman was 10³ M^–1⋅s^–1.

Scheme 1.

Cobalt and nickel hangman complexes.

The intramolecular PT should be mediated by the pK_a of the metal. Indeed, the basicity of the metal center relative to a given acidity of the proton relay may be a critical determinant in the HER (37). We now show that the nickel hangman porphyrin 1-Ni (Scheme 1) offers an improvement in catalytic activity over its cobalt analog owing to a change in the PCET mechanism. By comparing HER activity of the Ni hangman catalyst with the Co hangman catalyst, a unified HER mechanism begins to emerge for complexes that use a secondary coordination sphere to manage PCET.

Results and Discussion

Free-base porphyrins 1 and 2 were synthesized in good yields in relatively short synthesis times using a two-step statistical method to construct the hangman porphyrin (31). Insertion of nickel into the free-base porphyrin to generate 1-Ni was performed by 8–10-h microwave irradiation of 1 and excess NiBr₂ in a chloroform:methanol solvent mixture (4:1) at 65 °C. Purification was accomplished by column chromatography. Full synthetic procedures and characterization data including ¹H NMR spectra (SI Appendix, Figs. S2–S4), electrospray ionization-mass spectrometry (ESI-MS) and laser desorption-mass spectrometry (LD-MS) (SI Appendix, Figs. S5–S7), electronic absorption spectra (SI Appendix, Figs. S8–S10), and cyclic voltammogram (CV) data (SI Appendix, Figs. S11–S18) are provided in SI Appendix.

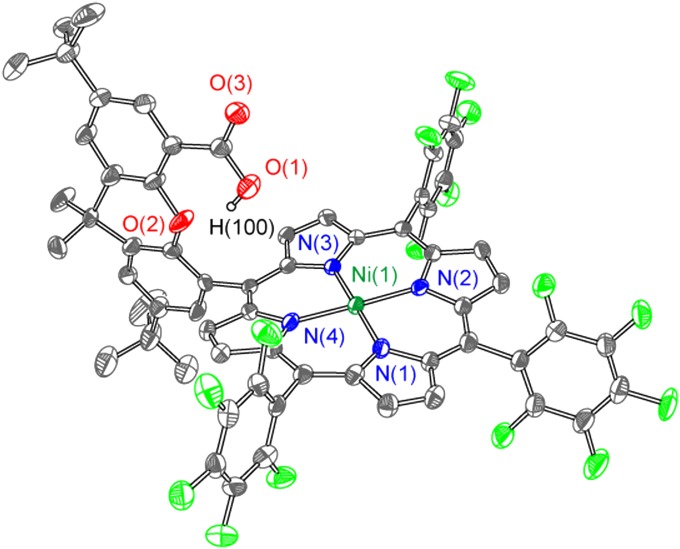
Compound 1-Ni was crystallized by slow evaporation of a dichloromethane–hexane solution; the crystal structure is shown in Fig. 1. The distance between the oxygen center of the hangman group and the metal center is 4.510 Å in the solid state. Other structural metrics are similar to those of a similar Co(II) hangman porphyrin possessing mesityl meso-substituents (32). One notable difference in the crystallographic structures of these two molecules is the presence of an apical ligand bound to cobalt. The absence of an apical ligand in the Ni complex is a result of the d⁸ electron count of the nickel; consequently the d_z² orbital is fully populated and thus unavailable for interaction with an apical ligand. The distance of the proton of the hanging group to the metal is 4.46 Å (Co) and 4.25 Å (Ni). This 0.21-Å difference in M−H distance is a result of a larger tilt angle of the xanthene relative to the porphyrin ring for the cobalt porphyrin (13.9° for Co, 7.1° for Ni), which positions the hanging group farther from the Co center. We believe this difference is likely due to packing effects in the solid state and thus of little consequence of the molecule’s behavior in solution. Thus, differences in subsequent HER chemistry between the Co and Ni complexes are attributed to electronic effects and not to an underlying structural difference between the two complexes.

Fig. 1.

Crystal structure of 1-Ni with thermal ellipsoids set at 50% probability. Selected internuclear distances (Å) and angles (°): Ni(1)−N(1) 1.951(3), Ni(1)−N(2) 1.940(3), Ni(1)−N(3) 1.951(3), Ni(1)−N(4) 1.951(3), Ni(1)−O(1) 4.510(6), N(1)−Ni(1)−N2 89.83(12), N(1)−Ni(1)−N(4) 90.31(12), N(2)−Ni(1)−N(3) 90.06(12), N(3)−Ni(1)−N(4) 89.87(13).

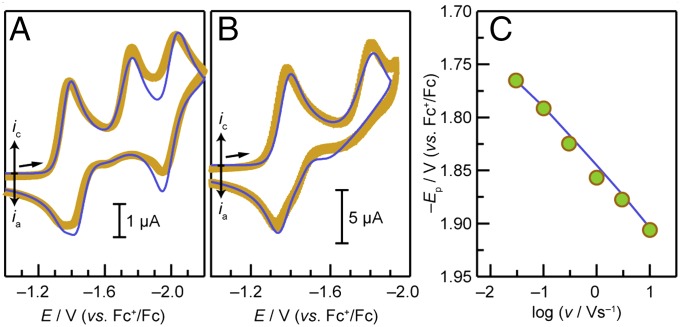
CVs of 1-Ni and 2-Ni in acetonitrile are shown in Fig. 2A. The CV of 2-Ni (Fig. 2A, – –, blue) simply displays two reversible waves centered at –1.39 and –1.96 V (all potentials are referenced to the standard reduction potential of the ferrocenium ion, Fc⁺/Fc); we ascribe these waves to the formal Ni^II/I (2-Ni/[2-Ni]^–) and Ni^I/0 ([2-Ni]^–/[2-Ni]^2–) redox couples, respectively. As shown in SI Appendix, Fig. S12, electrochemically reversible behavior is also observed for the A₄ porphyrin 3-Ni (Scheme 1); the reduction potentials are shifted positively as a result of the additional electron-withdrawing C₆F₅ substituent. The CV of 1-Ni (Fig. 2A,—, red) displays two reversible waves possessing midpoint potentials of –1.37 and –2.01 V that flank an irreversible wave with a peak potential of –1.76 V. By analogy to 2-Ni, we assign the first reversible wave observed in the case of 1-Ni to the formal Ni^II/I redox couple (e.g., 1-Ni/[1-Ni]^–) and the second reversible wave to the [1-Ni]^–/[1-Ni]^2– couple. The irreversible wave is associated with H₂ catalysis, and a detailed discussion of the processes associated with this wave is presented below.

Fig. 2.

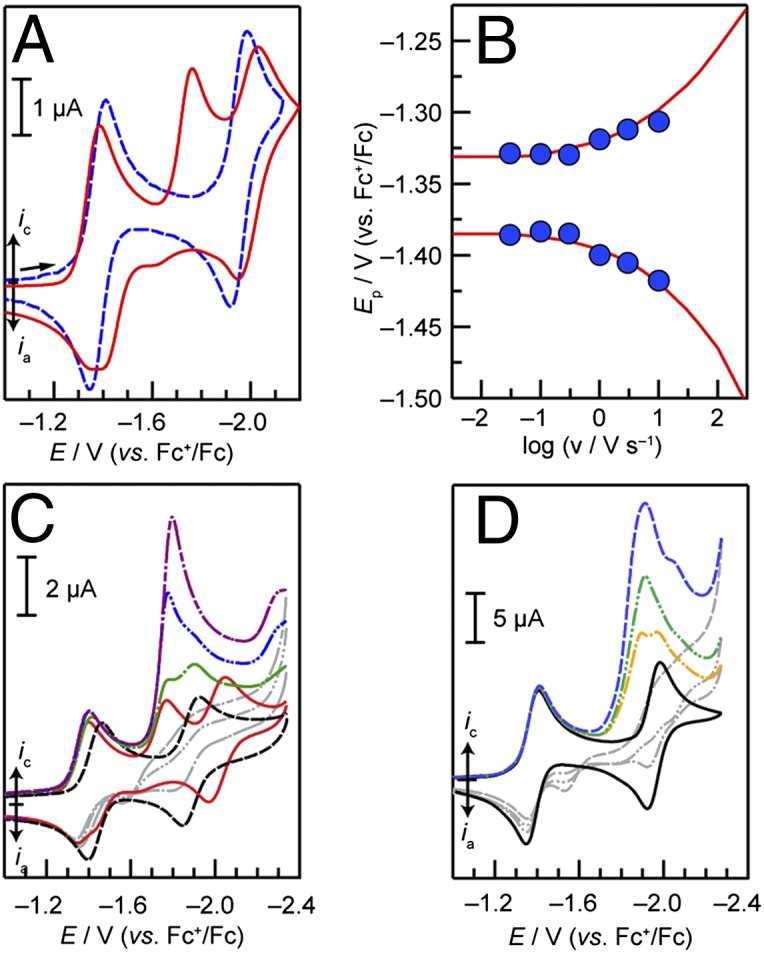
CV of 1-Ni and 2-Ni in 0.1 M TBAPF₆–acetonitrile electrolyte at a glassy carbon electrode. (A) CVs of 0.4 mM 1-Ni (red —) and 0.4 mM 2-Ni (– –, blue) at a scan rate of 30 mV/s. (B) Anodic (upper circles) and cathodic (lower circles) peak potentials (E_p) of the formal Ni(II/I) wave as a function of the logarithm of scan rate (v). The solid red line represents the simulation of the trumpet plot to a standard heterogeneous rate constant k_ET^o of 0.025 cm/s. The diffusion coefficient D of 1-Ni was determined to be 4.5 × 10⁻⁶ cm²/s from the peak current density as described in ref. 38. (C) CVs of 0.25 mM 1-Ni before (—, red) and after (– –, black) treatment with K₂CO₃ followed by addition of 0.6 (— ∙ —, green), 1.2 (— ∙∙, blue), and 1.8 (— - ∙, purple) molar equivalents of benzoic acid (scan rate: 30 mV/s). (D) CVs of 0.5 mM 2-Ni (—) upon titration with 0.5 (— ∙ —, orange) 1.0 (— ∙∙, green), and 2.0 (– –, blue) molar equivalents of benzoic acid (scan rate: 30 mV/s).

Variable scan rate voltammetry permits isolation of the standard heterogeneous ET rate constants (k_ET^o) associated with the electrochemically reversible processes of all complexes. Increasing separation between cathodic and anodic peak potentials as the scan rate is increased is indicative of deviation away from strict Nernstian behavior toward electrochemical irreversibility. Accordingly, the degree of separation for a given scan rate relies on k_ET° (38). CV simulation software (39) provides a reliable means of determining k_ET° from the “trumpet plot” generated by simulating CVs over a range of scan rates (40). Trumpet plots of the 1-Ni/[1-Ni]^– peak potentials (blue circles) as a function of the logarithm of the scan rate, shown in Fig. 2B, furnish a k_ET° value of 0.025 cm/s. Owing to the influence of the irreversible wave on the peak potential of the second reversible wave, the k_ET^o value for the [1-Ni]^–/[1-Ni]^2– couple was determined at a later stage from fits to the entire CV (vide infra). Similarly, k_ET^o values were obtained for the 2-Ni/[2-Ni]^– and [2-Ni]^–/[2-Ni]^2– reversible redox couples (both found to be about 0.06 cm/s, SI Appendix, Figs. S14 and S15) and the 3-Ni/[3-Ni]^– and [3-Ni]^–/[3-Ni]^2– couples (0.05 and 0.03 cm/s, respectively), SI Appendix, Figs. S16 and S17. The greater kinetic facility of the Ni^II/I reduction relative to the Co^II/I reduction is attributed to the requisite dissociation of a solvent [k°_ET = 0.01 cm/s (36)] ligand that is axially coordinated to the low-spin d⁷ Co^II molecule as observed in the solid-state (32). No axial ligand is expected from our theoretical computations nor observed in the solid-state structure (Fig. 1) of the low-spin d⁸ Ni^II species.

Titration of 1-Ni with benzoic acid results in the growth of the irreversible wave centered at –1.76 V (SI Appendix, Fig. S18), indicative of an electrocatalytic reaction. Treatment of 1-Ni with solid potassium carbonate to deprotonate the pendant acid group results in the elimination of the central irreversible feature (Fig. 2C, – –) as well as an ∼60-mV negative shift in the midpoint potential of the first reversible wave to –1.43 V. The midpoint potential of the second reversible wave shifts in the positive direction to ca. –1.88 V following treatment with K₂CO₃. These data confirm that the middle, irreversible peak is associated with an electrocatalytic reaction involving an acid species along with proton transfer from the hangman group. The observed negative shift in the first equilibrium potential is consistent with deprotonation of the pendant carboxylic acid group leading to an increase in the charge on the molecule as a whole, which disfavors reduction. Titration of the deprotonated 1-Ni with increasing amounts of benzoic acid leads to the return of the irreversible wave (Fig. 2C, – ∙ –, green, blue, and purple traces), and subsequent growth with increasing benzoic acid concentration is also in agreement with the occurrence of an electrocatalytic reaction involving an acid source. Indeed, chronocoulometry of a 0.4-mM solution of 1-Ni in the presence of 15 mM benzoic acid at –1.77 V leads to the generation of H₂ with a faradaic efficiency of 92% over the course of an electrolysis that passed a total of 20.0 C.

Titration of 2-Ni with benzoic acid also results in the emergence and growth of an irreversible catalytic wave as shown in Fig. 2D. However, this catalytic feature is offset toward more negative potentials relative to what is observed in 1-Ni. The presence of the pendant proton relay is therefore integral to the observance of a catalytic wave that is markedly shifted toward more positive potentials (i.e., the hangman effect).

The CV characteristics displayed in Fig. 2 A and C—specifically the irreversible catalytic wave and subsequent reversible wave—are reminiscent of what Savéant classifies as “total catalysis.” (41, 42) This term denotes a mechanistic regime wherein, owing to a high catalytic rate and/or a dearth of reactant, the rate of reactant consumption is very rapid, leading to control of the electrocatalytic response by diffusion of the reactant from the bulk electrolyte. This behavior results in the presence of two waves: (i) an irreversible wave involving the reactant-diffusion-controlled catalytic process, followed by (ii) a reversible wave associated with the molecular catalyst, centered at the potential where it appears in the absence of reactant. The catalytic rate constant influences the peak potential of the irreversible wave, but not the peak current (41, 42). In the case of 1-Ni, notwithstanding the absence of exogenous benzoic acid, one equivalent of acid from each hangman porphyrin is available. These acid functional groups should permit H₂ production, and catalytic turnover would regenerate the [1-Ni]^– state. Hence, we infer that the second reversible wave involves the formal Ni^I/0 reduction of the molecule in its deprotonated (hanging carboxylate group) state. We ascribe the positive shift in the second reduction potential upon addition of potassium carbonate to the greater stabilizing effect of the smaller and possibly ion-paired K⁺ countercations present in this case, compared with tetrabutylammonium cations that serve to provide charge balance upon electrochemical reduction. The effect of the more charge-dense potassium ions would be pronounced particularly in the reduction to the highly charged deprotonated and doubly reduced state.

Thin-layer spectroelectrochemical analysis of 3-Ni was undertaken to provide insight into the electronic structure of the Ni(II), Ni(I), and formally Ni(0) states of the porphyrin molecules. The UV-vis absorption spectra of the three species are shown in Fig. 3. Controlled potential electrolysis of 3-Ni in acetonitrile at –1.3 V cleanly generates the spectrum of [3-Ni]^– with good isosbestic points (SI Appendix, Fig. S19A). The bathochromic shift and concomitant loss of intensity of the Soret band along with the growth of new bands at 358 and 608 nm are consistent with spectra obtained by Savéant and coworkers for the one-electron reduction products of similar Ni porphyrins that were assigned as formal Ni(I) species based on UV-vis absorption and ESR data (43). These data therefore support the contention that the first reduction of 3-Ni to [3-Ni]^– is metal-centered. Electrolysis at –1.9 V generates the spectrum of the two-electron reduced species [3-Ni]^2–. The growth of a broad absorption band at 615 nm that extends into the near-infrared region (SI Appendix, Fig. S19B) is consistent with a ligand-centered second reduction (44). The absorption spectrum of 3-Ni is quantitatively recovered upon electrolysis at 0.0 V following the generation of [3-Ni]^2– (SI Appendix, Fig. S19C), supporting the CV data that indicate that the reduction processes are reversible.

Fig. 3.

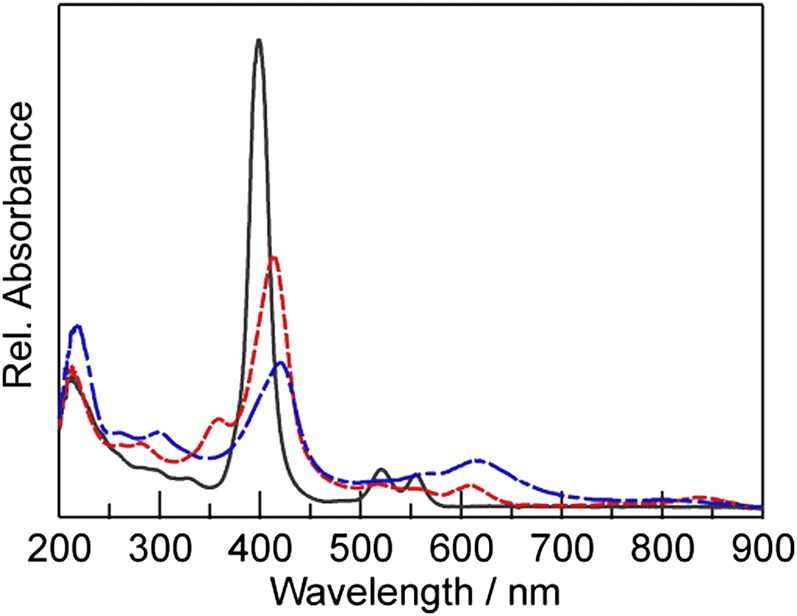
UV-vis absorption spectra of 3-Ni (dark gray —), [3-Ni]^– (red – –), and [3-Ni]^2– (royal blue — - —) in 0.1 M TBAPF₆ in acetonitrile obtained using thin-layer spectroelectrochemistry.

Density functional theory (DFT) calculations (see SI Appendix for full details on the computational method) were used to probe the electronic structure of the compounds in the different oxidation states. For computational tractability, the tert-butyl groups on the xanthene backbone and pentafluorophenyl meso-substituents of the porphyrin ring were truncated to methyl groups and chlorine atoms, respectively. These truncations were chosen based on Hammett constants (45) of similar values (SI Appendix), and we have exploited this protocol successfully in recent studies to compute the equilibrium potentials of intermediates involved in homogeneous hydrogen evolution (46).

We find that the Ni(II) closed-shell singlet of the 3-Ni resting state is 8.5 kcal/mol lower in energy than the triplet. In addition, upon reduction to [3-Ni]^–, the results of calculations using five different functionals (SI Appendix, Table S1) all agree that the spin density on Ni is near unity, suggesting that the unpaired electron is localized on the nickel center. DFT calculations on the doubly reduced molecule [3-Ni]^2– with seven different functionals (SI Appendix, Table S2) all show that only one electron is localized on Ni, and the triplet state is lower in energy than the closed-shell singlet. Fig. 4 displays the singly occupied molecular orbitals (SOMOs) calculated for [3-Ni]^– (Fig. 4A) and [3-Ni]^2– (Fig. 4 B and C), showing that in the case of the monoanion (S = 1/2), the electron is localized primarily on the σ*(d_x²–y²) orbital of the Ni center. Subsequent reduction to the dianion (S = 1) leads to the highest energy SOMO possessing electron density primarily localized on the porphyrin ligand, whereas the SOMO–1 resembles the SOMO for [3-Ni]^2–. Spin density plots of the mono- and dianion are displayed in SI Appendix, Fig. S20.

Fig. 4.

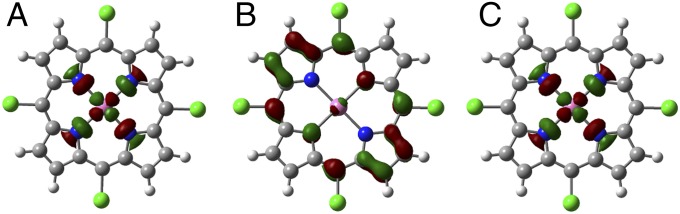
Calculated (B3P86 solvated phase; IsoValue: 0.05): (A) SOMO of [3-Ni]^– showing electron density localized on the nickel center. (B) SOMO and (C) SOMO–1 of [3-Ni]^2– showing that the second electron is localized primarily on the ligands.

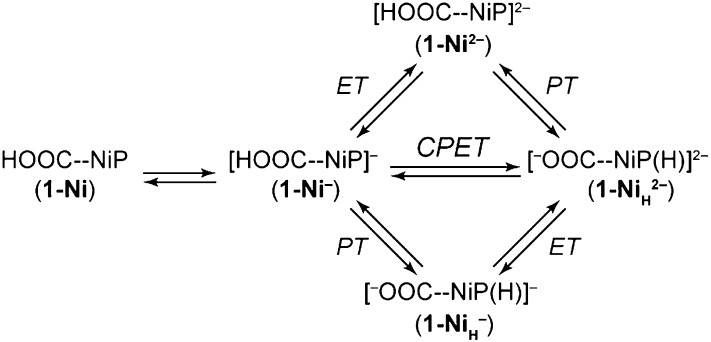
The electrocatalytic generation of hydrogen from the [1-Ni]^– resting state must proceed through an initial step consisting of either one of two stepwise PCET pathways or a concerted one. The stepwise (ETPT and PTET) and concerted (CPET) pathways from [1-Ni]⁻ leading to the generation of a formally Ni(II) hydride, [1-Ni_H]²⁻, are shown in Scheme 2 (where HOOC–NiP is synonymous with 1-Ni). Insight into the operative PCET pathway comes from modeling the CV responses in concert with using the insights garnered from DFT computations as a guide. We computed the equilibrium potentials E_eq of plausible intermediates using the experimentally determined Ni^II/I reduction potential of 1-Ni (–1.37 V) as a reference value (Table 1). The correspondence between experimental and computed equilibrium potentials of nonhangman porphyrins 2-Ni and 3-Ni is very satisfying, and gives us confidence in the relevance of the computational results. Moreover, the computed reduction potential for a putative Ni^IIH intermediate (calculated as –1.84 V) is found to lie between the reduction potentials of 1-Ni and [1-Ni]^–, within our voltage sweep window. As such, a subsequent reduction of this Ni^IIH to Ni^IH could be favored. Theoretical studies on the mechanism of hydrogen production by cobaloximes have revealed that the equilibrium potential of the Co^IIH–Co^IH couple in those systems may also lie between that of Co^II/I and Co^I/0 (47).

Scheme 2.

Stepwise (ETPT and PTET) and concerted (CPET) PCET from [1-Ni]^– leading to the generation of a formally Ni(II) hydride, [1-Ni_H]^2–. HOOC–NiP is synonymous with 1-Ni, indicating the presence of a proton on the carboxylate group in the second coordination sphere of the Ni²⁺ metal center.

Table 1.

Computed reduction potentials of nickel hangman porphyrins

Oxidized species	Sox	Reduced species	Sred	E0/V vs. Fc+/Fc*
HOOC–NiP	0	[HOOC–NiP]–	1/2	−1.37 (–1.37)†
[HOOC–NiP]–	1/2	[HOOC–NiP]2–	1	−1.85
[OOC–NiP]–	0	[OOC–NiP]2–	1/2	−1.40 (–1.43)
[OOC–NiP]2–	1/2	[OOC–NiP]3–	1	−2.01 (–1.99)
[OOC–Ni(H)P]–	1/2	[OOC–Ni(H)P]2–	1	−0.81
[OOC–Ni(H)P]2–	1	[OOC–Ni(H)P]3–‡	3/2	−1.84
2-Ni	0	[2-Ni]–	1/2	−1.34 (–1.39)
[2-Ni]–	1/2	[2-Ni]2–	1	−1.91 (–1.96)
3-Ni	0	[3-Ni]–	1/2	−1.32 (–1.27)
[3-Ni]–	1/2	[3-Ni]2–	1	−1.76 (–1.82)

Calculations were performed with DFT using the B3P86 functional, 6–31+G(d), and 6–31+G(d,p) basis sets, and conductor-like polarizable continuum model (C-PCM) solvation. Geometries were optimized in solution.

^*Experimental midpoint potential (E_1/2) values are given in parentheses.

^†These experimental and computational values are the same by construction because this is the reference reaction used in computation.

^‡This reduced species refers to the formally Ni(I) hydride; the spin density on nickel remains ∼2 (SI Appendix), indicating that the reduction is ligand-based.

We first set out to determine whether the ETPT framework that is operative in the case of 1-Co could account for the electrocatalytic behavior manifest in Fig. 2 A and C. In the context of such an ETPT mechanism (top route of Scheme 2), three critical parameters that control the electrochemical response are (i) the reduction potential of [1-Ni]^–, (ii) the associated standard heterogeneous ET rate constant, and (iii) the rate of the subsequent intramolecular PT. The experimentally measured equilibrium potential and standard ET rate constant of the nonhangman analog (i.e., the [2-Ni]^–/[2-Ni]^2– couple, which possesses E° = –1.96 V and k_ET° = 0.06 cm/s) provide an estimate for (i) and (ii). However, this still leaves the intramolecular PT rate constant (iii) as well any equilibrium–rate constant and reduction potential values associated with follow-up reactions (such as the protonation of a hydride to evolve H₂) as unknowns. If these are fast and post–rate-limiting they will not influence the electrokinetic response.

As in the case for the one-electron ET reactions, CV simulation is a powerful tool for gaining mechanistic insight into homogeneous electrocatalytic reactions, especially in cases where substrate limitation cannot be avoided. CV simulations of an ETPT pathway using the aforementioned parameters are shown in SI Appendix, Fig. S21. In these simulations, we also assumed that all bimolecular reactions proceed at the diffusion limit with a rate constant on the order of 10¹⁰ M^–1⋅s^–1. Moreover, the intramolecular rate constant $k_{PT}^{intra}$ is set to 10¹³ s^–1, such that it is many orders of magnitude faster than the bimolecular reactions (i.e., we ensure that the product of the diffusion-limited rate constant, 10¹⁰ M^–1⋅s^–1, and the concentration of the catalyst–substrate (<1 mM) will be much less than $k_{PT}^{intra}$). We also set the reduction potential of the Ni^IIH that is formed by protonation of the formally Ni⁰ species to be equal to –1.4 V, close to that of the Ni^II/I reduction potential. This value is considerably more positive than the potential at which catalysis is observed (∼–1.76 V) and also more positive than that computed by DFT (–1.84 V). These parameters (tabulated in Table S3) were specifically chosen to be representative of a best-case scenario for the ETPT mechanism. These governing factors will lead to the most positive peak potentials possible for an ETPT process, which proceeds through the [1-Ni]^2– intermediate: in a reaction scheme governed by these parameters the most negative reduction potential is that of [1-Ni]^–/[1-Ni]^2– and all bimolecular reactions proceed at the diffusion limit. Even though the resulting simulation reveals a voltammogram that displays the general total catalysis behavior, the ETPT model leads to voltammetric features that are not fully coincident with the experimental results (SI Appendix, Fig. S21A); anticipated peak potentials are too negative and peak current values remain too low to account for the experimental result. These observations are conserved over a scan rate range of two orders of magnitude (SI Appendix, Fig. S21B).

To explore the possibility of this ETPT mechanism further, we also simulated CVs using the computed [1-Ni]^–/[1-Ni]^2– and [1-Ni_H]^2–/[1-Ni_H]^3– E° values (–1.85 and –1.84 V, respectively; Table 1) as opposed to using that of the nonhangman analog. The resulting simulated voltammogram is shown in SI Appendix, Fig. S22. Using these computed parameters, a much slower intramolecular PT rate constant of 2,000 s^–1 is needed to replicate the peak potential of the irreversible catalytic wave (SI Appendix, Table S4). However, the simulations show that prominent peaks expected at 30 mV in the return sweep are inconsistent with experimental data. Thus, simulations of the ETPT pathway under any reasonable fitting condition do not match the experimental CVs of 1-Ni. We therefore turned our attention to the interrogation of the PTET and CPET mechanisms displayed in Scheme 2.

To assist in differentiating between the PTET and CPET mechanisms, we set out to measure the H–D isotope effect. In the case of the PTET mechanism, no significant isotope effect is expected because the proton transfer exists in a rapid preequilibrium, and any equilibrium isotope effect is expected to be too small to lead to a detectable change in peak position. In contrast, any change in the standard CPET rate constant k_CPET associated with H–D isotopic substitution would lead to a shift in peak position if that reaction were to be the rate-determining step. Indeed, as shown by CV simulations (SI Appendix, Fig. S23) a CPET-based framework accommodates the voltammetric behavior of 1-Ni, but the catalytic peak potential is very sensitive to k_CPET. Following treatment of 1-Ni with K₂CO₃ to deprotonate the pendant acid as described above, a batch of this deprotonated hangman porphyrin was titrated with C₆H₅COOH and an identical batch was titrated with C₆H₅COOD. The difference in catalytic peak potential in the case of the two isotopes is plotted as a function of the number of equivalents of acid titrated in SI Appendix, Fig. S24. Because we do not observe a significant isotope effect, we consider a rate-limiting concerted pathway to be unlikely. Instead, these data are consistent with the occurrence of a stepwise PTET from [1-Ni]^– to form the formally Ni(II)H intermediate. We note that we cannot entirely rule out the possibility of a rapid, reversible non–rate-limiting CPET at this time. In this case, isotopic substitution and consequent alteration of the heterogeneous rate constant would not give rise to a change in peak potential at these relatively slow scan rates. Additional computational studies are required to explore this possibility while considering the various potential proton-acceptor sites of the molecule.

Simulations of the PTET pathway are successful in replicating the experimental data with good fidelity as shown in Fig. 5. Simulation parameters are provided in Tables 2 and 3, and these values provide estimates of the thermodynamic and kinetic parameters that govern catalysis. According to these CV simulations, an intramolecular PT from the Ni^I resting state leads to a formal Ni^IIIH species, which exists in minor equilibrium. Subsequent ET furnishes Ni^IIH, followed by another reduction to Ni^IH. Protonation of the hydride by an acid source produces H₂ in a facile step. This contrasts the HER mechanism for the analogous 1-Co system and benzoic acid, which displays an ETPT mechanism for HER (35). The Co^I state is not protonated and only after Co⁰ is formed does the proton transfer to produce Co^IIH. A PTET pathway for 1-Co may be realized but only when strong acids such as p-toluenesulfonic (tosic) acid are used. The only ET step for which there is poor agreement between the computed equilibrium potential (–0.81 V) and experiment/simulation (ca. –1.57 V) is for the formally Ni^IIIH to Ni^IIH reduction (Table 2). The DFT calculations only considered cases where the proton is transferred to the metal center; the disparity between CV simulation (Table 2) and computation (Table 1) in this single reduction potential value thus suggests that the proton may not transfer directly to the metal center but rather to the macrocycle. Efforts to explore alternative proton accepting sites are underway. Nevertheless, the CV data and simulation provide compelling evidence for an operative PTET pathway.

Fig. 5.

Experimental (thick light-brown curves) and simulated (thin blue curves) CVs of a 0.4-mM solution of 1-Ni at a scan rate of (A) 30 mV/s and (B) 300 mV/s. Voltammograms were simulated according to a mechanistic framework consisting of a PTET pathway (Scheme 2) from 1-Ni^– to 1-Ni_H^2–, followed by reduction to 1-Ni_H^3–, which is subsequently protonated by the pendant acid group of another porphyrin molecule to liberate H₂. Parameters used in simulation are tabulated in Tables 2 and 3. (C) Variation of the experimental peak potential of the irreversible catalytic wave of 1-Ni as a function of scan rate (green circles) compared with the variation observed from simulated CVs (blue trace).

Table 2.

Parameters of heterogeneous/electrochemical reactions used in simulating PTET-based pathway

Oxidized species	Reduced species	Eosim*	kETo/cm s–1
HOOC–NiP	[HOOC–NiP]–	−1.37	0.025†
[HOOC–NiP]–	[HOOC–NiP]2–	−1.96‡	0.06‡
[OOC–NiP]–	[OOC–NiP]2–	−1.45§	0.025¶
[OOC–NiP]2–	[OOC–NiP]3–	–1.99	0.002†
[OOC–Ni(H)P]–	[OOC–Ni(H)P]2–	−1.57†	0.01†
[OOC–Ni(H)P]2–	[OOC–Ni(H)P]3–	−1.95†	0.05†

^*Reduction potentials are relative to the reduction potential of Fc⁺/Fc.

^†Obtained from simulating experimental CV data.

^‡Values estimated from that of nonhangman compound 2-Ni.

^§Value determined from treatment of 1-Ni with potassium carbonate, and further refined by simulating shoulder near anodic return peak of 1-Ni/[1-Ni]⁻ wave.

^¶Value set equal to that obtained from trumpet plots of the corresponding protonated species.

Table 3.

Parameters of homogeneous/chemical reactions used in simulating PTET pathway

Reactants	Products	Keq	kforward
[HOOC–NiP]–	[OOC–NiP(H)]–	9 × 10−3*	>105*
[OOC–NiP(H)]– + [OOC–NiP]3–	[OOC–NiP(H)]2– + [OOC–NiP]2–	1.25 × 107†	kdiff‡
[OOC–NiP(H)]2– + [OOC–NiP]3–	[OOC–NiP(H)]3– + [OOC–NiP]2–	4.74†	kdiff‡
[OOC–NiP(H)]3– + acid§	H2 + [OOC-NiP]2–conjugate base	>105	kdiff‡

^*Obtained from simulating experimental CV data.

^†These equilibrium constants are governed by the difference in reduction potentials of the two sets of species.

^‡The forward rate constants of these downhill reactions are assumed to be the diffusion-limited rate constant: 10¹⁰ M^–1⋅s^–1.

^§All nickel porphyrins with protonated hanging groups are permitted as acid sources in the mechanism.

The discrepancy in mechanistic pathway between 1-Co and 1-Ni could arise from a difference in basicity of the metal centers. It is interesting that for both 1-Co and 1-Ni, it is the d⁹ electronic configuration that is protonated (Co⁰ for 1-Co and Ni^I for 1-Ni). The presence of an electron in the in-plane metal-based orbital might provide a more favorable electrostatic environment that induces proton transfer. The contributions of electrostatic versus covalent factors in the HER mechanism have not yet been computationally disentangled. The results here suggest this may be a fruitful line of inquiry.

Conclusions

The effect of a pendant proton relay (hangman group) proximate to the catalytic center in nickel hangman porphyrins leads to an improvement in catalytic activity over analogous nonhangman molecules. The hangman effect is associated with the facilitation of a stepwise PTET mechanism, which is favored over the ETPT pathway that is observed in the case of the cobalt catalyst. Indeed, because Ni-based catalysis avoids generation of the formally metal(0) species, the nickel porphyrin offers an improvement in catalytic activity over the cobalt analog, which proceeds through a stepwise ETPT route via Co⁰. Computational and spectroelectrochemical results are consistent with the reduction of Ni(I) involving porphyrin ligand-based orbitals, such that the Ni(0) species is truly a Ni(I) porphyrin radical. Studies to shed more light on the nature of the hydrides formed during these PCET reactions as well as the stabilization of proposed intermediates by appropriate ligand design are underway. Such studies could shed more light on the requirements for facile H₂ evolution through PCET.

Materials and Methods

¹H NMR spectra (500 MHz) were recorded on samples in CDCl₃ at room temperature unless noted otherwise. Silica gel (60-µm average particle size) was used for column chromatography. THF (anhydrous), methanol (anhydrous), CH₂Cl₂ (anhydrous), benzoic acid (≥99.5%), and tetrabutylammonium hexafluoro-phosphate (TBAPF₆, ≥99.0%), and all other chemicals were used as received.

Electrochemical measurements were performed on a CH Instruments 760D Electrochemical Workstation using CHI Version 10.03 software. CV experiments were conducted in a nitrogen-filled glovebox, a glassy carbon button working electrode (area = 0.071 cm²), BASi Ag/AgNO₃ (0.1 M) reference electrode in 0.1 M TBAPF₆ acetonitrile solution at room temperature, and Pt mesh counterelectrode. All CVs were recorded with compensation for solution resistance. Bulk electrolysis was performed using a glassy carbon rod (7 mm × 5 cm) working electrode and a platinum mesh auxiliary electrode in a gas-tight electrochemical cell. The amount of H₂ gas produced in the headspace was analyzed by an Agilent 7890A GC.

UV-vis spectra were recorded at room temperature in quartz cuvettes in CH₂Cl₂ on a Varian Cary 5000 UV-vis-near-infrared (NIR) spectrophotometer. UV-vis spectroelectrochemical measurements were made using a quartz thin-layer cell (0.5-mm path length) at room temperature in a N₂-filled glovebox with an Ocean Optics USB4000 spectrophotometer and DT-Mini-2GS UV-vis-NIR light source.

Computed structures were optimized with DFT using a variety of exchange-correlation functionals. For computation tractability, the tert-butyl groups on the xanthene backbone and pentafluorophenyl meso-substituents of the porphyrin ring were truncated to methyl groups and chlorine atoms, respectively.

All simulated CVs were calculated using DigiElch 7 software (39). Symmetry factors–transfer coefficients were set to 0.5 for all ET steps. Additional experimental details are available in SI Appendix.