Quantitation of interactions between two DNA loops demonstrates loop domain insulation in E. coli cells

Significance

Genes are frequently regulated by interactions between proteins that bind to the DNA near the gene and proteins that bind to DNA sites located far away, with the intervening DNA looped out. In eukaryotic genomes, genes and their distant sites are intermingled in complex ways and it is not understood how the correct connections are formed. Using two pairs of DNA-looping sites in bacterial cells, we tested the idea that one DNA loop can either assist or interfere with the formation of another DNA loop. By measuring the strength of these interactions between loops, we showed that this mechanism is capable of directing a distant site to the correct gene and preventing it contacting the wrong gene.

Abstract

Eukaryotic gene regulation involves complex patterns of long-range DNA-looping interactions between enhancers and promoters, but how these specific interactions are achieved is poorly understood. Models that posit other DNA loops—that aid or inhibit enhancer–promoter contact—are difficult to test or quantitate rigorously in eukaryotic cells. Here, we use the well-characterized DNA-looping proteins Lac repressor and phage λ CI to measure interactions between pairs of long DNA loops in E. coli cells in the three possible topological arrangements. We find that side-by-side loops do not affect each other. Nested loops assist each other’s formation consistent with their distance-shortening effect. In contrast, alternating loops, where one looping element is placed within the other DNA loop, inhibit each other’s formation, thus providing clear support for the loop domain model for insulation. Modeling shows that combining loop assistance and loop interference can provide strong specificity in long-range interactions.

Transcription of genes is regulated by promoter-proximal DNA elements and distal DNA elements that together determine condition-dependent gene expression. In eukaryotic genomes, enhancers can be many hundreds of kilobases away from the promoter they regulate (1–3), and the intervening DNA can contain other promoters and other enhancers (4–7). How the regulatory influence of distal elements is exerted efficiently and specifically at the correct promoters is poorly understood.

Enhancers are clusters of binding sites for transcription factors and chromatin-modifying enzymes, and activate promoters by directly contacting them via DNA looping (8–12). Enhancer trap approaches and mapping of transcription factor binding and chromatin modifications have identified tens of thousands of enhancer elements in metazoan genomes (7, 13–16). Chromatin capture studies show that enhancers and promoters are connected in highly complex condition-dependent patterns (6, 15, 17). Although core enhancer and promoter elements can provide some specificity (18), enhancers are often able to activate heterologous promoters if they are placed near to each other. Indeed, this lack of specificity is the basis for standard enhancer assays and screens (7, 14, 19). Thus, additional mechanisms are clearly needed to target enhancers to the correct promoters over long distances and to prevent their interaction with the wrong promoters. Dedicated DNA-looping elements that can either assist or interfere with enhancer–promoter looping are thought to play a major role.

In theory, any DNA loop that brings the enhancer and promoter closer together should assist their interaction (Fig. 1A), because the efficiency of contact increases as the length of the DNA tether between the sites shortens (20–24). Promoter-tethering elements in Drosophila that allow activation by specific enhancers over long distances are proposed to form DNA loops between sequences near the enhancer and the promoter (18, 25). In the mouse β-globin locus, the Ldb1 protein binds to proteins at the locus control region and at the promoter and appears to form a bridge necessary for efficient enhancer–promoter contact (26). In bacteriophage λ, the CI protein forms a 2.3-kb DNA loop that brings a distal stimulatory site close to RNA polymerase at the PRM promoter (27). Enhancer–promoter targeting has also been demonstrated on plasmid constructs using heterologous looping proteins—e.g., with λ CI in human cells (28) and the Drosophila GAGA protein in human cells and in yeast (29, 30).

Fig. 1.

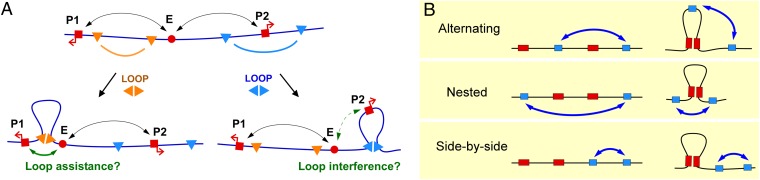
Interactions between DNA loops. (A) DNA-looping interactions between sites on the DNA, e.g., between an enhancer (E) and promoters (P1 and P2), are proposed to be affected by other DNA loops. Specific interactions between looping elements (triangles) can either assist enhancer–promoter looping by bringing the enhancer and promoter closer together (orange triangles) or are thought to interfere with enhancer–promoter looping by placing them in separate loop domains (blue triangles). (B) The three possible topological arrangements of two pairs of interacting sites on DNA. We tested in each case whether the formation of a loop between one pair of sites affects the propensity of the other sites to interact (and vice versa).

DNA looping also seems to be able to inhibit enhancer–promoter contact. Enhancer-blocking insulators are defined by their ability to prevent enhancer activation of the promoter when placed between the enhancer and the promoter. A large body of evidence is consistent with the idea that insulators work by binding proteins that form DNA loops to other insulators (31–35). This mechanism of insulator action is rationalized by the loop domain model (36), which proposes that the formation of a DNA loop creates a separate topological domain that inhibits interaction between any site within the loop and any site outside the loop (Fig. 1A). This model is the only one that can currently explain the requirement that an insulator must be between the enhancer and promoter to block activation, as well as observations that two insulators between the enhancer and promoter sometimes do not block activation (37, 38). The loop domain model is also a potential explanation (35) of the topologically associated domains (TADs) revealed by genome-wide mapping of DNA contacts by chromatin capture methods in genomes from mice to bacteria (39–45). Individual DNA sites between two domain boundaries interact more frequently with each other than they do with individual DNA sites in other TADs—i.e., domain boundaries act like insulators. Consistent with the loop domain model, domain boundaries interact with each other at high frequency and often contain known DNA-looping elements, being enriched for insulator protein binding sites, as well as for active promoters and enhancers (44).

Despite the fundamental significance of the loop domain model in explaining insulator action and the formation of TADs, unequivocal tests of the model in vivo have been hampered by the complexity of eukaryotic genomes and their gene regulatory elements. Evidence from more defined systems has supported the loop domain model. In a plasmid transfection system, a 344-bp DNA loop formed by a Tet repressor derivative around the SV40 enhancer inhibited its activation of a promoter 2 kb away (46). However, the small loop may have affected enhanceosome assembly in these experiments. In an in vitro system with E. coli proteins and supercoiled plasmids, a 630-bp DNA loop formed by the Lac repressor (LacI) around the NtrC enhancer element inhibited its activation of the glnA promoter 2.5 kb away (47). However, this effect has not been tested in vivo. In both studies, the lack of information about DNA-looping efficiencies prevents a quantitative analysis of loop interference.

To clearly test the loop domain model in vivo and to rigorously quantitate loop interaction effects, we measured interactions between large DNA loops formed in the E. coli chromosome by the two best-characterized DNA-looping proteins, LacI and bacteriophage λ CI. Previously (24), we quantitated looping efficiency of single DNA loops in vivo by assaying DNA loop-mediated LacI or CI repression of a reporter gene, and in vitro by the single molecule technique, tethered particle motion (TPM). Here, we have combined LacI and CI DNA loops in each of the three possible topologies (Fig. 1B) to show that alternating DNA loops interfere, nested DNA loops assist, and side-by-side loops do not affect one another’s formation. Fitting our data to a general statistical–mechanical model of loop interaction allowed calculation of the strength of looping assistance or interference.

Results

Quantitation of Interactions Between DNA Loops.

There are three topological ways to arrange two pairs of DNA-looping sites: alternating, nested, and side by side (Fig. 1B; note that we ignore the parallel/antiparallel orientation of the strands at the loop clamps). The expectation from the loop domain model is that in the alternating arrangement, the formation of one loop will interfere with the formation of the second loop. For nested loops, we expect that the formation of one loop would assist the formation of the second. If the interior loop forms first, then the linear distance (along the DNA), between the exterior loop sites becomes shorter. When the exterior loop is formed, the distance between the interior loop sites may or may not shorten (depending on the geometry), but they are nevertheless likely to become more spatially constrained because they become linked by a DNA tether on each side. We do not expect side-by-side loops to affect each other.

Previously we used in vivo reporter assays and statistical–mechanical modeling to extract key DNA-looping parameters for LacI and CI DNA loops (24), allowing calculation of the fraction of the time (averaged over many cells) that the DNA is in a looped state, which we term F. The rationale of this approach is shown in Fig. 2.

Fig. 2.

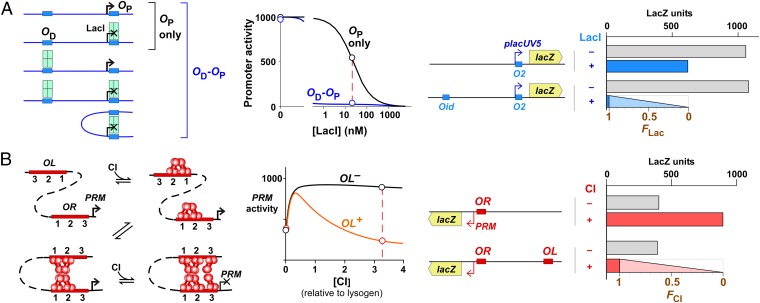
Measuring looping in vivo. (A, Left) A LacI tetramer represses the promoter by binding to a proximal lac operator (O_P). Repression can be improved by DNA looping between O_P and a distal lac operator (O_D) because a tetramer bound at O_D constitutes a high local concentration at O_P due to DNA tethering. The strength of the O_D effect depends on the operator combination, the LacI concentration and the length of the spacer DNA. (Right) The effect of O_D on reporter expression can be used to measure the fraction of time that the system spends in the looped state, F_Lac. In the absence of looping, F_Lac = 0, activity is the same with or without O_D. If the system were fully looped, F_Lac = 1, the activity of the O_D–O_P reporter would be reduced to background. (B) CI. (Left) Repression of the PRM promoter is dependent on DNA looping between OR and OL, because OR3 is too weak to be occupied by a CI dimer at physiological concentrations. (Right) As with LacI, the effect of OL on reporter expression can be used to measure the fraction of time that the system spends in the looped state, F_CI.

For LacI, repression of a PlacUV5 promoter with a single proximal lacO2 operator is relatively inefficient at low LacI concentrations. Repression is more efficient when a strong distal operator (Od) is present and DNA looping between the two operators can occur, aiding binding of the LacI tetramer to the proximal site (Fig. 2A). The fractional DNA looping F can be extracted from measurement of the efficiency of repression in the presence of the distal operator (24) (Materials and Methods).

For CI, the fraction of DNA looping can be obtained from measurements of CI regulation of the phage PRM promoter (24, 27, 48). At low CI concentrations, CI tetramers assemble at the OL and OR sites, and these DNA-bound tetramers can form an OL–OR DNA loop by CI octamerization (Fig. 2B). PRM is activated by binding of CI to OR2 (49), both in unlooped and looped states (27). However, repression of PRM by CI, which occurs at higher CI concentrations, is dependent on looping because repressive CI binding at the very weak OR3 operator relies on interactions with CI bound at stronger sites at OL (Fig. 2B). Again, the efficiency of repression of PRM in the presence of OL can be used to measure the fractional DNA looping F (24) (Materials and Methods).

Alternating Loops Interfere in Vivo.

We made lacZ reporters with an alternating arrangement of binding sites for LacI (O2 and Oid) and CI (OR and OL). For measuring LacI looping, lacZ was placed downstream of PlacUV5.O2; for measuring CI looping, lacZ was placed downstream of OR.PRM (Fig. 3A and Figs. S1A and S2). Two different alternating arrangements were made: symmetrical and asymmetrical (Fig. 3 B and C), with loop sizes ranging from 1,200 to 1,800 bp. The smallest distance between operators was 300 bp, which is well beyond the apparent 20- to 45-bp persistence length of DNA in E. coli (24, 50).

Fig. 3.

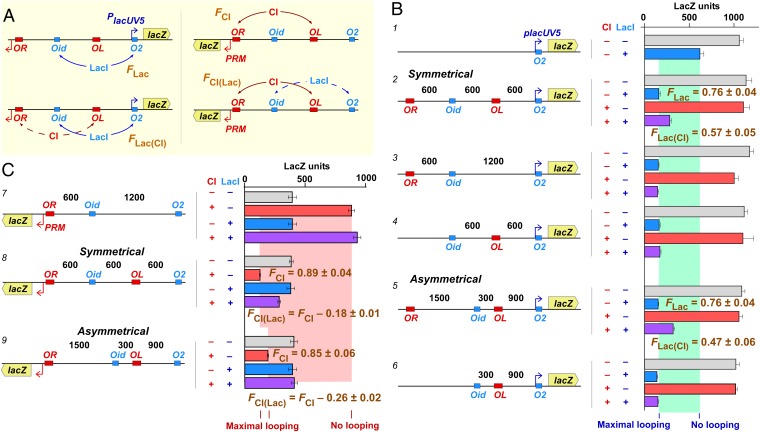
Loop interference by alternating loops. (A) Experimental strategy for measuring interactions between alternating loops. A lacZ reporter is placed downstream of PlacUV5 to measure the fraction of LacI-mediated Oid–O2 looping in the absence of CI (F_Lac) or in the presence of CI [F_Lac(CI)]. Similarly, the reporter is placed downstream of PRM to measure the fraction of CI-mediated OL–OR looping in the absence of LacI (F_CI) or in the presence of LacI [F_CI(Lac)]. (B) Effect of CI loops on LacI looping. Chromosomal reporters (distances in base pairs; Materials and Methods; Figs. S1A and S2) were exposed to fixed levels of LacI (18 nM) or CI (3.3 wild-type lysogenic units) expressed from other chromosomal constructs (Materials and Methods; Fig. S1B) (24). Histograms show steady-state LacZ units and 95% confidence intervals (n = 5–12). Construct 1 shows weak repression in the absence of looping to the distal operator. The presence of Oid 1,200 bp upstream improves repression in both the symmetrical constructs (2–4) and the asymmetrical constructs (5, 6), but this improvement is diminished when Oid is flanked by OL and OR and CI is present (constructs 2 and 5). The F_Lac and F_Lac(CI) values were calculated by fitting the four data points for each construct with a statistical–mechanical model of LacI repression (24) (Materials and Methods). Errors for F values are SDs. (C) Effect of LacI loops on CI looping. Experimental details are as in B except n = 9 for the LacZ units. In the absence of OL, CI activates PRM but does not repress it (construct 7). Repression by CI is improved in the presence of OL in the symmetrical construct (8) and the asymmetrical construct (9); as expected, repression is stronger for the 1,200-bp CI loop compared with the 1,800-bp CI loop (24). This improved repression is diminished when OL is flanked by Oid and O2 and LacI is present (additional controls for the symmetrical construct are given in Fig. S3). The F_CI and F_CI(Lac) values were calculated by fitting the four data points for each construct and the four data points of construct 7 with a statistical–mechanical model of CI repression (24) (Materials and Methods). F_CI(Lac) values are expressed relative to the corresponding F_CI values (errors are SDs).

We measured lacZ expression in the presence or absence of fixed concentrations of LacI (18 nM) and CI (3.3 wild-type lysogenic units), expressed from chromosomally integrated constructs (24, 27) (Fig. S1B).

In the absence of the distal operator, LacI repression was weak (Fig. 3B, construct 1). Repression improved substantially with a distal Oid operator 1,200 bp away (Fig. 3B, constructs 2–6), with the magnitude of the improvement indicating looping 76 ± 4% of the time (errors are 95% confidence limits). When the distal Oid was flanked by CI operators and CI was present, then LacI repression was reduced to levels indicating 57 ± 5% and 47 ± 6% looping for the symmetrical and asymmetrical constructs, respectively (Fig. 3B, constructs 2 and 5). Importantly, both CI operators were required for this loop inhibition (Fig. 3B, constructs 3, 4, and 6), implying that CI looping sequestered the distal lac operator.

A reciprocal effect was seen by assaying CI looping (Fig. 3C). In the absence of the distal OL operator, CI activated PRM some twofold (Fig. 3C, construct 7). The presence of OL 1,200 or 1,800 bp upstream enabled CI repression, indicative of 89 ± 4% or 85 ± 6% looping, respectively (Fig. 3C, constructs 8 and 9). Addition of LacI did not affect PRM regulation in the absence of OL (construct 7) but inhibited repression when OL was present and flanked by lac operators, with looping measured at 71 ± 5% or 59 ± 8% (constructs 8 and 9). Again, a single lac operator within the loop or outside the loop had no effect (Fig. S3).

These results show a loop interference effect for loops in the alternating arrangement, with CI or LacI sites effectively acting as insulators.

Nested Loops Give Loop Assistance.

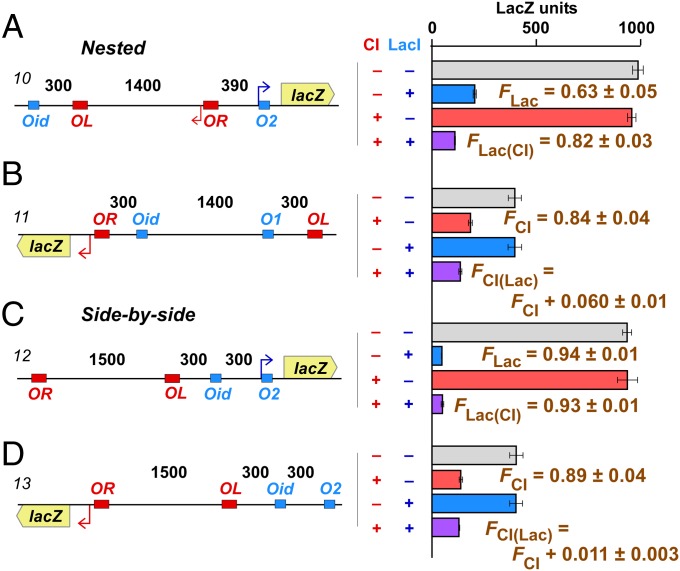
We made two different nested loop constructs, one with a 1,400-bp CI loop inside a 2,090-bp LacI loop (Fig. 4A, construct 10), and one with a 1,400-bp LacI loop (an Oid–O1 loop) inside a 2,000-bp CI loop (Fig. 4B, construct 11). Addition of CI improved LacI looping from 63 ± 5% to 82 ± 3% for the CI-inside construct. Addition of LacI improved CI looping from 84 ± 4% to 90 ± 5% for the LacI-inside construct.

Fig. 4.

Loop assistance by nested loops and no effect of side-by-side loops. Experimental details are as in Fig. 3. Histograms show steady-state LacZ units and 95% confidence intervals (n = 4–9). F_Lac and F_Lac(CI) values for each construct (10, 12) were calculated by fitting the four data points shown. The F_CI and F_CI(Lac) values were calculated by fitting the four data points for each construct (11 or 13) and the four data points of construct 7 (Fig. 3). F_CI(Lac) values are expressed relative to the corresponding F_CI values. Errors for F values are SDs. (A and B) Nested loops. Addition of the protein for the internal loop increases looping of the external loop. (C and D) Side-by-side loops. Addition of CI has no effect on LacI looping and vice versa.

Thus, in a nested arrangement, formation of the inside loop improved formation of the outside loop. Our reporter approach prevented us measuring the fraction of looping for the internal loop.

This experiment also replicates the insulator bypass experiment, which provides strong support for the loop domain model of insulator action. Placement of two insulators between an enhancer and promoter can relieve the enhancer blocking caused by a single insulator (37, 38). Under the loop domain model, looping between the tandem insulators would leave the enhancer and promoter in the same domain. In our experiments also, a single CI site placed between two LacI sites can inhibit their interaction (as long as it can loop to an outside site; Fig. 3), whereas two CI sites do not block interaction of the LacI sites, but in fact stimulate it.

Side-by-Side Loops Do Not Interact.

We also made reporters with a 1,500-bp CI loop and a 300-bp LacI loop placed next to each other and separated by 300 bp. We found that the presence of CI did not affect LacI looping (Fig. 4C), and the presence of LacI did not affect CI looping (Fig. 4D), confirming our expectation that side-by-side loops do not interact.

Model to Quantitate Loop Interactions.

Although it is clear from our data that alternating and nested loops interact, it is difficult to appreciate the strength of the interaction because none of the loops forms with 100% efficiency (i.e., F = 1). However, the measured F values obtained for each of the loop arrangements provide sufficient information to calculate the strength of the loop interference or assistance by use of a simple statistical mechanical model of loop interaction.

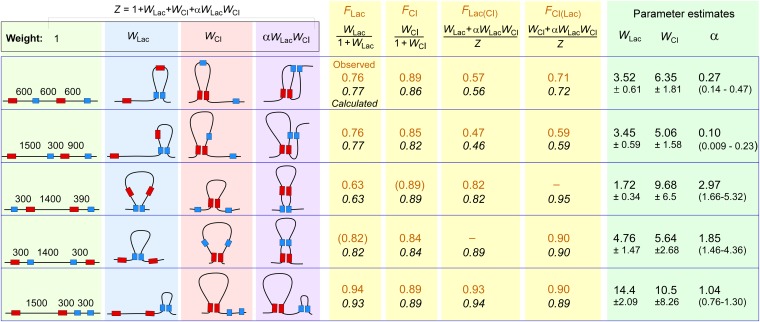
If we consider just one pair of operators, then the DNA can exist in either a looped or an unlooped state. This equilibrium is determined by the nature and concentration of the looping protein, the length and nature of the DNA between the operators, and the chemical environment. The propensity of loop formation relative to the unlooped ground state under these fixed conditions can be simply defined by a statistical weight W. The fraction looped is a function of this weight F = W/(1 + W). Each LacI loop and CI loop has its own weight, W_Lac or W_CI, that determines F_Lac or F_CI in the absence of the other protein (Fig. 5). Note that for LacI and CI, the looped and unlooped states are each mixtures of species (Fig. 2 A and B), which, for the purposes of the loop interaction analysis, it is not necessary to distinguish.

Fig. 5.

Modeling loop interaction. (Left) For each construct tested, the four possible looped species in the presence of both LacI and CI and their relative statistical weights. The fraction of each species is given by its weight divided by the partition sum, Z. Alpha (α) is the loop interaction factor: α > 1 indicates loop assistance (the double looped species forms more often than the product of individual loop weights); α < 1 indicates loop interference (the double looped species forms less often than the product of individual loop weights). (Center) Observed F values (brown) from Figs. 3 and 4, and the F values (italic) calculated from the equations shown using the fitted loop weights and α for each construct (Right). Observed F values in parentheses were estimated from other measurements (Fig. S4). W_Lac, W_CI, and α were fitted to minimize the difference between observed and calculated F values (Materials and Methods). W errors are SDs, and the ranges for the α estimates are the 2.5–97.5 percentiles (>900 fitting runs).

In the case where there are two pairs of operators, there are four loop states: all sites unlooped, only LacI sites looped, only CI sites looped, or both pairs of sites looped (Fig. 5). If the loops form independently of each other, i.e., they do not interact, then the statistical weight of the double-looped state is just the product of the individual loop weights W_Lac∙W_CI. However, if the loops do interact, a loop interaction factor α (Fig. 5) can be used to quantitate the direction and strength of the loop interaction, with the weight of the double-looped species represented by α∙W_Lac∙W_CI. Thus, when α < 1, there is loop interference, the double-looped species forms less frequently than expected; when α > 1, there is loop assistance, the double looped species forms more frequently than expected.

For each of the alternating loop arrangements, our in vivo measurements provide us with four F values: F_Lac, F_CI (for looping in the absence of the other loop), F_Lac(CI), and F_CI(Lac) (for looping in the presence of the other loop). By using a Monte Carlo fitting procedure, we were able to obtain convergent estimates for W_Lac, W_CI, and α that closely reproduced these F values (Fig. 5; Materials and Methods).

The obtained values for α, 0.27 (95% confidence interval 0.14–0.47) and 0.10 (0.01–0.23) for the symmetrical and asymmetrical alternating arrangements, respectively, indicate that the formation of one loop inhibits the formation of the other loop by 3.7- or 10-fold (1/α). Whether there is a real difference between the two geometries is not clear, because the errors in these estimates overlap.

For each of the nested loop arrangements, our measurements provide us with only two F values: F_Lac and F_Lac(CI) (for the CI-inside case) or F_CI and F_CI(Lac) (for the LacI-inside case). However, we can interpolate between other F measurements to estimate F_CI for the CI-inside case and F_Lac for the Lac-inside case (Fig. S4). For the CI-inside case where the CI loop is 1,400 bp, we used the F_CI values obtained for the 1,200-bp (Fig. 3C, construct 8), 1,500-bp (Fig. 4D, construct 13), 1,800-bp (Fig. 3C, construct 9), and 2,000-bp (Fig. 4B, construct 11), CI loops to give an estimate of F_CI = 0.89 (Fig. S4A). For the LacI-inside case, where we have no direct comparisons for the Oid–O1 looping, we interpolated between the j_LOOP values obtained from model fitting for the 300-bp (Fig. 4B, construct 12), the 1,200-bp (Fig. 3B, constructs 2 and 5), and 2,090-bp (Fig. 4B, construct 9), LacI loops (Fig. S4B). j_LOOP is the effective concentration of one site on the DNA relative to another site on the same DNA molecule, and is a critical parameter in determining loop efficiency (51). From this estimate of j_LOOP for a 1,400-bp loop, and our previous measurements of the dissociation constants for LacI at O1, it is possible to calculate F_Lac = 0.82 for the 1,400-bp Oid–O1 loop (24) (SI Materials and Methods). Having three F values for each nested construct allowed us to obtain convergent estimates for W_Lac, W_CI, and α in each case (Fig. 5). The values for α were 3.0 (1.7–5.3) and 1.9 (1.5–4.4) for the LacI-inside and CI-inside arrangements, respectively, indicating moderate loop assistance.

Analysis of the side-by-side loop data gave α ∼1 (0.76–1.30; Fig. 5), indicating a lack of loop interaction in this arrangement.

Loop Interference and Assistance in Vitro.

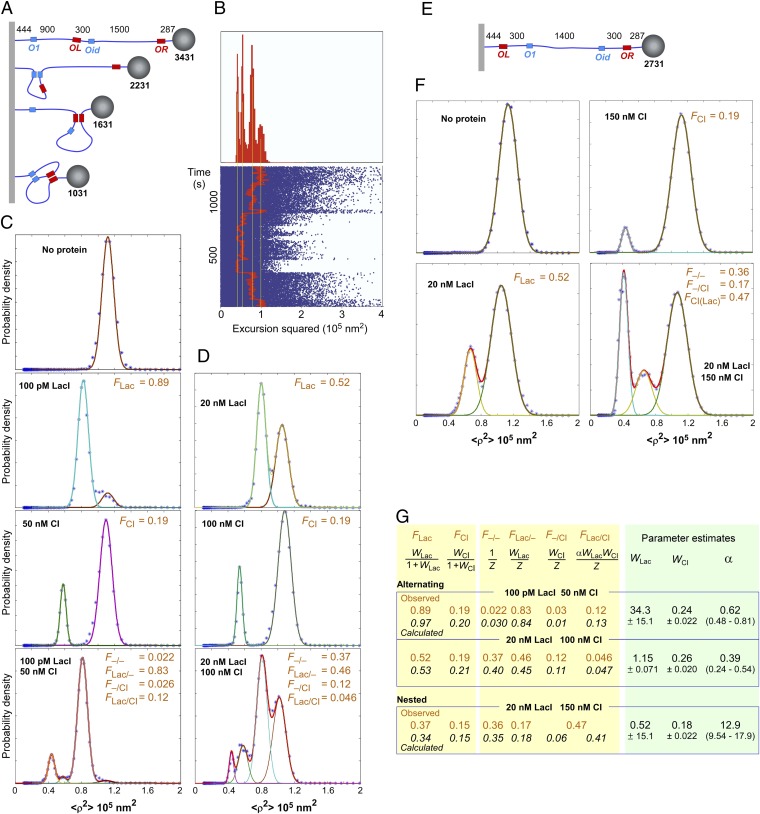
We used the TPM technique to detect and measure DNA looping in vitro (24, 52–54). For loop interference, we used a DNA tether with the asymmetrical looping arrangement that we used in vivo (Fig. 3B, construct 5, except Plac⁺.O2 was replaced with PLac^–.O1). This arrangement had been designed so that LacI or CI or both concurrent loops could be distinguished by their effect on the tether length (Fig. 6A), and therefore on the mean displacement of the attached bead. Recordings of the tether lengths vs. time for individual tethers exposed to both proteins exhibited discrete stepping between values expected for the unlooped and all three looped forms (Fig. 6B). By following multiple beads over time in the presence of LacI or CI, histograms of the probability vs. tether length were compiled (Fig. 6 C and D; Materials and Methods). Two combinations of LacI and CI concentrations (100 pM LacI + 50 nM CI and 20 nM LacI + 100 nM CI) were used, and each protein was also used alone at the same concentration. Estimates of the fraction of each looped species were obtained by fitting the histograms to Gaussian curves. Because it was possible to resolve all of the looped species, six F values were obtained for each condition (Fig. 6 B and C).

Fig. 6.

TPM analysis of alternating loops. (A and E) Setup of the TPM experiments to measure loop interference or assistance in vitro (not to scale). Distances in base pairs. DNA was attached to the coverslip by digoxigenin and to the bead by streptavidin (Materials and Methods). (B) An example of switching between tether lengths corresponding to unlooped, LacI or CI looped, or both CI and LacI looped states for one tether with 20 nM LacI and 100 nM CI over a 1,350-s observation interval. (Lower) Observed values of excursion squared (blue) along with an 8-s moving average (red) during an observation interval of 1,350 s. (Upper) Histogram for the entire observation in which four states corresponding to, from left to right, the doubly looped, CI looped, LacI looped, and unlooped tether appear. (C and D) Histograms of bead displacement <ρ²> for the alternating arrangement. F values were obtained as the area under each peak by Gaussian fitting. Histograms were compiled from analysis of 12–61 beads (total 109–1,332 min) under each condition. (F) As C and D, but for the nested arrangement. CI-His6 was used instead of CI. Histograms were compiled from analysis of 25–45 beads (total 224–877 min) under each condition. (G) Statistical–mechanical model of loop interaction (Fig. 5). The observed F values (brown) from C, D, and F, and the calculated F values (italic) using the equations shown and the fitted loop weights and α for each construct (Right). W_Lac, W_CI, and α were fitted to minimize the difference between the observed and calculated F values. W errors are SDs, and the ranges for the α estimates are the 2.5–97.5 percentiles (>900 fitting runs).

These data were analyzed using the statistical–mechanical loop interaction model to extract loop weights and α (Fig. 6G). An α of 0.62 (0.48–0.81) indicates ∼1.5-fold loop interference for the 100-pM LacI, 50-nM CI data, and an α of 0.39 (0.24–0.54) indicates ∼2.5-fold interference for the 20-nM LacI, 100-nM CI data, with overlapping 95% confidence intervals. We have more confidence in the 2.5-fold interference estimate because the four loop species were better balanced in the 20-nM LacI, 100-nM CI condition, and the match between data and prediction was better.

This interference effect was some fourfold weaker than the in vivo results with the same DNA, and the 95% confidence interval for the in vivo α estimate lies completely above the 95% interval for the in vitro estimate (Figs. 5 and 6G).

Loop assistance was examined by TPM with the Lac-inside nested construct (Fig. 6E; Plac⁺.O2 was replaced with PLac^–.O1). Again, data were collected in the presence of LacI alone, CI alone, or both proteins (Fig. 6F). The fraction of the CI-looped state was substantially increased in the presence of LacI. Note that this state is a mixture of two forms, with the state of the internal Lac loop invisible to TPM.

Fitting to the loop interaction model gave a large α value of ∼13 (9.5–18), indicative of strong loop assistance (Fig. 6G).

Discussion

Mechanism of Loop Interference.

Our results provide important support for the loop domain model and show that insulation is not restricted to complex regulatory elements in metazoan genomes but can occur by loop interference between relatively simple DNA-looping protein-binding sites. Further experiments will be needed to test whether the insulation effects we see for 1.2- and 1.8-kb loops extend to much longer loops.

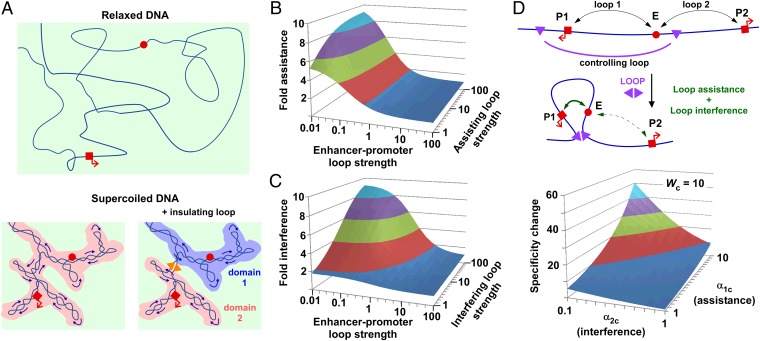
The asymmetrical alternating construct gave ∼10-fold loop interference in vivo, ∼fourfold stronger than the interference seen for the same construct in vitro, with nonoverlapping 95% confidence intervals for the in vitro and in vivo estimates of α; this implies an important role of some in vivo factor that affects DNA structure. Our favored explanation is DNA supercoiling, which would be present in our in vivo assays but absent in TPM. Brownian dynamics simulations show that DNA supercoiling compacts DNA such that the “search volume” for any two sites on the DNA to find each other is considerably reduced, perhaps by 10-fold to 100-fold (55, 56) (Fig. 7A). Enhancement of protein-mediated DNA looping by supercoiling has been shown in vitro (56–58) and also stimulates recombination between distant sites in vivo (59). Looping enhancement by supercoiling is also consistent with our measurements of a 5- to 10-fold increase in the efficiency of long-range LacI looping of DNA in vivo compared with relaxed DNA in vitro (24). Much of the enhancement of search volume by DNA supercoiling is likely to be lost when the sites are in separate topological domains (Fig. 7A), such as formed by a protein-mediated loop (60). Indeed, LacI loop inhibition of NtrC–promoter contact was dependent on DNA supercoiling of the plasmid template (47). Further experiments are needed to confirm the involvement of DNA supercoiling in the loop interference we measured in vivo. Of particular interest is whether the prevalent DNA supercoiling in eukaryotic genomes (61) plays a role in the efficiency and specificity of enhancer–promoter contact, or whether more complex mechanisms such as nucleosome–nucleosome interactions are also involved (62, 63).

Fig. 7.

Effect of DNA supercoiling and DNA loops on contact efficiency and specificity. (A) In unconstrained DNA (Upper), the red sites must find each other in a large, 3D common search volume (light green shading). DNA supercoiling (Lower) compacts the DNA and reduces this 3D space but also creates a reduced dimensionality common search volume due to the dynamic interwinding of DNA strands (darker shading). A protein-mediated DNA clamp (Right) prevents the supercoiling-induced interwinding between strands inside and outside the loop, separating the low dimensionality search volumes so that the sites must again search for each other in the larger 3D space. (B and C) The strength of loop assistance and loop interference in controlling enhancer–promoter looping is dependent on the strength of the enhancer–promoter loop (its weight) and the strength (weight) of the assisting or interfering loop. Derivations are given in Fig. S5. (D) A single DNA loop can assist the enhancer to make contact with one promoter and simultaneously interfere with its contact with another promoter, thus generating strong enhancer–promoter specificity. Note that α₁₃ is the loop interaction factor between loop 1 and loop 3 (assistance) and α₂₃ is the loop interaction factor between loop 2 and loop 3 (interference). The plot is for a controlling loop with strength W_c = 10. The specificity change due to the controlling loop does not depend on the strength of the enhancer–promoter loops. Derivations are given in Fig. S5.

We did not expect to see any loop interference in vitro with relaxed DNA, so the ∼2.5-fold loop interference effect is intriguing. Whether this supercoiling-independent effect is due to specifics of the TPM setup (e.g., the inability of the bead to pass through a loop) or contributes to loop interference in vivo is not clear. It has been proposed that entropic effects can drive DNA circles apart when they are in a confined volume (64).

Mechanism of Loop Assistance.

The loop assistance we observed in vivo is consistent with the distance-shortening effect of nested loops. The statistical weight of a looped species is directly related to the factor j_LOOP, the effective concentration of one looping site relative to the other, which quantitates the DNA-tethering effect (24, 51). We have shown that j_LOOP for LacI and CI loops over the 600- to 10,000-bp range in E. coli cells is roughly inversely proportional to the DNA separation (24). On this basis, j_LOOP for external sites of nested loops should increase by a factor proportional to the fold-change in separation. For the LacI-CI-CI-LacI arrangement (Fig. 4A, construct 10), this is 2,090/690 = 3.0 (ignoring any length addition due to the loop junction), whereas for the CI-LacI-LacI-CI arrangement (Fig. 4B, construct 11), this is 2,000/600 = 3.3, reasonably close to the fitted α = 3.0 and 1.9 values, respectively (Fig. 5). Note that the statistical–mechanical model implies that loop assistance is reciprocal—the formation of the inner loop is also stimulated by the formation of the outer loop. The formation of the external loop does not change the direct DNA tether between the internal sites, but provides a second DNA tether (containing the loop junction) that connects the internal sites. In our constructs, this second DNA tether provided a significant shortening of the distance between CI sites, being 2.3-fold (1,400/600) shorter than the unlooped distance.

The loop assistance in vitro, α = 13, was ∼twofold greater than we expected on the basis of distance shortening. In previous TPM experiments with LacI, we found that j_LOOP decreased with distance to the power 1.5 (24). Because the internal loop brings the CI sites 3.3-fold closer together (2,000/600 bp), we expected that the distance-shortening effect alone would give α = 3.3^1.5 = 6. The higher assistance seen may be due to specific angles imposed on the two 300-bp DNA “arms” as they exit the internal LacI tetramer (65), which, combined with the relative stiffness of DNA in vitro (persistence length ∼150 bp) (22), may tend to juxtapose the CI sites.

Maximizing Loop Interaction Effects.

The loop interactions in our in vivo experiments had relatively mild effects on regulation of transcription, with the largest expression changes roughly twofold; this is primarily because the LacI and CI loops were similar in strength, so that the primary gene regulatory loop—the one regulating the promoter—either resists the effects of the interfering loop or forms reasonably efficiently without help from the assisting loop. Modeling shows that the effect of a second interfering or assisting loop on a primary gene regulatory loop is maximized when the primary loop is weak (W₁ << 1) and the interfering/assisting loop is stronger than the primary loop W₂ >> W₁ (Fig. 7 B and C and Fig. S5). The maximum fold assistance is α and the maximal fold interference is 1/α. For nested loops, keeping the distance between each pair of different sites small and the length of the internal loop large should maximize α and at the same time help keep the primary loop weak. However, a long internal loop would also tend to make the assisting loop weak as well, so that mechanisms to strengthen the assisting loop, such as using strongly interacting proteins or multiple interacting sites, would help to maximize loop assistance. Thus, DNA-looping elements that target an enhancer to a promoter would be most effective if the enhancer–promoter interaction by itself is weak, if the targeting elements are located close to the promoter and enhancer, and if the targeting elements loop strongly to each other. Long distances between the enhancer and promoter may be useful in minimizing promoter activity and making it strongly dependent on loop assistance.

Similarly, the maximal regulatory effect of an interfering loop would be achieved if the primary loop is naturally weak and the interfering loop is very strong. Systematic testing will be required to determine whether different geometries of the alternating arrangement can increase loop interference beyond the 10-fold effect (α = 0.1) we saw. However, although looping efficiencies are not known, a 10-fold effect is potentially sufficient to account for observed insulator effects (33–35) and to explain the reductions in contact probability seen across TAD boundaries (39, 41).

Achieving Enhancer–Promoter Specificity by Loop Interactions.

Our analysis suggests that large changes in enhancer–promoter specificity could be caused by a single DNA loop that combines loop assistance and loop interference. We imagined an enhancer that is able to interact with either one of two promoters, with this contact regulated by a controlling loop that simultaneously assists the enhancer to loop to one promoter and interferes with looping to the other (Fig. 7D). We define a specificity change factor S, which is the fold change in promoter preference due to the presence of the controlling loop. Using a three-loop model, we can calculate that high S values (large changes in the specificity) are possible with moderate α factors and strengths of controlling loops (Fig. 7D and Fig. S5). Interestingly, the strengths of the enhancer–promoter loops are not important in determining the specificity change; the critical parameters are the α values for the assisting and interfering effects of the controlling loop on the enhancer–promoter loops, (α_1c and α_2c), as well as the strength of the controlling loop (W_c). The maximal specificity change obtainable is given by the ratio of the assisting and interfering α values (α_1c/α_2c), which is approached as the controlling loop gets stronger. Thus, interactions between DNA loops provide a potentially powerful mechanism for regulating enhancer–promoter specificity.

Materials and Methods

Strain Constructions.

The parent strain for all reporter assays was E4643, which was constructed from BW30270 (CGSC7925) MG1655 rph⁺ by precise deletion of lacIZYA (27). The PlacUV5.lacO2 and λOR.PRM promoters and the lacOid and λOL sequences were inserted into pIT-HF-CL.lacZO2^–, a modular DNA-looping lacZ reporter chassis (24) (Figs. S1A and S2) and integrated into the λattB site. LacI at ∼18 nM was expressed from a PlacI.lacI⁺ unit in pIT3-SH-lacI⁺ integrated at φHK022 attB (24) (Fig. S1A). Lambda CI was expressed from a PRM.cI pIT3-TO-λcI-OL3-4 construct integrated at 186 attB, which produces 3.3 ± 0.53 wild-type lysogenic units of CI (27) (Fig. S1B). Strains not expressing LacI or CI contained integrated empty vectors.

LacZ Assays.

A microtitre plate-based kinetic assay (66) was used, with strains grown at 37 °C to late log phase in minimal medium [1× M9 salts (10× M9 salts = 67.8g of NaH₂PO₄, 30.0g of KH₂PO₄ and 5g NaCl/L H₂O), 2 mM MgSO₄, 0.1 mM CaCl₂, 0.01 mM (NH₄)₂Fe(SO₄)₂·6H₂O, 0.4% glycerol].

TPM.

TPM experiments were performed as described previously (53). The DNA fragment was prepared using PCR with biotin- and digoxigenin-labeled primers and was attached to an anti–digoxigenin-coated coverslip and streptavidin-coated polystyrene beads (160 nm radius; Spherotech Inc.). The motion of multiple beads exposed to purified LacI (obtained from Kathleen Matthews, Rice University, Houston), CI or CI-His6 (67) in 10 mM Tris⋅HCl (pH 7.4), 200 mM KCl, 5% DMSO, 0.1 mM EDTA, 0.2 mM DTT, 0.1 mg/mL α-casein was recorded. Drift correction used immobile beads, and only symmetrically moving beads were analyzed further. The mean square excursion of each bead was calculated using the formula ${\langle {\rho }^2\rangle }_{8s}={\langle \left({\left(x-{\langle x\rangle }_{8s}\right)}^2+{\left(y-{\langle y\rangle }_{8s}\right)}^2\right)\rangle }_{8s}$. Histograms were compiled from combined recordings of multiple beads and the fractions of each species determined by Gaussian peak fitting.

Modeling.

In vivo F values were obtained by fitting the reporter data with previously described statistical–mechanical models of LacI- and CI-mediated DNA-looping regulation of PlacUV5 and λPRM to obtain the key DNA-looping parameters j_LOOP (for LacI) or ΔG_oct (for CI) for each construct (24). These and the fixed system parameters allow the fractions of all species to be determined and thus the fraction that are looped to be calculated.

For the loop interaction modeling, a Monte Carlo fitting procedure was used to find values for W_lac, W_CI, and α that minimized Σ((observed–expected)²/expected). Varied F values were used in repeated fittings to propagate the uncertainty in the F estimates.

Further details are provided in SI Materials and Methods and Figs. S1 and S2.