Importance of the DNA “bond” in programmable nanoparticle crystallization

Significance

The well-defined base-pairing interactions of DNA allow it to behave as a programmable bond on a nanoparticle scaffold and, when designed properly, these systems are able to form crystals through a process that closely mirrors the formation of atomic crystals. However, DNA-directed nanoparticle crystallization also offers a level of programmability that is not achievable in atomic systems as it enables precise and independent control over many components in a given system. This work focuses on understanding the nature of this DNA “bond,” how various parameters affect this bond, and the overall effects as seen through the crystallization behavior of the nanoparticles in an aggregate.

Abstract

If a solution of DNA-coated nanoparticles is allowed to crystallize, the thermodynamic structure can be predicted by a set of structural design rules analogous to Pauling’s rules for ionic crystallization. The details of the crystallization process, however, have proved more difficult to characterize as they depend on a complex interplay of many factors. Here, we report that this crystallization process is dictated by the individual DNA bonds and that the effect of changing structural or environmental conditions can be understood by considering the effect of these parameters on free oligonucleotides. Specifically, we observed the reorganization of nanoparticle superlattices using time-resolved synchrotron small-angle X-ray scattering in systems with different DNA sequences, salt concentrations, and densities of DNA linkers on the surface of the nanoparticles. The agreement between bulk crystallization and the behavior of free oligonucleotides may bear important consequences for constructing novel classes of crystals and incorporating new interparticle bonds in a rational manner.

Materials scientists have accomplished much by studying the way atoms and molecules crystallize. In these systems, however, the identity of the atom and its bonding behavior cannot be independently controlled, limiting our ability to tune material properties at will. In contrast, when a nanoparticle is modified with a dense shell of upright, oriented DNA, it can behave as a programmable atom equivalent (PAE) (1, 2) that can be used to synthesize diverse crystal structures with independent control over composition, scale, and lattice symmetry (3–14). The thermodynamic product of this crystallization process has been extensively studied by both experimental and theoretical means, and thus a series of design rules has been proposed and validated with a simple geometric model known as the complementary contact model (CCM). These rules allow one to predict the thermodynamically favored structure as the arrangement of particles that maximizes complementary contacts and therefore DNA hybridization (2, 6). These efforts have been very successful in predicting the thermodynamically favored product; recent studies have even demonstrated that PAEs can form single-crystal Wulff polyhedra that are analogous to those formed in atomic systems with the same crystallographic symmetry (15). However, the fact that there is a crystalline thermodynamic product does not mean that any choice of DNA and nanoparticles will result in crystalline systems in practice (3, 4). For example, crystallization has been observed for a relatively narrow class of PAEs (16) and in a manner that is primarily dependent upon the length of the DNA linker and temperature at which assembly occurs (8). Thus, absent from our understanding of these systems is a connection between the crystallization process and the properties of the DNA bonds that form the foundation of these structures.

Here, we study the crystallization process and find that the complexity of the polyvalent DNA interactions can be simply understood by considering the behavior of a single DNA bond. By systematically studying the roles of nucleobase sequence, solution ionic strength, DNA density, and temperature on crystallization, we find that the effects of these factors are mirrored by the rates of hybridization and dehybridization of free DNA. In addition to examining steady-state structures, we evaluate the formation and reorganization of these crystals in a time-resolved manner using small-angle X-ray scattering (SAXS) to study how crystallization dynamics are affected by each design variable. Finally, we develop a predictive model that allows one to compare the range of temperatures over which crystallization will occur for different conditions. In addition to providing an avenue for improving PAE crystallization and realizing new architectures, the effectiveness of this reductionist model suggests that this approach can be applied to study crystallization in a broader class of systems, thus making an impact in the materials by design community.

Results and Discussion

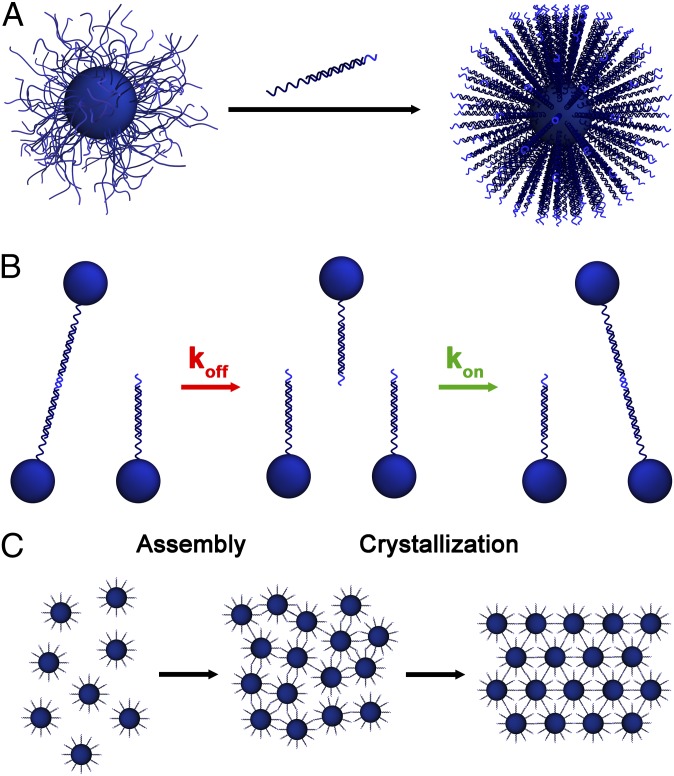
In these studies, crystals were generated using PAEs consisting of a 10-nm gold core surrounded by a dense shell of DNA that is composed of an 18-base-pair double-stranded region and a shorter single-stranded region that can participate in interparticle binding known as a “sticky end” (Fig. 1A; full sequences in Table S1) (4, 6). It is important to note that the double-stranded region of the DNA acts as a passive spacer that separates the sticky end from the particle surface so that it can engage in hybridization with the equivalent regions of other PAEs. Here, the use of a self-complementary sticky end means that all PAEs can interact with one another; these PAEs readily assemble into a disordered aggregate at room temperature. Subsequent thermal annealing allows the PAEs to reorganize into a crystalline superlattice (Fig. 1C and Fig. S1), where the thermodynamically favored crystal structure is a face-centered cubic (fcc) lattice, as this structure maximizes the number of interparticle connections possible for all nanoparticles in a crystal (4, 6).

Fig. 1.

(A) PAEs are synthesized by first densely functionalizing gold nanoparticles with thiol-modified oligonucleotides, then introducing linker strands, which contain a region that is complementary to the particle-bound sequence (dark blue region), and a short sticky end (light blue region), which is used to link PAEs. (B) Nanoparticle reorganization occurs through rapid hybridization (k_on) and dehybridization (k_off) of sticky ends between adjacent particles. (C) Initial duplex formation between sticky ends causes precipitation of the PAEs into a disordered aggregate (Assembly) which can reorganize into a crystal upon annealing (Crystallization).

In order for reorganization to occur, the interparticle DNA bonds must first dehybridize, freeing the nanoparticles to reposition themselves, and then rehybridize to a new set of sticky ends to ensure the particles remain bound within the aggregate (Fig. 1B). This suggests that the kinetics of DNA bond formation may be of great importance to crystallization. A surprising result from prior studies is that the thermodynamic product of this reorganization can be described using the hybridization behavior and thermodynamic properties of free oligonucleotides, if one takes into account the increased oligonucleotide and salt concentration (relative to the bulk) found at the surface of a PAE (16, 17). In this work, we hypothesize that the kinetics of particle reorganization in superlattices can be explained by examining the kinetics of free oligonucleotides. Specifically, we propose to explain reorganization kinetics based upon how the rates of hybridization (k_on) and dehybridization (k_off) change as a function of design variables including temperature, nucleobase sequence, oligonucleotide density, and solution ionic strength (18–20).

It is important to note that this hypothesized behavior is specific to systems wherein DNA linker strands are primarily rigid duplexes with short (typically between 1/10 and 1/6 the overall length of a DNA linkage) sticky ends. Although other designs have also been used to generate colloidal crystals, the DNA design strategy used in this work enables exquisite control over crystal symmetry and lattice parameters (6, 7, 14, 16), both of which have been difficult to realize experimentally to the same degree with systems where interparticle connections comprise long DNA linkages with large regions of single-stranded DNA (21, 22). This design is also crucial for the systematic study reported herein, where DNA bond kinetics between different crystal samples can be more readily compared without concerns about variations in DNA length or solution temperature, both of which can significantly impact the mobility, structure, and orientation of DNA strands containing long single-stranded regions. Indeed, in our design, where the sticky end comprises only a small portion of the DNA linker strands, the motion of the DNA linkers has been shown to be dominated primarily by the rigid duplex that holds them onto the particle (6–8).

Free DNA Analogy.

The central hypothesis of this work is that the hybridization kinetics of free DNA are qualitatively similar to the reorganization kinetics of PAE superlattices. The hybridization of self-complementary DNA is second order in nature and parameterized by the free energy of hybridization associated with the formation of a duplex from the sticky ends of the DNA linkers (ΔG). This value is related to the kinetics of DNA hybridization by the following equation:

$$\mathrm{\Delta }G=-RT\ln \left(k_{\mathrm{on}}/k_{\mathrm{off}}\right),$$

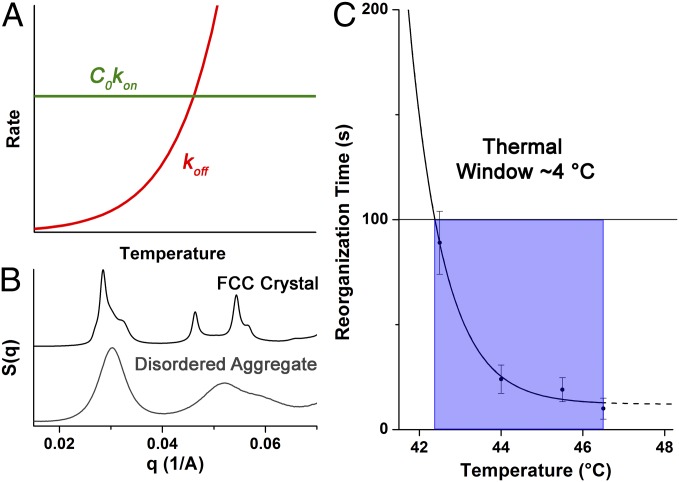
where R is the universal gas constant, T is the system temperature, and k_on and k_off are the rate constants of the hybridization and dehybridization reactions, respectively. Interestingly, k_on has been found to be nearly invariant with respect to temperature (18). Therefore, this equation can be used to define k_off in terms of ΔG and T. Additionally, DNA is characterized by a melting temperature (T_m) at which half the strands are hybridized. Given an initial oligonucleotide concentration C₀, at T_m, detailed balance requires that k_off = C₀k_on. When plotted vs. T, the intersection between k_off and C₀k_on is a graphical relationship of the melting temperature with T > T_m resulting in predominantly free DNA and T < T_m resulting in predominantly duplexed DNA (Fig. 2A). The reorganization rate of PAEs is expected to depend on the rate at which DNA dehybridizes and rehybridizes, and thus reorganization will accelerate with increasing k_off. This suggests that at the temperature range in which k_off ∼ C₀k_on, reorganization will be fastest, provided that the superlattice remains the thermodynamically favored configuration (i.e., the superlattice does not completely dissociate), and that this temperature should be the optimal annealing condition. In the subsequent sections, this model is experimentally tested.

Fig. 2.

(A) General heuristic image demonstrating the temperature dependences of both hybridization (C₀k_on) and dehybridization (k_off). When C₀k_on >> k_off, sticky ends exist primarily in the bound state. When C₀k_on and k_off are approximately equal, but C₀k_on > k_off, DNA connections between particles are readily broken and reformed, leading to reorganization within the aggregate. When k_off > C₀k_on, strands are primarily in the unbound state, which leads to aggregate melting. (B) Comparison of disordered and face-centered cubic SAXS patterns. (C) Example of the metric referred to as the “thermal window,” wherein particles reorganize on a reasonable timescale (100 s is chosen as an arbitrary point for qualitative comparison between all samples).

DNA Sticky End Sequence.

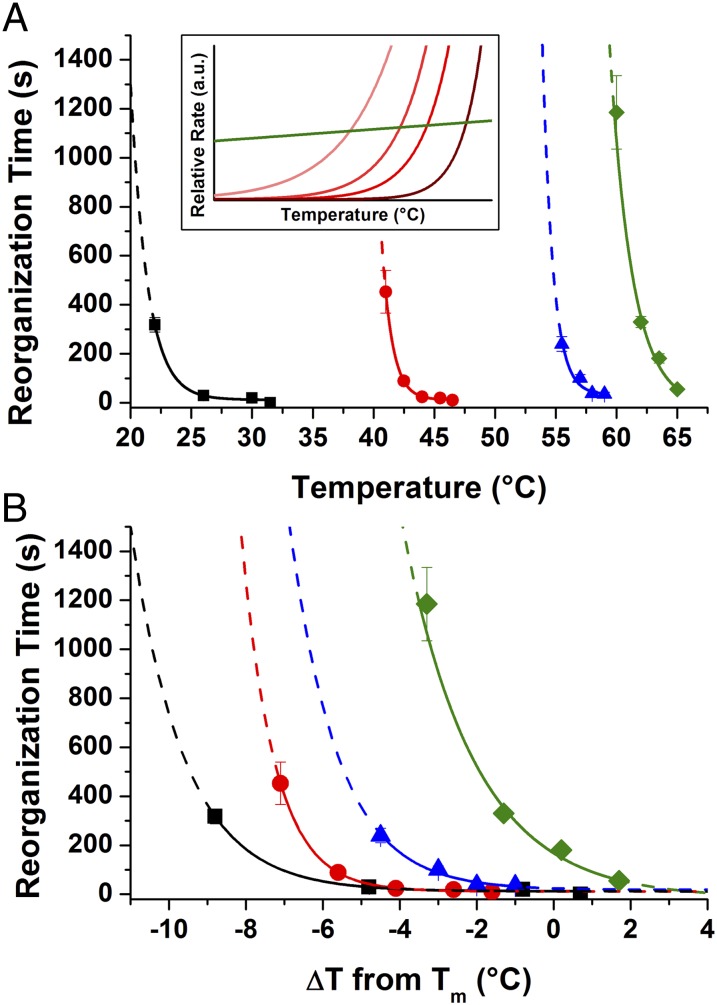
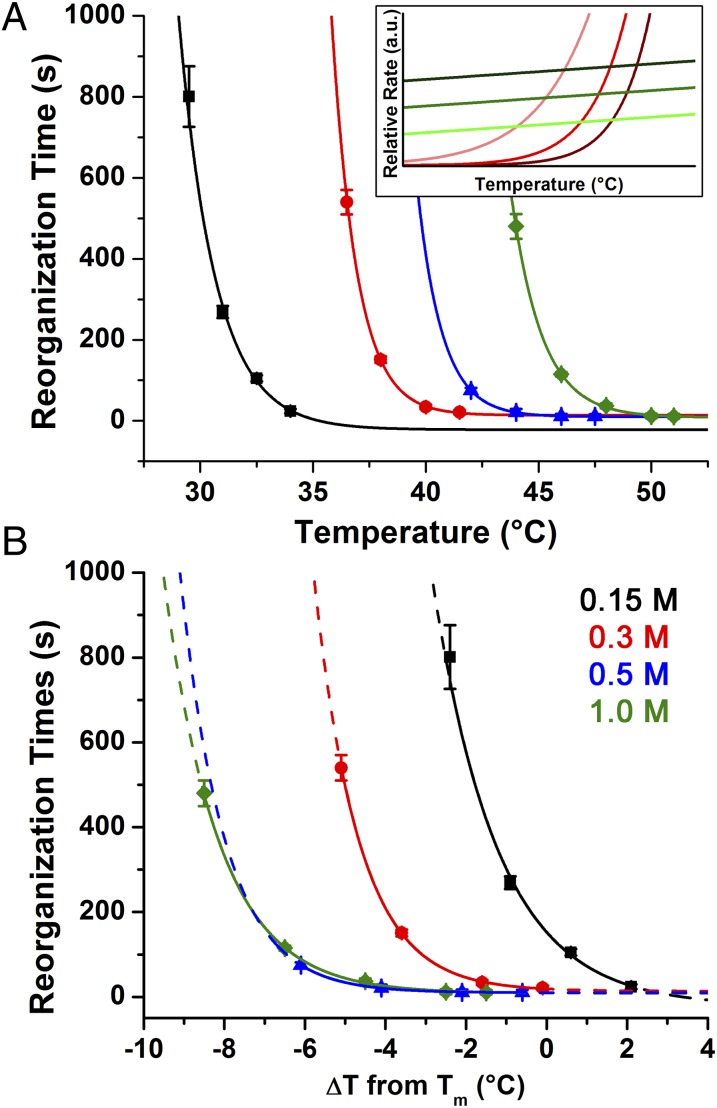
To study the effect of the DNA bond energy on reorganization kinetics, a series of PAE systems were synthesized with sticky ends with varying ΔG of hybridization, based on the free energy of a single sticky end interaction at 25 °C. As with free DNA, ΔG can be varied by adjusting the length of the sticky ends and/or their GC content (increasing strand length and increasing GC content each make ΔG more negative). Although the quality and domain size of the final crystals in fcc-forming systems obtained after extended annealing (up to 24 h at temperatures within ∼1 °C of their melting temperature) did not vary with ΔG values for an individual connection weaker than −90 kJ/mol (Fig. S2 and Table S2), we hypothesized that the kinetics of reorganization would depend strongly on ΔG owing to its effect on k_off. (Samples with ΔG of hybridization < −90 kJ/mol did not form ordered crystals, this “upper limit” of sticky end hybridization strength is discussed later in this section). Thus, four PAE systems were synthesized with individual sticky end ΔG values between −29 and −69 kJ/mol (23) (Fig. 3) and SAXS experiments were performed to observe the aggregates as they transitioned from a disordered to ordered arrangement at a given temperature.

Fig. 3.

Effects and trends of varying sticky end sequence on reorganization kinetics. Each sticky end is designated with a different color: Black: TGCA (T_m = 30.5 °C; ΔG = −28.9 kJ/mol); red: TAGCTA (T_m = 44.3 °C; ΔG = −33.9 kJ/mol); blue: TGCGCA (T_m = 57.0 °C; ΔG = −56.9 kJ/mol); and green: GCGCGC (T_m = 60.3 °C; ΔG = −69.0 kJ/mol); [NaCl] = 0.5 M for all samples. Lines are not quantitative fits, but rather guides for the eye: the solid portion of each line is within the experimentally examined temperature range and the dotted portion is an extrapolation beyond this regime. (A) Plot of the time required for crystallization versus absolute temperature. (B) Plot of the time required for crystallization versus relative temperature (each system’s T_m is set as 0). (A, Inset): Heuristic image showing the effects of increasing linker strength (light to dark traces: more negative ΔG of hybridization).

In a typical reorganization experiment, a sample was assembled into a disordered state at low temperature, then placed in the path of the X-ray beam where the system was rapidly heated to a desired annealing temperature (either just below, at, or slightly above the T_m) and SAXS patterns were repeatedly taken at intervals of several seconds. In all cases where the system had reached a sufficiently high temperature, a clear transition from a disordered aggregate to an fcc lattice was observed (Fig. 2B). The time point at which each system could be considered an fcc crystal (i.e., displaying diffraction peaks that are typical of fcc lattices, see Supporting Information) was then plotted as a function of temperature. When the rates of reorganization at different temperatures are compared for each of the four systems examined, it is clear that the “thermal window” of crystallization (Fig. 2C; i.e., the range of temperatures over which crystalline structures are achieved within a reasonable time scale) for these samples decreases with more negative ΔG values (Fig. 3A). This effect is more obvious when each PAE system is plotted relative to their respective melting temperature (Fig. 3B; see Table S3 for full data analysis).

Interestingly, these results are qualitatively consistent with our proposed analogy between the behavior of free DNA and nanoparticle superlattices. Examining the theoretical rates reveals two predictions (Fig. 3A, Inset). (i) Because the intersection of k_off and C₀k_on increases with stronger sticky end interactions (i.e., more negative ΔG values), T_m is also expected to increase; and (ii) because the slope of k_off becomes steeper at T_m for more negative ΔG, the region in which k_off ∼ C₀k_on becomes narrower as the magnitude of ΔG increases (19). Indeed, both of these predictions match the experimental trends. It is significant to note that the failure of systems with the strongest individual sticky ends tested (ΔG values ≤ −90 kJ/mol; Fig. S2) to crystallize after extended annealing at temperatures ∼1 °C below their T_m can also be explained by this effect, as this temperature was likely outside the annealing window for these systems.

Strikingly, in many systems, reorganization was observed at temperatures above T_m. Although the melting temperature determined by UV-Vis spectroscopy is not a perfect determinant of the melting temperature of an aggregate in a capillary during an SAXS experiment due to a difference in concentration (Supporting Information), aggregate reorganization was found to occur simultaneously with aggregate melting in many systems. A likely cause for this is that PAEs at the edge of an aggregate have fewer DNA linkages holding them in place, resulting in more rapid melting than particles within the center of the aggregate. This competition between melting and reorganization suggests that the “upper limit” of DNA bond strength beyond which no ordered crystals are formed is essentially a kinetic wall. In these systems, temperatures necessary to induce a disordered-to-ordered transition on an observable timescale are sufficiently high that the aggregate melts before crystallization is achieved. Thus, crystals have not been observed with these systems (3).

Number of Linkers.

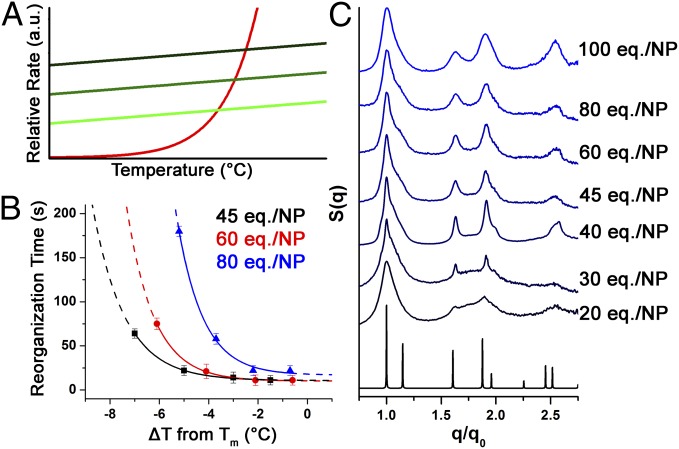
Increasing the number of DNA strands that can participate in bonding on each particle raises C₀k_on by virtue of the increased DNA density, but k_off is unaffected by DNA concentration (9, 16). Therefore, by adding more linkers, the practically flat C₀k_on curves are simply shifted up and intersect the unchanged k_off curve at higher values (Fig. 4A). Following this, one can expect slightly higher T_m and, because k_off has a higher slope at higher temperatures, a slightly narrowed annealing window.

Fig. 4.

(A) Heuristic image showing the kinetic effects of adding more linker equivalents [light to dark traces: increasing equivalents (eq.) per particle]. (B) Plot of the time required for crystallization versus relative temperature (each system's T_m is set as zero). (C) Comparison of normalized SAXS patterns for systems with different numbers of linker equivalents after overnight incubation at their optimal annealing conditions; [NaCl] = 0.5 M for all samples. The black trace is the predicted scattering pattern for a perfect fcc lattice.

In an initial set of experiments, different sets of particles with a range of linker loadings (from 20 to 100 equivalents per particle) were allowed to reach their maximum crystal qualities upon a 24-h incubation at their optimal annealing temperatures (Fig. 4C). Subsequent analysis with SAXS showed that samples in the low-loading regime (i.e., 20 and 30 equivalents) displayed broad features corresponding to a large number of disordered regions that are overlaid with weak but discernible narrow peaks attributable to small fcc domains. This mixed structure could be predicted considering that each particle in an fcc lattice has 12 neighbors; even a modest nonuniformity in the distribution of linker strands among the particles could lead to defects in the lattice. Assuming that the region of the particle surface corresponding to each linkage has a Poissonian distribution of DNA where the mean is the linker number divided by 12, in a system with 20 linker equivalents, less than 10% of particles will have DNA that can bind to all neighbors. Even for 30 linker equivalents, only 35% of particles will have DNA that can bind to each neighbor, while for 40 linker equivalents, over 65% of particles are expected to be able to bind to all of their neighbors. This simple statistical argument provides a rationale for the inability of low-linker–number systems to form uniform crystals.

Kinetics experiments were also carried out for three different DNA loadings within the regime that demonstrated reliable crystal formation (45, 60, and 80 equivalents of DNA per particle). The thermal windows for these systems narrow as the linker density increases, in agreement with our aforementioned hypothesis that reorganization is hindered when a larger number of DNA connections tether a particle in place (Fig. 4B; see Table S4 for full data analysis). Furthermore, within the regime of reliable crystal formation, we attribute the observed broadening of peaks as the linker loading increases (Fig. 4C) to the presence of smaller and less-perfect crystal domains (Table S2), suggesting that very dense DNA shells hinder the reorganization processes and limit the ability of particles to arrange themselves into large, perfect domains.

Salt Concentration.

Changing the solution salt concentration has multiple effects on reorganization because it affects both C₀k_on and k_off (Fig. 5A, Inset) (18, 20). Specifically, raising the salt concentration is expected to increase k_on because the additional charge screening minimizes the repulsion between negatively charged DNA strands, and it is also expected to lower k_off because the increased counterion concentration will help to stabilize the linkages once formed. To probe the effects of varying the solution cation concentration, samples were prepared using a standard linker sequence and number of linker equivalents (60 equivalents TAGCTA, ΔG = −33.9 kJ/mol) at 0.5 M NaCl. Once the particles were assembled, the solution salt concentration was adjusted to lie within the range of 150 mM to 2.0 M. The salt concentration was modified after assembling the particles to ensure that the physical characteristics and behavior of the particles (number of thiolated and linker strands per particle, etc.) during the preparation process were the same as the previous experiments that monitored linker sequence and number of linkers per particle. This range of salt concentrations represents the maximum range in which aggregates were found to be stable; lower values of salt concentration led to crystals that were not stable at room temperature and higher values resulted in aggregates that formed dense, black pellets that stuck to the walls of the containers in which they were stored.

Fig. 5.

(A) Plot of the time required for systems with different NaCl concentrations (exact concentrations listed in B) to transition from disordered to ordered versus absolute temperature. (B) Plot of the time frame of reorganization versus relative temperature, with each system’s T_m set at 0. (A, Inset) Heuristic image demonstrating the effect of increasing salt on both k_on and k_off (light to dark traces: increasing solution ionic strength).

When these samples were annealed at their respective optimal temperatures for 24 h, each formed fcc crystals of comparable quality and crystal domain size, indicating that changing these salt concentrations had no discernible effect on the ability of these systems to form ordered crystals (Fig. S3 and Table S2). When kinetics experiments were performed at four different salt concentrations, examination of their thermal windows showed that systems with increasing melting temperatures had broader thermal windows than those with lower melting temperatures (Fig. 5 A and B; see Table S5 for full data analysis). Although this result may seem counterintuitive given that the opposite was obtained upon increasing the ΔG of hybridization of the sticky ends, it is actually in agreement with our model. Because increasing the salt concentration raises both C₀k_on and k_off, the absolute rates of k_on and k_off at T_m (and thus the absolute rates of reorganization) are higher when a system with greater salt concentration is annealed at T_m. Thus, the annealing window is broadened at higher salt concentration.

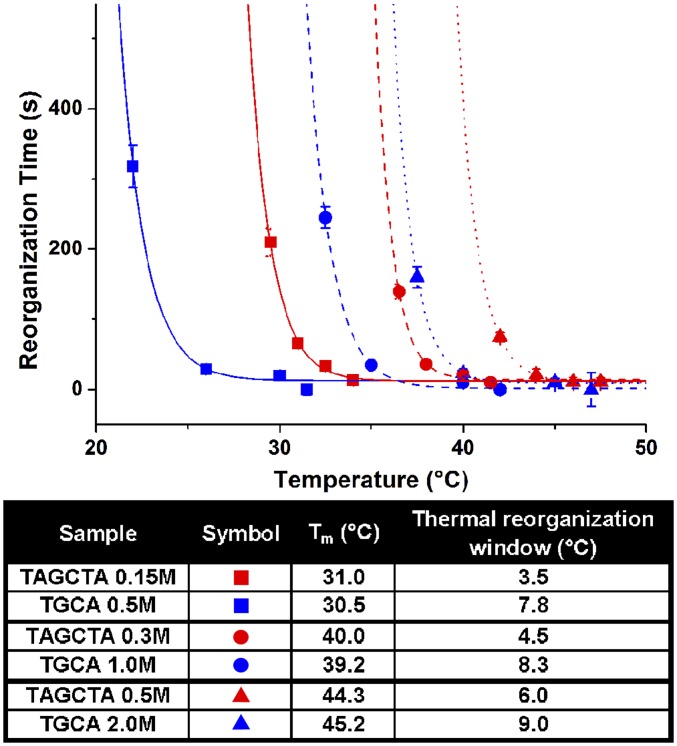
The way in which salt concentration affects the annealing properties provides an interesting and useful contrast to tuning T_m through linker strength or density, where increasing T_m also narrows the annealing window. To further illustrate this, we studied the kinetics of two systems with different sticky ends (and therefore different ΔG values) after tuning their salt concentrations such that their melting temperatures overlap. Because both experimental modifications of increasing the strength of individual sticky ends and lowering the salt concentration cause a narrowing of the thermal window (thus increasing the experimental difficulty of inducing crystallization), we hypothesized that the systems with the lowest magnitudes of ΔG and highest salt concentrations should prove easiest to anneal. Measurements of the reorganization rates for three such pairs of systems showed that the annealing window was lower (relative to T_m) and broader for the higher-salt–, lower-linker–strength system of each pair, consistent with our hypothesis (Fig. 6). Again, the effect of increased thermal stability with elevated salt concentrations leads to higher absolute rates of reorganization and thus widens the range of temperatures at which crystal formation can occur. More importantly, this demonstrates how modifying several design variables in a coordinated fashion can be used to tailor crystallization behavior in these systems, a feat that cannot be accomplished in traditional atomic- or molecular-based crystallization without altering the crystal type or symmetry achieved.

Fig. 6.

Comparison of thermal windows for two different sticky end sequences (TAGCTA, red traces, and TGCA, blue traces) whose melting temperatures have been modified by adjusting bulk solution salt concentration. Data are grouped into pairs of systems that have equivalent melting temperatures (denoted by matching data point shape and line type).

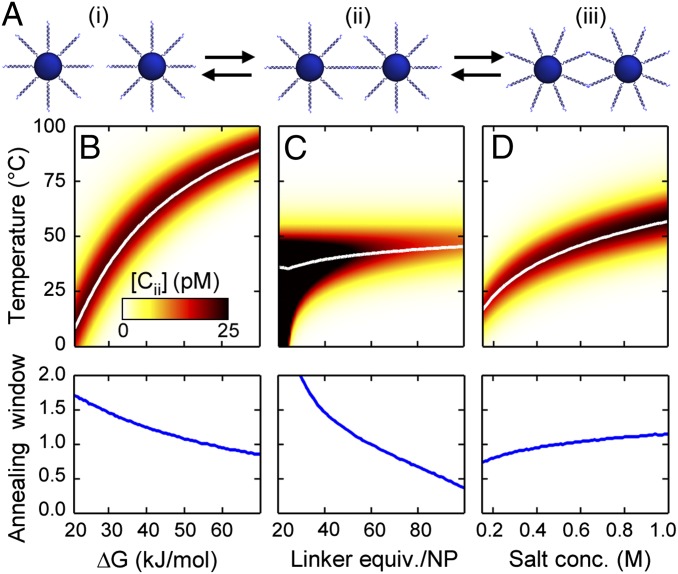
To gain further insight into the kinetics of the crystallization process, we have constructed a simplified model of DNA-mediated nanoparticle crystallization that includes multivalency. The multivalent effects can be captured in the simplest way possible by considering a three-state system where a pair of particles can either be free, bound to another particle by one DNA linkage, or bound by two DNA linkages (Fig. 7A). At low temperatures, the system will be completely in the doubly bound state. As the temperature rises, some strands begin to dissociate and some particles enter the singly bound state. At the T_m, where half of the available DNA bonds have broken, a given particle will transition between doubly bound, singly bound, and free states with a rate that is related to the population of the singly bound state. At even higher temperatures, all DNA linkages break and all particles enter the free state. If there is reorganization occurring, singly bound particles must be present, as this state allows for particles to move between free and fully bound states. Therefore, the concentration of the singly bound intermediate may be considered a proxy for the ability of a system to reorganize. Interestingly, this means that the predicted reorganization in a system could be estimated from experimentally derived thermodynamic data with no free parameters. Specifically, we treat the process of free particles binding as having the same ΔG as that of the sticky end with a concentration equal to that of the particles. The process of the second strand binding is assumed to have the same ΔG as free DNA, but now includes the higher effective concentration of linker strands in the vicinity of the particle (full quantitative workup in Supporting Information). It is interesting to note that the predicted variation of melting temperature and annealing window matches the observations discussed above (Fig. 7 B–D), suggesting a simple extension of the free DNA model, even one based solely on thermodynamic parameters, could be very useful in predicted PAE crystallization.

Fig. 7.

Implications of the proposed model of PAE reorganization. (A) Schematic showing the model in which particles can exist freely in solution (i), as singly bound intermediates (ii), or in a doubly bound state (iii). (B–D, Top) The average number of particles that exist as singly bound intermediates are shown at different linker free energies (B), linker equivalents (C), and salt concentrations (D), with the color scale representing concentration of ii. (Note: total particle concentration is 50 nM.) The white line indicates the computed melting temperature. (B–D, Bottom) The computed annealing window at different sticky end free energies (B), linker equivalents (C), and salt concentrations (D). These calculations are based on numerically solving the thermodynamic equations (Supporting Information).

Conclusions

The experiments described above indicate that there are a large number of design variables that can be used to control the process of PAE crystallization, including solution temperature, DNA sticky end sequence, number of bound linker strands per particle, and salt concentration. Given that each of these variables can be controlled independently, it would therefore be useful to determine the optimal conditions under which one can most reliably synthesize colloidal crystals using PAEs as building blocks. Although the specific conditions under which crystals need to be assembled may vary depending on their application, a general set of principles that make PAEs strong candidates for materials by design can still be established for this system.

In essence, crystallization is easiest when there is a broad thermal window, and is fastest when annealing occurs at a relatively high temperature. From these observations, the experiments probing the effects of variations in sticky end sequence provide the first principle of crystal design: the sticky ends of the DNA linkers should only be as strong as is necessary to stabilize an aggregate at the desired temperature range, thus maximizing the breadth of the thermal window. When considering the number of DNA linkers per particle, the trends at both extremes of linker density indicate that the highest quality crystals are most readily achieved with smaller numbers of linker equivalents per particle, provided that sufficient linkers are present to stabilize an ordered structure. Thus, the second design principle is the minimum linker density necessary to obtain homogenous loading (where all particles are capable of forming a lattice as a thermodynamic product) facilitates the formation of the highest quality crystals.

Finally, tuning the salt concentration provides a facile means of controlling the crystallization process postsynthetically, without the need to prepare multiple sets of DNA strands or different batches of DNA-functionalized particles. The melting temperature of the system increased with increasing salt concentration up to 2.0 M NaCl; the thermal window in which reorganization occurred also broadened with increasing salt concentration up to a value of 1.0 M NaCl. This translates to the third design principle: the ionic strength of the solution should be as high as possible without altering the macroscopic behavior of the crystals (for example, by flocculation).

In this work, we have analyzed the crystallization pathway for DNA-functionalized particles behaving as nanoscale PAEs, and found it to depend intricately on the thermodynamics of the DNA bonds. Importantly, this work has demonstrated that there are multiple synthetic and environmental handles that can be used to tune the interaction strength between nanoparticle building blocks, and that manipulating these variables allows us to control the relative ease with which crystals can be formed. These results should aid in the design of future crystals, as understanding the pathway by which a disordered aggregate becomes crystalline (as well as knowing which design parameters and conditions facilitate this process) enables better control of the annealing procedure, allowing for the establishment of design processes that encourage reliable, high-quality crystal syntheses. Moreover, the ability to stabilize a crystal under different environmental conditions (e.g., variations in solution ionic strength or temperature) improves their ability to be used in different contexts, such as epitaxial growth of crystals on surfaces (24), thermally addressable topotactic intercalation of multiple nanoparticle components (25), or assembly of Wulff polyhedra via slow cooling at high temperatures (15). We also established that studies of systems where DNA bonds are formed via transient interactions between small sticky ends at the tip of primarily rigid DNA duplexes not only enable more complex superlattice design, but also facilitate fundamental investigations of their crystallization behavior. We therefore encourage both the experimental and theoretical scientific communities to further examine the behavior of these PAEs using techniques that have been previously applied to systems using long DNA overlaps between particles, or primarily single-stranded DNA linkers (9, 10, 12, 21, 22, 26). Lastly, this work underscores the notion that PAEs present a highly programmable means of studying and controlling crystallization in a more facile and directable manner than their atomic counterparts, and thus are a useful tool for materials synthesis.