Interfacial gating triad is crucial for electromechanical transduction in voltage-activated potassium channels

Gating interaction analysis reveals a cluster of three conserved amino acids that couple structural transitions in the potassium channel voltage sensor to those in the pore.

Abstract

Voltage-dependent potassium channels play a crucial role in electrical excitability and cellular signaling by regulating potassium ion flux across membranes. Movement of charged residues in the voltage-sensing domain leads to a series of conformational changes that culminate in channel opening in response to changes in membrane potential. However, the molecular machinery that relays these conformational changes from voltage sensor to the pore is not well understood. Here we use generalized interaction-energy analysis (GIA) to estimate the strength of site-specific interactions between amino acid residues putatively involved in the electromechanical coupling of the voltage sensor and pore in the outwardly rectifying K_V channel. We identified candidate interactors at the interface between the S4–S5 linker and the pore domain using a structure-guided graph theoretical approach that revealed clusters of conserved and closely packed residues. One such cluster, located at the intracellular intersubunit interface, comprises three residues (arginine 394, glutamate 395, and tyrosine 485) that interact with each other. The calculated interaction energies were 3–5 kcal, which is especially notable given that the net free-energy change during activation of the Shaker K_V channel is ∼14 kcal. We find that this triad is delicately maintained by balance of interactions that are responsible for structural integrity of the intersubunit interface while maintaining sufficient flexibility at a critical gating hinge for optimal transmission of force to the pore gate.

INTRODUCTION

Voltage-gated ion channels (VGICs) control ion flux across biological membranes in a voltage-dependent manner and are critical for membrane excitability and cell signaling. Like many complex biological proteins, these proteins are modular with distinct structural domains that are involved in voltage sensing and ion conduction (Yellen, 1998; Bezanilla, 2000; Swartz, 2008). Structural and functional studies have highlighted the role of distinct regions and specific residues in determining ion conduction (Perozo et al., 1993; Heginbotham et al., 1994; Hackos et al., 2002; Kitaguchi et al., 2004) and voltage sensing (Aggarwal and MacKinnon, 1996; Seoh et al., 1996; Tao et al., 2010; Yarov-Yarovoy et al., 2012), but how these two modules communicate with each other to work in concert remains unclear.

High-resolution structures and structure–function studies on potassium and sodium channels have shown that the residues in the S4–S5 linker connecting the voltage-sensing domain (VSD) and the pore domain (PD) are important for coupling voltage sensing and pore gates (Lu et al., 2002; Long et al., 2005a,b; Soler-Llavina et al., 2006; Muroi et al., 2010; Chowdhury and Chanda, 2012b). However, the energetic contribution of specific residues in this crucial interface remains unclear in large part because of a lack of general methods to measure free energy of interactions (Chowdhury and Chanda, 2010, 2012b). Specific networks of residues in this region may be especially important for the great diversity in “coupling mechanisms” of VGICs. For example, the coupling of the VSD in the Shaker K_V channel is such that the channel gates can open only after all VSDs have activated (Zagotta et al., 1994; Sigg and Bezanilla, 1997; Islas and Sigworth, 1999). In contrast, in the well-characterized BK channels, the coupling is relatively weaker, which allows the channel gates to open even when all the VSDs are not activated, albeit with a low probability (Cox et al., 1997; Horrigan et al., 1999; Talukder and Aldrich, 2000). In contrast, in the hyperpolarization-activated HCN channel, activation of the VSDs causes the channel gates to close (Altomare et al., 2001; Chen et al., 2007; Ryu and Yellen, 2012). The different modes of coupling arise in these proteins, despite the fact that they are built on a common structural template.

In the accompanying study in this issue, we have described an experimental approach to determine the energetic contribution of residue-level interactions to the overall gating process of a VGIC (Chowdhury et al.). This approach combines mutant cycle analyses with the free energies of perturbations evaluated by measuring the conjugate displacement associated with a stimulus-driven conformational change in the protein (Chowdhury and Chanda, 2012a, 2013). For VGICs, we showed that the free energies of interaction between specific residues can be evaluated by measuring the median voltage of channel activation, from gating charge displacement versus voltage curves. To understand the molecular basis of electromechanical coupling, we focused on determining the energetic contributions of residues that are at the interface of the PD and voltage sensors. The specific network of residues was identified using a computational graph theoretical approach (Kannan and Vishveshwara, 1999) applied on the structure of the homologous K_V1.2/2.1 chimera channel. In this approach, every pair of residues in the structure was scored based on their proximity, which was subsequently used to group them into clusters. In addition, sequence conservation scores were applied as an orthogonal criterion to rank these clusters. Interaction energies between residues in the highest ranked cluster were calculated using generalized interaction-energy analysis (GIA). Our experimental measurements reveal that three residues in this cluster, R394, E395, and Y485, exhibit strong interresidue coupling (3–5 kcal) and that the pairwise (or binary) coupling between the residues are sensitive to the ternary perturbation. The three residues are structurally oriented in a way that the tyrosine residue is intercalated between the arginine and glutamate residues, thereby preventing them from interacting. Thus, this conserved interfacial gating triad constitutes a critical electromechanical transducer that mediates coupling between structural transitions in the voltage sensor to those in the pore.

MATERIALS AND METHODS

Mutagenesis and expression in Xenopus laevis oocytes

All mutations were generated in the cDNA of the inactivation-removed Shaker K_V channel (Δ6–46), bearing the W434F mutation, cloned into the pBSTA vector. Mutations were introduced by PCR using mismatch mutagenic primers (QuikChange; Agilent Technologies) and confirmed by sequencing. Mutant cDNAs were linearized using the NotI enzyme (New England Biolabs, Inc.) and transcribed into cRNAs using mMESSAGE mMACHINE T7 kit (Life Technologies).

Xenopus oocytes were extracted, defolliculated, and stored as described previously (Chowdhury et al., 2014). Oocytes were injected with 50 nl cRNA at a concentration of 50–200 ng/µl and stored at 18°C (as described in Chowdhury et al. [2014]) for 2–7 d before electrophysiological measurements.

Electrophysiology

Gating currents were measured either on a cut-open oocyte voltage clamp (COVC) or a two-electrode voltage (TEV) clamp set up. The external solution used for gating current measurements in both set-ups was 115 mM NMG-MES (N-methyl-d-glucamine methanesulfonate), 2 mM Ca-MES, and 10 mM HEPES, pH 7.4. The internal solution used for gating current measurements on the COVC set-up was 115 mM NMG-MES, 2 mM EGTA, and 10 mM HEPES, pH 7.4. The recording pipette resistance for all electrophysiological measurements was 0.2–0.5 MΩ. Analogue signals were sampled at 20–250 kHz with a Digidata 1440 or 1320 interface (Molecular Devices) and low-pass filtered at 10 kHz.

Gating currents were obtained by applying 50-ms-long depolarizing pulse to voltages from −120 to 20 mV (in 5-mV intervals). For measurements using COVC, the holding potential used was −120 mV, whereas on the TEV, the holding potential was −90 mV and the depolarizing pulse was preceded and followed by 50-ms hyperpolarization pulses to −120 mV. The capacitive transient and linear leak currents were subtracted online using the P/−4 or P/−8 method, with a subsweep holding potential of −120 or −90 mV (on COVC or TEV, respectively). After baseline readjustments, the on-gating current records were integrated over the duration of the depolarization pulse to obtain the gating charge displaced, which was used to compute the fractional gating charge displacement versus V curve (Q/Q_max vs. V or Q-V).

Data analysis

The fractional gating charge displacement curves for all of the mutants were obtained by averaging measurements performed on three to six oocytes. The median voltage of activation, V_M, for each normalized Q-V curve was extracted by calculating the area between the Q-V curve and the ordinate axis using the trapezoid method. For a Q-V curve with n points, the V_M is calculated as

$$V_M={\displaystyle {\sum }_{i=1}^{n-1}\frac{\left(Q_{i+1}-Q_i\right)\left(V_{i+1}+V_i\right)}{2}},$$

where Q_i and V_i is the i^th point on the Q-V curve. The net free energy of activation of the channel is calculated as ΔG_C = Q_maxFV_M, where Q_max is the maximum number of charges transferred during voltage-dependent activation of the channel. For all of our calculations, we used a Q_max of 13.2 because the sites of perturbations are not the primary gating charge–determining residues of the channel (Aggarwal and MacKinnon, 1996; Seoh et al., 1996). The uncertainty in ΔG_C was calculated as Q_maxFδV_M, where δV_M is the standard error of the V_M estimation.

The nonadditivity in a mutant cycle analysis was calculated using the median measure of free-energy change; this nonadditivity, ΔΔG_GIA, was calculated as

$$\Delta \Delta G_{GIA}=Q_{\max }F\left(V_{M\left|\right|W}+V_{M\left|\right|S12}-V_{M\left|\right|S1}-V_{M\left|\right|S2}\right),$$

where the subscripts, ||W, ||S12, ||S1, and ||S2, indicate the V_M for the WT channel and the double and two single mutants, respectively. The standard error associated with ΔΔG_GIA (δΔΔG_GIA) was calculated as

$$\delta \Delta \Delta G_{GIA}=Q_{\max }F\sqrt{{\left\{\delta {\left(V_M\right)}_{WT}\right\}}^2+{\left\{\delta {\left(V_M\right)}_{S1}\right\}}^2+{\left\{\delta {\left(V_M\right)}_{S2}\right\}}^2+{\left\{\delta {\left(V_M\right)}_{S12}\right\}}^2},$$

where δ(V_M)_WT, δ(V_M)_S1, δ(V_M)_S2 and δ(V_M)_S12 are the uncertainties (SEM) associated with V_M measurement of the WT and the single and double mutant channels, respectively.

Identification of conserved residue clusters using a graph theoretical approach

Using the structure of the K_V1.2/2.1 paddle chimera (PDB ID 2R9R, chain B; Long et al., 2007), we first derived the adjacency matrix, A, for the residues in the transmembrane segments of the protein. A is a square matrix whose elements, a_ij, were calculated as

$$a_{ij}=100\frac{N_{ac}\left(i,j\right)}{Norm\left(i\right)},$$

where N_ac(i,j) is the number of interatomic contacts between the side chains of residues “i” and “j,” an atomic contact being defined only when two atoms are within 4.5 Å of each other. Norm(i) is a parameter that depends on the specific type of residue at position i; it is related to the size of the specific amino acid. The Norm() values used for our purposes were the same as those reported previously (Kannan and Vishveshwara, 1999). A higher value of a_ij suggests an increased possibility that the two residues are interacting. By this formulation, A is not a symmetric matrix (because Norm(i) ≠ Norm(j), unless residues i and j are identical). Furthermore, because the channel is homotetrameric, there are four possible values for N_ac(i,j), depending on whether the residues are in the same or neighboring subunits. However, given the symmetric structure of the tetrameric channel, there will be four possible unique pairs, of which at least one pair will have the highest N_ac. Because our aim is to generate a sparse network, we chose to concentrate on the pair with the highest contact score to generate A. Once A is obtained, we generate a symmetric version of the adjacency matrix, S (with elements s_ij), as follows

$$s_{ij}=\{\begin{array}{c}0\hspace{0.17em}\text{when}\hspace{0.17em}\left|i-j\right|\le 5\\ \max \left(a_{ij},a_{ji}\right)\hspace{0.17em}\text{when}\hspace{0.17em}\left|i-j\right|>5\hspace{0.17em}\text{and}\hspace{0.17em}\max \left(a_{ij},a_{ji}\right)\ge lim\\ 0\hspace{0.17em}\text{when}\hspace{0.17em}\left|i-j\right|>5\hspace{0.17em}\text{and}\hspace{0.17em}\max \left(a_{ij},a_{ji}\right)<lim\end{array},$$

where “lim” is a cut-off value for the adjacency scores, used to “neutralize” residue pairs with a low number of interatomic contacts. For our purpose, we used a value of 7 for the limiting cut-off score. Additionally, the condition |i − j| ≤ 5 implies that scores were evaluated only for residues that are more than five residues apart in primary sequence. For our purposes, it was necessary to generate the symmetric version because asymmetry would imply that the graph represented by the raw adjacency matrix is directed, which in turn would make the subsequent clustering steps significantly more complex and hard to interpret. Additionally, the normalization factor Norm() is essential because raw N_ac scores cannot be used directly to determine and compare the significance (cut-off) levels (see Kannan and Vishveshwara [1999]).

Using the elements of symmetric adjacency matrix as weights, the residues of the K_V channel were grouped into different clusters. Clustering was performed using the ClusterOne program (Nepusz et al., 2012). Each cluster was constrained to comprise at least five amino acids and show strong clustering density (i.e., high degree of interconnectivity). Application of this approach shows that the 259 residues of the channel (residue numbers 158–417 corresponding to PDB ID 2R9R, chain B) can be first reduced into a graph with 109 nodes (each corresponding to a residue) and 98 edges (each edge indicating a connection, the “strength” of which reflects its adjacency score), which can be further subdivided into six clusters.

For the sequence conservation calculation, we used an alignment of ∼360 K_V channel sequences as was described previously (Lee et al., 2009). According to Halabi et al. (2009), for each position of the alignment we computed the conservation entropy (c.e.(i)) as follows:

$$c.e.\left(i\right)={\displaystyle \sum }_{j=1}^{20}{f}_j^i\text{ln}\left(\frac{f_j^i}{f_j^b}\right),$$

where $f_j^i$ is the frequency of amino acid j at position i of the sequence alignment and $f_j^b$ is the background frequency of the amino acid (deduced from the nonredundant database of the protein), and the summation runs over all 20 amino acids. The $f_j^b$ values previously reported by Halabi et al. (2009) were used here. c.e.(i) indicates the “enrichment” of a particular site in amino acids with respect to a background distribution of amino acids. We also calculated the frequency of occurrence of each amino acid in the multiple sequence alignment (as described previously [Halabi et al., 2009]) and found it to be close to the background frequency distribution, suggesting sufficient sampling of sequence for conservation analyses.

For each cluster, the mean and standard deviation of the conservation entropy scores were evaluated as

$${\mu }_{c.e.}\left(i\right)=\frac{{{\displaystyle \sum }}_{j=1}^{n_i}c.e.\left(j\right)}{n_i}$$

$${\sigma }_{c.e.}\left(i\right)=\sqrt{\frac{{{\displaystyle \sum }}_{j=1}^{n_i}{\left\{c.e.\left(j\right)-{\mu }_{c.e.}\left(i\right)\right\}}^2}{n_i-1}},$$

where n_i is the number of residues constituting the cluster and the summations (over j) are performed over the residues constituting the cluster (i).

Online supplemental material

Online supplemental figures show the adjacency matrix (Fig. S1), sequence alignment of Shaker with K_V 1.4 (Fig. S2), structure of the K_V 1.2/2.1 paddle chimera (Fig. S3), and family of gating current traces of different mutants (Fig. S4). The supplemental worksheet, included as a separate Excel file, provides the values for the complete adjacency matrix. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201411185/DC1.

RESULTS

Identification of sparse networks of conserved residues

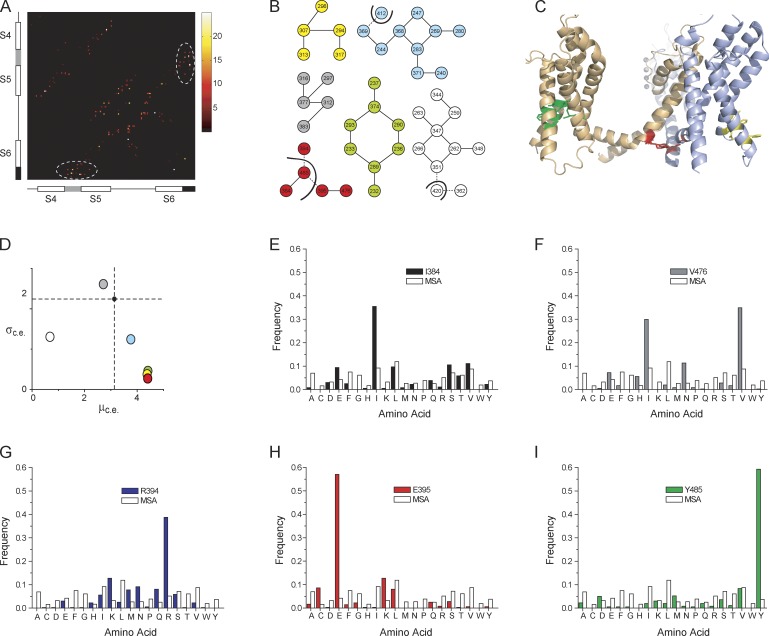
To identify putative interactors, we used a graph theoretical approach to identify sparse networks of spatially adjacent residues from high-resolution structures (Kannan and Vishveshwara, 1999). In this approach, distances between each pair of residues in a protein structure are first evaluated and then using proximity-based scores are clustered into groups. The crystal structure of the K_V channel paddle chimera (PDB ID 2R9R, chain B; Long et al., 2007) was used to construct an adjacency matrix, S (Fig. 1 A and Fig. S1). S is an N × N symmetric matrix, where N is the number of amino acids in a single subunit of the protein. Each element of S, s_ij (the i^th row and j^th column), is a score related to the number of atomic contacts formed by the side chains of residues “i” and “j” in the protein. In the S matrix (supplemental worksheet), part of which is represented as heat map in Fig. 1 A, we can make out that residues in certain regions of the protein (for instance, the S4–S5 linker and the S6 tail) are more tightly packed against each other than other regions. Using the elements of S as weights, the different residues of the protein were clustered into groups such that residues within each group have high interresidue contact scores, whereas residues between groups have relatively low interresidue contact scores (see Materials and methods for details). This approach identified six clusters in the K_V channel that are represented as a “graph” (i.e., a collection of nodes and edges) in Fig. 1 B. Each node, depicting a residue of the protein, is numbered according to the sequence position of the residue in the Shaker K_V channel (using the sequence alignment shown in Fig. S2). Except red, cyan, and white clusters, all other clusters are limited to residues within the same subunit. We should caution that in addition to other limitations, the ability of this algorithm to correctly identify interaction networks is dependent on the resolution of structures. In the case of the K_V channel paddle chimera, the relatively low resolution of the structure (Long et al., 2007) will introduce uncertainty to our predictions. In any case, our aim here is to use these algorithms to simply identify clusters that can be tested experimentally.

Figure 1.

Identification of a conserved cluster of contiguous residues in the K_V channel. (A) A heat map showing part of the symmetric version of the adjacency matrix showing the proximity scores between residues within the S4–S6 segments, deduced from the paddle chimera structure (PDB ID 2R9R, chain B). The proximity scores are colored from black to white according to the color legend shown alongside the matrix. The locations of the different helical segments are shown along the axes of the matrix, with the S4–S5 linker helix in gray and the tail end of the S6 helix in black. Within the matrix, the elements that depict the contacts between the S4–S5 linker and the S6 tail are shown within the dotted white ellipses. The heat map of the full sequence is shown in Fig. S1, and the full adjacency matrix is shown in the supplemental worksheet. (B) The full adjacency matrix that transforms the protein structure into a “graph” was clustered to find groups of residues with high interresidue contact density, which identifies six clusters. In each cluster, the circles (or nodes) represent an amino acid residue, numbered according to the Shaker K_V channel sequence (based on an alignment of Shaker and the paddle chimera; Fig. S2). The lines between the nodes (or edges) depict whether the two nodes have a proximity score greater than the cut-off. In the yellow, gray, and green clusters, all residues are within the same subunit. In the cyan, white, and red clusters, not all residues are in the same subunit; residues that belong to different subunits are separated by dark curved lines. The edges are solid for intrasubunit contacts and dashed for intersubunit contacts. (C) The green, yellow, and red clusters are mapped on the structure of the K_V channel, with the residues colored according to the cluster in B. For clarity, the intrasubunit green and yellow clusters, which are housed in the VSDs, are shown on different subunits. The red cluster lies at the intracellular interface between the two subunits. (D) For each of the six clusters, the standard deviation of the conservation entropy of the residues of a cluster (σ_c.e.) is plotted against the mean conservation entropy of the residues of the same cluster (μ_c.e.), derived from the multiple sequence alignment (MSA). Each circle represents a cluster and is colored according to B. The smaller dark circle, at the intersection of the two dashed lines, indicates the σ_c.e. and μ_c.e. for all of the residues of the protein (paddle chimera [2R9R, chain B] residues 158–417). (E–I) The frequency distribution of amino acids, at positions corresponding to each of the five residues of the intersubunit red cluster, derived from the MSA, is compared against the frequency distribution of amino acids in the overall MSA. The enrichment of particular amino acids at these positions underlies the high μ_c.e. and low σ_c.e. for the red cluster.

Each of these clusters were subsequently ranked in order of their evolutionary significance using sequence conservation scores (Halabi et al., 2009) derived from a multiple sequence alignment of 360 K_V channel sequences (Lee et al., 2009). For each cluster, two parameters were evaluated, µ_c.e. and σ_c.e. (Fig. 1 D), where µ_c.e. is the mean conservation score of the residues constituting a cluster and σ_c.e. is the standard deviation of the conservation scores of the residues in the cluster. A cluster with a high µ_c.e. and low σ_c.e. indicates that all of the residues comprising it are strongly conserved (as opposed to one with a high µ_c.e. and high σ_c.e., which indicates that the cluster comprises both strongly and poorly conserved residues) and is likely to be crucial for channel function. Of the six clusters, three (red, yellow, and green) are constituted by sites that also exhibit high evolutionary conservation. Fig. 1 C shows the location of the three clusters with high evolutionary scores on the structure of the K_V channel. The other three clusters are shown in Fig. S3. Each cluster is seen as a discrete entity, and the residues in a cluster are juxtaposed against each other. Of the three conserved clusters, the red cluster forms an intersubunit network, whereas the other two (yellow and green clusters) are completely housed within the VSD.

The red cluster is particularly significant because it is formed by residues (I384, R394, E395, V476, and Y485; numbered according to the Shaker K_V sequence) all at the intracellular interface between the S4–S5 linker and S6 helices. Fig. 1 (E–I) shows the distribution of the different amino acids at each of the five sites deduced from the sequence alignment. In comparison with the distribution of the amino acids in the total multiple sequence alignment (which closely follows the background distribution of amino acids in the nonredundant protein database), we find that the sites are strongly enriched in specific amino acids, which accounts for high μ_c.e. and low σ_c.e. for the cluster.

Energetic role of the interfacial gating triad evaluated using GIA

Of the different clusters identified using the computational approach, the red cluster is distinct because of several reasons. It comprises evolutionarily conserved residues, distributed at an intersubunit interface in a region of the protein previously hypothesized to be important for coupling voltage sensor motions to channel opening (Lu et al., 2002; Long et al., 2005b; Soler-Llavina et al., 2006; Muroi et al., 2010; Chowdhury and Chanda, 2012b). This raises the possibility that these sites might be important mediators of electromechanical coupling in voltage-gated potassium channels (Batulan et al., 2010; Haddad and Blunck, 2011). Within the red cluster, we observe that the arginine, glutamate, and tyrosine sites exhibit greater sequence conservation than the I384 and V476 sites. The isoleucine and valine are involved in intrasubunit contacts, whereas the other three sites form intersubunit contacts (Fig. 1 B). To understand the energetic role of these three residues in electromechanical coupling, we used the GIA approach to compute the interactions that underlie this triad (arginine, glutamate, and tyrosine), which also forms a highly conserved intersubunit contact. Additionally, we tested interaction between V476 with E395 because the 476 site features a strong enrichment in valine and the chemically similar isoleucine side chains.

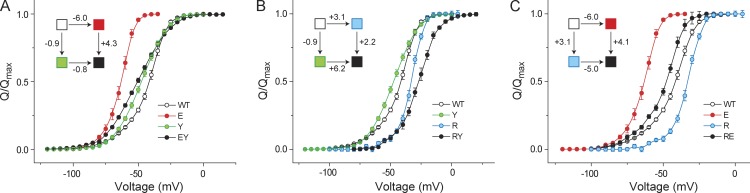
Each of the three residues was substituted to alanine individually and in pairwise combination, and for each mutant we measured the gating charge displacement versus voltage (Q-V) curve (see Fig. S4 for raw gating current records). For each pair (EY, RY, and RE) we compared the effects of the two single mutants with that of the double mutant. For instance, in the case of the EY pair (Fig. 2 A), we observed that although the E395A mutation causes a large leftward shift in the Q-V curve with respect to that of the WT channel, in the background of the Y485A mutation, E395A results in a much smaller shift (Table 1). Such a functional response is clearly reflective of nonadditivity of the two perturbations. The calculated energetic nonadditivity of the perturbations, in this case, turns out to be 5 kcal/mol (Table 2). Similarly, even in the case of the RY pair (Fig. 2 B), we observed a substantial nonadditivity of 3.1 kcal/mol (Table 2). In contrast, for the RE pair we found that the E395 mutation causes a substantial shift in the Q-V curves both in the presence and absence of the R394A mutation. The nonadditivity for the RE pair was found to be 1 kcal/mol, which is lower than the cut-off value for significant interactions. These results imply that both the arginine and glutamate residues strongly interact with the tyrosine residue, whereas they do not interact with each other.

Figure 2.

Pairwise interaction energies between residues of the interfacial triad using GIA. (A–C) GIA was used to measure the interaction energies between E395-Y485 (A), R394-Y485 (B), and R394-E395 (C). For each pair, the normalized Q-V curves of the single and double (alanine) mutants were measured, from which the V_M was extracted and used to calculate the free energy of perturbation. The thermodynamic cycle for each pair is shown in the inset, where each box corresponds to the WT or single or double mutants, colored according to the curves in each panel. The legends correspond to single-letter codes of the amino acids perturbed. Error bars represent SEM.

Table 1.

Median voltage of activation, V_M, and the net free energy of activation of mutants of the Shaker K_V channel

Mutant	VM (±SEM)	n	ΔGnet (±SEM)
	mV		kcal
WT	−44.7 (±1.0)	5	−13.6 (±0.3)
R394A	−34.6 (±1.0)	5	−14.0 (±0.3)
E395A	−64.6 (±0.9)	5	−19.6 (±0.3)
V476A	−61.0 (±0.9)	8	−18.5 (±0.2)
Y485A	−47.9 (±0.9)	5	−14.5 (±0.3)
R394A-E395A	−51.0 (±0.9)	6	−15.5 (±0.3)
R394A-Y485A	−27.4 (±0.9)	6	−8.3 (±0.3)
E395A-Y485A	−50.5 (±1.0)	4	−15.3 (±0.3)
E395A-V476A	−78.8 (±1.4)	4	−23.9 (±0.4)
V476A-Y485A	−61.4 (±1.6)	9	−18.6 (±0.5)
R394A-E395A-Y485A	−40.0 (±1.9)	4	−12.1 (±0.6)
E395A-V476A-Y485A	−66.6 (±0.6)	6	−20.2 (±0.2)

Gating currents for the mutants were measured either on a COVC or a TEV clamp set-up (bold). The V_M of the normalized Q-V curve, for all of the mutants (averaged from n oocytes), along with its SEM (δV_M) are reported for each mutant. ΔG_net was evaluated as Q_maxFV_M and its standard error as Q_maxFδV_M. For all mutants, a Q_max of 13.2 electronic charges was used for ΔG_net calculations.

Table 2.

Interaction energies between residue pairs evaluated using GIA

Site pairs	ΔΔGGIA	δΔΔGGIA
	kcal	kcal
R394-E395	1.05	0.58
R394-Y485	3.14	0.58
E395-Y485	5.27	0.58
E395-V476	0.64	0.65
V476-Y485	0.84	0.69
R394-E395 (Y485A)	−3.03	0.76
R394-Y485 (E395A)	−0.94	0.76
E395-Y485 (R394A)	1.15	0.76
E395-Y485 (V476A)	3.86	0.72

ΔΔG_GIA and its uncertainty (δΔΔG_GIA) for each pair of sites were calculated as described in Materials and methods. The first five rows correspond to mutant cycles in which the WT channel was the reference channel. For the last four rows, the control/reference channel is a mutant indicated in parenthesis and reflects the interaction energy between two residues in the presence of a third mutation.

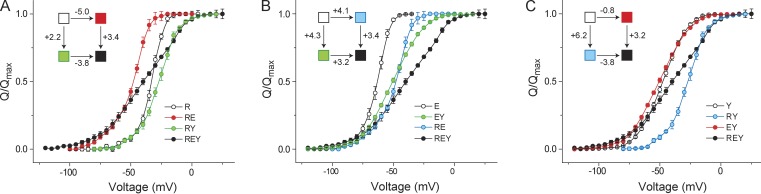
Next, we generated the triple mutant in which all three sites were mutated to alanine and we measured its Q-V curve. This allowed us to compute each of the three pairwise interactions, in the presence of a third perturbation (Fig. 3). In the presence of the R394A mutation, the E395A mutation caused a prominent leftward shift in the Q-V curves whether the Y485A mutation was present or absent (Fig. 3 A). The nonadditivity calculation shows that in the background of the R394A mutation, ΔΔG_GIA for the EY pair is 1.2 kcal/mol. Thus, there is a strong reduction in the interaction between E and Y in the background of the R394A mutation. Similarly, for the RY pair (Fig. 3 B) we observed that, in the presence of the E395A mutation, ΔΔG_GIA for the RY pair is −0.9 kcal/mol, which is 4 kcal/mol lower than the nonadditivity calculated in the absence of the mutation (Table 2). However, the RE pair exhibits a strong nonadditivity of −3 kcal/mol in the presence of the Y485A mutation. These results therefore imply that within the triad, ternary perturbations strongly influence each of the pairwise or binary nonadditivities.

Figure 3.

Ternary perturbation affects the pairwise interactions between residues in the interfacial triad. (A) GIA was used to measure the interaction energies between E395-Y485 in the presence of the R394A perturbation. The control or reference channel was the R394A mutant, and the three additional mutants (E, Y, and EY) were obtained in the background of R394A. For each of the four mutants, the normalized Q-V curves are shown along with the thermodynamic cycle in the inset (with each box representing the mutants colored as marked). (B and C) GIA for the R394-Y485 pair in the background of E395A mutation (B) and for the R394-E395 pair in the background of the Y485A mutation (C) showing the respective Q-V curves of the control/reference channel, the two single and the double mutation, and the thermodynamic cycle in the inset. Error bars represent SEM.

Valine 476 has no energetic influence on the gating triad

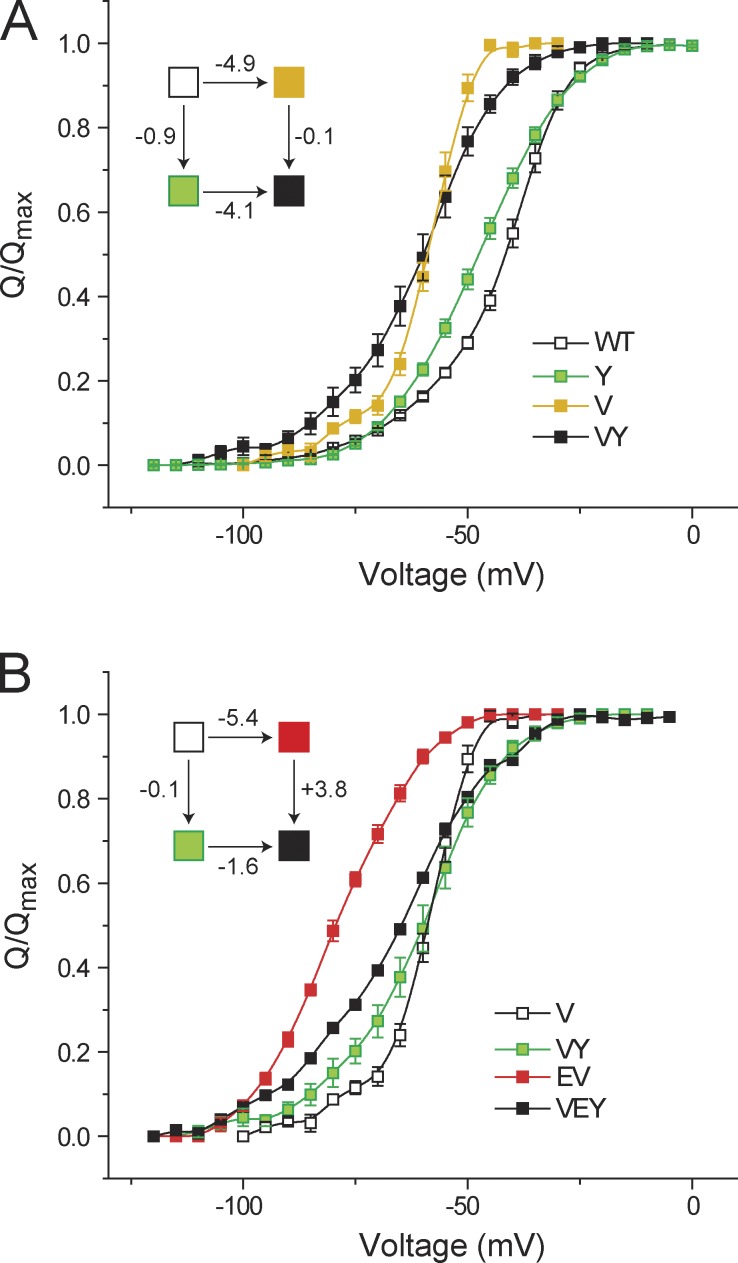
The valine residue (V476), which resides in the PD of the channel and is a part of the gating cluster, has been previously hypothesized to strongly interact with the glutamate residue (E395; Yifrach and MacKinnon, 2002; Barghaan and Bähring, 2009). However, in our companion paper (Chowdhury et al., 2014), ΔΔG_GIA measurements show that the contribution of such an interaction (if present) to the overall free-energy change of the protein is very small (<1 kcal). We further investigated whether V476 has any influence on the gating triad.

First, we generated the double mutant (V476A/Y485A), measured its Q-V curve (raw gating current records provided in Fig. S4), and performed GIA to measure the interaction between the sites V476 and Y485 (Fig. 4 A). Y485A perturbation caused small shifts in the Q-V curves in the WT channel as well as in the background of the V476A mutation, and the calculated ΔΔG_GIA between the two sites was found to be ∼0.8 kcal. This indicates that V476 does not share any substantial energetic linkage with the site Y485.

Figure 4.

Effect of V476 on the interaction between E395 and Y485. (A) Normalized Q-V curves to evaluate the interaction energy between V476 and Y485 using GIA, with the corresponding thermodynamic cycle in the inset. (B) Interaction energy between E395 and Y485 was assessed in the presence of the V476A mutation. The normalized Q-V curves for the single (E or Y) and double (EY) mutants, all in the background of the V476A mutation, are shown, along with the corresponding thermodynamic cycle. Error bars represent SEM.

Finally, we sought to determine whether V476 modulates the interaction between the sites E395 and Y485. To this end, we generated the triple mutant (E395A/V476A/Y485A) and measured its Q-V curve (Fig. 4 B). This was subsequently used to construct a mutant cycle, wherein the reference channel was the V476A mutant and the single and double perturbations (E395A, Y485A, and E395A/Y485A) were all in the background of the V476A mutation. For this cycle, ΔΔG_GIA was calculated to be 3.9 kcal/mol. This nonadditivity reflects the interaction energy between the EY pair in the background of the V476A mutation and is not significantly different from the interaction energy between the EY pair calculated in the WT channel background (Fig. 2 A). This suggests the V476 either does not interact with the gating triad or its interaction remains unchanged during channel activation.

DISCUSSION

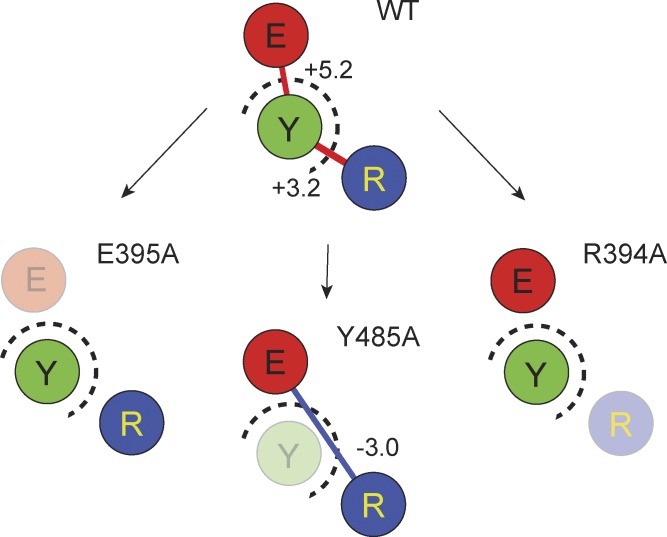
In this paper, we analyze an interaction network involving a conserved nexus of residues in the intracellular interface of Shaker potassium channel. The three critical residues constituting the triad are R394, E395, and Y485, wherein the latter belongs to the neighboring subunit and forms an intersubunit interaction with the other two. GIA calculations, performed by measuring the Q-V curves of the single, double, and triple mutants (summarized in Fig. 5), reveal that in the native channel the RY and EY pairs of residues interact with each other very strongly (3–5 kcal/mol), but the interaction is likely to be destabilizing toward the open state of the channel. In contrast, the RE pair does not seem to interact with one another in the native channel. Surprisingly, perturbation of the tyrosine residue led to the development of a strong interaction between the RE pair (∼3 kcal) that favors the open state of the channel. In contrast, the RY and EY interactions seem to disappear when the glutamate and arginine were perturbed, respectively. These interactions are not modulated by V476, which is the other conserved residue in the immediate vicinity.

Figure 5.

Summary of interactions at the triad. The three residues of the triad, R394, E395, and Y485, are shown as circles marked as R (blue), E (red), and Y (green), respectively. Intersubunit interface is marked with dashed circles. Each box represents the interactions between the residues in the WT channel or in the background of each of the three alanine mutants (mutated residues were made transparent). Unconnected circles imply that the interaction energy between them were not significant. The solid lines represent strong interactions with values in kcal/mol shown next to them. Lines are colored red for ΔΔG_GIA > 0 and blue for ΔΔG_GIA < 0.

Considerations for interpreting GIA data

As discussed in the companion piece, the interaction energy calculations require us to determine not just the V_M caused by perturbation but also the Q_max (Chowdhury et al., 2014). We have assumed that the Q_max is unchanged because all of these sites lie outside the region where the electric field drops sharply. The only residues that have been convincingly demonstrated to contribute to gating charges in the Shaker potassium channel are the first four arginines in the S4 segment (Aggarwal and MacKinnon, 1996; Seoh et al., 1996; Ahern and Horn, 2004). Nevertheless, we should add that it will be necessary to determine the Q_max to increase the accuracy of interaction energy measurements. Additionally, mutations may either slow down the gating charge movement or shift it far outside the measurable range. In both cases, the interaction energies will be underestimated. To increase the confidence that all transferrable gating charges have been counted when the Q_max appears less than WT, the following tests can be applied. Q-V curves should be measured to voltages large enough to saturate G-V curves. When mutation slows gating charge movement, gating currents should be measured by giving large pulses to accelerate slow components.

More generally, there are few other considerations regarding mutant cycle approach that should be kept in mind while interpreting GIA data. For instance, we should not expect mutant cycle to provide us an exact estimate of various contributions. Energetic contributions are typically probed by mutating the putative interactors to alanine. Such perturbations eliminate electrostatic and van der Waals contributions to interaction energies, and thus interpreting the physical origins of energetic nonadditivities might not always be very straightforward. Another consideration is that all mutant cycle approaches are based on the assumption that the free energy of the system is the sum of all interactions. This assumption is possibly not true (Mark and van Gunsteren, 1994), but it is necessary to understand the specific role of various amino acids in determining structure and forces that drive protein function.

A possible role of the interfacial gating triad

In light of the structure of the open Shaker channel, we can propose a mechanistic basis underlying the origin of these dynamic interactions. As seen in the structure of the open state of the paddle chimera (Fig. 6 A), the tyrosine residue is intercalated between the arginine and glutamate sites and thereby destabilizes the interaction between the two oppositely charged residues in the open state. Upon mutation to alanine, the room created by removal of the bulky phenolic side chain allows the arginine and glutamate to reorient themselves and interact with each other, which accounts for the nonadditivity between the RE pair in the absence of tyrosine (but not in its presence). In the native structure, the tyrosine itself is held in position by its interaction with the arginine and glutamate side chains; the underlying forces, although putatively repulsive (because of the positive ΔΔG_GIA) are oppositely directed, which holds the tyrosine in position. Mutation of the arginine (or glutamate) residue possibly results in an imbalance causing the tyrosine to swing out of position, thereby resulting in disruption of its interaction with glutamate (or arginine). It is important to mention that the positive interaction energy (nonadditivity) observed between the RY and EY pairs might not necessarily imply a repulsive interaction. ΔΔG_GIA reports the difference in the interresidue interaction energies between the initial (closed/resting) state and the final (open/activated) state of the channel (Chowdhury et al., 2014). Thus, positive ΔΔG_GIA simply indicates that the interaction energy between residue pairs is directed toward stabilizing the initial state with respect to the final state.

Figure 6.

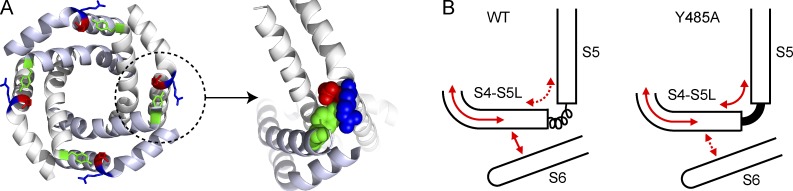
Possible role of the interfacial gating triad in electromechanical coupling in K_V channels. (A, left) A bottom-up view of the PDs of the K_V1.2/2.1 paddle chimera with the nonadjacent pairs of subunits colored similarly. The residues constituting the coupling cuff (R394, E395, and Y485) are depicted in a stick representation (and colored in blue, red, and green, respectively). (right) An enlarged view of the interfacial triad at a single intersubunit interface with the residues shown in CPK representation. (B) Cartoon of the S4-S5 linker and S5 hinge region in the WT channel and in the Y485A mutant. In WT, the hinge between the S4–S5 linker (S4–S5L) and the S5 is flexible, whereas in the Y485A mutant, the hinge is rigid. In WT, the force is transmitted from the S4 to the S4–S5L (curved solid red arrow) and relayed efficiently to the tail end of the S6 (straight solid red arrow), whereas only a small fraction is transmitted to the S5 (dashed curved red arrow). In the Y485A mutant, most of the force transmitted to the S4–S5L (from the S4) is lost in transmission to the S5 (curved solid red arrow) and only a small fraction is transmitted to the S6 (dashed straight red arrow). Thus, by altering the hinge-flexing energetics at the distal hinge of the S4–S5L, the Y485A mutation facilitates electromechanical transduction.

The gating triad, studied in this paper, has been previously suggested to contribute to electromechanical coupling in a study by Batulan et al. (2010). Based on OFF-gating current kinetics, they suggest that in the background of E395A, R394 and Y485 interact, which causes an open pore stabilization. Furthermore, the V476 site was also proposed to be essential for maintaining the structural integrity of the triad, although we find no evidence of such a role. Kinetics of the OFF-gating currents is informed by the stabilities of intermediate closed states, heights of multiple transition barriers, etc. that might have contributed to the observed deceleration of the OFF-gating currents by the E395A mutant.

What is the mechanistic role of the interfacial gating triad in relaying the structural changes to the channel gates? We speculate that this intersubunit interaction at the gating triad promotes electromechanical coupling at two levels. First, they form a “coupling cuff” around the pore gates that glues the intracellular moving parts of the neighboring subunits together (Fig. 6 A), thereby facilitating the final concerted transition that leads to channel opening (Zagotta et al., 1994; Ledwell and Aldrich, 1999). Second, this interfacial nexus is also important to maintain the flexibility of the distal gating hinge connecting the S4–S5 linker helix and the S5 transmembrane segment (Fig. 6 B). We speculate that this flexibility is important for electromechanical transduction in VGICs as a flexible hinge would facilitate energy flow to the S6 segment instead of contiguous S5, thereby allowing the lever-arm movement of the S4–S5 linker to efficiently close and open the channel gates (Chowdhury and Chanda, 2012b). Compromising the flexibility of the distal hinge by forming tight intrasubunit interactions, as observed in the Y485A mutation, impairs channel electromechanical coupling (Ding and Horn, 2002; Soler-Llavina et al., 2006; Muroi et al., 2010). By intercalating itself between R394 and E395, the Y485 residue forms a “coupling” nexus, allowing for facile transfer of information within and between the subunits of the K_V channel. Thus, this gating triad may serve as electromechanical switch that converts the electrical force acting on the S4 charges into a mechanical force that tugs at the tail end of the S6 segment, causing it to open/close.

Concluding remarks

Although our proposed mechanism is compatible with structure and known functional data, it can be further tested by a more exhaustive analysis of the residues in the intracellular gating interface. More importantly, pairwise interaction energies that contribute to the gating process as determined by the GIA approach are consistent with multistate gating models. This may allow direct comparison of experimentally measured residue-level interaction energies with those obtained from molecular dynamics simulation–based free-energy calculations. Additionally, they may help refine our understanding of structural changes during voltage gating. Applying the GIA approach to other members of the VGIC family will allow us to compare the strengths of interactions between the same amino acid pairs in homologous proteins. Molecular interactions are likely to be context dependent. For instance, in the EY pair nonadditivity depends on the presence of the arginine residue. Thus, equivalent sites in different proteins might interact differently depending on the context, and this diversity of interactions may result in distinct functional outcomes in homologous proteins.