Images as drivers of progress in cardiac computational modelling

Abstract

Computational models have become a fundamental tool in cardiac research. Models are evolving to cover multiple scales and physical mechanisms. They are moving towards mechanistic descriptions of personalised structure and function, including effects of natural variability. These developments are underpinned to a large extent by advances in imaging technologies. This article reviews how novel imaging technologies, or the innovative use and extension of established ones, integrate with computational models and drive novel insights into cardiac biophysics. In terms of structural characterization, we discuss how imaging is allowing a wide range of scales to be considered, from cellular levels to whole organs. We analyse how the evolution from structural to functional imaging is opening new avenues for computational models, and in this respect we review methods for measurement of electrical activity, mechanics and flow. Finally, we consider ways in which combined imaging and modelling research is likely to continue advancing cardiac research, and identify some of the main challenges that remain to be solved.

1. Introduction

From the first models of single cell electrophysiology (Noble, 1960, Noble, 1962) the field of cardiac modelling has experienced remarkable progress. Current models incorporate multi-physics phenomena (Hunter et al., 2003; Kohl and Noble, 2009; Nordsletten et al., 2011), combining electrophysiology (Trayanova, 2011), mechanics (Nash and Hunter, 2000), mechano-electric interactions (Hermeling et al., 2012; Hales et al., 2012), fluid flow (Taylor and Figueroa, 2009) and tissue perfusion (Lee and Smith, 2012). They characterize processes across scales, from nano to macro. Cardiac models increasingly incorporate subject-specific information, from ventricular anatomy to electrical and mechanical material properties (Ranjan et al., 2012, Sermesant et al., 2012, Krishnamurthy et al., 2013, Xi et al., 2013). Having proved their value for advancing our insight into mechanisms of (patho-) physiology (Hunter et al., 2001), models are now moving to applications in the clinic (Burnes et al., 2000, McDowell et al., 2012).

Healthy cardiac function depends on the interplay of multiple biophysical phenomena. The elucidation of mechanisms and their complex interrelations is particularly challenging when using a purely experimental approach. Mechanistic description, quantitative analysis, identification of causal interrelations, consideration of dynamic behaviour, and – in particular – prediction, are domains where computational modelling has started to play a prominent role in cardiac research. In this context, models enable one to integrate and interpret experimental data, to form and test hypotheses about cardiac function, and to assess physiological variables that may not be open to direct measurement due to their invasiveness or for technical reasons (e.g. lack of techniques to measure local stress in situ).

Electrophysiologically, cardiac cells can be divided into excitable (mainly cardiomyocytes; note that intra-cardiac neurons are generally excluded from cell-based cardiac modelling) and non-excitable (mainly fibroblasts, endothelial, immune and fat cells). In healthy myocardium, cardiomyocytes occupy ∼75% of tissue volume. The remainder is dominated by fibroblasts, accounting for ∼60–70% of all cardiac cells (Camelliti et al., 2005). The heart is an organ with built-in pacing and conduction capability, from the sinoatrial node, via the atrio-ventricular node and the specialised Purkinje system, to ventricular cardiomyocytes. The generated electrical wavefront triggers well-coordinated contraction of the muscle. On the cellular level, a wide range of cardiac EP models have been developed for the various cell sub-types involved in this process (e.g. (Zhang et al., 2000, Li and Rudy, 2011, Noble, 2011, Britton et al., 2013)), and the introduction and use of cell-level mark-up languages (like CellML) and associated tools are improving model exchange and re-use (Lloyd et al., 2004, Pitt-Francis et al., 2006, Garny et al., 2009, Gianni et al., 2010, Kerfoot et al., 2013). At the tissue level, cardiac EP models have traditionally considered the myocardial wall as a continuum (Garny et al., 2003, Clayton et al., 2011, Cooper et al., 2011), typically introducing anisotropy through conductivity tensors.

From a mechano-anatomical model perspective, the heart can be decomposed into active and passive components. The mechanically active component is formed by the contractile cardiomyocytes, while the mechanically passive component comprises intra-cellular visco-elastic structures (both in cardiomyocytes and non-myocytes) and the extra-cellular matrix which provides the deformable skeleton of the heart (Weber et al., 1994). Similarly to EP models, cardiac mechanical models traditionally represent this microstructure as a continuum, encoding microstructure in the anisotropy of the contractile and material properties (Hunter et al., 2003). More recent attempts have tried to incorporate the hetero-cellular nature of heart muscle (Xie et al., 2009), and the feedback from mechanical to electrical behaviour of the heart (Kohl et al., 1999, Kohl et al., 2006, Li et al., 2004).

From a fluid dynamics perspective, the ventricles are chambers whose inflow and outflow tracks are controlled by valves. Blood can be accurately represented as an incompressible fluid, and inside the cardiac chambers and big vessels its constitutive behaviour can be approximated by a Newtonian model.

Depending on the specific research question addressed, a cardiac model can represent a combination of the aforementioned three physical domains: EP, mechanics and fluidics. The two most common combinations are electro-mechanical (Trayanova, 2011) and fluid–solid interaction models (Taylor and Figueroa, 2009) for the study of the ventricles and main vessels, respectively.

The synergy between experimental methods (e.g. data from images and functional maps) and theory (computational models) is key in the generation of novel insight in cardiovascular science (Quinn and Kohl, 2013). The availability of novel imaging technologies, and the innovative use or extension of established ones, are main drivers of this progress. Recent years have seen dramatic improvements in imaging capabilities, and a rapid expansion of their application. Images cover most of the scales relevant to cardiac modelling, from subcellular structures (Iribe et al., 2009) to whole organs (Pope et al., 2008, Trayanova, 2011). Images have moved from characterizing static structures to providing dynamic measures of function (Townsend, 2008), including electrophysiology, mechanics and blood flow, and modern techniques even probe different aspects of metabolic activity (Taegtmeyer and Dilsizian, 2013). Image analysis methods, allowing the combination of images from multiple subjects, are gradually enabling the transition from individual to population studies (Young and Frangi, 2009).

For these reasons, imaging and modelling are increasingly linked. Development of computational models relies on information acquired from images. Image data have become drivers of progress in cardiac computational modelling in three general areas (Fig. 1). First, they capture anatomy, providing the structural information necessary to run simulations (MacLeod et al., 2009). Secondly, images provide functional information used to build, adjust and validate models (Carusi et al., 2012). When models are not able to reproduce the data contained in images, model limitations are identified, and new mechanisms may be unveiled (Kohl et al., 2010). Thirdly, images are used to estimate model parameters by data assimilation (Sermesant et al., 2006b), finding the model parameters that best explain the observed data. These parameters can then be fed back to experimental investigations, or be used as biomarkers. Models also feedback onto imaging methodologies providing a framework for integrating images across multiple scales, for interpreting measurements introducing the biophysics of the system and for linking data across different imaging platforms.

Fig. 1.

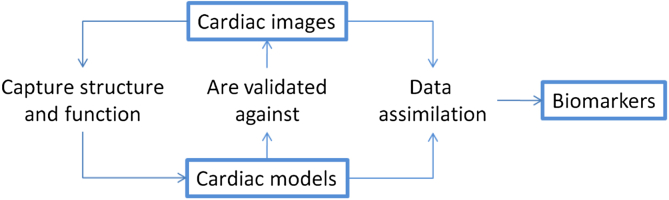
Conceptual scheme of how cardiac images interact with computational models to generate novel insight and drive research progress.

In this review, we concentrate primarily on the scales from tissue to whole organ. Subcellular structures rely on a separate set of imaging technologies (Iribe et al., 2009, Wong et al., 2013) and modelling approaches (Winslow et al., 2006, Gaur and Rudy, 2011), and while there are relevant conceptual similarities, these merit a review on their own. Rather than presenting an exhaustive list of papers, we aim at providing a consideration of the main trends in the field, highlighting in particular how the use of novel imaging technologies is opening up new possibilities for innovation. We illustrate this by offering representative examples covered in previous publications. We do not provide details about modelling, but instead refer the reader to recent reviews and original sources.

Following this introduction, the paper is organized as follows. Section 2 provides an overview of imaging modalities that have become established in clinical cardiac assessment, and of the ways in which they have been applied in combination with computational models. Sections 3, 4 focus on more experimental imaging techniques, illustrating specific areas in which progress in modelling has been made possible through advances in imaging technologies, and/or in which new imaging developments have been motivated by the needs of modelling research. This is separated into new imaging technologies currently pushing the boundaries of structural (Section 3) and functional (Section 4) characterization of the heart. Section 5 discusses current and future challenges and opportunities involving the combination of images and models in cardiovascular science and medicine.

2. Established clinical imaging technologies: An overview

Imaging has become an integral part of cardiac health and disease assessment. Several cardiac imaging modalities are now widely available in the developed world, and are used as part of standard procedures recommended by the relevant medical societies. As models evolve towards clinical application, data from these imaging modalities are commonly available to build personalised models. Understanding strengths and limitations (including those arising from clinical constraints) of the various techniques is fundamental for successful interrelation with computational modelling. This Section provides an overview of several well-established imaging technologies that have been used in combination with computer models, and discusses representative examples of their application in specific computational modelling studies.

2.1. Echocardiography

Echocardiography often is the first-resort imaging modality in the clinics, due to its low cost (Pennell et al., 2004), lack of ionising radiation, safety, rapid evaluation, easy transportation to the bedside and availability in the operating theatre. Handheld ultrasound systems have become available, providing even higher portability and encouraging routine use in the out-of-hospital setting. Transthoracic echocardiography, the most common echocardiographic investigation, is fully non-invasive, and even invasive transesophageal exams require only mild or no sedation, and involve no incisions. Echocardiographic images show a distinct texture of locally varying signal intensities, commonly referred to as speckle. Speckle tracking can be used to study tissue deformation and thus estimate strain and strain rate. This is useful for the assessment of systolic and diastolic function, and for the identification of regional motion abnormalities indicative of ischemia or scarring (Blessberger and Binder, 2010, Mondillo et al., 2011).

The uptake of echocardiographic data for model development has been limited so far, but insightful case examples exist: e.g. its use in combination with simple mechanical models to identify the contribution of the right ventricle to improved pump function induced by cardiac resynchronization therapy (Lumens et al., 2013), or to evaluate the relevance of different dyssynchrony indexes to predict the response to the same therapy (Lumens et al., 2012), or to predict the improvement in contractile behaviour after cardiac revascularization (Han et al., 2005). Echocardiography has recently benefited from further important advances in technology that will affect the development of computational models and give rise to novel insights. The development of gas-filled microbubbles for use as contrast agents has enabled the evaluation of perfusion (Bhatia and Senior, 2008). In addition, 3D echocardiography increasingly overcomes the limitations of 2D data, albeit generally at a cost of reduced spatio-temporal resolution. 3D echo can also provide data suitable for generation of valid anatomical models of the right ventricle and the cardiac valves (Lang et al., 2012).

2.2. Cardiac Magnetic Resonance Imaging

Cardiac Magnetic Resonance Imaging (MRI) can provide a rich set of data, including information on cardiac anatomy, mechanics, microstructure, perfusion, and other tissue properties. Consequently, MRI has been proposed as a “one-stop-shop” for the analysis of the heart (Poon et al., 2002), and it is considered the gold-standard for assessing cardiac anatomy and function. On the flip side, cardiac MRI is relatively slow, typically involving a combination of acquisitions over several cardiac cycles using the electrocardiogram (ECG) for gating. Long acquisition time also affects resolution, and MRI datasets typically consist of a number of two-dimensional slices acquired at different locations and orientations. MRI can introduce risks to patients with implanted devices which, in turn, can affect the quality of information acquired (Ainslie et al., 2014), though MRI-compatible devices have started to become more generally available (Wilkoff et al., Sommer, 2011).

The possibility of obtaining accurate anatomical and functional information from a single imaging modality, the relatively “clean” appearance of the images (in comparison to echocardiography), and the relatively widespread availability of MRI have led to its use in many cardiac modelling studies, e.g. (Plank et al., 2009, Vadakkumpadan et al., 2009, Conti et al., 2011, Bishop and Plank, 2012, Krishnamurthy et al., 2013), as will be illustrated in more detail in Sections 3, 4 below.

2.3. Computed Tomography (CT)

Computed Tomography (CT) provides excellent anatomical resolution, both spatial and temporal, but it involves exposure to ionizing radiation. It allows accurate assessment of cardiac functional properties such as left ventricular stroke volume and ejection fraction, and of morphological characteristics such as congenital heart disease, cardiac masses, regional wall motion, presence and location of thrombi, pericardial disease. In addition, CT has recently been proposed for perfusion assessment (Peebles, 2013). The quality and reproducibility of images enables the adoption of robust automatic segmentation solutions for cardiac chambers (Ecabert et al., 2008).

The excellent anatomical detail provided by this imaging modality has enabled detailed computational investigations, such as of the effects of vessel anatomy on blood flow (Taylor and Figueroa, 2009). Personalised models of the coronaries predict an important clinical marker, the flow reserve, without the need of catheterization, constituting an excellent example of successful translation of model-based imaging to clinical practice (Taylor et al., 2013). CT also provides the opportunity to build personalised ventricular models of subjects with implantable devices, such as a left ventricular assisted device, and then optimise the settings of the device by identifying the flow regime that maximises myocardial unloading and homogenisation of work (McCormick et al., 2014).

3. Anatomical model improvements driven by novel imaging techniques

While established imaging modalities will continue playing substantial roles in the development, application and validation of cardiac computational models, continued advances in imaging technologies are pushing the boundaries of model-based cardiac research. Novel technologies allow probing the heart at unprecedented resolution levels, measuring different aspects of cardiac function, and quantifying anatomical and functional variability in health and pathology. In the next two Sections we review specific aspects in which imaging technologies are driving progress in computational models. Section 3 focuses on anatomical characterization, discussing in particular three aspects: (i) the introduction of meso-scale anatomical structures, beyond the standard representation of ventricular and atrial cavities and walls; (ii) moving towards micro-scale, the characterization of cellular structures; and (iii) the quantification of anatomical variability using multi-subject studies and advanced computational statistical atlases.

3.1. Models including meso-scale anatomical structures

While models using simplified geometries have demonstrated their utility in elucidating fundamental mechanisms of cardiac function, a number of studies have shown the importance of finer-scale structures, including papillary muscles (Kim et al., 1999, Bishop et al., 2010b), blood vessels (Luther et al., 2011, Bishop et al., 2012), trabeculations (Bishop et al., 2010b, Sands et al., 2011), and the Purkinje network (Vigmond and Clements, 2007, Ten Tusscher and Panfilov, 2008, Romero et al., 2010, Bordas et al., 2011). Recognition of the importance of small structures, together with advances in computational methods, has motivated the development of high-resolution models. These models are generally made possible by high-resolution structural MRI scans (see Fig. 2), which at present are obtained ex vivo in fixed (Bishop et al., 2010b, Vadakkumpadan et al., 2010) or live tissue (Schuster et al., 2012, Hales et al., 2012, Odening et al., 2013).

Fig. 2.

Sample slices in three orthogonal directions from an ex vivo 3D MRI acquisition of a rabbit heart, from Bishop et al. (2010b). The original resolution of the images is 26.4 μm × 26.4 μm × 24.4 μm. LV, RV, LA, RA: Left (right) ventricle (atrium). AO: Aorta.

High resolution ex vivo MRI (also referred to as MRI microscopy) has been employed to obtain detailed ventricular geometries in experimental studies (Gurev et al., 2011), and to identify infarcted regions (Vadakkumpadan et al., 2010), leading to computational studies of the electrophysiological effect of the location, size and shape of infarcts. While ex vivo MRI microscopy offers the possibility of characterizing small structures, down to voxel sizes in the order of 10⁻⁸ m (Gilbert et al., 2012), it is limited in several aspects. Excision and fixing of the heart gives rise to deformations, which require nonlinear registration to the in vivo geometry for compensation (Plank et al., 2009). Ex vivo hearts experience a drift in their properties with time, even after chemical fixation, potentially leading to significant changes in MRI acquisitions (Hales et al., 2011). Fixation in different states of contraction has been demonstrated (Plank et al., 2009), but individual hearts can only be fixed in one state which complicates the analysis of cardiac motion effects in fine scale structures. That said, progress is being made in MRI microscopy of isolated perfused hearts, which are now yielding high-resolution data from multiple deformation states in one and the same sample (see (Hales et al., 2012) and the paper by Lohezic et al., 2014).

Detailed models of ventricular anatomy with high-resolution MRI have provided insights on the efficacy of defibrillation after infarction, finding that the change of properties in the peri-infarct zone explain the increased vulnerability (Rantner et al., 2012), and proposing low-voltage defibrillation protocols to convert ventricular fibrillation into tachycardia, and then terminate tachycardia (Rantner et al., 2013a). Computational modelling studies of the atria have also benefitted from the availability of high-resolution MRI scans, with models being applied to analysing the effects of tissue remodelling, the presence of fibrosis (McDowell et al., 2012, McDowell et al., 2013), and the arrangement of endocardial bundles (McDowell et al., 2011, Maesen et al., 2013) in atrial fibrillation.

Electric disorders, such as reentrant arrhythmias, are often closely associated with the presence of heterogeneities in the myocardium, and thus the study of such phenomena requires incorporation and analysis of the impact of finer-scale anatomical details within models. Experimental investigations have demonstrated that distinct anatomical features (such as papillary muscle insertion sites, endocardial trabecular invaginations, or large sub- epicardial blood vessels) play a potentially important role in stabilising reentrant arrhythmias (Pertsov et al., 1993, Kim et al., 1999, Valderrábano et al., 2001, Valderrábano et al., 2003, Nielsen et al., 2009), providing a substrate which attracts and anchors rotors. Recently, computational models derived from high-resolution MR and containing such levels of finer-scale anatomical detail (Bishop et al., 2010b), have been instrumental in providing a full three-dimensional understanding of these mechanisms (Bishop et al., 2010a, Bishop and Plank, 2012), and the circumstances under which they become important. Furthermore, structural heterogeneity is known to be of great importance during electrotherapy. Both computational bidomain studies (Hooks et al., 2002, Bishop et al., 2010a) and experimental optical mapping measurements (Fast et al., 1998, Fast et al., 2002) have shown how the interaction of conductivity discontinuities, represented by intramural blood vessels and extracellular cleft spaces, may induce 'virtual-electrode' polarisations within the tissue depth, suggesting this as a mechanism of more effective defibrillation (Luther et al., 2011, Bishop et al., 2012).

3.2. Myocardial microstructure

Our understanding of the spatial organization of myocardial tissue, and its impact on electrical and mechanical function, has greatly improved in recent years. Ventricular myocytes are grouped longitudinally in strands, usually referred to as ‘fibres’, and laterally arranged in layers, usually called ‘sheets’. This arrangement is closely linked to the specific shape of the cardiac myocyte and the extensive collagen network present in cardiac tissue (LeGrice et al., 1995, Spotnitz, 2000, Gilbert et al., 2007). This organization is fundamental for healthy cardiac electro-mechanical function. Of note, both electrical (Kanai and Salama, 1995) and mechanical (Waldman et al., 1988) behaviour are highly anisotropic within ventricular tissue, yet in combination with structurally determined differences in activation timing and stress-strain dynamics, they give rise to externally homogeneous function (as discussed in Solovyova et al. (2006) and by Solovyova et al. 2014).

Microscopy of histological sections has driven knowledge of cardiac cell distribution and morphological interrelations (Spotnitz, 1974), and this data modality remains a gold standard for micro-structural tissue characterization. Standard histology techniques, such as the use of trichrome stains to differentiate between myocytes, collagen and other cells (Plank et al., 2009), provide fundamental information about myocardial microstructure. On the other hand, histology has the important shortcoming that processing and mechanical slicing distort the tissue. These non-linear deformations pose significant challenges for 3D tissue reconstruction by alignment of adjacent 2D slices. Estimating cellular orientations in slices has a fundamental limitation also in that angles can only be measured reliably within the cutting plane of a slice. This can be partially compensated by use of non-parallel slices, but since these cannot be extracted from the same location in a single heart, any 3D description based on histology sections is necessarily incomplete. Nonetheless, mathematical models of whole-ventricular fibre distribution, based on histology (Nielsen et al., 1991, Legrice et al., 1997), have played important roles in cardiac modelling, from early models of cardiac electrophysiology to more recent electromechanical ones (Aguado-Sierra et al., 2011, Clayton et al., 2011).

High-resolution confocal microscopy has also been employed to image cell orientation and the 3D arrangement of laminar structures in small samples of myocardial tissue. In contrast to histology slices, confocal microscopy datasets can be obtained in 3D without physical slicing. Current technology is limited, however, to characterisation of small regions that are near the accessible surface, for example to study sarcomere lengths in sub-epicardial tissue in horizontal (Bub et al., 2010) and oblique orientations (Botcherby et al., 2013). Using confocal imaging of embedded tissue, combined with periodic removal of the imaged tissue layers, true 3D reconstruction of cardiac tissue is possible (Pope et al., 2008). Tissue structure distributions, obtained in this way, were introduced in 3D tissue slab electrophysiological simulations (Hooks et al., 2002), demonstrating that not only fibre direction but the anisotropy induced by sheet orientation may affect electrical propagation patterns across the tissue. Confocal imaging has also given further insight into cardiac collagen organisation, including description of extensive meshworks on laminar surfaces, convoluted fibres connecting adjacent layers, and longitudinal cords (Pope et al., 2008).

Diffusion Tensor MRI (DT-MRI) protocols are the state-of-the-art in non-destructive methods to obtain myocyte orientation in cardiac geometries (Sosnovik et al., 2009), initially in fixed hearts as pioneered in (Helm et al., 2005, Helm et al., 2006), but now also applied to in vivo human data acquisition, albeit not at microscopic resolution (Nielles-Vallespin et al., 2013). DT-MRI characterizes the diffusivity of water molecules in the myocardium, providing an indirect measure of tissue microstructure, and in particular of the alignment of privileged diffusion spaces in and around myocytes, and the barriers formed by their lateral arrangement into sheets (Scollan et al., 1998). Alternatives to DT-MRI that allow representing complex configurations such as crossing fibres or bifurcations have been proposed (Dierckx et al., 2009) . Direct characterisation of tissue structure in whole hearts is also possible to some extent by high resolution ex vivo T2* enhanced MRI (Gilbert et al., 2012).

Models of cardiac electrophysiology based on tissue structure distribution obtained from ex vivo DT-MRI acquired from a single subject (Vadakkumpadan et al., 2010), or statistical atlases based on ex vivo DT-MRI of multiple datasets (Relan et al., 2011), have been used to predict the evolution of arrhythmia in the infarcted rabbit (Vadakkumpadan et al., 2009) and human heart (Relan et al., 2011).

Given that high-resolution DT-MRI studies are only possible ex vivo, solutions have been proposed to build patient-specific fibre models by warping fibre atlases onto patient-specific gross cardiac geometries (McDowell et al., 2013). This approach is also supported by recent results suggesting limited relevance of personalised fibre descriptions for simulation of cardiac mechanics (Carapella et al., 2014). More recently, methods to extract smooth representations of tissue structure distribution from in vivo DT-MRI have been developed (Toussaint et al., 2013). This imaging modality has enabled the study of the microstructural regeneration capacity in mice, opening up the possibility of studying the longitudinal effects of interventions such as cell therapy or progression of diseases such as heart failure (Sosnovik et al., 2014).

The combination of realistic geometry from MRI microscopy with realistic tissue structure from DT-MRI is still uncommon, partly because of the high imaging and computational cost associated with both, and with the modelling framework. Simulation of the high-resolution geometry and structure information requires the use of parallel computing approaches and supercomputer facilities (Lafortune et al., 2012). Efforts to exploit this combination have recently started to be undertaken (Gurev et al., 2011, Gil et al., 2013), suggesting that the use of realistic tissue structure distribution will allow electro-mechanical models to predict more realistic global motion and regional strain/stress patterns.

Histology and DT-MRI offer complementary information and their combination can provide rich descriptions of histo-anatomy of the whole heart. Almost a decade ago, a first complete framework to combine histology, high-resolution ex vivo MRI, in vivo and DT-MRI was presented (Burton et al., 2006). Given the substantial deformations occurring between acquisitions (between in vivo and ex vivo scans and between MRI and histology), advanced image processing algorithms are required. Additionally, 2D slices need to be combined to produce a 3D representation that can be related to MRI findings, a process that is far from trivial (Gibb et al., 2012). In a related study, the sinoatrial node was reconstructed in human tissue by combined DT-MRI, histology and immuno-histochemistry imaging (Chandler et al., 2011). A similar methodology has been used to build a segmented anatomical and electrophysiological model of the atrioventricular node (Li et al., 2008), and of the sinoatrial node in rabbit (Dobrzynski et al., 2005). A framework to combine high-resolution MRI, DT-MRI and histology has been demonstrated in Plank et al. (2009) to build the most detailed anatomical whole ventricular models to date.

An illustrative example of synergy between imaging and modelling is illustrated by Hales et al. (2012). Computational models of cardiac mechanics typically fail to predict some aspects of cardiac contraction; in particular they tend to underestimate shortening in the apex-base axis, as well as the predominantly centripetal wall thickening. Laminar tissue structure was suggested as an explanation for this effect in Spotnitz (1974). Confirmation of this basic mechanism, generally missing as an explicit structure from models (changes in sheet angles occurring with contraction), was made possible by DT-MRI studies of individual hearts in two contraction states, using a unique imaging set-up constructed specifically for this purpose (Hales et al., 2012; updated to three mechanical states in the paper by Lohezic et al., 2014).

Atrial walls are much thinner than those of the left venctricle, and their microstructure is mainly characterised by bundles linking atrial sub-structures, and by a thin layer of cells (see recent reviews of atrial modelling in Dössel et al. (2012) and Trayanova (2014)). This microstructure is not well captured by the resolution offered by DT-MRI, but contrast enhanced micro CT has shown to be able to combine an excellent myocyte contrast and voxel resolution, 36 μm (Aslanidi et al., 2013). Realistic 3D atrial tissue models enable a detailed in-silico analysis of electrical disorders, and have recently led to the suggestion of mechanisms that facilitate initiation and maintenance of re-entrant excitation waves (Colman et al., 2013, Trayanova, 2014).

3.3. Analysis of variability

The inclusion of developmental, inter-individual, and disease-related variability in cardiac anatomy and function is an important task area for computational modelling (Britton et al., 2013). Images, and other measurements acquired on individual subjects, provide a subset of the parameters that affect or represent cardiac function. These parameters are usually complemented by standard values or published data acquired in previous studies. A quantitative description of the variability of these parameters is necessary to determine the extent to which the use of standard values affects the validity of model predictions. Estimations of uncertainty can be generated in this process, which may help to select appropriate studies for each specific research question.

Shape variability, for example, can be observed in collections of images, and then quantified through mathematical and statistical tools, including computational atlases. Medical atlases have found wide acceptance in the field of neuroanatomy (Thompson et al., 2000). Similar attempts to capture cardiac structural variability in the form of atlases have been proposed, from gross anatomy Fonseca et al. (2011) to microstructure Lombaert et al. (2012). Initially used as guides for segmentation algorithms (Heimann and Meinzer, 2009), they are now finding their way into computational modelling (Young and Frangi, 2009). Characterization of shape using models has been shown to help quantifying shape bias of imaging protocols (Medrano-Gracia et al., 2013), to allow differentiation of gestational age (Lewandowski et al., 2013), and to be a potential biomarker for adverse cardiovascular events (Lamata et al., 2013a).

4. From anatomy to function

Medical imaging has evolved from the capture of still images, mostly containing anatomical information, to the dynamic characterisation of function. This opens up a range of exciting possibilities in the field of cardiac research, and is arguably the technological area with the potential to produce the strongest driver for conceptual development, in particular through computer modelling.

This section continues the exploration of novel modelling developments, driven by emerging imaging techniques. Here, we focus on image-based characterization of cardiac function, and specifically on three cardiac processes of particular relevance: EP, ventricular wall mechanics, and blood flow inside the cardiac chambers and main vessels.

4.1. Excitation and conduction

Some of the most prevalent and severe cardiac diseases are characterized by EP disorders. The management of these patients requires structure-based information on atrial and ventricular EP, to estimate conduction blocks, re-entry circuits, pro-arrhythmic substrates, etc. General availability of data on cardiac electrical activity has traditionally been limited to the ECG or body surface potential maps. New imaging techniques support acquisition of high-resolution maps of electrical activity ex vivo and, with certain limitations, in vivo.

Electro-anatomical mapping systems (such as Ensite NaVx from St. Jude Medical, or CARTO from Biosense Webster, see Fig. 3a) have changed the way in which clinicians explore and visualize EP function of patients (Knackstedt et al., 2008, Chubb et al., 2014). These systems combine intra-cardiac catheter tip tracking with field potential recordings, and provide anatomically (relative to the endocardium) resolved EP information in vivo. Despite its limited anatomical fidelity, which is further affected by distortions caused by catheter tip interaction with the tissue (in particular in the thin-walled atria), and the difficulty of mapping the EP data to the cardiac anatomy reconstructed from other modalities, electro-anatomical maps can be used to estimate patient-specific electrical conductivity, and to identify regions of impaired electrical function (Chinchapatnam et al., 2008). Electro-anatomical maps are generated interactively in the catheter lab, and can therefore be used as an on-site guide for ablation procedures (Nademanee et al., 2004). Optimization of pacemakers can also benefit from this modality, since it enables the analysis of intrinsic and paced activation waves (Vatasescu et al., 2009). EP mapping technology also enables simultaneous recordings at several locations through multi-electrode basked catheters; they are generally used for the ventricle, and their non-contact data is less accurate.

Fig. 3.

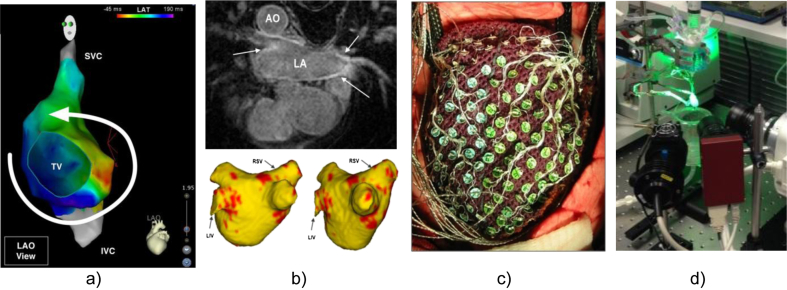
Imaging techniques to capture cardiac electrophysiological information. (a) Electro-anatomical map of the atrium, obtained by intra-cardiac catheter approaches, showing a re-entry circuit (Chubb et al., 2014; image courtesy of Dr. H. Chubb, KCL); (b) Functional MRI of the heart capturing the extent of fibrosis for ablation therapy of atrial arrhythmias (top), automatically segmented and reconstructed (bottom; Karim et al., 2014; image courtesy of Dr. R. Karim, KCL). AO: Aorta, LA: Left Atrium, RSV: Right Subclavian Vein, LIV: Left Innominate Vein. (c) Multi-electrode cardiac sock for human epicardiac potential mapping (Nash et al. 2006; image courtesy of Dr. M. Nash, University of Auckland); (d) Optical mapping set-up for ex vivo Langendorff-perfused rabbit heart (Bishop et al. 2014; image courtesy of Dr. R. Burton and Dr. G. Bub, University of Oxford).

EP maps obtained in this way have been adopted into models of the atria (Dössel et al., 2012), which are providing novel insight into atrial fibrosis as a substrate of atrial fibrillation (McDowell et al., 2012), and into models of the susceptibility to arrhythmias of the infarcted heart (McDowell et al., 2011, Karim et al., 2013, Karim et al., 2014). In combination with structural information obtained from other imaging modalities (like late gadolinium enhanced MRI, see Fig. 3b), EP maps have been used to predict risk of arrhythmia recurrence after ablation (Oakes et al., 2009). Access to advanced EP mapping systems is still developing. As they require an invasive procedure, and provide only partial information from extracellular field potentials, EP maps have not yet been widely adopted by the academic modelling community.

The interpretation of EP function measurements is greatly enhanced when combined with specialised structural characterization, facilitated by computational models. Late gadolinium-enhanced (LGE) MRI, also known as delayed enhancement MRI, is an imaging technique that can be used to assess scar location and size after myocardial infarction or ablation (see Fig. 3b). A landmark paper found a correlation between the amount of enhancement and the risk of recurrence after ablation (Oakes et al., 2009), and verified that the regions of greater enhancement were related to regions with low voltage from electroanatomic maps. LGE MRI has gradually been adopted for models of the atria (Dössel et al., 2012), which are providing novel insights about atrial fibrosis as a substrate for atrial fibrillation (McDowell et al., 2012) and the susceptibility to arrhythmia in the infarcted heart (McDowell et al., 2011). Models have successfully predicted ventricular tachycardia circuits (Ng et al., 2012), and suggest a significant potential to reduce ablation procedure time and complication rates by modelling-based pre-procedural planning of optimal ablation targets (Ashikaga et al., 2013). More specifically, models built to investigate tachycardia circuits have found the so-called ‘grey zone’ to be the arrhythmogenic substrate that promotes re-entry formation (Arevalo et al., 2013).

Multi-electrode cardiac socks record the electrical potential distribution directly from the epicardial surface of the heart. Resultant EP imaging data resolution is much better than in other patient-applicable recording techniques, such as the ECG. Electrode sock recordings have been used intra-operatively in humans (see Fig. 3c). They have been successfully applied to investigate the relevance of the latest activated region for cardiac resynchronisation pacing in the treatment of heart failure (Helm et al., 2007). The combination of EP data from cardiac socks with computational models has supported investigations into heterogeneous restitution properties, and their influence on vulnerability to, and stability of, re-entry in ventricular fibrillation (Nash et al., 2006). Cardiac sock recordings have also revealed differences between animal models and humans in the dynamics of ventricular fibrillation, and computational modelling has been applied to explain these by differences in action potential duration dynamics across species (ten Tusscher et al., 2009). One conclusion that has emerged from these studies is that the simpler spatial organization of human ventricular fibrillation is likely to have important implications for treatment and prevention, highlighting the necessity of combining experimental data and computational models to project between species. Cardiac socks have also been used for simultaneous imaging of endocardial and epicardial electrograms, revealing distinct characteristics of the re-entrant waveforms on each of the surfaces, and thus making a valuable contribution to the understanding of transmural mechanisms of ventricular fibrillation (Massé et al., 2007).

Imaging of EP activity using cardiac socks requires invasive procedures, and data can be substantially affected by artifacts. An alternative is the use of higher resolution surface electrode plaques, which are also invasive but provide finer-scale electrical data (Nademanee et al., 2004, Lee et al., 2014). In addition, transmural EP activity can be acquired through specialised arrays of multi-point recording needles (Valderrábano et al., 2001). These have highlighted, for example, that the so-called M-cells (myocytes with exceedingly long AP durations) would appear to be absent from human myocardium, again referring to the need for careful extrapolation between species (Taggart et al., 2003).

Stretchable electronics (Kim et al., 2011, Chung et al., 2014) constitute a new technology that may allow integration of voltage sensors on conventional balloon catheter membranes, opening up the possibility of high-density measurements with minimally invasive procedures. In a similar way, elastic integumentary membranes, produced via 3D printing to match the shape of the heart, may provide an improved picture of both EP and mechanical response (Xu et al., 2014).

Electrocardiographic imaging (ECGI) – the reconstruction of the electrical activity in the heart from body surface potentials – is a concept with high relevance for the clinical management of patients with cardiac electrophysiological disorders. Mathematically this is an “ill-posed” problem, which can be solved only with the use of appropriate constraints, including an accurate spatial representation of the interrelation of the heart as the electrical source, and the recording locations of mapping electrodes. The feasibility of this approach in humans was demonstrated in a study involved the combination of a vest with 224 electrodes, an accurate anatomical model from CT imaging, and a mathematical solver able to reconstruct electrical potentials, electrograms and isochrones on the heart's surface (Ramanathan et al., 2004). ECGI has since been used to evaluate electrical function in patients from paediatric candidates for cardiac resynchronization therapy (CRT) (Silva et al., 2009) to heart transplant recipients (Desouza et al., 2013), and it has moved to commercialisation (CardioInsight Technologies Inc., Cleveland, USA).

Optical mapping produces images with higher spatial resolution than cardiac socks, using photodetectors to record light emitted by fluorescent dyes that report functional properties (see Fig. 3d). Potentiometric dyes (Laughner et al., 2012) provide an image of trans-membrane voltage changes that can be used to measure activation, action potential duration (and, to some extent, shape), repolarization timing, and conduction velocity. Other fluorescent molecules can be used to measure ion concentrations and dynamics, such as for calcium (Kao et al., 2010). For a review of the state of the art in optical mapping, the reader is referred to (Herron et al., 2012).

Optical mapping has been used to study complex arrhythmias, including fibrillation. In combination with computer models, it has revealed mechanisms that accelerate or stabilize electrical disorders (Noujaim et al., 2007), helped to understand the effect of geometric factors on cardiac vulnerability to electric shocks (Rodríguez et al., 2005), and projected from optical mapping to surface ECG patterns in heart failure (Okada et al., 2011), to name but a few. Optical mapping is limited to acquisition of images that average voltages (or ionic concentrations) over a certain volume of sub-surface myocardium, and computational models have been critical for their characterization and interpretation (Bishop et al., 2006). There are dynamic differences between optically observed action potentials and the electrical activity in cells such as recorded with microelectrodes, with implications for the interpretation of optical recordings (Bishop et al., 2007). Both optical mapping and multi-electrode contact recordings provide unique data on the dynamics of electrical rotors and spiral waves, and contribute to further understanding of the mechanisms of normal and disturbed sino-atrial node pacemaking (Fedorov et al., 2010), atrio-ventricular conduction (Hucker et al., 2008), and of atrial and ventricular fibrillation (Vaquero et al., 2008) in human. From a model validation perspective, optical mapping has successfully predicted electrical activation waves on alternative pacing configurations (Relan et al., 2011). This has been used to compare cardiac EP models of variable complexities, leading to the proposal to coordinate model parameterization strategies to increase their predictive power (Camara et al., 2011).

In summary, with EP being one of the main targets of cardiac computational methods, the advent of techniques allowing the mapping of electrical activity beyond the standard ECG has been a game-changer in the field. A drawback is that available methods are either limited in spatio-temporal resolution, require invasive procedures, or are applicable to experimental settings only.

4.2. Contraction and relaxation

The concerted interplay of active ejection (systole) and passive relaxation/filling (diastole) of the ventricular chambers is fundamental for effective and efficient pump action of the heart. Management of diseases like heart failure requires accurate methods to characterise myocardial mechanics. Widely available clinical imaging modalities like MRI and ultrasound are used to observe cardiac contraction and relaxation (Ledesma-Carbayo et al., 2005, Brown et al., 2009, Geyer et al., 2010). Image segmentation provides metrics, such as ejection fraction, that can be compared to the clinical setting. Local measurements of strain have the potential to improve patient assessment beyond established global metrics, and they are particularly useful for validating mechanical models.

Considerable efforts have been dedicated to estimating motion from conventional imaging studies like cine MRI, using image registration between frames (see Fig. 4 a–c). Nevertheless, and despite considerable research efforts, image registration algorithms are limited by their assumptions (like the incompressibility of the myocardial walls, which is difficult to ascertain and – in the presence of intra-vascular fluid redistribution - may only be an approximation (Cheng et al., 2005)), the aperture problem (there are several solutions that fulfil the similarity criterion between images), and the possibility of convergence to non-optimal solutions. Cardiac mechanical models have been used to formulate and regularise the problem of image registration, and have thus helped in improving the accuracy and plausibility of the analysis of strain and deformation patterns (Sermesant et al., 2006a). A more accurate alternative is given by the use of motion sensitive MRI scans. Tagged MRI works by superimposing a grid pattern on cardiac MRI intensity; the grid points can then be followed through subsequent time points in the cardiac cycle. This technique has been used for generation and validation of computational models (Bovendeerd et al., 2009, Wang et al., 2009). More recent MRI acquisition protocols (like Diffusion Encoded with Stimulated Echoes [DENSE] or Strain Encoding [SENC] MRI) directly reveal displacement and strain, and reach higher resolution than tagged MRI (Wang and Amini, 2012, Simpson et al., 2013).

Fig. 4.

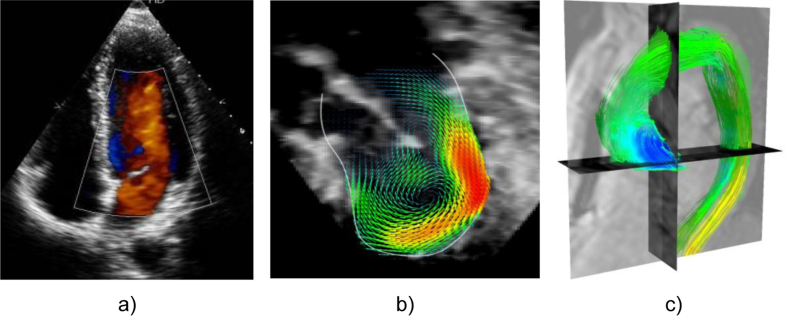
Illustration of techniques used to capture the mechanical information available in images. (a) Computational mesh of the left ventricle fitted to the domain of the myocardium from the end-diastolic frame of a MRI dynamic short axis stack (Lamata et al., 2011). (b) Tagged MRI frame of a short axis view of the left ventricle with an overlay of a colour encoded deformation field estimated from it by image registration (Chandrashekara et al., 2004). (c) Computational mesh fitted to in vivo DT-MRI data (Toussaint et al., 2013) at two instants of the cardiac cycle, systole (left) and diastole (right), with vectors pointing in the direction of the first eigenvector (fibre), colour encoded with respect to the elevation angle (red to blue, +45 to −45). (d) Echocardiographic speckle tracking (Ledesma-Carbayo et al., 2005). (e) Echocardiography-based electromechanical wave imaging (EWI), illustrating the motion maps (left) and the EWI isochrones (right; both colour coded from 0 ms, red, to 300 ms, blue; Provost et al., 2011b). (f) Elastography by the methods described in (Robert et al., 2009): the panel illustrates the shear modulus in a healthy volunteer at two time points of the cardiac cycle (image courtesy of Dr. R. Sinkus, KCL).

Motion measurements can be used for validation in cardiac electromechanical modelling by comparing predicted and observed deformation (Bovendeerd et al., 2009, Wang et al., 2009), or to estimate mechanical material properties of cardiac tissue (Wang et al., 2009, Xi et al., 2011, Xi et al., 2013). These constitutive properties are direct diagnostic biomarkers, and can also be used to personalise computational models for further analysis. However, the estimation of constitutive properties requires simultaneous knowledge of the amount of force (or pressure) that caused a deformation, and the deformation itself (Xi et al., 2014). A further challenge arises from the fact that that many cardiac tissue components display visco-elastic behaviour, so that steady state stress-strain relations only provide a partial picture. In turn, non-invasive estimation of central blood pressure, without the need of a catheter, is becoming feasible through recent advances in imaging and modelling. As the acoustic properties of microbubbles change with pressure, this can be captured by echocardiography techniques (Dave et al., 2012). On the other hand, maps of relative pressure can be estimated in theoretical models from flow data (Krittian et al., 2012).

From a modelling perspective, ventricular diastolic behaviour is simpler than systolic, as it is assumed to be dissociated from electrical activity. Contraction, in contrast, strongly depends on the timing of electrical activation. There are two main ventricular factors that influence diastolic ventricular filling, the ability of myocytes to relax after contraction, and the passive compliance (stiffness) of the ventricular wall. Separation of the relative contribution of these two processes has been aided by recent model analysis of MRI sequences (Xi et al., 2013). Extending these methods to the study of contraction will require simultaneous analysis of electrical and mechanical activities, which remains challenging for both imaging and modelling methods.

Among the more recent imaging techniques with interesting potential for computational model development, elastography has been developed to characterise tissue properties in vivo. The core concept of this technique is to image deformation, either with MRI (Elgeti and Sack, 2014), see Fig. 4f, or ultrasound (Hollender et al., 2012), in response to a known mechanical stimulus, and to determine the stiffness of the material. The challenge here is the control of the mechanical stimulus (usually a mechanical wave) across the beating and deforming wall of the heart, and the presence of tissue mechanical inhomogeneities at spatial scales that may not be captured by the imaging techniques.

Echocardiographic speckle tracking also captures deformation (see Fig. 4d), but the more commonly used 2D echo images do not lend themselves to mapping 3D mechanics. Nevertheless, speckle tracking can be combined with simplified 2D mechanical models, and this approach has been used to explain different patterns of circumferential strain in heart failure patients requiring CRT (Leenders et al., 2012). Analysis of left ventricular regional wall motion during stress echocardiography has proved to be a useful predictor of coronary artery disease and clinical prognosis, and has in turn been improved by computational models (Herz et al., 2010). Echocardiographic speckle tracking has also been used for validation of predicted deformation patterns for the study of left ventricular torsion (Evangelista et al., 2011).

Another echo-based technique is electromechanical wave imaging (EWI). EWI uses ultrafast echo sequences to capture transient strains in response to electrical activation at high temporal and spatial resolutions, to estimate cardiac activation sequences (Provost et al., 2011b, Provost et al., 2013), see Fig. 4e. The potential utility of EWI in the clinical setting is significant, especially in the context of arrhythmias, including fibrillation, that are associated with extremely fast and potentially lethal changes in cardiac electrical activation and regional motion. The additional ability to locate earliest pacing sites and ischemic regions makes EWI an interesting alternative to ECG mapping, at least for spatial characterisation of electrical activation patterns (Konofagou and Provost, 2012), as electrical and mechanical activation patterns often correlate to an extent that allows deformation-based diagnosis of diseases (Odening et al., 2013). The potential of EWI has only begun to be explored in computational modelling work. EWI patterns have been used to validate a biventricular electromechanical model, reporting good agreement between predicted and measured deformation (Provost et al., 2011a). Given its non-invasive nature and low costs, EWI may be promising for patient-specific modelling that aims to predict the effect of pathologies and/or pharmacological interventions on local electrical and mechanical activation patterns.

An aspect of cardiac mechanics that makes its study particularly suitable for a combined imaging and modelling approach is that fundamental biophysical parameters such as regional stress-strain characteristics are not open to direct experimental exploration, but can be derived from measurement through the use of computational models (Nash and Hunter, 2000). Results obtained in this way can then be fed back to experimental research on isolated cells (Iribe et al., 2007), and also used to investigate the behaviour of cardiomyocytes as mechano-sensors as well as activators (Cooper et al., 2000). This provides an excellent example of an aspect in which imaging and modelling need to work in combination, driving each other's progress.

In summary, in contrast to the limitations in imaging of electrical activity, methods to non-invasively visualize strain with reasonable resolution and accuracy are widely available. However, strain is only part of the picture: mechanical constitutive parameters and stresses (forces, pressure) play fundamental roles in the assessment of cardiac function in health and disease. Computational models have proved useful for this purpose, and their use is likely to play a prominent role in the advance of mechanical characterization methods.

4.3. Ventricular ejection and filling

Characterization of abnormal blood flow patterns and associated key physical parameters, like shear stress, pressure gradients or kinetic energy, are increasingly being adopted for clinical management of diseases like aortic coarctation or valve stenosis (Pedrizzetti et al., 2014).

Doppler ultrasound (see Fig. 5a) captures the blood velocity component parallel to the echo beam, and it is clinically used to assess the severity of obstructions in vessels or the left ventricular outflow track. The pressure gradient is the quantitative metric to characterise obstruction, and its computation typically only requires the peak velocity based on simplistic assumptions (the Bernoulli principle; Gersh et al., 2011). In contrast, computational fluid–solid interaction models can account for the complete mechanics of blood flow, formulated in the Navier–Stokes equations, and be developed from personalised geometries and suitable boundary conditions. These approaches have experienced remarkable progress during the past few years (Taylor and Figueroa, 2009). Prediction of the fractional flow reserve in the coronaries, for example, using geometrical information alone, is a remarkable success in this field (Taylor et al., 2013). The combination of Doppler US with an anatomical modality, MRI, has also enabled the personalization of models to paediatric patients, and the proposal of a metric based on kinetic energy for the assessment of the diastolic function in congenital diseases (de Vecchi et al., 2012).

Fig. 5.

Illustration of three main imaging technologies used to capture information on blood flow. (a) 2D Doppler echocardiography is widely used in the clinic; (b) 3D flow reconstructed in an infant with mitral stenosis using registration of multiple 3D Doppler acquisitions (Gómez et al., 2013) (c) Phase-contrast MRI, also known as 4D flow data, colour coded by the pressure maps computed from blood flow velocity data (Krittian et al., 2012) in a chronic dissection case.

3D Flow reconstruction is among the more recent imaging-related developments. The reconstruction of dense 3D velocity fields from multiple 3D ultrasound maps is feasible (Gomez et al., 2013), see Fig. 5b. This has the potential of becoming a key tool in computer modelling, providing boundary conditions (i.e. values that can be imposed so the model achieves a realistic prediction) and validating model results. Images of the deformation of the aorta are also commonly available, and it has been demonstrated recently that variations in distensibility along the aorta, and values of pulse wave velocity along the vessel, can be obtained from dynamic sequences of 3D ultrasound maps using image registration regularised by a one-dimensional wave equation (Barber et al., 2014).

Phase-Contrast MRI (PC-MRI, see Fig. 5c) provides a spatio-temporal description of blood velocity fields in a 3D domain (Markl et al., 2011). This can be used for the definition of boundary conditions, and for the validation of fluid-solid-interaction models. In a more data-driven approach, PC-MRI has also been used to estimate pressure fields (Krittian et al., 2012) and reveal characteristic patterns that differentiate healthy and diseased subjects (Lamata et al., 2013b), for example using wall shear stress signatures that identify patients with bicuspid aortic valve (Bissell et al., 2013), turbulent (Dyverfeldt et al., 2008) or laminar (Barker et al., 2013) viscous energy loss, etc. Pressure gradients estimated from PC-MRI have also been found to be a suitable surrogate readout (biomarker) to characterise the heart's ability to relax (Yotti et al., 2011).

4.4. Comprehensive integration of clinical data

Computational models support integration of different sources of clinical data and images. These can be used to build detailed in silico representations of cardiac physiology of individual subjects. Ultimately, this is the basis of personalised medicine, aiming to aid clinical activities from diagnostics to therapy planning. The vision here is that computational models may be used to explore various treatment options, and to tailor interventions to minimize procedure risk while maximizing patient benefit. Availability of patient-specific datasets is becoming a reality in the clinical domain, based on the combination of several imaging modalities, clinical information, and other relevant data (increasingly including genomic data).

An example is the combination of catheter-based electro-anatomical maps and MRI dynamic studies to assess anatomy, tissue deformation and scar location. Personalization of models using this clinical data can aid the management of heart failure patients, specifically the selection for CRT. In this way, the acute response to CRT has been predicted in two patients at different pacing configurations (Sermesant et al., 2012). Models, personalised on the basis of imaging data, have also helped to reveal the role that auto-regulatory mechanisms have in electro-mechanical coupling, and how they affect cardiac responses to CRT (Niederer et al., 2011). These personalised models have contributed to understanding how regional work redistributes in the ventricle after pacing (Niederer et al., 2012a), to identifying that efficient preloading is responsible for a significant stroke work improvement (Hu et al., 2013), and to evaluating the effects of novel pacing leads (Niederer et al., 2012b). Computational models have further been used to analyse abnormal contraction patterns in asynchronous hearts of animal models, and explained these patterns based on well-established electrical and mechanical properties of the myocardium (Kerckhoffs et al., 2008). Models have also recently been used to illustrate how pacing locations can be chosen to optimise both stroke work and ATP consumption (Hu et al., 2014).

5. Discussion: Challenges and opportunities

Recent advances in cardiac structure and function modelling have benefitted from novel imaging modalities and improvements in already established techniques. Enhanced spatio-temporal resolution, an increasing range of functional parameters that can be imaged, and growing signal-to-noise ratios complement anatomical descriptions and increase model utility. The ability to record multiple parameters simultaneously, and to combine different imaging modalities, enriches the information that can be included in conceptual models and quantitative simulations. All this has given rise to substantial developments in the cardiac modelling field.

Mechanisms fundamental to healthy cardiac function cover all scales from the sub-cellular level to the whole organ, and thus computational modelling needs to be multi-scale. In addition to the examples of ‘success stories’ mentioned so far, computational models can help to optimise the placement of implantable cardioverter-defibrillators wires (Rantner et al., 2013b; Rantner et al., 2013b), covering multiple scales from the integration of the full torso, reconstructed from either CT (Jolley et al., 2008) or MRI (Rantner et al., 2013b), to the detailed inclusion of sub-cellular EP mechanisms. An exciting area of development is the prediction at the organ scale of the effects at the level of drug–channel interactions (Moreno et al., 2011), with applications to improving the processes of drug screening (Clancy et al., 2007, Rodriguez et al., 2010, Zemzemi et al., 2013),including inter-species comparisons (O’Hara and Rudy, 2012). Models built from images enable the study of novel concepts, such as the impact of the bioelectric responses to illumination as a potential future mechanism to delivering safe and effective therapy (Boyle et al., 2013).

As models gradually include multi-physics descriptions of the different solid and fluid tissues involved in circulation, we can begin to make use of a broader range of imaging techniques that measure relevant aspects of cardiac physiology. An interesting, yet underutilized in the cardiac field, alternative is based on imaging not the electrical, but the magnetic field generated by the coordinated electrical activation cycle. This technology is used with great success in neurophysiological imaging (magnetoencephalography), and offers excellent temporal resolution and 3D localisation. This can be used to diagnose cardiac rhythm disturbances in particularly delicate settings, such as before birth in utero (Cuneo et al., 2008, Cuneo et al., 2013).

Despite notable progress towards personalization of models, based on comprehensive sets of available data (Taylor and Figueroa, 2009, Aguado-Sierra et al., 2011, Relan et al., 2011, McDowell et al., 2012, Sermesant et al., 2012, Krishnamurthy et al., 2013, Xi et al., 2013, Lamata et al., 2014), there is a need to improve automation and robustness of underlying processes (Aguado-Sierra et al., 2011), and to find the best compromise between the level of anatomical detail included and the stability of computational meshes and solutions (Lamata et al., 2013c). Research is driven by specific problems, and every study will need to assess the need of model personalization accordingly to the clinical or physiological hypothesis that is to be tested. Subsequently, the need for personalization and the restrictions of each imaging modality will need to be reconciled to determine the optimal imaging protocols (MacLeod et al., 2009).

Improvements in image acquisition techniques must be accompanied by corresponding advances in image analysis. Multi-scale, multi-physics and multi-modal image acquisition calls for novel methods to extract information from large datasets, across different resolutions, and to reliably integrate information from different scans. Fusion of information requires correct spatial and temporal alignment between image data, and careful interrelation with other clinical measurements, such as the ECG or blood pressure measurements, is needed. The integration of image data from different modalities raises the issue of modality robustness and repeatability, particularly in the case of clinical data. The need to balance the use of robust and trusted imaging methods that are ‘good enough’ to guide current clinical decision making with state-of-the-art ones that may be more prone to application and/or interpretation error needs to be carefully balanced.

Cardiac models are moving from deterministic to stochastic and/or population studies, recognising the importance of natural and pathological variability, from behaviour of individual cells to inter-subject and inter-species variations. Descriptions of standard anatomy and function, as well as their normal and pathological variability, can be condensed in the shape of atlases. These are expected to play an important role in complementing subject-specific data, which are necessarily limited in their resolution and information content. The creation of major repositories of cardiac imaging data (Petersen et al., 2013) could bring substantial rewards in this context. It is fundamental that data as well as methods are shared between groups in public databases. Initial efforts, from The Cardiac Atlas Project (Fonseca et al., 2011) to identification of reporting standards, e.g. MICEE (Quinn et al., 2011), are steps in the right direction, and it will be interesting to see whether they become standard practice in spite of the initial ‘extra effort’ involved in depositing relevant information.

While perhaps less apparent than the effects that improved imaging methods have had on models, there are also instances in which models have been significant drivers of progress in image acquisition and analysis. Examples include the improved understanding of scattering in optical mapping (Bishop et al., 2007), and the introduction of models in motion estimation techniques to assure that identified motion fields are physiologically feasible (Sermesant et al., 2006a). Synergies and complementarities between imaging and modelling will continue to develop, in particular where a close interaction between the two research fields is achieved. In fact, the majority of commercial imaging systems for clinical use already contains significant image analysis and (albeit somewhat rudimentary) modelling capabilities, that are bound to improve as part of technological progress.

The application of multiple imaging techniques to the same subject can be restricted by time and financial cost, as well as by invasiveness and real or perceived presence of harmful effects associated with individual techniques. In terms of technology development, the challenge ahead is to find optimal combinations of imaging and modelling, suitable to address specific questions in basic and applied research, as well as in the clinic. This will require a mind-set in which the standard sequence of ‘modelling follows imaging’ is substituted by a combined and interactive development of both, simultaneously.

Editors’ note

Please see also related communications in this issue by Prakosa et al. (2014) and Lohezic et al. (2014).