Temperature Dependence and Energetics of Single Ions at the Aqueous Liquid-Vapor Interface

Abstract

We investigate temperature-dependence of free energetics with two single halide anions, I⁻ and Cl⁻, crossing the aqueous liquid-vapor interface through molecular dynamics simulations. The result shows that I⁻ has a modest surface stability of 0.5 kcal/mol at 300 K and the stability decreases as the temperature increases, indicating the surface adsorption process for the anion is entropically disfavored. In contrast, Cl⁻ shows no such surface state at all temperatures. Decomposition of free energetics reveals that water-water interactions provide a favorable enthalpic contribution, while the desolvation of ion induces an increase in free energy. Calculations of surface fluctuations demonstrate that I⁻ generates significantly greater interfacial fluctuations compared to Cl⁻. The fluctuation is attributed to the malleability of the solvation shells, which allows for more long-ranged perturbations and solvent density redistribution induced by I⁻ as the anion approaches the liquid-vapor interface. The increase in temperature of the solvent enhances the inherent thermally-excited fluctuations and consequently reduces the relative contribution from anion to surface fluctuations, which is consistent with the decrease in surface-stability of I⁻. Our results indicate a strong correlation with induced interfacial fluctuations and anion surface stability; moreover, resulting temperature dependent behavior of induced fluctuations suggests the possibility of a critical level of induced fluctuations associated with surface stability.

I. INTRODUCTION

Beginning with the theoretical/computational view of the stability of specific ions at aqueous liquid-vapor interfaces put forth in the work of Berkowitz et al^1,2, Tobias and Jungwirth^3-15, Dang and coworkers^16-22, and recently more coarse-grained theories based on dielectric continuum^23-25, the discussion of specific-ion effects^16,17,19, particularly differential stabilities of halides at aqueous liquid-vapor interfaces and generally at hydrophobic interfaces, continues. The understanding of physical origins of differential stabilities of anions is of broad interest as specific-ion effects are implicated in processes ranging from protein denaturation, surface tension modulation, carbon nanomaterial self-association, and ion association with lipid bilayers and membranes²⁶. Efforts to present unifying explanations of the molecular, thermodynamic, and structural underpinnings of these effects has garnered significant attention from theory and experiment, and continues to do so. We refer to a sampling of the vast literature^{13,15,24,26-40}. In the context of differential stabilities of ions at the aqueous liquid-vapor interface, it is widely accepted that several factors conspire to give rise to interfacial stability in the case of the larger halides such as I⁻ and Br⁻, and lack thereof in the case of smaller halides such as F⁻ and Cl⁻ (reflecting the reverse canonical Hofmeister series). Major molecular/atomic properties implicated are ion size, ion polarizability, ion hydration properties (free energy and entropy), ion charge density, and solvent polarizability and dipole moment⁴¹. Recently, the surface potential of the liquid vapor interface originating from classical point charge descriptions of molecular electrostatic distributions has been implicated as a major factor in interfacial ion partitioning^42-47.

Affnity of ions to hydrophobic interfaces in a chemically-specific manner has been documented experimentally as well. Rankin et al, addressed differences in interactions between halide anions F⁻ and I⁻ and t-butyl alcohol (TBA) in aqueous solution using Raman spectroscopy with multivariate curve resolution (Raman-MCR)⁴⁸. The authors demonstrated that for 3M NaI solutions, roughly 64 percent of t-butyl alcohol molecules are affected by I⁻ based on a red-shift of the CH stretch Raman frequency of about 5 cm⁻¹ relative to t-butyl alcohol in pure water. Furthermore, computational modeling using EFP/MD and quantum mechanical QM/EFP1 methods showed that the alcohol interacts with I⁻ in the region of the alcohol headgroup (OH⁻) and near the aliphatic CH₃ groups. Interestingly, the authors observed no experimental indication of Na⁺ or F⁻ perturbations to the alcohol’s vibrational modes. Recently, Otten et al⁴⁹ used second harmonic generation (SHG) to probe surface adsorption thermodynamics for NaSCN (sodium thiocyanate) solutions, considering SCN⁻ as a prototypical chaotropic ion with unambiguous stability at the aqueous liquid-vapor interface. The authors demonstrated by fitting their SHG data to a Langmuir adsorption isotherm model, that the inherent enthalpy and entropy of adsorption for SCN⁻ are negative, in keeping with earlier simulations⁵⁰ and experiment. The negative adsorption enthalpy was considered to challenge currently held theoretical views of the thermodynamic underpinnings of these ion behaviors. Zhang et al. examined the influence of 11 sodium salts on the stability of poly(N-isopropylacrylamide).^51,52 Kosmotropic anions were shown to polarize the water molecules hydrating the macromolecule, whereas the chaotropic anions directly interact with the macromolecule. The former of these mechanisms resulted in salting-out of the macromolecule, whereas the latter influenced salting-in.^51,52 Similar results were observed from molecular dynamics simulations of model systems. Heyda et al¹² showed using extensive molecular dynamics simulations of N-methylacetamide (NMA) in the presence of monovalent cations and anions in water that the cations exhibit strong association with the carbonyl moiety of the peptide bond, while the anions do not interact with the amide group. Moreover, the larger anions, bromide and iodide, demonstrated preferential spatial correlation with the hydrophobic methyl group. This interaction was more evident in the simulations with polarizable force fields.

Finally, recent studies have illuminated the contributions of effects characteristic of hydrophobic hydration to halide interface propensity^25,42,53; moreover, fluctuations of water-hydrophobe interfaces have been linked to differential interfacial stabilities. With the recent connection of surface stability of select inorganic anions (iodide, and partially charge iodide, for instance) to interfacial fluctuations and spatial correlations thereof^49,54, there appears an intriguing mechanistic theme for ion-specific effects revolving around interfacial fluctuations induced by individual ions quite distant from the interface. This has broad implications in the context of discussing specific ion effects in a variety of circumstances. Thus, we also ask what differential influences single ions may have at distant interfaces.

Computational experiments measuring the reversible work (potential of mean force, PMF) for transferring single ions from bulk aqueous environment to the aqueous liquid-vapor interface have enjoyed a long history as a means to explore the origins of surface stability^16,18,21. As mentioned above, to date, only one temperature dependence study on monovalent halides has been presented in the literature⁵³. As mentioned in that work, the idea of negative adsorption entropy is independent of force field used to model the molecular components. This has also been demonstrated experimentally for NaSCN (as mentioned above). Thus, in this contribution, we first consider the temperature dependence of the potentials of mean force for single iodide and chloride anions in TIP4P-FQ water using classical umbrella sampling molecular dynamics simulations coupled with the Weighted Histogram Analysis Method (WHAM)⁵⁵. We then analyze local self- and cross-interaction (i.e., water-water and water-ion) energies underlying the observed potentials of mean force and temperature dependencies. Few studies in the literature have addressed the temperature dependence of single ion free energetics at the liquid-vapor interface, and we hope to compare and contrast the properties we observe with those discussed in earlier studies. We further consider solvent properties in the hydration shells of the two anions with the aim of comparing and contrasting radially dependent solvent properties such as water molecular dipole moment, water tetrahedrality, water-water interaction, and water-ion interaction energies; we hope to gain further insight into energetic and molecular structural origins of the differences in the surface stabilities of these two anions representing the neutral and chaotropic positions on the canonical Hofmeister series. These analyses will tie into recent work connecting local hydration properties and energetics of halide anions to surface propensity. Finally, we address aspects of the influence of the two anions on interface fluctuations in the spirit of Otten et al⁴⁹.

This study is organized as follows. In Section II we outline the methods, force fields, and related issues. We next present our results in Section III, including the potential of mean force along with its decomposition (Section III A) and L-V surface height fluctuations with the presence of single anion (Section III B). We conclude in Section IV.

II. METHODS

Molecular dynamics simulations were performed using the CHARMM package.⁵⁶ Simulations of liquid-vapor interfaces were performed in the NVT ensemble. Temperature was maintained at T = 280, 300, 320, 340, 360 K using Nosé-Hoover thermostat.⁵⁷ The simulation cell was rectangular with dimensions 24 Å × 24 Å × 100 Å, in which z is the direction normal to the liquid-vapor interface. A bulk slab consisting of 988 water molecules (represented by the polarizable TIP4P-FQ model⁵⁸) and a single ion (Cl⁻, I⁻) was positioned in the center of the simulation cell, resulting in two liquid-vapor interfaces. A rigid water geometry is enforced using SHAKE⁵⁹ constraints. We employ polarizable TIP4P-FQ⁵⁸ water model and non-polarizable anions treated as charged Lennard-Jones spheres. Polarization of water is treated with a charge equilibration Hamiltonian^60-63:

$$E_{\mathrm{elec}}=\sum _{i=1}^N\left({\chi }_i\right)q_i+\frac{1}{2}\sum _{i=1}^N\eta q_i^2+\frac{1}{2}\sum _{i\ne j}^N{J}_{ij}{q}_i{q}_j$$ (1)

where χ_i and η_i may be associated with atomic electronegativities and hardnesses, respectively; the J_ij terms represent a parameterized molecular Coulomb integral between pairs of atoms. Components of the molecular polarizability tensor are related to the inverse of the hardness matrix (constructed from the values of η_iand J_ijabove) as α_βγ=R_βJ⁻¹R_γwhere R_βrepresents the β Cartesian components of the atomic position vector⁶⁴.

The polarizable TIP4P-FQ water model employs a rigid geometry having an O-H bond distance of 0.9572 Å, an H-O-H bond angle of 104.52° and a massless, off-atom M site located 0.15 Å along the H-O-H bisector which carries the oxygen partial charge. Repulsion and dispersion interactions are modeled using a single Lennard-Jones (LJ) site located on the oxygen center having parameters R_min,O = 3.5459 Å and ε_O = 0.2862 kcal mol⁻¹.

Ions were treated as non-polarizable particles with interaction parameters based on those by Lamoureux and Roux⁶⁵ and validated for use with TIP4P-FQ^66-70. We acknowledge that the use of a mixed polarizable water model with non-polarizable anion representation may appear unorthodox, but we consider that the combination of this empirical model is well-validated and reproduces many of the currently-accepted experimental observables upon which the quality of such force fields are based. Furthermore, the use of an alternative force field model allows us to speak to the universality (or at least the broad commonality) of molecular and atomic features underlying observed behaviors such as surface stability and negative surface adsorption entropy. We summarize the parameters used in Table I. The non-bond interactions were treated via the standard Lennard-Jones “12-6” potential

$$E_{LJ}=\sum _{ij}{\epsilon }_{ij}\left(\frac{R_{\min ,ij}^{12}}{r_{ij}^{12}}-2\frac{R_{\min ,ij}^6}{r_{ij}^6}\right)$$ (2)

Lennard-Jones interactions were gradually switched off at interparticle distance of 11 Å, with a gradual switching between 10 Å and 11 Å using the switching function:

$$S\left(r_{ij}\right)=\{\begin{array}{cc}1\hfill & r_{ij}\le r_{\text{on}}\hfill \\ \frac{{(r_{\text{off}}^2-r_{ij}^2)}^2(r_{\text{off}}^2+2r_{ij}^2-3r_{\text{on}}^2)}{{(r_{\text{off}}^2-r_{\text{on}}^2)}^3}\hfill & r_{\text{on}}<r_{ij}\le r_{\text{off}}\hfill \\ 0\hfill & r_{ij}>r_{\text{off}}\hfill \end{array}\phantom{\}}$$ (3)

Charge degrees of freedom for the TIP4P-FQ water molecules were coupled to a thermostat at 1K with mass 0.000069 kcal mol⁻¹ ps² e⁻² using the Nosé-Hoover method and the charge degrees of freedom were propagated in an extended Lagrangian formalism; each water molecule was taken as a charge normalization unit (charge conserved with this unit), thus preventing any charge transfer between water molecules or between water and ion. We acknowledge recent developments of charge transfer models of water^71,72, and anticipate that application of charge transfer models to the study of specific-ion effects will soon be realized and further elucidate underlying mechanisms and physics. Conditionally convergent long-range electrostatic interactions were treated using Particle Mesh Ewald (PME)⁷³ approach with a 30 × 30 × 128 point grid, 6th order interpolation, and κ = 0.33. Dynamics were propagated using a Verlet leap-frog integrator with a 0.5 fs timestep. Total sampling time for each window was 15-20 ns; properties were calculated from all but the initial 0.5 nanosecond, which was treated as equilibration.

TABLE I.

Parameters used in this study.

	Rmin (Å)	ε (kcal/mol)	q (e)
Oa	3.5458	0.2862	−0.888
Cl−	4.9198	0.07658	−1
I−	5.5198	0.15910	−1

^aCharge presented here was on the M-site of TIP4P-FQ water molecule in the gas phase.

For potential of mean force calculations, our reaction coordinate, ξ₀, is the Cartesian z-component of the separation between the water slab center of mass and ion center of mass. In all simulations used for computing potentials of mean force, ions were restrained to z-positions from 10 Å to 35 Å relative to the water slab center of mass using a harmonic potential $U_{restraint}(z;z_{relative,ref})=\frac{1}{2}{k}_{restraint}{(z-z_{relative,ref})}^2$ with the force constant of 4 (kcal/mol)/Ų; this encompasses a range approximately 15 Å below the Gibbs Dividing Surface (GDS) to approximately 10 Å above it at 300 K; though one could probe separations further into the bulk (towards the center of the system) this distance is sufficient to probe the differences of interest in this study, and also in keeping with previous studies to which we compare our results. In the case of 360 K, the highest temperature in this study, GDS increases by 2 Å. The actual position of GDS at corresponding temperature, which is determined by half of bulk water oxygen density, is plotted in Figure 1 (to be discussed in Results Section). We note the recent connection of the potential of mean force to thermodynamic free energies⁷⁴:

$$\frac{dG\left({\xi }_0\right)}{d{\xi }_0}={\langle {\left(\frac{\partial U_{interaction}\left({\mathrm{r}}^N\right)}{\partial q_{\xi }}\right)}_{{\{q_m\ne \xi \}}^{N-1}}\rangle }_{{\xi }_0}-{\langle \frac{1}{\beta }{\left(\frac{\partial \ln \mid J\mid }{\partial \xi }\right)}_{{\{q_m\ne \xi \}}^{N-1}}\rangle }_{{\xi }_0}-\frac{1}{\beta }{\langle \sum _{m\ne \xi }^{N-1}\left[\delta (q_m-l_{U_m})\frac{d{l}_{U_m}\left(q_m\right)}{d{q}_{\xi }}\delta (q_m-l_{L_m})\frac{d{l}_{L_m}\left(q_m\right)}{d{q}_{\xi }}\right]\rangle }_{{\xi }_0}$$ (4)

where the interaction potential is taken to be a function of some set, of the size of the number of system degrees of freedom, of generalized coordinates, q_ξ. The reaction coordinate of interest in this case corresponds to q_ξ = ξ₀. The first term is the negative of the mean force whose integral over the domain of the reaction coordinate yields the potential of mean force. The second term arises from the volume scaling upon transforming from Cartesian to some generalized curvilinear space (represented in general by the set of generalized coordinates). The last term arises from interchange of the order of the differential and integral operators according to Leibniz rule. In the present study, as we retain the Cartesian z-component of the separation between centers of mass (the force is projected along this reaction coordinate), and the domain of the reaction coordinate is decoupled from those of the remaining coordinates (the derivatives in the Leibniz term are zero), the Jacobian and Leibniz terms vanish. Thus we discuss the PMF in terms of the free energy or reversible work for the remainder of the paper.

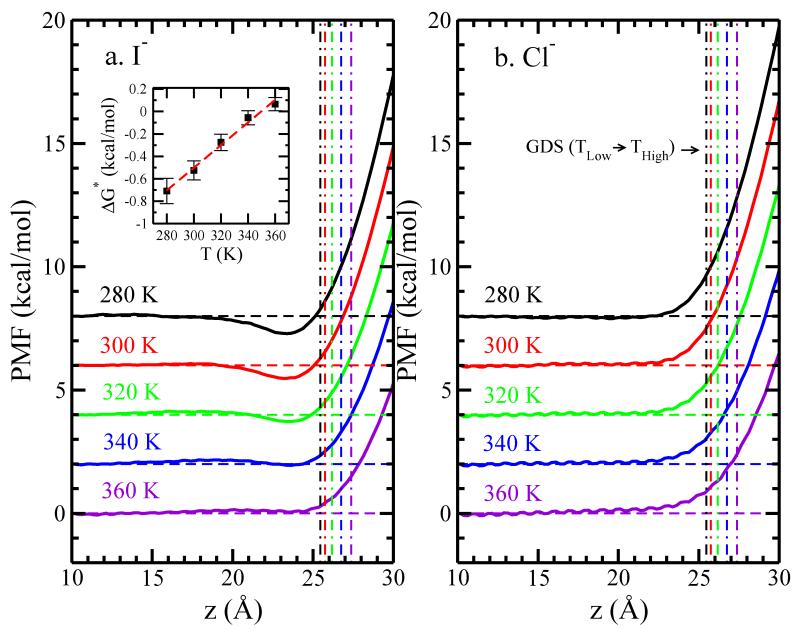
FIG. 1.

Potential of mean force for single (a) iodide and (b) chloride ions across the TIP4P-FQ LV-interface, relative to the value at z = 10.0 Å, which we consider sufficiently far away from the interface so as to represent bulk-like water region. Solid lines represent ions in TIP4P-FQ, a vertical offset of 2 kcal/mol is used to distinguish different temperature, each with a dashed horizontal line denoting zero. The inset shows the PMF minimum as the function of temperature for I⁻. The dashed line indicates the linear fitting result, with slope = 0.01 and intercept = −3.53.

III. RESULTS AND DISCUSSION

A. Potential of Mean Force and Solvation Structure

The potential of mean force (ΔG(z)) was calculated for each ion as a function of its z-position using WHAM⁵⁵ and is referenced to zero at z = 10Å; results of I⁻ and Cl⁻ at different temperatures are shown in Figure 1 a and b, respectively. For clarity, a vertical offset of 2 kcal/mol is added to distinguish the PMF at different temperatures. While Cl⁻ shows no pronounced minimum independent of temperature, I⁻ shows minima below the GDS at all temperatures except 360 K. We define ΔG* as the PMF at the minimum and plot it as a function of temperature, as shown in the inset of Figure 1a along with the uncertainty and the linear fitting result (ΔG* = ΔH* − TΔS*). We observe a positive slope for ΔG* versus T indicating ΔS* < 0. The uncertainties in potentials of mean force are determined using the approach of Zhu and Hummer⁷⁵:

$$\mathrm{var}\left[G\right({\xi }_{\mathrm{N}}\left)\right]\approx \sum _{i=1}^N\mathrm{var}\left[K\Delta \xi {\stackrel{‒}{z}}_i\right]$$ (5)

where ${\stackrel{‒}{z}}_i$ is the mean position of z in the i_th window, which can be obtained from block averages⁷⁶. The corresponding standard deviation σ[G(ξ_N)] is then the square root of var[G(ξ_N)]. In our case, G(z = 10 Å) = 0, therefore the window z = 35 Å is expected to have the largest uncertainty. The largest uncertainties for the systems are approximately 0.13 kcal/mol (shown in Supporting Information).

At 300 K, I⁻ shows a minimum of 0.5 kcal/mol, which is similar to the result for iodide at the L-V interface using non-polarizable ions in SPC/E water by Horinek et al^25,53. This also corresponds with the DFT-D value determined by Baer et al⁴³, though we do not discount that ours is a fortuitous result to some degree. In our simulation, we do not include explicitly the polarization of the I⁻, but we have taken care to faithfully capture the relative hydration free energetics of the individual ions to as great an extent as possible. Though not possible currently, it would be interesting to connect the hydration free energetics of ions using DFT-D methods in order to further assess and characterize such agreements between classical models and electron-density based models. Caleman et al⁵⁰ observed a significantly deeper free energy minimum (≈ 1.4 kcal/mol) for similar calculations but using water droplets and a polarizable force field based on classical Drude oscillators for water⁷⁷ and ions⁶⁵; the force fields used in that study were parameterized to optimally recapitulate experimental hydration free energies of ions in bulk water and ion-water binding energies and geometries of gas-phase water-ion dimer complexes⁶⁵. Later studies have concluded that the greater stability suggested by such classical models may arise from a representation of ion and water polarization response that is larger than the actual physical value. What appears in general, however, is that the location of the PMF minimum occurs prior to the GDS (defined in terms of the water density in most studies).

An intriguing property that seems to be universal amongst the single anion PMF’s estimated using various parametrized classical models (non-polarizable and polarizable, including the present study) is the emergence of a perceptible barrier before the surface-stable anions reach the Gibbs Dividing Surface^16,25,50,69; this barrier is even observed for polarizable ions at the water-CCl₄ interface¹⁸. Despite its prevalence, this feature has not been addressed to any significant extent. We conjecture at the present time that several factors (not necessarily confined to regions local to the ion and its vicinal hydration shell) give rise to a real physical barrier. The observation of this barrier even in the DFT-D study and the dielectric continuum theory-based predictions⁴³ provides further compelling motive to pursue this feature found in PMF’s based on numerous, widely differing interaction models. This is ongoing work and beyond the scope of the present study. Finally, unlike the study by Horinek^25,53, however, we do not observe a minimum as the I⁻ moves across the L-V interface at T = 360K. This suggests that underlying temperature-dependent properties of water-water and water-ion interactions are not equivalent; though not pursued presently, a comparison of the phase-equilibrium properties of the water-water interaction models used in the two studies would provide further insight as to the origins of this difference.

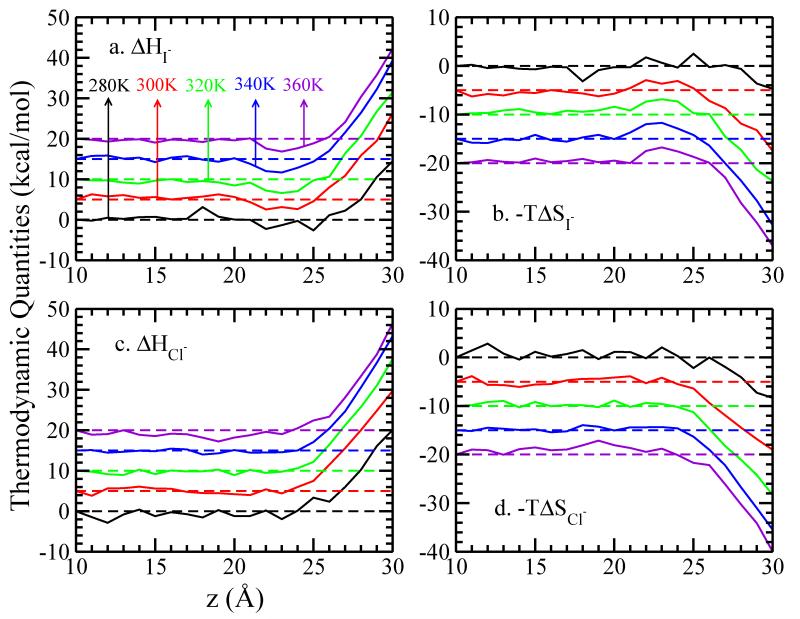
We next decompose our PMF into total enthalpic and total entropic components, acknowledging that this analysis is not a definitive exploration of the inherent driving forces for surface adsorption as observed via molecular simulations using classical force fields. It does allow some connection to previous studies using droplet based simulations⁵⁰ so as to allow one to draw conclusions about general behaviors and trends related to observed behaviors in anion surface propensities. In our system the pressure-volume work is negligible and so we will estimate enthalpic contributions with internal energy components. Furthermore, since we are interested in differences relative to specific positions in our simulation system, we will consider kinetic contributions to be equivalent at the endpoints, thus leaving us with interaction energy components as the determinants of the enthalpy changes. As in previous studies, we consider the enthalpy change ΔH(z) as the difference of average interaction potential energy^50,78,79 when the anion resides at position z and in bulk (z = 10 Å), ΔH(z) = ΔH(z_ion) − ΔH(z_bulk). The entropy change profile, ΔS(z), can therefore be estimated by subtracting enthalpy from free energy, −TΔS(z) = ΔG(z) − ΔH(z). Figure 2 shows the enthalpic component ΔH(z) and entropic component −TΔS(z) of the free energy for I⁻and Cl⁻. For clarity, we added 5 and −5 kcal/mol vertical offsets for ΔH(z) and −TΔS(z), respectively. At 300K, relative to when the ion is located in a bulk-like z-position, the total system enthalpy for states where I⁻ is surface-adsorbed is lower, while the enthalpy for Cl⁻ (not surface-enhanced in our study) effectively does not change at the GDS. Caleman et al⁵⁰ observe a similar, though slightly deeper, minimum for I⁻. Furthermore, the present relative enthalpies are not overly temperature sensitive. Entropy contributions are positive, suggesting inherent negative adsorption entropy as evidenced by the fitting slope of 0.01 kcal/mol/K obtained from a linear fit of the temperature versus PMF well-depth data. Negative surface adsorption entropy has been concluded from experiment⁴⁹ and from theory and simulations^25,49

FIG. 2.

Decomposition of (a)(c) enthalpic and (b)(d) entropic contributions to the potential of mean force of single iodide and chloride ion crossing the TIP4P-FQ LV-interface, relative to the value at z = 10.0 Å. A vertical offset of 5 kcal/mol is used in panel (a) and (c), while in panel (b) and (d) the vertical offset is −5 kcal/mol, for clarity.

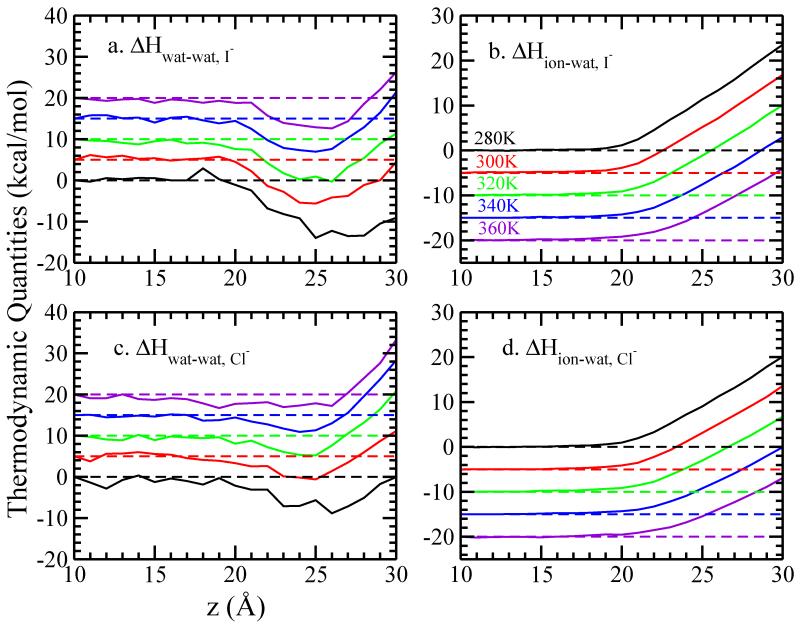
We further decompose ΔH(z) into water-water (w-w) and ion-water (i-w) contributions⁵⁰, which are represented by the averaged potential energy at each window. These potential energies are plotted relative to the window where the anion is restrained at z = 10 Å, such that

$$\Delta H\left(z\right)=\Delta H_{\mathrm{w}-\mathrm{w}}\left(z\right)+{\Delta }_{\mathrm{i}-\mathrm{w}}\left(z\right)$$ (6)

The results of ΔH_w-w(z) and ΔH_i-w(z) of I⁻ and Cl⁻ are shown in Figure 3. In the case of I⁻, ΔH_w-w(z) shows a significant minimum at z = 25 Å, which is closer to the GDS than the minimum of ΔG(z) and ΔH(z) at z = 23 Å; at this z-position, the ion-water interaction is positive, thus restricting the minimum of the total enthalpy to below the GDS. The combination of water-water and water-ion enthalpies (interaction energies) effectively cancel one another, leading to the flat profile of the Cl⁻total enthalpy, though Figure 3 indicates that the water-water interaction in the Cl⁻ case does reach a minimum at the GDS location. We define $\Delta H_{w-w}^{†}$ as the minimum of $\Delta H_{w-w},\Delta H_{i-w}^{†}=\Delta H_{i-w}\left(GDS\right)-\Delta H_{i-w}\left(10\mathrm{Å}\right)$ and $\Delta H_{i-w}^{‡}=\Delta H_{i-w}\left(35\mathrm{Å}\right)-\Delta H_{i-w}\left(10\mathrm{Å}\right)$ and list these values in Table II. Although no significant minimum for ΔG(z) and ΔH(z) has been found for Cl⁻, we still observe a minimum for ΔH_w-w(z). These minima, while shallower compared with those in the I⁻ system, show the same temperature dependence. For both anions, ΔH_i-w(z) terms monotonically increase as the ion approaches the vapor phase independent of temperature. We finally break down the total enthalpy into electrostatic and dispersion contributions. We can write Equation 6 as:

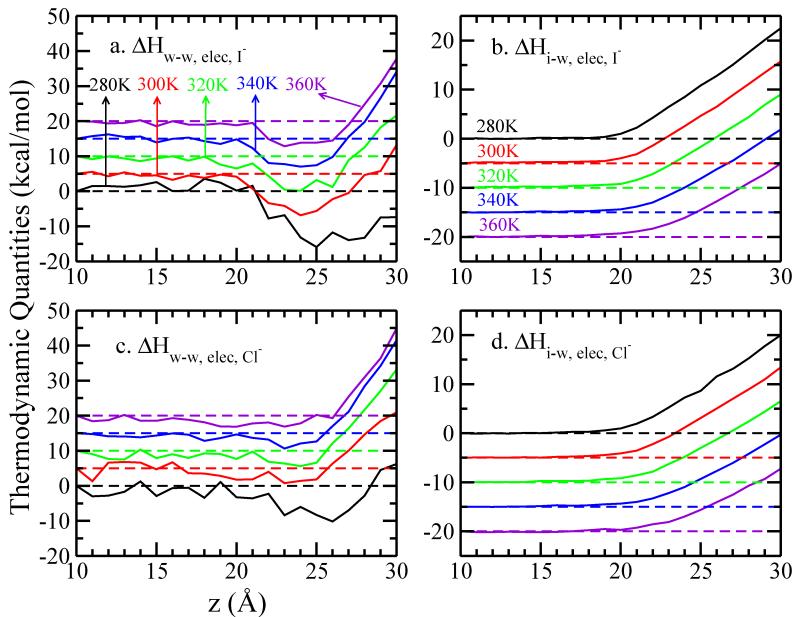
$$\Delta H\left(z\right)=\Delta H_{\mathrm{vdW}}\left(z\right)+\Delta H_{\mathrm{elec}}\left(z\right)=\Delta H_{\mathrm{vdW},w-w}\left(z\right)+\Delta H_{\mathrm{vdW},i-w}\left(z\right)+\Delta H_{\mathrm{elec},w-w}\left(z\right)+\Delta H_{\mathrm{elec},i-w}\left(z\right)$$ (7)

We plot the ΔH_elec,w-w(z) and ΔH_elec,i-w(z) terms in Figure 4. Again, we set z = 10 Å as the reference for both cases. Comparison of Figure 4 and Figure 3 shows that electrostatics dominate both water-water and ion-water interactions.

FIG. 3.

Decomposition of enthalpic contributions into (a)(c) water-water and (b)(d) ion-water interactions of single iodide and chloride ion crossing the TIP4P-FQ LV-interface, relative to the value at z = 10.0 Å. A vertical offset of 5 kcal/mol is used in panel (a) and (c), while in panel (b) and (d) the vertical offset is −5 kcal/mol, for clarity.

TABLE II.

Decomposition of ΔH(z) into water-water and ion-water components at some significant z-positions. Refer to text for the detail definition. The units are in kcal/mol.

System	$\Delta H_{w-w}^{†}$	$\Delta H_{i-w}^{†}$	$\Delta H_{w-w}^{‡}$
I−
280 K	−13.97	11.35	37.17
300 K	−10.62	10.18	34.90
320 K	−10.31	8.83	32.50
340 K	−8.04	7.42	29.58
360 K	−7.38	7.84	27.11
Cl−
280 K	−8.85	11.22	31.92
300 K	−5.61	8.11	30.02
320 K	−4.78	6.97	27.53
340 K	−4.08	4.10	25.38
360 K	−3.06	3.20	23.16

FIG. 4.

Decomposition of the electrostatic component of enthalpic contributions. Panel (a)(c) show the electrostatic contribution to the water-water interactions and (b)(d) refer to the ion-water interactions. Values are all relative to the value at z = 10.0 Å. A vertical offset of 5 kcal/mol is used in panel (a) and (c), while in panel (b) and (d) the vertical offset is −5 kcal/mol, for clarity.

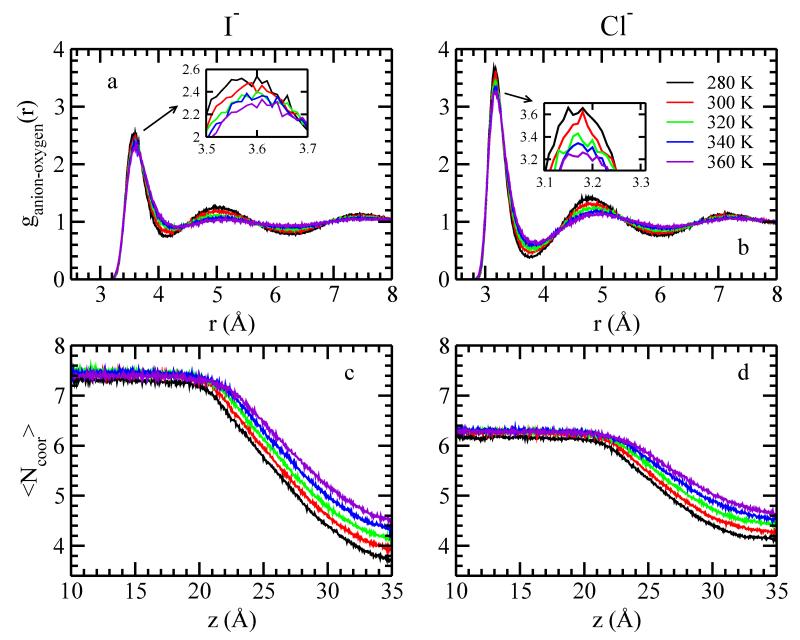
We consider the change in hydration of ions through the LV-interface by calculating the number of coordination water molecules as a function of z-position (〈N_coor〉, Figure 5 c and d); this addresses the difference of ΔH_i-w(z). We define the first solvation shell cutoff distance as the first minimum of the anion-oxygen radial distribution function, as shown in Figure 5 a and b. Moving through the GDS into the vapor, the coordination number decreases. All ions remain partially hydrated in the vapor; both anions maintain about four coordinating water molecules. Completely desolvated ions are not observed in our simulations. This is in agreement with calculations for transferring hydrated ion clusters from bulk water to 1,2-dichloroethane,⁸⁰ and simulations of ions across water/air interface¹⁶. As the larger ion, I⁻ inherently has more water molecules in the first solvation shell, and thus experiences greater changes in its coordination environment upon transfer into the vapor phase. Since the ion-coordinated water interaction is negative, this reduction of 〈N_coor〉 as the ion moves past the GDS result in the increase of ΔH_i-w(z). The larger change in 〈N_coor〉 for I⁻ necessarily leads to larger ΔH_i-w(z) for I⁻ than Cl⁻ at the same temperature. As the temperature increases, both ions show less reduction of 〈N_coor〉, and therefore leads to less ΔH_i-w.

FIG. 5.

Anion-oxygen radial distribution function (RDF) for (a) I⁻ (b) Cl⁻ at different temperature. Average number of coordinated water for (c) I⁻ (d) Cl⁻ at different temperature.

Thus far, our analysis of the global enthalpy change indicates that the balance of water-water and water-ion interactions through the interface result in the enthalpy minimum before the GDS in the I⁻ system. Since the water-water interaction component of the enthalpy yields the largest favorable contribution (Figure 3), we now adopt the analysis of Otten et al⁴⁹ to consider the origin of this contribution, and its sign, based on consideration of the average interaction energy of a water molecule with other water molecules in the system; we consider this average interaction energy for the regions where the water molecule is in a bulk-like region, at the liquid-vapor interfacial region, and in the hydration shell of the anion. The total water-water energy is $\langle U_{w-w}\left(z\right)\rangle ={\stackrel{‒}{\epsilon }}_{\mathrm{coor}}{N}_{\mathrm{coor}}\left(z\right)+{\stackrel{‒}{\epsilon }}_{L-V}{N}_{L-V}\left(z\right)+{\stackrel{‒}{\epsilon }}_{\text{bulk}}{N}_{bulk}\left(z\right)$, where $\stackrel{‒}{\epsilon }$ represents the average interaction energy of a water molecule with all the other water molecules in the corresponding environment. Here, N_coor indicates the number of water molecules within the first solvation shell of the ion, N_L–V refers to water molecules near the GDS but not within the first solvation shell of the ion, and finally, N_bulk refers to the water molecules that are in the bulk liquid (but not within the coordination criteria or near the L-V interface). ΔH_w-w(z) is therefore

$$\Delta H_{w-w}\left(z\right)={\stackrel{‒}{\epsilon }}_{\text{coor}}\Delta N_{\mathrm{coor}}\left(z\right)+{\stackrel{‒}{\epsilon }}_{L-V}\Delta N_{L-V}\left(z\right)+{\stackrel{‒}{\epsilon }}_{\text{bulk}}\Delta N_{\text{bulk}}\left(z\right)$$ (8)

where ΔN is the difference in the number of water molecules in the region indicated by the subscript to ΔN; here, we adopt the definition of ΔN = N(z) − N(z = 10Å). Since the total number of water molecules is fixed, we have ΔN_bulk= −(ΔN_coor + ΔN_L-V), therefore Equation 8 can be written as:

$$\Delta H_{w-w}\left(z\right)=({\stackrel{‒}{\epsilon }}_{\mathrm{coor}}-{\stackrel{‒}{\epsilon }}_{\text{bulk}})\Delta N_{\mathrm{coor}}\left(z\right)+({\stackrel{‒}{\epsilon }}_{L-V}-{\stackrel{‒}{\epsilon }}_{\text{bulk}})\Delta N_{L-V}\left(z\right)$$ (9)

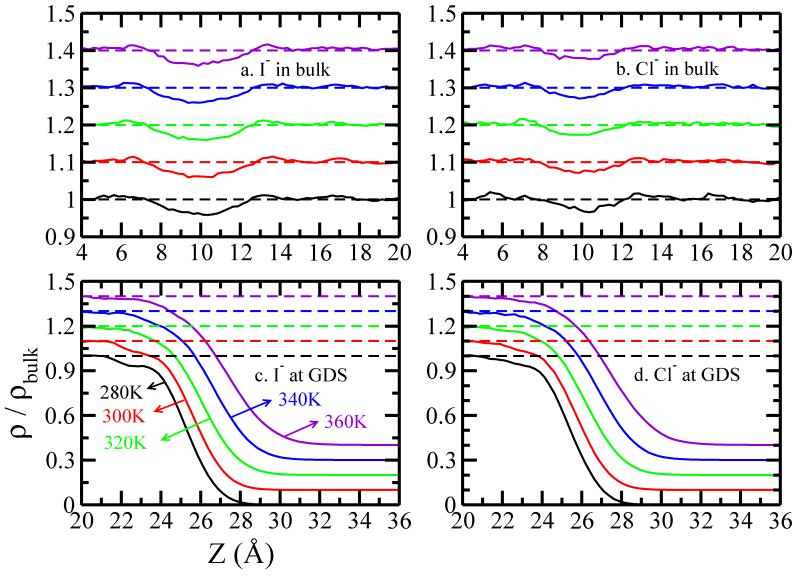
In Figure 6 we present the density profile of water oxygen atoms along the z-dimension when an ion is restrained in bulk (z=10Å) or at the GDS. From Figure 6 c, d and previous discussion, we have ΔN_L-V and ΔN_coor < 0. Since ${\stackrel{‒}{\epsilon }}_{\mathrm{coor}}$ and ${\stackrel{‒}{\epsilon }}_{L-V}$ are both more positive than ${\stackrel{‒}{\epsilon }}_{\text{bulkq}}$, we obtain that ΔH_w-w(GDS) is negative. This recapitulates the results of Otten et al⁴⁹.

FIG. 6.

Density profile of water oxygen along z-dimension, when (a) I⁻ (b) Cl⁻ is in the bulk (z_ion = 10 Å). The lower panels show the density profile along when (c) I⁻ and (d) Cl⁻ is at GDS, which is pushed toward the vapor phase as the temperature increases. An offset of 0.1 is added for clarity.

When the ion is in bulk, the number of bulk water molecules is reduced (the ions carve out a void that excludes water molecules); as the ion moves to GDS, water fills in the void, leading to ΔN_bulk > 0, which is a reflection of the change of ΔN_coor and ΔN_L-V. From Figure 6a and b we observe larger voids for I⁻ compared to those for Cl⁻, which explains why ΔH_w-w(GDS) is more stabilizing for the larger anion. The size of these voids is not sensitive to the temperature. However, due to lower water-water interaction at high temperature (as evidenced by the shift of GDS to larger value as the water cohesive energy is reduced at elevated temperatures), we expect a less stabilizing ΔH_w-w(GDS) at elevated temperatures, shown in Figure 3 a and c.

B. Surface Height Fluctuation and Entropy

From Figure 2 and earlier studies, it is acknowledged that surface-adsorption of anions at the aqueous liquid-vapor interface is an entropically disfavored process^49,53,54. Intriguing ideas about the origin of this negative entropy have emerged in the recent literature^49,54 relating to the suppression of the fluctuations of the interface. Using the idea of coarse-graining atomically-resolved interfaces, Otten et al⁴⁹ showed using molecular simulations the reduction of interface fluctuations and the concomitant negative ΔS_adsorption calculated from the covariance matrix of interface fluctuations. We thus explore the nature of interfacial fluctuations in the two anion systems. In particular, we are interested in observing how fluctuations of the interface vary as the two ions approach the GDS and move through it. Since we have systems with unequivocal differences in surface-stability (i.e., one anion is stable at 300K and the other shows no surface state), we hope to extract a strong correlation between surface stability and the perturbations induced by the two anions. We consider the fluctuations at 300K first to set a base line, and then consider the temperature dependence of induced interface fluctuations.

For an instantaneous surface snapshot, the local density profile can be defined as⁸¹:

$$\langle \rho ({\overrightarrow{r}}_{xy},z)\rangle \equiv \frac{1}{A\xi }\int d^2{\overrightarrow{r}}_{xy}^{\prime }\rho ({\overrightarrow{r}}_{xy}-{\overrightarrow{r}}_{xy}^{\prime },z)=\rho [z-h({\overrightarrow{r}}_{xy}\left)\right]$$ (10)

which describes the short-distance average of the density over an area A_ξ ≥ ξ² at position ${\overrightarrow{r}}_{xy}$. ξ is an inherent correlation length. Here we define $\delta h\left({\overrightarrow{r}}_{xy}\right)=h\left({\overrightarrow{r}}_{xy}\right)-z$ as a surface height function. With this definition, $\langle \delta h\left({\overrightarrow{r}}_{xy}\right)\rangle =0$. From individual snapshots/configurations we construct the coarse-grained instantaneous surface defined by Willard and Chandler⁸². Gaussian mass distributions are assigned to each water oxygen atom according to:

$$\Phi (\mathrm{r};\xi )={\left(2\pi {\xi }^2\right)}^{-d∕2}exp(-r^2∕2{\xi }^2)$$ (11)

where r is the magnitude of r, ξ is taken as 3.0 Å, and d is the dimensionality (3 in this case). At space-time point (r, t), we have the coarse-grained density as

$$\stackrel{‒}{\rho }(\mathrm{r},t)=\sum _j\Phi (\mid \mathrm{r}-{\mathrm{r}}_i(t)\mid ;\xi )$$ (12)

The interface is determined as the (d−1)-dimensional manifold with constant value c. In practice, we set up a series of spatial grid points (x, y, z) and compute the corresponding coarse-grained densities ρ(x, y, z) by Equation 12. We use a grid spacing in the x and y dimensions of 0.6 Å; for the z dimension the grid resolution is 0.1 Å. The surface is then obtained as the manifold by setting ρ(x, y, z) = ρ_bulk/2. With sufficient sampling, we can average these instantaneous surfaces (h_t(x, y), at time t) and get the mean surface 〈h(x, y)〉; furthermore, 〈δh(x, y)〉 = 0. Subtracting the mean values from the h_t(x, y), we obtain δh_t(x, y) and the height fluctuations $\delta h_{\mathrm{t}}^2(x,y)$. Using this framework to characterize interface fluctuations, we can probe the magnitudes of interface fluctuations when the ions reside at various positions along the reaction coordinate. We first consider how the two anions affect the interface as they approach the interface at 300K; then we discuss how these influences vary with temperature.

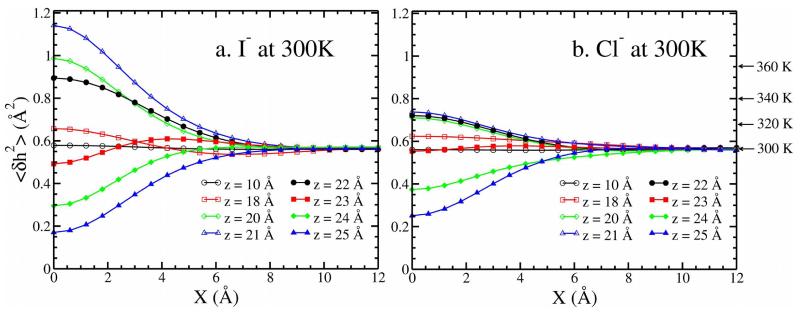
Figure 10, 11, 12 in Supporting Information show representative instantaneous surfaces, mean surfaces, and fluctuations derived based on the above approach. In Figure 7 (main text) we show for 300K the absolute magnitude of the mean interface fluctuation when I⁻ and Cl⁻ reside at various z positions. The X-axis is the distance along the X-dimension for a coordinate system originating at the center of the anion. At 300K, the inherent interface fluctuations for this water model are 0.56 (far way from the ion, X=12 Å. We use this value as a proxy to represent the pure water interface fluctuations, but we have confirmed independently that these match the system of a pure water liquid-vapor interface in the absence of ions. Interestingly, the pure water interfacial fluctuations we obtain for the TIP4P-FQ water model are quite close to those reported by Otten et al). Approaching the interface, the mean fluctuations increase, with I⁻ inducing significantly larger perturbation than Cl⁻. Since thermal fluctuations give rise to an inherent (absence of ions) level of interfacial fluctuations, we normalize the absolute mean surface fluctuations $(\langle \delta h^2(x,y)\rangle )$ with the value for pure water at the corresponding temperature $(\langle \delta h_{\text{pure}}^2)\rangle$. Thus, when the ratio between ≤δh²(x, y)≥ and $\langle \delta h_{\text{pure}}^2\rangle$ is (which defined as $\langle \delta h_{\mathrm{L}}^2\rangle$) equals 1, the effect of ion is zero. When $\langle \delta h_{\mathrm{L}}^2\rangle >1$ the surface height fluctuation is enhanced relative to pure water with the presence of ion; when $\langle \delta h_{\mathrm{L}}^2\rangle <1$, the surface height fluctuation is suppressed.

FIG. 7.

Surface height fluctuations, as functions of lateral displacement X (when the other lateral displacement Y is zero), for (a) I⁻ (b) Cl⁻ resides in different restrained window at 300 K. The arrows in the right axis indicate the inherent pure water fluctuations from 300 K to 360 K.

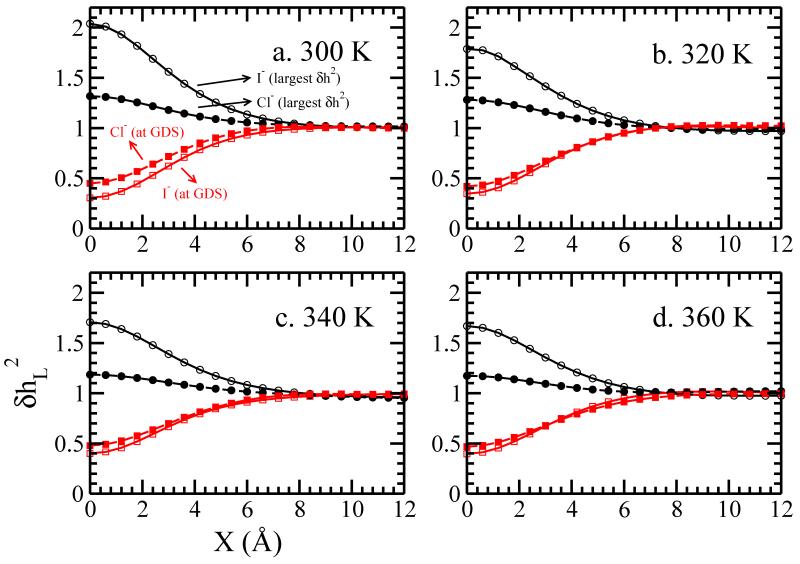
Figure 8 shows the normalized, mean-square amplitude of surface height fluctuations as a function of lateral distance × from the ion. Generally, when the ion is 4 Å below the GDS, the fluctuations are maximum just above/beneath the ion (X = 0 Å). As the ion moves closer to the GDS, the fluctuation is reduced; when the ion resides at the GDS (z=25Å), the fluctuations are suppressed relative to pure water. The enhancement of fluctuations is related to the solvent spatial perturbations by the anion. The radial distribution functions of Figure 6a and b demonstrate that the solvent around the ion is perturbed out to at least 8 Å away from the ion, suggesting that the presence of the ion generates interfacial perturbations before even reaching the vicinity of the GDS. As the ions approach the L-V interface, solvation shell water interferes with the interfacial water; inherent surface fluctuations are amplified, and reach a maximize when the edge of the first hydration shell (refer to the first minimum of RDF in Figure 5, which is approximately 3.8 and 4.2 Å for Cl⁻ and I⁻ at 300 K, respectively) coincides with the GDS.

FIG. 8.

Normalized surface height fluctuations, as functions of lateral displacement X (when the other lateral displacement Y is zero), for ions at (a) 300 K (b) 320 K, (c) 340 K and (d) 360 K. Only the windows with largest $\delta h_{\mathrm{L}}^2$ and the window of GDS are shown here. For other windows please refer to the supporting information.

From Figure 8a a lower enhancement of surface fluctuations is associated with Cl⁻ relative to I⁻. We posit that this is related to the coupling of the local anion solvation shell properties to the more distal solvent. The first solvation shell of Cl⁻ is more rigid and less “malleable” than that of I⁻. Indications for this are as follow. The radial distribution functions, Figure 5, show a more dramatic ordering of water in the first solvation shell of Cl⁻; this is widely known based on previous simulation studies⁶⁵. We have also confirmed (data not shown) that the lifetime of water molecules in the first solvation shell of Cl⁻ are longer than of those in I⁻’s first shell; furthermore, the velocity decorrelation times of first solvation shell water around Cl⁻ are shorter than for I⁻, and velocity correlation functions of first solvation shell water molecules around Cl⁻ retain an oscillatory “hump” indicative of water “rattling in a cage” formed from its closely packed nearest neighbors. Further evidence of the distinct environments of the first hydration shells of I⁻ and Cl⁻ are shown in Figure 17 and 18 of the Supporting Information. The average molecular dipole moment of water in the first solvation shell of Cl⁻ is significantly more enhanced than in the first shell of I⁻; the tetrahedrality of water in the first shells also demonstrates this difference. In total, these indications suggest that coordinated water molecules surrounding Cl⁻ are more “ordered” (vis-a-vis, rigid) compared to those around I⁻. This being the case, the local water molecules around Cl⁻ (first to second solvation shell) are not as deformable; thus, when Cl⁻ nears the interface, the shielding effect of first (and somewhat second) solvation shell water molecules prevents significant added fluctuations of the interface. In fact, since Cl⁻ shows no surface state, we interpret the slight enhancement of interface fluctuations in the Cl⁻ case to be insignificant. Since the surface stability observed for these two anions is binary (I⁻ = on, Cl⁻ = off), we consider that there is a possible threshold of induced fluctuations separating surface-stable anions. Interestingly, Otten et al demonstrate an ostensibly similar behavior in Figure S2 of the Supporting Information of that work.

We comment on the slight differences in the extent to which interfacial flucuations are suppressed once the ions reach the GDS and move through the interface. The slightly weaker suppression by Cl⁻, we suggest, is due to the less anisotropic solvation structure (refer to supporting information or Ref^69,83) of Cl⁻ at the GDS. For the case of I⁻, water molecules are rarely found above the ion, therefore the coarse-grained surfaces are mostly beneath I⁻; however, for Cl⁻ there are more instantaneous coarse-grained surfaces observed above the anion resulting in slightly higher fluctuations than the case of when I⁻ resides at the GDS.

In summary, though Cl⁻ induces a much more modest perturbation, we consider this a non-effect. Considering that the I⁻ is surface-stable and the Cl⁻ not, this seems to suggest that there may exist a force field dependent critical level of perturbation of the interface that distinguishes between surface-stable and non-surface stable species. This is conjecture at this time, but we continue to explore this idea with ongoing work. Nevertheless, the notion that Cl⁻ has no effect on interfacial fluctuations, correlating with its lack of surface stability, has implications when considering the temperature dependence of induced interfacial fluctuations, to which we now turn.

As temperature increases, the maximum of $\langle \delta h_{\mathrm{L}}^2\rangle$ for I⁻ drops from 2 to 1.65; on the other hand, the maximum of $\langle \delta h_{\mathrm{L}}^2\rangle$ for Cl⁻ is rather insensitive to temperature change, remaining approximately 1.3. Since the fluctuations of surface height can be decomposed into the ion-induced and water-inherent contributions, this indicates the fact that the proportion of ion-induced fluctuations is weakened as the temperature increases. We rationalize this by considering the mechanism through which I⁻ effects its perturbation. Since the perturbation of solvent structure amplifies the inherent interface fluctuations at lower temperatures, the increase of inherent fluctuations at higher temperatures reduces the impact of any solvent structural perturbation induced by the ion. Again, the reduction in the magnitude of interface fluctuation induced by I⁻ correlates with reduction in surface stability. Interestingly, we find that the absolute change in fluctuation magnitude from 12 Å to 0 Å is about 0.4, independent of temperature (for I⁻) (though the value we ascribe to the endpoints would change based on characteristics of the grid used to estimate the instantaneous interfaces, the argument would sill hold).

Finally, we provide some estimates of surface entropy related to enhanced interface fluctuations in the presence of anions. We use concepts from multivariate statistics as discussed by Otten et al to formulate entropy estimates. For a random variable x with continuous density f(x), the entropy can be written as⁸⁴

$$S\left(f\right)=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\cdots {\int }_{-\infty }^{\infty }\ln \left[f\right(x\left)\right]f\left(x\right)dx$$ (13)

where x = (x₁, x₂,…, x_N)^’. The density function of the multivariate normal distribution is given by

$$f\left(x\right)=\frac{1}{{\mid 2\pi \Sigma \mid }^{1∕2}}exp\{-\frac{1}{2}{(x-\mu )}^{\prime }{\Sigma }^{-1}(x-\mu \left)\right\}$$ (14)

Σ is the covariance matrix, Σ_ij = cov(x_i, x_j) = E[(x_i − μ_i)(x_j − μ_j)], where μ_i = E(x_i) is the expected value of the i_th entry of x. We can therefore rewrite the entropy as

$$\begin{array}{cc}\hfill S=& \frac{1}{2}\{N+N\ln (2\pi )+\ln \mid \Sigma \mid \}\hfill \\ \hfill =& \frac{1}{2}\{\ln e^N+\ln {\left(2\pi \right)}^N+\ln \mid \Sigma \mid \}\hfill \\ \hfill =& \frac{1}{2}\ln \{{\left(2\pi e\right)}^n\mid \Sigma \mid \}\hfill \\ \hfill =& \frac{N}{2}\ln \left(2\pi e\right)+\frac{1}{2}\ln \mid \Sigma \mid \hfill \end{array}$$ (15)

where |Σ| is the determinant of covariance matrix Σ. The surface entropy can therefore be estimated with surface height function δh = h − 〈h〉 since δh is normal distributed for each ion restrained-window (shown in Supporting Information). The covariance matrix (χ) is then defined as χ_ij = δh_iδh_j. The $\frac{N}{2}\ln \left(2\pi e\right)$ term is a constant for different windows with the same resolution of grid points (in other words, same N). Consequently, we get the entropy described by the fineness of the resolution of grid points:

$$S=constant+\frac{k_{\mathrm{B}}}{2}\ln \mid \chi \mid$$ (16)

where k_B is the Boltzmann constant. We obtain ΔS as ΔS(z) = S(z) − S(z = 10Å). For every 50 picoseconds, we compute 〈χ〉 and corresponding entropy. Eventually we use these to get the estimation of 〈S(z)〉 (for convergence of entropy please refer to the Supporting Information). The estimated 〈S(z)〉 for I⁻ and Cl⁻ between the window of highest fluctuations and bulk are listed in Table III. As expected, the entropy at the position of highest interface fluctuations, z₁, relative to the bulk, z = 10Å decreases with increasing temperature; values for Cl⁻ are smaller, also as anticipated based on differences in fluctuations. We reiterate that these are simply coarse estimates, with only qualitative descriptive value. These results recapitulate the idea put forth by Noah-Vanhoucke et al that surface stable anions, in part, derive their thermodynamic stability through collective properties associated with the fluctuations of the interface and coupling of these with those fluctuations induced by the anions. Based on ion-induced interface fluctuations, the authors conclude, there is an entropic benefit for moving a volume-excluding ion from bulk to a position within the interface below the GDS; the free energy penalty for loss of electrostatic water-ion interactions becomes dominant after the passage of the anion through the GDS and into the vapor-like regions⁵⁴.

TABLE III.

Estimated ΔS(z₁) and ΔS(z_GDS) obtained by the covariance matrix of surface height functions. z₁ indicates the window with largest fluctuations. The units are k_B.

System	ΔS(z1)	ΔS(zGDS)
I−
300 K	31.80	−30.07
320 K	28.96	−28.98
340 K	23.35	−16.11
360 K	14.45	−14.13
Cl−
300 K	19.27	−11.61
320 K	15.21	−12.16
340 K	11.84	−9.59
360 K	14.13	−9.06

IV. SUMMARY AND CONCLUSIONS

We have explored the enthalpic and entropic changes as two anions, I⁻ and Cl⁻, cross the aqueous liquid-vapor interface under infinite dilution conditions; this variation is extracted from calculations of the potential of mean force associated with the reversible work involved with the translocation process. We find, in accord with numerous earlier experimental and simulation studies, that I⁻ has a modest surface stability of 0.5 kcal/mole, whereas Cl⁻ shows no such surface state. Coincidentally, our estimate of the surface stability (relative to bulk) for I⁻ is, most likely fortuitously, in agreement with the recent estimate by Baer et al using DFT-D molecular dynamics (this is also in agreement with dielectric continuum theory approaches of Levin and coworkers). Decomposition of the potential of mean force is also in keeping with the results of Caleman et al and Otten et al. We see that at all temperatures, water-water interactions provide the sole favorable enthalpic contribution to the free energy while the water-ion interactions contribute a balancing destabilizing contribution until beyond the GDS, at which point the loss of water-ion interaction leads to the rapid increase in free energy. The temperature dependence study we present demonstrates that the surface adsorption process for anions is entropically disfavored, again in agreement with previous experiment and simulation studies. As suggested by Netz et al⁵³, the negative entropy of adsorption is independent of force field used, as further demonstrated in this study. Though the entropy is negative, we find that it is a small contribution to the entire process. We have explored one particular origin of this negative adsorption entropy, induced fluctuations of the aqueous liquid-vapor interface upon anion approach. We find that the surface-stable I⁻ induces significantly greater interfacial fluctuations (after accounting for inherent thermally-excited interface fluctuations) compared to Cl⁻; at 300K, the relative effect of I⁻ is a two-fold increase of interface fluctuations in the immediate vicinity of the anion. We posit that the essence of the dramatic difference in the two anions’ abilities to induce surface fluctuations lies in the properties of their respective local solvation shells, and the coupling of this local solvation shell with distal solvent. Specifically, Cl⁻, being more charge-dense, carries a more rigid, ordered solvation shell (as evidenced by several solvation shell water properties discussed in the main text); this rigidity to some extent is conferred to the second solvation shell as well. I⁻ carries a much more malleable solvation shell. Approaching the interface, the long-range perturbations induced by both anions are more effectively damped by the local solvation shells of Cl⁻ compared to that of I⁻; solvation structure perturbations are able to interact more easily with I⁻’s solvation shell due to its malleability. In this picture, our interpretation is that the minimal perturbation of the interface by Cl⁻ is a non-effect; this interpretation is consistent with the unequivocally different surface-stabilities of the two anions (as computed using the models and attendant assumptions we have chosen for this work).

An implication of the mechanism through which I⁻ effects its perturbations of the interface is that increasing temperature of the solvent, thus enhancing inherent thermally-excited fluctuations, should reduce the anions effect on surface fluctuations; likewise, since there is no effect from Cl⁻, its effect should show no temperature dependence. Our results demonstrate that the relative contributions to changes in interface fluctuations from I⁻ decrease with temperature, while no perceptible change is present for Cl⁻. This is again consistent with the decrease in surface-stability of I⁻ demonstrated by the disappearance of the free energy minimum before the GDS.